2. 中国石化石油物探技术研究院, 江苏南京 211103
2. Sinopec Geophysical Research Institute, Nanjing, Jiangsu 211103, China
与传统拖缆地震数据采集相比,海底地震勘探是一种多波多分量地震探测技术,它在气云区与盐下成像、岩性区分、裂缝检测和油气藏预测等方面优势明显[1-5]。虽然海底地震勘探有很多优势,但是如何利用海底多分量地震数据进行海底横波速度建模一直是困扰海上油气地震勘探的难题。
Scholte波是海底流—固界面处产生的一种界面波,是P波和SV波耦合作用的结果[6-9]。由于海底沉积物分层以及有限的水深,海底Scholte波的相速度和群速度随频率发生变化,有典型的频散特性[10],而且其频散特性受海底沉积层的纵、横波速度和水深控制[6, 11]。Scholte波能量主要集中在流—固界面处,在界面上方和下方呈指数衰减[12-13]。Glorieux等[14]通过物理实验发现,Scholte波与体波的耦合会发生泄漏,从而导致Scholte波能量明显损失。Woezel等[15]在实际海底多分量地震记录波形上观测到Scholte波有明显的频散现象,并对Scholte波的运动形式进行了分析。Muyzert[16]发现Scholte波在传播过程中以逆行椭圆质点运动。
海底Scholte波的频散特性被广泛用于估算浅海沉积物的横波速度结构[10]。Scholte波的频散特性对横波速度很敏感,这也是利用Scholte波反演海底横波速度结构的前提和优势[17-22]。建立精确的海水—海底弹性模型,理论推导该模型下的Scholte波频散特征,是利用Scholte波反演海底横波速度的基础,国内外众多学者开展了相关的研究。梁志强[23]、邵广周[24]研究了两层海底或三层海底的Scholte波频散曲线,并将其与数值模拟记录进行对比分析。罗夏云等[25]基于海底半无限空间模型分析Scholte波频散特性,并利用高阶交错网格有限差分算法实现了软硬海底的Scholte波波场模拟,确定了Scholte波能量集中频段,并与湖上试验数据进行对比分析。祝捍皓等[26]研究了半无限海底上覆沉积层的Scholte波传播特征,并分析了海底弹性参数对Scholte波传播特性的影响。
目前,关于Scholte波传播机理的研究大多基于半无限海底或半无限海底上覆盖单一沉积层等简单模型[27-30]。实际海底是复杂非均匀介质,因此将简单模型的Scholte波频散方程用于实际海底横波速度的反演会产生一定误差。Dong等[31]建立了多层海底模型,并利用刚度矩阵法推导了该模型的Scholte波频散方程,但是在海底分层数较多时,频散方程的求解变得复杂。为了降低多层海底模型频散方程求解的复杂度,本文从纵、横波的势函数出发,基于海水—海底分层模型不同界面的位移和应力连续性条件,推导Scholte波频散方程及其振幅深度分布方程,并分析海水深度及海底沉积物物性对Scholte波频散特征的影响。最后,基于东海实际海底弹性模型,通过数值模拟的方法从模拟记录中提取频散曲线,并与理论计算结果进行对比验证。
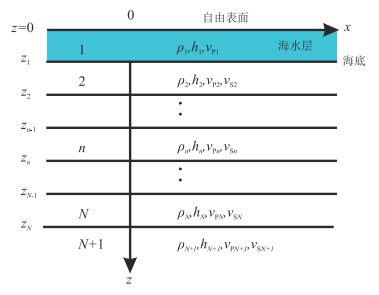
1 理论基础 1.1 水平层状海水—海底弹性模型中的频散方程推导Dong等[31]通过海底分层建立水平层状海水—海底弹性模型,如图 1所示。模型共有
|
图 1 水平层状海水—海底地质模型 |
第1层(海水表面)和第2层(海底顶面)界面为自由表面—液体—固体分界面,满足如下边界条件[25]
| $ \left\{\begin{array}{l}({\tau }_{zz}{)}_{1}{|}_{z=0}=0\\ ({\tau }_{zz}{)}_{1}{|}_{z={z}_{1}}=({\tau }_{zz}{)}_{2}{|}_{z={z}_{1}}\\ {w}_{1}{|}_{z={z}_{1}}={w}_{2}{|}_{z={z}_{1}}\\ ({\tau }_{xz}{)}_{2}{|}_{z={z}_{1}}=0\end{array}\right. $ | (1) |
式中:
| $ \left\{\begin{array}{l}{u}_{n-1}{|}_{z={z}_{n-1}}={u}_{n}{|}_{z={z}_{n-1}}\\ {w}_{n-1}{|}_{z={z}_{n-1}}={w}_{n}{|}_{z={z}_{n-1}}\\ ({\tau }_{zz}{)}_{n-1}{|}_{z={z}_{n-1}}=({\tau }_{zz}{)}_{n}{|}_{z={z}_{n-1}}\\ ({\tau }_{xz}{)}_{n-1}{|}_{z={z}_{n-1}}=({\tau }_{xz}{)}_{n}{|}_{z={z}_{n-1}}\end{array}\right. \quad 3\le n\le N+1 $ | (2) |
式中
| $ {\boldsymbol{J}}_{5}{A}_{1}={\boldsymbol{J}}_{4}^{\mathrm{T}}\left[\begin{array}{c}{A}_{2}\\ {B}_{2}\\ {C}_{2}\\ {D}_{2}\end{array}\right] $ | (3) |
式中
| $ {\boldsymbol{J}}_{5}=\left[\begin{array}{c}-{\rho }_{1}{v}_{P1}^{2}\left({\alpha }_{1}^{2}+{k}^{2}\right)\left({\mathrm{e}}^{\mathrm{i}{\alpha }_{1}{h}_{1}}-{\mathrm{e}}^{-\mathrm{i}{\alpha }_{1}{h}_{1}}\right)\\ {\alpha }_{1}\left({\mathrm{e}}^{\mathrm{i}{\alpha }_{1}{h}_{1}}-{\mathrm{e}}^{-\mathrm{i}{\alpha }_{1}{h}_{1}}\right)\\ 0\end{array}\right] $ |
| $ {\boldsymbol{J}}_{4}=\left[\begin{array}{ccc}{\rho }_{2}\left(2{v}_{\mathrm{S}2}^{2}{k}^{2}-{\omega }^{2}\right){e}^{i{\alpha }_{2}{h}_{1}}& {\alpha }_{2}{e}^{i{\alpha }_{2}{h}_{1}}& 2k{\alpha }_{2}{e}^{i{\alpha }_{2}{h}_{1}}\\ {\rho }_{2}\left(2{v}_{\mathrm{S}2}^{2}{k}^{2}-{\omega }^{2}\right){e}^{-i{\alpha }_{2}{h}_{1}}& -{\alpha }_{2}{e}^{-i{\alpha }_{2}{h}_{1}}& -2k{\alpha }_{2}{e}^{i{\alpha }_{2}{h}_{1}}\\ 2{\rho }_{2}{v}_{S2}^{2}k{\beta }_{2}{e}^{i{\beta }_{2}{h}_{1}}& -k{e}^{i{\beta }_{2}{h}_{1}}& -\left({k}^{2}-{\beta }_{2}^{2}\right){e}^{i{\beta }_{2}{h}_{1}}\\ -2{\rho }_{2}{v}_{S2}^{2}k{\beta }_{2}{e}^{-i{\beta }_{2}{h}_{1}}& -k{e}^{-i{\beta }_{2}{h}_{1}}& -\left({k}^{2}-{\beta }_{2}^{2}\right){e}^{-i{\beta }_{2}{h}_{1}}\end{array}\right] $ |
式中:
| $ \begin{array}{l}\left[\begin{array}{l}{u}_{n}\left|{}_{z={z}_{n}}\right.\\ {w}_{n}\left|{}_{z={z}_{n}}\right.\\ ({\tau }_{zz}{)}_{n}\left|{}_{z={z}_{n}}\right.\\ ({\tau }_{xz}{)}_{n}\left|{}_{z={z}_{n}}\right.\end{array}\right]={\left({\boldsymbol{M}}_{2, n}\right)}^{\mathrm{T}}\cdot {\left({\boldsymbol{M}}_{1, n}^{-1}\right)}^{\mathrm{T}}\left[\begin{array}{l}{u}_{n}\left|z={z}_{n-1}\right.\\ {w}_{n}\left|{}_{z={z}_{n-1}}\right.\\ ({\tau }_{zz}{)}_{n}\left|{}_{z={z}_{n-1}}\right.\\ ({\tau }_{xz}{)}_{n}\left|{}_{z={z}_{n-1}}\right.\end{array}\right]\\ ={\boldsymbol{G}}_{n}\left[\begin{array}{l}{u}_{n}\left|z={z}_{n-1}\right.\\ {w}_{n}\left|{}_{z={z}_{n-1}}\right.\\ ({\tau }_{zz}{)}_{n}\left|{}_{z={z}_{n-1}}\right.\\ ({\tau }_{xz}{)}_{n}\left|z={z}_{n-1}\right.\end{array}\right]\end{array} $ | (4) |
式中
| $ {\boldsymbol{G}}_{n}={\left({\boldsymbol{M}}_{2, n}\right)}^{\mathrm{T}}\cdot {\left({\boldsymbol{M}}_{1, n}^{-1}\right)}^{\mathrm{T}} $ |
| $ {\boldsymbol{M}}_{1, n}=\left(\begin{array}{cccc}-\mathrm{i}k& 0& {\rho }_{n}(2{v}_{\mathrm{S}n}^{2}{k}^{2}-{\omega }^{2})& 0\\ 0& \mathrm{i}{\alpha }_{n}& 0& 2k{\alpha }_{n}{\rho }_{n}{v}_{\mathrm{S}n}^{2}\\ 0& -\mathrm{i}k& 0& -{\rho }_{n}{v}_{\mathrm{S}n}^{2}({k}^{2}-{\beta }_{n}^{2})\\ -\mathrm{i}{\beta }_{n}& 0& 2k{\rho }_{n}{\beta }_{n}{v}_{\mathrm{S}n}^{2}& 0\end{array}\right) $ |
| $ {\boldsymbol{M}}_{2, n}=\left(\begin{array}{cccc}-\mathrm{i}k\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{P}n}& -{\alpha }_{n}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{P}n}& {\rho }_{n}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{P}n}(2{v}_{\mathrm{S}n}^{2}{k}^{2}-{\omega }^{2})& 2ik{\alpha }_{n}{\rho }_{n}{v}_{\mathrm{S}n}^{2}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{P}n}\\ k\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{P}n}& \mathrm{i}{\alpha }_{n}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{P}n}& \mathrm{i}{\rho }_{n}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{P}n}(2{v}_{\mathrm{S}n}^{2}{k}^{2}-{\omega }^{2})& 2k{\alpha }_{n}{\rho }_{n}{v}_{\mathrm{S}n}^{2}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{P}n}\\ {\beta }_{n}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{S}n}& -\mathrm{i}k\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{S}n}& 0& -{\rho }_{n}{v}_{\mathrm{S}n}^{2}({k}^{2}-{\beta }_{n}^{2})\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{S}n}\\ -\mathrm{i}{\beta }_{n}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{S}n}& k\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{S}n}& 2k{\rho }_{n}{\beta }_{n}{v}_{\mathrm{S}n}^{2}& -\mathrm{i}({k}^{2}-{\beta }_{n}^{2})\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{\mathrm{S}n}{\rho }_{n}{v}_{\mathrm{S}n}^{2}\end{array}\right). $ |
上式中
| $ \begin{array}{l}\left(\begin{array}{l}{u}_{N}\left|{}_{z={z}_{N}}\right.\\ {w}_{N}\left|{}_{z={z}_{N}}\right.\\ ({\tau }_{zz}{)}_{N}\left|z={z}_{N}\right.\\ ({\tau }_{xz}{)}_{N}\left|{}_{z={z}_{N}}\right.\end{array}\right)={\boldsymbol{G}}_{N}{\boldsymbol{G}}_{N-1}{\boldsymbol{G}}_{N-2}\cdots {\boldsymbol{G}}_{3}\left(\begin{array}{l}{u}_{2}\left|{}_{z={z}_{2}}\right.\\ {w}_{2}\left|{}_{z={z}_{2}}\right.\\ ({\tau }_{zz}{)}_{2}\left|z={z}_{2}\right.\\ ({\tau }_{xz}{)}_{2}\left|z={z}_{2}\right.\end{array}\right)\\ =\boldsymbol{H}\left(\begin{array}{l}{u}_{2}\left|{}_{z={z}_{2}}\right.\\ {w}_{2}\left|{}_{z={z}_{2}}\right.\\ ({\tau }_{zz}{)}_{2}\left|{}_{z={z}_{2}}\right.\\ ({\tau }_{xz}{)}_{2}{\left|z={z}_{2}\right.}_{}\end{array}\right)\end{array} $ | (5) |
上式中,
| $ \left(\begin{array}{l}{u}_{N}\left|{}_{z={z}_{N}}\right.\\ {w}_{N}\left|{}_{z={z}_{N}}\right.\\ ({\tau }_{zz}{)}_{N}\left|z={z}_{N}\right.\\ ({\tau }_{xz}{)}_{N}\left|z={z}_{N}\right.\end{array}\right)={\boldsymbol{J}}_{2}\left[\begin{array}{c}{B}_{N+1}\\ {D}_{N+1}\end{array}\right] $ | (6) |
其中
方程右侧
| $ \left(\begin{array}{l}{u}_{2}\left|{}_{z={z}_{2}}\right.\\ {w}_{2}\left|{}_{z={z}_{2}}\right.\\ ({\tau }_{zz}{)}_{2}\left|z={z}_{2}\right.\\ ({\tau }_{xz}{)}_{2}\left|{}_{z={z}_{2}}\right.\end{array}\right)={\boldsymbol{J}}_{3}^{\mathrm{T}}\left[\begin{array}{c}{A}_{2}\\ {B}_{2}\\ {C}_{2}\\ {D}_{2}\end{array}\right] $ | (7) |
| $ {\boldsymbol{J}}_{2}=\left(\begin{array}{cc}-\mathrm{i}k\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}{\alpha }_{N+1}{z}_{N})& \mathrm{i}{\beta }_{N+1}\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}{\beta }_{N+1}{z}_{N})\\ -\mathrm{i}{\alpha }_{N+1}\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}{\alpha }_{N+1}{z}_{N})& -\mathrm{i}k\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}{\beta }_{N+1}{z}_{N})\\ {\rho }_{N+1}(2{v}_{\mathrm{S}N+1}^{2}{k}^{2}-{\omega }^{2})\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}{\alpha }_{N+1}{z}_{N})& -2{\rho }_{N+1}{v}_{\mathrm{S}N+1}^{2}k{\beta }_{N+1}\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}{\beta }_{N+1}{z}_{N})\\ -2k{\rho }_{N+1}{v}_{\mathrm{S}N+1}^{2}{\alpha }_{N+1}\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}{\alpha }_{N+1}{z}_{N})& -{\rho }_{N+1}{v}_{\mathrm{S}N+1}^{2}({k}^{2}-{\beta }_{N+1}^{2})\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}{\beta }_{N+1}{z}_{N})\end{array}\right) $ |
| $ {\boldsymbol{J}}_{3}=\left(\begin{array}{cccc}-\mathrm{i}k{\mathrm{e}}^{\mathrm{i}{\alpha }_{2}{z}_{2}}& \mathrm{i}{\alpha }_{2}{\mathrm{e}}^{\mathrm{i}{\alpha }_{2}{z}_{2}}& {\rho }_{2}\left(2{v}_{\mathrm{S}2}^{2}{k}^{2}-{\omega }^{2}\right){\mathrm{e}}^{\mathrm{i}{\alpha }_{2}{z}_{2}}& 2k{\alpha }_{2}{\rho }_{2}{v}_{\mathrm{S}2}^{2}{\mathrm{e}}^{\mathrm{i}{\alpha }_{2}{z}_{2}}\\ -\mathrm{i}k{\mathrm{e}}^{-\mathrm{i}{\alpha }_{2}{z}_{2}}& -\mathrm{i}{\alpha }_{2}{\mathrm{e}}^{-\mathrm{i}{\alpha }_{2}{z}_{2}}& {\rho }_{2}\left(2{v}_{\mathrm{S}2}^{2}{k}^{2}-{\omega }^{2}\right){\mathrm{e}}^{-\mathrm{i}{\alpha }_{2}{z}_{2}}& -2k{\alpha }_{2}{\rho }_{2}{v}_{\mathrm{S}2}^{2}{\mathrm{e}}^{\mathrm{i}{\alpha }_{2}{z}_{2}}\\ -\mathrm{i}{\beta }_{2}{\mathrm{e}}^{\mathrm{i}{\beta }_{2}{z}_{2}}& -\mathrm{i}k{\mathrm{e}}^{\mathrm{i}{\beta }_{2}{z}_{2}}& 2{\rho }_{2}{v}_{\mathrm{S}2}^{2}k{\beta }_{2}{\mathrm{e}}^{\mathrm{i}{\beta }_{2}{z}_{2}}& -\left({k}^{2}-{\beta }_{2}^{2}\right){\rho }_{2}{v}_{\mathrm{S}2}^{2}{\mathrm{e}}^{\mathrm{i}{\beta }_{2}{z}_{2}}\\ -\mathrm{i}{\beta }_{2}{\mathrm{e}}^{-\mathrm{i}{\beta }_{2}{z}_{2}}& -\mathrm{i}k{\mathrm{e}}^{-\mathrm{i}{\beta }_{2}{z}_{2}}& -2{\rho }_{2}{v}_{\mathrm{S}2}^{2}k{\beta }_{2}{\mathrm{e}}^{-\mathrm{i}{\beta }_{2}{z}_{2}}& -\left({k}^{2}-{\beta }_{2}^{2}\right){\rho }_{2}{v}_{\mathrm{S}2}^{2}{\mathrm{e}}^{-\mathrm{i}{\beta }_{2}{z}_{2}}\end{array}\right) $ |
整理可得
| $ \left(\begin{array}{ccc}\boldsymbol{H}\cdot {\boldsymbol{J}}_{3}& {\boldsymbol{J}}_{2}& {0}_{4\times 1}\\ {\boldsymbol{J}}_{4}& {0}_{3\times 2}& {\boldsymbol{J}}_{5}\end{array}\right)\left[\begin{array}{c}{A}_{2}\\ {B}_{2}\\ {C}_{2}\\ {D}_{2}\\ {B}_{N+1}\\ {D}_{N+1}\\ {A}_{1}\end{array}\right]=0 $ | (8) |
为使线性方程组(式(8))的根不全为零,其系数矩阵满足行列式为0,即
| $ \mathrm{d}\mathrm{e}\mathrm{t}\left(\begin{array}{ccc}\boldsymbol{H}\cdot {\boldsymbol{J}}_{3}& {\boldsymbol{J}}_{2}& {0}_{4\times 1}\\ {\boldsymbol{J}}_{4}& {0}_{3\times 2}& {\boldsymbol{J}}_{5}\end{array}\right)=0 $ | (9) |
上式为水平层状海水—海底模型的Scholte波频散方程,求解该方程可得到该模型Scholte波的频散曲线。
群速度是频散波列中的一个重要概念,代表整个波列的传播速度。群速度
| $ U=c+k\frac{\mathrm{d}c}{\mathrm{d}k} $ | (10) |
为了分析Scholte波在海水和海底中传播的能量分布特征,本文研究了Scholte波振幅深度分布。将频散曲线中某个频率及其对应的相速度代入式(8)并假设
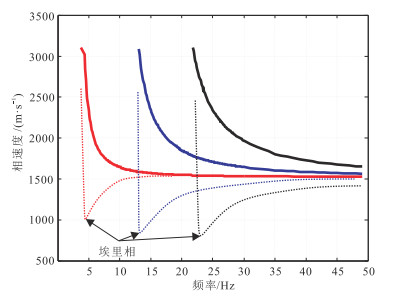
设水平层状海水—海底模型共有6层,其中第1层为海水,海水深度为100 m,第6层为海底弹性半空间,海底半空间上方共有4层沉积层,模型参数见表 1。基于水平层状海水—海底地质模型的Scholte波频散方程及振幅深度分布方程,计算该模型0~2阶Scholte波频散曲线和振幅深度分布,结果如图 2和图 3所示。
|
|
表 1 6层水平层状海水—海底模型参数 |
|
图 2 6层海水—硬海底层状模型的0~2阶Scholte波频散曲线 实线为相速度,虚线为群速度。红线代表基阶,蓝线代表1阶,黑线代表2阶。 |
|
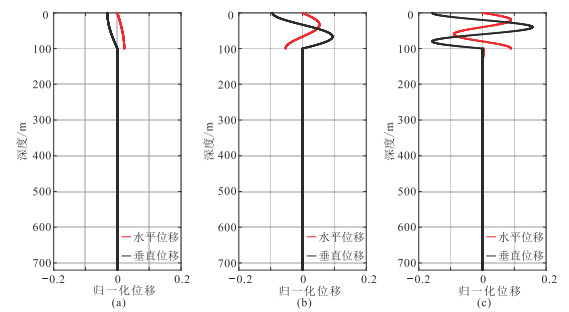
图 3 Scholte波埃里相水平位移和垂直位移随深度变化曲线 (a)0阶;(b)1阶;(c)2阶 |
图 2中,0~2阶Scholte波相速度和群速度都有明显的频散特性,且各阶Scholte波的相速度均存在截止频率。随着频率增高,先产生0阶(又称为基阶)Scholte波,其次是1阶Scholte波,然后是2阶Scholte波。Scholte波相速度从海底介质最大横波速度逐渐减小至海水纵波速度;群速度先降至最小值,然后逐渐增加,最后接近于海水纵波速度。群速度极小值点对应的波列为埃里震相,极小值点对应的频率和速度为埃里相频率和埃里相速度。埃里相具有能量强、速度低的特点,0阶Scholte波埃里相频率最低,2阶Scholte波埃里相频率最高。
Scholte波是沿着海水与海底分界面传播的一种界面波,其能量在空间传播随着距离海底的深度变化而变化。由于埃里相是Scholte波能量最强的波列,所以本文分析了0~2阶Scholte波埃里相的振幅深度分布特征,如图 3所示。海水中Scholte波振幅明显强于固体海底层状介质中的振幅,表明Scholte波能量主要集中在海水中。海水中的水平位移随深度的变化特征类似正弦函数,垂直位移随深度变化类似于余弦函数。在海水表面,没有水平位移,仅有垂向位移,且垂向位移始终为负;另外, 海水中的垂直位移大于水平位移,表明Scholte波在海水中的运动轨迹为逆进的长椭圆。在海水与海底分界面上,Scholte波水平位移不连续,垂直位移连续,这一特征与固—液界面的边界条件一致。在该分界面上,水平位移大于垂直位移。对比0~2阶Scholte波的振幅深度分布,在海水中0阶Scholte波埃里相位移最弱,2阶Scholte波埃里相位移最强;且随着阶数的增加,水平位移和垂直位移逐渐增加一个零点。
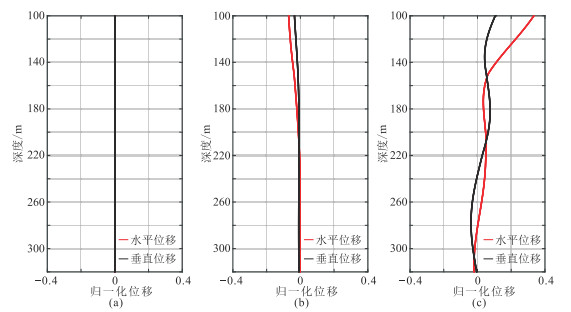
在固体海底中,0~2阶Scholte波水平位移和垂直位移分布特征如图 4所示。海水与海底分界面上,水平位移大于垂向位移,表明固体介质中Scholte波的运动轨迹为扁椭圆。对比0~2阶Scholte波位移,2阶Scholte波位移最强,0阶位移最弱。该特征与海水中Scholte波位移特征一致,说明在海水和固体海底中,均为2阶Scholte波位移最强,0阶Scholte波位移最弱。
|
图 4 Scholte波水平位移和垂直位移分布特征 (a)0阶;(b)1阶;(c)2阶 |
海水深度是水平层状海水—海底模型中的重要参数。针对浅海和深海两种不同模型,改变表 1中的海水深度依次为50,100,500及1000 m,其余参数不变,分别计算四种海水深度模型的Scholte波频散曲线及振幅深度分布。
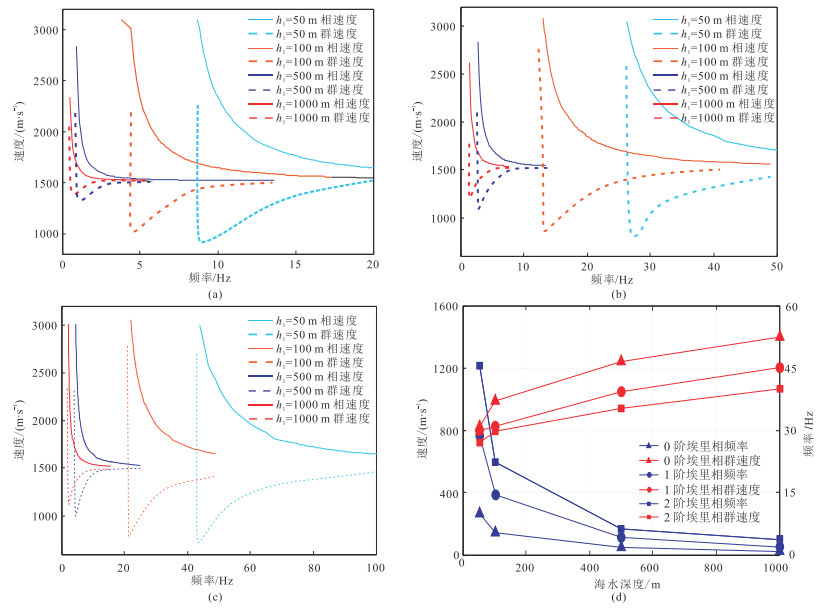
通过分析不同水深Scholte波频散曲线的变化(图 5a~图 5c),发现随着海水深度增加,0~2阶Scholte波频散曲线逐渐向低频方向移动。统计不同海水深度的埃里相频率和群速度,结果显示随着海水深度增加,0~2阶Scholte波均表现为埃里相频率逐渐降低、群速度逐渐增加的特征(图 5d)。随着海水深度增加,在更低频段内观察到Scholte波,且Scholte波强能量波列(埃里相)传播速度逐渐增加,接近海水纵波速度。同时,随着海水深度增加,0~2阶Scholte波频散特征减弱。当海水深度为500 m或1000 m时,随着频率增大,相速度由海底最大横波速度迅速降低至海水纵波速度,然后保持不变。结果表明,浅海Scholte波频散特征明显,随着海水深度增加,频散特征逐渐减弱。
|
图 5 海水深度变化时Scholte波频散曲线 (a)0阶;(b)1阶;(c)2阶;(d)埃里相频率和群速度随海水深度变化曲线 |
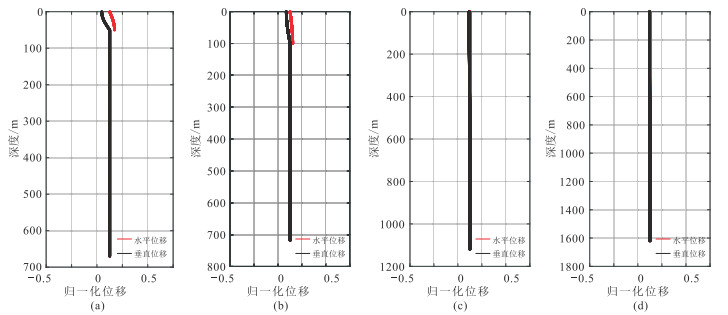
为了分析海水深度对Scholte波传播能量的影响,分别计算四种不同海水深度模型的0~2阶Scholte波埃里相振幅深度分布(图 6~图 8)。可以看出,各阶Scholte波的振幅随着海水深度的增加逐渐降低。
|
图 6 海水深度不同时0阶Scholte波振幅深度分布 (a)50 m;(b)100 m;(c)500 m;(d)1000 m |
|
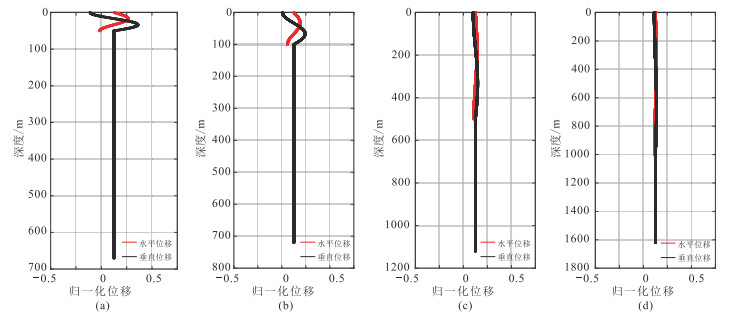
图 7 海水深度不同时1阶Scholte波振幅深度分布 (a)50 m;(b)100 m;(c)500 m;(d)1000 m |
|
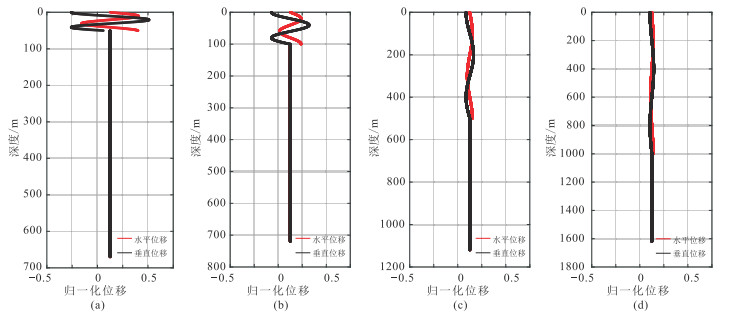
图 8 海水深度不同时2阶Scholte波振幅深度分布 (a)50 m;(b)100 m;(c)500 m;(d)1000 m |
综上所述,浅海Scholte波能量强,频散特征明显,因此在浅海环境利用Scholte波反演海底浅层横波速度的结果精度和可信度更高。
按照海底沉积物的物性,可以将海底分为软海底和硬海底。硬海底地层固结好,纵、横波速度较高。表 1所示模型中,海水附近没有低速层,是一种典型的硬海底。当海水附近为低速层时,此时的海底模型为软海底。为了分析海底沉积物物性对Scholte波频散特征的影响,改变表 1中2~6层的纵、横波速度及密度,其余参数不变,建立软海底地层模型并计算软海底Scholte波0~2阶频散曲线。软海底为未固结软性地层,纵、横波速度比值大[32-33]。粉砂质沉积物是一种典型的软海底沉积物,基于粉砂质沉积物的纵、横波速度随埋藏深度的经验公式[34-35],确定软海底地层纵、横波速度为
| $ \left\{\begin{array}{l}{v}_{\mathrm{P}}\left(z\right)=1800\cdot {z}^{0.015}\\ {v}_{\mathrm{S}}\left(z\right)=128\cdot {z}^{0.28}\end{array}\right. $ | (11) |
其中z为地层深度。基于经典Gardner公式,可得软海底模型中的地层密度[36]
| $ \rho \left(z\right)=310\cdot {v}_{\mathrm{P}}{\left(z\right)}^{0.25} $ | (12) |
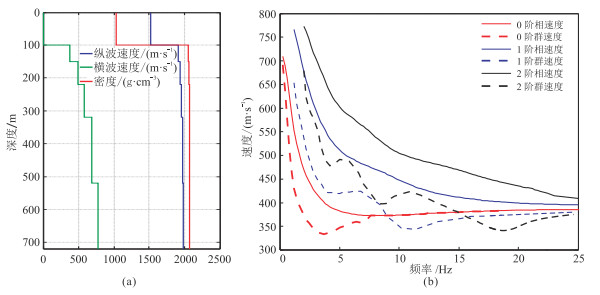
图 9为软海底模型各阶Scholte波频散曲线。与硬海底模型相比,软海底Scholte波频散曲线的相速度及群速度较低。随着频率增加,1~2阶Scholte波相速度由最大横波速度逐渐减小至最小横波速度;0阶Scholte波相速度随着频率增大出现先减小后增大的特征,相速度最小值低于海底沉积物的最小横波速度。
|
图 9 软海底模型(a)及0~2阶频散曲线(b) |
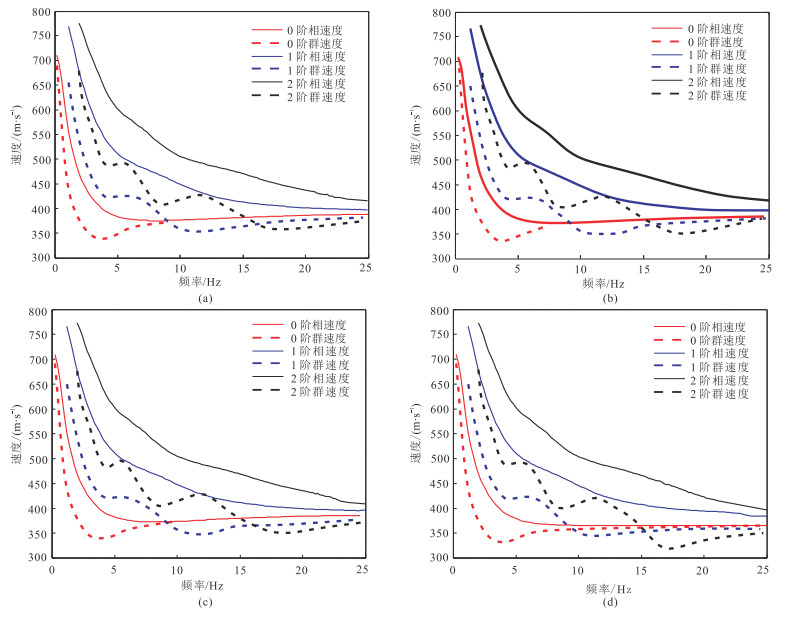
分析不同海水深度软海底模型的Scholte波频散曲线(图 10a~图 10c),发现软海底Scholte波频散特征受海水深度的影响很小。如果将软海底模型的海水层去掉,计算无海水层时的Rayleigh面波频散曲线(图 10d),发现软海底模型的Scholte波频散曲线与没有海水层覆盖时的Rayleigh面波频散曲线较为相似。
|
图 10 不同海水深度软海底Scholte波频散曲线 (a)50 m;(b)500 m;(c)1000 m;(d)0 m |
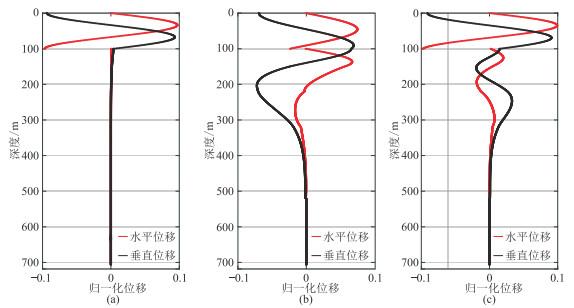
分析软海底模型的振幅深度分布(图 11),在海水中,水平位移与垂直位移大小相当,表明海水中Scholte波运动轨迹为近似圆形。固体海底中,0阶Scholte波能量较弱,1阶和2阶Scholte波能量强。与硬海底模型相比,软海底模型固体海底中Scholte波能量明显增强,且Scholte波位移随着深度增加先增大后减小,然后逐渐趋于零。
|
图 11 软海底Scholte波埃里相振幅深度分布图 (a)0阶;(b)1阶;(c)2阶 |
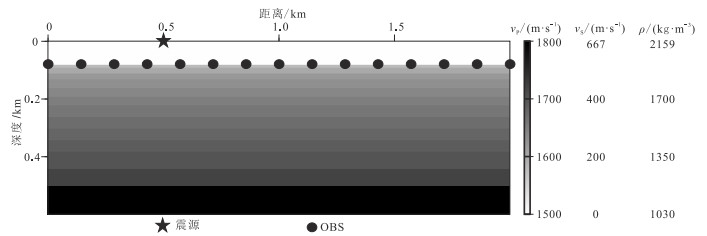
Wang等[18]利用在东海QY工区采集的海底OBN多分量地震数据中的Scholte波,对东海海底浅部沉积层进行了横波速度反演,获得了该工区海底浅层沉积层的纵、横波速度及地层分层信息(表 2)。谱元法(Spectral Element Method)通过离散化弹性波方程将连续的地震波问题转化为离散的数值问题,能够提供高精度的数值解,准确地模拟地震波传播的细节,适用于处理非均匀性和复杂地质结构的情况,广泛应用于复杂地表的弹性波数值模拟[37-38]。基于东海弹性模型,本文利用谱元法模拟海底多分量地震数据采集,波场模拟的观测系统见图 12。
|
|
表 2 东海工区海底浅层地层厚度和弹性参数 |
|
图 12 东海模型数值模拟观测系统图 |
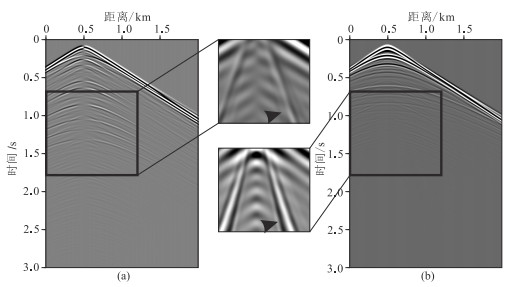
图 13为模拟的海底多分量地震记录,总记录长度为3 s。模拟的两个速度分量地震记录上Scholte波能量比直达波、反射波弱,很难直接观测。从模拟记录中截取局部记录,局部记录中可以清晰观测到Scholte波,有典型的频散特性。很多学者研究了从多分量地震记录中提取频散曲线的方法[10, 39-41]。本文基于多道面波分析的方法[41],从模拟的海底多分量地震记录中提取Scholte波频散能谱,可以清晰地观测到多阶Scholte波。将提取的Scholte波频散能谱与理论频散曲线对比,两者吻合度较高(图 14),验证了本文提出的Scholte波频散理论模型的准确性。
|
图 13 东海模型模拟的OBS多分量记录 (a)水平速度分量;(b)垂直速度分量 |

|
图 14 模拟数据中提取的频散能谱与理论频散曲线对比 蓝色虚线、红色虚线、黄色虚线分别为0阶、1阶、2阶Scholte波理论频散曲线。 |
基于海底弹性半空间中的纵、横波势函数和海水—海底不同界面处的应力、位移连续性条件,本文推导了水平层状海水—海底模型Scholte波频散方程及其振幅—深度分布方程,分析了软、硬海底及海水深度对Scholte波频散特征的影响,并将理论频散曲线与从模拟的海底多分量地震数据中提取的Scholte波频散曲线进行对比验证,取得以下几点认识。
(1)硬海底Scholte波具有明显的频散特性,能量主要集中在海水中,0阶能量最弱,2阶能量最强;随着海水深度增加,Scholte波频散特性减弱;软海底Scholte波也有明显的频散特性,但其频散特性与无海水覆盖时Rayleigh波频散特性类似;Scholte波频散特性受海水深度变化影响小,并且硬海底的Scholte波能量明显增强。
(2)相比于深海环境,浅海Scholte波能量更强,频散特征更明显,因此在浅海环境利用Scholte波反演海底浅层横波速度结果的精度和可信度更高。
(3)基于东海浅水弹性模型,从模拟的海底多分量地震数据中提取Scholte波的频散曲线与理论计算的频散曲线进行对比分析,两者非常吻合,验证了本文推导的Scholte波频散理论的正确性。
(4)基于水平分层海水—海底模型,本文提出的Scholte波频散理论为利用Scholte波频散特性反演海底横波速度提供了更准确的理论基础。
附录A 海底弹性半空间中的纵、横波势函数在图 1任意第
| $ \left\{\begin{array}{l}{\varphi }_{n}={f}_{\mathrm{P}n}\left(z\right)\mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\right(\omega t-kx\left)\right]\\ {\psi }_{n}={f}_{\mathrm{S}n}\left(z\right)\mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\right(\omega t-kx\left)\right]\end{array}\right. $ | (A-1) |
式中:
| $ \left\{\begin{array}{l}\frac{{\partial }^{2}\varphi }{\partial {t}^{2}}\cdot \frac{1}{{v}_{\mathrm{P}}^{2}}=\frac{{\partial }^{2}\varphi }{\partial {x}^{2}}+\frac{{\partial }^{2}\varphi }{\partial {z}^{2}}\\ \frac{{\partial }^{2}\psi }{\partial {t}^{2}}\cdot \frac{1}{{v}_{\mathrm{S}}^{2}}=\frac{{\partial }^{2}\psi }{\partial {x}^{2}}+\frac{{\partial }^{2}\psi }{\partial {z}^{2}}\end{array}\right. $ | (A-2) |
将式(A-1)代入式(A-2),可以得到任意
| $ \left\{\begin{array}{l}{\varphi }_{n}=({A}_{n}{\mathrm{e}}^{\mathrm{i}{\alpha }_{n}z}+{B}_{n}{\mathrm{e}}^{-\mathrm{i}{\alpha }_{n}z})\mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\right(\omega t-kx\left)\right]\\ {\psi }_{n}=({C}_{n}{\mathrm{e}}^{\mathrm{i}{\beta }_{n}z}+{D}_{n}{\mathrm{e}}^{-\mathrm{i}{\beta }_{n}z})\mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\right(\omega t-kx\left)\right]\end{array}\right. $ | (A-3) |
式中:
| $ \left\{\begin{array}{l}{\varphi }_{1}=({A}_{1}{\mathrm{e}}^{\mathrm{i}{\alpha }_{1}z}+{B}_{1}{\mathrm{e}}^{-\mathrm{i}{\alpha }_{1}z})\mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\right(\omega t-kx\left)\right]\\ {\psi }_{1}=0\end{array}\right. $ | (A-4) |
海底弹性半空间需要满足无穷远处振幅为零,则式(A-3)中,
| $ \left\{\begin{array}{l}{\varphi }_{N+1}={B}_{N+1}{\mathrm{e}}^{-\mathrm{i}{\alpha }_{n}z}\mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\right(\omega t-kx\left)\right]\\ {\psi }_{N+1}={D}_{N+1}{\mathrm{e}}^{-\mathrm{i}{\beta }_{n}z}\mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\right(\omega t-kx\left)\right]\end{array}\right. $ | (A-5) |
| [1] |
STEWART R R, GAISER J E, BROWN R J, et al. Converted-wave seismic exploration: methods[J]. Geophysics, 2002, 67(5): 1348-1363. DOI:10.1190/1.1512781 |
| [2] |
BOUSKA J. Advantages of wide-patch, wide-azimuth ocean-bottom seismic reservoir surveillance[J]. The Leading Edge, 2008, 27(12): 1662-1681. DOI:10.1190/1.3036972 |
| [3] |
MAVER K G. Ocean Bottom Seismic: strategic technology for the oil industry[J]. First Break, 2011, 29(12): 75-80. |
| [4] |
张永刚, 王赟, 王妙月. 目前多分量地震勘探中的几个关键问题[J]. 地球物理学报, 2004, 47(1): 151-155. ZHANG Yonggang, WANG Yun, WANG Miaoyue. Some key problems in the multi-component seismic exploration[J]. Chinese Journal of Geophysics, 2004, 47(1): 151-155. |
| [5] |
李向阳, 王九拴. 多波地震勘探及裂缝储层预测研究进展[J]. 石油科学通报, 2016, 1(1): 45-60. LI Xiangyang, WANG Jiushuan. Recent advances in multicomponent seismic and fractured reservoir characterization[J]. Petroleum Science Bulletin, 2016, 1(1): 45-60. |
| [6] |
EWING W M, JARDETZKY W S, PRESS F. Elastic Waves in Layered Media[M]. New York: McGraw-Hill, 1957.
|
| [7] |
PADILLA F, DE BILLY M, QUENTIN G. Theoretical and experimental studies of surface waves on solid-fluid interfaces when the value of the fluid sound velocity is located between the shear and the longitudinal ones in the solid[J]. The Journal of the Acoustical Society of America, 1999, 106(2): 666-673. DOI:10.1121/1.427084 |
| [8] |
卓乐芳. 固体—液体层分界面处的P、SV型面波[J]. 西安工程学院学报, 1999, 21(3): 71-73. ZHUO Lefang. P、SV typal surface waves at the interface of solid-aliquid layer[J]. Journal of Xi'an Engineering University, 1999, 21(3): 71-73. |
| [9] |
CARCIONE J M, HELLE H B. The physics and simulation of wave propagation at the ocean bottom[J]. Geophysics, 2004, 69(3): 825-839. DOI:10.1190/1.1759469 |
| [10] |
BOHLEN T, KUGLER S, KLEIN G, et al. 1.5D inversion of lateral variation of Scholte-wave dispersion[J]. Geophysics, 2004, 69(2): 330-344. DOI:10.1190/1.1707052 |
| [11] |
RAUCH D, KUPERMAN W A, JENSEN F B. Experimental and Theoretical Studies of Seismic Interface Waves in Coastal Waters[M]. Bottom-Interacting Ocean Acoustics, Springer, Boston, MA, 1980, 307-327.
|
| [12] |
SCHOLTE J G. The range of existence of Rayleigh and Stoneley waves[J]. Geophysical Journal International, 1947, 5(S5): 120-126. |
| [13] |
TOMAR G, STUTZMANN E, MORDRET A, et al. Joint inversion of the first overtone and fundamental mode for deep imaging at the Valhall oil field using ambient noise[J]. Geophysical Journal International, 2018, 214(1): 122-132. DOI:10.1093/gji/ggy122 |
| [14] |
GLORIEUX C, VAN DE ROSTYNE K, GUSEV V, et al. Nonlinearity of acoustic waves at solid-liquid interfaces[J]. The Journal of the Acoustical Society of America, 2002, 111(1): 95-103. DOI:10.1121/1.1420388 |
| [15] |
WOEZEL J L, EWING M, PEKERIS C L. Explosion Sounds in Shallow Water[M]. Pittsburgh: University of Pittsburgh Press, 1948.
|
| [16] |
MUYZERT E. Scholte wave velocity inversion for a near surface S-velocity model and PS-statics[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 1197-1200.
|
| [17] |
WANG Y, LI Z, YOU Q, et al. Shear-wave velocity structure of the shallow sediments in the Bohai Sea from an ocean-bottom-seismometer survey[J]. Geophysics, 2016, 81(3): ID25-ID36. DOI:10.1190/geo2015-0417.1 |
| [18] |
WANG Y, LI Z, GENG J, et al. Seismic imaging of S-wave structures of shallow sediments in the East China Sea using OBN multicomponent Scholte-wave data[J]. Geophysics, 2020, 85(6): EN87-EN104. DOI:10.1190/geo2019-0639.1 |
| [19] |
WANG Y, YOU Q, HAO T. Estimating the shear-wave velocities of shallow sediments in the Yellow Sea using ocean-bottom-seismometer multicomponent Scholte-wave data[J]. Frontiers in Earth Science, 2022, 10: 812744. DOI:10.3389/feart.2022.812744 |
| [20] |
SPICA Z J, NISHIDA K, AKUHARA T, et al. Marine sediment characterized by ocean-bottom fiber-optic seismology[J]. Geophysical Research Letters, 2020, 47(16): e2020GL088360. DOI:10.1029/2020GL088360 |
| [21] |
CHENG F, CHI B, LINDSEY N J, et al. Utilizing distributed acoustic sensing and ocean bottom fiber optic cables for submarine structural characterization[J]. Scientific Reports, 2021, 11(1): 5613. DOI:10.1038/s41598-021-84845-y |
| [22] |
LIOR I, SLADEN A, RIVET D, et al. On the detection capabilities of underwater distributed acoustic sensing[J]. Journal of Geophysical Research: Solid Earth, 2021, 126(3): e2020JB020925. DOI:10.1029/2020JB020925 |
| [23] |
梁志强. 层状介质中多模式面波频散曲线研究[D]. 陕西西安: 长安大学, 2006. LIANG Zhiqiang. Study on Multi-Modes Surface Wave Dispersion Curves in Bedding Media[D]. Chang'an University, Xi'an, Shanxi, 2006. |
| [24] |
邵广周. 多阶模式瑞利波频散特征与反演研究[D]. 陕西西安: 长安大学, 2009. SHAO Guangzhou. Study on Multiple-Mode Dispersion Characteristics of Rayleigh Waves and it's Inversion[D]. Chang'an University, Xi'an, Shanxi, 2009. |
| [25] |
罗夏云, 程广利, 张明敏, 等. 浅海Scholte波的频散特性研究[J]. 兵工学报, 2018, 39(9): 1786-1794. LUO Xiayun, CHENG Guangli, ZHANG Mingmin, et al. Research on dispersion characteristics of Scholte wave in shallow sea[J]. Acta Armamentarii, 2018, 39(9): 1786-1794. |
| [26] |
祝捍皓, 郑红, 林建民, 等. 海洋环境参数对Scholte波特性的影响[J]. 上海交通大学学报, 2016, 50(2): 257-264. ZHU Hanhao, ZHENG Hong, LIN Jianmin, et al. Influence of ocean environment parameters on Scholte wave[J]. Journal of Shanghai Jiaotong University, 2016, 50(2): 257-264. |
| [27] |
雷左, 孟路稳, 金丹, 等. 基于两种海底介质的地震波传播特性研究[J]. 海军工程大学学报, 2017, 29(6): 13-17. LEI Zuo, MENG Luwen, JIN Dan, et al. Propagation characteristics of seismic waves based on two kinds of seabed medium[J]. Journal of Naval University of Engineering, 2017, 29(6): 13-17. |
| [28] |
ALI H B, BIBEE L D. The influence of sediment layering and geoacoustics on the propagation of Scholte interface waves[C]. Proceedings of OCEANS'93, 1993, I105-I113.
|
| [29] |
QI Q. Attenuated leaky Rayleigh waves[J]. The Journal of the Acoustical Society of America, 1994, 95(6): 3222-3231. DOI:10.1121/1.409986 |
| [30] |
VINH P C. Scholte-wave velocity formulae[J]. Wave Motion, 2013, 50(2): 180-190. DOI:10.1016/j.wavemoti.2012.08.006 |
| [31] |
DONG Y, PIAO S, GONG L, et al. Scholte wave dispersion modeling and subsequent application in seabed shear-wave velocity profile inversion[J]. Journal of Marine Science and Engineering, 2021, 9(8): 840. DOI:10.3390/jmse9080840 |
| [32] |
CARLSON R L, SCHAFTENAAR C H, MOORE R P. Causes of compressional-wave anisotropy in carbonate-bearing, deep-sea sediments[J]. Geophysics, 1984, 49(5): 525-532. DOI:10.1190/1.1441688 |
| [33] |
BERGE P A, MALLICK S, FRYER G J, et al. In situ measurement of transverse isotropy in shallow-water marine sediments[J]. Geophysical Journal International, 1991, 04(2): 241-254. |
| [34] |
BUCKINGHAM M J. Compressional and shear wave properties of marine sediments: comparisons between theory and data[J]. Journal of the Acoustical Society of America, 2005, 117(1): 137-152. DOI:10.1121/1.1810231 |
| [35] |
HAMILTON E L. Sound velocity gradients in marine sediments[J]. The Journal of the Acoustical Society of America, 1979, 65(4): 909-922. DOI:10.1121/1.382594 |
| [36] |
GARDNER G H F, GARDNER L W, GREGORY A R. Formation velocity and density: the diagnostic basics for stratigraphic traps[J]. Geophysics, 1974, 39(6): 770-780. DOI:10.1190/1.1440465 |
| [37] |
KOMATITSCH D, TROMP J. Spectral-element simulations of global seismic wave propagation-I. Validation[J]. Geophysical Journal International, 2002, 149(2): 390-412. DOI:10.1046/j.1365-246X.2002.01653.x |
| [38] |
KOMATITSCH D, TROMP J. Spectral-element simulations of global seismic wave propagation-Ⅱ. Three-dimensional models, oceans, rotation and self-gravitation[J]. Geophysical Journal International, 2002, 150(1): 303-318. DOI:10.1046/j.1365-246X.2002.01716.x |
| [39] |
夏江海, 高玲利, 潘雨迪, 等. 高频面波方法的若干新进展[J]. 地球物理学报, 2015, 58(8): 2591-2605. XIA Jianghai, GAO Lingli, PAN Yudi, et al. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics, 2015, 58(8): 2591-2605. |
| [40] |
GANJI V, GUCUNSKI N, NAZARIAN S. Automated inversion procedure for spectral analysis of surface waves[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(8): 757-770. DOI:10.1061/(ASCE)1090-0241(1998)124:8(757) |
| [41] |
OLAFSDOTTIR E A, ERLINGSSON S, BESSASON B. Tool for analysis of multichannel analysis of surface waves (MASW) field data and evaluation of shear wave velocity profiles of soils[J]. Canadian Geotechnical Journal, 2018, 55(2): 217-233. DOI:10.1139/cgj-2016-0302 |



 杨小慧, 江苏省南京市江宁区上高路219号中国石化石油物探技术研究院,211103。Email:
杨小慧, 江苏省南京市江宁区上高路219号中国石化石油物探技术研究院,211103。Email: