0 引言

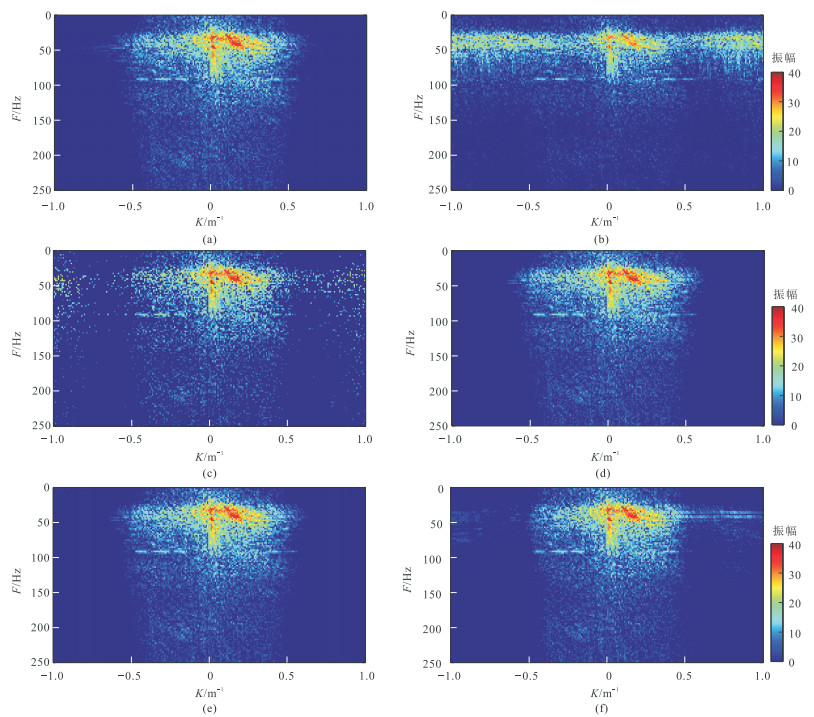
在理想情况下地震信号处理需要规则且致密的信号集。然而，受地表障碍物、禁采区、检波器失效等因素的影响，地震信号往往会出现缺失、分布不规则、稀疏采样等问题^[1]，降低了后续处理和成像精度。为此，国内外学者基于不同的数学理论相继提出了四类地震信号重建方法^[2]：①基于预测滤波的方法^[3-4]；②基于波动方程的方法^[5-6]；③基于降秩的方法^[7-8]；④基于变换域的方法^[9-11]。其中，基于压缩感知理论的变换域重建方法，因无需各种地质、地球物理等先验信息，而在地震信号重建领域得到广泛应用^[12-14]。压缩感知理论指出，若信号在某个变换域内具有稀疏性，则可设计一个与变换基不相关的观测矩阵将高维信号转化为低维观测值，并通过求解最优化问题实现缺失信号的重建^[15-16]。迭代收缩阈值(Iterative Shrinkage Thresholding，IST)算法和凸集投影(Projection onto Convex Sets，POCS)算法是构建最优化问题的两种主要方法^[17]。现有的IST算法收敛速度较慢、计算效率低^[18]。相比于IST算法，POCS算法在由稀疏变换规则和迭代阈值模型构建的凸集约束集合中，通过多次迭代设置合适的阈值，将完整信号特征的能量保留，滤除掉因信号缺失而产生的无关噪声，具有理论简单、容易实现、计算效率高的优点，被广泛应用于地震和重磁信号的高精度重建^[19-23]。

目前，广泛应用于地震信号POCS重建的稀疏变换主要有傅里叶变换、小波变换、曲波变换等^[24-26]。相比于傅里叶变换，小波变换和曲波变换使用的基函数能较好地表征地震信号的局部细节特征，重建精度更高，但由于其算法冗余度较大且计算效率低，因而无法快速、高效重建大规模缺失地震信号^[27]。只能展现信号的频域局部特征的傅里叶变换虽然计算效率高，适用于大规模地震信号的快速重建，但是重建效果不佳。研究表明：在POCS重建中，选择合适的阈值模型，可有效保留稀疏变换域中的完整信号特征，提高重建精度和效率。目前，广泛应用于F-K域POCS重建的线性和指数阈值模型由于无法有效重建弯曲同相轴，重建精度低^[28]。Gao等^[1]在Abma等^[29]的线性阈值模型基础上推导了指数阈值模型，减少了迭代次数、提高了重建效率；张华等^[19]在指数阈值模型的基础上提出一种修正指数阈值模型，可在一定程度上提高计算效率；Gao等^[20]提出了一种数据驱动阈值模型，可有效提高计算效率；黄小刚等^[30]在半径—斜率域中设置权函数作用于POCS的每次迭代，有效提高了POCS重建精度；刁塑等^[21]结合POCS采用倾角扫描方法拾取有效波能量进行地震信号重建，有效提高了重建精度，但计算效率有所降低。

在上述研究基础上，本文通过分析时—空域缺失地震信号的F-K谱特征，提出了适用于缺失地震信号重建的矩形与扇形区域阈值模型，其核心思想是将数值阈值转化为区域阈值，将区域窗口作为阈值进行迭代更新，以解决POCS重建中广泛使用的线性和指数阈值模型无法高效重建弯曲同相轴的问题，并通过数值试验对比分析了区域阈值模型相比于F-K域指数阈值模型和曲波域指数阈值模型在重建精度和计算效率方面的优越性。

1 方法原理 1.1 基于POCS的地震信号重建方法

不规则或稀疏的地震信号可描述为完整信号的稀疏采样^{[10, 15]}

$ {\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}=\boldsymbol{R}\boldsymbol{d} $

(1)

式中：d_obs为实测的不规则或稀疏地震信号；d为完整或规则的信号；R为由元素1和0构成的稀疏采样矩阵。

基于压缩感知理论，通常将地震数据重建表示为一个带有正则化项的优化问题^{[3, 31]}。对于该优化问题可构建目标函数

$ \varPhi \left(\boldsymbol{x}\right)={‖{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\boldsymbol{R}{\mathbf{F}}^{-1}\boldsymbol{x}‖}_{2}^{2}+\psi {‖\boldsymbol{x}‖}_{1} $

(2)

式中：$ {\mathbf{F}}^{-1} $为反傅里叶变换；$ \boldsymbol{x} $为完整信号$ \boldsymbol{d} $的估计在傅里叶域中的稀疏系数；$ \psi $为正则化参数。式(2)右端侧第一项表示在缺失信号与完整信号之间残差最小情况下，促使$ \boldsymbol{x} $向真值方向收敛；第二项表示对$ \boldsymbol{x} $施加L₁范数正则化约束，以保证计算结果的稀疏性^[17]。

本文采用POCS算法求解式(2)，分别将地震信号的傅里叶变换规则和迭代阈值模型设置为凸集约束集合$ {\boldsymbol{Q}}_{1} $和$ {\boldsymbol{Q}}_{2} $^[1]

$ {\boldsymbol{Q}}_{1}=\left\{\boldsymbol{x}:{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\boldsymbol{R}{\mathbf{F}}^{-1}\boldsymbol{x}=0\right\} $

(3)

$ {\boldsymbol{Q}}_{2}=\left\{\boldsymbol{x}:{‖\boldsymbol{\alpha }‖}_{1}\le {‖\boldsymbol{x}‖}_{1}\right\} $

(4)

式中$ \boldsymbol{\alpha } $为迭代阈值。在凸集约束集合中，将$ {\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}} $的傅里叶变换系数作为初始解进行多次迭代投影，以获得满足约束条件的解$ \tilde{\boldsymbol{x}} $^[32]。$ {\boldsymbol{Q}}_{1} $的投影过程是$ {\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}} $在傅里叶变换域内不断更新解的过程，可表示为^[33]

$ {\tilde{\boldsymbol{x}}}_{k-1}={\boldsymbol{x}}_{k-1}+\left(\boldsymbol{R}{\mathbf{F}}^{-1}{)}^{\mathrm{*}}\right({\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-\boldsymbol{R}{\mathbf{F}}^{-1}{\boldsymbol{x}}_{k}) $

(5)

式中：$ {(\cdot )}^{\mathrm{*}} $表示矩阵的伴随算子；$ {\tilde{\boldsymbol{x}}}_{k-1} $与$ {\boldsymbol{x}}_{k-1} $分别表示地震信号在第$ k-1 $次迭代时的更新解与初始解。$ {\boldsymbol{Q}}_{2} $的投影过程可视为阈值算子的应用，阈值算子可以将小于阈值的傅里叶系数置零，而保留大于阈值的傅里叶系数，并将其重新代入解区间^[34]，即

$ {\boldsymbol{x}}_{k}=\left\{\begin{array}{cc}{\tilde{\boldsymbol{x}}}_{k-1}& \left|{\tilde{\boldsymbol{x}}}_{k-1}\right|\ge {\lambda }_{k}\\ 0& \left|{\tilde{\boldsymbol{x}}}_{k-1}\right| < {\lambda }_{k}\end{array}\right. $

(6)

式中：$ \left|·\right| $表示取绝对值；$ k=1, \mathrm{ }2, \mathrm{ }\cdots , N $，N为最大迭代次数；$ {\lambda }_{k} $为阈值门限，在迭代过程中按一定规律不断变化。地震信号在POCS重建中广泛使用的线性阈值与指数阈值模型分别为^[1]

$ {\lambda }_{k}={\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\frac{(k-1)({\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}-\delta )}{N-1} $

(7)

$ {\lambda }_{k}={\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{e}\mathrm{x}\mathrm{p}{\left[\frac{(k-1)\left(\mathrm{l}\mathrm{n}\delta -\mathrm{l}\mathrm{n}{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)}{N-1}\right]}^{} $

(8)

式中：$ {\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}} $表示傅里叶变换系数中最大绝对值；$ \delta $为一个与缺失信号产生的噪声能量相关且接近零的极小值^[35]。地震信号POCS重建试验表明：指数阈值模型中的阈值变化要快于线性阈值模型，重建效率、精度更高^{[27, 32]}，因此本文选取指数阈值模型进行对比。

由式(5)和式(6)并结合阈值算子$ {\boldsymbol{T}}_{k} $可得^[1]

$ {\tilde{\boldsymbol{x}}}_{k}={\boldsymbol{T}}_{k}\left\{\mathbf{F}\left[\boldsymbol{R}{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}+(\boldsymbol{I}-\boldsymbol{R}){\mathbf{F}}^{-1}{\boldsymbol{x}}_{k-1}\right]\right\} $

(9)

式中$ \boldsymbol{I} $为单位矩阵。在每次迭代时逐渐减弱阈值$ {\boldsymbol{T}}_{k} $可重建具有稀疏地震信号特征的傅里叶变换系数，并结合傅里叶变换不断对变换系数$ {\boldsymbol{x}}_{k-1} $进行更新，从而得到第k次迭代后的傅里叶变换系数$ {\tilde{\boldsymbol{x}}}_{k} $。为得到时—空域中的重建后地震信号，对$ {\tilde{\boldsymbol{x}}}_{k} $进行傅里叶反变换，将重建后的时—空域地震信号代入式(9)，可得到时—空域地震信号POCS重建迭代公式为

$ {\boldsymbol{d}}_{k+1}={\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}+(\boldsymbol{I}-\boldsymbol{R}){\mathbf{F}}^{-1}{\boldsymbol{T}}_{k}\mathbf{F}{\boldsymbol{d}}_{k} $

(10)

式中：$ \boldsymbol{I}-\boldsymbol{R} $为缺失信号位置矩阵；$ {\boldsymbol{d}}_{k+1} $为第$ k+1 $次迭代后重建的时—空域地震信号。

1.2 区域阈值模型

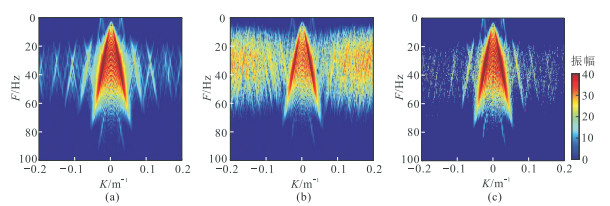
阈值模型是决定POCS重建精度和重建效率的关键因素之一。由于地震信号缺失引起的噪声能量在F-K谱中不一定弱于有效信号，因而线性阈值模型、指数阈值模型及其改进的数值阈值模型不是最优阈值模型^[27]。当其应用于POCS重建时，若某次迭代时的阈值高于有效信号能量，则部分有效信号的傅里叶变换系数将会被置零，从而导致无法被有效重建；若某次迭代的阈值低于由地震信号缺失引起的噪声能量，则不能完全滤除噪声，降低重建精度。图 1展示了一个三层模型的地震信号的完整数据、随机缺失40%地震信号和POCS重建后的F-K谱(指数阈值模型)。完整地震信号的能量主要集中在F-K谱中心位置处(图 1a)；而部分信号缺失引起的噪声杂乱分布在整个波数区间，且部分噪声能量高于有效波能量(图 1b)；由于部分噪声能量高于有效波，应用数值阈值模型的POCS进行重建时，不可避免会在F-K谱滤除部分有效波能量，重建精度不高(图 1c)。

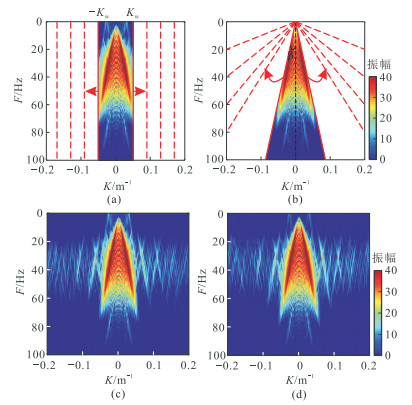
为解决上述问题，本文根据上述完整地震信号F-K谱和随机缺失部分地震信号的F-K谱特征，将数值阈值模型转换为区域阈值模型，提出适用于F-K域的矩形区域阈值模型和扇形区域阈值模型，其表达式分别为

$ {\boldsymbol{x}}_{k}(K, F)=\left\{\begin{array}{cc}{\tilde{\boldsymbol{x}}}_{k-1}& K\in [-{K}_{\mathrm{w}}, {K}_{\mathrm{w}}]\\ 0& \mathrm{其}\mathrm{它}\end{array}\right. $

(11)

$ {\boldsymbol{x}}_{k}(K, F)=\left\{\begin{array}{cc}{\tilde{\boldsymbol{x}}}_{k-1}& K\in [-L\mathrm{s}\mathrm{i}\mathrm{n}\beta , L\mathrm{s}\mathrm{i}\mathrm{n}\beta ]\\ 0& \mathrm{其}\mathrm{它}\end{array}\right. $

(12)

式(11)表示将$ \left[-{K}_{\mathrm{w}}, \right.\left.{K}_{\mathrm{w}}\right] $波数区间的傅里叶系数保留，将其他波数对应的傅里叶系数滤除；式(12)中L为扇形滤波器的边界线(图 2b中红线)，$ \beta $为边界线与纵轴方向的夹角，其表示在$ \left[-L\mathrm{s}\mathrm{i}\mathrm{n}\beta , \right. $$ \left.L\mathrm{s}\mathrm{i}\mathrm{n}\beta \right] $区域内对应的傅里叶系数保留，其他波数区域对应的傅里叶系数滤除。区域阈值模型采用的滤波器如图 2a、图 2b所示，该滤波器左右对称，将两条红线内波数区域对应的傅里叶系数保留，红线外波数区域对应的傅里叶系数滤除。迭代初期使用较小的区域阈值，从而筛选较大的傅里叶系数，之后按照一定的波数步长或一定的角度变化逐步增大滤波器的覆盖范围。如应用矩形区域阈值模型进行重建时，以波数步长0.001 m^-1进行扩大；使用扇形区域阈值模型进行重建时，以角度步长0.9°进行扩大；随着区域阈值的不断增大，允许更多的傅里叶系数通过，以逐步恢复微弱地震信号的特征。最后，滤波器覆盖范围不断增大，直至覆盖整个F-K谱。图 2c、图 2d为使用矩形和扇形区域阈值模型的F-K域POCS经50次迭代后重建信号的F-K谱。对比图 1c与图 2c、图 2d可见，F-K域区域阈值模型的POCS重建精度更高，与图 1a所示的完整地震信号的F-K谱差异更小。

1.3 重建流程和重建信号质量评价

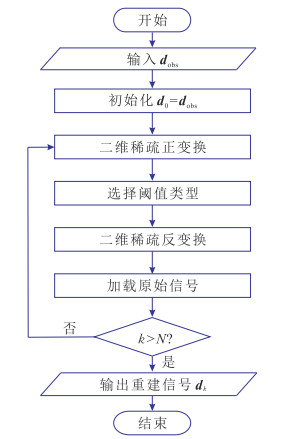
依据上述理论，本文构建的地震信号F-K域POCS重建流程如图 3所示。

本文采用Gao等^[20] 提出的迭代误差评价重建时—空域地震信号质量，其计算公式为

$ {\varepsilon }_{k+1}=\frac{{‖{\boldsymbol{d}}_{k+1}-\boldsymbol{d}‖}_{2}^{2}}{{‖\boldsymbol{d}‖}_{2}^{2}} $

(13)

式中$ {\varepsilon }_{k+1} $为第$ k+1 $次的迭代误差。为进一步分析POCS重建质量，采用平均绝对误差(Mean Absolute Error，MAE)、信噪比(Signal-to-noise Ratio，SNR)和峰值信噪比(Peak Signal-to-noise Ratio，PSNR)三个指标进行定量分析^[36-37]。MAE、SNR、PSNR分别为

$ \mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{mn}\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}\left|d(i, j)-{d}_{\mathrm{r}\mathrm{e}\mathrm{c}}(i, j)\right| $

(14)

$ \mathrm{S}\mathrm{N}\mathrm{R}=10\times \mathrm{l}\mathrm{g}\frac{\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}{\left[d(i, j)\right]}^{2}}{\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}{\left[{d}_{\mathrm{r}\mathrm{e}\mathrm{c}}(i, j)-d(i, j)\right]}^{2}} $

(15)

$ \mathrm{P}\mathrm{S}\mathrm{N}\mathrm{R}=10\times \mathrm{l}\mathrm{g}\frac{\mathrm{m}\mathrm{a}\mathrm{x}{\left(\boldsymbol{d}\right)}^{2}}{\mathrm{M}\mathrm{A}\mathrm{E}} $

(16)

式中：m为地震信号样点数；n为道数；d_rec表示重建信号。

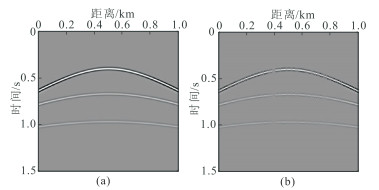
2 数值算例 2.1 区域阈值模型的优势分析

为验证本文提出的F-K域区域阈值模型的POCS重建效果，采用主频为30 Hz的Ricker子波合成一个三层模型的地震道集，如图 4a所示。该道集共有401道，道间距为2.5 m，每道751个采样点，采样间隔为2 ms。对地震道集进行40%的随机缺失，并在横向0.4 km处设置了一个连续10道的缺失区域，如图 4b所示。

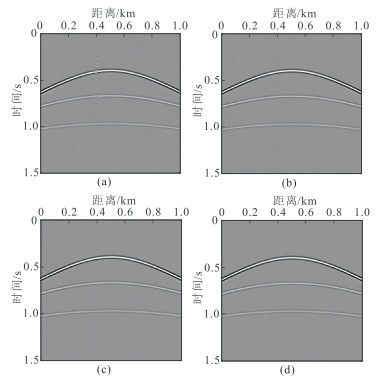
分别使用F-K域指数阈值模型、矩形区域阈值模型和扇形区域阈值模型及曲波域指数阈值模型的POCS重建方法对图 4b重建。100次迭代后重建的地震道集如图 5所示。F-K域指数阈值模型的POCS重建结果在连续缺失区域有着明显的截断和纵向伪影(图 5a)；F-K域矩形区域阈值模型、扇性区域阈值模型和曲波域指数阈值模型均能有效重建缺失地震信号，重建同相轴平滑、完整，基本没有能量缺失，重建效果大致相当(图 5b~图 5d)。

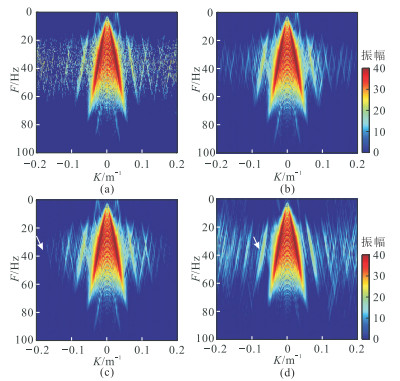
图 6为四种方法重建道集的F-K谱。与图 1a的F-K谱相比，F-K域指数阈值模型的POCS重建结果丢失部分有效能量，在远离中心区域有较明显的干扰噪声(图 6a)；而F-K域矩形区域阈值模型与扇形区域阈值模型POCS重建结果的F-K谱与图 1a相比，无明显噪声(图 6b、图 6c)；但扇形区域阈值模型重建结果的F-K谱在远离中心处缺失部分有效能量，如图 6c中白色箭头所指；曲波域指数阈值模型的POCS重建结果的F-K谱中在白色箭头所指处部分有效能量被剔除，干扰强且分布在整个F-K谱中(图 6d)。

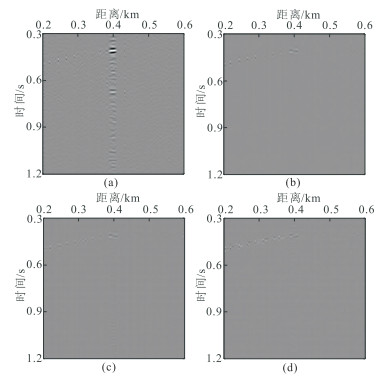
为进一步对比分析不同阈值模型的重建效果，利用完整地震道集减去不同阈值模型重建结果，其残差道集如图 7所示。使用F-K域指数阈值模型的POCS重建存在较大的误差，在400 m连续缺失区域能看见明显的伪影(图 7a)；曲波域指数阈值模型与F-K域矩形区域阈值模型和扇形区域阈值模型的POCS重建误差大致相当(图 7b~图 7d)；但仔细对比可见，矩形区域阈值模型和扇形区域阈值模型在有些位置的误差更小。

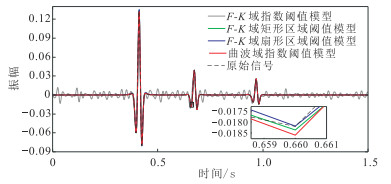
提取横向位置410 m处(连续缺失处)四种方法重建结果与原始数据的单道波形如图 8所示。由图可见，F-K域指数阈值模型的POCS重建结果与原始信号的差异较为明显，重建效果差；F-K域矩形区域阈值模型、扇形区域阈值模型的POCS重建结果与曲波域指数阈值模型的POCS重建精度高，与原始信号单道波形拟合较好；由0.660s附近的局部放大图可知：F-K域区域阈值模型的POCS重建精度要略高于曲波域指数阈值模型的POCS重建精度。

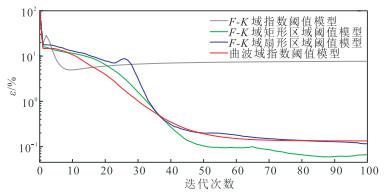
图 9为根据式(13)计算的迭代相对误差曲线，可见：F-K域指数阈值模型的POCS重建误差在初始时下降很快，但50次迭代后重建误差稳定在7.58%；曲波域指数阈值模型的POCS重建误差缓慢下降，经过100次迭代后误差约为0.13%；F-K域扇形区域阈值模型的POCS重建在约30次迭代时阈值模型恰使F-K谱中大部分能量完全通过，迭代重建误差快速下降，随后缓慢下降，经100次迭代后迭代误差与曲波域指数阈值模型的POCS接近，约为0.12%；F-K域矩形区域阈值模型的POCS重建误差缓慢下降，在90次迭代后趋于平稳，其迭代误差小于F-K域扇形区域阈值模型和曲波域指数区域阈值模型，约为0.06%。

由此可见，相比于F-K域和曲波域指数阈值模型，F-K域区域阈值模型的POCS重建误差更小，精度更高；矩形区域阈值模型的重建误差比扇形区域阈值模型更小。

利用式(14)、式(15)、式(16)计算重建道集与原始完整道集之间的MAE、SNR、PSNR及重建计算时间的统计如表 1所示。由表可知：F-K域矩形区域阈值模型、扇形区域阈值模型与曲波域指数阈值模型POCS重建的MAE、SNR和PSNR基本相当，MAE要远小于F-K域指数阈值模型，且SNR和PSNR更高；F-K域矩形区域阈值模型、扇形区域阈值模型的POCS重建计算时间要远小于曲波域指数阈值模型，计算效率提高了约90%。由此可见，F-K域矩形区域阈值模型和扇形区域阈值模型的POCS重建算法能在保证精度的同时，缩短计算时间，显著提高了计算效率。

2.2 实际数据测试

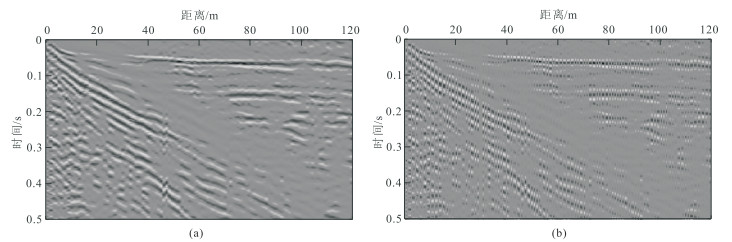
采用图 10a所示的经滤波和增益等常规处理后的实际地震道集测试本文的F-K域区域阈值模型POCS重建方法的实用性。该实际数据共241道，道间距为0.5 m，每道251个样点，采样间隔为2 ms。图 10b为随机缺失40%的道集，且在30 m附近连续缺失了3道。与完整道集相比，道的缺失导致同相轴不连续。

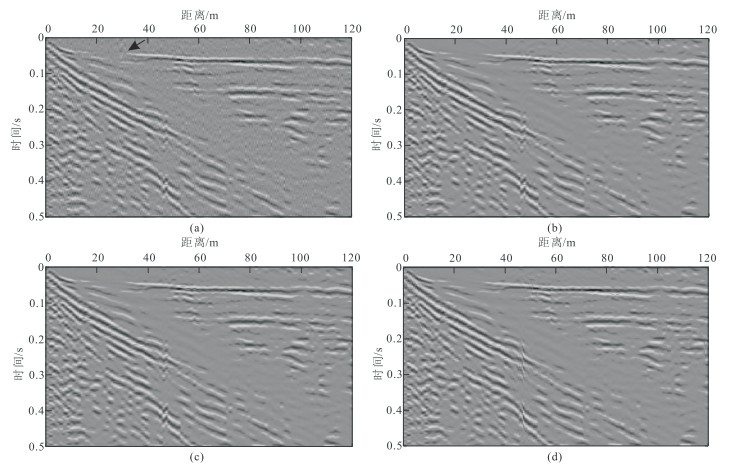
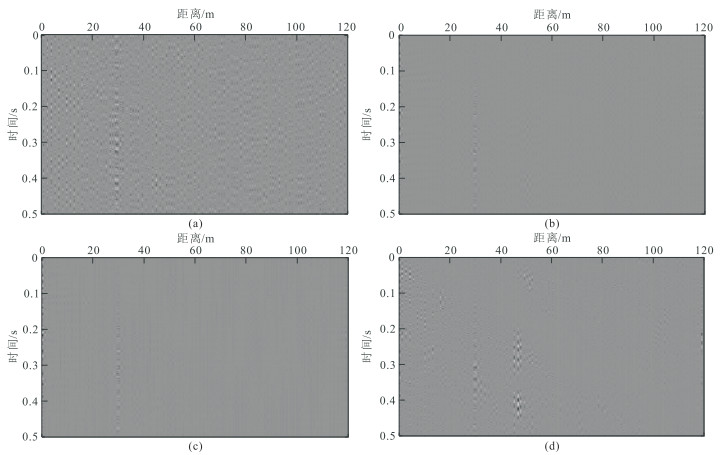
利用上述四种阈值模型的POCS算法对图 10b中的缺失地震道集进行重建，100次迭代的重建结果和残差分别如图 11和图 12所示。F-K域指数阈值模型的POCS重建结果的同相轴完整且连续，但在缺失处存在纵向伪影(图 11a黑色箭头处)，整个剖面都存在明显误差(图 12a), 重建效果最差；曲波域指数阈值模型的POCS虽能较好重建连续缺失地震道(图 11d)，但整体上存在不小的误差(图 12d), 重建效果较好；F-K域矩形区域阈值模型和扇形区域阈值模型的POCS重建地震道集同相轴光滑且连续，误差较小, 具有更好的重建效果，(图 11b、图 11c、图 12b、图 12c)。

在F-K域和曲波域指数阈值模型的POCS重建误差道集中，误差不仅在30 m连续缺失处存在，在其他道缺失处也广泛存在(图 12a、图 12d)；F-K域矩形区域阈值模型和扇形区域阈值模型的POCS重建仅在连续缺失处存在较小的误差，重建效果更好(图 12b、图 12c)。

图 13为实测地震道集、缺失地震道集、四种方法重建结果的F-K谱对比。与完整地震道集F-K谱(图 13a)相比，缺失地震道集的F-K谱在中心处存在部分有效能量缺失，且在远离中心处存在广泛分布的噪声(图 13b)；四种阈值模型均能有效重建F-K谱中心处的有效能量，但F-K域和曲波域指数阈值模型的POCS重建不能较好地滤除远离中心处的噪声(图 13c、图 13f)；F-K域矩形区域阈值模型和扇形区域阈值模型POCS重建后的F-K谱(13d、图 13e)与完整地震道集(图 13a)相比，无明显噪声，重建精度更高、效果更好。

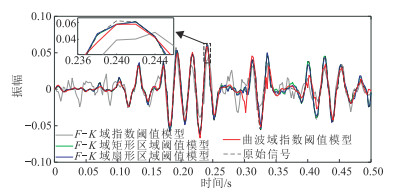
提取四种阈值模型POCS重建地震道集在横向30 m处的波形，与原始道集的单道对比如图 14所示。由图可见，F-K域指数阈值模型的POCS重建结果与原始地震道集相比存在明显扰动，重建效果较差；曲波域指数阈值模型的POCS重建效果得到改善，但重建精度仍低于F-K域矩形区域阈值模型和扇形区域阈值模型。由0.240 s处的波峰子图可见，F-K域矩形区域阈值模型和扇形区域阈值模型的POCS重建结果与原始道集的拟合效果更好。

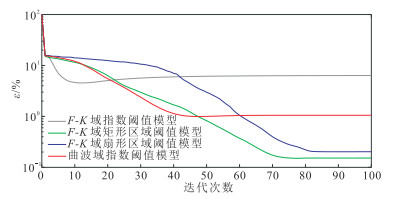
图 15为四种POCS阈值模型迭代相对误差曲线。F-K域指数阈值模型的POCS重建误差初始快速下降，在40次迭代后误差稳定在6.22%附近；曲波域指数阈值模型的POCS重建经过更多次迭代后误差趋于稳定，但小于F-K域指数阈值模型，约为1.05%；F-K域矩形区域阈值模型和扇形区域阈值模型的POCS重建稳定、误差接近，分别为0.15%与0.20%，远小于前两个模型。由此可见，对于实际地震道集，F-K域矩形区域阈值模型和扇形区域阈值模型的POCS重建虽然需要更多的迭代次数，但重建精度要远高于F-K域和曲波域指数阈值模型。

表 2为四种方法重建道集与原始完整道集之间的MAE、SNR、PSNR峰值信噪比及重建计算时间对比。由表可知，F-K域矩形区域阈值模型与扇形区域阈值模型的POCS重建精度相当，其重建精度和计算效率高于F-K域和曲波域指数阈值模型，计算时间分别约为曲波域指数阈值模型的2.4%和4.2%。

3 结论

(1) 本文首先根据压缩感知理论，推导了地震信号POCS重建时—空域迭代公式及其计算流程。在此基础上，根据时—空域缺失地震信号的F-K谱特征，引入矩形与扇形区域滤波窗口作为阈值进行迭代更新，将数值阈值转化为区域阈值，提出了一种基于区域阈值模型的地震信号POCS重建方法。

(2) 数值试验结果表明：相比于F-K域指数阈值模型的POCS重建，F-K域区域阈值模型对连续缺失信号的重建精度更高；相比于F-K域扇形区域阈值模型，F-K域矩形区域阈值模型的重建精度和计算效率均略高；F-K域区域阈值模型的POCS重建精度与曲波域指数阈值模型相当，但计算效率提高了约90%。