2. 东北石油大学人工智能能源研究院, 黑龙江大庆 163318;
3. 东北石油大学物理与电子工程学院, 黑龙江大庆 163318
2. Artificial Intelligence Energy Research Institute, Northeast Petroleum University, Daqing, Heilongjiang 163318, China;
3. School of Physics and Electronic Engineering, Northeast Petroleum University, Daqing, Heilongjiang 163318, China
地震速度反演精度是偏移成像的关键。目前,地震速度反演的主要方法有叠加速度分析、偏移速度分析、层析速度反演和全波形反演及深度学习方法等。
Garotta等[1]提出的常规叠加速度分析方法是常用的速度建模方法之一。张明等[2]、徐文君等[3]、王瑞林等[4]改进了叠加速度模型方法,但是在复杂地质条件下精度明显不足。偏移速度分析可结合速度分析与偏移成像进行速度建模,早期主要是利用Kirchhoff积分法[5-7]实现,但精度较低。后续具有更高精度的基于波动方程的偏移速度分析方法成为主流[8-9],但是效果受迭代精度和计算效率的影响较大。层析成像方法可分为以射线理论为基础的射线层析[10-11]和以波动理论为基础的绕射层析[12-14]两种类型,其中射线层析的结果分辨率较低,绕射层析的计算量过大。全波形反演[15-17]基于波动方程,利用观测到的数据与模拟数据的最优匹配以建立地下介质的模型,反演结果精度高,但过度依赖初始速度模型,迭代过程较复杂,耗时较长。
深度学习技术为速度建模提供了高效利用海量地震数据的手段。Araya-polo等[18]提出了基于深度神经网络(Deep Neural Networks,DNN)的二维速度建模方法,将提取的道集数据特征作为网络输入,具有较高精度,但特征提取部分受人为因素影响较大。韩明亮等[19]将地震反射波形和速度谱作为U-Net的输入,克服单独使用反射波形或速度谱时存在的建模不稳定和精度不足的问题。张兵[20]将速度谱作为神经网络的输入数据,将时间域层速度作为标签数据,设计了一种编码—解码结构的神经网络模型,直接将速度谱映射为时间域层速度。以上方法主要是利用现有经典网络结构调整输入与标签信息进而实现反演。Mosser等[21]将反演问题看作不同域之间的转换,使用深度卷积生成对抗网络,实现了地震数据域与速度模型域之间的转换,但结果的精度还具有较大提升空间。Zhang等[22]设计了VelocityGAN网络,将物理驱动方法的逆过程转化为图像之间的映射,直接从原始地震波形数据生成高质量的速度图像,提高了生成的速度模型精度。Feng等[23]针对全波形反演(Full-waveform Inversion,FWI)中的局部极小值问题,基于全卷积网络(Fully Convolutional Networks,FCN)开发了一种多尺度数据驱动方法,相较传统FWI具有更高的精度和更少的计算时间。Li等[24]认为深度学习反演的映射关系存在弱对应的问题,提出SeisInvNet网络,通过学习增强地震道中的空间对应关系重构速度模型,这在一定程度上提高了精度。
综上所述,基于深度学习的速度反演方法面临以下挑战:①时间域(地震数据)与空间域信息(速度模型)之间的语义映射对应性较弱, 使网络在学习该映射关系时存在多解性;②采集到的原始地震记录中存在噪声,神经网络将地震数据映射到速度模型时缺少有效引导,导致反演精度下降。
特征强化是通过提高特征表示能力进而增强模型性能的方法。特征叠加、特征增强、特征融合等方法都可以视为特征强化的手段,可以在深度学习中提高学习特征的有效性和表现力,从而解决深度学习技术运用到速度反演领域所面临问题。本文将对空间位置信息更敏感的U-Net[25-26]作为基础网络,结合特征强化的思想改进U-Net,提出了一种深度神经网络反演方法:①为解决传统反演模型多解性问题,本文基于特征叠加的思想,叠加多炮地震数据特征并设计特征提取模块,保留更多的地震数据与速度模型之间的映射关系,使提取的特征图与目标模型之间的映射关系更加明确。通过设计多尺度模块,使用不同尺寸卷积核处理特征图,并对提取的不同特征进行融合,以增强网络特征学习能力。②为解决神经网络缺乏引导的问题,采用注意力门代替跳跃连接,以增强网络学习速度模型的重点特征,提高关键特征质量。引入残差学习策略,并基于预激活和瓶颈残差的思想,设计预激活瓶颈残差结构,引入跨层连接,强化特征表达,以避免梯度消失和模型退化,提高网络鲁棒性。使用理论速度模型作为样本进行网络试算,验证本文方法的有效性。然后在含噪数据及标准模型中进行测试,验证方法的抗噪性和泛化能力。
1 方法原理 1.1 多炮特征叠加特征叠加是将多个数据源提取的特征进行堆叠以提高特征表示,获得更加全面、丰富的数据表示。
在地震勘探中,与速度模型对应的三维地震记录一般为[S,R,T],其中S为震源数量,R为接收器数量,T为采样时间步长。由于从震源到接收器的波场传播路径是固定的,这使每个震源对应的地震剖面[1,R,T] 不同,而每个地震剖面包含的信息有限,只能为部分速度模型提供支持。现有方法通常用S作为初始卷积层的通道数,导致提取的每个通道的特征映射与速度模型的对应关系不适定,使神经网络难以将数据域转换为空间域。因此,本文对多炮地震数据进行变形操作,即网络输入的是[1,S×R,T] 格式的地震数据,其中初始卷积层的输入通道为1。这在不破坏原始地震数据的情况下,保留了接收器与震源之间的空间关系,使提取的特征图与速度模型之间的对应关系更加明确,减少了求解反演问题的多解性。
基于特征叠加的思想,将来自不同震源的多个地震数据沿着1个维度叠加,形成新的输入数据。将每个震源对应的不同的地震剖面叠加到相同的特征空间中,便于模型对整体数据进行学习和分析。
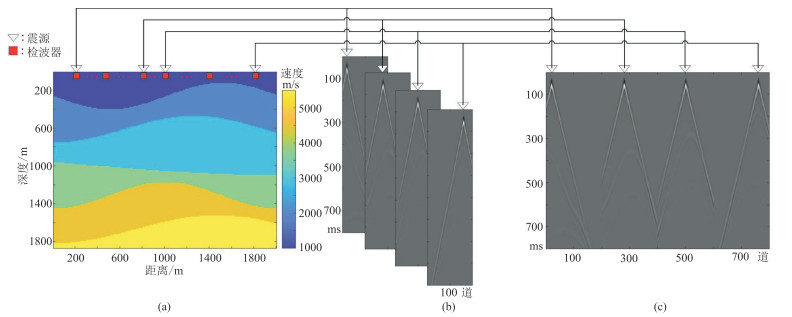
如图 1所示,图 1a为具有4个震源的速度模型,图 1b为[S,R,T] 格式的三维地震数据,每个震源对应不同的地震剖面[1,R,T],接收器与震源之间的空间关系不明确。图 1c为[1,S×R,T] 格式的二维地震数据,接收器与震源之间的空间关系较为清晰,增加了有效特征的约束,可以减少解空间的大小,提高求解的准确性。
|
图 1 速度模型与地震数据的对应关系 (a)速度模型;(b)三维地震记录[S,R,T],每个震源对应不同的地震剖面[1,R,T];(c)二维地震记录[1,S×R,T] |
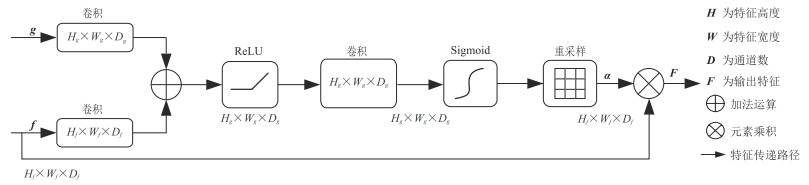
传统的U-Net采用跳跃式连接,将浅层卷积提取的低层次特征与深层卷积提取的相同尺度的高层次特征进行融合,可以为上采样提供无法恢复的空间信息。然而,在速度反演领域,神经网络的主要任务是将时域地震数据映射到空间域速度模型,由浅层卷积层提取的时域地震数据的低层特征不适合直接并入空间域速度模型的高层特征中,网络在缺少引导的情况下使用跳跃连接会导致地震记录中的噪声信息被重复使用。基于特征强化的思想,通过注意力门(Attention Gates,AGs)[27]代替跳跃连接,使用上采样得到的深层特征引导网络,以全局视角给将要拼接的低层特征每个元素不同的权重,帮助神经网络降低不相关的低层次特征的干扰,改进拼接特征的质量,增强对速度模型相关特征的学习。如图 2所示,AGs方法通过分析深层特征(g)提供的语义信息计算得到注意力系数(
|
图 2 注意力门流程图 |
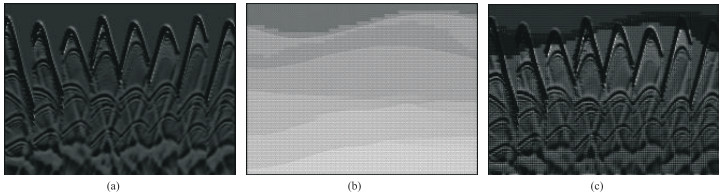
图 3a是从地震数据中提取的低维时域特征,图 3b是经过深层卷积后解码得到的高维空间域特征,经过注意力门后的特征如图 3c所示,包含了经过加权后的低层特征。图 3c和图 3b进行通道上的拼接后输入到下一层卷积,为卷积层提供了增强的特征和缺失的细节信息,引导网络重点学习速度模型相关特征。
|
图 3 输入注意力门的特征图 (a)浅层特征;(b)深层特征;(c)经过注意力门后的特征 |
特征融合通常将不同来源、不同尺度的特征信息进行组合,以提高模型性能。基于特征融合的思想,使用多尺度卷积核,在不同感受野下对地震数据特征进行提取,可以捕获更多的细节和结构信息,并将提取的特征进行通道拼接,使下一卷积层得到更丰富的全局特征表示。多尺度卷积通过使用不同的卷积核对图像特征进行提取,并从全局视角对图像特征信息进行编码和解码,从而提高网络性能。其中,规模大的卷积核具有更大的感受野,可以提取更多的信息,用于稀疏地震数据的初始特征提取;规模小的卷积核具有更少的参数和更低的内存需求。
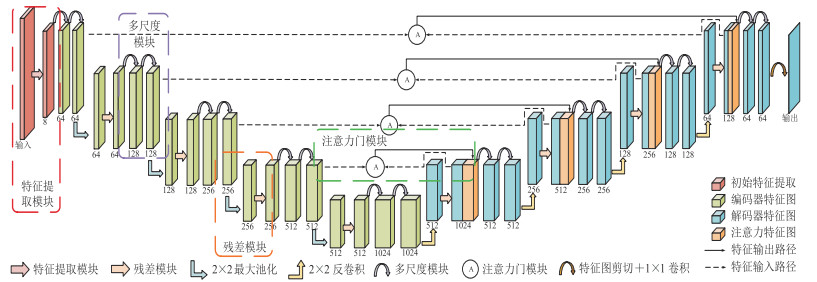
2 网络结构本文提出的FEU-Net(Feature Enhancement U-Net)结构包括特征提取模块、多尺度模块、注意力门模块和残差模块4个部分(图 4)。
|
图 4 FEU-Net结构图 每个柱状体下标注的数字为特征通道数。 |
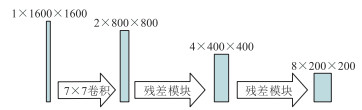
特征提取模块由1个卷积核(7×7的卷积层)和2个3×3尺度的残差块组成(图 5)。经过预处理后的地震数据尺寸过大,将其输入网络主体前需要使用特征提取模块减小数据尺寸。同时,该模块可以对时域地震记录进行初始特征提取。
|
图 5 特征提取模块结构 1×1600×1600表示特征图尺寸。 |
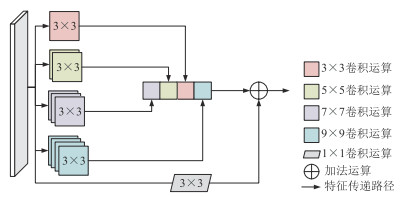
多尺度模块(图 6)由1个3×3、5×5、7×7卷积层和1个9×9卷积层并行组成,以此增强网络的多尺度断层检测能力。同时,在模块中增加1个1×1的卷积层,使网络能够获取更多的空间信息。
|
图 6 多尺度模块结构 |
对于大卷积核使训练参数过多而导致网络计算效率下降的问题,可以使用多个小卷积核的组合代替较大的卷积核。多个小卷积核连续卷积的效果和单个大卷积核卷积的作用相同,2个3×3的卷积层堆叠后的感受野为5×5,3个3×3的卷积层堆叠后的感受野为7×7,故可以通过小尺寸卷积层的堆叠替代大尺寸卷积层,并且在感受野不变的同时使网络堆叠更深,以增加网络的拟合能力。因此,为减少网络的内存需求,多尺度模块中的5×5、7×7和9×9卷积层分别替换为具有等价效果的2个3×3、3个3×3和4个3×3卷积序列。
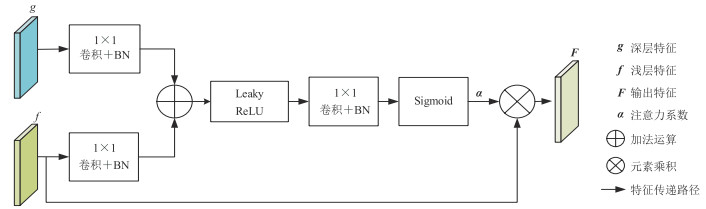
2.3 注意力门模块注意力门模块的结构如图 7所示。使用注意力门计算输入浅层特征
|
图 7 注意力门模块结构 |
残差结构通过跨层连接实现对跨层信息的传递,使梯度更容易反向传递回前面的层,同时将上一层的输入与当前层的输出相加,减少地震数据在网络传递过程中有效信息的损失,提高特征的表达能力。常规残差模块随着网络深度增加,在提取从地震数据到速度模型的映射关系时,相邻两个层之间的特征差别越来越小,梯度逐渐消失。因此,需要对常规残差模块进行改进。
瓶颈残差模块(Bottleneck Residual Block)[28]依次由1×1、3×3、1×1的3个卷积层堆叠而成,1×1的卷积用于降低或升高特征的维度,3×3的卷积在相对较低的维度可以更有效、更直观地提取特征。同时,2个1×1的卷积代替一部分常规残差模块中3×3卷积的作用,减少参数的数量,从而达到提高计算效率的目的。
预激活残差单元(Pre-activation ResBlock)[29]将ReLU激活函数放入残差块内部,数据进入每个模块(Block)时先经过批量归一化(BN)和ReLU激活函数再进行卷积。实验数据表明,使用预激活残差单元的网络比基本残差单元更容易优化。考虑到地震数据的类型为实数,而U-Net中使用的ReLU激活函数会使网络中过多的神经元失活,因此使用Leaky ReLU作为激活函数[30]。
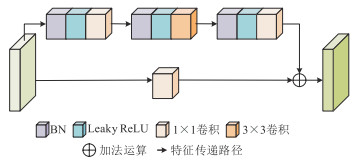
基于上述思想,本文设计了预激活瓶颈残差模块(图 8)。由图可见,输入x进入残差路径,先经过1层BN和Leaky ReLU进行预激活,然后通过1×1卷积降维处理。降维后的数据通过BN和Leaky ReLU开展3×3卷积进行特征提取,最后由1×1卷积将特征维度复原,并和直接映射路径的数据进行add操作,即为预激活瓶颈残差模块的输出。因此, 在解决模型退化的同时引入跨层连接强化了特征的表达。
|
图 8 预激活瓶颈残差模块结构 |
为了验证本文方法反演的有效性,首先使用正演程序模拟生成的简单速度模型进行反演,并将U-Net与FEU-Net的反演结果进行对比。
随机生成最小层数为4、最大层数为7、最小速度为1500m/s、最大速度为4500m/s的速度模型,并设置断层和盐丘体参数生成断层和盐丘速度模型。根据生成的速度模型,采用20 Hz的雷克子波,生成采样时间间隔为1ms、总采样时间为1600 ms的地震数据。将得到的数据按照8:1:1的比例划分为训练集、验证集、测试集,输入网络进行训练。
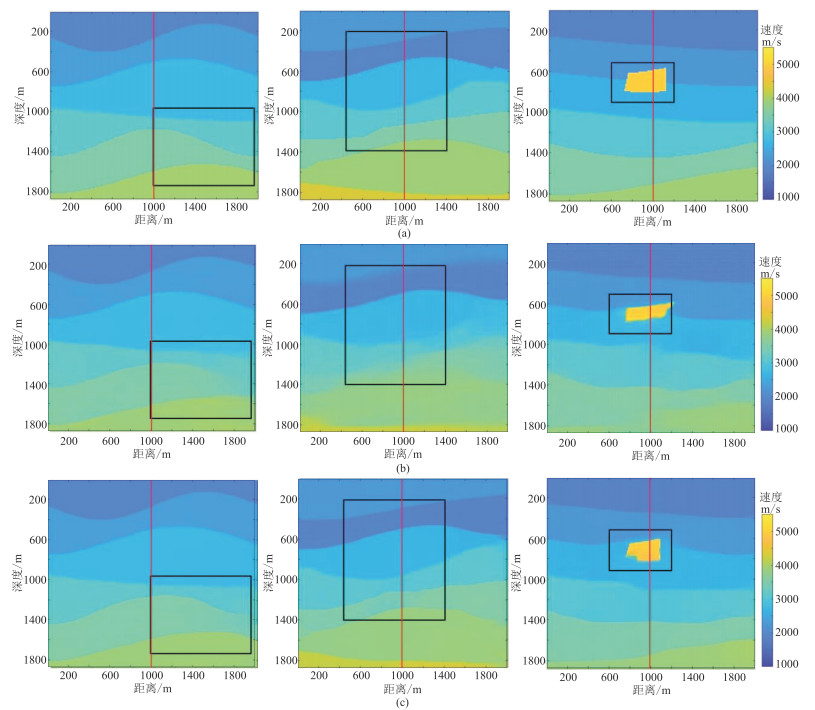
在测试集中,任意选取1个普通速度模型样本、1个断层速度模型样本和1个盐丘速度模型样本(图 9a),对比U-Net(图 9b)和FEU-Net(图 9c)的反演结果,可知本文方法得到普通速度模型的反演结果更准确,断层速度模型的边界更清晰,盐丘速度模型盐丘体具更高的精度(黑色方框)。这表明了本文方法通过强化特征,有效增强了地震数据与速度模型之间的映射关系,使网络可以反演出准确的背景速度和地质体尺度及位置信息。
|
图 9 不同速度模型及其U-Net与FEU-Net的反演结果对比 (a)速度模型;(b)U-Net反演结果;(c)FEU-Net反演结果 左为普通速度模型,中为断层速度模型,右为盐丘速度模型。 |
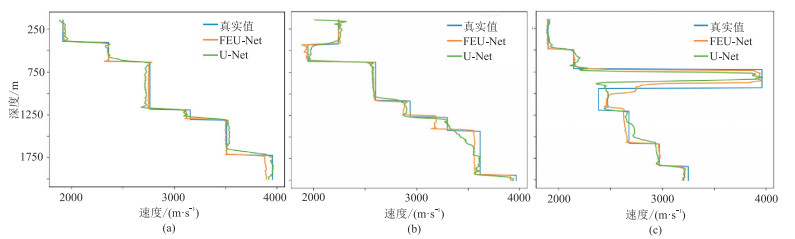
图 10是从图 9普通速度模型、断层速度模型和盐丘速度模型中红线处提取的单道速度值。在浅层,FEU-Net反演重建的速度模型结果与真实值基本一致,曲线较为平滑,而U-Net反演结果局部产生较大误差并且存在较为明显的波动。在深层,两者的反演结果与真实值都存在一定的差别,但FEU-Net反演的结果较U-Net更加稳定, 前者反演的结果是较为平滑的折线,而后者为波动的曲线。另外,由MAE(平均绝对误差)、MSE(均方误差)、SSIM(结构相似度)和SNR(信噪比)函数评价指标结果(表 1)可见,FEU-Net反演结果的4个评价指标均优于U-Net。
|
图 10 不同速度模型U-Net与FEU-Net反演结果的单道速度值对比 (a)普通速度模型;(b)断层速度模型;(c)盐丘速度模型 |
|
|
表 1 U-Net和FEU-Net反演结果的4种评价指标对比 |
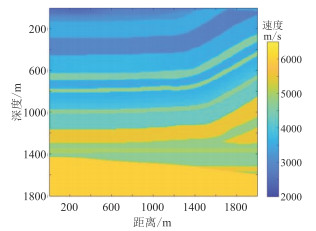
实际采集到的原始地震数据通常含有无规律噪声。为了测试本文方法的抗噪性,在SEG/EAGE推覆体数据集中选取任意1个原始地震数据样本(图 11),分别加入噪声等级r(噪声信号标准差与原始信号标准差之比)为0.01、0.03、0.05、0.07、0.10、0.30的随机噪声。
|
图 11 SEG/EAGE推覆体数据 |
由表 2可知,在噪声强度较小时(r为0.01~0.10),对4种评价指标的影响较小;在噪声强度较大时(r为0.30),MSE和MAE的数值上升幅度增大,SSIM和SNR的数值大幅下降。
|
|
表 2 不同噪声等级下FEU-Net反演结果的4种评价指标对比 |
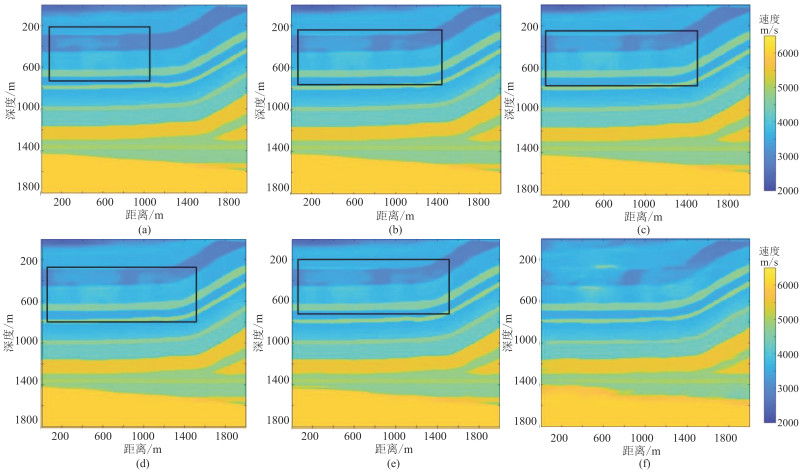
由图 12可见,噪声强度较小时(r为0.01~0.10),本文算法反演出了比较准确的速度模型,在黑色矩形框区域存在少量伪影,表现出了良好的抗噪性;噪声强度较大时(r为0.30),本文算法仍然具有一定的抗噪能力,网络学习到了整体的速度信息。
|
图 12 FEU-Net在不同噪声等级的反演结果对比 (a)0.01;(b)0.03;(c)0.05;(d)0.07;(e)0.10;(f)0.30 |
通过在网络中引入多个尺度的卷积,可以在不同的空间尺度上捕获有关图像结构的信息,从而提高对噪声的容忍度。同时残差模块将输入信息与卷积输出信息相加,使残差模块能够在前向传递时传递输入的特征,神经网络更具有鲁棒性,网络在处理带有噪声的数据时能够更好地保持稳定性。
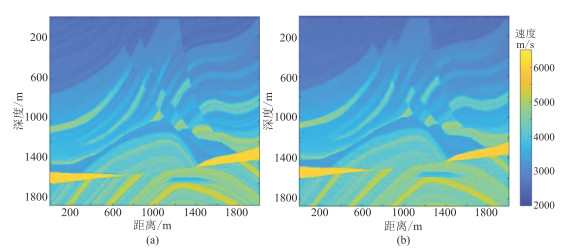
3.3 Marmousi模型泛化测试为了进一步验证本文方法的泛化性,利用Marmousi二维模型对FEU-Net算法进行测试。下采样后的Marmousi模型如图 13a所示。Marmousi数据集中的速度模型更复杂,结构与之前的训练数据集有很大不同,因此,FEU-Net使用Marmousi训练集重新训练30个Epoch以微调神经网络的参数,然后使用Marmousi的样本进行反演。
|
图 13 Marmousi模型(a)及其FEU-Net反演结果(b) |
从图 13可见,本文方法在底部高速体区域反演出了较为准确的地质信息,在浅层速度体区域也有较好的表现(图 13b)。本文方法通过强化地震数据中的有效特征,加强神经网络的特征学习能力,使网络表现出了一定的泛化能力。
4 结束语本文提出FEU-Net的深度神经网络地震速度反演方法,对多炮地震数据特征叠加处理,使提取的特征与速度模型的对应关系更加清晰;使用特征提取模块,过滤不适合连接速度模型的底层特征;引入注意力门代替跳跃连接,增强网络特征学习能力;引入多尺度模块,用不同尺寸的卷积核使网络可以学习到更多的特征融合信息;引入预激活瓶颈残差模块,在增加网络深度的同时避免了网络退化。实验结果证明了FEU-Net的优越性。与同类算法相比,本文反演模型具有更高的清晰度,且网络模型具有一定的抗噪性和泛化能力。
| [1] |
GAROTTA R, MICHON D. Continuous analysis of the velocity function and of the normal-moveout corrections[J]. Geophysical Prospecting, 1967, 15(4): 584-597. DOI:10.1111/j.1365-2478.1967.tb01805.x |
| [2] |
张明, 薛诗桂. 基于物理模型的起伏地表构造成像叠加速度分析研究[J]. 地球物理学进展, 2013, 28(3): 1417-1424. ZHANG Ming, XUE Shigui. Stacking velocity analysis of structure imaging with relief surface based on seismic physical model[J]. Progress in Geophysics, 2013, 28(3): 1417-1424. |
| [3] |
徐文君, 殷俊锋, 王华忠, 等. 基于稀疏反演理论的自动叠加速度反演方法[J]. 地球物理学报, 2017, 60(7): 2791-2800. XU Wenjun, YIN Junfeng, WANG Huazhong, et al. Automatic estimation of stacking velocity based on sparse inversion[J]. Chinese Journal of Geophysics, 2017, 60(7): 2791-2800. |
| [4] |
王瑞林, 冯波, 吴成梁, 等. 基于CMP道集智能化的初始速度建模方法研究[J]. 石油物探, 2021, 60(5): 763-772. WANG Ruilin, FENG Bo, WU Chengliang, et al. Intelligent initial velocity model building based on CMP gathers[J]. Geophysical Prospecting for Petroleum, 2021, 60(5): 763-772. DOI:10.3969/j.issn.1000-1441.2021.05.007 |
| [5] |
ROSS H N. Prestack Gaussian-beam depth migration[J]. Geophysics, 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
| [6] |
胡治权, 曹俊兴, 姚维益. 基于射线参数估计的快速2D Kirchhoff叠前深度偏移[J]. 物探化探计算技术, 2008, 30(5): 368-373, 348. HU Zhiquan, CAO Junxing, YAO Weiyi. High-efficiency 2D Kirchhoff pre-stack migration based on the ray-parameter estimation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2008, 30(5): 368-373, 348. DOI:10.3969/j.issn.1001-1749.2008.05.005 |
| [7] |
杜启振, 李芳, 侯波, 等. 角度域弹性波Kirchhoff叠前深度偏移速度分析方法[J]. 地球物理学报, 2011, 54(5): 1327-1339. DU Qizhen, LI Fang, HOU Bo, et al. Angle-domain migration velocity analysis based on elastic-wave Kirchhoff prestack depth migration[J]. Chinese Journal of Geophysics, 2011, 54(5): 1327-1339. DOI:10.3969/j.issn.0001-5733.2011.05.022 |
| [8] |
ZHANG K, LI Z C, ZENG T S, et al. Residual curvature migration velocity analysis for angle domain common imaging gathers[J]. Applied Geophysics, 2010, 7(1): 49-56, 99. DOI:10.1007/s11770-010-0006-1 |
| [9] |
秦宁, 王延光, 杨晓东, 等. 基于角道集剩余曲率分析的层析速度建模[J]. 石油地球物理勘探, 2015, 50(1): 61-66. QIN Ning, WANG Yanguang, Yang Xiaodong, et al. Tomography velocity model building based on ADCIG's residual curvature[J]. Oil Geophysical Prospecting, 2015, 50(1): 61-66. |
| [10] |
李勇德, 董良国, 刘玉柱. 一种新的预条件伴随状态法初至波走时层析[J]. 地球物理学报, 2017, 60(10): 3934-3941. LI Yongde, DONG Liangguo, LIU Yuzhu. First-arrival traveltime tomography based on a new preconditioned adjoint-state method[J]. Chinese Journal of Geophysics, 2017, 60(10): 3934-3941. DOI:10.6038/cjg20171021 |
| [11] |
沈天晶, 胡叶正, 黄旭日, 等. 共聚焦点层析成像方法[J]. 石油地球物理勘探, 2021, 56(5): 1074-1085. SHEN Tianjing, Hu Yezheng, HUANG Xuri, et al. Research on tomography method based on common focus point[J]. Oil Geophysical Prospecting, 2021, 56(5): 1074-1085. |
| [12] |
DAHLEN F A, HUNG S H, NOLET G. Fréchet kernels for finite-frequency traveltimes—I. Theory[J]. Geophysical Journal International, 2000, 141(1): 157-174. DOI:10.1046/j.1365-246X.2000.00070.x |
| [13] |
XIE X B, YANG H. The finite-frequency sensitivity kernel for migration residual moveout and its applications in migration velocity analysis[J]. Geophysics, 2008, 73(6): S241-S249. DOI:10.1190/1.2993536 |
| [14] |
陈云鹏. 海南地幔柱P波有限频层析成像研究[D]. 黑龙江哈尔滨: 哈尔滨工业大学, 2020. CHEN Yunpeng. Hainan Mantle Plume from P Wave Finite Frequency Tomography[D]. Harbin Institute of Technology, Harbin, Heilongjiang, 2020. |
| [15] |
张天泽, 韩立国, 张盼, 等. 基于自适应步长OBFGS算法的快速时间域全波形反演[J]. 物探化探计算技术, 2018, 40(1): 1-7. ZHANG Tianze, HAN Liguo, ZHANG Pan, et al. Fast time domain full waveform inversion based on self-adaptive step OBFGS algorithm[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2018, 40(1): 1-7. DOI:10.3969/j.issn.1001-1749.2018.01.01 |
| [16] |
YONG P, LIAO W Y, HUANG J P, et al. Misfit function for full waveform inversion based on the Wasserstein metric with dynamic formulation[J]. Journal of Computational Physics, 2019, 399: 108911. DOI:10.1016/j.jcp.2019.108911 |
| [17] |
杨瑞冬, 黄建平, 杨振杰, 等. 基于双对角通量校正的多尺度全波形反演[J]. 石油地球物理勘探, 2022, 57(5): 1120-1128. YANG Ruidong, HUANG Jianping, YANG Zhenjie, et al. Multi-scale full waveform inversion based on double diagonal flux correction transport[J]. Oil Geophysical Prospecting, 2022, 57(5): 1120-1128. |
| [18] |
ARAYA-POLO M, JENNINGS J, ADLER A, et al. Deep learning tomography[J]. The Leading Edge, 2018, 37(1): 58-66. DOI:10.1190/tle37010058.1 |
| [19] |
韩明亮, 邹志辉, 马锐. 利用反射地震资料和多尺度训练集的深度学习速度建模[J]. 石油地球物理勘探, 2021, 56(5): 935-946. HAN Mingliang, ZOU Zhihui, MA Rui. Deep learning-driven velocity modeling based on seismic reflection data and multi-scale training sets[J]. Oil Geophysical Prospecting, 2021, 56(5): 935-946. |
| [20] |
张兵. 基于卷积神经网络和叠加速度谱的地震层速度自动建模方法[J]. 石油物探, 2021, 60(3): 366-375. ZHANG Bing. Automatic seismic interval velocity building based on convolutional neural network and velocity spectrum[J]. Geophysical Prospecting for Petroleum, 2021, 60(3): 366-375. DOI:10.3969/j.issn.1000-1441.2021.03.002 |
| [21] |
MOSSER L, KIMMAN W, DRAMSCH J, et al. Rapid seismic domain transfer: Seismic velocity inversion and modeling using deep generative neural networks[C]. Extended Abstracts of 80th EAGE Conference & Exhibition, 2018, 1-5.
|
| [22] |
ZHANG Z P, WU Y, ZHOU Z, et al. VelocityGAN: subsurface velocity image estimation using conditional adversarial networks[C]. 2019 IEEE Winter Conference on Applications of Computer Vision(WACV), Waikoloa, 2019, 705-714.
|
| [23] |
FENG S H, LIN Y Z, WOHLBERG B. Multiscale data-driven seismic full-waveform inversion with field data study[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-14. |
| [24] |
LI S C, LIU B, REN Y X, et al. Deep learning inversion of seismic data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(3): 2135-2149. DOI:10.1109/TGRS.2019.2953473 |
| [25] |
RONNEBERGER O, FISCHER P, BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015, Cham, 2015, 234-241.
|
| [26] |
李阳, 韩立国, 周帅, 等. 基于深度学习U-net网络的重力数据界面反演方法[J]. 地球物理学报, 2023, 66(1): 401-411. LI Yang, HAN Liguo, ZHOU Shuai, et al. Gravity data density interface inversion based on U-Net deep learning network[J]. Chinese Journal of Geophysics, 2023, 66(1): 401-411. |
| [27] |
OKTAY O, SCHLEMPER J, FOLGOC L L, et al. Attention U-Net: Learning where to look for the pancreas[EB/OL]. (2018-04-11)[2023-06-05]. https://arxiv.org/abs/1804.03999.
|
| [28] |
SANDLER M, HOWARD A, ZHU M, et al. MobileNetV2: Inverted residuals and linear bottlenecks[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, Salt Lake City, 2018.
|
| [29] |
HE K M, ZHANG X Y, REN S Q, et al. Identity mappings in deep residual networks[C]. Computer Vision-ECCV 2016, Cham, 2016, 630-645.
|
| [30] |
张岩, 周一帆, 宋利伟, 等. 基于物理约束U-Net网络的地震数据低频延拓[J]. 石油地球物理勘探, 2023, 58(1): 31-45. ZHANG Yan, ZHOU Yifan, SONG Liwei, et al. Low frequency continuation of seismic data based on physically constrained U-Net network[J]. Oil Geophysical Prospecting, 2023, 58(1): 31-45. |



 董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院,163318。Email:
董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院,163318。Email: