2. 山东能源集团南美有限公司, 山东青岛 266580;
3. 中国石化胜利油田分公司勘探开发研究院, 山东东营 257022
2. Shandong Energy Group South America Co., Ltd, Qingdao, Shandong 266580, China;
3. Exploration and Development Research Institute, Shengli Oilfield Company, SINOPEC, Dongying, Shandong 257022, China
地震勘探是探明地下构造的最有效的地球物理方法之一。多次散射波一直是研究的热点,在很长一段时间里多次散射波被认为是噪声,会在成像剖面上产生假象,从而干扰地震解释。常规成像方法如Kirchhoff偏移[1-2]、逆时偏移(RTM)[3-4]都是基于单次散射假设,即利用一次反射波进行成像[5],因此使用这些偏移方法前,压制多次波成为不可或缺的环节。全波场偏移方法的提出打破了多次波是噪声的固有印象,将多次波与一次波联合成像,成像信息更丰富。研究表明正确利用表面相关多次波可有效提升地下照明范围[6-8]。
全波场偏移是基于多次散射、面向目标、数据驱动的成像方法。通过迭代求解全波场方程,将地震响应聚焦于地下某一点,得到该点的上、下行格林函数,利用成像条件进行成像。全波场偏移可以实现单边聚焦、重构包含一次波和多次波、相对精确的格林函数,成像结果不包含多次波造成的假象[9-10]。
全波场方法最早起源于Marchenko[11]在1955年一维量子力学领域中提出的、一种新的格林函数估计方法。Berkhout[12]提出WRW模型,全波场成像的概念首次出现,但受限于当时的条件,之后其研究重心放在多次波的压制上。直到1993年Berkhout[6]首次提出包含表面相关多次波的偏移方法,证明该方法在避免常规偏移中多次波干扰的同时,可利用多次波提升偏移精度。在此基础上,Berkhout等[8, 13]实现了一次波和表面相关多次波的同时偏移,压制了多次波造成的假象。与此同时,Wong等[14]提出了相似方法实现一次波场和表面相关多次波的成像。Broggini等[9]使用全波场方程求解一维介质内任意虚拟源与表面接收点间的格林函数,实现了在地下介质的任意位置重构虚拟震源,大大拓展了地震干涉(Seismic Interferometry,SI)法[15]的应用范围,因而称之为超越地震干涉(Beyond Seismic Interferometry,BSI)法。值得注意的是BSI法最早研究的是层间多次波,这不同于Berkhout等[8, 13]提出的方法,但二者最终走向都是全波场成像。之后,Berkhout[16-17]将偏移理论推广到混合多次散射波场,将其称为递归全波场偏移。Wapenaar等[18-19]推导了三维全波场方程,并将其用于观测面沉降,论证全波场方法用于观测面沉降的可能性。Wapenaar等[20-21]继续发展BSI方法,提出面向目标的多分量单边全波场方程,探讨了聚焦函数分别产生P波和S波独立聚焦点的过程。Singh等[22-23]通过在全波场方程中添加表面相关多次波项,成功将表面相关多次波用于成像。2015年Verschuur等[24]指出尽管去除多次波的技术已相对成熟,但在数据丢失且存在噪声时,闭环成像过程即全波场成像是唯一获得可靠成像结果的方法。王通等[25-26]实现被动源数据的全波场偏移方法,并通过稀疏变换提升计算效率。秦宁等[27]将一次波和层间多次波进行联合成像。近几年,对于全波场成像方法的研究逐渐从理论研究走向实际应用,Ravasi等[28]、Jia等[29]、Wapenaar等[30]分别将该方法成功应用于北海、墨西哥湾和Vøring盆地的地震数据。此外,中国近年注重散射波成像的研究[31-33]。散射波场能刻画地下非均质地质体,反映小尺度地质体信息,通过偏移可得到相位正确和分辨率高的成像结果,这也是全波场成像发展的路径之一。
在全波场偏移方法的发展过程中对于成像条件的研究相对较少。da Costa Filho等[34-35]改进了全波场偏移成像条件,将上、下行格林函数互相关修改为下行格林函数与直达波的互相关,即零延迟互相关成像条件,可有效压制上、下行格林函数互相关产生的假象[36-37]。韩冬等[38]提出了改进多维反褶积的成像条件,提高了成像质量。De Paula等[39]系统讨论了互相关成像条件、零延迟互相关成像条件、多维反褶积三种成像条件,发现:多维反褶积成像条件相较于其他两种成像条件,能够进一步压制构造假象,补偿振幅能量, 得到成像精度更高的结果,对于复杂构造适应较好,但其计算成本高;零延迟互相关成像条件相较于互相关成像条件对于层间多次波的压制有所加强,但复杂构造多次波造成的假象依旧严重。为克服上述难题,基于零延迟互相关成像条件,本文提出一种保幅逆散射成像条件,以实现复杂构造的高精度地震成像。通过对已知直达波估计与下行格林函数互相关成像条件即零延迟互相关条件添加拉普拉斯滤波及照明项,衰减后向散射并补偿深部能量,提高了对于复杂构造的成像精度、增强了适应能力。
1 全波场偏移方法全波场地震偏移打破单次散射假设限制,将多次散射波用于成像。基于数据驱动的全波场偏移方法凭借其能够重构包含一次波和多次波的格林函数的优势,在观测面沉降、波场重建、多次波压制以及全波场成像方面应用较广。
1.1 地下观测面格林函数重建全波场偏移方法最核心的内容是将地震响应和采集面与成像点之间的直达波作为输入数据,迭代求解地下任一成像点与地表采集阵列之间的格林函数。
格林函数表示时空脉冲源经地下介质到达检波点的波场,记为
|
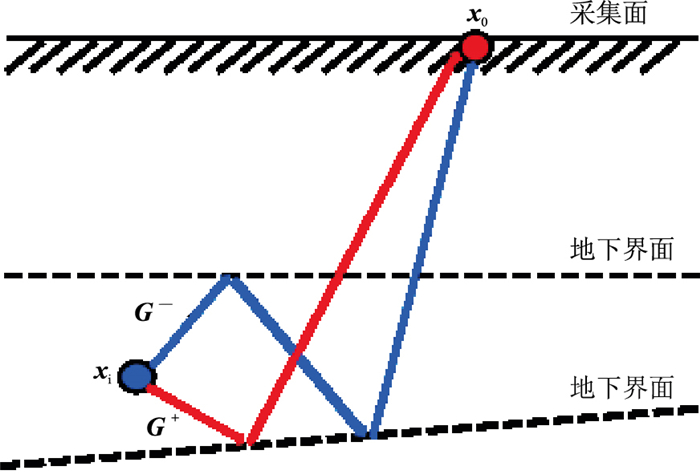
图 1 上行格林函数和下行格林函数 |
上、下行格林函数
| $ G({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)={G}^{-}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)+{G}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t) $ | (1) |
全波场偏移方法是数据驱动的,只需要已知地震反射响应
| $ \begin{array}{l}{G}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)=-{f}^{-}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, t)+\\ {\int }_{\partial {D}_{0}}{f}^{+}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, t)\otimes R({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{0}^{\text{'}}, t)\mathrm{d}{\boldsymbol{x}}_{0}^{\text{'}}\end{array} $ | (2) |
| $ \begin{array}{l}{G}^{-}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)={f}^{+}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, -t)-\\ {\int }_{\partial {D}_{0}}R({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{0}^{\text{'}}, t)\otimes {f}^{-}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, -t)\mathrm{d}{\boldsymbol{x}}_{0}^{\text{'}}\end{array} $ | (3) |
式中:
由式(2)和式(3)可以看出,求解上、下行聚焦函数并代入全波场方程后即可求得上、下行格林函数。全波场偏移方法迭代求解聚焦函数,Wapenaar等[19]定义了下行聚焦函数
| $ {f}_{}^{+}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, t)={T}_{}^{-1}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0}, t) $ | (4) |
式中
| $ {T}_{}^{-1}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0}, t)={T}_{\mathrm{d}}^{-1}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0}, t)+{M}_{k}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t) $ | (5) |
将成像点到地表的直达波的逆时波场
| $ {f}_{1}^{+}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, t)={T}_{\mathrm{d}}^{-1}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0}, t) $ | (6) |
式中
而上行聚焦函数
| $ \begin{array}{l}{f}_{1}^{-}({x}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, t)=\theta ({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)\times \\ \ \ {\int }_{\partial {D}_{0}}\left[R({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{0}^{\text{'}}, t)\otimes {f}_{1}^{+}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, t)\right]\mathrm{d}{\boldsymbol{x}}_{0}^{\text{'}}\end{array} $ | (7) |
式中
| $ \theta ({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)=\left\{\begin{array}{l}1\ \ \mathrm{ }-{T}_{\mathrm{d}}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0}) < t < {T}_{\mathrm{d}}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0})\\ 0\ \ \mathrm{其}\mathrm{它}\end{array}\right. $ | (8) |
再迭代计算散射尾波
| $ \begin{array}{l}{M}_{k}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, -t)=\theta ({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)\times \\ {\int }_{\partial {D}_{0}}\left[R({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{0}^{\text{'}}, t)\otimes {f}_{k-1}^{+}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{\mathrm{i}}, -t)\right]\mathrm{d}{\boldsymbol{x}}_{0}^{\text{'}}\end{array} $ | (9) |
式中k为迭代次数。下行聚焦函数
| $ {f}_{k}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)={f}_{1}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)+{M}_{k}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t) $ | (10) |
将尾波
| $ \begin{array}{l}{f}_{k}^{-}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)={f}_{1}^{-}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)+\theta ({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)\times \\ \ \ {\int }_{\partial {D}_{0}}R({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{0}^{\text{'}}, t)\otimes {M}_{k}^{+}({\boldsymbol{x}}_{0}^{\text{'}}, {\boldsymbol{x}}_{i}, t)\mathrm{d}{\boldsymbol{x}}_{0}^{\text{'}}\end{array} $ | (11) |
应用式(6)和式(7)求得上、下行聚焦函数初始值,代入式(9)和式(11)可得到1~k次尾波和上行聚焦函数。迭代求解式(9)和式(11),直至散射尾波和上行聚焦函数收敛。将尾波代入式(10)可求得下行聚焦函数,再代入式(2)、式(3)可得上、下行格林函数,最后代入式(1)即可得到总的格林函数。该格林函数表示地下成像点有一虚拟源、检波器在地表采集的信号。
1.2 直达波场计算全波场偏移成像的另一个重要的输入是地下成像点与地表检波点之间的直达波。直达波可以通过旅行时与震源子波卷积获得。利用求解程函方程
| $ {\left[\nabla \tau \left(\boldsymbol{x}\right)\right]}^{2}=\frac{1}{{v}^{2}\left(\boldsymbol{x}\right)} $ | (12) |
可以计算旅行时。式中:
| $ {T}_{\mathrm{d}}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0}, t)=\mathrm{\delta }\left[t-\tau ({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0})\right]\otimes w\left(t\right) $ | (13) |
式中w为震源子波。相较于有限差分求解直达波场,使用该方法能够大大降低计算成本,提高效率。
1.3 保幅逆散射成像条件全波场成像条件大致可分为互相关成像条件与多维反褶积成像条件两类。本文对互相关成像条件进行改进。互相关成像条件最简单的形式是上、下行格林函数的互相关[19],即
| $ {I}_{1}\left({\boldsymbol{x}}_{\mathrm{i}}\right)=\sum\limits_{{\boldsymbol{x}}_{0}}\sum\limits_{t}{G}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t){G}^{-}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t) $ | (14) |
da Costa Filho等[35]发现上行格林函数中的多次波和下行格林函数互相关时,会在成像结果上产生严重的串扰噪声,提出零延迟互相关成像条件,即将估计的直达波与下故行格林函数进行互相关
| $ {I}_{2}\left({\boldsymbol{x}}_{\mathrm{i}}\right)=\sum\limits_{{\boldsymbol{x}}_{0}}\sum\limits_{t}{T}_{\mathrm{d}}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0}, t){G}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t) $ | (15) |
韩冬等[38]和顾智炜[41]对两者进行了较为详细的分析,发现零延迟互相关成像条件相较于常规互相关成像条件能够大大压制串扰噪声,但对于复杂的构造假象依旧严重。多维反褶积成像条件应运而生,但高计算成本使其应用受限。根据以上情况,本文提出保幅逆散射成像条件,在保证计算成本的前提下提高复杂构造成像精度。改进后的成像条件为
| $ \begin{array}{l} {I}_{3}\left({\boldsymbol{x}}_{\mathrm{i}}\right)=\\ \sum\limits_{{\boldsymbol{x}}_{0}}\sum\limits_{t}\left\{\frac{{v}_{\mathrm{m}\mathrm{i}\mathrm{g}}^{2}\left({\boldsymbol{x}}_{\mathrm{i}}\right)}{2E({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0})}{\nabla }^{2}\left[{T}_{\mathrm{d}}({\boldsymbol{x}}_{\mathrm{i}}, {\boldsymbol{x}}_{0}, t){G}^{+}({\boldsymbol{x}}_{0}, {\boldsymbol{x}}_{\mathrm{i}}, t)\right]\right\} \end{array}$ | (16) |
式中:
为验证保幅逆散射成像条件全波场偏移的可行性,设计了简单的散射体模型,如图 2所示。模型网格点数为501

|
图 2 散射体速度模型 |
|
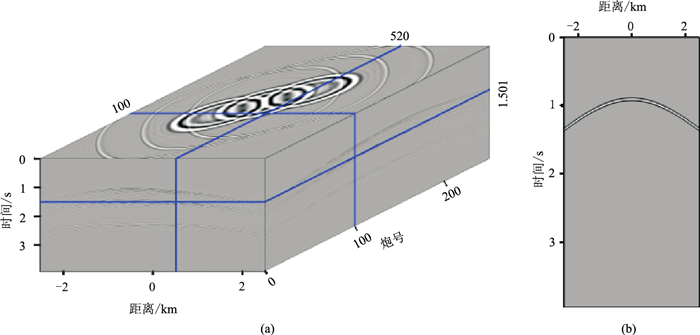
图 3 散射体模型检波点记录全波场偏移的输入 (a)正演记录;(b)(0,2.28 km)处到地表接收阵列的直达波 |
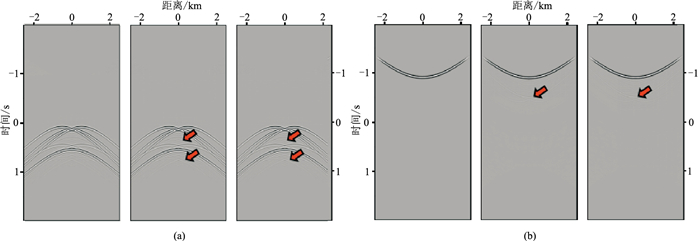
(0,2.28 km)是介质内部确定的成像点,该点到地表采集阵列的直达波如图 3b所示,也是检波点的全波场偏移的另一个输入,是利用背景速度场通过程函方程计算旅行时后与子波褶积得到。值得注意的是,这里使用的子波不同于正演时使用的Ormsby子波,而是主频为25 Hz的Ricker子波。该点的上、下行聚焦函数如图 4所示,对比不同迭代次数的聚焦函数,可以发现聚焦函数在第3次迭代时已经达到相对收敛状态(对比第3、第5次迭代结果,红色箭头处无明显变化),基于此可确定迭代次数。上、下行格林函数如图 5所示,对比发现随着迭代次数增加,干扰逐渐减弱(红色箭头所示),与聚焦函数类似,第3次与第5次迭代之间很难看出差别,这是由于迭代后期干扰能量十分微弱。该现象在图 6b、图 6c的成像结果中也有所体现。
|
图 4 散射体模型点(0,2.28 km)不同迭代次数的上(a)、下(b)行聚焦函数 左、中、右的迭代次数分别为1、3、5。 |

|
图 5 散射体模型点(0,2.28 km)不同迭代次数的上(a)、下(b)行格林函数 左、中、右的迭代次数分别为1、3、5。 |
|
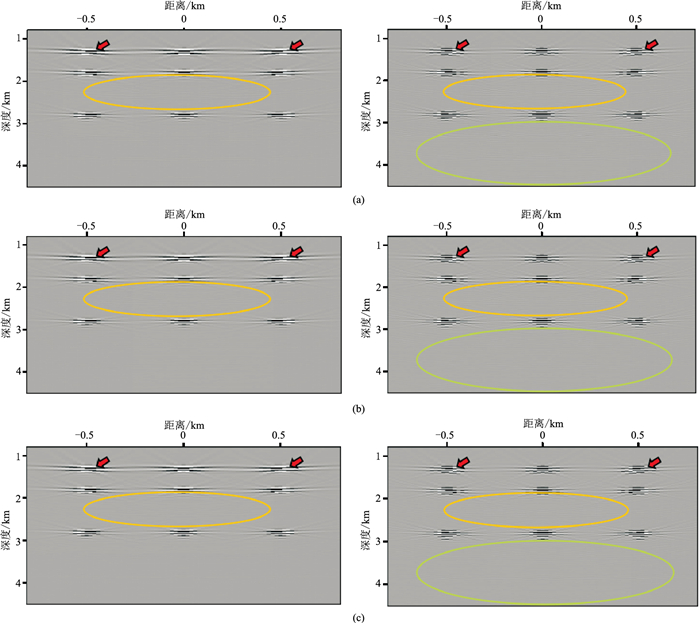
图 6 散射体模型不同迭代次数常规互相关成像条件(左)与保幅逆散射成像条件(右)的局部成像结果对比 (a)1次;(b)3次;(c)5次 |
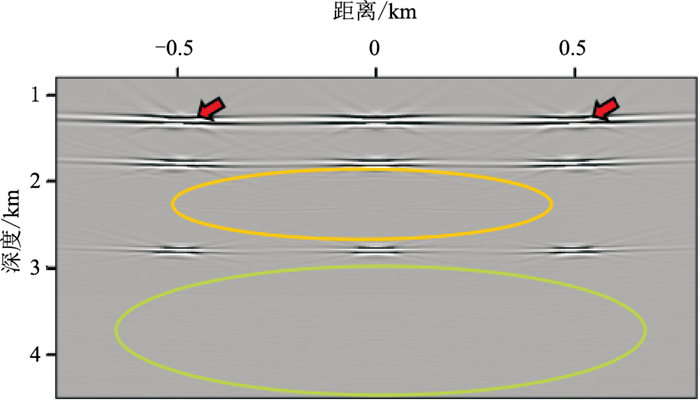
对散射点模型共进行5次迭代,应用常规互相关成像条件(式(10))和本文保幅逆散射成像条件(式(11))的偏移结果如图 6所示(为更清楚地展示成像效果,仅截取图 2中红框范围显示)。对比图 6左与图 6右可见,保幅逆散射成像条件相较于常规互相关成像条件的偏移结果的能量更聚焦(红色箭头所指)。由于保幅逆散射成像条件对深部能量进行了补偿,相较于图 6 a左,图 6 a右的橙色椭圆范围内多次波假象更强;随着迭代次数的增加,二者都能有效压制多次波,与第1次迭代相比,第3次迭代明显压制了深层的假象(图 6 a右、图 6 b右绿色椭圆内);第5次迭代(图 6 c)相较于第3次迭代(图 6 b),橙色椭圆内假象得到进一步压制,成像质量更高。由图 7不难看出,基于单次散射的RTM结果中多次波假象明显(橙色和绿色椭圆内),且散射点之间干扰严重,浅层不够聚焦,成像效果明显不如全波场偏移。
|
图 7 散射体模型的RTM成像结果 |
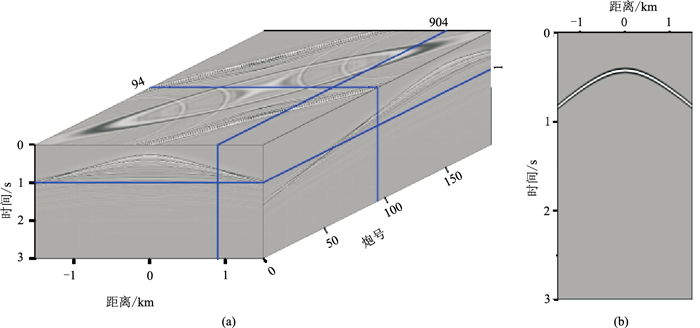
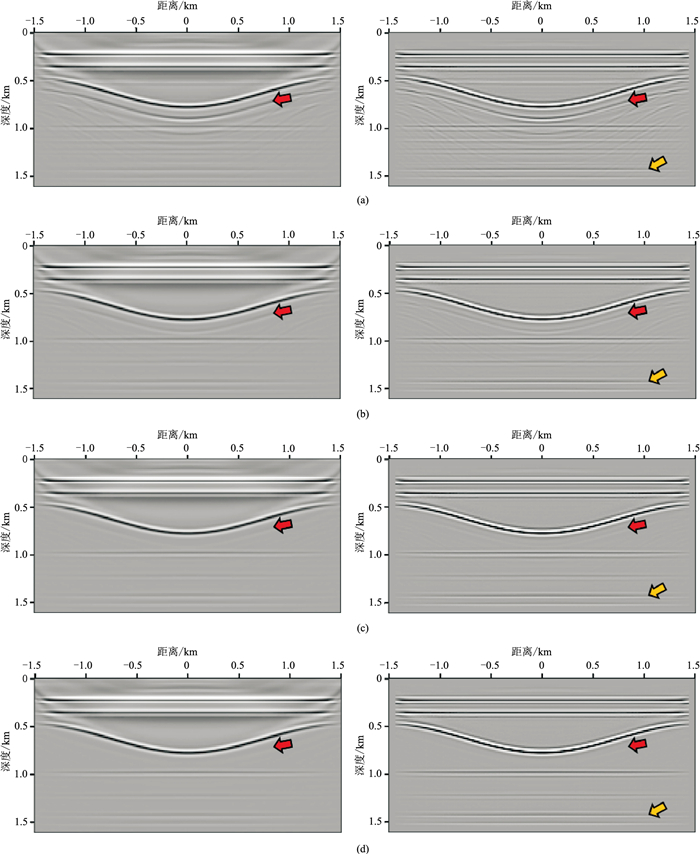
选用全波场成像研究领域典型的凹陷模型[23, 26](图 8 a)测试保幅逆散射成像条件对于复杂构造的适应性。模型密度范围为1000~5000 kg/m3,与速度呈线性变化,当速度为1.5 km/s时密度为1000 kg/m3,速度每增加0.1 km/s,密度增大400 kg/m3。模型网格点数为375×201,网格尺寸为8 m,共模拟188炮,每炮188道,间距为16 m。图中红点标注为一成像点。图 8 b为平滑速度场,用于计算直达波。采用与散射体模型相同的方法模拟炮记录(图 9 a)和成像点到达地表的直达波(图 9 b)。应用全波场方法迭代求解上下行聚焦函数、上下行格林函数,其第1、5、10、20次迭代结果如图 10所示。由图 10 a、图 10 b可见,随着迭代次数的增多,聚焦函数逐渐收敛,干扰逐渐减弱(红色箭头所示),能量更加聚焦(橙色箭头所示)。格林函数在第20次迭代时主轴能量更加聚焦(图 10 c、图 10 d橙色箭头所示),干扰能量更弱(图 10c、图 10 d红色箭头所示)。图 11是不同成像条件全波场偏移结果。对比左、右图可以看出,对于凹陷模型,常规成像条件的结果中假象更明显(红色箭头所示),保幅逆散射成像条件压制了多次波假象(红色箭头所示);同等的迭代次数下保幅逆散射成像结果中界面的能量更强;保幅逆散射成像条件的结果在浅层低频干扰少、界面更清晰;保幅逆散射成像条件对于深层能量进行了补偿,深层界面也更清晰(橙色箭头所示)。相较于RTM成像结果(图 12),全波场成像方法较彻底地压制了多次波假象(红色箭头处),干扰更少,深层界面更清晰,成像效果更好。

|
图 8 真实(a)和平滑(b)凹陷速度模型 |
|
图 9 凹陷模型检波点记录全波场偏移的输入 (a)全接收反射响应;(b)图 8a红点到地表接收阵列的直达波 |

|
图 10 图 8红点不同迭代次数的上(a)、下(b)行聚焦函数及上(c)、下(d)行格林函数 从左往右迭代次数依次为1、5、10、20。 |
|
图 11 凹陷模型不同迭代次数常规互相关成像条件(左)与保幅逆散射成像条件(右)的偏移结果对比 (a)1次;(b)5次;(c)10次;(d)20次 |

|
图 12 凹陷模型RTM成像结果 |
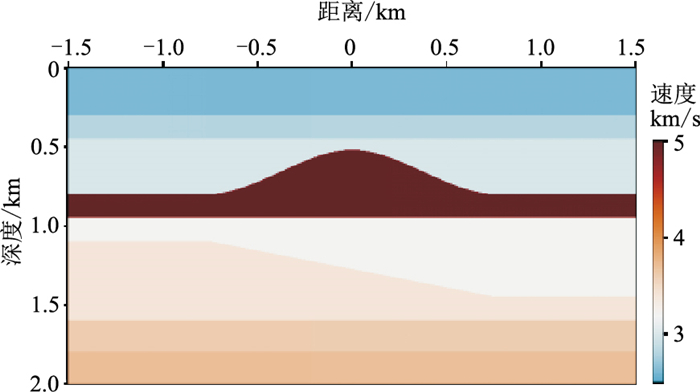
为进一步证明保幅逆散射成像条件的对于复杂构造的有效性,建立有盐丘速度畸变和大倾角界面的模型(图 13)。模型网格数为601
|
图 13 盐丘速度模型 |
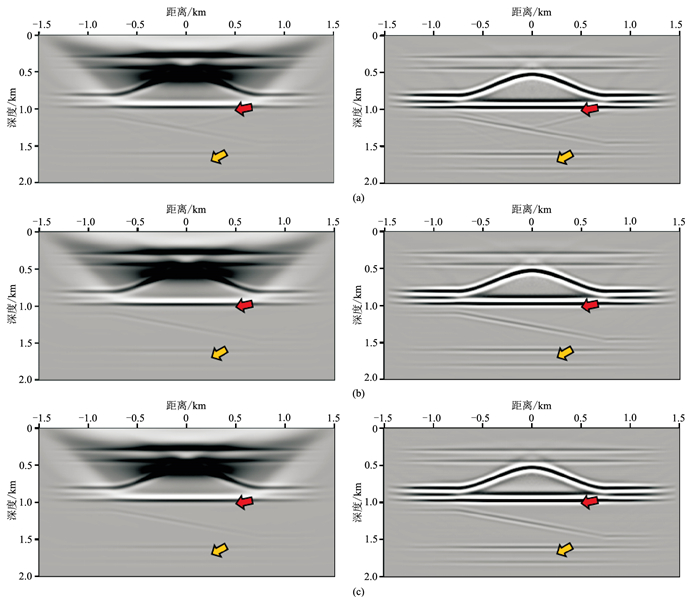
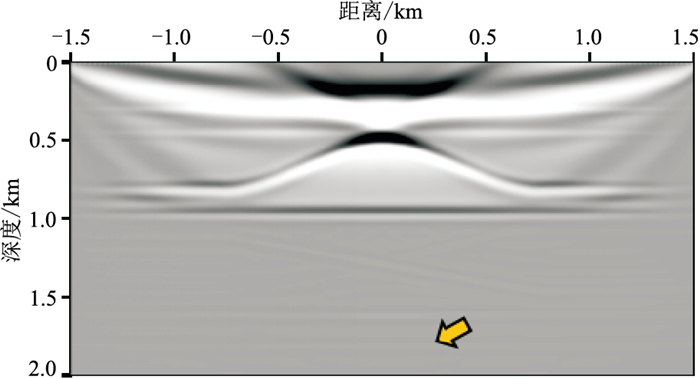
求解格林函数时,分别进行1、3、5次迭代,常规互相关成像条件及改进后的成像条件的成像结果如图 14所示。可以看出,倾斜层和盐丘构造界面成像清晰,说明全波场偏移对于该模型具有良好的适用性。对比左、右图可见,保幅逆散射成像条件能够消除盐丘高速体对深层界面的屏蔽作用,去除浅层低频干扰,补偿深部能量,改善深部成像效果(橙色箭头所示)。第1次迭代时,保幅逆散射成像条件的多次波假象相较于常规互相关成像条件更为明显(图 14a);但随着迭代次数的增加,多次波假象逐渐被压制(图 14b~图 14d红色箭头所示)。盐丘模型的常规RTM成像结果(图 15) 与全波场偏移(图 14c)相比,浅层干扰严重,深部层受盐丘高速体影响成像效果差(黄色箭头所示)。
|
图 14 盐丘模型常规互相关成像条件(左)与保幅逆散射成像条件(右)不同迭代次数全波场偏移结果对比 (a)1次;(b)3次;(c)5次 |
|
图 15 盐丘模型RTM成像结果 |
本文基于逆散射成像理论,对现有全波场偏移的成像条件进行了改进。改进后的保幅逆散射成像条件对于复杂构造具有更高的成像精度和更强的适应性,实现了复杂构造高精度地震成像。模型测试结果验证了方法的可行性、有效性以及对复杂模型适用性。
(1) 基于多次散射的全波场偏移成像方法相较于基于单次散射的常规偏移方法,比较彻底地压制了多次波假象,低频干扰更少,极大地提高了浅层成像精度,改善了深部成像效果。
(2) 保幅逆散射成像条件相较于常规互相关成像条件,对于简单模型,能量更聚焦,对于复杂模型,能够在保证浅层准确成像的基础上,更彻底地压制深层多次波假象,并补偿了深部界面的成像能量。
需要指出的是,本文提出的成像条件是对于全波场偏移常规互相关成像条件的基本改进,具有一定的理论研究价值。但对于模型边界的处理以及考虑实际资料应用的复杂性,基于保幅逆散射的全波场偏移方法的实用性还需要进一步研究。
| [1] |
SCHNEIDER W A. Integral formulation for migration in two and three dimensions[J]. Geophysics, 1978, 43(1): 49-76. DOI:10.1190/1.1440828 |
| [2] |
KUO J T, DAI T F. Kirchhoff elastic wave migration for the case of noncoincident source and receiver-reply[J]. Geophysics, 1984, 49(8): 1223-1238. DOI:10.1190/1.1441751 |
| [3] |
BAYSAL E, KOSLOFF D D, SHERWOOD J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [4] |
CHANG W F, MCMECHAN G A. Reverse-time migration of offset vertical seismic profiling data using the excitation‑time imaging condition[J]. Geophysics, 1986, 51(1): 67-84. DOI:10.1190/1.1442041 |
| [5] |
SAVA P, HILL S J. Overview and classification of wavefield seismic imaging methods[J]. The Leading Edge, 2009, 28(2): 170-183. DOI:10.1190/1.3086052 |
| [6] |
Berkhout A J. Migration of multiple reflections[C]. SEG Technical Program Expanded Abstracts, 1993, 12: 1022-1025.
|
| [7] |
GUITTON A. Shot-profile migration of multiple reflections[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 1296-1299.
|
| [8] |
VERSCHUUR D J, BERKHOUT A J. Seismic data analysis in the forward and inverse data space[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 3536-3540.
|
| [9] |
BROGGINI F, SNIEDER R, WAPENAAR K. Focusing the wavefield inside an unknown 1D medium: Beyond seismic interferometry[J]. Geophysics, 2012, 77(5): A25-A28. DOI:10.1190/geo2012-0060.1 |
| [10] |
靳中原. 多源地震波场重构与Marchenko成像研究[D]. 吉林长春: 吉林大学, 2018.
|
| [11] |
MARCHENKO V A. On reconstruction of the potential energy from phases of the scattered waves[J]. Doklady Akademii Nauk SSSR, 1955, 104(5): 695-698. |
| [12] |
BERKHOUT A J. Seimic Migration: Imaging of Acoustic Energy by Wavefield Extrapolation, Part A: Theoretical Aspects[M]. 2nd Edition. Amsterdam: Elsevier, 1982.
|
| [13] |
BERKHOUT A J. Combining full wavefield migration and full waveform inversion[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 3321-3325.
|
| [14] |
WONG M, BIONDI B, RONEN S. Imaging with multiples using least-squares reverse time migration[J]. The Leading Edge, 2014, 33(9): 970-972, 974, 976. DOI:10.1190/tle33090970.1 |
| [15] |
BROGGINI F, SNIEDER R. Connection of scattering principles: A visual and mathematical tour[J]. European Journal of Physics, 2012, 33(3): 593-613. DOI:10.1088/0143-0807/33/3/593 |
| [16] |
BERKHOUT A J. Combining full wavefield migration and full waveform inversion, a glance into the future of seismic imaging[J]. Geophysics, 2012, 77(2): S43-S50. DOI:10.1190/geo2011-0148.1 |
| [17] |
BERKHOUT A J. Review paper: An outlook on the future of seismic imaging, Part Ⅱ: Full-wavefield migration[J]. Geophysical Prospecting, 2014, 62(5): 931-949. DOI:10.1111/1365-2478.12154 |
| [18] |
WAPENAAR K, BROGGINI F, SLOB E, et al. Three-dimensional single-sided Marchenko inverse scattering, data-driven focusing, Greens function retrieval, and their mutual relations[J]. Physical Review Letters, 2013, 110(8): 084301. DOI:10.1103/PhysRevLett.110.084301 |
| [19] |
WAPENAAR K, THORBECKE J, VAN DER NEUT J, et al. Marchenko imaging[J]. Geophysics, 2014, 79(3): WA39-WA57. DOI:10.1190/geo2013-0302.1 |
| [20] |
WAPENAAR K. Single-sided Marchenko focusing of compressional and shear waves[J]. Physical Review E, 2014, 90(6): 063202. DOI:10.1103/PhysRevE.90.063202 |
| [21] |
WAPENAAR K, SLOB E. On the Marchenko equation for multicomponent single-sided reflection data[J]. Geophysical Journal International, 2014, 199(3): 1367-1371. DOI:10.1093/gji/ggu313 |
| [22] |
SINGH S, SNIEDER R, BEHURA J, et al. Marchenko imaging: Imaging with primaries, internal multiples, and free‑surface multiples[J]. Geophysics, 2015, 80(5): S165-S174. DOI:10.1190/geo2014-0494.1 |
| [23] |
SINGH S, SNIEDER R, VAN DER NEUT J, et al. Accounting for free-surface multiples in Marchenko imaging[J]. Geophysics, 2017, 82(1): R19-R30. DOI:10.1190/geo2015-0646.1 |
| [24] |
VERSCHUUR D J, BERKHOUT A J. From removing to using multiples in closed-loop imaging[J]. The Leading Edge, 2015, 34(7): 744-759. DOI:10.1190/tle34070744.1 |
| [25] |
王通, 王德利, 王睿, 等. 基于被动源数据的包含多次波的全波场偏移成像方法研究[C]. 2016中国地球科学联合学术年会论文集(二十三)——专题46: 地震波传播与成像, 北京, 2016.
|
| [26] |
王通. 稀疏约束反演多次波压制及偏移成像方法研究[D]. 吉林长春: 吉林大学, 2017.
|
| [27] |
秦宁, 王常波, 梁鸿贤, 等. 一次波和层间多次波联合成像方法[J]. 石油地球物理勘探, 2022, 57(6): 1375-1383. QIN Nin, WANG Changbo, LIANG Hongxian, et al. Joint imaging method of primaries and internal multiples[J]. Oil Geophysical Prospecting, 2022, 57(6): 1375-1383. DOI:10.13810/j.cnki.issn.1000-7210.2022.06.012 |
| [28] |
RAVASI M, VASCONCELOS I, KRITSKI A, et al. Target-oriented Marchenko imaging of a North Sea field[J]. Geophysical Journal International, 2016, 205(1): 99-104. DOI:10.1093/gji/ggv528 |
| [29] |
JIA X, GUITTON A, SNIEDER R. A practical implementation of subsalt Marchenko imaging with a Gulf of Mexico data set[J]. Geophysics, 2018, 83(5): S409-S419. DOI:10.1190/geo2017-0646.1 |
| [30] |
WAPENAAR K, BRACKENHOFF J, THORBECKE J, et al. Virtual acoustics in inhomogeneous media with single-sided access[J]. Scientific Reports, 2018, 8(1): 2497. DOI:10.1038/s41598-018-20924-x |
| [31] |
胡自多, 雍学善, 刘威, 等. 地震散射偏移方法[J]. 石油地球物理勘探, 2020, 55(3): 584-590. HU Ziduo, YONG Xueshan, LIU Wei, et al. Seismic scatterring data migration based on scattering wave equation[J]. Oil Geophysical Prospecting, 2020, 55(3): 584-590. DOI:10.13810/j.cnki.issn.1000-7210.2020.03.013 |
| [32] |
姜晓宇, 宋涛, 甘利灯, 等. 散射成像在小尺度缝洞体识别中的应用——以川中古隆起灯影组为例[J]. 石油地球物理勘探, 2022, 57(1): 206-211. JIANG Xiaoyu, SONG Tao, GAN Lideng, et al. Application of scattering imaging in small‑scale fracture cavity recognition: A case study of Dengying Formation in central Sichuan paleo-uplift[J]. Oil Geophysical Prospecting, 2022, 57(1): 206-211. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.022 |
| [33] |
张羽茹, 张志军, 李尧, 等. 叠前散射波形态滤波分离方法[J]. 石油地球物理勘探, 2023, 58(1): 114-120. ZHANG Yuru, ZHANG Zhijun, LI Yao, et al. Pre-stack scattered wave separation method based on morphological filtering[J]. Oil Geophysical Prospecting, 2023, 58(1): 114-120. DOI:10.13810/j.cnki.issn.1000-7210.2023.01.012 |
| [34] |
DA COSTA FILHO C A, RAVASI M, CURTIS A, et al. Elastodynamic Green's function retrieval through single-sided Marchenko inverse scattering[J]. Physical Review E, 2014, 90(6): 063201. DOI:10.1103/PhysRevE.90.063201 |
| [35] |
DA COSTA FILHO C A, RAVASI M, CURTIS A. Elastic P-and S-wave autofocus imaging with primaries and internal multiples[J]. Geophysics, 2015, 80(5): S187-S202. DOI:10.1190/geo2014-0512.1 |
| [36] |
薛东川. 几种叠前逆时偏移成像条件的比较[J]. 石油地球物理勘探, 2013, 48(2): 222-227. XUE Dongchuan. Imaging condition comparison of prestack reverse‑time migration[J]. Oil Geophysical Prospecting, 2013, 48(2): 222-227. |
| [37] |
LOMAS A, CURTIS A. An introduction to Marchenko methods for imaging[J]. Geophysics, 2019, 84(2): F35-F45. DOI:10.1190/geo2018-0068.1 |
| [38] |
韩冬, 李博, 许璐, 等. 基于改进多维反褶积的Marchenko成像方法[C]. SPG/SEG南京2020年国际地球物理会议论文集(中文), 江苏南京, 2020, 403-406.
|
| [39] |
DE PAULA R, REVELO D E, PESTANA R C, et al. Marchenko redatuming and imaging by multidimensional deconvolution(MDD)[C]. Extended Abstracts of 83rd EAGE Annual Conference & Exhibition, 2022, 1-5.
|
| [40] |
VAN DER NEUT J, WAPENAAR K, THOR BECKE J, et al. Practical challenges in adaptive Marchenko imaging[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 4505-4509.
|
| [41] |
顾智炜. 基于聚焦源的地震复杂构造多次波去除方法研究[D]. 浙江杭州: 浙江大学, 2021.
|
| [42] |
THORBECKE J, SLOB E, BRACKENHOFF J, et al. Implementation of the Marchenko method[J]. Geophysics, 2017, 82(6): WB29-WB45. DOI:10.1190/geo2017-0108.1 |



 杨继东,山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
杨继东,山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: