0 引言

地震正演模拟通过分析地震波在地球介质中的传播过程，研究地震波的传播特性与地球介质参数的关系，从而最优逼近实际观测地震记录^[1]。地震正演模拟对人们正确认识地震波的传播规律具有重要的理论和实际意义^[2-4]。

波动方程是地震正演模拟的基础。由于在各向异性介质中qP波和qSV波是耦合在一起传播的，因此人们研究了各向异性介质qP波解耦波动方程，如声学近似及其改进方法^[5-7]、近似配方法等^[8-9]。Alkhalifah^[5-6]提出了声学假设近似，即令沿TI介质对称轴的qSV波速度近似为0，建立了相应的qP波波动方程并进行了数值模拟，但存在两个不足：一是方程中存在退化的qSV波解，不是纯qP波波动方程；二是方程不适用于ε < δ（ε和δ为Thomsen参数^[10]，ε是度量qP波各向异性强度的参数，δ是连接qP波相速度和qSV波相速度的过渡性参数）的介质；随后人们改进了该方程。Fowler等^[11]对比和分析了基于声学假设近似的qP波波动方程，提出了适合于ε < δ介质的qP波波动方程。Chu等^[12]令${V}_{\mathrm{S}0}^{2}=\frac{4}{3}{V}_{\mathrm{P}0}^{2}\left|\varepsilon -\delta \right|$（${V}_{\mathrm{P}0}$和${V}_{\mathrm{S}0}$分别为qP波和qSV波沿VTI介质对称轴（$z$轴）方向的相速度^[10]）改进声学近似，推导了TTI介质纯qP波波动方程。Duveneck等^[13]和Zhang等^[14]从虎克定律出发，分别提出了基于声学近似的TTI介质稳定qP波波动方程，并用于逆时偏移。Cheng等^[15-16]利用偏振方向投影方法推导了各向异性介质纯qP和qSV波波动方程。郭成锋等^[17]利用改进的TTI介质纯P波波动方程进行正演模拟与逆时偏移。Xu等^[18]利用标量算子S实现了基于声学近似的纯qP波波动方程正演模拟；杨鹏等^[19]在此基础上利用改进的椭圆差分算子进行TI介质qP波正演模拟和逆时偏移；胡书华等^[20]进一步提出了TTI介质稳定的纯qP波波场模拟方法。张庆朝等^[21]研究了对称轴任意空间取向TI介质qP和qSV波解耦的波动方程。徐世刚等^[22]推导了一种简化的三维TTI介质黏滞纯声波波动方程。Xu等^[23]和Stovas等^[24]在研究TI介质qP波相速度、慢度和程函方程时提出了一种改进的声学近似方法，该方法适用于ε < δ的VTI介质；Liang等^[25]利用这种改进声学近似方法建立了qP波频散关系，结合标量算子推导了VTI介质改进声学近似纯qP波二阶波动方程，并进行规则网格高阶有限差分模拟，表明该方程在ε≥δ、ε < δ的VTI介质中都是稳定的。Shan等^[26]推导了基于改进声学近似的HTI介质纯qP波波动方程并进行了数值模拟。

本文基于改进的声学近似^[23-26]，结合椭圆分解^[19-20]，建立了纯qP波解耦频散关系，利用改进声学近似和椭圆分解的标量算子S_ia推导了VTI介质改进声学近似纯qP波一阶速度—应力波动方程，然后采用交错网格有限差分算法进行数值模拟，最后分析了精确和近似频散关系的精度。

1 改进声学近似qP波一阶速度—应力波动方程

将平面波解代入VTI介质弹性波波动方程并忽略体力项，得到VTI介质的Christoffel方程。该方程要有非零解，其系数矩阵行列式必须为零。通过求解分别得到qP波和qSV波的精确频散关系^[25]

${\omega }_{\mathrm{P}}^{2}=\frac{1}{2}\left\{{V}_{\mathrm{P}0}^{2}\left[(1+2\varepsilon ){k}_{x}^{2}+{k}_{z}^{2}\right]+\\{V}_{\mathrm{S}0}^{2}({k}_{x}^{2}+{k}_{z}^{2})+\sqrt{D}\right\}$

(1)

${\omega }_{\mathrm{S}\mathrm{V}}^{2}=\frac{1}{2}\left\{{V}_{\mathrm{P}0}^{2}\left[(1+2\varepsilon ){k}_{x}^{2}+{k}_{z}^{2}\right]+\\{V}_{\mathrm{S}0}^{2}({k}_{x}^{2}+{k}_{z}^{2})-\sqrt{D}\right\}$

(2)

其中

$\begin{array}{l}D={\left\{{V}_{\mathrm{P}0}^{2}\left[\right(1+2\varepsilon ){k}_{x}^{2}-{k}_{z}^{2}]-{V}_{\mathrm{S}0}^{2}({k}_{x}^{2}-{k}_{z}^{2})\right\}}^{2}+\\ 4({V}_{\mathrm{P}0}^{2}-{V}_{\mathrm{S}0}^{2})\left[\right(1+2\delta ){V}_{\mathrm{P}0}^{2}-{V}_{\mathrm{S}0}^{2}]{k}_{x}^{2}{k}_{z}^{2}\end{array}$

(3)

式中：ω_P、ω_SV分别为qP波、qSV波的圆频率；${k}_{x}=k\mathrm{s}\mathrm{i}\mathrm{n}\theta$、${k}_{z}=k\mathrm{c}\mathrm{o}\mathrm{s}\theta$分别为波矢量$\boldsymbol{k}={k}_{x}{\boldsymbol{e}}_{x}+{k}_{z}{\boldsymbol{e}}_{z}$沿$x$、$z$方向的波数，e_x、e_z分别为$x$、$z$方向的单位失量，$k$为$\boldsymbol{k}$的模，$\theta$为$\boldsymbol{k}$与$z$轴的夹角。

式（1）、式（2）含有根号运算，形式较复杂，难以直接转换为时—空域波动方程。Alkhalifah^[5-6]在研究VTI介质qP波相速度、动校正和波动方程时提出了著名的声学假设近似，即令${V}_{\mathrm{S}0}=0$，从而得到qP波的近似相速度和频散关系方程。Xu等^[23]和Stovas等^[24]在研究VTI介质qP波相速度、慢度和程函方程时，提出了一种改进的声学近似方法，其思想不是令${V}_{\mathrm{S}0}=0$，而是令qSV波沿各个方向的相速度${V}_{\mathrm{S}}$=0。Liang等^[25]和Shan等^[26]利用该思想建立了基于改进声学近似的VTI介质和HTI介质纯qP波二阶波动方程。本文在Liang等^[25]的基础上，将这种改进声学近似方法的思想引入qP波频散关系和一阶波动方程推导。令各个方向的ω_SV为0，即

${\omega }_{\mathrm{S}\mathrm{V}}^{2}=\frac{1}{2}\left\{{V}_{\mathrm{P}0}^{2}\left[(1+2\varepsilon ){k}_{x}^{2}+{k}_{z}^{2}\right]+\\{V}_{\mathrm{S}0}^{2}({k}_{x}^{2}+{k}_{z}^{2})-\sqrt{D}\right\}=0$

(4)

求解式（4），可得

${V}_{\mathrm{S}0}^{2}=\frac{-2(\varepsilon -\delta ){V}_{\mathrm{P}0}^{2}{k}_{x}^{2}{k}_{z}^{2}}{(1+2\varepsilon ){k}_{x}^{4}+{k}_{z}^{4}+2(1+\delta ){k}_{x}^{2}{k}_{z}^{2}}$

(5)

在声学近似中，${V}_{\mathrm{S}0}$≡0；由上式可知，在改进声学近似中，${V}_{\mathrm{S}0}$不再是常数，而是$\theta$和$\varepsilon , \delta$的函数。将式（5）代入式（1），可得基于改进声学近似的qP波频散关系

${\omega }_{\mathrm{P}\mathrm{i}\mathrm{a}}^{2}={V}_{\mathrm{P}0}^{2}\left[(1+2\varepsilon ){k}_{x}^{2}+{k}_{z}^{2}\right](1+{S}_{\mathrm{i}\mathrm{a}})$

(6)

式中${S}_{\mathrm{i}\mathrm{a}}$是基于改进声学近似和椭圆分解的标量算子，其表达式为

${S}_{\mathrm{i}\mathrm{a}}=\frac{-2(\varepsilon -\delta ){k}_{x}^{2}{k}_{z}^{2}({k}_{x}^{2}+{k}_{z}^{2})}{\left[(1+2\varepsilon ){k}_{x}^{2}+{k}_{z}^{2}\right]\left[(1+2\varepsilon ){k}_{x}^{4}+{k}_{z}^{4}+2(1+\delta ){k}_{x}^{2}{k}_{z}^{2}\right]}$

(7)

令平面波的传播方向单位失量为$\boldsymbol{n}=({n}_{x}, {n}_{z})$=$\left({k}_{x}/k, {k}_{z}/k\right)$，则

${S}_{\mathrm{i}\mathrm{a}}=\frac{-2(\varepsilon -\delta )\left({n}_{x}^{2}+{n}_{z}^{2}\right)}{\left[(1+2\varepsilon ){n}_{x}^{2}+{n}_{z}^{2}\right]\left[(1+2\varepsilon ){n}_{x}^{4}+{n}_{z}^{4}+2(1+\delta ){n}_{x}^{2}{n}_{z}^{2}\right]}$

(8)

由于传播方向在空间域的渐近项^[18]为$\boldsymbol{n}\approx \nabla P/\left|\nabla P\right|=\left(\frac{\partial P}{\partial x}{\boldsymbol{e}}_{x}+\frac{\partial P}{\partial z}{\boldsymbol{e}}_{z}\right)/\left|\frac{\partial P}{\partial x}{\boldsymbol{e}}_{x}+\frac{\partial P}{\partial z}{\boldsymbol{e}}_{z}\right|$，则

${S}_{\mathrm{i}\mathrm{a}}\approx \frac{-2(\varepsilon -\delta ){\left(\frac{\partial P}{\partial x}\right)}^{2}{\left(\frac{\partial P}{\partial z}\right)}^{2}\left[{\left(\frac{\partial P}{\partial x}\right)}^{2}+{\left(\frac{\partial P}{\partial z}\right)}^{2}\right]}{\left[(1+2\varepsilon ){\left(\frac{\partial P}{\partial x}\right)}^{2}+{\left(\frac{\partial P}{\partial z}\right)}^{2}\right]\left[(1+2\varepsilon ){\left(\frac{\partial P}{\partial x}\right)}^{4}+{\left(\frac{\partial P}{\partial z}\right)}^{4}+2(1+\delta ){\left(\frac{\partial P}{\partial x}\right)}^{2}{\left(\frac{\partial P}{\partial z}\right)}^{2}\right]}$

(9)

式中P为qP波波场。将式（9）代入式（6），再乘以qP波频率—波数域波场$\tilde{P}({k}_{x}, {k}_{z}, \omega )$并进行傅里叶反变换，得到基于改进声学近似的qP波时间—空间域波动方程

$\frac{{\partial }^{2}P}{\partial {t}^{2}}={V}_{\mathrm{P}0}^{2}(1+2\varepsilon )(1+{S}_{\mathrm{i}\mathrm{a}})\frac{{\partial }^{2}P}{\partial {x}^{2}}+{V}_{\mathrm{P}0}^{2}(1+{S}_{\mathrm{i}\mathrm{a}})\frac{{\partial }^{2}P}{\partial {z}^{2}}$

(10)

为了方便数值模拟，将上式转换为一阶方程，得到VTI介质改进声学近似qP波速度—应力波动方程

$\left\{\begin{array}{l}\frac{\partial P}{\partial t}=\rho {V}_{\mathrm{P}0}^{2}\frac{\partial U}{\partial x}+\rho {V}_{\mathrm{P}0}^{2}\frac{\partial W}{\partial z}\\ \frac{\partial U}{\partial t}=\frac{1}{\rho }(1+2\varepsilon )(1+{S}_{\mathrm{i}\mathrm{a}})\frac{\partial P}{\partial x}\\ \frac{\partial W}{\partial t}=\frac{1}{\rho }(1+{S}_{\mathrm{i}\mathrm{a}})\frac{\partial P}{\partial z}\end{array}\right.$

(11)

式中：t为时间；ρ为密度；U、W分别为x、z方向的速度分量。

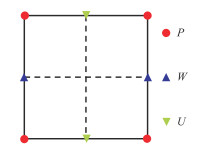
2 VTI介质改进声学近似qP波速度—应力波动方程交错网格差分算法

针对式（11），采用交错网格对计算域离散化，将P定义在主网格点，将U、W定义在交错网格点（图 1）。令$x$和$z$方向的网格间距分别为$\mathrm{\Delta }x$和$\mathrm{\Delta }z$，对于空间一阶偏导数$\partial /\partial x$和$\partial /\partial z$，其空间$2N$阶差分格式分别为

$\left\{\begin{array}{l}{D}_{x}^{+}P=\frac{1}{\mathrm{\Delta }x}\sum\limits_{n=1}^{N}{c}_{n}({P}_{i+n, j}^{l}-{P}_{i-n+1, j}^{l})\\ {D}_{z}^{+}P=\frac{1}{\mathrm{\Delta }z}\sum\limits_{n=1}^{N}{c}_{n}({P}_{i, j+n}^{l}-{P}_{i, j-n+1}^{l})\\ {D}_{x}^{\mathrm{c}}P=\frac{1}{\mathrm{\Delta }x}\sum\limits_{n=1}^{N}{c}_{n}^{\mathrm{c}}({P}_{i+n, j}^{l}-{P}_{i-n, j}^{l})\\ {D}_{z}^{\mathrm{c}}P=\frac{1}{\mathrm{\Delta }z}\sum\limits_{n=1}^{N}{c}_{n}^{\mathrm{c}}({P}_{i, j+n}^{l}-{P}_{i, j-n}^{l})\\ {D}_{x}^{-}U=\frac{1}{\mathrm{\Delta }x}\sum\limits_{n=1}^{N}{c}_{n}({U}_{i-\frac{1}{2}+n, j}^{l+\frac{1}{2}}-{U}_{i+\frac{1}{2}-n, j}^{l+\frac{1}{2}})\\ {D}_{z}^{-}W=\frac{1}{\mathrm{\Delta }z}\sum\limits_{n=1}^{N}{c}_{n}({U}_{i, j-\frac{1}{2}+n}^{l+\frac{1}{2}}-{U}_{i, j+\frac{1}{2}-n}^{l+\frac{1}{2}})\end{array}\right.$

(12)

式中：$\mathrm{\Delta }x$、$\mathrm{\Delta }z$分别为$x$、$z$方向的空间采样率；${D}_{x}^{+}, {D}_{x}^{-}, {D}_{x}^{\mathrm{c}}$分别表示沿$x$方向的前向差分、后向差分、中心差分；${D}_{z}^{+}, {D}_{z}^{-}, {D}_{z}^{\mathrm{c}}$分别表示沿$z$方向的前向差分、后向差分、中心差分；${c}_{n}$为前向和后向差分的系数^[27]；${c}_{n}^{\mathrm{c}}$为中心差分系数^[28]；下标$i$、$j$分别为$x$、$z$方向的空间离散坐标，上标$l$表示第$l$个采样时刻。

同理，时间差分为

$\left\{\begin{array}{l}\frac{\partial P}{\partial t}=\frac{1}{\mathrm{\Delta }t}({P}_{i, j}^{l+1}-{P}_{i, j}^{l})\\ \frac{\partial U}{\partial t}=\frac{1}{\mathrm{\Delta }t}({U}_{i+\frac{1}{2}, j}^{l+\frac{1}{2}}-{U}_{i+\frac{1}{2}, j}^{l-\frac{1}{2}})\\ \frac{\partial W}{\partial t}=\frac{1}{\mathrm{\Delta }t}({W}_{i, j+\frac{1}{2}}^{l+\frac{1}{2}}-{W}_{i, j+\frac{1}{2}}^{l-\frac{1}{2}})\end{array}\right.$

(13)

式中$\mathrm{\Delta }t$为时间采样率。将式（12）和式（13）代入式（11），得到VTI介质改进声学近似qP波速度—应力波动方程的差分格式

$\left\{\begin{array}{l}{P}_{i, j}^{l+1}={P}_{i, j}^{l}+\rho {V}_{\mathrm{P}0}^{2}\mathrm{\Delta }t\left({D}_{x}^{-}U\right)+\rho {V}_{\mathrm{P}0}^{2}\mathrm{\Delta }t\left({D}_{z}^{-}W\right)\\ {U}_{i+\frac{1}{2}, j}^{l+\frac{1}{2}}={U}_{i+\frac{1}{2}, j}^{l-\frac{1}{2}}+\frac{1}{\rho }\mathrm{\Delta }t(1+2\varepsilon )(1+{S}_{\mathrm{d}})\left({D}_{x}^{+}P\right)\\ {W}_{i, j+\frac{1}{2}}^{l+\frac{1}{2}}={W}_{i, j+\frac{1}{2}}^{l-\frac{1}{2}}+\frac{1}{\rho }\mathrm{\Delta }t(1+{S}_{\mathrm{d}})\left({D}_{z}^{+}P\right)\end{array}\right.$

(14)

其中${S}_{\mathrm{d}}$为${S}_{\mathrm{i}\mathrm{a}}$的差分形式，即

${S}_{\mathrm{d}}=\frac{-2(\varepsilon -\delta )\left({D}_{x}^{\mathrm{c}}{P)}^{2}\right({D}_{z}^{\mathrm{c}}{P)}^{2}}{(1+2\varepsilon )({D}_{x}^{\mathrm{c}}{P)}^{2}+({D}_{z}^{\mathrm{c}}{P)}^{2}}\times \frac{({D}_{x}^{\mathrm{c}}{P)}^{2}+({D}_{z}^{\mathrm{c}}{P)}^{2}}{(1+2\varepsilon )({D}_{x}^{\mathrm{c}}{P)}^{4}+({D}_{z}^{\mathrm{c}}{P)}^{4}+2(1+\delta )\left({D}_{x}^{\mathrm{c}}{P)}^{2}\right({D}_{z}^{\mathrm{c}}{P)}^{2}}$

(15)

3 数值示例 3.1 频散关系分析

为了验证式（11）的效果，分析式（6）的精度。设计了三个VTI介质模型（模型A~模型C），${V}_{\mathrm{P}0}=3000\;\mathrm{m}/\mathrm{s}$，${V}_{\mathrm{S}0}=1500\;\mathrm{m}/\mathrm{s}$，$\varepsilon \mathrm{、}\delta$如表 1所示。

模型A~模型C的频散关系分析结果（图 2~图 4）表明：①模型A的声学近似频散关系^[5]和改进声学近似频散关系（式（6））分析结果（图 2a）的相对误差小于1×10^-15（图 2b），这与计算机字长误差相当，说明这两种近似频散关系在椭圆各向异性介质中与精确频散关系（式（1））是等价的，这与理论分析吻合。②模型B、模型C的两种近似频散关系分析结果与式（1）十分接近（图 3 a、图 4 a），相对误差均小于0.5%（图 3 b、图 4 b），说明这两种近似频散关系的精度均很高。③对于$\varepsilon > \delta$的VTI介质，式（6）的相对误差略大于声学近似（图 3 b）；对于$\varepsilon < \delta$的VTI介质，式（6）的相对误差小于声学近似（图 4 b）。

3.2 正演模拟

根据VTI介质弹性波速度—应力波动方程^[27]、声学近似qP波一阶波动方程^[13]和改进声学近似qP波一阶波动方程（式（11）），利用交错网格有限差分算法对模型A~模型C进行正演模拟。

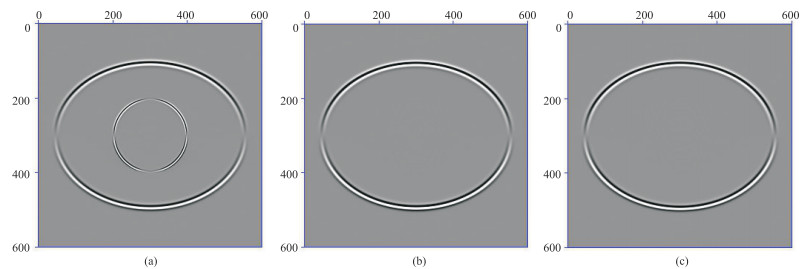
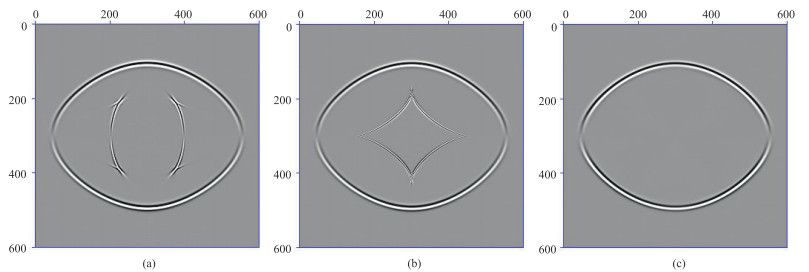
图 5~图 7分别为模型A~模型C的波场快照，图 8为由波场快照提取的x=380处的波形曲线。由图可见：①在模型A中，qP波波前面呈椭圆形，qSV波波前面呈圆形，声学近似（图 5 b、图 8 a）和改进声学近似（图 5 c、图 8 a）的qP波波场特征与弹性波的qP波波场（图 5a、图 8a）基本相同，并且不存在qSV波波场。②在模型B中，声学近似（图 6 b、图 8 b）和改进声学近似（图 6 c、图 8 b）的qP波波场特征与弹性波的qP波波场（图 6 a、图 8 b）吻合较好；图 6 b中存在退化的qSV波波场，说明图 6 b不是纯qP波，图 6c中不存在退化的qSV波波场，说明图 6 c是纯qP波。③在模型C中，声学近似的波场（图 7b、图 8 c）存在数值溢出，无法模拟qP波，改进声学近似（图 7 c、图 8 c）的qP波波场特征与弹性波的qP波波场（图 7 a、图 8 c）吻合较好，不存在退化的qSV波波场。上述模拟结果说明式（11）很好地刻画了纯qP波波场，并且与改进声学近似qP波二阶方程^[25]类似，同样适用于ε≥δ、ε < δ的VTI介质。

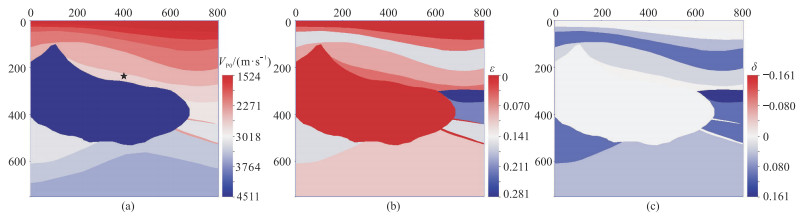
将式（11）应用于Hess模型（图 9）。图 10为Hess模型的波场快照，图 11为由图 10提取的x=450处的波形曲线。由图可见：①声学近似qP波波场（图 10 b、图 11）特征与弹性波的qP波波场（图 10 a、图 11）吻合较好，但是图 10 b中存在退化qSV波（图 10 b中白色箭头和图 11中红色箭头处），从而无法认识qP波的传播规律。②改进声学近似的qP波波场（图 10c、图 11）特征与弹性波的qP波波场（图 10 a、图 11）吻合较好，且不存在退化qSV波，说明式（11）也适用于复杂VTI介质，能够更精确地描述声波在VTI介质中的传播。

4 结束语

本文根据改进声学近似和椭圆分解推导了qP波解耦频散关系，利用标量算子的空间域渐近近似建立了改进声学近似qP波一阶速度—应力波动方程，采用交错网格有限差分算法实现了VTI介质纯qP波正演模拟。理论分析和数值示例表明，基于改进声学近似的qP波一阶速度—应力波动方程不包含退化qSV波，为纯qP波方程。该方程与Liang等^[25]推导的二阶方程性质类似，在$\varepsilon \ge \delta$和$\varepsilon < \delta$的VTI介质中均是稳定的，并且在均匀介质和复杂VTI介质中均能有效地模拟qP波传播规律。