直光纤及螺旋缠绕光纤三维地震响应机制
1. 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
2. 山东能源集团南美有限公司, 山东青岛 266580;
3. 中国石化胜利油田分公司勘探开发研究院, 山东东营 257022
2. 山东能源集团南美有限公司, 山东青岛 266580;
3. 中国石化胜利油田分公司勘探开发研究院, 山东东营 257022
本文于2023年3月31日收到，最终修改稿于同年11月6日收到。
本项研究受国家自然科学基金优秀青年项目（海外）“油气勘探地球物理”（ZX20230152）、山东能源集团深层高温地热重大科技项目“山东省深层高温地热资源形成机制、分布规律研究及地热资源调查评价”（SNKJ2022A06-R23）、中国石油重大科技专项项目“深层复杂高陡构造成像关键技术”（ZD2019-183-003）联合资助。
杨继东, 山东省青岛市黄岛区长江西路66号中国石油大学（华东）地球科学与技术学院，266580。Email：jidong.yang@upc.edu.cn。
摘要：分布式光纤（DAS）测量轴向应变或应变率，其中直光纤接收的是单分量信号，对垂直于光纤入射的波的响应不敏感，螺旋缠绕光纤可接收多分量信号，可以解决上述响应不敏感问题。首先，分析了直光纤及缠绕角分别为35.3°、54.7°的螺旋缠绕光纤的P波、SV及SH波的理论轴向应变率响应；其次，利用三维弹性有限差分模拟了轴向应变率响应；然后，在地表、水平井、竖直井布设DAS，利用均匀模型、双层模型及西南页岩气模型模拟直光纤、缠绕角分别为35.3°、54.7°的螺旋缠绕光纤的地震响应，并将DAS轴向应变率响应与常规检波器的速度z分量、压力分量对比。结果表明：①直光纤接收单分量信息，在垂直于光纤方向接收的波的响应较弱，而螺旋缠绕光纤接收多分量信息，因此在垂直于光纤方向接收的波的响应较强；②缠绕角为35.3°的螺旋缠绕光纤地震记录中无S波响应，其波形与常规检波器压力分量相似，在成像中可以利用声波方程成像。
关键词：直光纤 螺旋缠绕光纤 缠绕角 轴向应变率响应 有限差分模拟
Three-dimensional seismic response mechanism of straight and helically wound optical fibers
1. School of Geosciences, China University of Petroleum (East China), Qingdao, Shandong 266580, China;
2. Shandong Energy Group South America Co., Qingdao, Shandong 266580, China;
3. Research Institute of Exploration and Development, ShengLi Oilfield Company., SINOPEC, Dongying, Shangdong 257022, China
2. Shandong Energy Group South America Co., Qingdao, Shandong 266580, China;
3. Research Institute of Exploration and Development, ShengLi Oilfield Company., SINOPEC, Dongying, Shangdong 257022, China
Abstract: Distributed Acoustic Sensing (DAS) measures axial strain or strain rate, and straight optical fibers receive a single component signal and are insensitive to the response of waves incident perpendicularly to the fiber. Helically wound optical fibers can receive multi-component signals, which can solve the problem of insensitive response. Firstly, the theoretical axial strain rate responses of P-wave, SV, and SH waves of straight optical fibers and helically wound optical fibers with winding angles of 35.3° and 54.7° are analyzed. Secondly, the axial strain rate response is simulated using the three-dimensional elastic finite difference method. Finally, DAS is deployed on the surface, horizontal wells, and vertical wells, and the seismic responses of straight optical fibers and helically wound optical fibers with winding angles of 35.3° and 54.7° are simulated using uniform models, double-layer models, and southwest shale gas models. The axial strain rate response of DAS is compared with the velocity z component and pressure component of conventional detectors. The results show that: ① Straight optical fibers receive single component information, but the response of waves received in the direction perpendicular to the optical fiber is weak, while helically wound optical fibers receive multi-component information, so the response of waves received in the direction perpendicular to the optical fiber is strong; ②there is no S-wave response in the helically wound optical fiber seismic record with a winding angle of 35.3°, and its waveform is similar to the pressure component of a conventional detector. The acoustic equation can be used for imaging.
Keywords:
straight optical fiber helically wound optical fiber winding angle axial strain rate response finite difference modeling
0 引言
1.1.2 螺旋缠绕光纤
1.2 有限差分模拟
2.2 双层模型
2.3 页岩气模型
3 结论
分布式光纤（Distributed Acoustic Sensing，DAS）采集是一种新型的地震采集技术，因具有频带宽、耐高温与高压、成本较低、可长时间监测等特点而广泛用于地震勘探。Mestayer等[1]利用VSP现场测试DAS，测试数据与检波器数据、声波测井数据的对比结果表明，就信噪比和分辨率而言，走时VSP数据的图像几乎与传统钻孔地震检波器的图像等效。Parker等[2]证明DAS采集数据的可重复性良好，在实验室及现场测试了远离光纤定位，并对比了数字光纤分布系统（iDAS）和检波器地面地震接收记录。Daley等[3]现场测试了DAS VSP采集及地表地震采集。李彦鹏等[4]通过分析井中现场地震勘探资料，指出DAS数据与常规检波器的z分量速度资料的一致性很好，并证实固井光缆的耦合性更好。Bakulin等[5]提出了一种使用DAS的新型集成陆地成像系统，该系统可以同时进行陆地近地表表征和地下成像。Molenaar等[6]利用致密气井作业的DAS记录实时监测井内作业，还能捕捉整个水力压裂过程的动态变化。
DAS接收的信号是光纤的轴向应变或应变率，由于直光纤只能接收单分量信息，当波的传播方向垂直于光纤时，光纤对信号不敏感。Hornman等[7]指出螺旋缠绕光纤可接收多分量信息，解决了波的传播方向垂直于直光纤时对波不敏感的问题。Kuvshinov[8]详细介绍了螺旋缠绕光纤的原理、螺旋缠绕光纤与地震波的相互作用以及提高光纤灵敏度的方法。Innanen[9]针对标准螺旋缠绕光纤形状及其2螺旋扩展，分析了张量应变重建中标距长度、重建间隔选取以及P波和S波间的相互作用。Eaid等[10-11]使用一个几何模型设计复杂纤维几何结构，论证了螺旋缠绕光纤对切应变不敏感，且可以忽略，并在此基础上进行全波形反演。
正演模拟可指导DAS实际勘探的观测系统设计、后期数据处理和解释[12-15]。目前，DAS的研究大多是针对实测数据[16-18]。马国旗等[19]基于离散光纤瑞利散射干涉模型，对井中DAS数据进行数值模拟。曹丹平等[20]探讨了不同旋转角度和缠绕角度的三分量振动信号对光纤轴向应变的影响，并对螺旋缠绕光纤接收信号进行数值模拟。郑伋[21]研究了DAS的弹性波场响应特征，并采用两种方式进行数值模拟。姚艺等[22]探讨了不同震源机制的DAS响应特征。Wu[23]使用三维有限差分模拟DAS记录。
1 方法原理 1.1 DAS理论响应 1.1.1 直光纤设地震波的传播方向余弦为
P波速度、SV波速度、SH波速度分别为
| $ \left\{\begin{array}{l}{V}_{x, \mathrm{P}}=\mathrm{i}kcA\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}{O}_{\mathrm{P}\mathrm{S}}\\ {V}_{y, \mathrm{P}}=\mathrm{i}kcA\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}{O}_{\mathrm{P}\mathrm{S}}\\ {V}_{z, \mathrm{P}}=\mathrm{i}kcA\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{2}{O}_{\mathrm{P}\mathrm{S}}\end{array}\right. $ | (1) |
| $ \left\{\begin{array}{l}{V}_{x, \mathrm{S}\mathrm{V}}=-\mathrm{i}kcA\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{2}{O}_{\mathrm{P}\mathrm{S}}\\ {V}_{y, \mathrm{S}\mathrm{V}}=-\mathrm{i}kcA\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{2}{O}_{\mathrm{P}\mathrm{S}}\\ {V}_{z, \mathrm{S}\mathrm{V}}=\mathrm{i}kcA\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}{O}_{\mathrm{P}\mathrm{S}}\end{array}\right. $ | (2) |
| $ \left\{\begin{array}{l}{V}_{x, \mathrm{S}\mathrm{H}}=\mathrm{i}kcA\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}{O}_{\mathrm{P}\mathrm{S}}\\ {V}_{y, \mathrm{S}\mathrm{H}}=-\mathrm{i}kcA\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}{O}_{\mathrm{P}\mathrm{S}}\\ {V}_{z, \mathrm{S}\mathrm{H}}=0\end{array}\right. $ | (3) |
式中：k为波数；c为相速度；A为振幅因子；
将速度对空间坐标求导得到应变率，进而分别得到P波、SV波、SH波的轴向应变率
| $ \begin{array}{l}{\dot{\varepsilon }}_{\theta , \mathrm{P}}={k}^{2}cA(\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{2}+\\ \frac{1}{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{2}-\\ \frac{1}{2}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}+\\ \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\varphi }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{2}-\\ \frac{1}{2}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}+\\ \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\varphi }_{2}){O}_{\mathrm{P}\mathrm{S}}\end{array} $ | (4) |
| $ \begin{array}{l}{\dot{\varepsilon }}_{\theta , \mathrm{S}\mathrm{V}}=\frac{{k}^{2}cA}{2}(-\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}-\\ \frac{1}{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}-\\ \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}2{\varphi }_{2}-\\ \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}-\\ \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}2{\varphi }_{2}+\\ \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}){O}_{\mathrm{P}\mathrm{S}}\end{array} $ | (5) |
| $ \begin{array}{l}{\dot{\varepsilon }}_{\theta , \mathrm{S}\mathrm{H}}=\frac{{k}^{2}cA}{2}(\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}-\\ \mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}2{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}-\\ \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{2}-\\ \mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}+\\ \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{2}){O}_{\mathrm{P}\mathrm{S}}\end{array} $ | (6) |
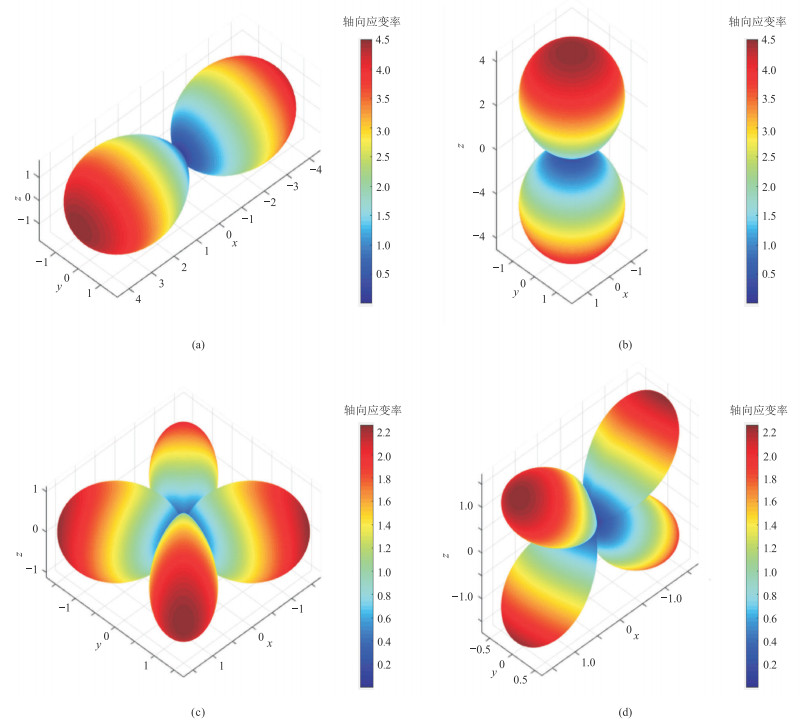
从直光纤轴向应变率响应可以看出，直光纤对垂直于光纤传播的入射波不敏感（图 1）。
|
图 1 直光纤轴向应变率 （a）光纤水平布设的P波响应；（b）光纤竖直布设的P波响应；（c）光纤水平布设的SH波响应；（d）光纤水平布设的SV波响应 |
在螺旋缠绕光纤中，剪切应变在测量长度内的贡献可以忽略不记[10-11]，因此螺旋缠绕光纤的轴向应变率为
| $ {\dot{\varepsilon }}_{\mathrm{T}\mathrm{T}}={A}_{xx}{\dot{\varepsilon }}_{xx}^{'}+{A}_{yy}{\dot{\varepsilon }}_{yy}^{'}+{A}_{zz}{\dot{\varepsilon }}_{zz}^{'} $ | (7) |
其中
| $ {A}_{xx}={{\int }_{-L/2}^{L/2}\left(\boldsymbol{t}\cdot \boldsymbol{i}\right)}^{2}\mathrm{d}{s}^{'} $ |
| $ {A}_{yy}={\left(\boldsymbol{t}\cdot \boldsymbol{j}\right)}^{2}\mathrm{d}{s}^{'} $ |
| $ {A}_{zz}={\left(\boldsymbol{t}\cdot \boldsymbol{k}\right)}^{2}\mathrm{d}{s}^{'} $ |
式中：下角“T”代表光纤的切向；
将速度转换为应变率，再进行坐标旋转得到缠绕角分别为35.3°、54.7°螺旋缠绕光纤的P波、SV波、SH波的轴向应变率
| $ \left\{\begin{array}{l}{\dot{\varepsilon }}_{\theta , \mathrm{P}}^{35.3°}={k}^{2}cA{O}_{\mathrm{P}\mathrm{S}}\\ {\dot{\varepsilon }}_{\theta , \mathrm{S}\mathrm{V}}^{35.3°}=0\\ {\dot{\varepsilon }}_{\theta , \mathrm{S}\mathrm{H}}^{35.3°}=0\end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l}{\dot{\varepsilon }}_{\theta , \mathrm{P}}^{54.7°}={k}^{2}cA(3\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{2}+\\ \frac{3}{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{2}-\\ \frac{3}{2}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}+\\ 3\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\varphi }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{2}-\\ \frac{3}{2}\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}+\\ 3\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\varphi }_{2}+1){O}_{\mathrm{P}\mathrm{S}}\\ {\dot{\varepsilon }}_{\theta , \mathrm{S}\mathrm{V}}^{54.7°}=\frac{{k}^{2}cA}{2}(-3\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}+\\ \frac{3}{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}-\\ 3\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}2{\varphi }_{2}+\\ 3\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}-\\ 3\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}2{\varphi }_{2}+\\ 3\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{2}){O}_{\mathrm{P}\mathrm{S}}\\ {\dot{\varepsilon }}_{\theta , \mathrm{S}\mathrm{H}}^{54.7°}=\frac{{k}^{2}cA}{2}(3\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}-\\ 3\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}2{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}-\\ 3\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{2}-\\ 3\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1}\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}{\theta }_{2}\mathrm{s}\mathrm{i}\mathrm{n}2{\varphi }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{2}+\\ 3\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{1}\mathrm{s}\mathrm{i}\mathrm{n}{\varphi }_{2}){O}_{\mathrm{P}\mathrm{S}}\end{array}\right. $ | (9) |
由式(8)可知，缠绕角为35.3°的螺旋缠绕光纤对S波没有响应，且很好地解决了P波垂直于光纤入射时对波不敏感的问题（图 2）。由式（9）可知，缠绕角为54.7°的螺旋缠绕光纤对垂直于光纤入射的波有响应，且可接收S波（图 3）。
|
图 2 缠绕角为35.3°的螺旋缠绕光纤的P波轴向应变率 |
|
图 3 缠绕角为54.7°的螺旋缠绕光纤轴向应变率 （a）光纤水平布设的P波响应；（b）光纤竖直布设的P波响应；（c）光纤水平布设的SH波响应；（d）光纤水平布设的SV波响应 |
使用三维弹性交错网格有限差分进行模拟。各向同性介质三维弹性波一阶速度—应力方程为
| $ \left\{\begin{array}{l}\rho \frac{\partial {v}_{x}}{\partial t}=\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\\ \rho \frac{\partial {v}_{y}}{\partial t}=\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\\ \rho \frac{\partial {v}_{z}}{\partial t}=\frac{\partial {\sigma }_{xx}}{\partial x}+\frac{\partial {\sigma }_{yy}}{\partial y}+\frac{\partial {\sigma }_{zz}}{\partial z}\\ \frac{\partial {\sigma }_{xx}}{\partial t}=\left(\lambda +2\mu \right)\frac{\partial {v}_{x}}{\partial x}+\lambda \left(\frac{\partial {v}_{y}}{\partial y}+\frac{\partial {v}_{z}}{\partial z}\right)\\ \frac{\partial {\sigma }_{yy}}{\partial t}=\left(\lambda +2\mu \right)\frac{\partial {v}_{x}}{\partial x}+\lambda \left(\frac{\partial {v}_{y}}{\partial y}+\frac{\partial {v}_{z}}{\partial z}\right)\\ \frac{\partial {\sigma }_{zz}}{\partial t}=\left(\lambda +2\mu \right)\frac{\partial {v}_{x}}{\partial x}+\lambda \left(\frac{\partial {v}_{y}}{\partial y}+\frac{\partial {v}_{z}}{\partial z}\right)\\ \frac{\partial {\sigma }_{xy}}{\partial t}=\mu \left(\frac{\partial {v}_{x}}{\partial y}+\frac{\partial {v}_{y}}{\partial x}\right)\\ \frac{\partial {\sigma }_{yz}}{\partial t}=\mu \left(\frac{\partial {v}_{z}}{\partial y}+\frac{\partial {v}_{y}}{\partial z}\right)\\ \frac{\partial {\sigma }_{xz}}{\partial t}=\mu \left(\frac{\partial {v}_{x}}{\partial z}+\frac{\partial {v}_{z}}{\partial x}\right)\end{array}\right. $ | (10) |
式中：ρ为密度；
在交错网格下对式（10）进行差分离散，可以得到各分量的差分格式。后文将常规检波器接收的速度 z分量及压力分量与DAS接收的轴向应变率进行对比。
DAS测量光纤的轴向应变或应变率，本文均采用应变率。将应变—位移方程两边同时对时间求导，可以由速度得到轴向应变率
| $ {\dot{\varepsilon }}_{ij}=\frac{1}{2}\left({v}_{ij}+{v}_{ji}\right)i, j=x, y, z $ | (11) |
然后进行坐标旋转，将光纤轴向转到x轴正方向，得到光纤的轴向应变率
| $ {\dot{\varepsilon }}_{\theta }=\boldsymbol{R}\dot{\varepsilon }{\boldsymbol{R}}^{\mathrm{T}} $ | (12) |
式中：
| $ \boldsymbol{R}=\left(\begin{array}{ccc}cos{\theta }_{2}& sin{\theta }_{2}& 0\\ -sin{\theta }_{2}& cos{\theta }_{2}& 0\\ 0& 0& 1\end{array}\right)\times \left(\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}& 0& -\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}\\ 0& 1& 0\\ \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}& 0& \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\end{array}\right) $ | (13) |
对于直光纤，
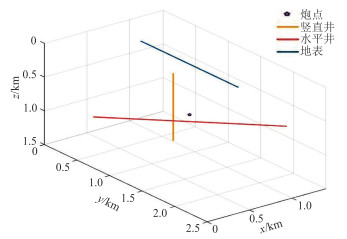
利用均匀模型（图 4）模拟直光纤、缠绕角分别为35.3°、54.7°的螺旋缠绕光纤的轴向应变率及常规检波器的速度z分量、压力分量，光纤分别布设在地表、水平井及竖直井。
|
图 4 均匀模型观测系统 模型尺寸为2500 m×1500 m×1500 m，网格尺寸为5 m×5 m×5 m，纵波速度为3500 m/s，横波速度为2000 m/s，密度为2000 kg/m3，时间采样间隔为0.5 ms。震源为主频20 Hz的雷克子波，位于（1250 m，750 m，750 m）。 |
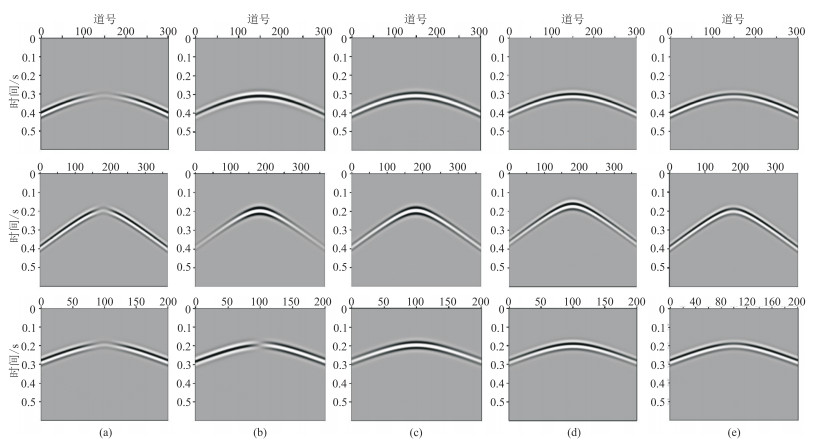
图 5为在地表、水平井及竖直井接收的均匀模型单炮地震记录。由图可见：①在直光纤地震记录中，当入射波垂直于光纤时，振幅非常小，这是由于波的传播方向垂直于直光纤时对波不敏感造成的（图 5a）。②在缠绕角为35.3°（图 5 d）、54.7°（图 5 e）的螺旋缠绕光纤地震记录中，当入射波垂直于光纤时，对振幅的影响较小，这是由于螺旋缠绕光纤可以接收多分量信息所致。③对比图 5 a、图 5 d、图 5 e、常规检波器速度z分量（图 5 b）以及常规检波器压力分量(图 5 c)可知，虽然图 5 a、图 5 d、图 5 e的振幅及相位与图 5 b、图 5 c有一定差别，但在整体上是吻合的。
|
图 5 在地表（上）、水平井（中）及竖直井（下）接收的均匀模型单炮地震记录 （a）直光纤；（b）常规检波器速度 |
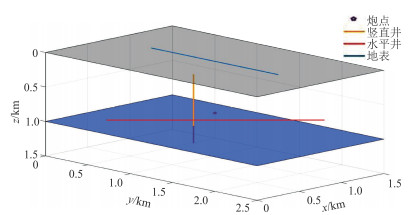
将均匀模型1000 m以下充填纵波速度为5700 m/s、横波速度为3400 m/s、密度为2500 kg/m3的地层，得到双层模型（图 6）。利用双层模型模拟直光纤、缠绕角分别为35.3°、54.7°的螺旋缠绕光纤的轴向应变率及常规检波器的速度 z分量、压力分量，光纤分别布设在地表、水平井及竖直井。
|
图 6 双层模型观测系统 时间采样间隔为0.4 ms，其他参数同图 4。 |
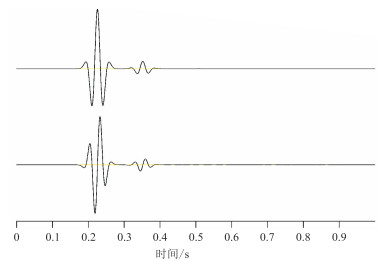
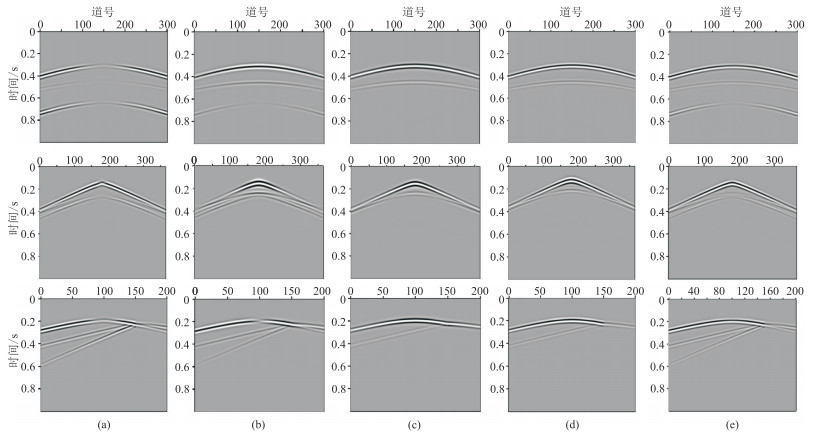
图 7为在地表、水平井及竖直井接收的双层模型单炮地震记录。由图可见：①在直光纤地震记录中存在直达波、反射P波、反射S波（图 7a）以及透射P波、透射S波(图 7a下)，当入射波垂直于光纤时振幅较弱。②在缠绕角为35.3°的螺旋缠绕光纤地震记录（图 7d）中没有反射S波和透射S波，与振幅响应吻合，波形与常规检波器压力分量（图 7c）相同；图 7d上与图 7c上的波形的振幅及相位存在一定差别（图 8）。③在缠绕角为54.7°的螺旋缠绕光纤地震记录中可见直达P波、反射P波、反射S波（图 7e）以及透射P波、透射S波（图 7e下），且不存在波的传播方向垂直于直光纤时对波不敏感的现象，波形与常规检波器速度 z分量（图 7b）相同。
|
图 7 在地表（上）、水平井（中）及竖直井（下）接收的双层模型单炮地震记录 （a）直光纤；（b）常规检波器速度 |
2.3 页岩气模型
建立了西南页岩气模型（图 9），观测系统如图 10所示。利用西南页岩气模型模拟直光纤、缠绕角分别为35.3°、54.7°的螺旋缠绕光纤的单炮地震记录，光纤分别布设在地表、水平井及竖直井。
|
图 9 西南页岩气模型 （a）速度模型；（b）密度模型 模型尺寸为7900 m×3900 m×5700 m，网格尺寸为10 m×10 m×10 m，页岩位于红色箭头处。震源为主频为15 Hz的雷克子波，采样间隔为0.6 ms。 |
|
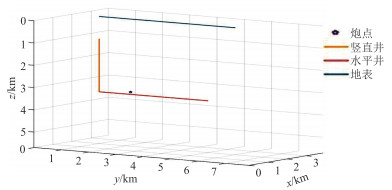
图 10 西南页岩气模型观测系统 震源位于页岩层中，且与水平井在同一水平面。 |
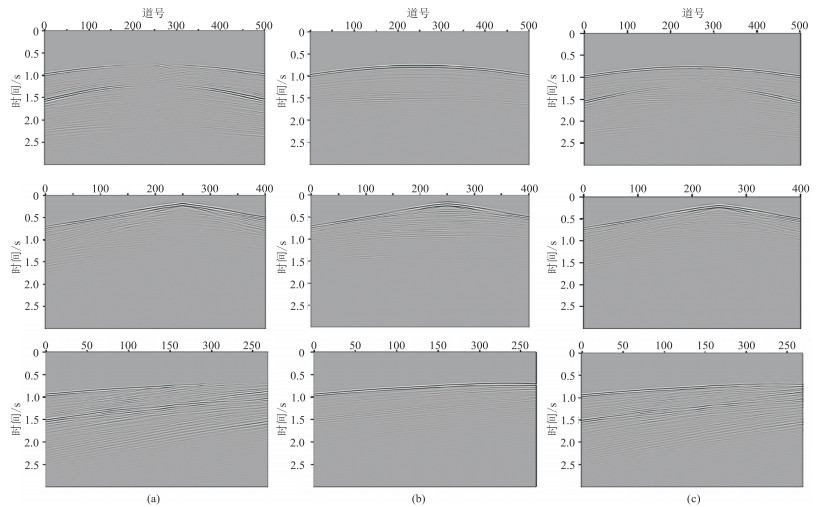
图 11为在地表、水平井及竖直井接收的西南页岩气模型单炮地震记录。由图可见：在与入射波垂直的直光纤附近响应较弱，可见P波、S波响应（图 11a）；在缠绕角为35.3°的螺旋缠绕光纤地震记录中无S波（图 11b）；在缠绕角为54.7°的螺旋缠绕光纤地震记录中存在P波、S波（图 11c）。
|
图 11 在地表（上）、水平井（中）及竖直井（下）接收的西南页岩气模型单炮地震记录 （a）直光纤；（b）缠绕角35.3°的螺旋缠绕光纤；（c）缠绕角54.7°的螺旋缠绕光纤 |
本文首先分析了直光纤及两种螺旋缠绕光纤的P波、SV及SH波的理论轴向应变率响应，然后利用三维弹性有限差分模拟了轴向应变率响应，并与常规检波器的速度 z分量、压力分量对比，得到以下认识：
（1）直光纤接收单分量信息，在垂直于光纤方向接收的波的响应较弱，而螺旋缠绕光纤可接收多分量信息，因此在垂直于光纤方向接收的波的响应较强；
（2）缠绕角为35.3°的螺旋缠绕光纤地震记录中无S波响应，其波形与常规检波器压力分量相似，在成像中可以利用声波方程成像。
参考文献
| [1] |
MESTAYER J, COX B, WILLS P, et al. Field trials of distributed acoustic sensing for geophysical monitoring[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 4253-4257.
|
| [2] |
PARKER T, SHATALIN S, FARHADIROUSHAN M. Distributed acoustic sensing-A new tool for seismic applications[J]. First Break, 2014, 32(2): 61-69. |
| [3] |
DALEY T M, FREIFELD B M, AJO-FRANKLIN J, et al. Field testing of fiber-optic distributed acoustic sensing (DAS) for subsurface seismic monitoring[J]. The Leading Edge, 2013, 32(6): 699-706. DOI:10.1190/tle32060699.1 |
| [4] |
李彦鹏, 李飞, 李建国, 等. DAS技术在井中地震勘探的应用[J]. 石油物探, 2020, 59(2): 242-249. LI Yanpeng, LI Fei, LI Jianguo, et al. Application of distributed acoustic sensing in borehole seismic exploration[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 242-249. DOI:10.3969/j.issn.1000-1441.2020.02.010 |
| [5] |
BAKULIN A, GOLOKOV P, SMITH R, et al. Smart DAS upholes for simultaneous land near-surface characterization and subsurface imaging[J]. The Leading Edge, 2017, 36(12): 1001-1008. DOI:10.1190/tle36121001.1 |
| [6] |
MOLENAAR M M, HILL D J, WEBSTER P, et al. First downhole application of distributed acoustic sensing for hydraulic-fracturing monitoring and diagnostics[J]. SPE Drilling & Completion, 2012, 27(1): 32-38. |
| [7] |
HORNMAN K, Kuvshinov B N, Zwartjes P M, et al. Field trial of a broadside-sensitive distributed acoustic sensing cable for surface seismic[C]. Extended Abstracts of 75th EAGE Conference & Exhibition, 2013, DOI: DOI.org/10.3997/2214-4609.20130383.
|
| [8] |
KUVSHINOV B. Interaction of helically wound fiber‐optic cables with plane seismic waves[J]. Geophysical Prospecting, 2016, 64(3): 671-688. DOI:10.1111/1365-2478.12303 |
| [9] |
INNANEN K. Determination of seismic-tensor strain from Helical Wound Cable-Distributed Acoustic Sensing cable with arbitrary and nested-helix winds[C]. SEG Technical Program Expanded Abstracts, 2017, 36: 926-930.
|
| [10] |
EAID M V, LI J, INNANEN K A. Modeling the response of shaped DAS fibres to microseismic moment tensor sources[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 4698-4702
|
| [11] |
EAID M V, KEATING S D, INNANEN K A. Multi-parameter seismic elastic full waveform inversion with combined geophone and shaped fiberoptic cable data[J]. Geophysics, 2020, 85(6): R537-R552. DOI:10.1190/geo2020-0170.1 |
| [12] |
陈亮, 黄建平, 王自颖, 等. 应用自适应变网格紧致差分的地震波数值模拟及逆时偏移[J]. 石油地球物理勘探, 2023, 58(3): 641-650, 712. CHEN Liang, HUANG Jianping, WANG Ziying, et al. Seismic numerical simulation and reverse time migration with adaptive variable-grid and compact difference method[J]. Oil Geophysical Prospecting, 2023, 58(3): 641-650, 712. |
| [13] |
徐世刚, 包乾宗, 任志明. 简化的三维TTI介质黏滞纯声波方程及其数值模拟[J]. 石油地球物理勘探, 2022, 57(2): 331-341. XU Shigang, BAO Qianzong, REN Zhiming. A simplified pure visco acoustic wave equation for 3D TTI media and its numerical simulation[J]. Oil Geophysical Prospecting, 2022, 57(2): 331-341. |
| [14] |
贾宗锋, 吴国忱, 李青阳, 等. 标量波方程广义有限差分正演模拟[J]. 石油地球物理勘探, 2022, 57(1): 101-110. JIA Zongfeng, WU Guochen, LI Qingyang, et al. Forward modeling of scalar wave equation with generalized finite difference method[J]. Oil Geophysical Prospecting, 2022, 57(1): 101-110. |
| [15] |
杨尚倍, 白超英, ZHOU Bing. 时间域广义2.5D一阶波动方程曲网格有限差分法数值模拟[J]. 石油地球物理勘探, 2021, 56(6): 1262-1278. YANG Shangbei, BaI Chaoying, ZHOU B. Curvilinear-grid finite-difference numerical simulation method for generalized first-order 2.5D time-domain wave equation[J]. Oil Geophysical Prospecting, 2021, 56(6): 1262-1278. |
| [16] |
LELLOUCH A, LINDESEY N J, ELLSWORTH W L, et al. Comparison between distributed acoustic sensing and geophones: Downhole microseismic monitoring of the FORGE geothermal experiment[J]. Seismological Research Letters, 2020, 91(6): 3256-3268. DOI:10.1785/0220200149 |
| [17] |
MA Y, LI W. Comparing DAS and geophone data and imaging for monitoring CO2 sequestration[C]. Second International Meeting for Applied Geoscience & Energy, 2022, 524-528.
|
| [18] |
梁兴, 王松, 刘成, 等. 光纤传感技术在昭通山地页岩气勘探开发实践中的应用进展[J]. 石油物探, 2022, 61(1): 32-40. LIANG Xing, WANG Song, LIU Cheng, et al. Progress of the application of optical fiber sensing technology in shale gas exploration and development practice in the Zhaotong mountain area[J]. Geophysical Prospecting for Petroleum, 2022, 61(1): 32-40. |
| [19] |
马国旗, 曹丹平, 尹教建, 等. 分布式声传感井中地震信号检测数值模拟方法[J]. 石油地球物理勘探, 2020, 55(2): 311-320. MA Guoqi, CAO Danping, YIN Jiaojian, et al. Numerical simulation of detecting seismic signals in DAS wells[J]. Oil Geophysical Prospecting, 2020, 55(2): 311-320. |
| [20] |
曹丹平, 律军军, 孙上饶, 等. 基于螺旋缠绕光纤的分布式声波传感三分量信号采集机理研究[J]. 石油物探, 2022, 61(1): 60-69. CAO Danping, LYU Junjun, SUN Shangrao, et al. Three-component signal acquisition mechanism of distributed acoustic sensing based on helically winding fiber-optic[J]. Geophysical Prospecting for Petroleum, 2022, 61(1): 60-69. |
| [21] |
郑伋. 分布式光纤传感器(DAS)弹性波场响应特征研究[D]. 北京: 北京中国地质大学(北京), 2019.
|
| [22] |
姚艺, 王一博, 王伟君, 等. 分布式光纤声波传感微振动响应特征[J]. 地球物理学报, 2023, 66(2): 713-730. YAO Yi, WANG Yibo, WANG Weijun, et al. Micro-vibration response characteristics of Distributed Acoustic Sensing[J]. Chinese Journal of Geophysics, 2023, 66(2): 713-730. |
| [23] |
WU C. 3D finite-difference elastic modeling for DAS VSP and microseismic surveys[C]. First International Meeting for Applied Geoscience & Energy Expanded Abstracts, 2021, DOI: 10.1190/segam2021-3589262.1.
|