2. 东华理工大学地球物理与测控技术学院, 江西南昌 330013
2. School of Geophysics and Measurement-Control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China
受到外部环境的影响和采集条件的限制,地震数据中往往存在大量的随机噪声,对后续地震资料处理和解释造成严重影响,因此随机噪声压制是地震数据处理过程中不可或缺的关键步骤。在以振幅信息为基础的精细地震勘探中,保幅性是衡量随机噪声压制方法优越性的关键指标[1-2]。
目前地震数据处理中常用的去噪方法可分为滤波类、变换类、深度学习类、反演类等方法。滤波类主要是通过不同的滤波器对地震数据进行平滑处理,如高斯滤波[3]、中值滤波[4]等,该类方法在处理地震数据时会破坏细节信息和突变信息,导致模糊输出[5]。变换类是将数据变换至特定的变换域中,通过噪声和有效信号在变换域中的差异进行信噪分离,如傅里叶变换[6]、小波变换[7-8]、曲波变换[9-10]等,但噪声和有效信号在各种变换域中一般存在不同程度的混叠,因此不恰当的滤波阈值会损伤有效信号。深度学习类是近期研究的热点,该类方法具有非常优越的保幅性,但前提是需要大量样本数据进行模型训练,计算成本较高,且去噪模型在不同地区地震数据应用时存在迁移性问题[11-13]。反演类是将去噪结果视为待反演参数构造相应的反演目标函数,然后对目标函数进行优化求解实现去噪过程[14-15]。为了提高反演过程的稳定性和反演结果的保幅性,需要在目标函数中加入合适的约束项,例如全变分(Total Variation,TV)正则化。TV正则化模型最早是为了解决图像去噪过程中边界保护问题而提出[16],即在滤除随机噪声的同时保护图像中的突变信息,有利于保护地震数据中的断层、岩性尖灭等不连续信息。对于非突变点,该方法假设相邻道在横向上的振幅差异主要由随机噪声引起,而地震数据同相轴在横向上具有较好的相似性,因此该方法在地震随机噪声压制中获得了广泛应用[17-18]。
理论上,在正则化模型中如果噪声引入越多而有效信号引入越少,则其保幅性越好。然而,常规的TV正则化去噪模型由水平和垂直方向的一阶导数构成,处理存在弯曲同相轴且振幅横向渐变的叠前地震数据时, 保幅性较差,存在两方面的问题:①即使地震数据中不含噪声,弯曲同相轴中的有效信息也会被水平导数引入TV正则化模型;②叠前数据中振幅随炮检距渐变的AVO特征同样也会被水平一阶导数引入TV正则化模型。目标函数优化过程中使TV函数趋向极小值,则势必会破坏上述被引入的有效信息[19-21]。为了提高常规TV去噪方法的保幅性,许多学者针对上述问题做了大量研究。针对问题①,提出了方向TV(Directional TV,DTV)正则化模型[22-24],该方法将图像纹理的延伸方向引入TV函数,针对地震数据则需要事先估计同相轴的局部倾角信息。针对问题②,提出了高阶TV(High-order TV,HTV)去噪模型[25-27],即用高阶导数替代常规TV去噪模型中的一阶导数,对横向渐变的信息具有较好的保幅效果,消除了常规TV去噪结果中的“阶梯效应”。为了同时解决问题①和问题②,Liu等[28]将DTV与HTV模型结合,提出了高阶方向TV (High-order Directional TV,HDTV)模型,与常规TV、DTV和HTV模型相比,具有明显的优势。当在TV去噪模型中同时考虑同相轴弯曲和振幅横向渐变时,可以获得最佳的保幅效果。然而,地震数据局部倾角信息的计算本身会受到噪声的严重影响,例如目前广泛应用的PWD(Plane Wave Destruction)方法[29],当噪声水平较高时,为了提高计算稳定性,必须增大计算窗口,但这会引起明显的平均效应,压制了同相轴局部倾角的细节变化,将这种局部倾角信息用于TV去噪模型时会引入额外的计算误差。
叠前CMP道集中同相轴的弯曲使相邻地震子波之间的相似性很难在去噪算法中恰当利用,造成很多去噪方法的保幅性欠佳,因此Chen等[30]利用局部倾角信息将CMP道集中弯曲同相轴拉平后再进行去噪,提高了保幅性。地震资料处理过程中动校正(NMO)是必不可少的环节。NMO后弯曲同相轴被拉平,不会在去噪过程中引入额外的计算,同时NMO对噪声的鲁棒性较强,避免了局部倾角信息的计算,因此,本文提出在叠前NMO域进行高阶TV去噪。合成地震数据和实际地震资料处理结果表明,本文方法比常规TV去噪方法保幅性更高。
1 方法原理 1.1 算法流程及有效性分析本文方法首先利用NMO将CMP道集中的弯曲同相轴拉平,然后对NMO域中的地震数据进行高阶TV正则化去噪,最后通过反NMO还原CMP道集,得到最终去噪结果。为了考查NMO拉平前、后一阶和二阶导数剖面中有效信号是否被压制,进而分析算法有效性,图 1给出了实际CMP道集及NMO拉平后的结果。由图可见,几何扩散、黏弹衰减等因素导致远道信噪比较低。图 2a为NMO拉平前的横向一阶和二阶导数剖面,其中一阶导数剖面中存在明显的有效信息(黑色箭头所示),而二阶导数剖面中黑色箭头处的有效信息明显减少,说明用二阶导数构造的TV去噪模型携带的有效信息少,保幅性高[31]。图 2b为NMO拉平后的横向一阶和二阶导数剖面,二者均无明显的有效信息,说明NMO拉平后进行TV去噪的保幅性更高。
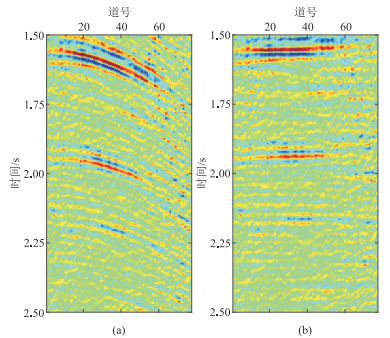
|
图 1 NMO前(a)、后(b)的部分叠前CMP道集 |
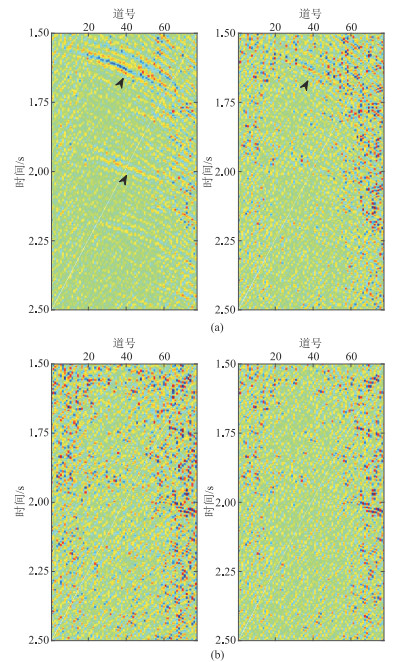
|
图 2 叠前CMP道集NMO前(a)、后(b)的横向导数对比左:一阶;右:二阶 |
综上所述,在NMO域中对叠前CMP道集进行高阶TV去噪的保幅性更高,证明了本文算法思路的有效性。
1.2 高阶TV正则化去噪目标函数及优化求解方法本文使用二阶导数构造各向异性高阶TV正则化去噪模型的目标函数
| $ J\left(\boldsymbol{u}\right)=\frac{1}{2}\left|\right|\boldsymbol{u}-\boldsymbol{s}|{|}_{2}^{2}+\lambda {‖{\boldsymbol{D}}_{x}\boldsymbol{u}‖}_{1}+\mu {‖{\boldsymbol{D}}_{y}\boldsymbol{u}‖}_{1} $ | (1) |
式中:
式(1)不可导,因此无法直接利用传统梯度类算法进行优化求解。本文采用分裂Bregman优化框架[32]将该目标函数分裂为三个目标函数交替优化求解。
| $ \left\{\begin{array}{l}{J}_{1}\left({\boldsymbol{u}}^{k+1}\right)=\frac{1}{2}{‖{\boldsymbol{u}}^{k+1}-\boldsymbol{s}‖}_{2}^{2}+\frac{\gamma }{2}‖{\boldsymbol{d}}_{x}^{k}-{\boldsymbol{D}}_{x}{\boldsymbol{u}}^{k+1}-\\ {{\boldsymbol{b}}_{x}^{k}‖}_{2}^{2}+\frac{\gamma }{2}{‖{\boldsymbol{d}}_{y}^{k}-{\boldsymbol{D}}_{y}{\boldsymbol{u}}^{k+1}-{\boldsymbol{b}}_{y}^{k}‖}_{2}^{2}\\ {J}_{2}\left({\boldsymbol{d}}_{x}^{k+1}\right)=\frac{\gamma }{2}{‖{\boldsymbol{d}}_{x}^{k+1}-{\boldsymbol{D}}_{x}{\boldsymbol{u}}^{k+1}-{\boldsymbol{b}}_{x}^{k}‖}_{2}^{2}+\lambda {‖{\boldsymbol{d}}_{x}^{k+1}‖}_{1}\\ {J}_{3}\left({\boldsymbol{d}}_{y}^{k+1}\right)=\frac{\gamma }{2}{‖{\boldsymbol{d}}_{y}^{k+1}-{\boldsymbol{D}}_{y}{\boldsymbol{u}}^{k+1}-{\boldsymbol{b}}_{y}^{k}‖}_{2}^{2}+\mu {‖{\boldsymbol{d}}_{y}^{k+1}‖}_{1}\end{array}\right. $ | (2) |
式中:k为迭代次数;中间变量的初值
式(2)中的J1为二次函数,对其求导并令导数为零后,可得
| $ {\boldsymbol{u}}^{k+1}={\boldsymbol{Q}}^{-1}{\boldsymbol{p}}^{k} $ | (3) |
式中:
| $ \left\{\begin{array}{l}{\boldsymbol{d}}_{x}^{k+1}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\left({\boldsymbol{D}}_{x}{\boldsymbol{u}}^{k+1}+{\boldsymbol{b}}_{x}^{k}, \lambda /\gamma \right)\\ {\boldsymbol{d}}_{y}^{k+1}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\left({\boldsymbol{D}}_{y}{\boldsymbol{u}}^{k+1}+{\boldsymbol{b}}_{y}^{k}, \mu /\gamma \right)\end{array}\right. $ | (4) |
变量
| $ \left\{\begin{array}{l}{\boldsymbol{b}}_{x}^{k+1}={\boldsymbol{b}}_{x}^{k}+{\boldsymbol{D}}_{x}{\boldsymbol{u}}^{k+1}-{\boldsymbol{d}}_{x}^{k+1}\\ {\boldsymbol{b}}_{y}^{k+1}={\boldsymbol{b}}_{y}^{k}+{\boldsymbol{D}}_{y}{\boldsymbol{u}}^{k+1}-{\boldsymbol{d}}_{y}^{k+1}\end{array}\right. $ | (5) |
软阈值算子soft对向量
| $ \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\{\boldsymbol{z}, \alpha \}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(\boldsymbol{z}\right)\circ \mathrm{m}\mathrm{a}\mathrm{x}\left[\mathrm{a}\mathrm{b}\mathrm{s}\left(\boldsymbol{z}\right)-\alpha \boldsymbol{\varGamma }, 0\right] $ | (6) |
式中:sign(·)和abs(·)分别表示对向量中的各元素取符号运算和求绝对值运算;
上述高阶TV正则化反演去噪的具体步骤如下:
(1) 输入
(2) 初始化:
(3) 当
(4) 重复步骤(3)直到
采用不同阶次的差分算子会得到相应的高阶TV正则化去噪方法。本文以二阶为例给出
| $ {\boldsymbol{D}}_{x}={\left[\begin{array}{cccccccc}-1& \stackrel{n-1\mathrm{个}0}{\stackrel{⏞}{\cdots }}& 2& \stackrel{n-1\mathrm{个}0}{\stackrel{⏞}{\cdots }}& -1& & & \\ & -1& \cdots & 2& \cdots & -1& & \\ & & \ddots & \ddots & \ddots & \ddots & \ddots & \\ & & & -1& \cdots & 2& \cdots & -1\end{array}\right]}_{n(m-2)\times nm} $ | (7) |
| $ {\boldsymbol{D}}_{y}={\left[\begin{array}{cccc}{\boldsymbol{D}}_{2}& & & \\ & {\boldsymbol{D}}_{2}& & \\ & & \ddots & \\ & & & {\boldsymbol{D}}_{2}\end{array}\right]}_{m\times m} $ | (8) |
式中
| $ {\boldsymbol{D}}_{2}={\left[\begin{array}{cccccc}-1& 2& -1& & & \\ & -1& 2& -1& & \\ & & \ddots & \ddots & \ddots & \\ & & & -1& 2& -1\end{array}\right]}_{(n-2)\times n} $ | (9) |
如要构造更高阶次的差分算子,可以根据式(7)和式(8)的形式进行类推。
使用合成地震数据(图 3a)验证本文方法的保幅去噪性能。合成地震数据共38道,每道样点数为522,采样间隔为1 ms。道集含三条弯曲同相轴,其中第一条曲率较大。对不含噪数据加入高斯白噪声,得到信噪比为20 dB的含噪地震数据(图 3 b),其中同相轴受到不同程度的噪声污染。含噪数据经NMO处理后,同相轴能量主要集中在水平方向(图 3 c)。
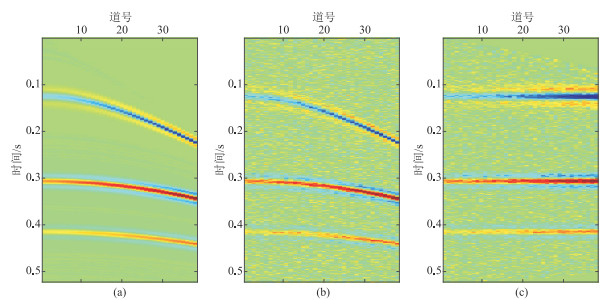
|
图 3 合成地震道集 (a)原始不含噪数据;(b)信噪比为20 dB的加噪数据;(c)NMO拉平后 |
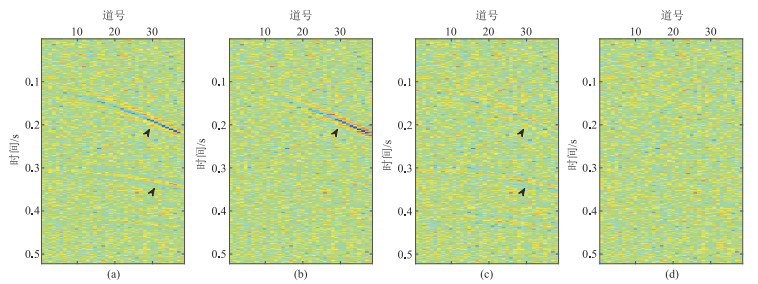
图 4和图 5分别为四种方法去噪结果和滤除的噪声。常规一阶TV去噪方法的处理结果(图 4 a)不理想,同相轴振幅失真严重,滤除的噪声中(图 5 a)存在明显的有效信息。NMO前二阶TV去噪方法对于弯曲度小的同相轴振幅信息有较好的保护效果(图 4 b),但其滤除噪声(图 5 b)中曲率大的同相轴信息较为明显,保幅性较差。NMO域一阶TV去噪的结果(图 4 c)相比常规一阶TV去噪的结果同相轴振幅信息得到了较好的保留,但去噪结果存在明显的“阶梯效应”(箭头所指),因此滤除的噪声(图 5 c)中存在少量有效信息。相比之下,NMO后二阶TV方法(本文方法)去噪后的结果(图 4 d)同相轴振幅横向过渡自然,“阶梯效应”被压制,滤除的噪声中(图 5 d)基本不存在有效信息,对弯曲同相轴信息的保幅性能最高,去噪结果与不含噪数据最接近,说明本文方法效果最好。
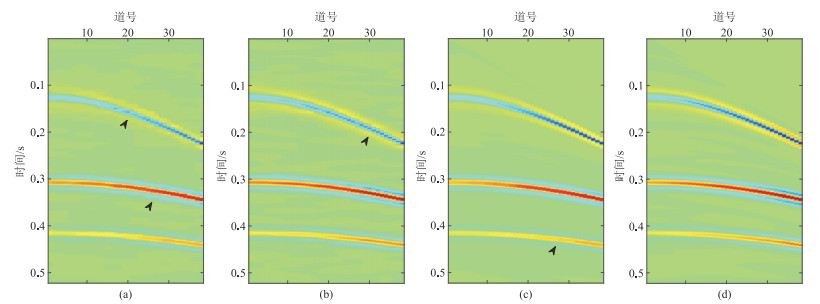
|
图 4 合成道集四种方法去噪结果对比 (a)常规一阶TV;(b)NMO前二阶TV;(c)NMO域一阶TV;(d)本文方法 |
|
图 5 合成数据四种方法去除的噪声对比 (a)常规一阶TV;(b)NMO前二阶TV;(c)NMO域一阶TV;(d)本文方法 |
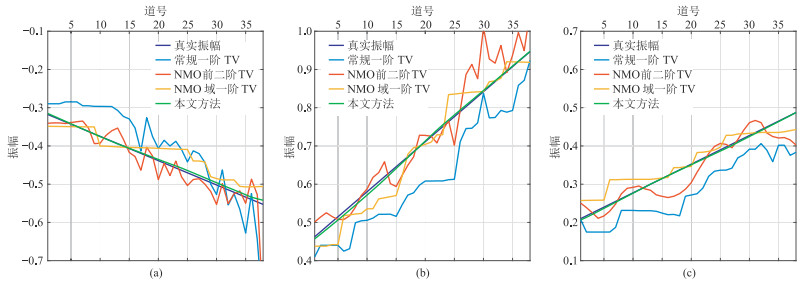
图 6为四种方法去噪后三条同相轴的振幅曲线与真实曲线对比。真实振幅呈线性变化,常规一阶TV去噪结果与真实振幅之间差异最大;NMO前二阶TV比常规一阶TV去噪结果更接近真实振幅曲线,但仍有较大差异;NMO域一阶TV比常规一阶TV去噪结果更接近真实振幅,但表现出了明显的“阶梯”状;本文方法去噪后的振幅最接近真实曲线,保幅性最高。
|
图 6 合成数据四种方法去噪后三条同相轴的振幅与真实曲线对比 (a)第一条(弯曲度较大);(b)第二条(弯曲度较小);(c)第三条(弯曲度最小) |
采用峰值信噪比(PSNR)、结构相似性(SSIM)和均方根误差(RMSE)三种指标衡量各方法的保幅去噪效果。三者的计算公式为
| $ \mathrm{P}\mathrm{S}\mathrm{N}\mathrm{R}=10\times \mathrm{l}\mathrm{g}\frac{{255}^{2}\times m\times n}{\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}{\left[\widehat{s}(i, j)-u(i, j)\right]}^{2}} $ | (10) |
| $ \mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}=\frac{\left(2{\mu }_{\widehat{s}}{\mu }_{u}+{c}_{1}\right)\left(2{\sigma }_{\widehat{s}u}+{c}_{2}\right)}{\left({\mu }_{\widehat{s}}^{2}+{\mu }_{u}^{2}+{c}_{1}\right)\left({\sigma }_{\widehat{s}}^{2}+{\sigma }_{u}^{2}+{c}_{2}\right)} $ | (11) |
| $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{NM}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}{\left[\widehat{s}(i, j)-u(i, j)\right]}^{2}} $ | (12) |
式中:
表 1为不同信噪比和不同噪声类型数据四种方法去噪结果的三个指标统计,结果表明,无论何种噪声类型,也无论信噪比高低,本文方法的去噪效果均最优。
|
|
表 1 不同信噪比和不同噪声类型数据去噪结果的定量指标对比 |
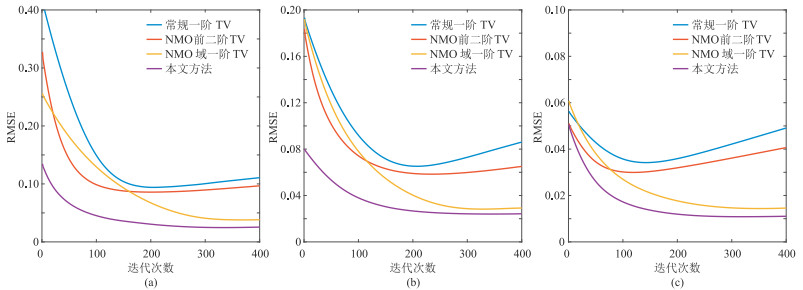
实际地震数据中随机噪声大都符合高斯分布,图 7为四种方法处理含高斯分布噪声、不同信噪比数据的RMSE迭代收敛曲线,常规一阶TV和NMO前二阶TV去噪结果的RMSE值呈先下降、后上升的趋势,这是由于随机噪声压制完成后弯曲同相轴的有效信息和横向渐变信息也被压制,说明保幅性低。在处理不同信噪比的数据时,本文方法均在迭代约300次后达到收敛;在相同的迭代次数下,本文方法的RMSE值最小,进一步证明了本文方法具有更高的保幅去噪性能。
|
图 7 不同信噪比合成数据四种去噪方法的RMSE迭代收敛曲线对比 (a)5 dB;(b)10 dB;(c)20 dB |
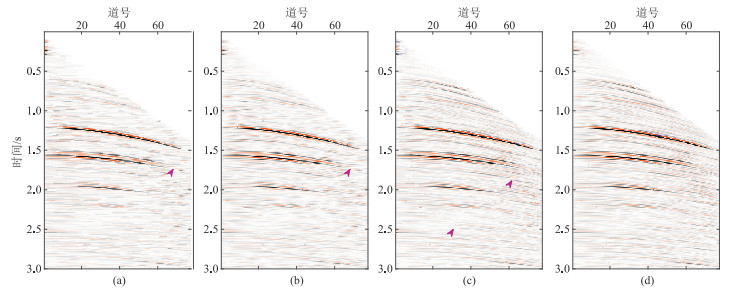
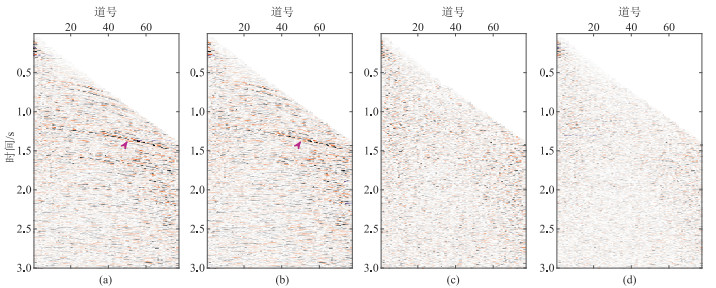
实际叠前CMP道集(图 8a)共有77道,每道的采样点数为3001个,采样间隔为1 ms,炮检距范围为59~4620 m。该数据信噪比较低,深部反射波同相轴受噪声影响变得模糊、杂乱(紫色箭头所示),连续性差。图 8b为NMO拉平结果,同相轴能量集中在水平方向。图 9和图 10分别为四种方法的去噪结果和滤除的噪声,可以看出:常规一阶TV和NMO前二阶TV的去噪结果(图 9a和图 9b)中同相轴有效信息破坏较为严重,连续性没有得到有效改善,滤除的噪声(图 10a和图 10b)中包含明显的弯曲同相轴信息(箭头所示);NMO域一阶TV相较于常规一阶TV去噪对弯曲同相轴的保幅性更高,滤除的噪声(图 10c)中基本无弯曲同相轴的信息,但去噪结果中(图 9c)存在较明显的“阶梯效应”(箭头所示);本文方法去噪的结果(图 9d)同相轴最连续,深部的反射波同相轴也清晰可见,滤除的噪声剖面(图 10d)中基本无有效同相轴信息,同时“阶梯效应”得到了有效压制,实际去噪效果与合成数据一致。
|
图 8 NMO前(a)、后(b)实际叠前CMP道集 |
|
图 9 实际叠前道集四种方法去噪结果对比 (a)常规一阶TV;(b)NMO前二阶TV;(c)NMO域一阶TV;(d)本文方法 |
|
图 10 实际叠前道集四种方法滤除的噪声对比 (a)常规一阶TV;(b)NMO前二阶TV;(c)NMO域一阶TV;(d)本文方法 |
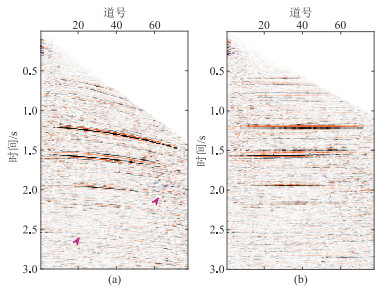
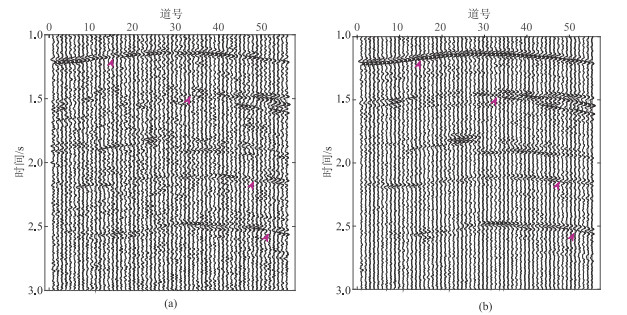
大炮检距信号对流体性质敏感,在叠前AVO分析中起着至关重要的作用。图 11为本文方法去噪前、后远道(第63~第77道)叠加剖面对比。去噪前剖面中噪声影响明显,同相轴有多处错断(箭头处),尖灭点等构造信息也无法准确识别。经本文方法去噪后,噪声得到了有效压制,剖面更清晰,同相轴也更连续,证明了本文方法的实用性。
|
图 11 本文方法去噪前(a)、后(b)远道(第63~第77道)叠加剖面对比 |
综上所述,本文方法在去除随机噪声的同时能够保护有效信息,特别是弯曲同相轴和振幅渐变信息,体现出比常规TV去噪方法更高的保幅性。
4 结束语在NMO域中,弯曲同相轴被拉平,由二阶导数构造的TV正则化去噪模型能更精确地保留振幅的横向渐变信息。在分裂Bregman框架下给出了二阶TV正则化反演目标函数的快速优化求解算法。
合成地震数据和实际地震资料处理结果表明,与其他TV去噪模型相比,本文方法可有效去除不同强度的随机噪声,消除同相轴弯曲和“阶梯效应”造成的振幅失真,从而显著提高地震剖面的信噪比,具有优于其他TV方法的保幅去噪性能,为后续地震解释及AVO分析提供了有力保障。
| [1] |
熊定钰, 赵海珍, 陈海云, 等. 保持地震记录叠前AVO属性的噪声衰减方法[J]. 石油地球物理勘探, 2010, 45(6): 856-860. XIONG Dingyu, ZHAO Haizhen, CHEN Haiyun, et al. Noise attenuation method based on the preserved pre-stack AVO attribute[J]. Oil Geophysical Prospecting, 2010, 45(6): 856-860. |
| [2] |
熊晓军, 简世凯, 李翔, 等. 叠前道集优化处理技术及其应用[J]. 西南石油大学学报(自然科学版), 2017, 39(6): 55-62. XIONG Xiaojun, JIAN Shikai, LI Xiang, et al. Prestack gather optimization technique and application[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2017, 39(6): 55-62. |
| [3] |
WU N, LI Y, YANG B. Noise attenuation for 2-D seismic data by radial-trace time-frequency peak filtering[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(5): 874-878. DOI:10.1109/LGRS.2011.2129552 |
| [4] |
董烈乾, 汪长辉, 李长芬, 等. 利用自适应中值滤波方法压制混叠噪声[J]. 地球物理学进展, 2018, 33(4): 1475-1479. DONG Lieqian, WANG Changhui, LI Changfen, et al. Blending noise removal utilizing an adaptive median filter[J]. Progress in Geophysics, 2018, 33(4): 1475-1479. |
| [5] |
国胧予, 刘财, 刘洋. 滤波类方法衰减地震数据噪声[J]. 地球物理学进展, 2018, 33(5): 1890-1896. GUO Longyu, LIU Cai, LIU Yang. Filtering methods attenuate seismic data noise[J]. Progress in Geophysics, 2018, 33(5): 1890-1896. |
| [6] |
TARY J B, HERRERA R H, HAN J, et al. Spectral estimation: What is new? What is next?[J]. Reviews of Geophysics, 2014, 52(4): 723-749. DOI:10.1002/2014RG000461 |
| [7] |
周怀来. 基于小波变换的地震信号去噪方法研究与应用[D]. 四川成都: 成都理工大学, 2006. ZHOU Huailai. Research and Application of Seismic Signal Denoising Method Based on Wavelet Transform[D]. Chengdu University of Technology, Chengdu, Sichuan, 2006. |
| [8] |
蔡剑华, 王先春, 胡惟文. 基于经验模态分解与小波阈值的MT信号去噪方法[J]. 石油地球物理勘探, 2013, 48(2): 303-307. CAI Jianhua, WANG Xianchun, HU Weiwen. A method for MT data denoising based on empirical mode decomposition and wavelet threshold[J]. Oil Geophysical Prospecting, 2013, 48(2): 303-307. |
| [9] |
CANDÈS E, DONOHO D. Continuous curvelet transform Ⅱ: Discretization and frames[J]. Applied and Computational Harmonic Analysis, 2005, 19(2): 198-222. DOI:10.1016/j.acha.2005.02.004 |
| [10] |
张恒磊, 张云翠, 宋双, 等. 基于Curvelet域的叠前地震资料去噪方法[J]. 石油地球物理勘探, 2008, 43(5): 508-513. ZHANG Henglei, ZHANG Yuncui, SONG Shuang, et al. Curvelet domain-based prestack seismic data denoise method[J]. Oil Geophysical Prospecting, 2008, 43(5): 508-513. |
| [11] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869, 877. HAN Weixue, ZHOU Yatong, CHI Yue. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869, 877. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [12] |
张岩, 李新月, 王斌, 等. 基于深度学习的鲁棒地震数据去噪[J]. 石油地球物理勘探, 2022, 57(1): 12-25. ZHANG Yan, LI Xinyue, WANG Bin, et al. Robust seismic data denoising based on deep learning[J]. Oil Geophysical Prospecting, 2022, 57(1): 12-25. |
| [13] |
李佳, 王维波, 盛立, 等. 应用双向长短时记忆神经网络的微地震信号降噪方法[J]. 石油地球物理勘探, 2023, 58(2): 285-294. LI Jia, WANG Weibo, SHENG Li, et al. Denoising of microseismic signal based on bidirectional long short-term memory neural network[J]. Oil Geophysical Prospecting, 2023, 58(2): 285-294. |
| [14] |
时磊, 刘俊州, 韦婉婉, 等. 基于贝叶斯反演的叠前数据同时插值和保幅去噪方法研究[J]. 地球物理学进展, 2019, 34(6): 2309-2314. SHI Lei, LIU Junzhou, WEI Wanwan, et al. Research on simultaneous interpolation and amplitude-preserving denoising based on Bayesian inversion of prestack data[J]. Progress in Geophysics, 2019, 34(6): 2309-2314. |
| [15] |
任浩, 李宗杰, 薛姣, 等. 基于稀疏反演的多道匹配追踪地震信号去噪方法及其应用[J]. 石油物探, 2019, 58(2): 199-207. REN Hao, LI Zongjie, XUE Jiao, et al. Multichannel matching pursuit based on sparse inversion for seismic data denoising and its application[J]. Geophysical Prospecting for Petroleum, 2019, 58(2): 199-207. |
| [16] |
RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D: Nonlinear Phenomena, 1992, 60(1): 259-268. |
| [17] |
OSHER S, BURGER M, GOLDFARB D, et al. An iterative regularization method for total variation-based image restoration[J]. Multiscale Modeling & Simulation, 2005, 4(2): 460-489. |
| [18] |
陈勇, 韩波, 肖龙, 等. 多尺度全变分法及其在时移地震中的应用[J]. 地球物理学报, 2010, 53(8): 1883-1892. CHEN Yong, HAN Bo, XIAO Long, et al. Multiscale total variation method and its application on time-lapse seismic[J]. Chinese Journal of Geophysics, 2010, 53(8): 1883-1892. DOI:10.3969/j.issn.0001-5733.2010.08.014 |
| [19] |
CHAN T F, ESEDOGLU S, PARK F E. Image decomposition combining staircase reduction and texture extraction[J]. Journal of Visual Communication and Image Representation, 2007, 18(6): 464-486. DOI:10.1016/j.jvcir.2006.12.004 |
| [20] |
LEFKIMMIATIS S, BOURQUARD A, UNSER M. Hessian-based norm regularization for image restoration with biomedical applications[J]. IEEE Transactions on Image Processing, 2012, 21(3): 983-995. DOI:10.1109/TIP.2011.2168232 |
| [21] |
Kong D H, Peng Z M. Seismic random noise attenuation using shearlet and total generalized variation[J]. Journal of Geophysics and Engineering, 2015, 12(6): 1024-1035. DOI:10.1088/1742-2132/12/6/1024 |
| [22] |
BAYRAM İ, KAMASAK M E. Directional total variation[J]. IEEE Signal Processing Letters, 2012, 19(12): 781-784. DOI:10.1109/LSP.2012.2220349 |
| [23] |
ZHANG H, WANG Y Q. Edge adaptive directional total variation[J]. The Journal of Engineering, 2013, 2013(11): 61-62. DOI:10.1049/joe.2013.0116 |
| [24] |
WANG D H, GAO J H, LIU N H, et al. Structure-oriented DTGV regularization for random noise attenuation in seismic data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(2): 1757-1771. DOI:10.1109/TGRS.2020.3001141 |
| [25] |
LYSAKER M, LUNDERVOLD A, TAI X C. Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time[J]. IEEE Transactions on Image Processing, 2003, 12(12): 1579-1590. DOI:10.1109/TIP.2003.819229 |
| [26] |
STEIDL G. A note on the dual treatment of higher-order regularization functionals[J]. Computing, 2006, 76(1): 135-148. |
| [27] |
LYSAKER M, TAI X. Iterative image restoration combining total variation minimization and a second-order functional[J]. International Journal of Computer Vision, 2006, 66(1): 5-18. DOI:10.1007/s11263-005-3219-7 |
| [28] |
LIU X Y, LI Q, YUAN C, et al. High-order directional total variation for seismic noise attenuation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-13. |
| [29] |
FOMEL S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(6): 1946-1960. |
| [30] |
CHEN Y K, HUANG W L, ZHOU Y T, et al. Plane-wave orthogonal polynomial transform for amplitude-preserving noise attenuation[J]. Geophysical Journal International, 2018, 214(3): 2207-2223. |
| [31] |
郝亚炬, 张鹏, 文晓涛, 等. 横向二阶导数TV正则化三维反射系数反演[J]. 石油地球物理勘探, 2023, 58(3): 680-689. HAO Yaju, ZHANG Peng, WEN Xiaotao, et al. 3D reflectivity inversion method based on TV regularization of lateral second-order derivatives[J]. Oil Geophysical Prospecting, 2023, 58(3): 680-689. |
| [32] |
GOLDSTEIN T, OSHER S. The split Bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343. |
| [33] |
CHEN Y P, PENG Z M, LI M H, et al. Seismic signal denoising using total generalized variation with overlapping group sparsity in the accelerated ADMM framework[J]. Journal of Geophysics and Engineering, 2019, 16(1): 30-51. |



 郝亚炬, 江西省南昌市广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
郝亚炬, 江西省南昌市广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email: