2. 中国石油勘探开发研究院西北分院, 甘肃兰州 730020
2. Northwest Branch, Research Institute of Exploration and Development, PetroChina, Lanzhou, Gansu 730020, China
沉积相智能地震识别方法以有监督的深度学习(DL)为主,瓶颈在于如何获取大量优质的地质体标签,目前样本的标定方式主要有两种:专家人工标注和正演模拟数据增广。
Wu等[1]利用正演模拟构建了断层的地震响应,并作为断层标签数据,提出了FaultSeg3D神经网络,将断层识别作为二分类问题,使用交叉熵损失函数优化模型,从而更有效地预测三维地震图像中的断层分布,进一步证明了神经网络从合成数据中学习到了各类断层反射特征;随后,Wu等[2]又提出了一种有监督的卷积神经网络(CNN),在训练图像中模拟地质构造和塌陷古岩溶特征作为标签,用于溶蚀孔洞的识别中。
对于盐丘的智能地震识别方法同样以神经网络方法为主。Waldeland等[3]将二维地震剖面视为二维图像,分割为多个像素点并作为标签数据,再利用CNN对盐丘体进行分类。Shi等[4]利用盐丘边界拾取和数据增广制作标签数据集,无需人工制作标签数据,利用CNN的三维图形分割来识别盐丘。
对于河道砂体的智能地震识别,Ao等[5]对比了支持向量机、神经网络和决策树等方法在预测性能、鲁棒性和特征优化方面各自的优势,并利用改进的随机森林算法由多地震属性识别河道砂体,在渤海西部地震数据取得了较好的应用效果。另外,对于岩性识别,Singh等[6]利用有监督和无监督的机器学习算法识别测井曲线的岩性分类,在阿拉斯加北坡的测试中,提高了岩性识别精度。
随着人工智能技术的发展,一些学者也开始关注DL的局限性,利用知识图谱(KG)引入更多的逻辑拓扑关系。
Gardner等[7]通过DL将KG中的关系组合成一个更紧凑的图结构,描述了如何将向量空间相似性引入KG, 并利用随机游走推理出拓扑关系。另外,陈曦等[8]提出了一种规则增强的KG表示学习方法,该方法首先通过KG规则挖掘的方法提取一组可代表KG语义信息的Horn逻辑规则,随后通过基于规则的物化推理方法将相应的隐藏语义信息注入到KG表示学习模型中。杨存等[9]提出一种基于少量样本学习的DL训练策略,将低频模型约束引入到网络训练中,为KG和DL方法融合提供了可能性[10-12]。Qian等[13]提出一种新的KG构建方法“TransAt”,引入注意力机制,当预测两个实体间的关系时,首先检查实体的类别,然后才会关注细粒度的关系以及相关属性。An等[14]提出了一种利用文本增强KG的学习方法,可利用文本信息来表征不同三元组中具有不同表示形式的关系和实体。
现有的KG,特别是信息提取部分,主要是针对文本数据的,这导致KG在地学领域中的应用主要集中在对地质文档及相关资料的搜索上。Zhu等[15]基于开放链接数据,实现从文档中提取本体并生成地质领域词汇,设计了地质数据的KG框架,再根据提取的本体进行实体信息抽取,建立了地质文档的KG。Fan等[16]提出了一种基于DL的命名实体识别模型,构建了地质灾害文献KG。Qiu等[17]提出了一种地质文档分析方法,使用了自动化技术来浏览地质文档和搜索相关的语义知识,改进了文档的搜索和管理。张富利等[18]设计了一套基于KG的勘探开发知识管理系统,针对勘探领域不同成果之间的关联性,实现快速检索,具有较强的辅助作用。
综上所述,针对其他类型的数据,如地质、测井和地震数据的KG相关研究较少,也反映了地学领域数据体本身要素多和关系复杂等特点。目前的沉积相智能识别技术主要还是依靠DL方法,KG与地学的结合仍然是新兴事物,构建KG在地质体识别任务上的工作仍处于一个初级阶段,还需大量的研究工作。
鉴于KG可以更加合理地对地质先验知识进行组织,并进一步提供了逻辑拓扑类知识挖掘的手段,本文依据专家的地质认识建立了丘状体及多期次前积体标签,将地质先验知识引入了KG体系,实现了地质先验知识数字化,形成了KG引导的沉积微相地震识别技术,在川中磨溪地区开展实际应用,实现了灯影组三—四段(后文简称灯三段—灯四段)碳酸盐岩微生物丘状体及多期次前积体的智能识别。
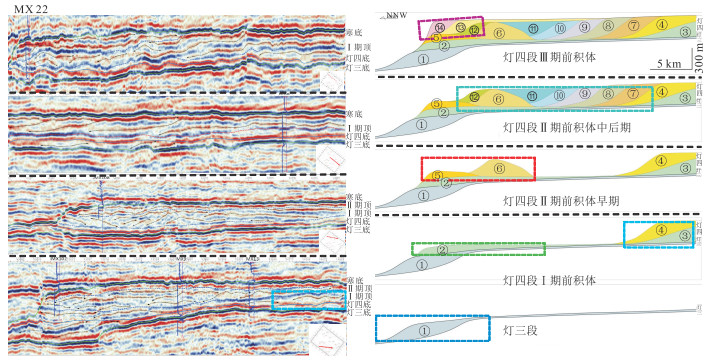
1 沉积微相标签的构建本文以川中磨溪地区灯三段和灯四段沉积模式为例。该工区灯三段早期的海平面较低,后来发生了海侵,使得灯三段的海平面逐步上升。灯四段Ⅰ期在工区东南部出现,Ⅱ期在工区中部由东南向西北逐期推进,Ⅲ期主要分布于工区北部。灯四段Ⅰ期的早期仍存在明显的负向地貌填充现象,而在其晚期出现前积体往南北方向推进的现象。在灯四段Ⅱ期,前积体向南北方向推进的幅度变缓,而横向推进的速度加快,由早期的南北向推进逐渐转变为了北西方向,且推进的距离也较远。当横向推进到Ⅰ期以西及裂陷槽以东的部分时,在第Ⅱ段的后期推进的方向又重新回到北方。灯四段Ⅲ期是在Ⅱ期已经形成的具有一定陡度的前积体坡之后,往裂陷槽的方向继续推进。
灯三段—灯四段沉积序列分为五个阶段(图 1右):沉积序列①为灯三段,是缓坡;灯四段Ⅰ期前积体划分出沉积序列②~④;灯四段Ⅱ期前积体早期,划分出微生物丘滩体⑤和⑥;接着为灯四段Ⅱ期前积体的中后期,划分出沉积序列⑦~⑫;灯四段第Ⅲ期前积体,将该部分位于上层的沉积序列⑬和⑭划分出来。上述依据沉积模式、环境与特征划分的沉积序列,与前文各期的描述相互对应。由不同沉积相划分的地震反射特征在振幅、频率、连续性和同相轴终止等关系上存在一定的差异,利用这一特点将地震反射特征划分为前积、丘状和平行等三类。
|
图 1 四川盆地磨溪地区灯三段—灯四段沉积序列示意图 |
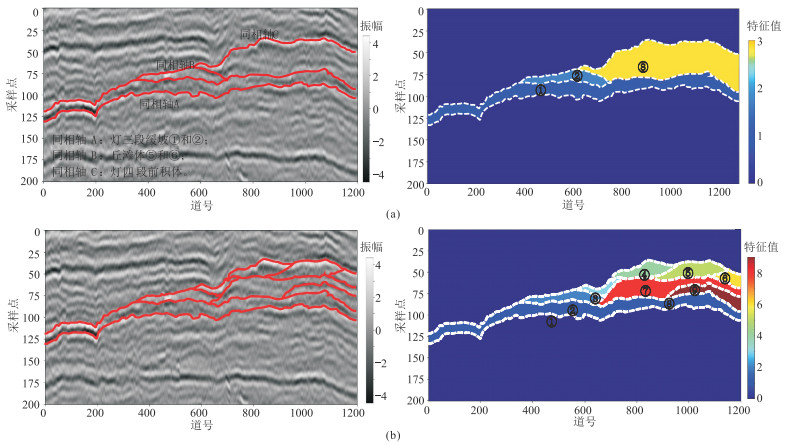
利用地震相反射特征对地震相分类进行标定(图 2a左),图中的同相轴A对应图 1中沉积序列①和②,同相轴B对应了图 1中的微生物丘滩体⑤和⑥,同相轴C对应图 1中的相应的灯四段前积体⑦~⑫。不同类别的前积体反射特征(图 2b左)具有差异性,其岩相也具有一定的区别。在前积体坡折部位主要发育白云岩,而坡折部位向陆一侧发育藻砂屑云岩,在斜坡与坡脚部分以深水相泥晶云岩和泥质云岩为主。丘状反射主要分布于灯四段的Ⅰ期与Ⅱ期的前积体之间,表现为上凸的丘状,内部为弱振幅杂乱反射。平行反射特征分布于灯四段Ⅱ期沉积的中后期,具有高连续性、低频和中强振幅的反射特征,该区薄层状硅质岩较发育,上部发育藻云岩,以纹层结构为主,具有一定的储集能力,中下部发育薄层泥晶云岩夹硅质岩,物性较差。
|
图 2 灯影组层序格架(左)与标签特征值分布(右) (a)四分类解释方案;(b)十分类解释方案 |
该工区勘探目标为丘状体和多期次前积体,根据专家解释标定了四分类和十分类的沉积微相标签,准则如下:①宁缺毋滥,优选多解性少的剖面进行分类表征,尽量保证参与训练的标签数据的正确性;②依据井震标定、测井分层和专家的地质认识对剖面进行层序格架解释,剖面的选取应尽可能垂直于目标构造走向且均匀分布,例如间隔100条主测线或联络线;③依据地震反射特征和沉积模式对地震数据进行分类,不同反射特征需存在可解释的层序界面,不整合面必须依据专家解释方案参考相邻剖面来确定其尖灭点位置,用不同的特征值填充各类别的沉积微相。
四分类解释方案(图 2a右)将灯三段缓坡对应标签特征值设置为1,碳酸盐岩微生物丘滩体的标签特征值为2,灯四段多期次前积体标签的特征值统一设置为3,背景的标签特征值为0。
十分类解释方案(图 2b右)将灯三段的标签特征值设置为1,灯四段Ⅰ期前积体的标签特征值为9,丘状体的标签特征值为2,灯四段Ⅱ期前积体早期的标签特征值为3,灯四段Ⅱ期前积体中后期的标签特征值为5、6、7和8,灯四段Ⅲ期前积体的标签特征值为4,背景值的标签特征值为0。
工区联络线方向共计500条测线,其中12条测线作为训练数据。生物礁体分布受控于台地边缘,碳酸盐岩微生物丘滩体在地震剖面上呈现丘状反射结构,但是不同期次前积体的地震反射特征极其相似且地层尖灭点分布不规律,进一步导致了专家解释的标签数据的数量较少,对于DL方法来说具有极大的挑战性。
对于少量样本问题,必须要利用层序地层格架生成低频趋势模型来约束训练过程,保证预测结果的正确性。另一方面,也需要针对预测目标优化卷积神经网络,局部聚焦于前积体不同期次的地震反射特征,提高智能分类的精度。
2 适用于沉积相识别的网络结构 2.1 引入残差模块的U-Net结构U-Net主要用于语义分割或图像识别,由对称的编码器和解码器组成,具有结构简单、高效且训练参数少等优点,与VGG和SegNet等网络结构相比,深度略显不足,能够获取的局部特征受到了限制。
网络训练时,为了提取丰富的局部特征,大多采取加深网络层数的方式。一般来说,模型层数越深,误差应该越小,然而实际上深层的误差有可能比浅层大,梯度随着网络深度的递增越容易发散。只增加网络深度,训练效果有时不会提升,还会出现网络退化,产生图像细节丢失和梯度消失等问题。
残差模块具有独特的结构,不直接进行卷积运算,采用跳跃连接多个卷积层以串联的方式进行特征提取,在一定程度上避免了梯度消失,结构更加合理,可以适当改变网络深度来匹配目标数据的特征信息,可随着网络深度递增而局部聚焦于前积体不同期次,解决了专家解释标签数据数量不足而导致的卷积神经网络性能不增反退等问题。
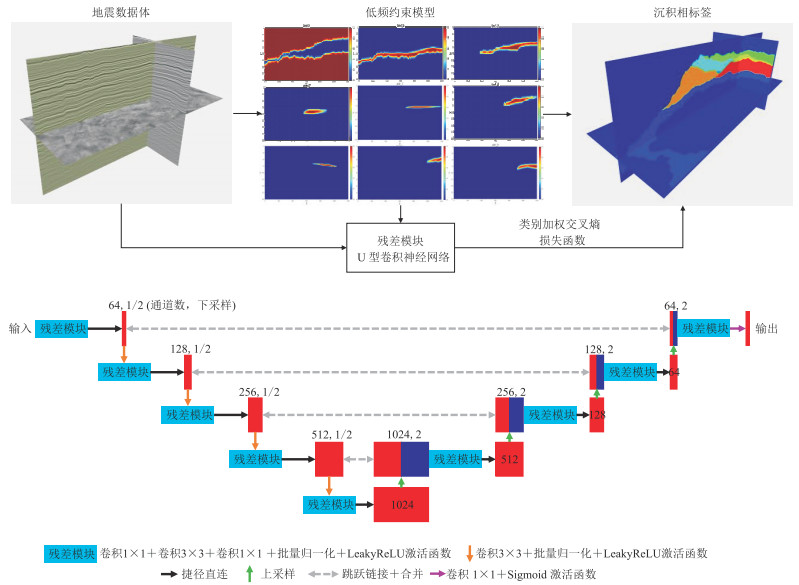
残差模块U型CNN结构仍然保留了对称的编码器和解码器(图 3),输入为地震数据,输出为少量专家标定的标签。数据进入网络之前,必须由层序地层格架生成低频趋势模型来约束训练过程,即按照地震相分类的特征值将低频模型表征到不同的向量空间,再沿着联络线方向抽取固定尺度的地震数据以及对应的低频约束模型作为网络输入,将多分类问题转化成二分类问题。
|
图 3 引入残差模块的U-Net结构 |
编码器部分负责提取地震数据的反射特征,利用多分辨率残差模块替换卷积层,每一次下采样都增加了一个1×1的“捷径”,每一次上采样也增加了一个1×1的“捷径”,残差模块通过上述捷径直连两个3×3卷积层,可获得多个特征图,之后再连接批量归一化和激活函数。
解码器部分恢复和重构地震数据的反射特征,每一次上采样之前需要收缩网络,获得与编码器相同尺寸的数据,即图中跳跃链接操作。上采样将特征图恢复到与编码器相对称的特征图尺寸,网络收缩与扩张的部分,每一层输出结果也需要先进行批量归一化,再利用激活函数提高非线性映射能力。输出由一个1×1的卷积层和一个Sigmoid激活函数组成,加入1×1的卷积层的目的是为了确保输出的特征图与输入的地震数据尺寸相互匹配。
本文采用二维卷积,卷积核大小根据目标数据和特征尺度确定。批量归一化一般在卷积层之后、激活函数之前,目的是缓解地震特征的剧烈变化。如卷积层的输出为
| $ \mu =\frac{1}{m}{x}_{i} $ | (1) |
上一层输出数据的标准差可表示为
| $ {{\sigma }_{\beta }}^{2}=\frac{1}{m}\sum\limits_{i=1}^{m}({x}_{i}-{\mu }_{\beta }{)}^{2} $ | (2) |
那么归一化处理可表示为
| $ {\widehat{x}}_{\mathrm{i}}=\frac{{x}_{i}+{\mu }_{\beta }}{\sqrt[]{{{\sigma }_{\beta }}^{2}}+\varepsilon } $ | (3) |
式中
| $ {y}_{i}=\gamma {\widehat{x}}_{\mathrm{i}}+\beta $ | (4) |
式中
本文采用LeakyReLU和Sigmoid激活函数,分别表示为
| $ f\left({x}_{i}\right)=\left\{\begin{array}{c}{x}_{i}\text{ }{x}_{i}\ge 0\\ \frac{{x}_{i}}{\alpha }\text{ }{x}_{i} < 0\end{array}\right. $ | (5) |
| $ f\left({x}_{i}\right)=\frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }(-{x}_{i})} $ | (6) |
式中
图 3中的直连层用来解决网络的退化问题,若上一层的输出为
| $ {y}_{i}=F({x}_{i},{W}_{H}) $ | (7) |
式中:
在输入和输出层之间增加一条路径
| $ {y}_{i}=F\left({x}_{i},{W}_{H}\right)T\left({x}_{i},{W}_{T}\right)+{x}_{i}C\left({x}_{i},{W}_{C}\right) $ | (8) |
对于二分类问题,令
| $ {y}_{i}=F\left({x}_{i},{W}_{H}\right)T\left({x}_{i},{W}_{T}\right)+{x}_{i}(1-T)\left({x}_{i},{W}_{T}\right) $ | (9) |
通过引入加权路径可知,残差
本文在编码器中利用卷积层实现下采样,与之相应地在解码器中利用上采样恢复数据下采样之前的尺寸(图 3中黄色箭头所示)。跳跃链接以及合并操作用来合并不同的特征图(图 3中灰色箭头所示)。
残差模块可解决不同类型的沉积微相地震反射特征的相似性强导致的卷积层提取不同尺度的地震特征困难等问题,由多个串联的3×3卷积层组成,可提取出多尺度的地震反射特征,还加入了一个1×1卷积层提取空间位置信息。根据分类目标而增加网络中滤波器的数量,可避免浅层的内存需求过大而堆积到网络的深层。
损失函数用来衡量预测值与标签之间的差异程度,该函数值越小,模型的鲁棒性越好。模型训练时,通过前向传播输出预测值,再计算出单批次的预测值和标签之间的差异值,即损失函数值。通过损失函数值反向传播并更新各个参数,以降低标签与预测值之间的差异值,使模型的预测值向标签方向逼近,从而达到学习的目的。
本文采用交叉熵损失函数,针对二分类问题的预测结果只有两种,每个类别的预测概率为
| $ L=\frac{1}{m}\sum\limits_{i}-[{y}_{i}\mathrm{l}\mathrm{n}{p}_{i}+(1-{y}_{i}\left)\mathrm{l}\mathrm{n}\right(1-{p}_{i}\left)\right] $ | (10) |
式中
对于多分类问题,可将上述二分类表达式进行扩展,表示为
| $ L=\frac{1}{m}\sum\limits_{i}{L}_{i}=-\frac{1}{m}\sum\limits_{i}\sum\limits_{c=1}^{m}{y}_{ic}\mathrm{l}\mathrm{n}{p}_{ic} $ | (11) |
式中:
| $ \mathrm{l}\mathrm{n}{p}_{ic}=\mathrm{l}\mathrm{n}\frac{{\mathrm{e}}^{{x}_{ic}}}{\sum\limits_{c=1}^{m}{\mathrm{e}}^{{x}_{ic}}} $ | (12) |
式中
| $ {L}_{i}=-\sum\limits_{c=1}^{m}{y}_{ic}\mathrm{l}\mathrm{n}{p}_{ic} $ | (13) |
| $ L=\frac{1}{m}\sum\limits_{{}_{i}}{L}_{i} $ | (14) |
类别交叉熵损失函数针对多分类问题时,可以给不同类别赋予不同的权重系数,用一个1维的向量表示,该向量长度为类别数m,每个值对应每一类的权重,用于解决样本的类别不均衡问题。将沉积微相的十个分类通过one-hot编码到不同向量空间后,每个向量空间只表征一种相,那么权重系数的向量长度为10,损失函数也可以对每一类单独计算,通过双向传播向标签数据靠拢,实现每一类地震相在层序界面的均衡分割。
2.2 网络训练和预测在上述四分类和十分类沉积微相的标签的基础上,本文对比了常规U-Net网络和残差模块U型网络的训练和预测效果。在训练之前先定义相同迭代次数,采用自适应步长的Adam优化器加速训练,初始学习率设置为0.01。
四分类解释方案(图 4a)分别用常规U型网络和残差模块U型网络训练,从损失函数图中可以看出,两种网络的损失函数都具有较好的收敛过程,但是残差模块U型网络损失函数下降更快,可提高400倍,准确率则无明显差别。十分类解释方案(图 4b)随着目标类别增多,第一轮迭代的损失函数由14000增加到70000,对网络的特征提取能力提出了更高的要求。

|
图 4 两种解释方案的损失函数(左)和学习率曲线(右) (a)四分类方案U-Net(上)和残差模块U-Net(下);(b)十分类方案U-Net(上)和残差模块U-Net(下) |
与四分类相比,当特征值由4增到10时(图 4b),残差模块U型网络的初始损失函数值由25增加到400,损失函数的收敛速度降低了10倍。但是随着迭代更新次数的增加,训练获得了较好的收敛过程,在第14次迭代时,损失函数值均小于0.1。另外,本文采用可变学习率,初始值为0.01,当损失函数在第12次迭代时已不能够优化模型,所以将学习率降为0.005,期望能够进一步提高精度。
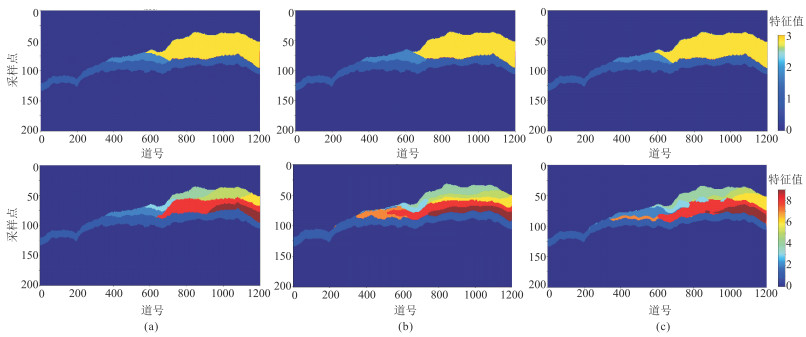
以联络线1403测线为例,四分类解释方案(图 5上)中的碳酸盐岩微生物丘滩体主要分布于台地边缘,多期次前积体整体划分为1类。常规U型网络识别结果(图 5b上)和残差模块U型网络识别结果(图 5c上)差异不大,只在相边界存在一定差别,丘状体在空间位置上符合地质认识,残差模块U-Net的识别结果与标签(图 5a上)更接近,四类地震相之间的层序界面识别精度也较高。
|
图 5 四分类(上)和十分类(下)的沉积微相识别结果对比 (a)沉积微相标签;(b)常规U-Net识别结果;(c)残差模块U-Net识别结果红色、深红色、浅绿色、蓝绿色、绿色、黄色和浅黄色分别代表灯三段不同期次的前积体。 |
同为联络线1403测线,十分类解释方案(图 5下)的浅蓝色代表微生物丘滩体,多期次前积体则分成7类。常规U-Net(图 5b下)和残差模块U-Net(图 5c下)都不理想,虽然地震相都能够划分并识别,但是识别结果不能够准确反映各个期次前积体的反射构型。残差模块U型网络的分类结果略好,更接近标签数据,但是各期次之间仍存在穿层问题,部分期次的前积体叠置关系与专家的地质认识不吻合。
因为不同期次的前积体地震反射特征相似性强,且地层尖灭点分布不规律,导致标签数据的数量少、质量差,故仅依靠DL很难进一步提高沉积微相的识别精度。
3 知识图谱引导沉积微相识别 3.1 引入地质先验知识构建知识图谱DL是一种数据挖掘方法,对于标签数据的依赖性极强。假如标签数据数量少、质量差或分布不均匀,则会导致预测结果存在误差。另外,DL只能通过标签表征数据类型先验知识,如反射特征和地震相边界的空间位置。逻辑类的先验知识,如上述的多期次前积体之间的相互叠置关系,CNN很难提取其特征进行训练,预测结果也需要依靠人工判断其合理性。
KG的优势在于能够表征逻辑类的地质先验知识,如地层接触关系和叠置关系等,故可将地质先验知识转化为“拓扑关系”,实现对地下地质模型的计算机高层逻辑认知。
KG的知识表征形式分为模式层和数据层。为了便于计算机理解地质先验知识以及地质对象之间的拓扑关系,可将不同类别的地震相转换为几何对象,并用几何对象的一维、二维和三维空间位置来描述沉积模式对应的拓扑关系。
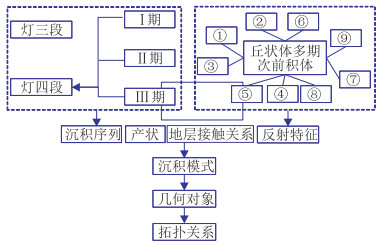
3.1.1 模式层模式层就是以本体的形式存储具有普适性的专家地质先验知识,先依据先验知识对灯三段和灯四段各个期次进行更加细致划分得到的前积体类别,那么节点就是9种不同类别的地震相,而边则是地震相之间的拓扑关系(图 6)。
|
图 6 模式层中地质先验知识的计算机表征 |
模式层首先表征丘状体及多期次前积体的9类地震相之间存在沉积模式、沉积序列、接触关系、产状和反射特征等拓扑关系,并针对它们之间的关系进行计算机建模,以网络结构的形式组织离散的信息和对应关系,完成对地质先验知识的搜索。以沉积序列这一类的地质先验知识为例,各期次间的叠置关系可以表征为特征值在空间内的排列次序,如灯三段发育较早,在灯四段的下方,那么特征值1需设定在特征值2的下方。灯四段Ⅰ期比灯四段Ⅱ期前发育早,特征值9需在特征值2至8的下方,灯四段Ⅱ期标签特征值2至8需在灯四段Ⅲ期标签特征值4的下方。另外,对于地层接触关系这一类的地质先验知识,不同期次之间尖灭点位置也可以表征为特征值之间的交点,如丘状体的特征值2与灯三段的特征值1存在交点,而不能够与灯四段Ⅲ期的特征值4存在交点。
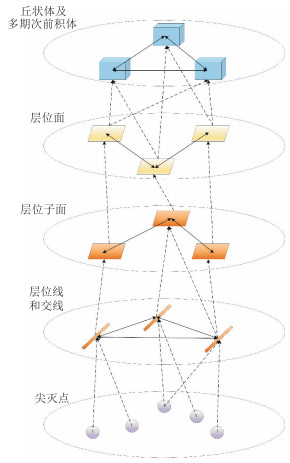
3.1.2 数据层数据层则是从目标地震数据中提取的拓扑关系,以多层网络表征的不同维度地质对象之间的关系,从下到上分为五层,每层的节点分别指尖灭点、层位线、层位子面、层位面和地震相体,而边则表征的是地质对象之间的拓扑关系(图 7)。
|
图 7 数据层中目标数据之间拓扑关系的计算机表征 |
因为KG并不关注层序格架具体的空间位置和几何形态,只关注实体与实体之间关系,为了模型的简单化,更加便于计算机实现,数据层的构建可以只关注各个节点之间的拓扑关系,将层序格架化曲为直,用线框模型表征即可。
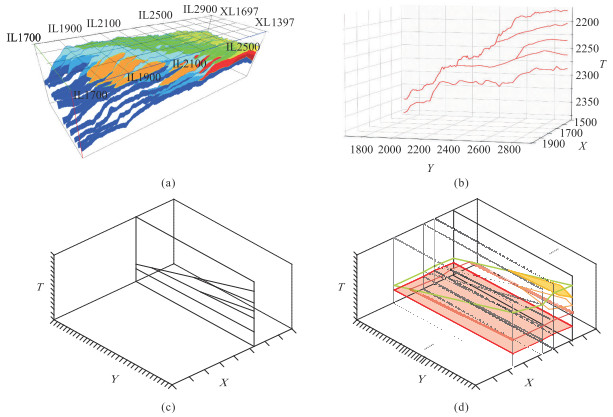
首先按照十分类解释方案提取标签数据体的层序格架(图 8a、图 8b),其次按照联络线方向找到所有尖灭点位置,将层位线分割成层位子线,并将每一条层位子线抽象成直线,得到该层位线对应的线框图(图 8c)。如果无法确定尖灭点具体位置,也可以先粗略计算一个点。最后,根据点构成线,线构成子面,子面构成面,面构成块的逻辑关系,将所有剖面的线框图进行组合得到线框模型(图 8d),即实现了地震相分类到几何对象实体之间的转换。
|
图 8 提取线框模型的过程示意图 (a)三维标签数据;(b)层序格架;(c)二维线框模型;(d)三维线框模型。 |
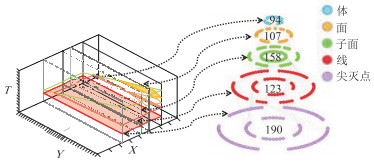
线框模型(图 9左)和数据层(图 9右)二者之间就是实体和拓扑关系的两种不同的可视化形式,线框模型更容易被计算机理解,而数据层则更容易表达线、面和块之间不同维度的拓扑关系。
|
图 9 线框模型(左)和数据层(右)结构可视化表征形式 |
另外,由于数据层是基于目标数据提取的沉积序列、接触关系、产状和反射特征等地质信息,存在不满足地质规律的情况,例如有些尖灭点真实位置无法确定,所以暂时只能得到一个不完备的数据层(图 9右),共计包含190个尖灭点节点,123个线节点,158个子面节点,107个面节点和94个体节点。
鉴于上述数据层的不完备性,可能存在一部分有歧义的地层接触关系,所以需要与模式层中的知识进行相互验证,将模式层和数据层的信息进行知识碰撞并融合,再根据模式层知识对数据层中的错误节点位置进行修正,得到完备数据层。
数据层提取尖灭点位置时,存在顶超和底超两种可能性,由于无法从目标数据中判断真实的尖灭点解释方案(图 10a),则数据层中的该节点和拓扑关系都存在多解性,可根据模式层中的地层接触关系定义修正数据层中错误的节点。另外,如果专家判断后认为数据层提取到了该尖灭点的真实位置,可在模式层中加入新的节点更新模式层。

|
图 10 模式层与数据层的知识碰撞与融合过程 (a)模式层修正数据层中尖灭点的位置;(b)数据层提取尖灭点位置更新模式层。蓝色曲面表示不整合面,红色点表示尖灭点。 |
由于标签剖面不是连续的,某些层序界面只在当前剖面存在,而相邻标签剖面却不存在,则推断层序界面在这两张标签剖面之间存在一个不整合面(图 10b)。这时只能确定该尖灭点的范围,那么可以采取两种方式更新知识图谱:①模式层如果存在对该地层接触关系的表征,则可按照模式层的定义,在相邻标签数据中指定一个尖灭点位置并导入数据层中;②如果模式层中没有对该地层的接触关系进行表征,则说明数据层提取到了新的地质认识,那么也可以重新评估模式层,同时对数据层进行内部推理,只要与模式层的其他节点以及节点间的拓扑关系不冲突,则可将该尖灭点对应的数据层节点以及拓扑关系升级为模式层,完成知识图谱更新。
模式层的各个节点之间表征了本工区相关的沉积模式、沉积序列、接触关系、产状和反射特征等专家地质先验知识,可依据这些拓扑关系修正数据层所有的节点,也可根据数据层中提取的地质认识更新模式层。无论采用哪种方式,直到数据层中的所有节点都满足模式层的定义,就得到了完备的数据层(图 11),共计210个尖灭点,149个线节点,191个子面节点,126个面节点和112个体节点。

|
图 11 完备的知识图谱数据层 |
通过KG模式层和数据层之间的知识碰撞、修正和更新,帮助计算机理解了逻辑类的地质先验知识,得到了完备的数据层,以数据库的形式存储,可在CNN中作为约束条件和质控手段引导沉积相的识别。
利用完备的数据层所表征的线框模型,可进一步生成初始低频约束模型,将其表征到不同的向量空间之后,可作为约束条件参与残差模块U型CNN训练当中,此时低频约束模型中各个期次前积体之间的叠置关系是基于逻辑类的地质先验知识得到的,比少量样本学习中利用人工标定的低频约束模型更为准确。
另一方面,预测结果也不再需要人工质控,可利用完备的线框模型作为质控手段,依靠计算机辨别预测结果的准确性。上述的地学KG是利用自顶向下与自底向上相结合的方式构建,可根据地质认识的提升而随时优化,也可从目标数据中提取新的地质认识而逐步更新。
如表 1所示,对比常规U-Net、残差模块U-Net和KG引导的残差模块U-Net之间的输入数据量和参数量可以明显看出,利用残差模块优化的U-Net网络模型,由于残差模块增加了不同尺度的卷积层和直连层,导致向前和向后传播的数据量增加了约2.7倍,相应的耗时也增加了2.6倍。但是KG对于网络模型来说并没有增加额外的运算量,只在输入端增加了11.97 MB的知识图谱数据层,并转化为低频约束参与模型训练,相对于单批次数据的数据量总和10.9 GB来说无足轻重,对于网络训练耗时影响极小。
|
|
表 1 单批次输入数据量和参数量对比 |
如表 2所示,由常规U-Net、残差模块U-Net和KG引导的残差模块U-Net之间的第10次迭代损失函数值对比可知,残差模块U-Net相较于常规U-Net有所降低,而KG约束下的残差模块U-Net训练损失值下降到0.03,验证损失值则下降到0.06。无论是训练损失还是验证损失,在10次迭代时已经小于0.1,进一步证明了上述两种方法对于沉积微相的分类识别精度来说都有不同程度的提高,特别是KG约束下的网络模型帮助计算机理解了逻辑类的地质先验知识,网络训练时收敛速度更快。
|
|
表 2 模型第10次迭代的损失函数值对比 |
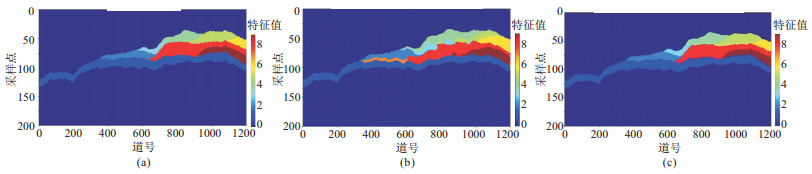
对于十分类解释方案,只依靠残差模块U型网络进行沉积微相分类(图 12b)是无法达到地质专家预期的,分类结果与标签数据(图 12a)相差较大且存在穿层问题,各个期次前积体间的叠置关系更是与标签数据存在较大误差。
|
图 12 引入地质先验知识前、后的识别结果对比 (a)标签数据;(b)残差模块U型网络识别结果;(c)KG引导的DL识别结果 |
与残差模块U型网络的识别结果相比,引入知识图谱约束后的多期次前积体识别(图 12c)精度较高,不同期次前积体之间的叠置关系与标签数据趋于一致,说明在数字化地质先验知识的引导下,预测结果符合地质规律,同时也提高了分类的准确性。
引入KG可以减少语义分割网络因数据驱动特点而导致的局限性,增加了逻辑类地质先验知识后,更加准确地完成沉积微相智能识别任务。
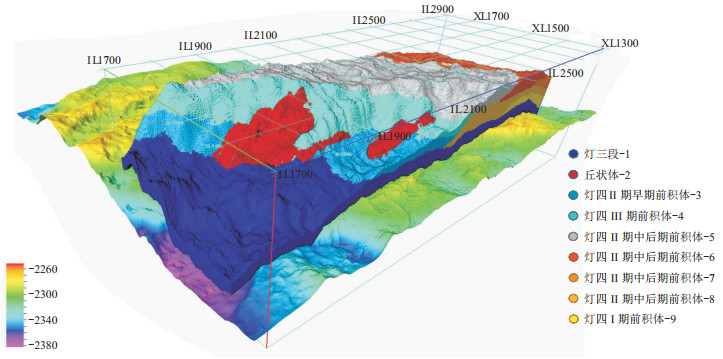
KG和DL两种人工智能方法相结合后,网络模型既能够从多属性输入的训练中学习到特征,又能契合真实数据所在工区的特定地质情况,对上述三维地震数据进行网络训练和预测后,得到碳酸盐岩微生物丘滩体及多期次前积体的三维空间分布智能识别结果(图 13)。
|
图 13 灯影组三—四段沉积微相三维空间分布智能识别结果 |
只依靠DL方法预测多期次前积体的空间分布仍然存在诸多问题,本文引入逻辑拓扑类的地质先验知识,采用自顶向下与自底向上的方式构建KG体系,以数据驱动与先验知识驱动相结合的方式,实现了对碳酸盐岩微生物丘滩体及前积体的智能识别。
通过构建知识图谱实现地下复杂沉积模式的计算机高级认知,以知识图谱中包含的人类认知作为约束条件实现沉积微相智能地震识别,有效解决了深度学习方法标签数据难以获取的问题。将专家的地质先验知识引入知识图谱后,提高了沉积微相的预测精度,预测结果更加符合地质认识。
| [1] |
WU X, LIANG L, SHI Y. et al. FaultSeg3D: using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. DOI:10.1190/geo2018-0646.1 |
| [2] |
WU X, YAN, QI J, et al. et al. Deep learning for characterizing paleokarst collapse features in 3-d seismic images[J]. Journal of Geophysical Research Solid Earth, 2020, 125(9): E2020JB019685. DOI:10.1029/2020JB019685 |
| [3] |
WALDELAND A U, JENSEN A C, GELIUS L J, et al. Convolutional neural networks for automated seismic interpretation[J]. The Leading Edge, 2018, 37(7): 482-560. |
| [4] |
SHI Y, WU X, FOMEL S. SaltSeg: Automatic 3D salt segmentation using a deep convolutional neural network[J]. Interpretation, 2019, 7(3): 1A-T725. DOI:10.1190/INT-2019-0729-FE.1 |
| [5] |
AO Y, LI H, ZHU L, et al. Identifying channel sand-body from multiple seismic attributes with an improved random forest algorithm[J]. Journal of Petroleum Science and Engineering, 2019, 173: 781-792. DOI:10.1016/j.petrol.2018.10.048 |
| [6] |
SINGH H, SEOL Y, MYSHAKIN E M. Automated well-log processing and lithology classification by identifying optimal features through unsupervised and supervised machine-learning algorithms[J]. SPE Journal, 2020, 25(5): 2778-2800. DOI:10.2118/202477-PA |
| [7] |
GARDNER M, TALUKDAR P, KRISHNAMURTHY J, et al. Incorporating vector space similarity in random walk inference over knowledge bases[C]. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), 2014, 397-406.
|
| [8] |
陈曦, 陈华钧, 张文. 规则增强的知识图谱表示学习方法[J]. 情报工程, 2017, 3(1): 26-34. CHEN Xi, CHEN Huajun, ZHANG Wen. Rule-augmented representation learning approach in knowledge graph[J]. Technology Intelligence Engineering, 2017, 3(1): 26-34. |
| [9] |
杨存, 孟贺, 叶月明, 等. 沉积相智能地震识别技术研究及应用[J]. 石油地球物理勘探, 2023, 58(3): 528-539. YANG Cun, MENG He, YE Yueming, et al. Research and application of intelligent seismic identification technology of sedimentary facies[J]. Oil Geophysical Prospecting, 2023, 58(3): 528-539. |
| [10] |
李素华, 李蓉, 石国山, 等. 四川盆地井研地区栖霞组白云岩储层识别及有利区预测[J]. 石油物探, 2023, 62(4): 708-720. LI Suhua, LI Rong, SHI Guoshan, et al. Identification and favorable area prediction of dolomite reservoir of Middle Permian Qixia Formation in Jingyan area, Sichuan Basin[J]. Geophysical Prospecting for Petroleum, 2023, 62(4): 708-720. |
| [11] |
周琨. 根据低角度前积地震反射特征划分分流砂坝型浅水三角洲相带[J]. 石油地球物理勘探, 2023, 58(4): 961-969. ZHOU Kun. Division of distributary sandbar-type shallow-water delta facies belts based on low-angle progradation seismic reflection characteristics[J]. Oil Geophysical Prospecting, 2023, 58(4): 961-969. |
| [12] |
刘宝鸿, 郭彦民, 田志, 等. 利用地震相控反演预测辽河坳陷兴隆台潜山中生界致密砂砾岩优质储层[J]. 石油地球物理勘探, 2022, 57(增刊2): 100-109. LIU Baohong, GUO Yanmin, TIAN Zhi, et al. Prediction of high-quality tight sandy conglomerate reservoirs in Mesozoic of Xinglongtai buried hill, Liaohe Depression by seismic facies-controlled inversion[J]. Oil Geophysical Prospecting, 2022, 57(S2): 100-109. |
| [13] |
QIAN W, FU C, ZHU Y, et al. Translating embeddings for knowledge graph completion with relation attention mechanism[C]. Proceedings of the 27th International Joint Conference on Artificial Intelligence, 2018, 4286-4292.
|
| [14] |
AN B, CHEN B, HAN X P, et al. Accurate text-enhanced knowledge graph representation learning[C]. Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 2018, 745-755.
|
| [15] |
ZHU Y, ZHOU W, XU Y, et al. Intelligent learning for knowledge graph towards geological data[J]. Scientific Programming, 2017, 2017: 5072427. |
| [16] |
FAN R, WANG L, YAN J, et al. Deep learning-based named entity recognition and knowledge graph construction for geological hazards[J]. ISPRS International Journal of Geo-information, 2019, 9(1): 15. DOI:10.3390/ijgi9010015 |
| [17] |
QIU Q, XIE Z, WU L, et al. Automatic spatiotemporal and semantic information extraction from unstructured geoscience reports using text mining techniques[J]. Earth Science Informatics, 2020, 13(4): 1393-1410. DOI:10.1007/s12145-020-00527-9 |
| [18] |
张富利, 张恩莉, 向永慧, 等. 知识图谱技术在石油天然气勘探开发知识管理中的应用探讨[J]. 信息系统工程, 2020(1): 128-131. ZHANG Fuli, ZHANG Enli, XIANG Yonghui, et al. Application of knowledge graph technology in knowledge management of oil and gas exploration and development[J]. China CIO News, 2020(1): 128-131. |



 杨存, 浙江省杭州市西溪路920号中国石油杭州地质研究院,310023。Email:
杨存, 浙江省杭州市西溪路920号中国石油杭州地质研究院,310023。Email: