0 引言

地震勘探是了解地质构造的有效手段，在油气勘探中发挥着重要的作用。受地理因素及经济条件的限制，采集的地震数据通常沿空间坐标分布不规则，或受技术因素的影响出现坏道或缺失，严重影响了后续地震资料的处理、解释工作。因此，重建缺失的地震数据具有重要的实际意义。

近年来，提出了很多地震数据重建的方法，包括传统方法和深度学习方法。传统方法可以大致分成四类：基于波动方程的方法^[1-2]；基于变换域的方法，如基于小波变换的方法^[3]和基于傅里叶变换的方法^[4]；预测误差滤波方法^[5]；基于低秩的方法^[6-7]。传统方法对先验知识以及计算成本的要求较高，限制了它们在实际中的应用。

随着深度学习在图像处理中显示出巨大的潜力，基于深度学习的数据驱动插值方法在地球物理领域得到广泛的应用^[8-13]。在地震数据重建方面，Mandelli等^[14]采用卷积自编码网络实现了叠前地震数据的重建；Oliveira等^[15]使用条件生成对抗网络解决叠后地震数据集中的插值问题；Chai等^[16]引入U-Net模型用于重建随机缺失以及规则缺失的地震数据。由于常用的卷积运算只能捕捉到局部特征，对全局信息利用不充分。为此，Pan等^[17]提出了基于部分卷积的深度学习网络，通过分层的区域学习机制实现数据的重构；Fang等^[18]在U-Net框架的基础上提出纹理损失以保证局部结构信息的准确性；Li等^[19]将注意力机制融入U-Net进行缺失地震道的重建。上述方法在一定程度上弥补了卷积运算提取局部特征的不足，但是采样层的池化操作也可能会破坏地震反射的详细特征。Liu等^[20]考虑地震资料的多尺度特征，提出一种基于小波残差的深度学习模型，有效提高了地震数据的重建精确。

考虑到常用的卷积运算不能充分利用全局信息，池化操作也会造成特征图信息的丢失，本文提出了小波通道注意力网络。基于U-Net的优越性，采用哈尔小波变换(Haar Wavelt Transform，HWT)代替池化操作，逆小波变换(Inverse Wavelt Transform，IWT)代替上采样操作。HWT能促进多尺度特征的提取，IWT避免了特征图重建过程的信息丢失。高效通道注意力(ECA)模块能够捕捉不同通道特征图的相关性，从而有效地利用全局信息。通过对地震数据的增广处理，即通过翻转及加噪方式，提高网络模型的泛化能力和鲁棒性。合成和实际地震数据的实验结果表明，与具有代表性的深度学习方法相比，本文的小波通道注意力网络的重建结果精度更高。

1 方法 1.1 哈尔小波变换

小波变换是一种有效的特征提取工具，在计算机视觉任务中得到了广泛的应用^[21-22]。受多级小波卷积神经网络^[21]的启发，本文将HWT融入网络模型，以便恢复地震数据的纹理信息。HWT是一种简单且计算高效的算法，其低通滤波器$ \boldsymbol{L} $和高通滤波器$ \boldsymbol{H} $可表示为

$ \left\{\begin{array}{l}\boldsymbol{L}=\frac{1}{\sqrt{2}}\left[\begin{array}{c}\mathrm{1,1}\end{array}\right]\\ \boldsymbol{H}=\frac{1}{\sqrt{2}}\left[\begin{array}{c}-\mathrm{1,1}\end{array}\right]\end{array}\right. $

(1)

对于输入的特征图x，经过滤波器进行采样可以获得四个子带图像x₁、x₂、x₃和x₄，分别表示低频分量和带有方向特征的高频分量。其中，低频部分含有地震数据的主要特征信息，而高频部分捕获了更复杂的纹理细节。由于HWT的正交特性，IWT操作可以确保在不丢失信息的情况下恢复特征图。IWT可表示为

$ \boldsymbol{x}=\mathrm{I}\mathrm{W}\mathrm{T}({\boldsymbol{x}}_{1},{\boldsymbol{x}}_{2},{\boldsymbol{x}}_{3},{\boldsymbol{x}}_{4}) $

(2)

1.2 高效通道注意力模块

注意力机制是优化神经网络的重要研究方向。在不显著增加模型复杂度的基础上，注意力机制可以加强网络对数据本质特征的关注。然而，大多数现有方法专注于开发更复杂的注意力模块以实现网络对数据本质特征的关注，不可避免地增加了模型的复杂度。为弥补卷积运算提取局部特征的不足，本文采用高效通道注意力模块^[23]促进模型对全局信息的关注。

ECA是一个轻量级的即插即用模块，避免了维度降低对于学习通道注意力的影响，在图像检测和分割任务中表现出良好的泛化能力。特征图通过全局平均池化后，ECA模块首先自适应地确定卷积核大小k，再执行一维卷积，然后用一个Sigmoid函数得到各个通道特征图的权重$ {\omega }_{i} $，最后将权重$ \boldsymbol{\omega }=\left[{\omega }_{1},{\omega }_{2},\cdots ,{\omega }_{C}\right] $与原始输入特征图$ \boldsymbol{y}=\left[{\boldsymbol{y}}_{1},{\boldsymbol{y}}_{2},\cdots ,{\boldsymbol{y}}_{C}\right] $对应元素相乘，得到特征图的输出，C表示通道维数。

对于给定的通道维数$ C $，卷积核大小k可以自适应地确定

$ k=\psi \left(C\right)={\left|\frac{\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}C}{\gamma }+\frac{b}{\gamma }\right|}_{\mathrm{o}\mathrm{d}\mathrm{d}} $

(3)

式中：超参数$ \gamma $和$ b $分别设为2和1；$ {\left|t\right|}_{\mathrm{o}\mathrm{d}\mathrm{d}} $表示最接近$ t $的奇数。

在ECA模块中，只考虑第i个通道特征图$ {\boldsymbol{y}}_{i} $与其k个相邻通道特征图间的信息交互，$ {\boldsymbol{y}}_{i} $的权重$ {\omega }_{i} $表示为

$ {\omega }_{i}=\sigma \left(\sum\limits_{j=1}^{k}{\omega }_{i}^{j}{\boldsymbol{y}}_{i}^{j}\right)\begin{array}{cc}& \end{array}{\boldsymbol{y}}_{i}^{j}\in {\boldsymbol{\varOmega }}_{i}^{k} $

(4)

式中：$ \sigma $为Sigmoid函数；$ {\boldsymbol{\varOmega }}_{i}^{k} $表示$ {\boldsymbol{y}}_{i} $的k个相邻特征图；$ {\boldsymbol{y}}_{i}^{j} $为$ {y}_{i} $的$ k $个相邻特征图中第$ j $个特征图; $ {\omega }_{i}^{j} $为$ {\boldsymbol{y}}_{i}^{j} $的权重。

为进一步提高性能，通道之间共享权重参数，即

$ {\omega }_{i}=\sigma \left(\sum\limits_{j=1}^{k}{\omega }^{j}{\boldsymbol{y}}_{i}^{j}\right)\begin{array}{cc}& \end{array}{\boldsymbol{y}}_{i}^{j}\in {\boldsymbol{\varOmega }}_{i}^{k} $

(5)

式中$ {\omega }^{j} $为$ {\boldsymbol{y}}_{i} $的$ k $个相邻通道特征图的共享权重。

ECA模块通过执行快速一维卷积实现通道之间的信息交互，得到特征图$ \boldsymbol{y} $的权重

$ \omega =\sigma \left[\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}{1}_{k}\left(\boldsymbol{y}\right)\right] $

(6)

式中Conv1_k 表示一维卷积，只涉及到$ k $个参数。

2 模型架构

小波通道注意力网络的整体架构如图 1所示。网络模型基于U-Net，由编码器、解码器和跳跃连接(Skip-connection)三部分构成。本文采用HWT取代U-Net中的采样操作，进一步提升地震数据的重建精度。在编码器阶段，HWT用于提取特征图的多尺度特征，使特征图的宽高减半而通道数量变成原来的四倍。解码器阶段，IWT用于生成上采样的特征图。小波卷积网络包含多个卷积注意力模块(Con-ECA)。该模块由两个3×3的双重卷积块(DoubleConv3×3)和ECA模块构成，用于提高模型捕捉全局特征信息的能力。除最后一个3×3的卷积(Conv3×3)层外，在每个卷积层之后使用批量归一化(BatchNorm)和ReLU函数，以增强模型泛化能力和非线性映射能力。

3 数值实验

应用合成和实际地震数据验证小波通道注意力网络的地震数据重建有效性，并与U-Net^[16]、基于坐标注意力机制的U-Net网络(CA-U-Net)^[19]、基于小波变换的卷积神经网络(MWCNN)^[21]对比。四种网络均在均方误差(MSE)损失函数指导下训练。实验基于GPU加速的PyTorch框架，在Windows10环境的GTX3060处理器下运行。网络模型使用Adam优化算法，学习率设为10^-3、批量大小为64。为了定量分析网络模型的有效性，使用信噪比(SNR)、MSE、结构相似性(SSIM)评估地震数据重建效果。MSE定义为

$ \mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{N}{‖\boldsymbol{x}-\widehat{\boldsymbol{x}}‖}_{2} $

(7)

式中：N为数据样点数；x和$ \widehat{\boldsymbol{x}} $分别表示完整地震数据和重建的地震数据。MSE值越小表明重建质量越高。SNR定义为

$ \mathrm{S}\mathrm{N}\mathrm{R}=20\times \mathrm{l}\mathrm{g}\frac{{‖\boldsymbol{x}‖}_{2}}{{‖\boldsymbol{x}-\widehat{\boldsymbol{x}}‖}_{2}} $

(8)

SNR越高意味着重建精度越高。SSIM用作度量两个图像之间的相似性，定义为

$ \mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}=\frac{2{\mu }_{\boldsymbol{x}}{\mu }_{\widehat{\boldsymbol{x}}}+{c}_{1}}{{{\mu }_{\boldsymbol{x}}}^{2}+{{\mu }_{\widehat{\boldsymbol{x}}}}^{2}+{c}_{1}}\times \frac{2{\tau }_{\boldsymbol{x}\widehat{\boldsymbol{x}}}+{c}_{2}}{{{\tau }_{\boldsymbol{x}}}^{2}+{{\tau }_{\widehat{\boldsymbol{x}}}}^{2}+{c}_{2}} $

(9)

式中：$ {\mu }_{\boldsymbol{x}} $和$ {\mu }_{\widehat{\boldsymbol{x}}} $分别表示x和$ \widehat{\boldsymbol{x}} $的均值；$ {\tau }_{\boldsymbol{x}} $和$ {\tau }_{\widehat{\boldsymbol{x}}} $表示x和$ \widehat{\boldsymbol{x}} $的标准差；$ {\tau }_{\boldsymbol{x}\widehat{\boldsymbol{x}}} $表示x和$ \widehat{\boldsymbol{x}} $的协方差；c₁和c₂为常数，以避免分母接近于0时造成不稳定。

3.1 合成地震数据处理

从公开的人工合成地震数据SEG C3中随机选取500个单炮记录作为数据集，每炮有201道，每道201个采样点，时、空采样间隔分别为8 ms和12.5 m。训练集、验证集和测试集中的炮集数量分别为400、50和50。在每个炮集中随机设置60%~80%缺失道，并将地震数据归一化。在训练阶段，为了确保内存的使用，采用滑动窗口机制将炮集处理为9000个128×128大小的切片，并对50%的切片做数据增广处理。

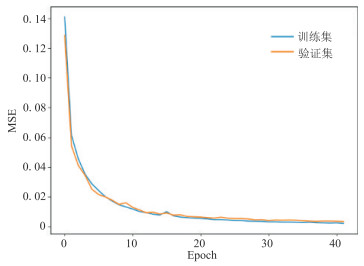
由图 2可见，随着训练周期(Epoch)的增加，小波通道注意力网络在训练集和验证集上的MSE损失逐渐降低，表明网络模型的训练过程是有效的；随着训练的进行，网络模型表现出了高度的稳定性。

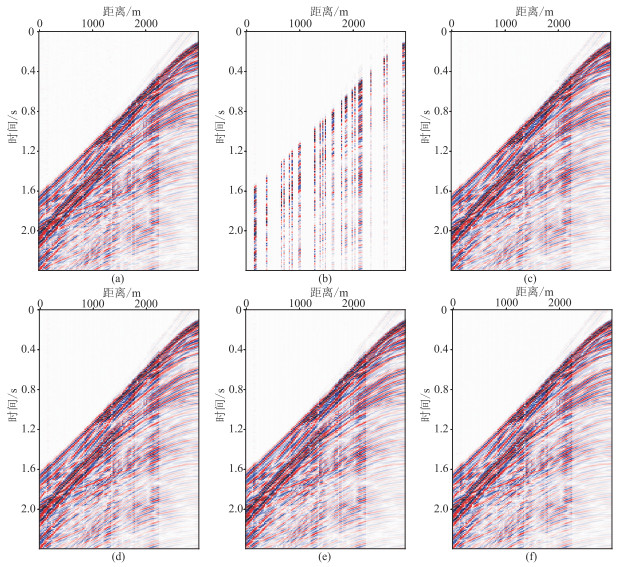
模型训练结束后，随机选取测试集中单炮记录(图 3a、图 3b)进行重建，四种网络模型的重建结果结果如图 3c~图 3f所示。可以看出：面临缺失间隙较大的情况，仅依赖卷积操作提取到的局部信息，U-Net模型很难恢复缺失区域的地震道(图 3c红色椭圆形区域)；在注意力机制的帮助下，CA-U-Net模型促进了信息的充分利用，但取得的效果仍不能令人满意(图 3d)；MWCNN因小波变换的嵌入避免了采样过程中的信息丢失，在一定程度上提高了模型对弱地震信号的恢复(图 3e)。相比于MWCNN，本文的小波通道注意力网络恢复了更真实的纹理信息，在合成数据实验中的重建结果更精确(图 3f)。

图 4为合成数据不同方法的重建误差。不难看出，相比于其他三种深度学习方法，本文的小波通道注意力网络的重建误差最小(图 4d)，重建结果更接近完整地震数据，尤其是方框处。表 1为四种网络模型重建结果的定量指标对比，本文网络模型的SSIM、SNR和MSE三个指标均最优。

3.2 实际地震数据处理

应用美孚阿沃维京地堑12号线数据进一步测试本文的小波通道注意力网络的性能。随机选取400个完整炮集，每炮120道，每道600个采样点，时间采样间隔为4 ms。以8∶1∶1比例划分训练集、验证集和测试集。与合成地震数据实验相同，对炮集做60%~80%随机道缺失和归一化处理。

表 2为实际数据四种网络模型重建结果的定量指标统计，可以看出，本文的网络模型的三个指标均优于其他三种模型，表明小波通道注意力网络可以产生更高质量的重建结果。四种网络模型重建的单炮记录如图 5所示。为了仔细比较不同模型的重建结果的差异，抽取两条相邻的重建地震道与原始地震道的对比如图 6所示。尽管四种模型的单炮记录重建结果没有明显差异，但本文的小波通道注意力网络(图 6d)重建结果与原始道最接近、最合理。

合成和实际地震数据实验结果表明，本文的小波通道注意力网络的地震数据重建精度最高。

4 结束语

本文提出了小波通道注意力网络模型用于随机缺失地震数据的重建。用哈尔小波变换取代了传统的采样层，实现了模型对多尺度特征的提取，避免了上采样特征图的信息丢失。此外，高效通道注意力模块提升了网络模型的重建性能。合成和实际地震数据实验结果表明，与具有代表性的三种深度学习方法相比，本文的小波通道注意力网络地震数据重建结果精度最高、效果最佳。