2. 广东石油化工学院石油工程学院, 广东茂名 525000
2. School of Petroleum Engineering, Guangdong University of Petrochemical Technology, Maoming, Guangdong 525000, China
地震属性是指由叠前或叠后地震数据,经过一定的数学公式变换为有关地震波的几何形态、运动学特征、动力学特征和统计学特征的特殊测量值。地震储层预测是有效描述地震属性参数与储层参数关系的方法。地质工作者通过提取和分析特定时窗内地震属性区分岩性特征,从而识别储层岩性。利用地震属性识别储层岩性时,往往只能优选一种或几种地震属性作为参考,会损失大量有效信息,而且由于地震属性特征受多种因素影响,应用多种地震属性识别储层岩性时存在多解性,致使储层岩性识别难度极大。
针对基于地震属性识别储层岩性时有效信息损失和多解性等问题,人工智能地震属性岩性识别方法应运而生[1-4]。文献[5-7]以地震属性数据为输入样本,采用BP神经网络识别储层岩性,但受梯度下降法的局限,BP网络在训练时易陷入局部极小值,难以达到全局最优解。文献[8]采用概率神经网络基于地震属性识别储层岩性,由于难以估计概率神经网络的概率函数,导致隐层节点数和空间复杂度均较高。文献[9]采用深度信念网络基于地震属性识别储层岩性,由于深度信念网络采用多层受限玻尔兹曼机构造,训练方法的本质仍然是梯度下降法,因此也易陷入局部极值。文献[10]采用卷积神经网络,首先利用叠后地震数据预测河道砂体分布,然后利用叠前地震数据预测河道内部储层类型及分布;但卷积神经网络需要采集一维序列样本或二维图像样本,因此样本构造过程相对复杂。因此,简单、实用且精度较高的岩性识别算法始终是该领域的追求目标。
T-S模型是一种模糊推理方法,它模拟了人脑的思维过程,不仅分类精度较高而且可解释性强,广泛用于分类领域。确定T-S模型的参数是训练该模型的中心任务,目前的常用方法是梯度下降法和智能优化算法。鉴于梯度下降法易陷入局部极值、普通群智能优化算法易早熟收敛,本文提出一种基于量子衍生涡流算法(Quantum Vortex Search Algorithm, QVSA)和T-S模糊推理模型的岩性识别方法,QVSA具有操作简单、收敛速度快、寻优能力强等优点。首先利用QVSA优化T-S模糊推理模型的各种参数;然后利用主成分分析方法降低获取的地震属性维度;再利用优化的T-S模糊推理模型识别储层岩性。实验结果表明,利用所提方法识别储层岩性的效果较好,岩性识别正确率高于普通BP网络方法,验证了方法的可行性和有效性。
1 QVSA涡流搜索算法(Vortex Search Algorithm, VSA)是2015年提出的一种新型优化算法[11],具有操作简单、收敛速度快、寻优能力强的优点。
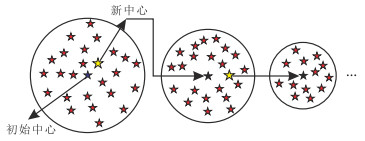
1.1 VSAVSA受涡流现象启发,建模时将最优解作为涡流中心,采用逆不完全伽马函数[12]缩减涡环半径,通过逐步迭代使涡流中心逐步逼近优化问题的最优解。该算法的寻优过程(图 1)简述如下。
|
图 1 VSA的搜索过程 |
(1) 产生初始解
VSA建模在搜索过程中涡环的半径逐渐缩小,并将最外涡环的中心设为搜索空间中心,该中心即为初始解。
(2) 产生候选解
候选解集
(3) 当前解更新
从候选解集
(4) 半径缩减方法
VSA的每步迭代都采用逆不完全伽马函数[12]
| $ {\sigma }_{t}={\sigma }_{0}(1/\lambda )\gamma (\lambda ,{a}_{t}) $ | (1) |
式中:λ为随机变量;at为分辨率参数,
借助逆不完全伽马函数的优良特性,可使搜索过程的前半程侧重于全局探索,后半程侧重于局部开发,从而达到探索与开发间的合理平衡。
1.2 QVSAQVSA是VSA与量子计算融合的结果,旨在利用量子计算方法提升VSA的寻优能力。QVSA利用量子比特对候选解编码,利用量子比特在Bloch球面上的绕轴旋转更新候选解,通过不断迭代、寻优直到满足算法的终止条件。
(1) 涡流中心初始化
为不失一般性,本文以最小值优化为例。最初的涡流中心可用量子比特初始化
| $ |{\mu }_{0}〉=\left(|{\varphi }_{1}〉,\mathrm{ }\cdots \mathrm{ },\mathrm{ }|{\varphi }_{D}〉\right) $ | (2) |
其中
| $ |{\varphi }_{d}〉={\left(\mathrm{c}\mathrm{o}\mathrm{s}\frac{{\theta }_{d}}{2}\text{ }{\mathrm{e}}^{\mathrm{i}{\phi }_{d}}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{\theta }_{d}}{2}\right)}^{\mathrm{T}} $ |
式中:
采用泡利矩阵σ=(σx σy σz)(σx、σy、σz分别为σ在x、y、z方向的分量)测量
| $ {x}_{d}=〈{\phi }_{d}\left|{\sigma }_{x}\right|{\phi }_{d}〉=\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{d}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{d} $ | (3) |
| $ {y}_{d}=〈{\varphi }_{d}\left|{\sigma }_{y}\right|{\varphi }_{d}〉=\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{d}\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_{d} $ | (4) |
| $ {z}_{d}=〈{\varphi }_{d}\left|{\sigma }_{z}\right|{\varphi }_{d}〉=\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{d} $ | (5) |
由于
| $ {X}_{d}=\frac{1}{2}\left[\mathrm{m}\mathrm{i}{\mathrm{n}}_{d}\right(1-{x}_{d})+\mathrm{m}\mathrm{a}{\mathrm{x}}_{d}(1+{x}_{d}\left)\right] $ | (6) |
式中
(2) 候选解的产生
QVSA将
| $ \begin{array}{l}|{\widehat{\varphi }}_{d}〉={\boldsymbol{R}}_{y}[{\delta }_{d}\left(t\right)\left]\right|{\varphi }_{d}〉\\ =\left(\begin{array}{l}\mathrm{c}\mathrm{o}\mathrm{s}\frac{{\delta }_{d}\left(t\right)}{2}-\mathrm{s}\mathrm{i}\mathrm{n}\frac{{\delta }_{d}\left(t\right)}{2}\\ \mathrm{s}\mathrm{i}\mathrm{n}\frac{{\delta }_{d}\left(t\right)}{2}\text{ }\mathrm{c}\mathrm{o}\mathrm{s}\frac{{\delta }_{d}\left(t\right)}{2}\end{array}\right)\times |{\varphi }_{d}〉\end{array} $ | (7) |
| $\left|\hat{\varphi}_d\right\rangle=\boldsymbol{R}_z\left[\delta_d(t)\right]\left|\varphi_d\right\rangle=\left(\begin{array}{cc} 1 & 0 \\ 0 & \mathrm{e}^{\mathrm{i} \delta_d(t)} \end{array}\right) \times\left|\varphi_d\right\rangle$ | (8) |
式中:Ry为绕y轴的旋转矩阵;Rz为绕z轴的旋转矩阵。将
(3) 最优解的更新
假定
(4) 算法终止条件
本文采用限定迭代次数作为终止条件,即无论优化结果如何,算法都将一直运行,直至达到预定义的最大迭代次数。
2 基于QVSA的T-S推理模糊模型构建方法 2.1 T-S推理模糊模型1985年,Takagi等[14]提出了一种基于模糊推理规则的评价模型,该模型的突出优点是,在模型输出端不需采用去模糊化处理,基于对所有模糊规则的综合,可直接获得数值结果。第
若
| $ {u}^{i}={p}_{0}^{i}+{p}_{1}^{i}{I}_{1}+{p}_{2}^{i}{I}_{2}+\cdots +{p}_{n}^{i}{I}_{n} $ | (9) |
式中:
对于
| $ \left\{\begin{array}{l}{u}^{i}={p}_{0}^{i}+{p}_{1}^{i}{I}_{1}+{p}_{2}^{i}{I}_{2}+\cdots +{p}_{n}^{i}{I}_{n}\\ \mu \left({u}^{i}\right)={\mu }_{{\boldsymbol{A}}_{1}^{i}}\left({x}_{1}\right){\mu }_{{\boldsymbol{A}}_{2}^{i}}\left({x}_{2}\right)\cdots {\mu }_{{\boldsymbol{A}}_{n}^{i}}\left({x}_{n}\right)\end{array}\right. $ | (10) |
此时,综合所有
| $ u=\frac{\sum\limits_{i=1}^{m}\mu \left({u}^{i}\right){u}^{i}}{\sum\limits_{i=1}^{m}\mu \left({u}^{i}\right)} $ | (11) |
综上所述,建立T-S模糊推理模型,关键在于确定式(9)中模糊规则的前件参数(高斯隶属度函数的中心、方差)和后件参数
在T-S模型中,模糊规则数目随输入变量个数增多呈指数增长,变量个数一般较多,传统方法(如梯度法)不易得到理想结果。因此,本文采用QVSA优化、确定这些参数。假设T-S模型有n个输入指标,下面阐述T-S模型的构建方法。
(1) 构造训练样本集
为便于描述,假定储层共有
(2) 构造目标函数
目标函数是构造和评价T-S模型的工具,通常以T-S模型的参数为自变量,而函数值则能反映T-S模型的质量。因此,本文选用T-S模型的错误识别样本数作为目标函数。首先对T-S模型的实际输出实施四舍五入取整操作,然后将实际输出和期望输出不一致的样本数(即识别错误的样本数)作为目标函数,即
| $ E=\sum\limits_{k=1}^N g\left(\hat{o}_k, o_k\right) \quad g\left(\hat{o}_k, o_k\right)= \begin{cases}1 & \hat{o}_k \neq o_k \\ 0 & \hat{o}_k=o_k\end{cases} $ | (12) |
式中:
(3) 构造T-S模糊推理模型
为降低T-S模糊推理模型的计算复杂度,对于n个输入指标,均选取“低(L)”和“高(H)”这2个模糊语言变量,采用高斯型模糊集隶属函数。因此,n个输入指标共可构造
1) 若
2)若
︙
(4) 优化确定T-S模糊推理规则参数
根据式(9),每条模糊规则含有
利用QVSA构建的T-S模糊推理模型识别实际储层岩性,并与普通BP网络储层岩性识别方法对比,以检验方法的效果。
3.1 基础资料处理研究区为松辽盆地北部中央坳陷区三肇凹陷西北部的卫星油田实验区,全区整体构造形态大致呈“西高东低”的斜坡,面积约为36.22 km2。目的层为下白垩统姚家组一段葡萄花油层,为盆地北部的大型朵叶状三角洲沉积,部分属于泛滥平原下游的大型河流沉积。岩性以一套粉砂岩夹灰、灰绿色泥岩及过渡岩为主,储层呈砂泥岩薄互层、钙质夹层交互组合。
选取370口井的目标时间单元样本进行测井解释,同时在精细合成记录标定的基础上,按照不同时间单元的时间深度提取26种地震属性:1)平均能量;2)平均信噪比;3)平均绝对振幅;4)平均瞬时频率;5)平均瞬时相位;6)平均波峰振幅;7)平均反射强度;8)相关长度;9)能量半衰时;10)峰态振幅;11)最大绝对振幅;12)最大波峰振幅;13)最大波谷振幅;14)最大值;15)平均振幅;16)最小值;17)正负样点比;18)均方根振幅;19)能量半衰斜率;20)瞬时频率斜率;21)反射强度斜率;22)振幅厚度;23)总绝对振幅;24)总振幅;25)总能量;26)振幅方差。
储层包括砂岩、泥岩两类岩性,分别用1、0编码,样本数量分别为242个和128个。部分储层的原始数据如表 1所示。基于这些样本数据,采用QVSA构建T-S模糊推理模型,使其逼近储层岩性指标与类属之间的复杂映射关系,以识别大量测试样本的未知岩性。
|
|
表 1 储层岩性识别的部分原始样本数据 |
考虑到描述样本数据的26个指标(地震属性)对岩性识别的贡献不同,甚至存在冗余指标。为降低模型复杂度并提高识别精度,采用主成分分析方法筛选部分指标构建T-S模糊推理模型。根据主成分分析方法的原理[15-17]得到每个指标对岩性识别的贡献率,将这些指标按相关性的大小降序排列,再做部分和与归一化处理,结果如表 2所示。
|
|
表 2 26个指标的主成分分析结果 |
根据表 2,综合指标贡献率和T-S模糊推理模型的复杂度,经过反复测试认为,前8个指标的贡献率总和占全部指标集的75%以上,因此最终选择前8个指标构建T-S模糊推理模型(表 3)。
|
|
表 3 构建T-S模糊推理模型的部分原始样本数据 |
岩性识别本质上属于分类问题,采用T-S模糊推理模型实现。对基于智能计算(神经网络、模糊推理、T-S模型)的分类问题,应保持各类样本数量均衡,否则多样本类会“淹没”少样本类。前文的砂岩、泥岩样本数量并不均衡(分别为242和128),因此做如下规定:128个泥岩样本(岩性编码为0)全部使用,随机选取242个砂岩样本(岩性编码为1)的128个使用。此时两类样本数量均衡,由T-S模糊推理模型训练256个样本。为考察T-S模糊推理模型的泛化能力,在每类128个样本中随机挑选64个作为训练集训练网络,使其逼近样本特征和岩性类别之间的映射关系,其余样本作为验证集考察模型的泛化能力,此时训练集和验证集的样本数相等,且都是二类均衡的。
3.4 T-S模糊推理模型的构建过程根据前文的T-S模糊推理模型构造方法,每个指标均选择“高”“低”两个模糊集,每个模糊集均采用高斯型隶属函数,8个指标可构造
首先为每个参数限定搜索范围。各指标“高”“低”模糊集中心范围的设置方法如下。首先,计算各指标数据的中值
|
|
表 4 各指标“低”“高”模糊集中心、方差的取值范围 |
所有模糊规则的后件参数均取区间
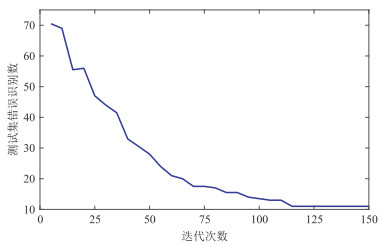
|
图 2 验证集错误识别样本数随迭代次数变化曲线 |
图 3为QVSA优化T-S模型得到的8个指标的“高”“低”模糊集隶属度曲线。由图可见,每个指标的两个模糊集均存在“交叉”,同时分区性明显,因此可以较好地实施模糊推理。

|
图 3 QVSA优化T-S模型得到的8个指标的“高”“低”模糊集隶属度曲线 |
应用训练好的网络识别研究区700000个地震属性采样点的储层岩性,并与普通BP网络储层岩性识别方法对比(表 5),以检验方法的效果。BP网络的结构设置为:输入层为8个节点,输出层为1个节点;经过多次实验,最终确定隐层节点数为20;隐层和输出层节点的激励函数均为Sigmoid,损失函数为交叉熵;迭代次数为150,采用随迭代次数单调下降的学习速率(初值为0.05、终值为0.01),惯性因子为0.9。
|
|
表 5 本文方法和BP网络方法的识别效果对比 |
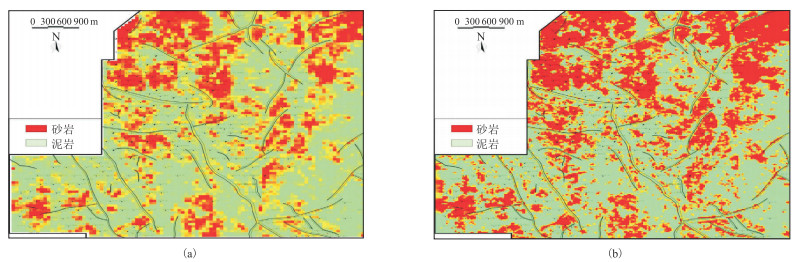
为增强对比结果的客观性,采用正确率、查准率、查全率、F1分数作为评估指标,这些指标可根据混淆矩阵(图 4)定义[18]。实验结果表明,本文方法的识别正确率达到92%,比普通BP网络方法高5.1%,同时其他三项指标也较BP网络方法提升明显。图 5为BP神经网络方法和T-S模糊推理方法的岩性识别效果。由图可见,T-S模糊推理方法的储层岩性识别效果(图 5 b)优于普通BP网络方法(图 5a)。

|
图 4 混淆矩阵的定义 |
|
图 5 BP神经网络方法(a)和T-S模糊推理方法(b)的岩性识别效果 |
为更准确地识别储层岩性,本文提出一种基于量子衍生涡流算法和T-S模糊推理模型的岩性识别方法。BP网络方法的固有缺陷在于训练过程易陷入局部极小值,从而不易“学会”储层岩性特征与其类属之间的复杂映射关系。T-S模糊推理方法模拟了人脑的推理过程,本文采用具有全局搜索能力的QVSA优化T-S模糊推理模型参数,可以较好地获得储层岩性特征与其类属之间的映射关系,从而有效提高了岩性识别精度。实验结果表明,利用反映储层特征的8个地震属性识别储层岩性时,本文所提方法的识别正确率达到92.0%,比普通BP网络方法高5.1%,同时查准率、查全率、F1分数等指标也较BP网络方法提升明显。然而QVSA需要种群寻优,而不是个体寻优,从而增加了模型的计算复杂度,降低了计算效率,即T-S模糊推理模型以牺牲计算效率换取较高的识别精度。
| [1] |
李海山, 杨午阳, 伍新明, 等. 基于深度学习的相对地质时间体估计方法[J]. 石油地球物理勘探, 2023, 58(2): 277-284. LI Haishan, YANG Wuyang, WU Xinming, et al. Relative geological time volume estimation method based on deep learning[J]. Oil Geophysical Prospecting, 2023, 58(2): 277-284. |
| [2] |
李素华, 余洋, 李蓉, 等. 神经网络反演在火山岩储层预测中的应用[J]. 石油地球物理勘探, 2023, 58(2): 392-402. LI Suhua, YU yang, LI Rong, et al. Application of neural network inversion in prediction of volcanic rock reservoir[J]. Oil Geophysical Prospecting, 2023, 58(2): 392-402. |
| [3] |
夏文鹤, 谢万洋, 唐印东, 等. 砂样岩屑图像特征的岩性智能高效识别[J]. 石油地球物理勘探, 2023, 58(3): 495-506. XIA Wenhe, XIE Wanyang, TANG Yindong, et al. Intelligent and efficient lithology identification based on image features of returned cuttings[J]. Oil Geophysical Prospecting, 2023, 58(3): 495-506. |
| [4] |
李建华, 钱丽萍, 钱丽欣, 等. 基于岩石归类分析的多属性基岩岩性预测及效果[J]. 石油地球物理勘探, 2022, 57(增刊2): 70-73. LI Jianhua, QIAN Liping, QIAN Lixin, et al. Multi-attribute bedrock lithology prediction and effect based on rock classification analysis[J]. Oil Geophysical Prospecting, 2022, 57(S2): 70-73. |
| [5] |
王棣, 杜世通. 用神经网络预测二维地震剖面的地层岩性[J]. 石油地球物理勘探, 1996, 31(3): 400-409. WANG Di, DU Shitong. Lithology prediction of 2-D seismic section by neural network technique[J]. Oil Geophysical Prospecting, 1996, 31(3): 400-409. |
| [6] |
姜岩, 周再林, 秦月霜. 地震属性分析的神经网络岩性识别技术及应用[J]. 大庆石油地质与开发, 2000, 19(5): 39-41. JIANG Yan, ZHOU Zailin, QIN Yueshuang. Neural-network lithology identification technique of seismic attitude analysis and its application[J]. Petroleum Geology & Oilfield Development in Daqing, 2000, 19(5): 39-41. |
| [7] |
杨远宏. 基于SSA-BP神经网络的岩性识别研究[J]. 长春工程学院学报(自然科学版), 2021, 22(1): 87-91. YANG Yuanhong. The study on lithology recognition based on SSA-BP neural network[J]. Journal of Changchun Institute of Technology(Natural Sciences Edition), 2021, 22(1): 87-91. |
| [8] |
张绍红. 概率神经网络技术在非均质地层岩性反演中的应用[J]. 石油学报, 2008, 29(4): 549-552. ZHANG Shaohong. Application of probabilistic neural network technique to lithology inversion of heterogeneous stratum[J]. Acta Petrolei Sinica, 2008, 29(4): 549-552. |
| [9] |
李国和, 郑阳, 李莹, 等. 基于深度信念网络的多采样点岩性识别[J]. 地球物理学进展, 2018, 33(4): 1660-1665. LI Guohe, ZHENG Yang, LI Ying, et al. Lithology recognition of multi-sampling points based on deep belief network[J]. Progress in Geophysics, 2018, 33(4): 1660-1665. |
| [10] |
张国印, 王志章, 林承焰, 等. 基于小波变换和卷积神经网络的地震储层预测方法及应用[J]. 中国石油大学学报(自然科学版), 2020, 44(4): 83-93. ZHANG Guoyin, WANG Zhizhang, LIN Chengyan, et al. Seismic reservoir prediction method based on wavelet transform and convolutional neural network and its application[J]. Journal of China University of Petroleum (Edition of Natural Science), 2020, 44(4): 83-93. |
| [11] |
DOĞAN B, ÖLMEZ T. A new metaheuristic for numerical function optimization: Vortex search algorithm[J]. Information Sciences, 2015, 293(3): 125-145. |
| [12] |
ARCHIE G E. Electrical resistivity log as an aid in determining some reservoir characteristic[J]. Transactions of the AIME, 1942, 146(1): 54-62. DOI:10.2118/942054-G |
| [13] |
LI P, ZHAO Y. A quantum-inspired vortex search algorithm with application to function optimization[J]. Natural Computing, 2019, 18(3): 647-674. DOI:10.1007/s11047-018-9704-z |
| [14] |
TAKAGI T, SUGENO M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1985, 15(1): 116-132. |
| [15] |
JOLLIFFE I T. Principal Component Analysis[M]. New York: Springer Verlag, 1986.
|
| [16] |
PEARSON K L. On lines and planes of closest fit to systems of points in space[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1901, 2(11): 559-572. DOI:10.1080/14786440109462720 |
| [17] |
HOTELLING H. Analysis of a complex of statistical variables into principal components[J]. Journal of Educational Psychology, 1933, 24(6): 417-441, 24(7): 498-520.
|
| [18] |
LIU X, SONG H. Automatic identification of fossils and abiotic grains during carbonate microfacies analysis using deep convolutional neural networks[J]. Sedimentary Geology, 2020. DOI:10.1016/j.sedgeo.2020.105790 |



 王伟, 广东省茂名市茂南区科创路1号广东石油化工学院石油工程学院,525000。Email:
王伟, 广东省茂名市茂南区科创路1号广东石油化工学院石油工程学院,525000。Email: