2. 有色资源与地质灾害探测湖南省重点实验室, 湖南长沙 410083;
3. 中南大学地球科学与信息物理学院, 湖南长沙 410083;
4. 湖南继善高科技有限公司, 湖南长沙 410208
2. Key Laboratory of Non-Ferrous and Geological Hazard Detection, Changsha, Hunan 410083, China;
3. School of Geosciences and Info-Physics, Central South University, Changsha, Hunan 410083, China;
4. Hunan Geosun Hi-technology Co., Ltd., Changsha, Hunan 410208, China
中国的石油和天然气对外依赖度居高不下,东部老油田区普遍进入油气生产中后期,非常规、超低渗资源成为重要战略接替资源。非常规、超低渗资源受大深度、低孔隙度、低渗透率等资源禀赋制约,必须经过大规模压裂改造才能形成经济产能[1-2]。准确、实时地监测、描述压裂改造裂缝的几何参数是压裂工艺设计和压裂效果评估的关键依据,也一直是学术界和工业界的难题之一。
目前主流压裂监测方法包括微震监测、分布式光纤监测、示踪剂监测、电磁法监测等。微震监测通过接收地下地震波场信号,运用震源定位技术推断岩石破裂位置,确定裂缝长度、方位等参数。由于获取的地震事件点代表岩石破裂前沿,无法描述压裂液和支撑剂的运移位置,得到的储层改造体积(Stimulated Reservoir Volume, SRV)远大于压裂液波及的有效改造体积(Effective Stimulated Reservoir Volume, ESRV);同时,微震信号弱、随机性强,震源信号拾取和事件定位较困难[3-8]。分布式光纤监测技术利用的是压裂造成井中温度场、声波场、应力场的变化,通过识别光波的光学特性(如振幅、相位等)异常,监测裂缝形态,但该方法难以定量推断裂缝几何参数、评估远场裂缝,且成本高昂[9-12]。示踪剂监测技术通过定期检测压裂返排液中示踪剂的浓度,分析注入液与返排液的浓度变化,评价不同压裂层段产出差异,对裂缝的缝高、缝宽等参数进行表征,但该方法无法描述缝长,因而无法精细刻画裂缝形态,且难以实现实时监测[13-16]。
电磁法对低阻体的走向、改造体积变化引起的电性异常敏感,压裂液呈低阻特征,电磁法水力压裂监测应用前景广阔。Bevc等[17]通过盐水实验验证了井地电磁法监测浅层地下水流动的可靠性;王志刚等[18]利用时频电磁监测技术,在地形平坦、电磁干扰小、地质构造简单、水平井较浅的试验区开展实验,验证了该方法的应用效果;李静和等[19]利用有限元法模拟并分析了地下目标体的电磁响应空间分布特征,提出并验证了接触式激发极化法在油气储层压裂监测领域的可行性;Pardo等[20]基于有限元研究了K型地电模型的井地电磁响应特征,获得了电磁监测最优频率;刘海飞等[21]推导了任意线电流源背景电位的计算公式,运用有限元进行三维正演模拟,证明了利用井地电位法对中浅层剩余油分布及注水前沿推进位置的预测是可行的,结果也是可靠的;Bai等[22]基于有限差分法构建了三维地电模型,推导了不同深度、不同方位的线电流源在地表产生的电位计算公式;王爱国等[23]基于充电导体理论[24]提出了稳定电场压裂裂缝监测技术,利用高精度电位法监测仪器实现了裂缝方位和长度的实时监测;Beskardes等[25]构建了复杂三维裂缝网络模型,研究模型的裂缝长度及孔径分布与电阻率响应的关系;杨沁润等[26]开展了大斜度井和水平井的井地三维电阻率数值模拟和反演研究,分析了倾斜线源及水平线源对地面响应的影响,有效识别了注水运移方向。综上,基于电磁法的压裂裂缝监测理论研究趋于成熟且应用广泛,但针对大深度条件下的电磁响应特征和电磁监测适用性截至目前还没有明确答案。中国非常规、超低渗资源埋藏较深,非常规水力压裂施工与监测环境复杂,针对大深度储层改造环境,电磁法监测技术的可行性亟须论证。
本文融合充电导体与电偶极源扩散电磁场理论,通过构建多组不同裂缝深度和不同裂缝长度的压裂模型,分析地面电磁响应总场与异常场的分布特征。通过对电磁压裂裂缝监测技术开展实测分析,讨论电磁监测技术的可行性,以期为电磁监测方法和应用探索新的发展方向。
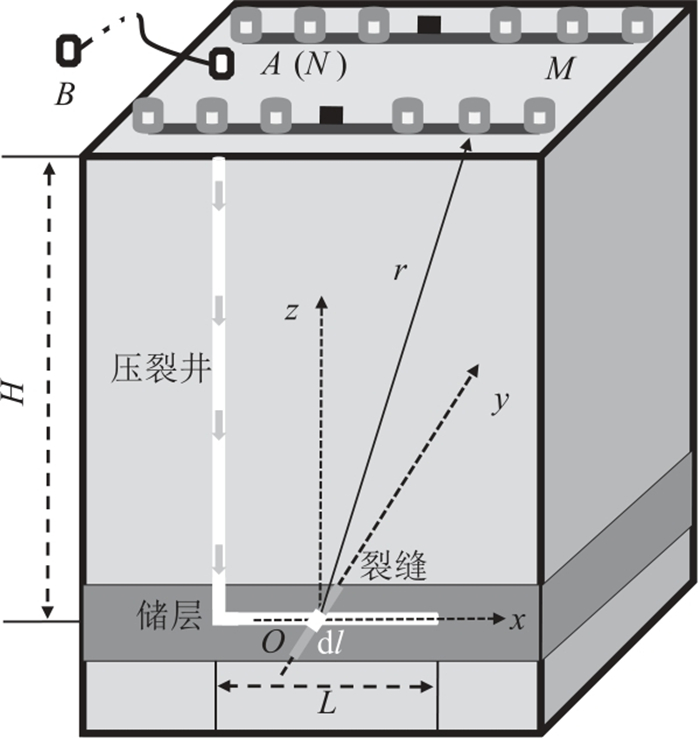
1 方法原理基于电偶极源扩散电磁场理论,假设地下半空间为均匀各向同性介质,向井筒供入低频电流(图 1)。地下形成由井筒(包括直井和水平井)与裂缝组成的线源,可将线源等效为若干个电偶极源的线性叠加,全空间电偶极源的电位表达式为
| $U(\boldsymbol{r})=\frac{\mathrm{e}^{\mathrm{i} k r}(1-\mathrm{i} k r)}{4 \pi \sigma r^3}(\boldsymbol{r} \cdot P)$ | (1) |
|
图 1 电磁压裂裂缝监测模型示意图 |
式中:r为矢径,即电偶极子中心点与测点M之间的矢量距离;r
L0表示水平井长度;A-B表示供电电极对,其中A位于井口,B位于无穷远处;M-N为测量电极对,N为参考电极,位于井口,M所在位置即测点;H表示井孔长度;L表示裂缝长度。
将长度为L的线源等效为n个电偶极源的线性叠加,则空间任意点M的电位为
| $ U\left(M\right)=\sum\limits_{j=1}^{n}\frac{{\mathrm{e}}^{\mathrm{i}kr}(1-\mathrm{i}kr)}{4\mathrm{\pi }\sigma {r}^{3}}(\boldsymbol{r}·\boldsymbol{P}) $ | (2) |
测量电极M、N之间的电位差
厘清充电导体压裂模型电磁响应地面分布特征是实现电磁监测的前提。利用式(2)建立不同裂缝深度与不同裂缝长度的压裂模型,模型参数设置为:H=1000 ~ 4000 m,L0=1000 m,L=0~200 m,
裂缝深度是影响电磁监测应用效果的关键因素。假设L=200 m,分别建立裂缝深度H为1000、2000、3000、4000 m的压裂模型,对比、分析无裂缝与有压裂情况下模型的电磁响应特征。模拟的场包括由压裂井(直井和水平井)产生的背景场和裂缝增长形成的异常场,总场即为背景场与异常场的标量叠加场。
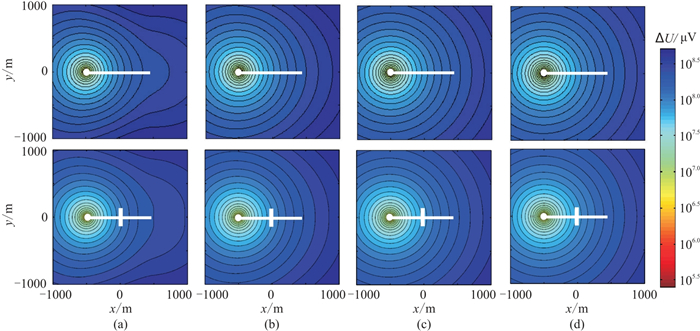
2.1.1 总场分析图 2为深度分别为1000、2000、3000、4000 m时无裂缝及有裂缝时模型总场
|
图 2 无(上)、有(下)裂缝时不同深度ΔU平面图 (a)H=1000 m; (b)H=2000 m; (c)H=3000 m; (d)H=4000 m |
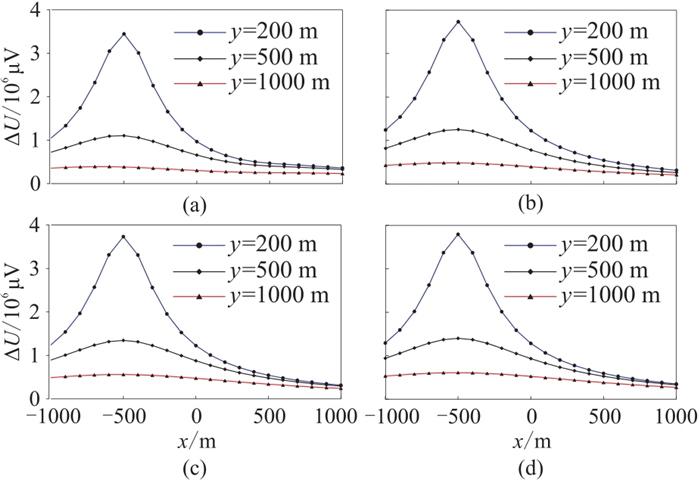
图 3为裂缝长度L=200 m、不同深度模型的测线y=200、500、1000 m的
|
图 3 L=200 m时不同裂缝深度模型的总场曲线 (a)H=1000 m; (b)H=2000 m; (c)H=3000 m; (d)H=4000 m |
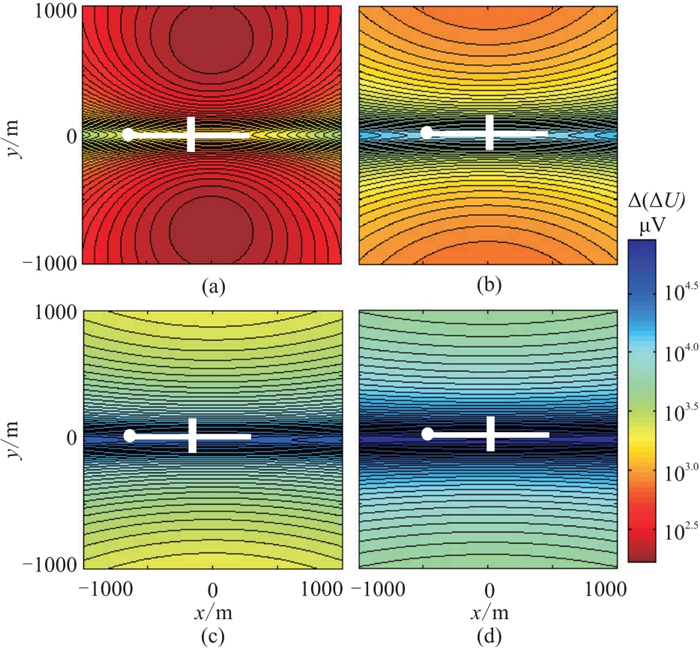
假设裂缝长度L=200 m,计算裂缝位于不同深度下模型的异常场
|
图 4 L=200 m时不同深度裂缝模型的 |
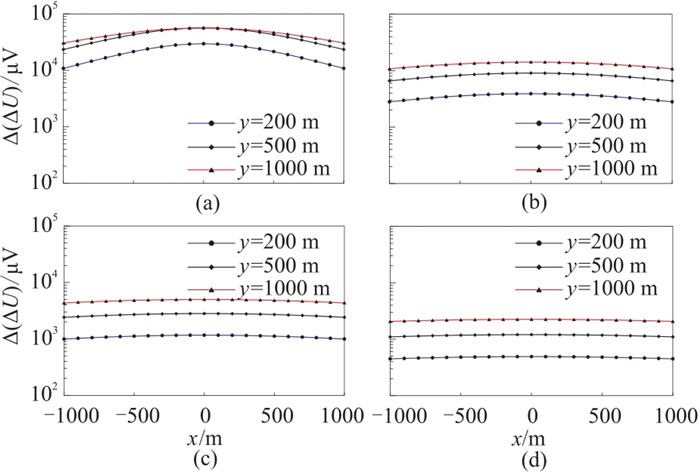
为定量分析异常场的分布特征,提取y=200、500、1000 m三条测线的异常场值(图 5)。由图可见,异常场曲线呈对称分布,极大值出现在裂缝中心位置,极大值的大小与裂缝深度、测线位置均有关。结合图 4的异常平面分布特征,当裂缝深度为1000 m时,裂缝在地面产生的异常最大值出现在y=500~1000 m范围内;当裂缝深度大于2000 m时,裂缝在地面产生的异常最大值超过y≤1000 m的范围。
|
图 5 裂缝位于不同深度时不同测线的异常场曲线 (a)H=1000 m; (b)H=2000 m; (c)H=3000 m; (d)H=4000 m |
由图 5还可以发现,y值越小,曲线越平缓。表 2为裂缝位于不同深度时y=200、500、1000 m测线上相邻测点(点距为100 m)间的最小异常差。可见,当裂缝深度小于2000 m时,相邻测点间的最小异常差不超过50 μV;深度越大,相邻测点间的最小异常差越小,且与y呈负相关;裂缝深度大于3000 m时,相邻测点的异常差值非常小,不足10 μV。
|
|
表 2 裂缝位于不同深度时相邻测点间的最小总场异常差 |
裂缝长度识别是压裂监测的核心内容之一。为分析电磁监测方法对裂缝长度的识别精度,分别建立裂缝深度为1000 m和4000 m时裂缝逐渐增长的压裂模型,分析缝长变化如何影响电磁响应特征。
2.2.1 总场分析图 6~图 7分别为裂缝深度在1000 m和4000 m时不同缝长模型总场平面等值线图。对比等值线形态与总场强度,总场强度对裂缝长度的增长不敏感。当裂缝深度为1000 m时,随着裂缝长度的增加,等值线形态及场值变化均十分微弱,对于长度不大于200 m的裂缝,几乎难以识别。当裂缝深度为4000 m时,随着裂缝长度的增加,总场值无明显变化。

|
图 6 H=1000 m时不同裂缝长度模型总场平面图 (a)L=0; (b)L=40 m; (c)L=80 m; (d)L=120 m; (e)L=160 m; (f)L=200 m |
|
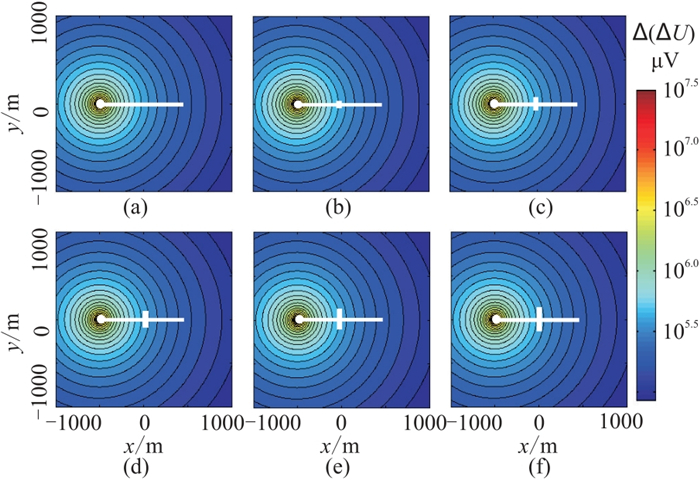
图 7 H=4000 m时不同裂缝长度模型总场平面图 (a)L=0; (b)L=40 m; (c)L=80 m; (d)L=120 m; (e)L=160 m; (f)L=200 m |
为进一步定量评价电磁监测对裂缝长度的识别精度,构建4组不同裂缝深度(1000、2000、3000、4000 m)的裂缝增长模型,每组模型均包括无裂缝、缝长100 m、缝长200 m三种情况。地面观测点均位于y=1000 m测线。4组模型的总场曲线见图 8。

|
图 8 裂缝不同深度、不同长度模型测线y=1000 m总场曲线 (a)H=1000 m; (b)H=2000 m; (c)H=3000 m; (d)H=4000 m |
以测点(1000, 1000)处的总场作为参考,分别计算沿测线y=1000 m范围内裂缝深度为1000、2000、3000、4000 m、裂缝长度每增长100 m时总场的增长率,分别为11.29%、3.25%、1.01%、0.40%,证明电磁监测总场变化对裂缝长度的变化不敏感。
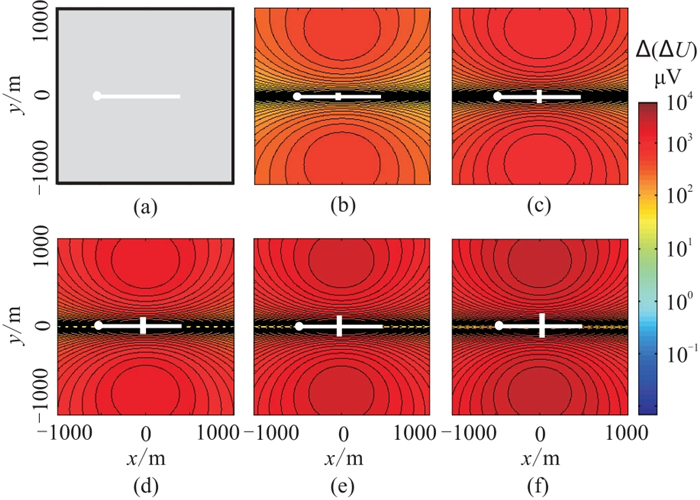
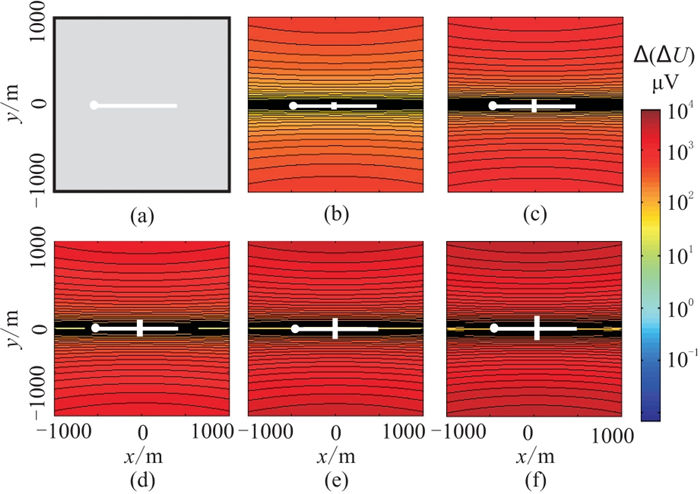
2.2.2 异常场分析图 9~图 10分别展现了裂缝深度分别为1000 m和4000 m、不同裂缝长度模型的异常场平面图。对比等值线形态和异常场强度,可见随着裂缝增长,异常场场值增大,但等值线形态不变。裂缝深度为1000 m时,在测区范围内可以获得裂缝在地面产生的异常最大值;裂缝深度增至4000 m时,测区范围内无法获得裂缝在地面产生的异常最大值,且距低值带越远,场值越大。
|
图 9 H=1000 m时不同裂缝长度模型异常场平面图 (a)L=0; (b)L=40 m; (c)L=80 m; (d)L=120 m; (e)L=160 m; (f)L=200 m |
|
图 10 H=4000 m时不同裂缝长度模型异常场平面图 (a)L=0; (b) =40 m; (c)L=80 m; (d)L=120 m; (e)L=160 m; (f)L=200 m |
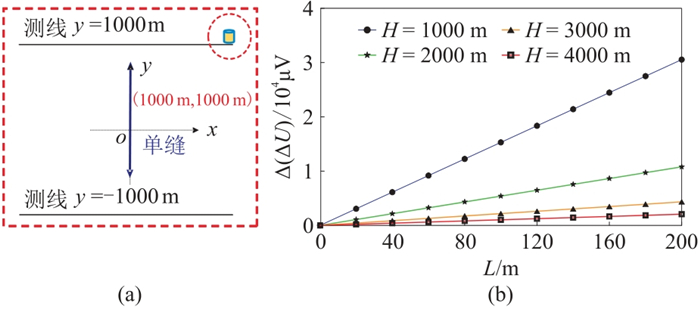
为分析不同裂缝长度下的电磁响应特征,提取裂缝位于不同深度时测点(1000 m, 1000 m)的电位异常差△(△U)(图 11)。由图可见:测点电位与裂缝长度呈线性正相关;裂缝深度越小,电位越大。裂缝深度为2000 m时,裂缝长度每增加20 m,电位涨幅大于1000 μV,异常占比大于5‰。当裂缝深度达到4000 m时,电位涨幅仅为206 μV,异常占比不足1‰。
|
图 11 裂缝位于不同深度的模型示意图(a)及总场异常差随裂缝长度的变化曲线(b) |
综上,基于充电导体理论,采用井中供电—地面接收的电磁监测方法存在诸多局限性:①背景场高于异常场至少两个数量级,总场对裂缝增长引起的电磁响应变化不敏感,且裂缝越深,敏感性越差;②异常场随裂缝深度的增加迅速衰减,严重制约了电磁法裂缝监测深度;③裂缝在地面投影位置的中垂线附近,异常场存在低值带,一定范围内,距离低值带越远则异常场越强,在实际勘探中应对此位置的信号进行采集,可沿平行于低值带的剖面进行观测,但测线与低值带间的距离应大于H/2;④相邻测点的异常场差异与深度呈负相关,裂缝越深,数据的抗噪能力越弱,若通过加大点距的方式提高数据质量,会降低对裂缝的识别精度。因此,实际工作中,测点间距应大于H/20。
3 应用实例为了分析电磁压裂裂缝监测技术的实用性,针对野外压裂施工环境复杂、模型构建困难等因素,开展1:10000的等比例砂槽实验,构建裂缝长度逐渐增长的压裂等效模型。模型中,直井、水平井及裂缝均采用铁片模拟(铁片宽度0.5 cm,厚度0.1 cm),直井长200 cm,水平井长200 cm,裂缝分5段,每段裂缝长5 cm,裂缝长度通过开关控制(开关闭合,裂缝相连)。电磁观测系统如图 12所示。采用井口供电、地面双测线接收的监测方式,供电电极A(正极)位于井口,电极B(负极)位于相对无穷远处(距A极500 cm),测量电极M和N用铁钉替代。共布设16个测点,组成2条测线,测线线距50 cm,点距10 cm。裂缝从水平井端逐渐增长,其地面投影与14号测点和6号测点共线,实验实景如图 13所示。

|
图 12 砂槽实验观测系统俯视图 |

|
图 13 砂槽实验实景图 (a)裂缝埋置;(b)裂缝模拟;(c)观测系统布置 |
实验过程共进行了880 s。实验开始前,所有开关处于断开状态,处于无裂缝状态。实验开始后,依次在80、160、240、320、400 s闭合开关,在480 s后所有开关依次断开。
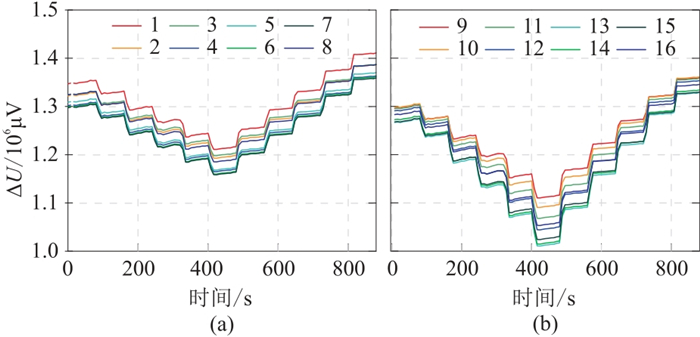
图 14为实测总场
|
图 14 砂槽实验实测总场曲线 (a)1~8号测点;(b)9~16号测点 |
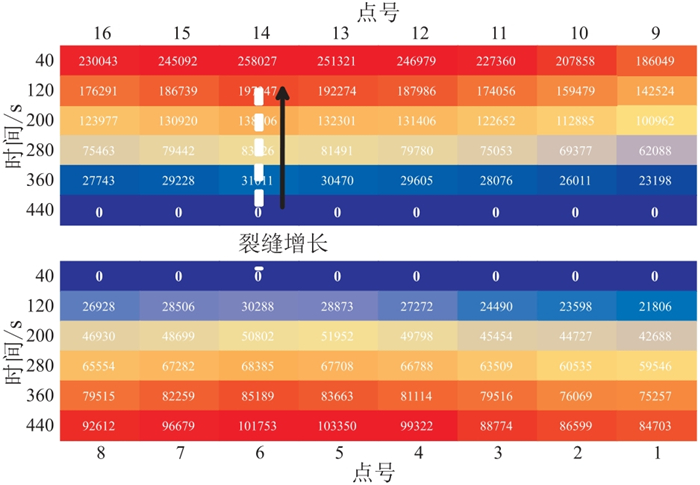
分别选取每段裂缝形成10 s后的总场值,并以无裂缝(20 s时刻)时的场值为背景场,计算各测点的异常值(图 15)。由图可见,距离测点较远的裂缝产生的异常较小;14号与6号测点的异常相差不大。裂缝长度增至25 cm时,9~14号测点中,14号测点异常值整体最高,最大值达258027 μV;1~8号测点中,6号测点的异常最大,最大值达101753 μV,但仍不足14号测点最大值的1/2。
|
图 15 裂缝长度增加时的异常场等值图 |
取背景值为1×106 μV,计算裂缝长度每增长5 cm时(顺序增加第①、②、③、④、⑤段裂缝)14号和6号测点的总场异常的变化率,结果见表 3。由表可见,裂缝长度增大所产生的电磁总场异常相对背景场较弱,占比不足7%;测点距离裂缝越远,异常变化越小,异常场易受干扰。
|
|
表 3 测点总场异常变化率 |
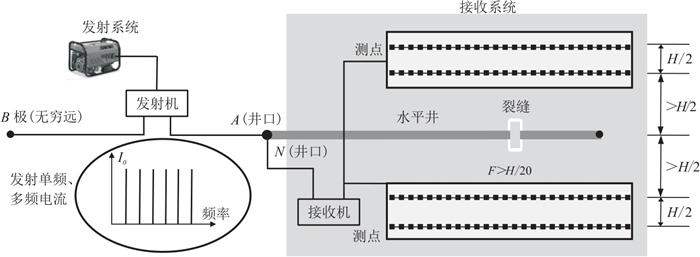
针对电磁裂缝监测系统的布设问题,依据相关理论成果与实践经验,基于前述数值模拟与实测分析结果,本文提出一种电磁监测观测系统布设方式,具体方案见图 16。该方式包括发射系统和接收系统两部分。发射系统发射单频或多频电流,电极A置于井口,电极B(负极)置于无穷远。接收系统中的参考电极N置于井口附近,利用多个电极M组成至少2条平行于水平井的测线,测线与水平井的距离应大于H/2。当测线分布在水平井两侧时,可选择对称测线进行剖面测量,当测线分布在水平井同一侧时,线距应大于H/5。这两种测线布设方式的测点间距F均大于H/20。此外,测线长度应根据监测裂缝的深度和水平井的长度确定,一般每条测线测点数不少于40,测线范围应超出水平井端点位置(原理井口方向)至少3个测点。
|
图 16 观测系统布设建议方案 |
本文首先采用线源等效电偶极子线性叠加方式,构建了基于充电导体的压裂模型,计算不同裂缝深度与长度模型的总场和异常场,分析其地面电磁响应特征。具体得到以下结论:①利用井—地电磁法进行压裂监测,压裂模型产生的背景场远大于异常场,因此通过分析总场的变化监测裂缝长度的变化是可行的;②裂缝的深度越大,地面观测的异常场越弱;③地面观测的异常场在裂缝在地面投影的中垂线附近存在低值带;④相邻测点间的异常场差值与裂缝的深度呈负相关。
通过搭建压裂监测物理模型进行实测分析,验证了理论分析结果的正确性,结合前人的理论成果与实践经验,提出一种井中激发—地面接收的测网式电磁监测观测系统。测量电极位于水平井上方距井口较远的位置,且满足中心两测线的距离大于裂缝深度等条件。该系统野外施工简单快捷,区域异常信号强,监测深度大。
对于深度较大(>4000 m)的非常规油气压裂监测,电磁法存在诸多局限性。本文采用均匀各向同性介质及理想充电导体构建的压裂模型相对简单,在实际复杂多变的地质条件下,对于大深度条件下的充电导体压裂模型的适应性有待进一步研究。
| [1] |
窦立荣, 李大伟, 温志新, 等. 全球油气资源评价历程及展望[J]. 石油学报, 2022, 43(8): 1035-1048. DOU Lirong, LI Dawei, WEN Zhixin, et al. History and outlook of global oil and gas resources evaluation[J]. Acta Petrolei Sinica, 2022, 43(8): 1035-1048. |
| [2] |
王勇, 汤勇, 李士伦, 等. 多级压裂水平井周期性注气吞吐提高页岩油气藏采收率——以北美Eagle Ford非常规油气藏为例[J]. 天然气工业, 2023, 43(1): 153-161. WANG Yong, TANG Yong, LI Shilun, et al. Cyclic gas injection huff-n-puff in multi-stage fracturing horizontal wells to improve recovery of shale reservoirs: Taking Eagle Ford unconventional reservoir in North America as an example[J]. Natural Gas Industry, 2023, 43(1): 153-161. |
| [3] |
LI L, TAN J, WOOD D A, et al. A review of the current status of induced seismicity monitoring for hydraulic fracturing in unconventional tight oil and gas reservoirs[J]. Fuel, 2019, 242: 195-210. DOI:10.1016/j.fuel.2019.01.026 |
| [4] |
刘曰武, 高大鹏, 李奇, 等. 页岩气开采中的若干力学前沿问题[J]. 力学进展, 2019, 49(1): 1-236. LIU Yuewu, GAO Dapeng, LI Qi, et al. Mechanical frontiers in shale-gas development[J]. Advances in Mechanics, 2019, 49(1): 1-236. |
| [5] |
刘星, 金衍, 林伯韬, 等. 利用微地震事件重构三维缝网[J]. 石油地球物理勘探, 2019, 54(1): 102-111. LIU Xing, JIN Yan, LIN Baitao, et al. A 3D fracture network reconstruction method based on microseismic event[J]. Oil Geophysical Prospecting, 2019, 54(1): 102-111. DOI:10.13810/j.cnki.issn.1000-7210.2019.01.012 |
| [6] |
LYU B, NAKATA N. Iterative passive-source location estimation and velocity inversion using geometric-mean reverse-time migration and full-waveform inversion[J]. Geophysical Journal International, 2020, 223(3): 1935-1947. DOI:10.1093/gji/ggaa428 |
| [7] |
房大志, 谷红陶, 钱劲, 等. NC区块页岩气水平井压裂微震实时监测[J]. 地球物理学进展, 2022, 37(2): 577-587. FANG Dazhi, GU Hongtao, QIAN Jin, et al. Real-time microseismic monitoring for the hydraulic fracture of horizontal wells at NC block[J]. Progress in Geophysics, 2022, 37(2): 577-587. |
| [8] |
刘卫东, 刘腾蛟, 纪拥军, 等. 利用微地震监测成果判断砂砾岩油藏压裂裂缝井间连通性——以准噶尔盆地玛湖油田为例[J]. 石油地球物理勘探, 2022, 57(2): 395-404. LIU Weidong, LIU Tengjiao, JI Yongjun, et al. Determination of inter-well connectivity of fractured fractures in glutenite reservoirs by microseismic monitoring results: a case study of Mahu Oilfield in the Junggar Basin[J]. Oil Geophysical Prospecting, 2022, 57(2): 395-404. |
| [9] |
KARRENBACH M, COLE1 S, RIDGE A, et al. Fiber-optic distributed acoustic sensing of microseismicity, strain and temperature during hydraulic fracturing[J]. Geophysics, 2019, 84(1): D11-D23. DOI:10.1190/geo2017-0396.1 |
| [10] |
ZHANG Z, FANG Z, STEFANI J, et al. Modeling of fiber optic strain responses to hydraulic fracturing[J]. Geophysics, 2020, 85(6): A45-A50. DOI:10.1190/geo2020-0083.1 |
| [11] |
苟量, 张少华, 余刚, 等. 光纤地球物理技术的发展现状与展望[J]. 石油物探, 2022, 61(1): 15-31. GOU Liang, ZHANG Shaohua, YU Gang, et al. Optical fiber geophysics: development status and future prospects[J]. Geophysical Prospecting for Petroleum, 2022, 61(1): 15-31. DOI:10.3969/j.issn.1000-1441.2022.01.002 |
| [12] |
隋微波, 刘荣全, 崔凯. 水力压裂分布式光纤声波传感监测的应用与研究进展[J]. 中国科学(技术科学), 2021, 51(4): 371-387. SUI Weibo, LIU Rongquan, CUI Kai. Application and research progress of distributed optical fiber acoustic sensing monitoring for hydraulic fracturing[J]. Scientia Sinica Technologica, 2021, 51(4): 371-387. |
| [13] |
SCOTT M P, JOHNSON R P, DATEY A, et al. Evaluating hydraulic fracture geometry from sonic anisotropy and radioactive tracer Logs[C]. SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Queensland, Australia, 2010, SPE-133059-MS.
|
| [14] |
DUENCKEL R J, SMITH H D, WARREN W A, et al. Field application of a new proppant detection technology[C]. SPE Annual Technical Conference and Exhibition, Denver, Colorado, USA, 2011, SPE-146744-MS.
|
| [15] |
TANG H, KILLOUGH J E, HEIDARI Z, et al. A new technique to characterize fractures in tight reservoirs using neutron porosity logs enhanced by electrically transported contrast agents[C]. SPE Annual Technical Conference and Exhibition, Dubai, UAE, 2016, SPE-181509-MS.
|
| [16] |
钟萍萍, 陆峰, 游雨奇, 等. 基于示踪剂监测的压裂裂缝体积的拟合方法及应用[J]. 钻采工艺, 2022, 45(4): 109-113. ZHONG Pingping, LU Feng, YOU Yuqi, et al. Fitting method of fracture volume calculation based on tracer monitoring and its application[J]. Drilling & Production Technology, 2022, 45(4): 109-113. |
| [17] |
BEVC D, MORRISON H F. Borehole-to-surface electrical resistivity monitoring of a salt water injection experiment[J]. Geophysics, 1991, 56(6): 769-777. DOI:10.1190/1.1443094 |
| [18] |
王志刚, 张林, 许健华, 等. 时频电磁技术在水力压裂监测中的应用[C]. CPS/SEG北京2018国际地球物理会议暨展览电子论文集, 2018, 1300-1304. WANG Zhigang, ZHANG Lin, XU Jianhua, et al. The use of time-frequency domain electromagnetic (TFEM) technique to monitor hydraulic fracturing[C]. CPS/SEG Beijing 2018 International Geophysical Conference & Exposition Electronic Papers, 2018, 1300-1304. |
| [19] |
李静和, 何展翔, 穆桐. 接触式激发极化法油气储层压裂监测有限元模拟[J]. 石油地球物理勘探, 2022, 57(3): 719-727. LI Jinghe, HE Zhanxiang, MU Tong. Finite element stimulation for fracturing monitoring of oil and gas reservoirs by using contact induced polarization method[J]. Oil Geophysical Prospecting, 2022, 57(3): 719-727. |
| [20] |
PARDO D, TORRES-VERDÍN C, ZHANG Z. Sensitivity study of borehole-to-surface and crosswell electromagnetic measurements acquired with energized steel casing to water displacement in hydrocarbon-bearing layers[J]. Geophysics, 2008, 73(6): F261-F268. DOI:10.1190/1.2993538 |
| [21] |
刘海飞, 陈德鹏, 戴前伟, 等. 连续电性介质线源井—地电位三维有限元数值模拟[J]. 桂林理工大学学报, 2011, 31(1): 28-38. LIU Haifei, CHEN Depeng, DAI Qianwei, et al. 3D FEM modeling of borehole-surface potential with line current source in semi-underground space of continuous variation of conductivity[J]. Journal of Guilin University of Technology, 2011, 31(1): 28-38. |
| [22] |
BAI Z, TAN M J, ZHANG F L. Three-dimensional forward modeling and inversion of borehole-to-surface electrical imaging with different power sources[J]. Applied Geophysics, 2016, 13(3): 437-448. DOI:10.1007/s11770-016-0575-8 |
| [23] |
王爱国, 张胜传, 余洲, 等. 稳定电场压裂裂缝监测技术[J]. 石油学报, 2016, 37(增刊2): 87-92. WANG Aiguo, ZHANG Shengchuan, YU Zhou, et al. Fracturing fissure monitoring technology in stable electric field[J]. Acta Petrolei Sinica, 2016, 37(S2): 87-92. |
| [24] |
何裕盛. 地下动态导体充电法探测概论[J]. 物探与化探, 2000, 24(2): 105-118. HE Yusheng. A preliminary discussion on the "mise-a-la-masse" detection of underground dynamic conductor[J]. Geophysical and Geochemical Exploration, 2000, 24(2): 105-118. |
| [25] |
BESKARDES G D, WEISS C J. Modelling DC responses of 3-D complex fracture networks[J]. Geophysical Journal International, 2018, 214(3): 1901-1912. DOI:10.1093/gji/ggy234 |
| [26] |
杨沁润, 谭茂金, 李桂山, 等. 大斜度井和水平井井地三维电阻率数值模拟和联合反演[J]. 地球物理学报, 2020, 63(12): 4540-4552. YANG Qinrun, TAN Maojin, LI Guishan, et al. Numerical simulation and joint inversion of three-dimensional borehole-to-surface resistivity of high deviated or horizontal wells[J]. Chinese Journal of Geophysics, 2020, 63(12): 4540-4552. |



 李富, 湖南省长沙市岳麓区麓山南路932号中南大学地球科学与信息物理学院,410083。Email:
李富, 湖南省长沙市岳麓区麓山南路932号中南大学地球科学与信息物理学院,410083。Email: