0 引言

断裂系统在油气运移、构造成藏中起着重要作用，地质建模、储层反演以及油气数值模拟等亦离不开断层面的精细解释。随着地震勘探规模不断扩大、勘探周期日益缩短，对断层精细解释要求大幅提高，如何快速提升断层解释效率和刻画精度成为现代油气资源勘探亟待解决的关键问题。

传统的断层解释主要由专业研究人员根据经验，联合地震、地质、测井等多种资料，在断点数据体的辅助下手动标出断层位置。这种断层解释模式推动了断点数据体刻画技术的快速发展。目前，断点数据体刻画技术主要有传统方法和智能预测方法两种。传统方法包括各类相干属性提取，如地震不连续性分析^[1-4]、基于小波变换^[5]、基于DOA^[6]、基于高阶统计量^[7-8]、C3改进^[9]、基于构造导向滤波与梯度结构张量等多种相干属性^[10]，这些传统方法有利于构造解释以及油气勘探开发。而智能预测方法基于U型网络、残差网络、迁移学习等对断点体进行智能识别^[11-16]，大大提高了断点识别的工作效率。

以上方法都可以识别出断点并形成相应的三维数据体，进而清晰地反映断点的空间展布。但是这些技术无法实现单一断层的自动提取，也不能替代专业人员完成基于地质建模的断层解释。从三维断点数据体中拆分单条断层并且实现该条断层的精准提取，仍是断层解释的难点。

在断层组合和提取方面，国外学者的相关文献很少，国内学者进行了简单的尝试。严哲^[17]提出了一种断层自适应分离方法，可以分离没有交错关系或有简单交错关系的断层。张进超^[18]提出了基于曲线相似性的断层智能组合和提取算法，可以分离没有交错关系的断层，但无法对交错断层进行有效提取。陈雷等^[19]采用自动确定聚类数的自适应聚类线性回归算法提取有简单交错关系的断层。蔡宇飞^[12]提出一种基于视频流的断层智能组合方法，使用迭代渐进式神经网络实现断层的智能组合，可以分离并提取有交错关系的断层。但对于更复杂的断层或者品质较差资料的断层提取仍有待进一步研究。

本文提出一种基于α-shape和多边形偏置的断层自动提取方法，该方法具有以下技术优势：①在构造地质理论指导下，通过人机交互明确目标断层确切位置，断层划分精确；②基于$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $算法的断点边界识别技术，能准确识别断层平面边界，剔除分叉断层的影响；③基于倾角约束多边形偏置算法的断点三维边界识别技术，能克服倾角变化引起的断点位置偏移现象，实现断层空间边界精确刻画；④利用精确的断层空间边界和目标断层重合度阈值约束区域生长算法的范围，实现高效、可靠的复杂断层提取。在实际工区的测试应用结果表明，本文方法不仅适用于相离断层或者简单相交断层的识别，对复杂断裂带的断层提取也有较好效果，为地质建模、储层反演以及油气数值模拟奠定了重要数据基础。

1 方法原理

为了区分目标断层与分叉断层并实现目标断层的准确三维提取，本文提出了基于$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $和多边形偏置的断层自动提取方法。研发$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $断点边缘提取算法和倾角约束多边形偏置算法，实现断层空间边界精确刻画；以该边界为约束条件设置目标断层重合度阈值，约束区域生长算法的延展范围，完成目标断层的三维自动提取。

1.1 基于人机交互和α-shape算法的断层平面边界识别

1983年，Edelsbrunner等^[20]提出$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $算法。该算法对平面点集进行Delaunay三角剖分，然后判断每条边的有效性，保留下来的有效边即为平面点集的凹轮廓。受其启发，本文将$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $算法应用于断点边缘提取。以断裂系统为研究对象，通过人机交互设置种子点和阻隔点，区分目标断层与分叉断层。

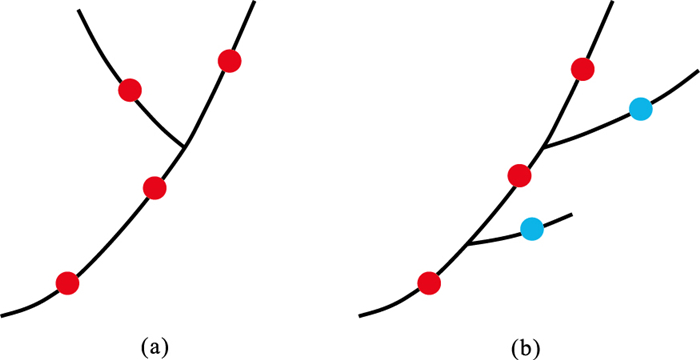
首先，在断点体的初始时间切片上选择目标断层。图 1是人机交互选择目标断层示意图，设置红色点为种子点，蓝色为阻隔点。图 1a用种子点明确标识“Y”字形断层所在位置；图 1b是主断裂选择示意图，只在主断裂位置设置种子点，在分叉断层上则设置了阻隔点。

其次，在初始时间切片上目标断层准确拾取的基础上，使用$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $算法识别目标断层的边界形状。$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $是在凸包的基础上添加了一个参数$ \alpha $，当参数$ \alpha $取值无穷大时，点集的$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $无限接近于凸包，当$ \alpha $逐步变小时，点集的$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $会倾向于在一定位置凹陷进去，更加契合断点集的轮廓。对于给定的断点集S与参数$ \alpha $，$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $算法通过以下方式实现。

（1）计算断点集S的Delaunay三角剖分$ \mathrm{D}\mathrm{T}\left(S\right) $。

（2）如图 2a所示，对于$ \mathrm{D}\mathrm{T}\left(S\right) $的所有边e，边的两个端点分别为p(x_p, y_p)和q(x_q, y_q)，求两个半径为$ \alpha $的圆$ {B}_{pq1} $和$ {B}_{pq2} $，圆心分别为$ {C}_{pq}\left(1\right) $和$ {C}_{pq}\left(2\right) $，有

$ \begin{aligned} C_{p q}(1,2)= & {\left[\frac{x_p+x_q}{2} \pm \sqrt{\alpha^2-\left(\frac{\|\boldsymbol{e}\|}{2}\right)^2}\left(\frac{y_p-y_q}{2}\right)\right.}, \\ & \left.\frac{y_p+y_q}{2} \pm \sqrt{\alpha^2-\left(\frac{\|\boldsymbol{e}\|}{2}\right)^2}\left(\frac{x_p-x_q}{2}\right)\right] \end{aligned} $

(1)

式中$ ‖\boldsymbol{e}‖ $为边长。

如果至少有一个圆在其内部不包含来自断点集S的点，则边e是有效边界，否则是无效边，该边将被删除（图 2b）。

（3）判定为有效边界的所有边的并集即为断点集S的$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $，最终保留的边如图 2c所示。

1.2 基于倾角约束多边形偏置算法的断层空间边界识别

2005年，Chen等^[21]提出多边形偏置算法，通过计算每个区域的卷绕数实现任意多边形的偏置求取。受其启发，本文将该算法与构造认识充分融合，研发了受倾角约束的断层多边形偏置算法。

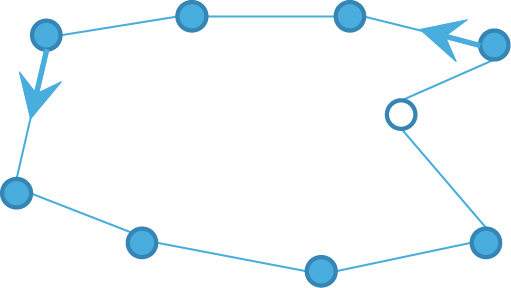
输入一组非自相交、不重叠的多边形，规定每个多边形都是有方向的且外围轮廓为逆时针方向、内部轮廓为顺时针方向。如图 3所示，沿多边形方向行进时，如果在该顶点左转，则定义该顶点为凸点；如果在该顶点右转，则定义为凹点。

设T是一组由一个或多个轮廓组成的有向多边形，$ {e}_{i} $为多边形的第i条边，t是T内部的任意点，$ \boldsymbol{R} $是从t到无穷远与T的所有顶点都不相交的任意射线，则$ \boldsymbol{R} $相对于T的卷绕数ω(R, T)为

$ \mathrm{\omega }(\boldsymbol{R}, \boldsymbol{T})=\sum\limits_{{e}_{i}\in \boldsymbol{T}}\mathrm{\varphi }(\boldsymbol{R}, {e}_{i}) $

(2)

其中$ \mathrm{\varphi }(\boldsymbol{R}, {e}_{i}) $定义为

$ \mathrm{\varphi }\left(\boldsymbol{R}, {e}_{i}\right)=\left\{\begin{array}{c}0, \ \ \ \ \ \ \ \ \ \ \ \ \ \boldsymbol{R}\mathrm{不}\mathrm{与}{e}_{i}\mathrm{相}\mathrm{交}\\ 1, \mathrm{以}t\mathrm{点}\mathrm{为}\mathrm{准}, \boldsymbol{R}\mathrm{与}{e}_{i}\mathrm{逆}\mathrm{时}\mathrm{针}\mathrm{相}\mathrm{交}\\ -1, \mathrm{以}t\mathrm{点}\mathrm{为}\mathrm{准}, \boldsymbol{R}\mathrm{与}{e}_{i}\mathrm{顺}\mathrm{时}\mathrm{针}\mathrm{相}\mathrm{交}\end{array}\right. $

(3)

由式（2）、式（3）可知，对于具有相同起点的所有射线$ \boldsymbol{R} $，ω(R, T)取相同的值；对于单个连接区域中的所有点，ω(R, T)具有相同的值；当有多个轮廓定义多边形时，可以将关于每个轮廓的卷绕数相加得到多边形的卷绕数。图 4显示了使用两条不同的射线计算点t的卷绕数的示例，可以看出，对于来自点t的任意射线，点t处的卷绕数都为+1。

之后定义卷绕规则。卷绕规则定义了如奇数(Add)、非零(Nonzero)、正(Positive)、负(Negative)等类别，可以将区域划分为内部或外部。如果一个区域计算的卷绕数落入所选类别，则将其归类为内部。本文选择正卷绕规则，即只有具备正卷绕数的区域才被归类为多边形内部。

受断层倾角影响，直接利用当前时间切片上目标断层的平面边界来框定相邻时间切片上的目标断层范围存在一定问题。结合构造认识，将断层倾角变化与多边形偏置算法融合，基于当前时间切片上目标断层的平面边界，实现了相邻时间切片上目标断层边界的准确刻画。方法原理如下。

（1）假设当前时间切片上目标断层边界都是逆时针方向多边形。多边形每条边向其法线方向(即边的右侧)偏移距离为d（即多边形偏置范围）, 有

$ d=\frac{L}{\mathrm{t}\mathrm{a}\mathrm{n}\beta }+\varepsilon $

(4)

式中：$ L $是相邻两切片之间的纵向距离；$ \beta $是断层倾角；$ \varepsilon $是可调节的正数。

（2）外偏置边（红色实线）与原始边（蓝色虚线）的示意图如图 5a所示。对于凸点，通过以该凸点为中心的逆时针方向的弧连接偏移线段的端点；对于凹点，将该凹点连接到偏置边的端点，偏置边与原始边共享该凹点（图 5b)。

（3）计算每个区域相对于偏置曲线的卷绕数。具有正卷绕数的区域位于偏置多边形的内部（图 5c)，这些区域并集的边界就是偏置多边形（图 5d)。

（4）应用倾角约束多边形偏置算法，可以获得相邻时间切片上目标断点的展布边界（偏置多边形）。随着当前时间切片的不断迭代，偏置多边形不断更新，将所有偏置多边形取并集，即可获得目标断层的空间边界。

1.3 基于约束区域生长算法的断层自动提取 1.3.1 区域生长算法

区域生长是指将成组的像素或区域发展成更大区域的过程，也就是把与每个种子点有相似属性（强度、灰度级、纹理颜色等）的相邻像素合并到同一区域。其中包含两个关键问题：①确定生长过程中将相邻像素纳入的准则，比如灰度图像的差值、彩色图像的颜色等；②确定生长的停止条件，一般无法满足所定义的生长需求即为生长停止。

1.3.2 基于约束区域生长算法的断层自动提取

复杂断裂带断层空间展布形态变化较大，针对目标断层，本文将基于α-shape和多边形偏置算法得到的断层边界作为约束条件，约束断层区域生长范围，精确刻画目标断层空间展布形态。方法原理简述如下：

（1）输入断点体，在当前时间切片上通过人机交互设置目标断层种子点和阻隔点；

（2）将种子点存入一个队列中，在该队列存储待生长的种子点；

（3）依次弹出种子点并判断种子点与平面周围邻域的关系，如距离队列中种子点较近，属于断点生长值取值范围，则判断为相似的点作为下次生长的种子点；

（4）判断该种子点是否超出断层空间边界，超出边界则当前时间切片上的断点停止生长，否则继续生长；

（5）设置断层重合度阈值η（相邻时间切片和当前时间切片目标断层重合的点数/相邻时间切片目标断层总点数）。若重合度大于阈值，则进入下一时间切片继续断点生长；否则目标断层停止断点生长。

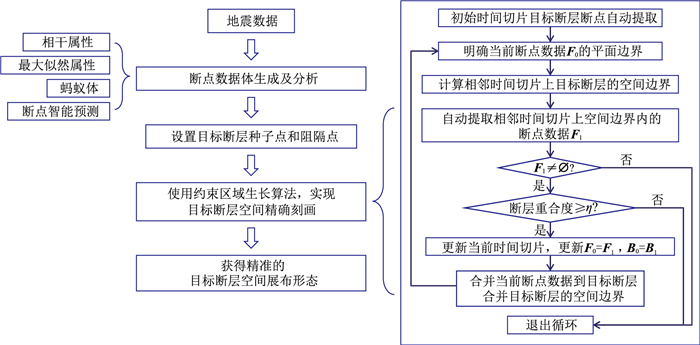
2 方法流程

为了区分目标断层与分叉断层并实现目标断层的准确三维提取，本文采用基于$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $算法和倾角约束多边形偏置算法的断层识别技术，实现断层空间边界的精确刻画；并以该边界为约束条件设置目标断层重合度阈值，约束区域生长算法的延展范围，完成目标断层的三维自动提取。具体方法实现流程如图 6所示。

2.1 断点数据体生成及分析

利用传统方法提取相干和高阶累计量等属性，以智能预测方法（如基于U型网络的断点数据体识别等）生成断点数据体；对比、分析不同类型断点数据体的准确性及其与地震数据体的对应关系，优选刻画精度最高的断点数据体用于后续方法研究。

用python程序分析该数据体中断点位置的值域范围，将数据体的值域归一化到[0, 1]，设置阈值区分断点和非断点。

2.2 设置目标断层种子点

针对目标断层，在三维地震数据上观察该断层所贯穿的时间范围，在该范围内选定一张断层刻画较为清晰的时间切片做为初始时间切片。在初始时间切片上，通过人机交互设置目标断层的种子点和阻隔点，明确目标断层所在位置。

2.3 利用约束区域生长算法实现目标断层空间精确刻画

（1）初始时间切片目标断层断点数据自动提取。将目标断层命名为F（初始为空集∅），将目标断层空间边界命名为B（初始为空集）。在初始时间切片上，从种子点出发，遇到阻隔点停止，利用区域生长算法实现目标断层断点数据的自动追踪，并记录为F₀（包括大地坐标X、大地坐标Y、时间）。

（2）明确当前时间切片断点数据F₀的平面边界。利用平面$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $边缘提取算法得到当前时间切片上目标断层断点数据F₀的凹包边界B₀；

（3）明确相邻时间切片目标断层的空间边界。利用倾角约束的多边形偏置算法得到凹包外扩多边形B₁，避免由于断层偏移漏掉相邻时间切片上的目标断层断点数据。

（4）搜索相邻时间切片上凹包外扩多边形B₁内的断点数据F₁。针对相邻时间切片，利用区域生长算法搜索位于凹包外扩多边形B₁范围内的断点，并记录为F₁。

（5）判断F₁是否为空集。若F₁是空集，则目标断层提取任务结束；否则进入下一步骤。

（6）判断F₁是否属于目标断层。针对凹包外扩多边形B₁范围内的断点数据F₁，设置目标断层重合度阈值η。若重合度大于阈值$ \eta $则进入下一步骤，否则目标断层提取任务结束。

（7）将相邻时间切片更新为当前时间切片，将F₁更新为F₀，将B₁更新为B₀。

（8）合并当前断点数据到目标断层，合并目标断层的空间边界。

把F₀拼接到F，即$ \boldsymbol{F}=\boldsymbol{F}\bigcup {\boldsymbol{F}}_{0} $；把B₀合并到B，即$ \boldsymbol{B}=\boldsymbol{B}\bigcup {\boldsymbol{B}}_{0} $。

（9）重复（2）~（8）操作，直到不存在目标断层的断点，即F₁为空集。最终获得精准的目标断层空间展布形态。

3 方法试算

针对某工区剖面上的三条断层，应用上述流程开展方法试算。

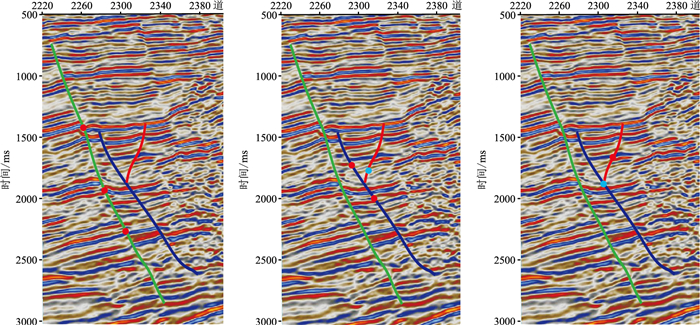
如图 7所示，针对不同颜色目标断层，分别设置了不同数目的种子点和阻隔点。绿色断层(图 7左)设置了三个种子点；蓝色断层（图 7中）设置了两个种子点和一个阻隔点；红色断层（图 7右）设置了一个种子点和一个阻隔点。

之后，对地震数据体提取相干属性，明确相干数据体上断点的值域范围，并将断点值域归一化到[0, 1]区间。根据经验可知断点生长值范围在0.4~0.9，断层重合度阈值范围在0.3~0.6，多边形偏置范围需根据断层倾角确定。表 1统计了该区较好的7个参数组合，依据断层自动提取结果与专家解释成果的吻合度确定其中最优组合是：断点生长值为0.52、断层重合度阈值为0.4、多边形偏置范围为10%。

断层自动提取的最优参数组合不是一成不变的，需根据不同地区、不同层系的断层特征，开展针对性参数组合分析。图 8为采用本文断层自动提取方法获得的三条目标断层的空间展布形态，可见，绿色断层和蓝色断层的倾向较为一致，红黄色断层的倾向与蓝色断层近乎垂直，并与蓝色断层相交，类似于“Y”字形。

4 实际应用

将本文方法应用在胜利油田征6、辛50地区实际地震资料断层解释中，与某商业软件和人工解释结果相比，本文方法断层提取效果更好、工作效率更高。

4.1 征6地区断层自动提取

针对征6地区某时间切片上的一条东西走向目标断层（图 9a黑色虚线椭圆内），应用某商业软件和本文方法分别开展断层自动提取。从断层提取效果看，受断层走向和倾向的影响，某商业软件将目标断层分割成多条零碎小断层，而且提取结果不能涵盖整条断层（图 9b）；而本文方法能够完整、准确地提取目标断层（图 9c）。

使用本文方法完成了对征6地区5条断层空间展布特征的精准刻画（图 10）。

4.2 辛50地区断层自动提取 4.2.1 断点数据体优选

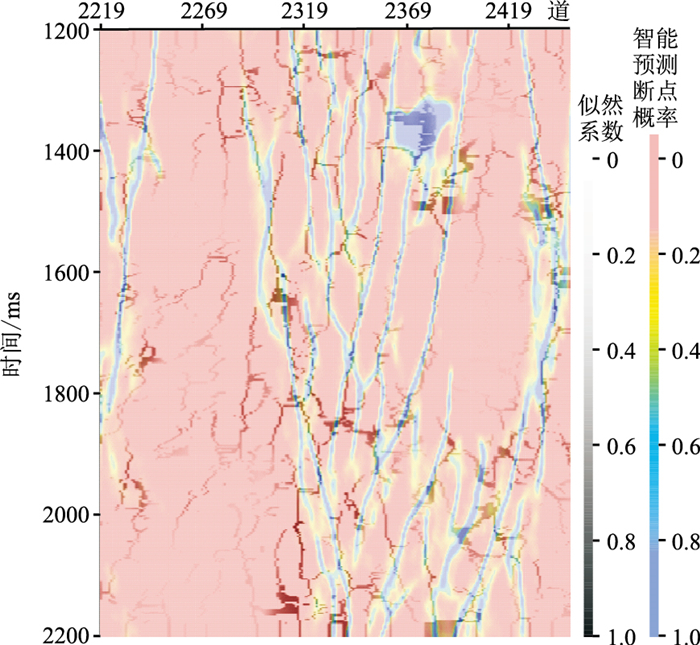
为了更准确地识别、提取辛50地区目的层段断层数据，对该区不同的断点数据体进行分析和优选。图 11是最大似然属性叠合地震剖面图，最大似然系数色标值越大表示成为断层的可能性越高。可以看出，最大似然属性体较为准确地表征出该区断裂系统展布。图 12是最大似然属性与智能预测结果的剖面叠合对比，图中彩色色棒表示智能预测断点概率，红黄色表示成为断点的概率低，蓝紫色表示成为断点的概率高。从两种预测体的叠合结果可见，在大部分位置两者具有很高的一致性，但是最大似然属性体上存在很多小弯曲，断层刻画多解性强；而智能预测数据体能更加完整而直观地表征断层，最终优选智能预测结果直接用于断层提取。

4.2.2 断层自动提取

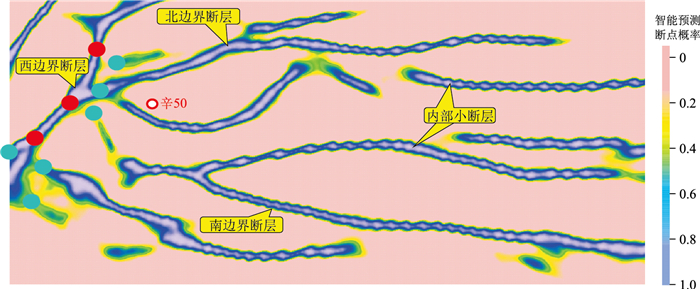
针对辛50地区边界断层以及内部小断层，在智能预测数据体辅助下，应用本文方法开展断层自动提取。图 13是辛50地区1732 ms时间切片上的西边界断层的种子点和阻隔点设置情况。因为西边界断层附近有很多分叉断层，所以要设置足够多的阻隔点。接下来确定断点生长值、断层重合度阈值和多边形偏置范围三参数，遍历所有的参数组合，选择针对每条目标断层的最优参数组合。最终应用本文方法准确而快速地识别出北边界、西边界和南边界断层以及两条内部小断层（图 14）。

在辛50地区采用人工解释断层的方式，需要2名研究人员历时3天才能完成这5条断层的准确解释；而采用本文方法只需要1名研究人员，并且可将断层解释时间缩短50%以上，大幅提高了工作效率。

在实际应用过程中，不论对于简单断层还是复杂断层，本文方法都具有较好的应用效果。但是对于复杂断层，需要设置足够多的阻隔点，并优选最佳参数组合才能实现目标断层的精准刻画。

5 结束语

本文提出一种基于$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $和多边形偏置算法的断层自动提取方法。通过人机交互设置种子点和阻隔点，消除了分叉断层对目标断层的影响；通过$ \alpha \mathrm{⁃}\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e} $算法定义了断层平面轮廓；将多边形偏置算法与断层倾角的变化相结合，研发了断层空间边界预测技术；在断层空间边界和断层重合度阈值的约束下，实现了基于约束区域生长算法的断层自动提取。

在胜利油田实际地震数据的应用结果表明，与某商业软件相比，本文方法断层提取结果更完整、更准确；与人工解释相比，该方法大幅提升了工作效率。另外，该方法不仅适用于断层分离或简单的交叉断层识别，而且适用于复杂断裂带的断层自动提取。但是对于复杂断层，需要设置足够的阻隔点并优选最优参数组合才能实现对目标断层的精准刻画。