2. 油气资源与勘探技术教育部重点实验室(长江大学), 湖北武汉 430100;
3. 中国石油大学(北京)地球物理学院, 北京 102249;
4. 中国石油勘探开发研究院, 北京 100083
2. Key Laboratory of Exploration Technologies for Oil and Gas Resources, Ministry of Education, Yangtze University, Wuhan, Hubei 430100, China;
3. College of Geophysics, China University of Petroleum (Beijing), Beijing 102249, China;
4. Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100083, China
品质因子Q描述了地下介质的本质特征,是地下介质的基本物理参数之一[1-3],通常用于表征地下介质的吸收衰减程度。其估算(或反演)所依据的是地震波在不同空间位置的频率变化。与地震波走时信息相比,地震波的频率信息更容易受到地层吸收之外的其他因素干扰。因此,Q估算是一项非常基础又颇具挑战性的研究工作[4-5]。
目前,许多科研工作者已经发展了多种Q反演方法,按照作用域可将这些方法分为三大类,即时间域[6]、频率域[7-15]和时频域Q反演方法[16-20]。
其中,时间域Q反演方法的主要依据是: 地震子波随着传播距离或时间的增加,子波的振幅、宽度等特征会发生变化,利用这些变化量可以反推地层的Q。Gladwin等[6]通过分析脉冲信号在吸收衰减过程中的上升时间变化,推导出上升时间与品质因子的关系,即上升时间法。噪声的存在会降低上升时间确定的准确性,从而影响Q反演的精度和稳定性。
频率域Q反演方法的主要依据是: 地震波的吸收衰减效应会引起地震信号频谱特征的变化,通过量化频谱变化可以估计地层的Q。Bath[7]分析不同时刻的两个地震子波的对数谱比值,提出了谱比法(SR),这也是目前工业界应用最为广泛的方法之一。Quan等[9]利用地震波的吸收衰减会导致子波质心频率向低频端移动这一特征,提出了质心频移法(CFS),该方法较SR有更强的抗噪性,但是该方法假设地震子波振幅谱为高斯谱,这在一定程度上降低了Q的反演精度,限制了其应用和推广。
时频域Q反演方法的主要依据是: 地震波的吸收衰减是传播时间和频率的二元函数,可以利用时频分析工具建立时频谱与品质因子的关系,进而反演地层的Q。Reine等[16]比较了利用固定时窗时频变换(短时傅里叶变换和Gabor变换)与可变时窗时频变换(小波变换和S变换)进行Q反演结果的差异,表明了可变时窗时频变换在一定程度上可提高Q反演的稳定性和精度。
在上述方法中,SR和CFS由于计算简单、使用灵活,成为了目前生产应用最为广泛的两种Q反演方法。但是,它们主要依靠地震振幅谱的单一属性(对数谱比斜率或者质心频率)对Q进行反演,很容易受到地震噪声和波场干涉等因素的影响。
近年来,基于最优化理论的Q反演已经成为重要的发展趋势[21-23]。Blias[24]将最小二乘反演框架引入Q估算,并通过最小化吸收参数目标函数得到了更加稳定的Q估算结果。Dutta等[25]基于时间域的黏滞声波波动方程,实现了基于波动方程的Q层析反演。Takam Takougang等[26]利用全波形反演框架实现了对速度和Q的联合反演。从理论上讲,基于全波形反演的Q建模是目前最为先进的Q反演技术(因为反演算法中用到了全波场信息),但是该方法需要提供地震子波,而且待反演的速度模型和Q模型存在耦合问题,这些因素都限制了其在工业界的大范围推广和应用。
为了兼顾Q反演方法的理论优越性和算法实用性,本文提出了一种基于重构震源振幅谱一致性的Q反演方法。首先将地震信号沿射线路径向震源位置反向传播,并进行吸收补偿,然后利用地震信号在震源位置重构的振幅谱一致性进行地层吸收参数反演。与全波形Q反演方法相比,该方法并未用到全波场信息,而是舍弃了不稳定的相位信息,只采用振幅谱信息,算法稳定性和实用性更好。同时,不同于SR和CFS采用单一参数(对数谱比斜率或者质心频率)刻画振幅谱信息,本文方法采用振幅谱全部信息参与反演,具备更强的抗噪性和适应能力。
1 方法原理地震波传播过程可以由如下线性系统描述
| $ {R}_{j}\left(f\right)={G}_{j}\cdot S\left(f\right)\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left(-f{\int }_{\mathrm{r}\mathrm{a}\mathrm{y}}\frac{{\rm{ \mathsf{ π} }}}{Qv}\mathrm{d}l\right) $ | (1) |
式中:Rj (f)表示第j个检波器接收信号的振幅谱,f为频率变量;Gj表示第j个检波器对应的与地层吸收无关的项,包括几何扩散、反射/透射损失、耦合响应、仪器响应等;S( f)表示输入信号的振幅谱;v表示地震波传播速度;ray表示传播路径;dl表示传播路径上的位移增量。
下面以微测井观测系统为例,详细介绍地震波在吸收介质中的传播过程以及本文方法的原理。
图 1a为微测井观测系统和单炮激发的射线追踪路径,其中,炮点放置在深度为45 m的井底,检波点放置在地表,最小偏移距为10 m,最大偏移距为150 m,检波点间距为10 m。根据速度模型可以进行射线追踪,得到地震波传播的射线路径。图 1b为振幅归一化之后的地震单炮记录,可以看出,随着偏移距的增大,地震记录的吸收衰减现象更明显,地震记录波形变“胖”。为了进一步展示随着偏移距变化的地震数据频率差异,对单炮地震记录的每一道进行傅里叶变换,并求取振幅谱,可以得到随偏移距变化的振幅谱(图 1c)。由图 1c可见,随着地震波传播距离的增大,地震信号的主频向低频方向移动,不同道之间的振幅谱表现出明显的差异。
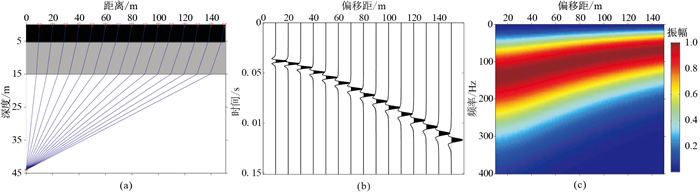
|
图 1 微测井正演模拟过程 (a)微测井观测系统和射线传播路径;(b)振幅归一化之后的地震单炮记录;(c)随偏移距变化的振幅谱 |
由于地层的吸收衰减效应,检波点接收的地震记录振幅谱表现出明显的差异。为了消除这种差异,可以将检波点地震信号向震源位置进行反向传播,并沿反向传播路径补偿其吸收衰减,最后可以得到每道地震信号在震源位置的重构振幅谱
| $ {\tilde{S}}_{j}\left(f\right)={R}_{j}\left(f\right)\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left(f{\int }_{\mathrm{r}\mathrm{a}\mathrm{y}}\frac{{\rm{ \mathsf{ π} }}}{Qv}\mathrm{d}l\right) $ | (2) |
式中
图 2展示了分别利用准确的与有误差的品质因子模型进行震源振幅谱重构的结果。假设给定的品质因子模型是准确的(图 2a左),则不同地震道
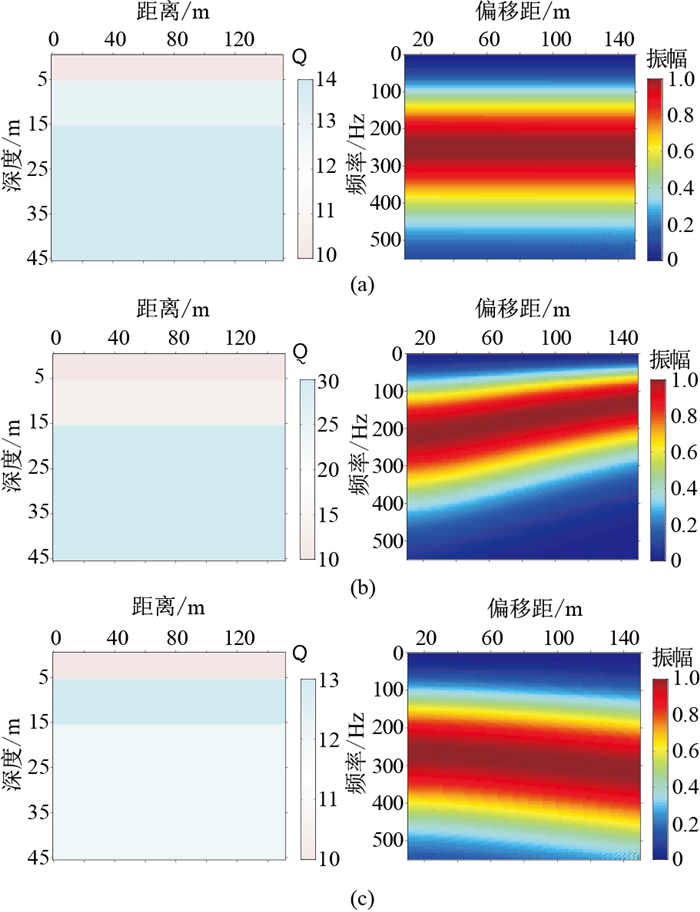
|
图 2 不同品质因子Q值模型(左)与其对应的 |
上述实验表明:无论是欠补偿情况,还是过补偿情况,每道记录对应的
为了建立地层品质因子Q与
| $ B(f, Q)=\frac{1}{{N}_{r}}\sum\limits_{j=1}^{{N}_{r}}{\tilde{S}}_{j}(f, Q) $ | (3) |
式中Nr为检波器个数。需要注意的是,本文并不是以真实的震源振幅谱作为参考值,而是以所有
进一步利用如下的方差函数定量描述不同地震道
| $ E\left(Q\right)=\sum\limits_{j=1}^{{N}_{r}}{\left[{\tilde{S}}_{j}(f, Q)-B(f, Q)\right]}^{2} $ | (4) |
在上式中,参考振幅谱B(f, Q)代表不同地震道
显然,当反演的品质因子模型等于真实模型时,每道数据
上述目标函数的求解不是传统的线性问题,很难通过梯度类方法解决。对于此类问题,可以通过全局寻优算法完成。目前的全局寻优算法种类繁多(如遗传算法、模拟退火算法、神经网络算法、蚁群算法等),本文选择模拟退火算法对上述目标函数进行求解。考虑到该算法已经较为通用且十分成熟,本文对该算法不进行详细赘述,其详细实施流程见参考文献[27]。
需要注意的是,虽然本文方法是以微测井观测系统为例进行推导,但是该方法不仅可以用于近地表Q值反演,同样也可以用于VSP数据和反射波数据的Q值反演。原因在于: 该方法的核心是将检波点数据沿传播路径反向延拓并补偿至震源位置处,进而比较
首先,利用图 3a所示的近地表模型进行测试分析。该模型分为3层,即低速层、降速层和高速层,每层的地层参数如表 1所示。近地表微测井观测系统采集参数为:激发井的深度为45 m,炮点从井深44 m到井深2 m间隔2 m依次激发。检波器均匀布置在地表,最小偏移距为10 m,最大偏移距为150 m,检波点距为10 m。激发子波选用峰值频率为250 Hz的零相位雷克子波。
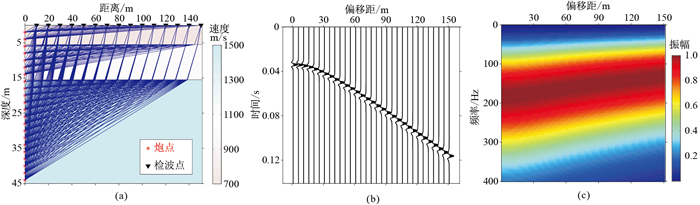
|
图 3 近地表模型和正演模拟 (a)近地表模型及射线路径;(b)考虑吸收衰减的合成地震记录;(c)地震记录对应的振幅谱 |
|
|
表 1 近地表模型参数 |
根据近地表速度模型和正演观测系统,利用射线追踪正演模拟可以确定地震波的传播路径。根据射线路径和品质因子Q模型,可以进一步计算地震波在各层中的传播时间和吸收衰减量,从而模拟得到衰减后的地震记录(考虑到本文讨论的Q反演方法都没有用到相位信息,在正演模拟中忽略吸收衰减效应产生的相位畸变)。图 3b展示了激发深度为40 m的单炮记录。可以看出,随着偏移距的增加,地层的吸收衰减效应更加严重,地震反射同向轴略微变“胖”。对衰减地震记录每一道做傅里叶变换,可以得到其对应的频谱(图 3c)。
分别利用SR、CFS和本文方法计算地层的品质因子,估算结果如表 2所示。可以看出,三种方法都能获得很好的Q值估算结果,且基于源谱一致性的Q反演方法具有更高的反演精度。
|
|
表 2 无噪声情况下三种方法的Q反演结果 |
为了测试三种Q估算方法的抗噪性,分别在合成数据中加入5%、10%和20%的随机噪声。对于每种含噪声数据,分别利用3种方法进行200次的独立测试,并计算Q反演结果的平均值和标准差。平均值反映了Q反演方法的精度,标准差反映了Q反演方法的稳定性和抗噪性。
在5%噪声情况下,三种方法的Q反演结果(平均值和标准差)如表 3所示。为了更加直观地比较效果,将上述结果用误差直方图(图 4a)展示。由图可见,在低噪声背景下,三种方法也能获得较为合理的Q反演结果,而本文方法具有更小的标准差,说明本文方法的抗噪性更强。
|
|
表 3 5%噪声情况下三种方法的Q反演结果 |

|
图 4 加入不同噪声情况下三种方法的Q因子反演结果 (a)5%随机噪声;(b)10%随机噪声;(c)20%随机噪声 |
在10%噪声情况下,三种方法的反演结果(平均值和标准差)如表 4和图 4b所示。此时,三种方法计算的Q误差都有所提高,可靠性随之减弱,但是本文方法的可靠性明显优于另外两种方法。
|
|
表 4 10%噪声情况下三种方法的Q因子反演结果 |
在20%噪声情况下,三种方法的Q反演结果(平均值和标准差)如表 5和图 4c所示。此时,三种方法的估算精度和可靠性均有所降低。
|
|
表 5 20%噪声情况下三种方法的Q因子反演结果 |
从这三组实验可以看出,随着加入噪声的增强,基于SR和CFS的Q反演结果的精度和可靠性明显降低,而本文方法优势逐渐凸显出来,这也证明了本文方法的稳定性更高和抗噪能力更强。
2.3 子波对Q因子的影响考虑到实际地震子波并非雷克子波,本文方法不依赖地震子波的任何假设,因而在理论上具有优越性。为了说明这一问题,分别利用可控震源子波和俞氏子波进行测试、分析。
图 5a和5b分别展示了利用可控震源子波和俞氏子波合成的地震炮集记录。在这两种情况下,分别利用三种Q因子反演方法计算地层的品质因子,估算结果如图 5c和5d所示。

|
图 5 利用不同类型子波激发合成的单炮记录以及对应的Q因子反演结果 (a)可控震源子波合成单炮记录;(b)俞氏子波合成单炮记录;(c)可控震源子波地震记录对应的Q因子反演结果;(d)俞氏子波地震记录对应的Q因子反演结果 |
当地震子波为可控震源子波时,SR估算的3层品质因子分别是12.34、21.55和48.32;CFS估算的3层品质因子分别是11.17、18.38和52.45;本文方法计算结果分别为10.05、20.23和50.42。
当地震子波为俞氏子波时,SR计算的3层品质因子分别是9.91、20.64和49.02;CFS计算的3层品质因子分别是12.03、23.12和53.74;本文方法计算结果分别为9.96、20.09和50.25。
对比分析可知:CFS受子波影响较大,主要原因在于CFS假设震源子波振幅谱为高斯函数,而SR和本文方法受到激发子波类型的影响较小,在实际资料处理中具有更强的适应性。
在实际情况中,子波的干涉是难以避免的。为探究子波干涉对本文方法的影响,可采用干涉后的地震数据作为输入进行测试、分析。
图 6a和6b分别展示了子波干涉后的单炮记录和对应的振幅谱。可以发现,子波干涉不仅使地震反射特征发生畸变(形成复合波),还影响了地震数据的频率特征(形成多峰值振幅谱)。子波干涉对频率的改造作用会严重影响Q值反演方法的可行性和估算精度。基于该数据,首先利用SR和CFS分别计算地层的品质因子,结果都出现了很大的误差,甚至估算出负Q值,这不符合理论。然后,利用本文方法计算,可得到误差较小的的Q值反演结果(图 6c)。

|
图 6 子波干涉情况下的Q因子反演结果 (a)子波干涉后的单炮记录;(b)单炮记录对应的振幅谱;(c)根据子波干涉后的数据计算Q因子反演结果;(d)利用Q因子反演结果反向补偿得到的重构振幅谱 |
为了更好地分析本文方法克服子波干涉影响的原因,利用图 6c所示的Q值模型对图 6b所示检波点振幅谱进行反向补偿,得到震源位置CFS(图 6d)。可以发现,CFS具有较好的一致性,且具有两个明显的峰值(分别为210 Hz和390 Hz)。其中,峰值频率为210 Hz的振幅谱部分主要反映了真实震源振幅谱的特征,峰值频率为390 Hz的振幅谱部分主要反映了相邻信号的干涉效应。考虑到初至信号与相邻信号传播时间十分相近,传播路径差异很小,即两者经历了相似的吸收衰减。因此,当反演的Q值模型接近于真实Q值模型时,反传补偿过程不仅可以消除初至子波的吸收衰减效应(得到震源子波),也可以校正相邻子波的吸收衰减效应(得到后续震源子波)。此时,每道CFS即为两个相邻震源子波干涉的结果,虽然该CFS不再是单纯的震源振幅谱(而是复合震源振幅谱),但是该振幅谱依旧具有很好的一致性,同时具有很小的方差。由此可见,子波干涉效应并未(大幅度)改变真实Q值模型和CFS方差最小值的对应关系。也就是说,即使在子波干涉情况下,也可以通过最小化方差目标函数,得到接近于真实Q值模型的反演结果,这也是本文方法可以在一定程度上克服干涉影响的原因。
3 实际资料应用将本文方法应用于M区块,对近地表观测数据进行处理和分析。
图 7是M区块井地联合微测井系统示意图。观测系统参数如下:激发井深为30 m,激发点深度由深至浅依次为30、28、26、24、22、20、18、16、14、12、10、9、8、7、6、5、4、3、2.5、2、1.5、1、0.5 m,总计23炮。接收井与激发井相距为5 m,接收井深为3 m。共布设了10个检波器,井底检波器为第1道,井口检波器为第2道,第3道至第10道沿二维测线非等间隔布设,检波器距离激发井最大距离为85 m。
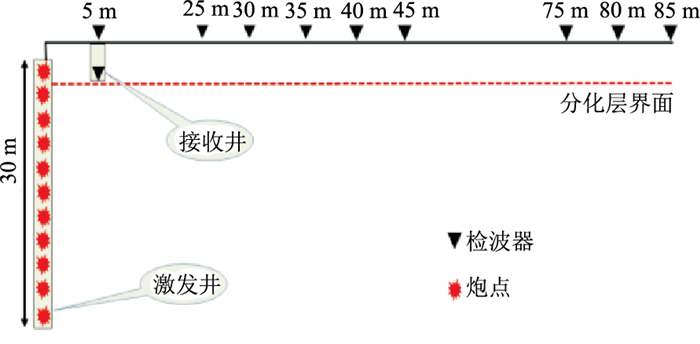
|
图 7 井地联合微测井观测系统示意图 |
图 8a是激发深度为30 m的共炮点道集,第1道和第2道分别是井底和井口接收的地震波信号,其波形和频率差异基本反映了低速层对地震信号的改造作用。第2道~第10道均为地面接收的地震波信号,由于它们均经历了近乎相同的低速层吸收作用,因此其波形和振幅谱差异反映了降速层和高速层对地震信号的改造作用。
|
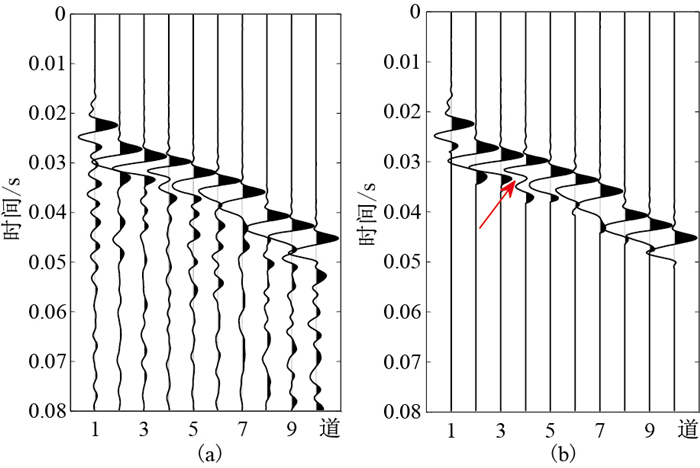
图 8 近地表野外观测数据 (a)激发深度为30 m的共炮点道集;(b)截取的直达波记录 |
在进行Q因子反演之前,需要按照一定的时窗将初至波信号分离出来。图 8b是截取的直达波地震记录。由图可见,第4道受到了严重的波场干涉(红色箭头处),应该予以剔除。值得注意的是,对地震信号的分析和编辑,是一项非常重要的基础工作,需要结合地震信号在时间域和频率域的特性,剔除干扰较为严重的地震道,确保参与反演的地震数据的合理性,否则很难保证反演结果的可靠性。
拾取初值波旅行时,利用速度层析反演进行近地表速度结构建模。图 9显示了M区块近地表速度反演结果。整体而言,该区近地表为3层结构,即低速层、降速层和高速层。低速层速度为400~800 m/s,除东北方向小部分区域速度较高外,其他区域速度变化较为平缓;降速层速度为500~1300 m/s,速度整体变化较为平缓;高速层速度为1400~2000 m/s,西北方向速度高,东南方向速度低。

|
图 9 近地表速度结构模型 (a)低速层;(b)降速层;(c)高速层 |
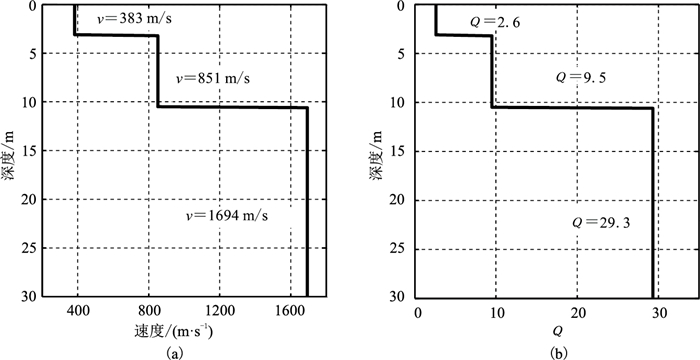
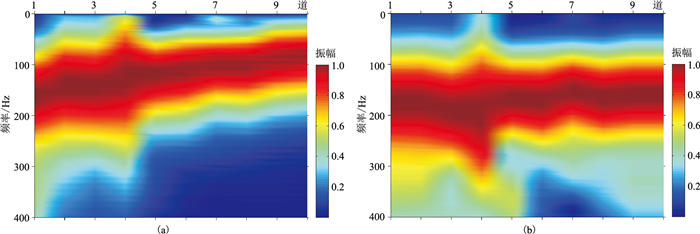
在此基础上,利用本文方法进行了吸收参数估算和反演。图 10a显示了本测点的速度层析反演结果,基于该速度模型,利用本文方法进一步反演近地表吸收参数,得到该测点的Q因子模型(图 10b)。利用这两个模型,可以将直达波地震信号沿射线路径向震源位置反向传播,并沿反向传播路径进行吸收补偿,重构出震源位置地震信号的振幅谱。图 11展示了吸收补偿前、后地震记录的振幅谱。从图中可以看出,经过吸收补偿之后,地震记录振幅谱的一致性得到了较好的恢复。也就是说,利用该吸收参数模型可以较好地消除地层吸收的影响,这从侧面证明了该吸收参数模型的可靠性。
|
图 10 近地表参数最终反演结果 (a)速度;(b)Q因子 |
|
图 11 根据图 10中速度和品质因子进行补偿前(a)、后(b)的直达波振幅谱 |
对M区块的所有微测井数据都按照上述流程处理,可以得到整个工区的近地表Q因子模型。图 12显示了该区块3个层的品质因子空间变化情况。其中,低速带品质因子平均值约为2.5,最小和最大值分别约为1.0和5.0。降速带品质因子平均值约为8.0,最小和最大值分别约为4.0和13.0。高速层品质因子平均值约为25.0,最小和最大值分别约为14.0和35.0。该结果与相邻区块一致,从侧面证明了本文方法反演结果的准确性。

|
图 12 近地表吸收结构模型 (a)低速层;(b)降速层;(c)高速层 |
需要指出的是,就本文开展的实验工作而言,品质因子和地层速度呈正相关。速度越大,品质因子也越大。但这种相关性在不同地区、不同地层存在较大差异。近地表的土质组分、压实程度、孔隙结构和潜水面变化等都对品质因子产生影响。因此,开展深入细致的近地表吸收结构调查,消除近地表吸收对地震数据分辨率和保幅性能的影响具有非常重要的现实意义。
4 结论(1)本文提出了一种基于重构震源振幅谱一致性的Q因子反演方法,其核心思想是将地震信号沿射线路径向震源位置反向传播并进行吸收补偿,然后利用地震信号在震源位置重构振幅谱的一致性进行地层吸收参数反演。
(2)不同于谱比法和质心频移法只提取地震信号振幅谱的某个特定属性,本文方法直接利用振幅谱进行反演,具有更高的稳定性和更强的抗噪性。此外,本文方法既不需要已知震源子波,也不需要对子波进行任何假设,具有较强的适用能力。
(3)模型数据测试和实际资料应用均表明:相较于谱比法和质心频移法,本文方法具有更强的抗噪性和更高的反演精度,能够为后续的吸收补偿提供更高精度的吸收结构模型。
| [1] |
王小杰, 印兴耀. 基于零相位子波地层Q值估计[J]. 地球物理学进展, 2011, 26(6): 2090-2098. WANG Xiaojie, YIN Xinyao. Estimation of layer quality factors based on zero‑phase wavelet[J]. Progress in Geophysics, 2011, 26(6): 2090-2098. |
| [2] |
赵秋芳, 云美厚, 朱丽波, 等. 近地表Q值测试方法研究进展与展望[J]. 石油地球物理勘探, 2019, 54(6): 1397-1418. ZHAO Qiufang, YUN Meihou, ZHU Libo, et al. Progress and outlook of near-surface quality factor Q measurement and inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1397-1418. DOI:10.13810/j.cnki.issn.1000-7210.2019.06.026 |
| [3] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法[J]. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near-surface Q value estimation and quantitative amplitude compensation[J]. Oil Geophysical Prospecting, 2019, 54(5): 988-996. DOI:10.13810/j.cnki.issn.1000-7210.2019.05.006 |
| [4] |
张瑾, 张国书, 王彦国, 等. 利用泰勒级数展开的振幅谱积分差值的Q值估计方法[J]. 石油地球物理勘探, 2022, 57(2): 320-330. ZHANG Jin, ZHANG Guoshu, WANG Yanguo, et al. Amplitude spectral integral difference method for Q estimation based on Taylor series expansion[J]. Oil Geophysical Prospecting, 2022, 57(2): 320-330. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.009 |
| [5] |
李拥军, 宋炜, 唐传章, 等. 复数域匹配追踪近地表Q值估计及深度学习建模[J]. 石油物探, 2021, 60(1): 123-135. LI Yongjun, SONG Wei, TANG Chuanzhang, et al. Complex domain-matching pursuit for near-surface Q-estimate and deep learning modeling[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 123-135. DOI:10.3969/j.issn.1000-1441.2021.01.012 |
| [6] |
GLADWIN M T, STACEY F D. Anelastic degradation of acoustic pulses in rock[J]. Physics of the Earth and Planetary Interiors, 1974, 8(4): 332-336. DOI:10.1016/0031-9201(74)90041-7 |
| [7] |
BATH B M. Spectral Analysis in Geophysics[M]. New York: Elsevier, 1974.
|
| [8] |
杨登锋, 刘军, 吴静, 等. 加权谱比法Q值估计[J]. 石油地球物理勘探, 2022, 57(3): 593-601. YANG Dengfeng, LIU Jun, WU Jing, et al. Q-factor estimation by weighted spectral ratio method[J]. Oil Geophysical Prospecting, 2022, 57(3): 593-601. DOI:10.13810/j.cnki.issn.1000-7210.2022.03.010 |
| [9] |
QUAN Y, HARRIS J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(3): 895-905. DOI:10.1190/1.1444197 |
| [10] |
张立彬, 王华忠, 马在田. 基于积分中值参变量法的质心频移Q值估算[J]. 石油物探, 2010, 49(3): 213-221. ZHANG Libin, WANG Huazhong, MA Zaitian. A centroid frequency shift method of Q estimation based on mean value theorem of integrals[J]. Geophysical Prospecting for Petroleum, 2010, 49(3): 213-221. |
| [11] |
杨登锋, 秦成岗, 汪瑞良, 等. 能量谱质心频移法Q值估计[J]. 石油地球物理勘探, 2016, 51(5): 863-867. YANG Dengfeng, QIN Chenggang, WANG Ruiliang, et al. Q factor estimation based on the centroid frequency shift of energy spectrum[J]. Oil Geophysical Prospecting, 2016, 51(5): 863-867. DOI:10.13810/j.cnki.issn.1000-7210.2016.05.003 |
| [12] |
ZHANG C, ULRYCH T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(5): 1542-1547. DOI:10.1190/1.1512799 |
| [13] |
余青露, 居兴国, 李进, 等. 基于峰值频率法的组合法估计叠前Q值[J]. 地球物理学进展, 2015, 30(4): 2090-2098. YU Qinglu, JU Xingguo, LI jin, et al. A combination method of Q factor estimation based on peak frequency shift method[J]. Progress in Geophysics, 2015, 30(4): 2090-2098. |
| [14] |
WANG Y. Q analysis on reflection seismic data[J]. Geophysical Research Letters, 2004, 31(17): 606-609. |
| [15] |
王静, 姚正新, 张彦斌, 等. VSP全井段Q值估计[J]. 石油地球物理勘探, 2018, 53(增刊2): 58-64. WANG Jing, YAO Zhengxin, ZHANG Yanbin, et al. Whole-well length VSP Q estimation[J]. Oil Geophysical Prospecting, 2018, 53(S2): 58-64. DOI:10.13810/j.cnki.issn.1000-7210.2018.S2.010 |
| [16] |
REINE C, VAN DER BAAN M, CLARK R. The robustness of seismic attenuation measurements using fixed- and variable-window time-frequency transforms[J]. Geophysics, 2009, 74(2): WA123-WA135. DOI:10.1190/1.3043726 |
| [17] |
刘国昌, 陈小宏, 杜婧, 等. 基于整形正则化和S变换的Q值估计方法[J]. 石油地球物理勘探, 2011, 46(3): 417-422. LIU Guochang, CHEN Xiaohong, DU Jing, et al. Seismic Q estimation using S-transform with regularized inversion[J]. Oil Geophysical Prospecting, 2011, 46(3): 417-422. |
| [18] |
刘喜恒, 刘国昌, 崔永谦, 等. 局部时频变换横向约束Q值估计方法[J]. 石油地球物理勘探, 2016, 51(5): 868-874. LIU Xiheng, LIU Guochang, CUI Yongqian, et al. Q estimation with lateral constraint based on local time-frequency transform[J]. Oil Geophysical Prospecting, 2016, 51(5): 868-874. DOI:10.13810/j.cnki.issn.1000-7210.2016.05.004 |
| [19] |
郝亚炬, 黄捍东, 文晓涛, 等. 广义S域Q值估计方法及其在油气检测中的应用[J]. 石油地球物理勘探, 2017, 52(5): 1059-1066. HAO Yaju, HUANG Handong, WEN Xiaowen, et al. Q estimation in the generalized S domain and its application in the hydrocarbon detection[J]. Oil Geophysical Prospecting, 2017, 52(5): 1059-1066. DOI:10.13810/j.cnki.issn.1000-7210.2017.05.020 |
| [20] |
许李囡, 高静怀, 杨阳, 等. 基于S变换和变分法的品质因子Q估计方法[J]. 石油地球物理勘探, 2022, 57(1): 82-90. XU Linan, GAO Jinghuai, YANG Yang, et al. Quality factor Q estimation based on S transform and variational method[J]. Oil Geophysical Prospecting, 2022, 57(1): 82-90. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.009 |
| [21] |
金子奇, 孙赞东. 改进的衰减旅行时层析方法估计Q值[J]. 石油物探, 2018, 57(2): 222-230. JIN Ziqi, SUN Zandong. Improved attenuated traveltime tomography for Q estimation[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 222-230. DOI:10.3969/j.issn.1000-1441.2018.02.007 |
| [22] |
严又生, 宜明理, 魏新, 等. 井间地震速度和Q值联合层析成像及应用[J]. 石油地球物理勘探, 2001, 36(1): 9-17. YAN Yousheng, YI Mingli, WEI Xin, et al. Joint tomographic imaging for cross-hole seismic velocity and Q value[J]. Oil Geophysical Prospecting, 2001, 36(1): 9-17. |
| [23] |
刘国昌, 李超. 基于多射线联合反演的速度无关叠前地震数据Q值估计[J]. 地球物理学报, 2020, 63(4): 1569-1584. LIU Guochang, LI Chao. Velocity-independent prestack seismic Q estimation based on multi‑ray joint inversion[J]. Chinese Journal of Geophysics, 2020, 63(4): 1569-1584. |
| [24] |
BLIAS E. Accurate interval Q-factor estimation from VSP data[J]. Geophysics, 2012, 77(3): WA149-WA156. DOI:10.1190/geo2011-0270.1 |
| [25] |
DUTTA G, SCHUSTER G T. Wave-equation Q tomography[J]. Geophysics, 2016, 81(6): R471-R484. DOI:10.1190/geo2016-0081.1 |
| [26] |
TAKAM TAKOUGANG E M, CALVERT A J. Seismic velocity and attenuation structures of the Queen Charlotte Basin from full‑waveform tomography of seismic reflection data[J]. Geophysics, 2012, 77(3): B107-B124. DOI:10.1190/geo2011-0243.1 |
| [27] |
SEN M K, STOFFA P L. Nonlinear one-dimensional seismic waveform inversion using simulated annealing[J]. Geophysics, 1991, 56(10): 1624-1638. DOI:10.1190/1.1442973 |



 李国发,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email:
李国发,北京市昌平区府学路18号中国石油大学(北京)地球物理学院,102249。Email: