2. 中国石油大学(北京)油气资源与工程全国重点实验室, 北京 102249;
3. 中国石油大学(北京)地球科学学院, 北京 102249;
4. 中国石化胜利油田分公司, 山东东营 257015
2. National Key Laboratory of Petroleum Resources and Engineering, China University of Petroleum (Beijing), Beijing 102249, China;
3. College of Geosciences, China University of Petroleum(Beijing), Beijing 102249, China;
4. Shengli Oil Field Company, SINOPEC, Dongying, Shandong 257015, China
地震属性能有效反映地下地质信息,在油气勘探、开发的各个阶段均扮演着重要角色,已广泛应用于构造与地层解释[1-3]、储层预测[4-6]、烃类检测[7-8]等方面。目前地震属性分析技术主要有两个研究方向[9],分别是研发新的地震属性[10-11]和发展地震多属性融合技术[6, 12-13]。地震属性种类繁多,能够在不同角度表征油气储层。新研发的地震属性易与现有的地震属性之间存在“明显”的数据冗余问题,由此增加了研发“高优势”地震属性的难度。相反,地震多属性融合技术在储层预测领域已取得良好的应用效果,其方法众多,可大致分为线性模型融合、非线性模型融合和颜色模型融合(如RGB颜色模型)等[9, 14-15]。近年来,随着人工智能技术的迅速发展,机器学习方法逐步用于地震多属性融合。此类方法主要是通过学习井点储层的先验信息,建立井、震数据之间的非线性映射关系,再利用支持向量机(SVR)[16-17]、BP神经网络[18]、极限学习机[19-20]和随机森林[21]等机器学习方法定量预测储层。
常见的地震属性融合方法主要是基于单类机器学习算法,缺少对多类算法的集成[16-18, 21]。由于地下储层结构复杂、非均质性强[22-23],不同油气田甚至同一油气田的不同位置或不同层段,适合的融合算法也不同,因此亟需探索多算法集成的属性融合方法,以提升地震属性融合方法的泛化能力。
为此,本文提出了一种基于Stacking集成学习的分频地震属性融合方法,旨在提高储层预测精度。首先,将地震资料进行分频处理,分析不同频段数据体的地震属性特征;其次,采用相关性分析和无监督聚类技术,优选地震属性;然后,设计Stacking框架,集成Bagging-SVR(Bg-SVR)、Multi-Layer Perceptron(MLP)、LightGBM(LGB)、Bagging-K Nearest Neighbor(Bg-KNN)和核主成因多层感知机(KPCA-MLP)模型,并利用集成后的模型融合多个频段的地震属性,实现储层定量预测;最后,使用线性公式定量分析等方法评估Stacking模型的预测性能,并通过渤海湾盆地埕岛油田河流相储层的实例应用验证Stacking分频属性融合方法的可靠性。
1 储层智能预测模型首先,优选在储层预测领域具有良好应用效果并存在明显差异的几类模型:SVR、KNN(K Nearest Neighbor)、LGB和MLP;然后,根据储层预测需求,分别对SVR、KNN和MLP模型进行改进,并综合这几类模型优势设计出Stacking集成学习框架,以得到更准确、稳定的预测结果。
2.1 常规预测模型 2.1.1 单类模型算法(1) Bg-SVR和Bg-KNN模型。传统的SVR和KNN模型在小样本预测方面均具有独特的优势。其中,SVR模型可利用核函数(通常是径向基函数)将地震数据从低维映射到高维,并在高维空间建立回归拟合模型,实现地震属性到储层信息的非线性映射;KNN模型能够基于相邻井点的数据关系,充分挖掘井震数据特征。但在储层预测时,SVR模型的非线性表达能力容易受少数几个支撑向量的影响,而KNN模型也只是考虑了邻近几口井的样本数据。因此, 上述两类模型的泛化能力仍有不足,需要进一步改进。
大量研究实例表明集成学习模型普遍具备更好的预测性能[24],其中Bagging模型便是一种能够降低模型泛化误差的集成方式。这种方式通常是基于同类模型的集成,在地震属性融合时,能够实现地震数据样本、特征的随机抽选,可提高模型的泛化性能。
因此,本文利用Bagging算法,以相同的方式分别对SVR模型和KNN模型进行改进。以改进的KNN模型,即Bg-KNN模型为例(图 1),其预测流程可分为4步:①训练时,进行

|
图 1 Bg-KNN模型结构 |
(2) MLP模型。MLP模型是一种前馈式监督学习神经网络,包含输入层、隐层和输出层。如图 2所示,该MLP模型的输入层为6分量,输出层为1分量,具有4个隐层,每层分别包含10、6、4和3个神经元,并选用
| $ {C}_{v}^{h}=\sum\limits_{g}{w}_{gv}^{h}f\left({C}_{g}^{h-1}\right)+{b}_{v}^{h} $ | (1) |

|
图 2 MLP网络结构 |
式中:
误差反向传播表达式为
| $ {\delta }_{v}^{h}=f\left({C}_{g}^{h}\right)\sum\limits_{v}{w}_{gv}^{h+1}{\delta }_{v}^{h+1} $ | (2) |
误差
(3) LGB模型。LGB模型是基于梯度提升决策树的集成算法,能够通过梯度下降算法更新残差,随着迭代次数增加,可拟合复杂的钻井、地震数据。此外,LGB模型还在原有梯度提升树算法上进行了改进, 采用互斥特征捆绑稀疏化地震属性特征以增强模型的数据处理性能。
2.1.2 KPCA-MLP组合模型算法原理当数据维度较高、非线性关系复杂时,模型容易为了追求拟合效果而出现过拟合现象。为此,设计了一个兼备高效数据降维和强非线性拟合能力的KPCA-MLP模型(图 3)。

|
图 3 KPCA-MLP网络结构 |
KPCA模型可利用核函数将地震属性样本向高维特征空间映射,并在高维空间实现数据降维,其核函数可表示为
| $ \boldsymbol{k}({\boldsymbol{x}}_{i},{\boldsymbol{x}}_{j})=\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{‖{\boldsymbol{x}}_{i}-{\boldsymbol{x}}_{j}‖}^{2}}{2{\sigma }^{2}}\right) $ | (3) |
式中:
KPCA-MLP模型便是在MLP模型的输入端加入了KPCA模型(图 3),利用KPCA模型对输入数据进行非线性降维与特征提取,然后基于MLP模型分析KPCA模型提取的主成分,从而有效挖掘复杂数据特征信息。因此,本文将使用KPCA-MLP模型算法进一步处理Bg-SVR、MLP、LGB和Bg-KNN模型的预测结果。
2.2 Stacking集成学习模型结构尽管上述几类模型在储层预测中具有良好的应用性能,但这些模型多属于单类预测模型,并且设计的组合模型(图 3)也未能基于高效架构实现多模型融合。因此,各模型的预测精度容易呈现边际效用递减的趋势[25]。为了提高储层预测准确率,本文将采用Stacking集成学习方式,实现多模型优势互补、深度协同。
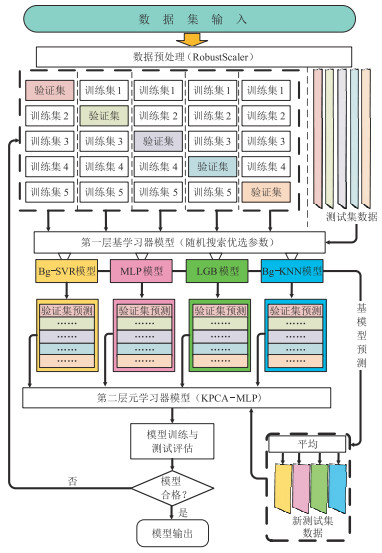
该Stacking集成学习模型主要包含两层结构(图 4)。第一层结构由多个基学习器模型组成,为了使各模型间能够“取长补短”,需选取泛化效果良好且存在明显差异的几类模型,因而将Bg-SVR、MLP、LGB和Bg-KNN作为基学习器模型。第二层结构由元学习器模型组成,其数据集来自上层的预测结果。若直接将基学习器模型的训练集预测结果作为元学习器的输入,可能会造成过拟合。因此,在第一层的基学习器模型训练前,利用5折交叉验证将数据划分为不重叠的5等份。当每个基学习器训练时,选取不重复的4等份作为训练集,余下的1等份作为验证集。训练完毕后,将5份基于验证集的预测结果重新组合,以得到与原数据集相同样本量的新数据集。新数据集来源于上层模型对验证集的预测结果,因此具有较强的客观性。
|
图 4 Stacking集成学习流程 |
然而,各基学习器模型的自身性能不同,当部分模型预测误差较大时,会增加元学习器输入数据的噪声,直接影响模型的预测精度。鲍海波等[26]提出了为预测结果赋予权重的方法以抑制各模型中预测效果较差的部分,能够提高集成模型的预测性能。但这种方式是一种主观的线性加权,并且赋予的权重值也难以充分表征各模型的预测性能。为了降低噪声数据的影响、充分挖掘基学习器模型预测结果的关键信息和拟合复杂的非线性数据,本文将选用KPCA-MLP模型作为元学习器模型。
Stacking模型的实现流程(图 4)如下。
(1) 利用RobustScaler对输入的地震属性进行数据预处理,即
| $ {\boldsymbol{x}}^{\text{'}}=\frac{\boldsymbol{x}-\mathbf{m}\mathbf{e}\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{n}}{\mathrm{I}\mathrm{Q}\mathrm{R}} $ | (4) |
式中:
(2) 使用5折交叉验证随机划分数据集,并利用Bg-SVR、MLP、LGB和Bg-KNN模型分别训练数据,训练过程中基于随机搜索[27]为每个基学习器模型优选超参数。
(3) 将交叉验证的验证集在基学习器上的预测结果组合为新训练数据集。
(4) 利用KPCA-MLP模型处理新训练数据集,生成训练集的最终预测结果。
(5) 将测试集经过训练好的基学习器处理、数据平均和训练好的KPCA-MLP模型处理等步骤,得到测试集的预测结果。
(6) 根据训练集和测试集的预测结果,评估模型合理性,若合格,便输出模型;反之,则返回步骤(2)。
3 分频地震属性融合方法以埕岛油田中区为研究区,基于Stacking集成学习模型,开展分频地震属性智能融合储层预测方法。
研究区面积约30 km2,主力含油层馆陶组上段为河流相沉积,砂体较薄,储层非均质性强,平均埋深约为1500 m。地震资料主频为33 Hz,频宽为17~49 Hz。
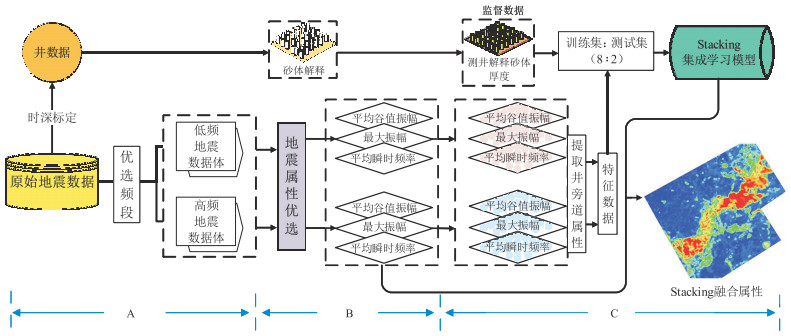
具体应用过程中,本文方法主要包含3个模块:地震频段优选、地震属性优选和多属性智能融合储层预测(图 5)。
|
图 5 基于Stacking集成学习的分频属性融合方法 |
不同频段地震数据体蕴含不同的地质信息,深度挖掘不同频段地震数据与储层之间的关系,有利于提高储层预测精度。
根据不同厚度储层的振幅与频率关系[4, 9, 14]可知:当砂体厚度小于1/4波长时,振幅与砂体厚度具有明显的正相关趋势;高频地震信息的分辨率较高,能够更好地反映薄砂体分布特征;低频数据体的分辨率较低,能够更好地反映厚砂体分布特征。采用小波分频技术,可将原始地震资料分为不同频段的地震数据体(图 5,A部分),但在分频的过程中需要注意两个原则:①分频数据体的总频宽需控制在原始地震资料的有效带宽内,以保留有效信息;②分频数据体数量不宜太多,防止地震数据冗杂[9]。综合考虑不同频段的地震信息,可降低地震资料的多解性。
由于馆陶组上段砂体厚度差异大,原始地震资料难以识别薄层砂体,所以在分频时需在有效频宽内尽可能保留高频数据体。对原始地震数据体(图 6 a)进行分频,高频地震数据的主频为40 Hz(图 6 b),对应的频宽为30 ~ 50 Hz,可反映原始数据中的高频信息。为了避免分频数据体过多和有效信息缺失,优选出主频为20 Hz、频宽为13 ~ 30 Hz的低频数据体(图 6 c),可反映原始数据中的低频信息。优选的两个分频数据体总频宽可覆盖原始地震数据,既保留了原始数据的有效信息,又减少了重复信息。

|
图 6 研究区不同地震数据体馆陶组上段频谱分析 (a)原始地震数据体;(b)高频地震数据体;(c)低频地震数据体 |
不同地震属性能够从不同角度表征储层特征,其中振幅类属性可以有效指示岩性、刻画砂体厚度;相位类属性有助于识别储层边界、断层等;频率类属性更适合反映储层在垂向上的岩性变化[6, 9, 28]。由于部分地震属性间共线性较强(较强的相关性),因而在地震多属性融合前需要优选属性(图 5,B部分)。
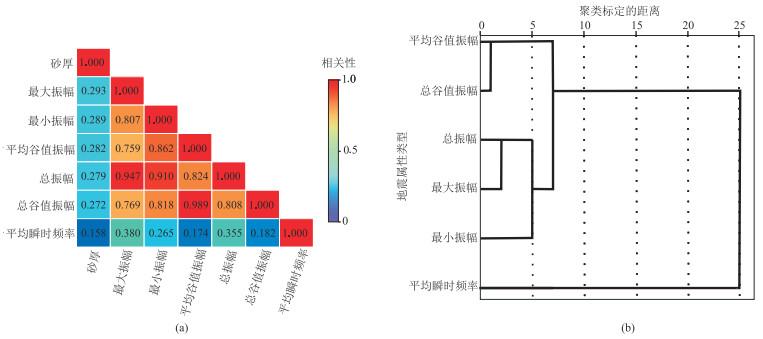
选取测井资料齐全的317口井,从井旁道目的层段提取不同类别的12种地震属性,分析各属性与砂体厚度相关性,共得到6种与砂体厚度相关系数大于0.15的地震属性(图 7 a);然后利用无监督聚类技术将6种地震属性进一步划分为3类(图 7 b),结合各类地震属性与砂体厚度的相关系数(图 7 a),最终优选出的敏感属性分别为平均谷值振幅、最大振幅和平均瞬时频率。
|
图 7 地震属性分析 (a)地震属性与砂体厚度相关性分析;(b)地震属性聚类 |
从分频地震数据体中分别提取上述三种属性。以最大振幅为例,可以看出,原始数据体最大振幅高值区能体现主河道砂体的分布,但反映的砂体连续性差,并且河道边界不清晰(图 8 a)。由于目的层段砂体较薄,低频数据体的最大振幅只能体现主河道上局部厚砂体的分布(图 8 b)。高频数据体的最大振幅高值区明显增多,主河道边界更加清晰(图 8 c),砂体连续性也更好(图 8 c红色箭头所指)。

|
图 8 馆陶组上段不同地震数据体最大振幅属性 (a)原始数据体;(b)低频数据体;(c)高频数据体 |
计算半径为25 m范围的井旁道地震属性值,将测井资料解释的砂体厚度与井旁道地震属性作为智能属性融合的数据样本,按照8:2的比例分别划分为训练集和测试集;再利用Stacking集成学习模型(图 5,C部分)融合低频、高频地震属性(平均谷值振幅、最大振幅和平均瞬时频率),建立砂体厚度与分频地震属性数据的映射关系;最后,将训练好的Stacking模型应用于馆陶组上段储层的定量预测。
4 方法评估 4.1 井点储层预测结果井点处的储层预测结果能够用于定量化评估模型预测精度和可靠性。为证实Stacking集成学习模型具备较强的预测性能,将Bg-SVR、MLP、LGB和Bg-KNN等4个基学习器模型作为参照组进行对比。训练过程中各模型的超参数设置见表 1。
|
|
表 1 各模型主要超参数 |
评估指标除了皮尔逊相关系数(
| $ \mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{m}\sum\limits_{i=1}^{m}\left|{y}_{i}-{\widehat{y}}_{i}\right| $ | (5) |
| $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{m}\sum\limits_{i=1}^{m}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}} $ | (6) |
| $ \mathrm{R}2\_\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=1-\frac{\sum\limits_{i=1}^{m}{\left({y}_{i}-{\widehat{y}}_{i}\right)}^{2}}{\sum\limits_{i=1}^{m}{\left({y}_{i}-\stackrel{-}{y}\right)}^{2}} $ | (7) |
| $ \mathrm{R}2\_\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{d}=1-\frac{\left(1-\mathrm{R}2\_\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\right)\left(m-1\right)}{m-p-1} $ | (8) |
式中:
由图 9可见,Bg-SVR、MLP、LGB和Bg-KNN模型属性融合预测结果与实际砂体厚度的

|
图 9 不同模型的预测误差 |
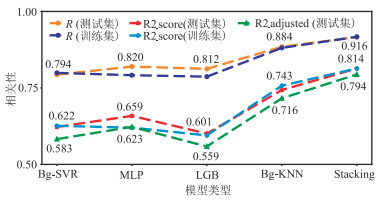
以测试集为例,Stacking集成模型的属性融合结果与实际砂体厚度的
|
图 10 不同模型的相关性指标 |
|
|
表 2 本文模型较单类模型的相关性指标提升率 |
地震多属性融合储层预测时需要将模型建立的井震数据映射关系应用于全研究区,因而基于多属性融合的储层预测准确度受映射关系影响。通常来说,模型在训练集上学习数据特征,然后利用测试集检验模型的合理性。本文的训练集和测试集都是按照特定比例随机、均匀划分,因而当模型在训练集和测试集的预测结果与真实砂体厚度之间展现相似的数据分布规律时,便可证明该模型建立的井震映射关系具有可靠性。为了有效评估模型的可靠性,本文利用线性关系式定量表征这种映射关系,即
| $ {\widehat{y}}_{i}=a{y}_{i}+{b}_{i} $ | (9) |
式中:
|
|
表 3 线性拟合公式分析 |
原始数据体最大振幅属性与砂体厚度相关性较低(图 11a),虽然能够初步反映主河道的展布趋势,但是河道边界模糊,并且属性高值区连续性较差(图 12a)。

|
图 11 不同地震属性与实际砂体厚度相关性 (a)原始数据体最大振幅属性;(b)Stacking融合属性 |
|
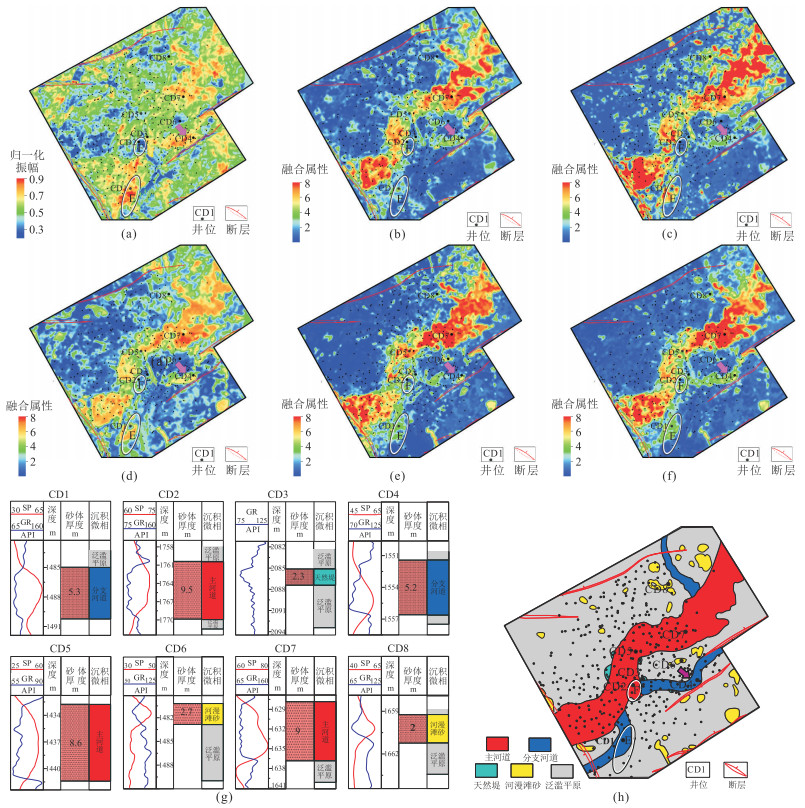
图 12 地震属性分析结果与沉积微相 (a)标注后的原始数据体最大振幅属性;(b)~(f)分别代表基于Bg-SVR、MLP、LGB、Bg-KNN和Stacking的分频属性融合结果;(g)单井综合解释;(h)沉积微相平面图 |
Bg-SVR模型的属性融合图上可见河道形态(图 12b),主河道的边界较为清晰,但在CD5井处显示为属性低值,指示河道断开,与单井砂体解释结论不符(图 12g)。同时,该属性图中的E区域的属性呈现零散分布,无明显的分支河道形态(图 12b)。MLP和LGB模型的属性融合结果展现出主河道砂体连续性较好(图 12c,图 12d),能够准确表现E区域的分支河道展布特征,但是与Bg-SVR模型的属性融合结果(图 12b)相比,MLP和LGB的属性融合结果中主河道外的属性分布更为杂乱。根据测井解释结果,在CD2井附近发育厚砂体(图 12g),在F区域内,MLP模型的属性融合结果展现了“大面积”的低值分布(图 12c),并且图 12b和图 12d的对应位置也体现了不同程度的属性低值特征,反映的砂体连续性较差。Bg-KNN算法能基于相邻井的空间位置关系,挖掘井旁道地震属性和储层信息特征。如图 12e所示,Bg-KNN模型的属性融合图中主河道分布更加明确,主河道外的属性杂乱度明显降低,同时F区域的砂体连续性变好。由于分支河道对应的属性为窄条带状,其邻近区域尤其是边界位置的属性差异较大,因而基于Bg-KNN的属性融合方法难以通过分析邻近空间数据精确预测分支河道砂体(图 12e紫色箭头所指区域)。
与单类预测模型的属性融合结果相比,Stacking集成模型的属性融合结果在E、F区域的砂体连续性更好,属性图的高值区形态清晰,分支河道砂体展布特征也更加明确。同时,该模型的属性融合结果的单井吻合率更高,与实际砂体厚度相关性也可达到0.92(图 11b)。一方面是因为优选的单类模型自身预测性能较强,另一方面是由于各模型在属性分析时存在相应的“预测短板”,而Stacking模型能高效融合多个单类模型并实现“优势互补”,由此提升了集成模型的预测精度。
根据Stacking集成模型的属性融合结果(图 12f),结合单井沉积微相解释结果(图 12g),可刻画出目的层沉积微相平面展布特征(图 12h)。由图可见,主河道呈宽条带状分布,分支河道为窄条带状分布,在主河道北西方向发育1条分支河道,南东方向发育有2条分支河道,分支河道延伸较远且有一定摆动幅度。主河道摆动不频繁,两侧均发育有天然堤,河漫滩砂呈孤立状分布在泛滥平原内部,展现了典型的河流相沉积特征。
5 结论(1) 基于Stacking集成学习的分频地震属性融合方法,能够综合考虑不同频段的“优势”地震属性信息,并可以对多个差异化模型“取长补短”,有利于提高储层预测精度。
(2) 本文提出的线性公式定量分析法,可以有效评估模型的预测性能。在埕岛油田的实例应用中,相对于单类预测模型,Stacking集成学习模型的预测性能和可靠性均有显著提升,其属性融合结果高值区形态清晰,砂体连续性更好。
(3) 本文基于Stacking分频属性融合储层预测方法具有良好的应用前景,可为类似研究区的储层预测提供借鉴。
| [1] |
陈芊澍, 文晓涛, 何健, 等. 基于极限学习机的裂缝带预测[J]. 石油物探, 2021, 60(1): 149-156, 174. CHEN Qianshu, WEN Xiaotao, HE Jian, et al. Prediction of a fracture zone using an extreme learning machine[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 149-156, 174. |
| [2] |
董少群, 曾联波, 杜相仪, 等. 致密碳酸盐岩储集层裂缝智能预测方法[J]. 石油勘探与开发, 2022, 49(6): 1179-1189. DONG Shaoqun, ZENG Lianbo, DU Xiangyi, et al. An intelligent prediction method of fractures in tight carbonate reservoirs[J]. Petroleum Exploration and Development, 2022, 49(6): 1179-1189. |
| [3] |
李婷婷, 侯思宇, 马世忠, 等. 断层识别方法综述及研究进展[J]. 地球物理学进展, 2018, 33(4): 1507-1514. LI Tingting, HOU Siyu, MA Shizhong, et al. Overview and research progress of fault identification method[J]. Progress in Geophysics, 2018, 33(4): 1507-1514. |
| [4] |
岳大力, 李伟, 王军, 等. 基于分频融合地震属性的曲流带预测与点坝识别——以渤海湾盆地埕岛油田馆陶组为例[J]. 古地理学报, 2018, 20(6): 941-950. YUE Dali, LI Wei, WANG Jun, et al. Prediction of meandering belt and point-bar recognition based on spectral-decomposed and fused seismic attributes: A case study of the Guantao Formation, Chengdao Oilfield, Bohai Bay Basin[J]. Journal of Palaeogeography, 2018, 20(6): 941-950. |
| [5] |
曾亚丽, 龙盛芳, 吴朦朦, 等. 基于GeoEast地震属性分析的储层预测技术及其在环县地区页岩油勘探开发中的应用[J]. 石油地球物理勘探, 2022, 57(增刊1): 196-201. ZENG Yali, LONG Shengfang, WU Mengmeng, et al. Reservoir prediction technique based on GeoEast seismic attribute analysis and its application in shale oil exploration and development in Huanxian[J]. Oil Geophysical Prospecting, 2022, 57(S1): 196-201. |
| [6] |
钟晗. 地震属性在储层预测中的应用研究[D]. 北京: 中国石油大学(北京), 2018. ZHONG Han. The Application of Seismic Attributes in the Reservoir Prediction[D]. China University of Petroleum (Beijing), Beijing, 2018. |
| [7] |
张树林. 海上多波多分量地震烃类直接检测方法研究及应用[J]. 物探化探计算技术, 2000, 22(3): 200-206. ZHANG Shulin. A direct hydrocarbon detecting method and application of offshore multiwave and multicomponent seismic data[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2000, 22(3): 200-206. |
| [8] |
郑江峰, 彭刚, 孙佳林, 等. 基于90°相移的振幅和频率属性融合法油气检测[J]. 石油物探, 2019, 58(1): 130-138. ZHENG Jiangfeng, PENG Gang, SUN Jialin, et al. Fusing amplitude and frequency attributes for hydrocarbon detection using 90° phase shift data[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 130-138. |
| [9] |
岳大力, 李伟, 杜玉山, 等. 河流相储层地震属性优选与融合方法综述[J]. 地球科学, 2022, 47(11): 3929-3943. YUE Dali, LI Wei, DU Yushan, et al. Review on optimization and fusion of seismic attributes for fluvial reservoir characterization[J]. Earth Science, 2022, 47(11): 3929-3943. |
| [10] |
CHEN Q, SIDNEY S. Seismic attribute technology for reservoir forecasting and monitoring[J]. The Leading Edge, 1997, 16(5): 445-448. DOI:10.1190/1.1437657 |
| [11] |
HART B S. Channel detection in 3-D seismic data using sweetness[J]. AAPG Bulletin, 2008, 92(6): 733-742. DOI:10.1306/02050807127 |
| [12] |
张家乐, 程冰洁, 徐天吉, 等. 应用地震属性主成分分析识别古河道[J]. 石油地球物理勘探, 2023, 58(1): 190-195. ZHANG Jiale, CHENG Bingjie, XU Tianji, et al. Identification of paleochannels by seismic attribute principal component analysis[J]. Oil Geophysical Prospecting, 2023, 58(1): 190-195. |
| [13] |
MCARDLE N J, ACKERS M A. Understanding seismic thin-bed responses using frequency decomposition and RGB blending[J]. First Break, 2012, 30(12): 57-65. |
| [14] |
李伟, 岳大力, 胡光义, 等. 分频段地震属性优选及砂体预测方法——秦皇岛32-6油田北区实例[J]. 石油地球物理勘探, 2017, 52(1): 121-130. LI Wei, YUE Dali, HU Guangyi, et al. Frequency-segmented seismic attribute optimization and sandbody distribution prediction: an example in North Block, Qinghuangdao 32-6 Oilfield[J]. Oil Geophysical Prospecting, 2017, 52(1): 121-130. |
| [15] |
ZENG H. Thickness imaging for high-resolution stratigraphic interpretation by linear combination and color blending of multiple-frequency panels[J]. Interpretation, 2017, 5(3): T411-T422. DOI:10.1190/INT-2017-0034.1 |
| [16] |
LI W, YUE D, WANG W, et al. Fusing multiple frequency-decomposed seismic attributes with machine learning for thickness prediction and sedimentary facies interpretation in fluvial reservoirs[J]. Journal of Petroleum Science and Engineering, 2019, 177: 1087-1102. DOI:10.1016/j.petrol.2019.03.017 |
| [17] |
YUE D, LI W, WANG W, et al. Fused spectral-decomposition seismic attributes and forward seismic modelling to predict sand bodies in meandering fluvial reservoirs[J]. Marine and Petroleum Geology, 2019, 99: 27-44. DOI:10.1016/j.marpetgeo.2018.09.031 |
| [18] |
蔡义峰, 熊婷, 姚卫江, 等. 地震多属性分析技术在薄层砂体预测中的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 140-145. CAI Yifeng, XIONG Ting, YAO Weijiang, et al. Thin sandstone prediction with seismic multi-attribute analysis[J]. Oil Geophysical Prospecting, 2017, 52(S2): 140-145. |
| [19] |
蔡国刚, 杨光达, 周艳, 等. 机器学习驱动的地震多属性分析表征扇三角洲沉积[J]. 科学技术与工程, 2021, 21(29): 12454-12460. CAI Guogang, YANG Guangda, ZHOU Yan, et al. Sedimentary facies characterization of fan delta based on machine learning driven multi-seismic attributes analysis[J]. Science Technology and Engineering, 2021, 21(29): 12454-12460. |
| [20] |
张宪国, 吴啸啸, 黄德榕, 等. 极限学习机驱动的地震多属性融合识别曲流带单一点坝[J]. 石油地球物理勘探, 2021, 56(6): 1340-1350. ZHANG Xianguo, WU Xiaoxiao, HUANG Derong, et al. Single point bar interpretation in meandering belt with extreme learning machine driven multiple seismic attributes fusion[J]. Oil Geophysical Prospecting, 2021, 56(6): 1340-1350. |
| [21] |
曲志鹏, 王芳芳, 张云银, 等. 基于关联规则与随机森林的地震多属性砂体厚度预测[J]. 地质科技通报, 2021, 40(3): 211-218. QU Zhipeng, WANG Fangfang, ZHANG Yunyin, et al. Thickness prediction of seismic multi-attributes sand based on association rules and random forests[J]. Bulletin of Geological Science and Technology, 2021, 40(3): 211-218. |
| [22] |
陈欢庆, 王珏, 杜宜静. 储层非均质性研究方法进展[J]. 高校地质学报, 2017, 23(1): 104-116. CHEN Huanqing, WANG Jue, DU Yijing. Advances of research methods on reservoir heterogeneity[J]. Geological Journal of China Universities, 2017, 23(1): 104-116. |
| [23] |
石鹏. 委内瑞拉JN-4区块储层非均质性研究[D]. 山东青岛: 中国石油大学(华东), 2015. SHI Peng. The Reservoir Heterogeneity Research in JN-4 Block, Venezuela[D]. China University of Petroleum (East China), Qingdao, Shandong, 2015. |
| [24] |
徐继伟, 杨云. 集成学习方法: 研究综述[J]. 云南大学学报(自然科学版), 2018, 40(6): 1082-1092. XU Jiwei, YANG Yu. A survey of ensemble learning approaches[J]. Journal of Yunnan University (Natural Sciences Edition), 2018, 40(6): 1082-1092. |
| [25] |
史佳琪, 张建华. 基于多模型融合Stacking集成学习方式的负荷预测方法[J]. 中国电机工程学报, 2019, 39(14): 4032-4041. SHI Jiaqi, ZHANG Jianhua. Load forecasting based on multi-model by Stacking ensemble learning[J]. Proceedings of the CSEE, 2019, 39(14): 4032-4041. |
| [26] |
鲍海波, 吴阳晨, 张国应, 等. 基于特征加权Stacking集成学习的净负荷预测方法[J]. 电力建设, 2022, 43(9): 104-116. BAO Haibo, WU Yangchen, ZHANG Guoying, et al. Net load forecasting method based on feature-weighted Stacking ensemble learning[J]. Electric Power Construction, 2022, 43(9): 104-116. |
| [27] |
BERGSTRA J, BENGIO Y. Random search for hyper parameter optimization[J]. Journal of Machine Learning Research, 2012, 13(1): 281-305. |
| [28] |
ZENG H. Geologic significance of anomalous instantaneous frequency[J]. Geophysics, 2010, 75(3): P23-P30. DOI:10.1190/1.3427638 |



 岳大力, 北京市昌平区府学路18号中国石油大学(北京)人工智能学院,102249。Email:
岳大力, 北京市昌平区府学路18号中国石油大学(北京)人工智能学院,102249。Email: