2. 中国石化石油工程地球物理公司华东分公司, 江苏南京, 210000
2. Huadong Branch, SINOPEC Geophysical Corporation, Nanjing, Jiangsu 210000, China
微地震监测技术已经广泛应用于矿山安全预警[1]、水力压裂储层改造[2]以及二氧化碳封存监控[3]等工程领域,是优化施工方案、保障施工安全的重要手段。在施工过程中介质由于应力发生变化而破裂,并产生微小的地震信号,通过分析这些地震信号可以获知介质破裂的规律和特征[4]。目前主要是利用微地震信号的初至信息对破裂事件进行定位,初至信息对后续裂缝解释工作的精确度有极大影响,因此准确地拾取到微地震信号的初至是微地震监测中关键的一步。
微地震信号初至拾取算法主要有能量比法、AIC(Akaike Information Criteria)算法、偏振分析法、分形维数法及机器学习类方法等。能量比法[5-6]是应用最为广泛的初至拾取算法,该算法根据微地震信号的能量与背景噪声的差异拾取初至,算法原理简单且拾取效率高,但是算法的拾取精度不高且抗噪性较差。有学者在能量比法的基础上提出了改进算法在一定程度上弥补了该算法的缺陷[7-9]。AIC算法[10]基于噪声和有效信号在统计特征上的差异识别有效信号的初至。该算法的优点是识别精度高,但是该算法无法检测是否存在微地震信号,将小波变换与AIC算法结合可以有效地解决这一问题[11-12]。偏振分析法利用了微地震信号与噪声在偏振特征上的差异识别信号的初至[13-15],其中微地震信号是线性偏振而噪声没有明显的偏振方向。该方法利用了微地震信号的多分量信息,但是拾取精度受数据信噪比影响较大。图形学中的分形维数理论也被应用于初至拾取中并取得了良好的效果[16-17]。有效信号和噪声的分形维数不同,其中噪声的分形维数是常数而有效信号的是变化的,因此可以根据分形维数的变化识别有效信号初至。另外作为近几年的热点问题机器学习方法也被应用于微地震事件的初至识别中,如支持向量机[18-19]和神经网络等算法[20-22]。虽然机器学习算法识别准确率高且受数据信噪比的影响小,但是这类方法通常比较复杂且应用效率低,目前还难以用于微地震监测现场的快速拾取。
对于微地震数据现场快速拾取而言,拾取算法不仅要具有较高的精确度,还要保证一定的拾取效率。为了提高能量比算法的拾取精度,张唤兰等[23]将能量比算法和AIC算法相结合,通过AIC算法的二次拾取提高拾取率和精度,但依然没有解决能量比算法抗噪性差的问题。另外,微地震事件通常具有多个震相(P波和S波),此时如果算法的触发阈值不合适会造成初至的误拾和漏拾。并且在算法触发后无法判断具体是哪种震相,宋维琪等[24]将能量比算法与偏振分析相结合解决了算法的多震相识别问题,但是这种方法增加了算法的复杂度从而降低了拾取效率。
针对上述问题,本文提出了一种利用聚类提高微地震信号初至拾取稳定性的算法。在改进的能量比(Modified Energy Ratio,MER)算法的基础上,应用DBSCAN(Density-based Spatial Clustering of Applications with Noise)算法对一次拾取结果进行优化,从而提高最终拾取结果的稳定性、抗噪性和精度。DBSCAN是一种聚类算法,可以对多震相事件的初至加以区分,解决了微地震信号多震相拾取的问题。利用不同类型的实际数据对本文算法进行测试,结果验证了算法的有效性。本文改进算法拾取效率较高,可以满足现场微地震信号实时拾取的要求。
1 方法原理微地震信号的初至拾取算法主要是基于有效信号与背景噪声在能量和传播特征上的差异而提出的[25],越能突出两者差异的算法越有效。在实际应用中,由于能量比算法和AIC算法简单易实现被广泛使用。本文主要基于这两种算法实现微地震信号的初至拾取,用DBSCAN算法提高了初至拾取的稳定性。
1.1 MER算法MER算法是一种时域初至拾取算法[5]。该算法基于长短时窗能量比法(STA/LTA)改进而来,解决了STA/LTA算法只能检测有效信号而无法准确拾取初至的问题。MER算法的基本原理是利用前后两个长度相同的时窗扫描信号,并计算两个时窗内信号的能量比值。当扫描时窗通过微地震初至位置时,能量比值会大幅增加,且能量比值的峰值位置通常出现在初至附近。
对于微地震信号X=(x1,x2,…,xn),MER算法的能量比定义为
| $ {r}_{i}=\frac{\sum\limits_{j=i-{n}_{\mathrm{w}}}^{i}{x}_{j}^{2}}{\sum\limits_{j=i}^{i+{n}_{\mathrm{w}}}{x}_{j}^{2}} $ | (1) |
| $ {R}_{i}={\left|{x}_{i}\times {r}_{i}\right|}^{3} $ | (2) |
式中:ri表示在信号X在i时刻的能量比;Ri表示改进的能量比;nw表示时窗长度。
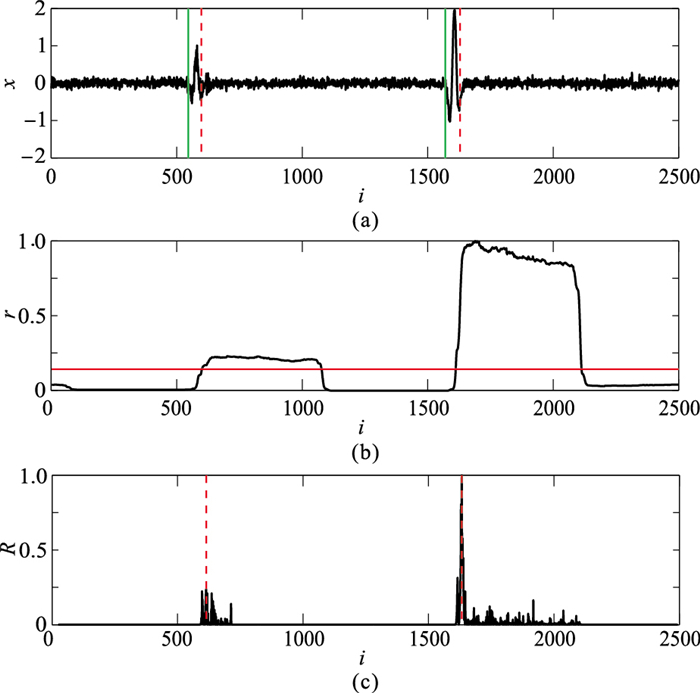
图 1为MER算法对模拟微地震信号初至的拾取结果。模拟信号(图 1a)包含了一个能量较弱的P波震相和一个能量较强的S波震相,在两个震相的初至位置能量比r(图 1b)和改进的能量比R(图 1c)均增大,但是R的峰值更加明显且与信号初至位置更接近。
|
图 1 模拟微地震信号的MER算法初至拾取结果 (a)微地震模拟信号,两个红色虚线分别表示算法拾取的P波和S波初至,两个绿色实线分别表示信号的起跳位置;(b)r曲线,红色实线表示触发阈值;(c)R曲线,红色虚线指示算法识别的初至位置。 |
AIC是由日本统计学家赤池弘治提出的一种用于衡量统计模型拟合程度的理论[26]。经过地球物理学家改进后,该理论被用于地震波初至拾取[10]。该理论拾取地震波初至的主要原理是根据统计特征上的差异区分有效信号与噪声。在初至位置有效信号与噪声的拟合程度最低,可以据此定位噪声与有效信号的交接位置。因此AIC算法拾取初至的精度较高,并且拾取结果更接近有效信号的起跳位置。
对于一个有n个采样点的微地震数据,其AIC函数计算表达式为
| $ \begin{array}{l}{A}_{i}=i\mathrm{l}\mathrm{g}C\left[x\left(1, k\right)\right]+\\ \ \ \ \ \ \ \ \ (n-k+1)\mathrm{l}\mathrm{g}C\left[x\left(k+1, n\right)\right]\end{array} $ | (3) |
式中:
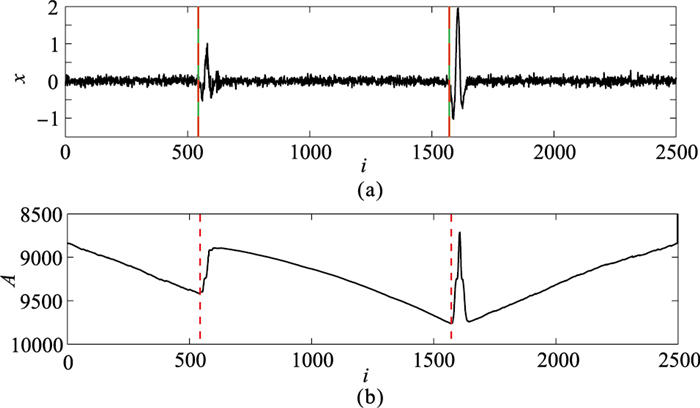
图 2为AIC算法在微地震模拟数据上的应用实例,AIC函数在P波和S波初至位置出现极小值。
|
图 2 模拟微地震信号的AIC算法拾取结果(a)及其AIC曲线(b) 两条红色虚线分别表示拾取的P波和S波初至位置,绿线表示真实的初至位置。 |
DBSCAN是一种根据数据分布找到数据的密集区域并分类的无监督学习算法[27]。该算法对数据的分布没有要求,克服了如K均值等聚类算法只能识别凸数据集的缺点。而且该算法无须预先确定类别数量,可以自适应判断数据的类别。DBSCAN算法具较好的抗噪性,可以将类别内数据与噪声点分开[25, 28],从而提高聚类的准确度。
DBSCAN算法的原理是通过搜索数据集中每个样本的邻域来区分样本的类别。对于初至数据集Y,有如下定义:
(1) ε邻域:对于Y的样本点yi,其邻域为所有与yi距离小于邻域半径ε的样本点的集合;
(2) 核心点:对于给定的邻域最小样本数M,若样本点yi的邻域内至少包含了M个样本,那么yi为核心点;
(3) 直接密度可达:若样本点yi为核心点,则其邻域内的样本对于yi是直接密度可达;
(4) 密度可达:若样本点yp和yq与yi是直接密度可达,则yp与yq为密度可达;
(5) 密度相连:若样本点yp和yq与同一个样本点密度可达,则yp与yq密度相连;
(6) 边界点:若样本点yi的ε邻域内样本点少于M,且yi在其他核心点的邻域内,则yi为边界点;
(7) 簇类:最大密度相连的样本点的集合;
(8) 噪声点:不属于任何簇类的样本点。
DBSCAN算法会将数据分为核心点、边界点和噪声点,并将密度相连的样本点分为簇类。如图 3所示,若M为3,样本点k1和k2为核心点,b1和b2为边界点,c为噪声点,则b1、k1、k2、b2为一个簇类。其中b1与k1、k1、k2、k2与b2是直接密度可达,b1与b2是密度可达且密度相连。算法的主要流程是首先找到数据集中的一个核心点,从核心点出发找到与之密度可达的样本点形成一个簇类。当发现边界点时,寻找其他未在簇类中的核心点并重复之前的操作直到数据搜索完毕。

|
图 3 DBSCAN算法示意图 蓝点:核心点;黄点:边界点;红点:噪声点;黑圈:邻域范围 |
对于实际的微地震数据,由于算法存在一定的局限性,使用单一算法往往无法得到理想的效果。MER算法的优势在于可以识别有效事件,但是该算法的拾取精度较低,易受到噪声干扰。而AIC算法拾取精度较高,但是无法识别有效事件,且拾取受时窗影响较大。将这两种算法结合使用,MER算法不仅弥补了AIC算法无法识别有效事件的缺点,而且可以给AIC算法提供一个初始结果,从而降低时窗对算法的影响。同时,AIC算法提高了拾取精度,弥补了MER拾取精度低的缺点。两种算法直接组合(MER+AIC算法)的具体做法是,首先利用MER算法识别出微地震有效信号以及初至的大致位置,然后在MER算法确定的初至位置附近开一个时窗并使用AIC算法拾取微地震信号的初至。对于高信噪比信号,两种算法的直接组合可以提高初至拾取精度(图 4a);但对于低信噪比数据,MER算法可能会出现错误的拾取,从而导致最终结果也不正确(图 4b)。

|
图 4 MER+AIC算法在实际高(a)和低(b)信噪比数据上的拾取结果 蓝圈为MER算法的拾取结果;红点为AIC算法的拾取结果;红框为AIC算法的计算时窗。 |
利用DBSCAN算法将MER和AIC算法有机的串联起来,保留两个算法互补关系的同时进一步降低了MER算法拾取结果的错误率,从而提高最终初至拾取的精度。对于同一个微地震事件,初至有规律分布:对于地面观测系统,初至分布呈双曲线;对于井中观测系统,初至分布近似直线。本文改进算法具体的步骤是:
(1) 利用MER算法拾取微地震信号初至,获得一个初步的结果;
(2) 利用DBSCAN算法对初步拾取结果进行聚类分析。由于错误的拾取结果通常会偏离初至的分布规律,因此会被DBSCAN算法作为噪声点剔除,而符合初至分布规律的拾取结果会被聚类;
(3) 对类别中的初至分布进行拟合,插值补齐被剔除的初至,以保证MER算法的拾取结果在合理的初至范围内;
(4) 以第(3)步的结果作为中心点开时窗,应用AIC算法获得更精确的初至位置。
除了可以提高拾取精度以外,本文改进算法的另一个优点在于当微地震数据中包含多组震相的初至时,DBSCAN算法可以将不同震相的初至区分开。该算法不仅提高了初至拾取的效率,还保证了有效信号的完整性。此外,DBSCAN算法的计算效率高,几乎不增加额外的运算时间,适用于现场实时拾取。
2 理论模型测试为了说明算法的改进效果,本文利用理论模型数据对算法进行测试。理论模型数据采用均匀介质模拟了地面接收的微地震数据,观测系统为单排列10道,道距90 m。微地震震源位于排列中心的正下方,垂深为750 m。图 5为MER、MER+AIC算法对无噪和含5%、25%随机噪声(随机噪声的均方根振幅为原始信号的5%和25%)数据的拾取结果对比。对于无噪数据(图 5 a),MER算法的拾取结果集中在有效波形的最大振幅附近,与真实的初至存在较大误差。MER+AIC算法的拾取结果集中在有效波形的起跳位置,更接近真实初至。对于含噪5%数据,两种算法的拾取结果与无噪时几乎相同,说明这两种算法都具有一定的抗噪能力(图 5b)。当数据含25%噪声时,两种算法的拾取精度均下降,MER算法的拾取结果会出现误差较大的“飞点”(如第2、第6、第9道),影响了AIC拾取结果的精度,使得最终拾取结果误差较大(图 5c)。

|
图 5 无噪(a)、含噪5%(b)和含噪25%(c)数据的拾取结果 蓝叉、红点分别是MER算法和MER+AIC算法的拾取结果,绿线是使用聚类算法后的拟合结果。 |
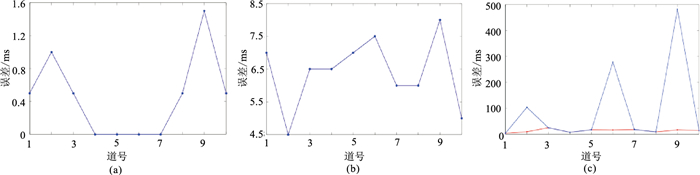
为了解决MER+AIC算法对低信噪比数据的拾取误差较大的问题,本文利用DBSCAN算法对MER算法拾取结果进行聚类,剔除误差大的“飞点”,再进行曲线拟合(图 5中的绿线)。本文改进算法与MER+AIC算法拾取结果对比如图 6所示。对于无噪和含5%噪声的理论数据,改进算法拾取结果与MER+AIC算法相同。对于含25%噪声的理论数据,改进算法提高了拾取结果精度。图 7为MER+AIC算法和本文改进算法对不同信噪水平合成数据的拾取绝对误差对比。对于无噪和含噪5%的理论数据,两种算法的误差相同,噪声的增加降低了拾取精度(图 7a、图 7b)。当信噪比较低时,本文改进算法减小了拾取错误率,提高了拾取的稳定性(图 7c)。

|
图 6 MER+AIC算法(蓝点)与本文算法(红点)对无噪(a)、5%含噪(b)和25%含噪(c)理论数据的初至拾取结果对比 |
|
图 7 MER+AIC算法(蓝线)和改进算法(红线)对无噪(a)、含噪5%(b)和含噪25%(c)数据初至拾取结果的绝对误差对比 |
使用两个工区的典型微地震监测记录对本文改进算法进行测试,分析算法对于不同观测系统的适用性,以及算法对于多震相初至拾取的有效性。
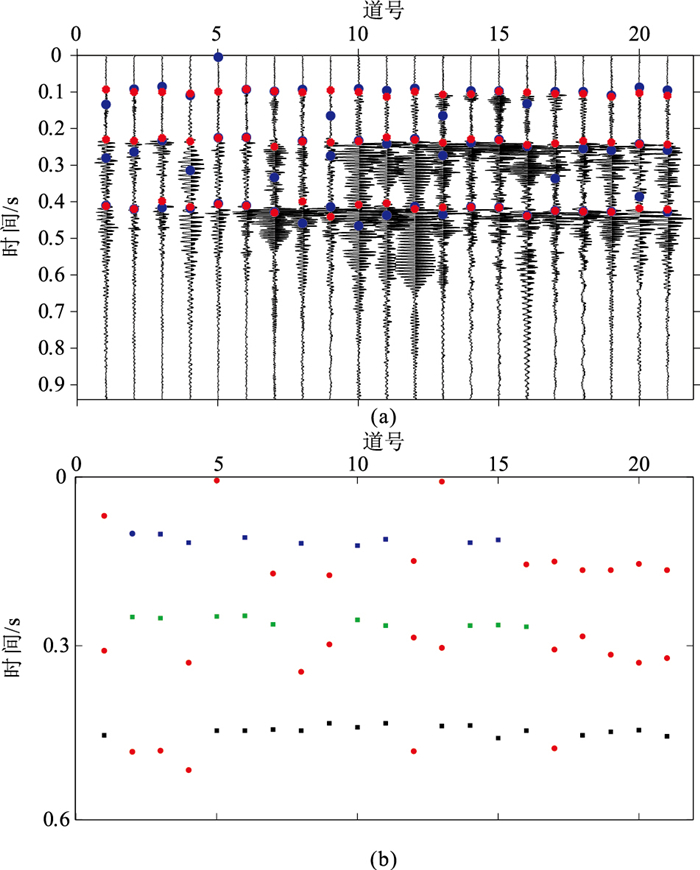
3.1 地面观测单震相微地震数据在中国东部A工区采用地面星型排列接收水力压裂微地震监测信号(数据1),共十二个排列、1618道。原始数据的信噪比较低,有效事件被强能量的高频噪声掩盖。经过10~50 Hz带通滤波和异常振幅压制后可以识别到有效事件的初至。图 8a为其中一个排列接收的微地震有效信号,可以看出:信噪比较低,背景干扰能量较强,且尾波及反射波能量与有效波相当;不同道接收的有效信号能量不一致,近道能量比远道弱,增加了初至识别的难度。
|
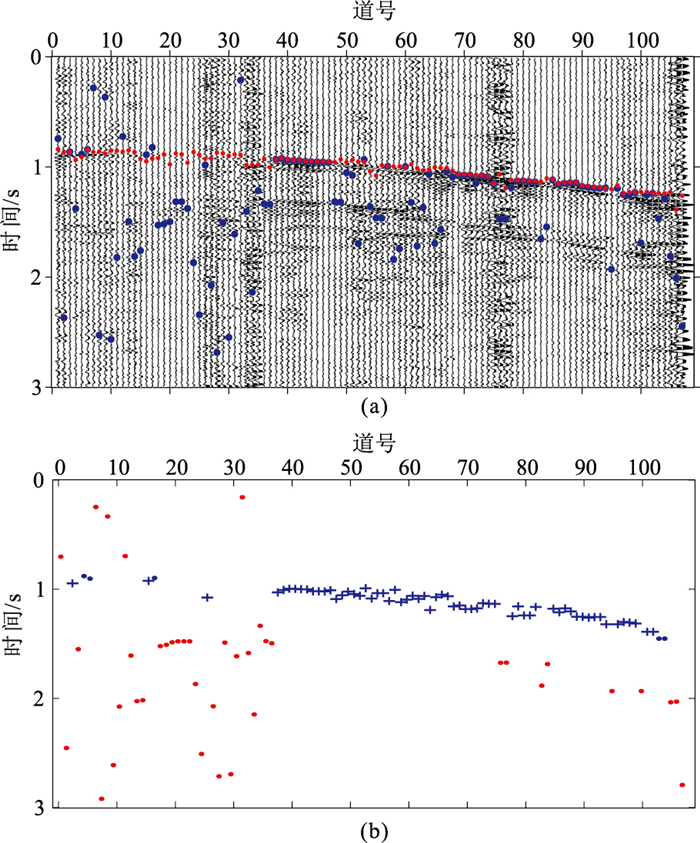
图 8 实际数据1初至拾取实验 (a)微地震记录及本文算法(红色圆点)与MER+AIC算法(蓝色圆点)拾取结果对比;(b)DBSCAN聚类算法对初至规律的分析结果(蓝色十字和圆点为有效初至,红色点号为剔除的噪声点) |
扫描时窗长度是MER算法重要参数,对信噪比较为敏感。当信噪比较高时采用较小的扫描时窗长度,而当信噪比较低时采用较大的扫描时窗长度拾取结果更理想[29-30]。由于数据1的各道数据信噪比差别较大,经过测试选择扫描时窗长度为100 ms(50个样点)。图 8a中红色圆点和蓝色圆点为数据1的初至拾取结果。第1~第37道有效事件的能量较弱、信噪比较低,MER+AIC算法拾取结果的错误率很高,第38道之后虽然拾取的错误率大幅降低,但仍然存在较大误差。本文的改进算法首先将MER算法拾取结果中误差较小的结果(图 8b蓝十字和圆点所示)通过聚类算法识别出来,剔除误差较大的结果(图 8b红色圆点所示),再拟合出初至的分布规律,以降低MER算法的拾取错误率,从而提高最终拾取结果的准确度。如图 8a中红色圆点所示,第1~第37道的拾取结果得到了改善,且能量较强的有效事件初至可以定位到起跳位置,表明本文算法可以提高初至拾取的抗噪能力。
3.2 井中观测双震相微地震数据中国西南B工区的水力压裂微地震监测数据(数据2)采用井中接收的观测方式,共21道(图 9a)。由图 9a可以看出,井中观测的微地震事件能量较强且信噪比较高,可以清晰地识别出事件的初至。微震事件包含P波和S波两个震相,S波能量大于P波。虽然该微震事件中两个震相的信噪比较高,但是较强的尾波会影响算法的拾取精度,拾取结果更接近尾波的强能量位置(图 9a蓝点所示)。

|
图 9 实际数据2初至拾取实验 (a)微地震记录及本文改进算法(红色圆点)与MER+AIC算法(蓝色圆点)的拾取结果对比;(b)DBSCAN聚类算法对初至规律的分析结果(蓝色圆点为P波有效初至,绿色圆点为S波有效初至,红色圆点为剔除的噪声点) |
通过测试选择MER算法的扫描时窗长度为20 ms(10个采样点)。从拾取结果(图 9a)可以看出:对于高信噪比数据,MER算法拾取结果的错误率降低,但是当数据尾波能量较强时算法的最终拾取误差仍较大。改进算法有效解决了拾取精度低的问题,并且可以自动分离出两个震相的初至。具体而言,首先利用DBSCAN聚类算法对MER拾取结果进行分析,聚类算法成功将两个震相的初至分开(图 9b),并且剔除了误差较大的拾取结果(红色圆点)。然后可以根据两个簇类的平均初至时间确定出P波和S波对应的簇类。再对两个簇类进行拟合插值补齐被剔除的初至点,最后使用AIC算法再进行初至精细拾取。最终拾取结果(图 9a红色圆点所示)更接近初至波起跳位置,极大地提高了初至拾取的精确度。
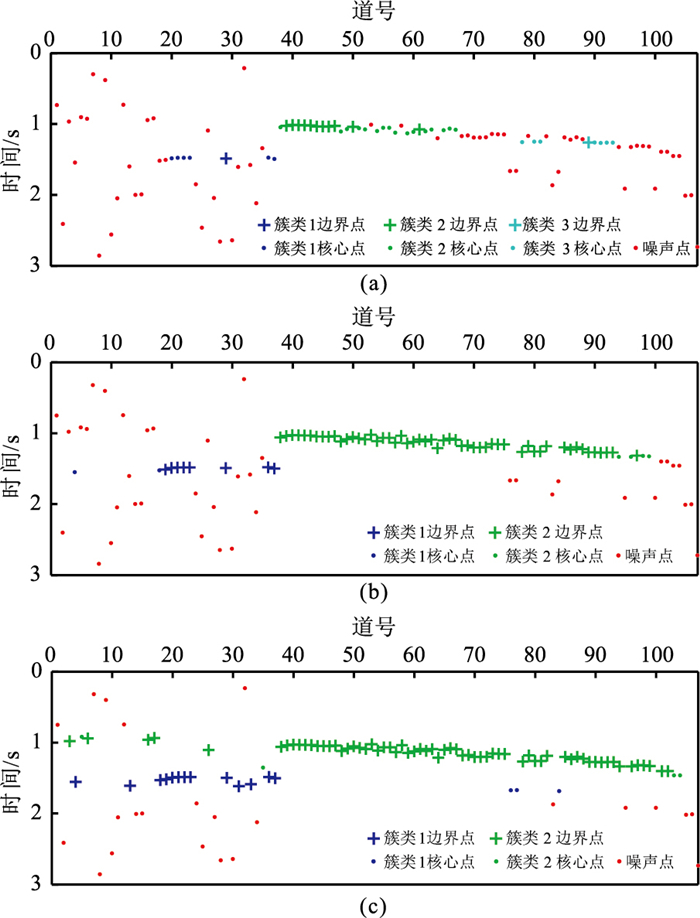
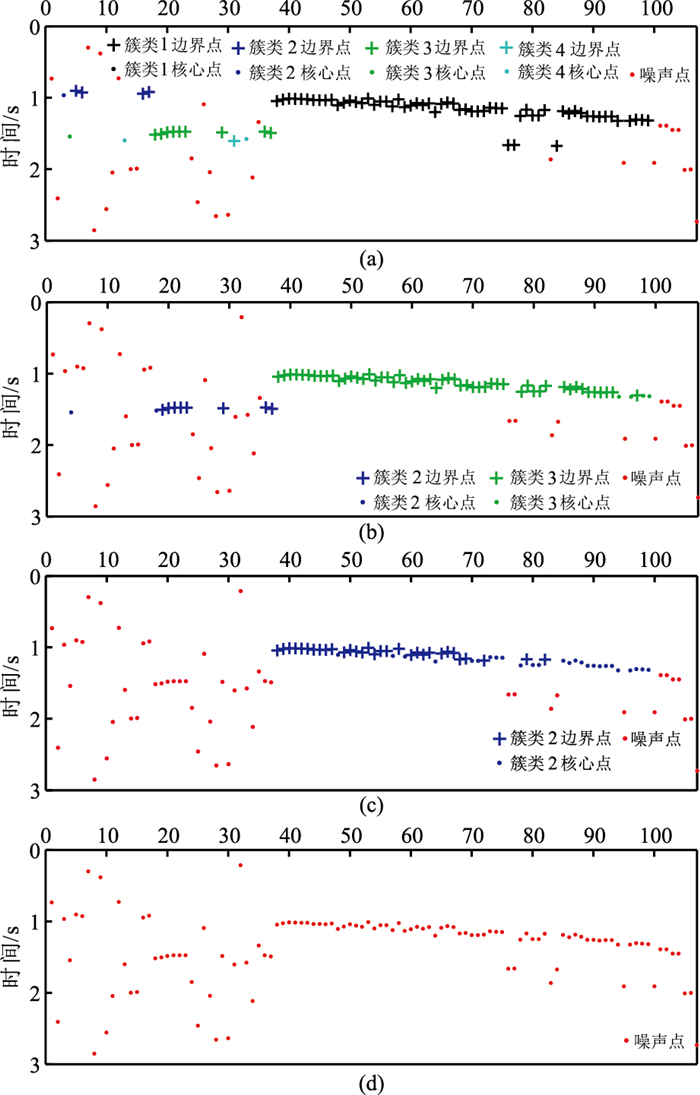
3.3 井中观测多震相微地震数据数据3与数据2来自同一工区,同样采用井中21道接收的观测方式。当两个微地震事件发生的间隔时间较小时,在记录中波形通常会重叠(图 10a)。由图可以看出,后一个微地震事件的P波信号被前一个事件的S波掩盖,记录上只能看到三个震相。对这种数据的初至拾取通常要额外划分窗口,利用本文提出的改进算法可以自动划分出这三个震相。虽然井中观测数据信噪比较高,但是初至拾取算法容易受到强振幅尾波的影响,增大了初至拾取的误差。通过测试选择MER算法的扫描时窗长度为20 ms(10个采样点)。图 10a中蓝点是MER+AIC算法的拾取结果,在强振幅尾波出现的记录道上初至拾取结果偏离了信号的起跳位置。
|
图 10 实际数据3初至拾取实验 (a)微地震记录及本文改进算法(红色圆点)与MER+AIC算法(蓝色圆点)拾取结果对比;(b)DBSCAN聚类算法对初至规律的分析结果(蓝色圆点为P波有效初至,绿色圆点为与P波对应的横波初至,黑色圆点为另一个事件的横波(S2)有效初至,红色圆点为剔除的噪声点) |
利用DBSCAN聚类分析算法对MER算法初步拾取结果进行分析,如图 10b所示。其中P波和对应的S波在第16~第21道的拾取误差较大,被聚类算法当作噪声点剔除。经过校正后初至拾取的精度得到了提高。MER算法拾取的错误点(第5道P波初至)也得到了纠正。另外,DBSCAN算法较好的解决了多震相初至难以准确识别的问题,尤其是针对图 10a所示的连续出现的多震相初至识别应用效果较好。在多震相识别中,如果通过触发阈值控制多震相初至的识别,通常会出现误触发或者漏触发的现象。聚类算法可以剔除误触发的初至,并补齐漏触发的初至,有效的提高算法对于多震相初至拾取的稳定性。
3.4 拾取效果分析对比MER+AIC算法和本文提出的改进算法的拾取结果与人工拾取结果之间的相对误差(图 11)可以看出,改进算法极大改善了初至的拾取精度。对于信噪比较低的数据1(图 11a),改进算法的拾取相对误差在±0.15以内,而MER+AIC算法的拾取误差较大。MER+AIC算法拾取结果的均方根误差为0.331 s,改进算法拾取结果的均方根误差为0.001 s。对于高信噪比的数据2(图 11b),改进算法的拾取结果几乎与人工拾取结果一致,MER+AIC算法拾取结果中P波初至的均方根误差为1.03×10-3 s,S波初至的均方根误差为1.36×10-3 s;改进算法拾取结果中P波初至的均方根误差为5.01×10-6 s,S波初至的均方根误差为7.85×10-5 s。其中S波初至的均方根误差略大于P波初至,可能是P波的尾波影响了S波初至拾取。改进算法可以将拾取误差降低2~3个量级。对于三震相的微地震数据3(图 11c),两个算法对后一事件的S波拾取结果误差均较小,而MER+AIC算法对于P波和其对应的横波的拾取结果误差均较大。MER+AIC算法拾取结果中P波初至的均方根误差为9.29×10-4 s,对应的横波初至的均方根误差为1.97×10-3 s,后一事件的横波初至的均方根误差为3.99×10-4 s;改进算法拾取结果中P波初至的均方根误差为4.16×10-5 s,对应的横波初至的均方根误差为6.42×10-5 s,后一事件的横波初至的均方根误差为1.53×10-4 s。可见,改进算法将P波和对应横波的初至误差降低了约2个量级。

|
图 11 MER+AIC算法与本文改进算法拾取相对误差交会图 (a)数据1;(b)数据2;(c)数据3。红点代表P波,蓝点代表对应的S波,绿点代表后一事件S波。 |
对于实际数据,本文改进算法与MER+AIC算法用时统计如表 1所示,可以发现,加入DBSCAN算法后的运行时间并没有太大的改变,约增加了10 ms,对于微地震监测现场实时拾取是完全可以接受的。
|
|
表 1 MER+AIC算法和本文改进算法运算时间统计 |
由DBSCAN算法的原理可知,算法中有两个参数需要预先确定,分别是邻域半径(ε)和邻域最小样本数(M)。
4.1 邻域半径对聚类效果的影响邻域半径是指在样本空间中某一样本点的邻域边界到样本点的距离。这个参数决定了邻域内可以包含的样本点数量,将直接影响聚类效果。如果ε取值过小可能无法将有效的初至分在同一个类别中,反之则可能将误差较大的初至包含在有效的初至类别中。ε的选取主要由样本点的分布密度决定,因此与样本点之间的距离有关。不同信噪比的数据初至分布特征不同,本文分别对不同信噪比的数据进行了ε参数测试。图 12为ε取不同值时数据3中后一事件横波(第三个震相)初至的聚类分析结果,其中M参数固定为5。对于高信噪比微地震数据,MER算法拾取的错误率和误差均较小,仅有个别偏离较远的初至点。从图中可以看出,当ε=5时(图 12a)邻域内没有足够的初至点,因此所有初至都被当作噪声点,说明ε取值太小。当ε=20时(图 12c),领域范围过大使得误差较大的初至被聚类为有效初至,说明ε取值太大。当ε=15时能将有效初至和误差较大的初至分离(图 12b),说明ε取值适当。
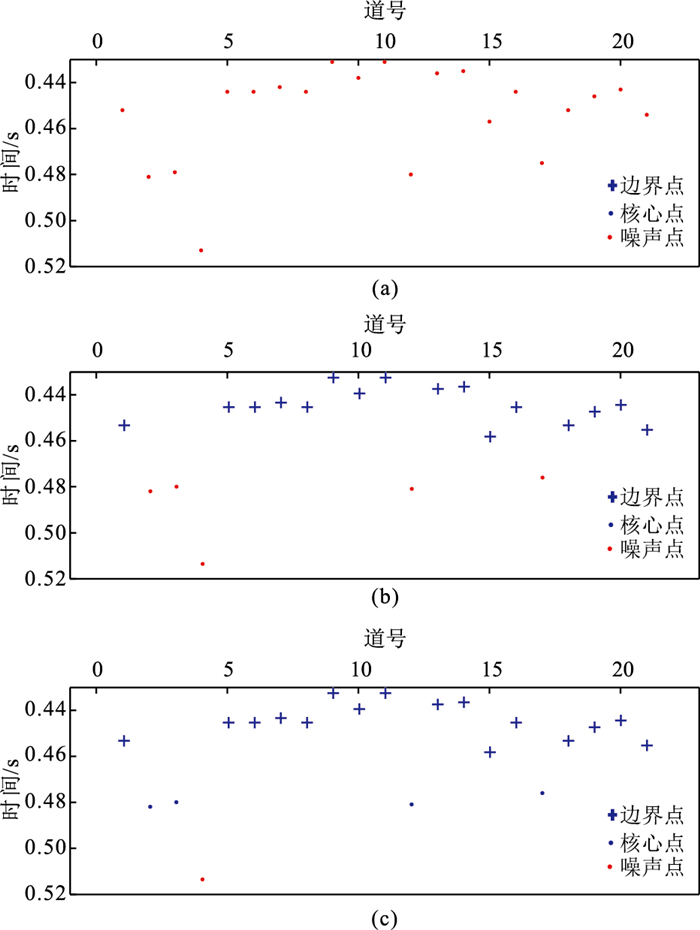
|
图 12 ε=5(a)、15(b)、20(c)时数据3中第三震相的MER算法拾取初至的聚类结果 |
对于低信噪比数据,MER算法的拾取结果中包含较多错误并且误差较大,使得初至分布较为分散,此时算法对于ε的变化较为敏感。图 13为ε=10、20、60时数据1的MER算法拾取初至的聚类结果,其中M=5。从图中可以看出,当ε值较小时大量有效初至被归类为噪声点(图 13a);而当ε值取的较大时,一些误差较大且较密集分布的初至点会形成另一个簇类(图 13c)。图 13中的19~39道的初至分布较为密集,聚类算法将这些初至单独分为一类,通过调整ε值难以将这些初至归为噪声点。
|
图 13 ε=10(a)、20(b)、60(c)时数据1的MER算法拾取初至的聚类结果 |
邻域最小样本数(M)主要影响核心点的数量。当ε固定时,M越大核心点越少,则被归类为同一簇类的点就越少。图 14为M=2、5、10时数据3中第三震相的MER算法拾取初至的聚类结果,其中ε=15。从图中可以看出,M较小时,由于难以满足核心点的形成条件部分误差较大的初至点被聚类为另一个簇类。随着M增大,当达到最佳聚类效果后结果没有明显的变化。

|
图 14 M=2(a)、5(b)、10(c)时数据3中第三震相的MER算法拾取初至的聚类结果 |
对低信噪比数据(数据1),MER算法拾取初至存在误差初至点密集分布,仅调整ε无法获得理想的聚类效果,可以适当增大M减少核心点数量,使密集分布的误差初至无法形成簇类。图 15为M=2、5、10、20时数据1的MER算法拾取初至的聚类结果,其中ε固定为20。从图中可以看出:当M较小时所形成的簇类会增加,这是核心点数目增加导致的,一些误差较大但是分布较为密集的初至被定义为核心点并且以此为中心形成了新的簇类(图 15a);随着M逐渐增加,形成的簇类数目逐渐减少(图 15b),最终只有大量密集分布的初至会形成簇类(图 15c);当M继续增大时,所有点已经无法形成簇类(图 15d)。
|
图 15 M=2(a)、5(b)、10(c)、20(d)时数据1 MER算法拾取初至的聚类结果 |
由以上分析可以知,参数ε和M存在耦合关系,需要选取合适的值才能使DBSCAN算法达到较好的聚类效果。为了满足微地震事件初至现场快速拾取的需求,需要自适应确定适合的参数。可以通过参数ε控制簇类中初至的密集程度,以此排除误差较大的初至;参数M主要影响簇类的数量,选取适当可以避免分布较为密集的噪声点被误判为有效初至。
为了避免邻域包含噪声点,邻域半径最好小于任意噪声点与有效初至的最小距离。在此条件下可以通过各个有效初至之间的距离来确定ε值。当有效初至点的邻域内正好包含一个最近的有效初至点时,DBSCAN算法正好可以沿着有效初至的分布方向聚类,这样可以保证将密集分布的有效初至聚成一类。此外,还要考虑到M参数的影响,避免出现ε值过小导致核心点过多,误差初至形成另一个簇类(如图 15所示)。
为综合考虑两个参数ε和M对聚类效果的影响,本文提出了一个根据M参数自适应确定ε参数的方法。对于给定的参数M,ε计算公式为
| $ \varepsilon =M\times \mathrm{M}\mathrm{e}\mathrm{d}\left({\boldsymbol{d}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right) $ | (4) |
式中:dmin表示任意一个初至点与其最近邻的初至点之间的距离;Med(·)表示取中位数。通过初至之间最小距离的中位数可以得到密集分布的有效初至之间的距离,再根据参数M扩大邻域半径ε。这样既可以保证邻域内不包含误差初至,又可以防止密集分布的误差初至聚为一类。在实际应用中参数M可以选择经验值5,根据实际聚类效果适当调整。
如果MER算法拾取的初至中误差过大导致密集分布的有效初至较少,则无论如何调整ε和M都无法使聚类效果达到最佳。此时建议选择较小的M和ε,尽量保证有效初至可以被聚为一类,而其他误差较大的初至可能会形成多个不同的簇类(如图 15a),但是这些错误的簇类中初至点的数量通常较少,可以设定一个样本数阈值,当簇类中样本数低于这个阈值时该簇类中的样本被归为噪声点。
5 结论本文利用DBSCAN聚类算法改进现有微地震信号初至拾取算法。首先利用MER算法对初至进行一次拾取,然后利用DBSCAN算法对一次拾取的结果进行优化,通过聚类算法区分误差较小的初至和误差较大的初至。再对小误差初至进行拟合并根据拟合的分布规律校正误差较大的初至。最后以优化后的初至为中心开时窗,利用AIC算法对初至进行精细拾取。三组实际数据测试结果表明,改进算法提高了初至拾取精度,增强了算法的抗噪能力。同时,聚类算法很好的解决了多震相初至难以识别的问题,可以有效区分不同震相的初至。另外,聚类算法的加入并没有增加过多的计算量,因此该算法可以满足现场实时拾取的要求。
本文分析了邻域半径(ε)和邻域最小样本数(M)对拾取结果的影响,ε主要影响算法对于大误差初至的识别能力,M主要影响簇类的数量。根据分析结果给出了参数的自适应选取方法,为算法的推广使用提供了便利。
| [1] |
张尔辉, 朱权洁, 缪华祥, 等. 基于微震技术的矿山地压活动监测及预警研究[J]. 金属矿山, 2020, 28(8): 172-181. ZHANG Erhui, ZHU Quanjie, MIU Huaxiang, et al. Study on monitoring and predicting of mine ground pressure activities based on microseismic technology[J]. Metal Mine, 2020, 28(8): 172-181. |
| [2] |
刘卫东, 刘腾蛟, 纪拥军, 等. 利用微地震监测成果判断砂砾岩油藏压裂裂缝井间连通性——以准噶尔盆地玛湖油田为例[J]. 石油地球物理勘探, 2022, 57(2): 395-404. LIU Weidong, LIU Tengjiao, JI Yongjun, et al. Determination of inter‑well connectivity of fractured fractures in glutenite reservoirs by microseismic monitoring results: a case study of Mahu Oilfield in the Junggar Basin[J]. Oil Geophysical Prospecting, 2022, 57(2): 395-404. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.016 |
| [3] |
赵改善. 二氧化碳地质封存地球物理监测: 现状、挑战与未来发展[J]. 石油物探, 2023, 62(2): 194-211. ZHAO Gaishan. Geophysical monitoring for geological carbon sequestration: present status, challenges, and future development[J]. Geophysical Prospecting for Petroleum, 2023, 62(2): 194-211. |
| [4] |
桂志先, 朱广生. 微震监测研究进展[J]. 岩性油气藏, 2015, 27(4): 68-76. GUI Zhixian, ZHU Guangsheng. Research advances of microseismic monitoring[J]. Lithologic Reservoirs, 2015, 27(4): 68-76. |
| [5] |
ALLEN R V. Automatic earthquake recognition and timing from single traces[J]. Bulletin of the Seismological Society American, 1978, 68(5): 1521-1532. DOI:10.1785/BSSA0680051521 |
| [6] |
RUTLEDGE J T, PHILLIPS W S, MAYERHOFER M J. Faulting induced by forced fluid injection and fluid flow forced by faulting: An interpretation of hydraulic-fracture microseismicity, Carthage Cotton Valley Gas Field[J]. Bulletin of the Seismological Society of America, 2004, 94(5): 1817-1830. DOI:10.1785/012003257 |
| [7] |
CHEN Z, STEWART R. A multi-window algorithm for real‑time automatic detection and picking of P-phases of microseismic events[C]. CSEG National Convention Abstracts, 2005, 355-358.
|
| [8] |
WONG J, HAN L J, BANCROFT J C, et al. Automatic time picking of first arrivals on noisy microseismic data [C]. CSEG Conference Abstracts, 2009, 1-5.
|
| [9] |
RODRIGUEZ I V. Automatic Time-picking of Microseismic Data Combining STA/LTA and the Stationary Discrete Wavelet Transform[D]. University of Alberta, Canada, 2011.
|
| [10] |
MAEDA N. A method for reading and checking phase times in auto-processing system of seismic wave data[J]. Zisin, 1985, 38(3): 365-379. DOI:10.4294/zisin1948.38.3_365 |
| [11] |
ZHANG H, THRUBER C, ROWE C. Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single‑component recording[J]. Bulletin of the Seimological Society of America, 2003, 95(5): 1904-1912. |
| [12] |
宋维琪, 吕世超. 基于小波分解与Akaike信息准则的微地震初至拾取方法[J]. 石油物探, 2011, 50(1): 14-21. SONG Weiqi, LYU Shichao. Automatic detection method of microseismic event based on wavelet decomposition and Akaike infornation criteria[J]. Geophysical Prospecting for Petroleum, 2011, 50(1): 14-21. DOI:10.3969/j.issn.1000-1441.2011.01.002 |
| [13] |
SOMA N, TAKEHARA T, ASANUMA H, et al. Precise automatic wave picking technique for onsite microseismic monitoring in hot dry rock development[J]. Geothermal Resources Council Transactions, 2004, 28(6): 239-244. |
| [14] |
MORIYA H. Precise arrival time detection of polarized seismic waves using the spectral matrix[J]. Geophysical Prospecting, 2008, 56(5): 667-676. DOI:10.1111/j.1365-2478.2008.00713.x |
| [15] |
吴治涛, 骆循, 李仕雄. 联合小波变换与偏振分析自动拾取微地震P波到时[J]. 地球物理学进展, 2012, 27(1): 131-136. WU Zhitao, LUO Xun, LI Shixiong. United wavelet transform and polarization analysis automatically identify micro seismic P-arrival[J]. Progress in Geophysics, 2012, 27(1): 131-136. |
| [16] |
BOSCHETI F, DERTITH M D, LIST R D. A fractal based algorithm for detecting first arrivals on seismic traces[J]. Geophysics, 1996, 61(4): 1095-1102. DOI:10.1190/1.1444030 |
| [17] |
常旭, 刘伊克. 地震记录的广义分维及其应用[J]. 地球物理学报, 2002, 45(6): 879-886. CHANG Xu, LIU Yike. The generalized fractal dimension of seismic records and its application[J]. Chinese Journal of Geophysics, 2002, 45(6): 879-886. |
| [18] |
JIA R, SUN H, PENG Y, et al. Automatic event detection in low SNR microseismic signals based on multi-scale permutation entropy and a support vector machine[J]. Journal of Seismology, 2017, 21(4): 735-748. DOI:10.1007/s10950-016-9632-2 |
| [19] |
QU S, GUAN Z, VERSCHUUR E, et al. Automatic high resolution microseismic event detection via supervised machine learning[J]. Geophysical Journal International, 2020, 222(1): 1881-1895. |
| [20] |
ZHU W, BEROZA G C. PhaseNet: a deep-neural-network‑based seismic arrival‑time picking method[J]. Geophysical Journal International, 2019, 216(1): 261-273. |
| [21] |
张逸伦, 喻志超, 胡天跃, 等. 基于U-Net的井中多道联合微地震震相识别和初至拾取方法[J]. 地球物理学报, 2021, 64(6): 2073-2085. ZHANG Yilun, YU Zhichao, HU Tianyue, et al. Multi-trace joint downhole microseismic phase detection and arrival picking method based on U‑Net[J]. Chinese Journal of Geophysics, 2021, 64(6): 2073-2085. |
| [22] |
邓飞, 蒋沛凡, 蒋先艺, 等. 应用图像语义分割网络的微地震事件识别和初至拾取方法[J]. 石油地球物理勘探, 2022, 57(5): 1011-1019. DENG Fei, JIANG Peifan, JIANG Xianyi, et al. Microseismic event recognition and first break picking method based on image semantic segmentation network[J]. Oil Geophysical Prospecting, 2022, 57(5): 1011-1019. DOI:10.13810/j.cnki.issn.1000-7210.2022.05.004 |
| [23] |
张唤兰, 朱光明, 王云宏. 基于时窗能量比和AIC的两步法微震初至自动拾取[J]. 物探与化探, 2013, 37(2): 269-273. ZHANG Huanlan, ZHU Guangming, WANG Yunhong. Automatic microseismic event detection and picking method[J]. Geophysical and Geochemical Exploration, 2013, 37(2): 269-273. |
| [24] |
宋维琪, 冯超. 微地震有效事件自动识别与定位方法[J]. 石油地球物理勘探, 2013, 48(2): 283-288. SONG Weiqi, FENG Chao. Automatic identification and localization of micro seismic effective events[J]. Oil Geophysical Prospecting, 2013, 48(2): 283-288. |
| [25] |
BORAH B, BHATTACHARYYA D K. An improved sampling-based DBSCAN for large spatial databases[C]. IEEE International Conference on Intelligent Sensing & Information Processing, 2004, 92-96.
|
| [26] |
AKAIKE H T. A new look at the statistical model identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723. DOI:10.1109/TAC.1974.1100705 |
| [27] |
ESTER M, KRIEGEL H P, SANDER J, et al. A density‑based algorithm for discovering clusters in large spatial databases with noise[C]. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, 1996, 226-231.
|
| [28] |
WADHWA A, THAKUR M K. Modified DBSCAN using particle swarm optimization for spatial hotspot identification[C]. Eleventh International Conference on Contemporary Computing, IEEE Computer Society, 2018, 1-3.
|
| [29] |
吴治涛, 李仕雄. STA/LTA算法拾取微地震事件P波到时对比研究[J]. 地球物理学进展, 2010, 25(5): 1577-1582. WU Zhitao, LI Shixiong. Comparison of STA/LTA P-pickers for micro seismic monitoring[J]. Progress in Geophysics, 2010, 25(5): 1577-1582. |
| [30] |
刘晗, 张建中. 微震信号自动检测的STA/LTA算法及其改进分析[J]. 地球物理学进展, 2014, 29(4): 1708-1714. LIU Han, ZHANG Jianzhong. STA/LTA algorithm analysis and improvement of microseismic signal automatic detection[J]. Progress in Geophysics, 2014, 29(4): 1708-1714. |



 龚屹,江苏省南京市建邺区金融城9号中国石化华东油气分公司勘探开发研究院,210000。Email:
龚屹,江苏省南京市建邺区金融城9号中国石化华东油气分公司勘探开发研究院,210000。Email: