2. 中国地质大学(武汉)科技部地球深部钻探与深地资源开发国际联合研究中心, 湖北武汉 430074;
3. 中国石油新疆油田公司, 新疆克拉玛依 834000;
4. 成都理工大学数学地质四川省重点实验室, 四川成都 610059
2. National Center for International Research on Deep Earth Drilling and Resource Development, Ministry of Science and Technology China University of Geosciences (Wuhan), Wuhan, Hubei 430074, China;
3. PetroChina Xinjiang Oilfield Company, Karamay, Xinjiang 834000, China;
4. Geomathematics Key Laboratory of Sichuan Province, Chengdu University of Technology, Chengdu, Sichuan 610059, China
准确的岩石力学参数在油气勘探与开发中发挥着重要作用,如井位选择、井壁稳定分析、井眼轨迹优化、压裂改造等 [1-6]。室内岩心实测是确定岩石力学参数最基本、最直接的方法,但是岩心试验数据有限且离散,不能完全反映钻井中地层岩石力学参数的变化趋势,不利于钻井、压裂等工程应用[7],因而在实践中更多的是采用地球物理测井预测方法。
常用的岩石力学参数测井预测方法有:基于弹性波动理论的预测方法和基于岩石力学参数的岩石物理响应机制建立的预测方法[8]。Gui等[9]结合室内试验和测井资料预测页岩地层脆性指数;王英伟等[10]根据室内试验获取动、静态岩石力学参数转换关系,对致密砾岩储层开展岩石力学参数预测;郭思强[11]利用纵波速度计算致密砂岩动态岩石力学参数,结合室内试验实现了动、静态力学参数之间的转换;邓晗等[12]对疏松砂岩储层的单轴抗压强度(Uniaxial Compressive Strength,UCS)与深度、声波时差、密度(ρ)等测井数据进行相关性分析,构建了多元线性回归模型并应用于实际资料;孙佳成等[13]对致密砂岩开展室内试验,实现了动、静态岩石力学参数之间的转换,计算得到岩石力学参数测井预测剖面。
岩石力学参数测井预测模型的建立通常基于实验室获得的半经验关系[14]。众多学者的研究表明,不同经验公式具有明显的区域性特点且易受岩性影响[14-18],而对于富有机质页岩、碳酸盐岩、致密砂岩等复杂岩性地层,由于其具有岩石成分和结构复杂、强非均质性、孔隙结构复杂等特征[19-22],因此地球物理测井预测方法精度较低,这为复杂岩性地层岩石力学参数预测带来较大挑战。
随着人工智能技术的快速发展,岩石力学参数预测方法出现智能化趋势。不同学者以声波时差、密度、孔隙度(ϕ)、渗透率等作为输入参数,针对不同岩性地层,采用不同机器学习算法开展岩石力学参数预测。Asadi[23]针对砂岩地层采用BP神经网络预测UCS;Matin等[24]基于随机森林(Random Forest,RF)模型实现了对凝灰岩样品弹性模量(E)和UCS的准确预测;Barzegar等[25]采用支持向量机(Support Vector Machine,SVM)预测凝灰岩样品UCS;He等[26]采用卷积神经网络(Convolutional Neural Network,CNN)预测大理岩和灰岩的UCS;Mahmoodzadeh等[27]采用决策树(Classification and Regression Tree,CART)和长短时记忆(Long-Short Term Memory,LSTM)网络分别预测砂岩岩样的内聚力(C)和内摩擦角(φ)。
上述研究说明了不同机器学习算法均可用于岩石力学参数预测。然而,仅构建单一算法模型进行岩石力学参数预测,可能会受到模型不规范、过度拟合、样本大小等因素影响[28],因此部分学者采用不同机器学习算法相结合的方式开展岩石力学参数预测。Mahmoodzadeh等[27]采用粒子群算法优化长短时记忆(Particle Swarm Optimization Long-Short Term Memory,PSO-LSTM)网络实现了砂岩内聚力和内摩擦角的高精度预测;Nasiri等[29]采用Shapley加法解释(Shapley Additive Explanations,SHAP),结合XGBoost预测凝灰岩UCS和弹性模量;Maryam等[30]采用布谷鸟算法优化人工神经网络(Cuckoo Optimization Algorithm-Artificial Neural Network,COA-ANN), 对灰岩的UCS和弹性模量进行预测。不同智能算法的结合进一步提升了预测模型的精度和适应性,然而目前的研究仅关注于少数几个岩石力学参数的预测,且多数针对单一岩性地层,对于复杂岩性地层多个岩石力学参数的同步预测的方法较少见于文献。
近年来,组合预测方法成为机器学习中一种最有效、最流行的预测技术[28]。组合预测方法采用多种预测模型对同一问题进行预测,然后赋予各单项预测模型合适的权系数并进行组合,从而提取各单项预测模型有效信息,优化预测效果,提高模型预测精度[31-32]。基于此,本文将组合预测的思想应用到复杂岩性地层岩石力学参数预测当中。
本文以准噶尔盆地玛湖凹陷风城组为例,首先,开展基于传统方法的岩石力学参数预测,通过室内岩石力学实验所获取的不同岩性岩样密度、声波速度参数以及UCS、弹性模量、泊松比(μ)、内聚力、内摩擦角、抗张强度(σt)、脆性指数(B)、断裂韧性(KIC)等岩石力学参数,构建岩石力学参数预测模型并开展预测;然后,采用BP、XGBoost、SVM、RF、CNN、CART、LSTM等不同机器学习算法,预测岩石力学参数并分析不同机器学习算法的预测效果;在此基础上,提出一种不同岩石力学参数的自适应权重组合预测方法,通过对不同岩石力学参数选取不同预测基模型,赋予权重并进行组合,以期实现对复杂岩性地层不同岩石力学参数的同步准确预测。
1 传统岩石力学参数预测方法准噶尔盆地玛湖凹陷风城组为多源混合细粒沉积,主要岩性为白云质粉砂岩、白云质泥岩、白云质细砂岩、凝灰质细砂岩、熔结凝灰岩等[33-34]。对研究区4口井岩样(深度为4300 ~ 5000 m)开展室内试验,获得其密度;然后开展岩石力学测试,主要包括单轴/三轴压缩测试(单轴抗压强度、弹性模量、泊松比、内聚力、内摩擦角、脆性指数)、巴西劈裂测试(抗张强度)、人字形切槽巴西圆盘法测试(断裂韧性)等,同时获取每一个岩样的纵波时差(∆tc)、横波时差(∆ts)。经过室内岩石力学试验和数据处理,共获得单轴抗压强度、弹性模量、泊松比、脆性指数(应力—应变曲线计算得到[35])、断裂韧性等数据各25组,抗张强度数据45组,内聚力、内摩擦角数据各30组。
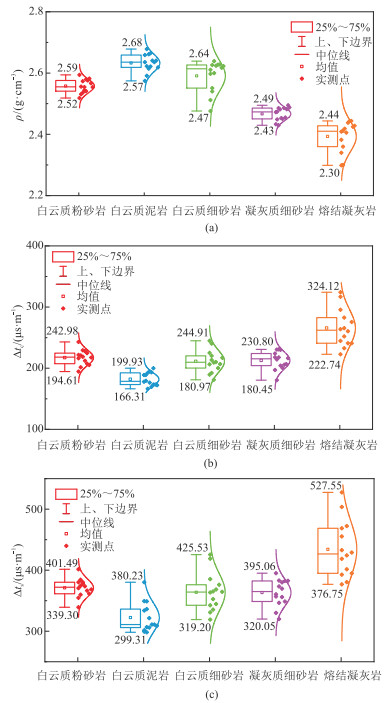
不同岩性岩样的密度及声学特征如图 1所示,岩石力学参数分布特征如图 2所示。由图 1和图 2可见,不同岩性岩样的岩石物理参数和岩石力学参数分布范围差异较明显,且部分相同岩性岩样的岩石物理参数、岩石力学参数的差异也较大,这可能与风城组纵向上岩性频繁变化、同一岩性岩样非均质性强、纹层发育等因素有关[34]。
|
图 1 不同岩性岩样的密度及声学特征 (a)密度;(b)纵波时差;(c)横波时差。图中曲线表示正态分布。 |

|
图 2 不同岩性岩样的岩石力学参数分布特征 (a)单轴抗压强度;(b)弹性模量;(c)泊松比;(d)抗张强度;(e)内聚力;(f)内摩擦角;(g)脆性指数;(h)断裂韧性 |
根据弹性波动理论和岩石物理响应特征,通过回归分析纵波时差、横波时差、密度等参数与不同岩石力学参数之间的关系,可建立不同岩石力学参数的预测模型(表 1)。
|
|
表 1 不同岩石力学参数预测模型 |
根据不同岩石力学参数预测模型(表 1)开展预测,并采用决定系数(R2)、平均相对误差(MRE)和均方根误差(RMSE)评价预测效果。评价指标公式分别为
| $ {R}^{2}=1-\frac{\sum\limits_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i}{)}^{2}}{\sum\limits_{i=1}^{n}({y}_{i}{-\stackrel{-}{y})}^{2}} $ | (1) |
| $ \mathrm{M}\mathrm{R}\mathrm{E}=\frac{1}{n}\sum\limits_{i=1}^{n}\left|\frac{{y}_{i}-{\widehat{y}}_{i}}{{y}_{i}}\right|\times 100\% $ | (2) |
| $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i}{)}^{2}} $ | (3) |
式中:
传统方法对不同岩石力学参数的预测效果如表 2所示。由表可见,不同岩石力学参数预测值与实测值的R2 < 0.4、MRE > 20%、RMSE较大,这说明基于弹性波动理论和岩石力学参数的岩石物理响应特征的传统预测方法对复杂岩性地层的适应性较差。
|
|
表 2 传统方法预测不同岩石力学参数效果评价 |
不同机器学习算法在岩石力学参数预测中的应用结果如表 3所示。由表可见,针对不同岩性岩石,可以选择不同机器学习算法得到较高精度的预测结果,这说明不同机器学习算法均能用于岩石力学参数预测。然而,针对复杂岩性地层,不同机器学习算法的适用性尚有待进一步研究。因此,本文采用BP、RF、SVM、CNN、CART、LSTM、XGBoost等7种机器学习算法,分别构建岩石力学参数预测模型并开展预测。通过比较不同机器学习算法的预测效果,寻找预测复杂岩性地层岩石力学参数的最优机器学习算法。
|
|
表 3 不同机器学习算法在不同岩石力学参数预测中的应用效果 |
基于室内实验获取的岩样岩性、密度、纵波时差、横波时差数据以及不同岩石力学参数数据,可建立用于机器学习算法模型的数据库。考虑到岩石力学参数的岩石物理响应特征及其受岩性影响的特点,本文将岩性、纵波速度、横波速度、密度作为机器学习的输入参数,各个岩石力学参数作为输出参数。同时,为了训练模型并评估不同模型预测结果的准确性,将数据库随机分成两组,即训练集(80%)和测试集(20%)。
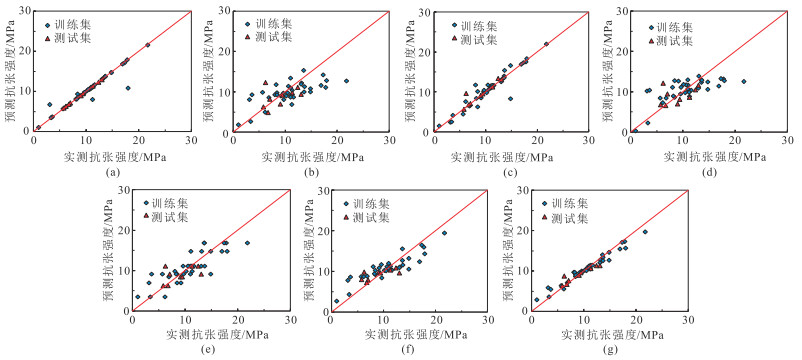
基于不同机器学习算法开展模型训练和测试,并计算预测值与实测值的R2、MRE和RMSE。图 3为不同机器学习算法预测抗张强度的结果。由图可见,不同机器学习算法预测效果有所不同,其中SVM、LSTM和XGBoost算法的预测效果较好,其他机器学习算法的预测效果较差。
|
图 3 不同机器学习算法预测抗张强度结果 (a)SVM;(b)BP;(c)LSTM;(d)CNN;(e)CART;(f)RF;(g)XGBoost |
进一步计算不同机器学习算法预测抗张强度结果与实测值的R2、MRE和RMSE,结果如表 4所示。由表可见,在训练阶段中,SVM算法的R2、RMSE、MRE分别为0.90、1.45、6.65%;LSTM算法的R2、RMSE、MRE分别为0.90、1.49、10.90%;XGBoost算法的R2、RMSE、MRE分别为0.97、1.06、14.55%。上述结果与图 3中展示的预测结果相吻合。
|
|
表 4 不同机器学习算法预测抗张强度效果评价 |
在测试阶段,SVM算法的预测效果最好,R2达到1.00,RMSE仅为0.10,MRE仅为1.21%。测试阶段的效果反映了模型在开展实际应用时的效果,因此所训练的SVM模型能更加准确地实现抗张强度的预测。
表 5展示了不同机器学习算法模型在测试阶段预测不同岩石力学参数的效果。通过对比可以发现,针对不同岩石力学参数,不同机器学习算法的预测效果存在差异。以MRE作为主要评价指标,同时考虑较高的R2值和较低的RMSE值,则单轴抗压强度的预测最优机器学习算法模型为SVM,弹性模量为BP,泊松比为RF,抗张强度为SVM,内聚力为XGBoost,内摩擦角为LSTM,脆性指数为SVM,断裂韧性为LSTM。以上结果进一步说明了针对复杂岩性地层不同岩石力学参数的预测最优机器学习算法有所不同,采用单一机器学习算法难以实现对不同岩石力学参数的准确预测。
|
|
表 5 不同机器学习算法预测不同岩石力学参数效果 |
为了实现对复杂岩性地层不同岩石力学参数的同步准确预测,本文采用基于Pearson相关系数的自适应权重组合预测方法。该方法主要是通过对不同岩石力学参数选择不同的基模型、赋予相应权重并进行组合,其中预测精度越高的基模型权重越大。该方法的关键在于不同岩石力学参数的基模型选择以及基模型的权重确定。单个岩石力学参数的预测基模型选择流程如图 4所示。首先通过不同机器学习算法模型对岩石力学参数开展预测,然后以R2≥0.60且MRE < 20%为指标对模型进行筛选,筛选后的模型即为该岩石力学参数的预测基模型。为了减小计算复杂度,本文选择的基模型不超过4个。对不同岩石力学参数重复图 4的流程,便可选出每个岩石力学参数的预测基模型。

|
图 4 基模型选择流程图 m为算法模型个数。 |
基模型的权重通过Pearson相关系数确定。根据基模型的预测结果可计算预测值与实测值的Pearson相关系数。Pearson相关系数反映两个向量间的线性相关性,即向量A=[a1, a2, …, ak]与B=[b1, b2, …, bk]之间的Pearson相关系数
| $ p=\frac{k\sum\limits_{i=1}^{k}{a}_{i}{b}_{i}-\sum\limits_{i=1}^{k}{a}_{i}\sum\limits_{i=1}^{k}{b}_{i}}{\sqrt{k\sum\limits_{i=1}^{k}{a}_{i}^{2}-{\left(\sum\limits_{i=1}^{k}{a}_{i}\right)}^{2}}\sqrt{k\sum\limits_{i=1}^{k}{b}_{i}^{2}-{\left(\sum\limits_{i=1}^{k}{b}_{i}\right)}^{2}}} $ | (4) |
式中k为向量维数。计算得到Pearson相关系数后,每个基模型的权重计算公式为
| $ w_j=\frac{{p}_{j}}{\sum\limits_{j=1}^{N}p_j} $ | (5) |
式中:wj为第j个基模型权重系数;pj为第j个基模型的Pearson相关系数;N为基模型个数。经过优选和权重计算,各岩石力学参数的预测基模型及其权重系数如表 6所示。根据表 6可以构建不同岩石力学参数的自适应权重组合预测模型。单个岩石力学参数的组合预测模型为
| $ g=\sum\limits_{j=1}^{N}w_j g_j $ | (6) |
|
|
表 6 不同岩石力学参数的预测基模型及其权重系数 |
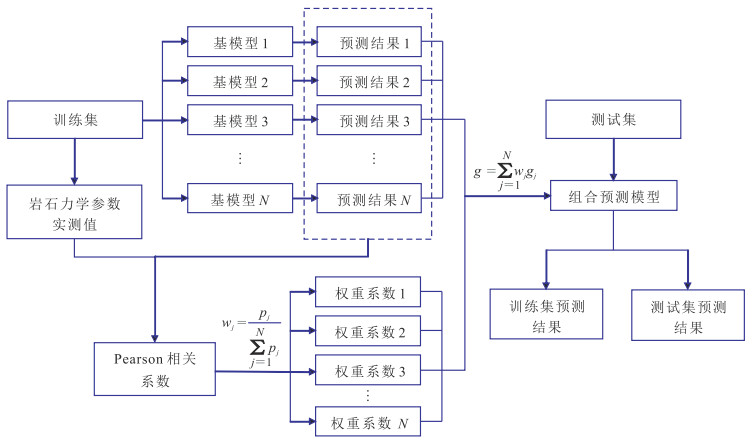
式中gj为第j个基模型。自适应权重组合预测模型的具体流程如图 5所示。
|
图 5 自适应权重组合预测流程图 |
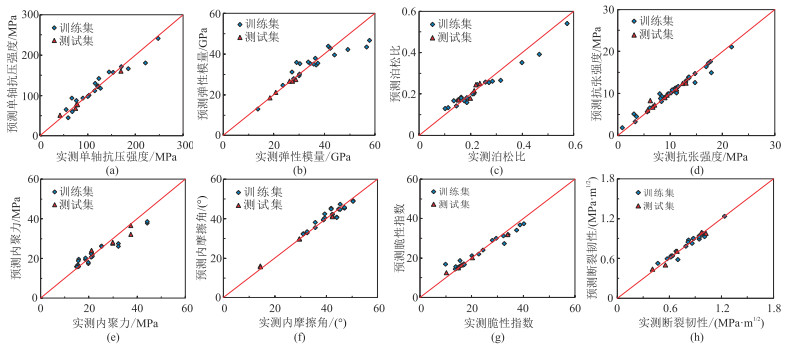
据图 5所示流程对不同岩石力学参数开展自适应权重组合预测,并计算预测值与实测值(图 6)的R2、RMSE和MRE(表 7)。由图 6可见,不同岩石力学参数的预测值与实测值之间的相关性均较高,预测效果均较好。
|
图 6 不同岩石力学参数预测值与实测值的关系 (a)单轴抗压强度;(b)弹性模量;(c)泊松比;(d)抗张强度;(e)内聚力;(f)内摩擦角;(g)脆性指数;(h)断裂韧性 |
|
|
表 7 自适应权重组合预测效果评价 |
从表 7中可以发现,不同岩石力学参数自适应权重组合预测结果的R2均较高,绝大部分大于0.90;不同岩石力学参数的RMSE均较低;除训练集中泊松比预测结果的MRE为10.30%外,其他岩石力学参数预测结果的MRE均小于10.00%。以上结果进一步说明:通过对不同岩石力学参数开展自适应权重组合预测可以提高机器学习算法对不同岩石力学参数的预测精度和适应性,从而实现对复杂岩性地层不同岩石力学参数的同步准确预测。
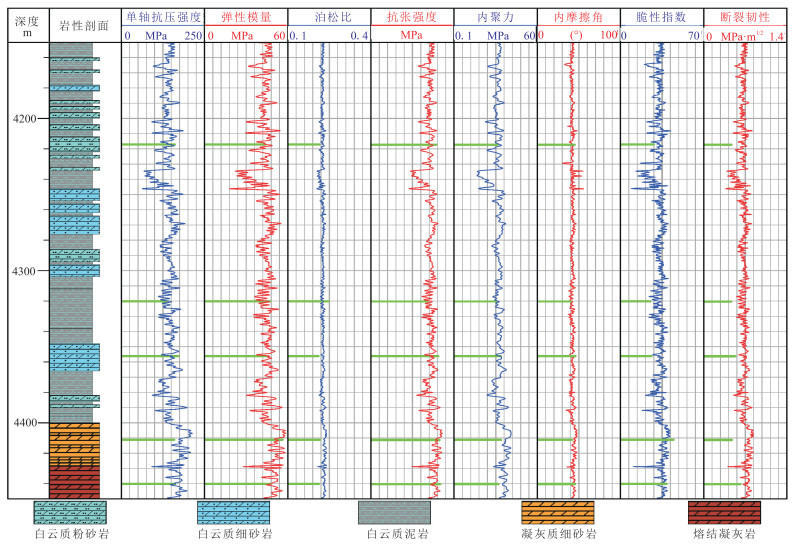
基于自适应权重组合预测方法得到玛湖凹陷风城组不同岩石力学参数的测井剖面如图 7所示。由图可见,某深度处预测值与实测值(绿色横线)吻合度较高。
|
图 7 玛湖凹陷风城组地层不同岩石力学参数的测井剖面 |
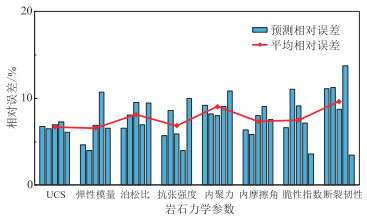
由图 8可见,不同岩石力学参数预测结果的平均相对误差均小于10.00%,其中单轴抗压强度平均相对误差为6.71%,弹性模量为6.57%,泊松比为8.11%,抗张强度为6.82%,内聚力为9.05%,内摩擦角为7.34%,脆性指数为7.51%,断裂韧性为9.64%,以上结果证明了本文所提出的自适应权重组合预测方法的适用性。
|
图 8 预测曲线与实测点的相对误差 |
本文基于室内岩石力学实验所获取的不同岩性岩样密度、声波速度参数以及抗压强度、弹性模量、泊松比、内聚力、内摩擦角、抗张强度、脆性指数、断裂韧性等岩石力学参数,采用传统预测方法、基于机器学习算法的预测方法和自适应权重组合预测法,对复杂岩性地层不同岩石力学参数进行预测,得到的结论如下:
(1) 传统预测方法在复杂岩性地层岩石力学参数的预测中适应性较差,预测精度较低;
(2) 不同机器学习算法对复杂岩性地层不同岩石力学参数的预测效果存在差异,单一机器学习算法难以实现对多个岩石力学参数的同步准确预测;
(3) 通过构建自适应权重组合预测模型,开展岩石力学参数预测,能够有效地提升机器学习算法的泛化性能,从而实现复杂岩性地层多个岩石力学参数的同步准确预测。
本文实例中仅选用了几种常用的机器学习算法去构建自适应权重组合预测模型。根据本文所提出的方法,也可选择更多的机器学习算法模型作为预测基模型以构建基模型库,进一步提高复杂岩性地层岩石力学参数的预测精度,同时实现更多岩石力学参数的同步准确预测。
| [1] |
任岩, 曹宏, 姚逢昌, 等. 吉木萨尔致密油储层脆性及可压裂性预测[J]. 石油地球物理勘探, 2018, 53(3): 511-519. REN Yan, CAO Hong, YAO Fengchang, et al. Brittleness and fracability prediction for tight oil reservoir in Jimsar Sag, Junggar Basin[J]. Oil Geophysical Prospecting, 2018, 53(3): 511-519. |
| [2] |
YONG R, CHANG C, ZHANG D, et al. Optimization of shale-gas horizontal well spacing based on geology-engineering-economy integration: A case study of Well Block Ning 209 in the National Shale Gas Development Demonstration Area[J]. Natural Gas Industry B, 2021, 8(1): 98-104. DOI:10.1016/j.ngib.2020.07.006 |
| [3] |
石林, 史璨, 田中兰, 等. 中石油页岩气开发中的几个岩石力学问题[J]. 石油科学通报, 2019, 4(3): 223-232. SHI Lin, SHI Can, TIAN Zhonglan, et al. Several rock mechanics problems in the development of shale gas in PetroChina[J]. Petroleum Science Bulletin, 2019, 4(3): 223-232. |
| [4] |
熊健, 林海宇, 唐勇, 等. 砂砾岩油藏影响压裂效果关键地质力学因素研究及应用[J]. 石油地球物理勘探, 2021, 56(5): 1048-1059. XIONG Jian, LIN Haiyu, TANG Yong, et al. A case study of key geomechanical factors affecting fracturing effect in sandy conglomerate reservoirs[J]. Oil Geophysical Prospecting, 2021, 56(5): 1048-1059. |
| [5] |
朱海燕, 宋宇家, 唐煊赫. 页岩气储层四维地应力演化及加密井复杂裂缝扩展研究进展[J]. 石油科学通报, 2021, 6(3): 396-416. ZHU Haiyan, SONG Yujia, TANG Xuanhe. Research progress on 4-dimensional stress evolution and complex fracture propagation of infill wells in shale gas reservoirs[J]. Petroleum Science Bulletin, 2021, 6(3): 396-416. DOI:10.3969/j.issn.2096-1693.2021.03.032 |
| [6] |
任岩, 曹宏, 姚逢昌, 等. 岩石脆性评价方法进展[J]. 石油地球物理勘探, 2018, 53(4): 875-886. REN Yan, CAO Hong, YAO Fengchang, et al. Review of rock brittleness evaluation methods[J]. Oil Geophysical Prospecting, 2018, 53(4): 875-886. |
| [7] |
钟自强, 刘向君, 刘诗琼, 等. 砾岩地层岩石力学参数测井预测模型构建与应用[J]. 科学技术与工程, 2018, 18(8): 181-186. ZHONG Ziqiang, LIU Xiangjun, LIU Shiqiong, et al. Logging prediction model of rock mechanical parameters and its applications in conglomerate formation[J]. Science Technology and Engineering, 2018, 18(8): 181-186. |
| [8] |
CHEN L, CHEN X, YANG Y, et al. Cuttings-test method for predicting rock strength[J]. Energy Reports, 2022, 8: 3964-3969. DOI:10.1016/j.egyr.2022.03.005 |
| [9] |
GUI J, GUO J, SANG Y, et al. Evaluation on the anisotropic brittleness index of shale rock using geophysical logging[J/OL]. Petroleum, 2022[2022-06-08]. https://www.sciencedirect.com/science/article/pii/S2405656122000463.
|
| [10] |
王英伟, 王林生, 覃建华, 等. 致密砾岩储层岩石力学参数及地应力测井评价方法研究[J]. 测井技术, 2021, 5(6): 624-629. WANG Yingwei, WANG Linsheng, QIN Jianhua, et al. Log evaluation method of rock mechanics and in-situ stress characteristics of tight conglomerate formations[J]. Well Logging Technology, 2021, 5(6): 624-629. |
| [11] |
郭思强. 大庆油田T30井区扶余油层致密储层岩石力学参数建模[J]. 大庆石油地质与开发, 2020, 39(5): 169-174. GUO Siqiang. Rock mechanical parameter modeling of Fuyu tight oil reservoir in Well Block T30 of Daqing Oilfield[J]. Petroleum Geology & Oilfield Development in Daqing, 2020, 39(5): 169-174. |
| [12] |
邓晗, 孟召兰, 王尧, 等. 渤海油田砂岩储层岩石力学参数预测经验公式研究[J]. 海洋石油, 2020, 40(2): 61-66, 95. DENG Han, MENG Zhaolan, WANG Yao, et al. Study on empirical formulas for predicting rock mechanical parameters of sandstone reservoirs in Bohai Oilfield[J]. Offshore Oil, 2020, 40(2): 61-66, 95. |
| [13] |
孙佳成, 高向东. 基于测井曲线的临兴区块致密砂岩力学性质研究[J]. 内蒙古石油化工, 2020, 46(5): 96-99. SUN Jiacheng, GAO Xiangdong. Study on the mechanical properties for the tight sandstone in Linxing block-area based on logging curve[J]. Inner Mongulia Petrochemical Industry, 2020, 46(5): 96-99. |
| [14] |
WAN Y, ZHANG H, LIU X, et al. Prediction of mechanical parameters for low-permeability gas reservoirs in the Tazhong Block and its applications[J]. Advances in Geo-Energy Research, 2020, 4(2): 219-228. DOI:10.26804/ager.2020.02.10 |
| [15] |
KHOSRAVI M, TABASI S, HOSSAM ELDIEN H, et al. Evaluation and prediction of the rock static and dynamic parameters[J]. Journal of Applied Geophysics, 2022, 199: 104581. DOI:10.1016/j.jappgeo.2022.104581 |
| [16] |
MOHAMMAD M I. Predictive models and feature ranking in reservoir geomechanics: A critical review and research guidelines[J]. Journal of Natural Gas Science and Engineering, 2020, 82: 103493. DOI:10.1016/j.jngse.2020.103493 |
| [17] |
CHANG C, ZOBACK M, KHAKSAR A. Empirical relations between rock strength and physical properties in sedimentary rocks[J]. Journal of Petroleum Science and Engineering, 2006, 51(3/4): 223-237. |
| [18] |
MOHAMAD E T, JAHED ARMAGHANI D, MOMENI E, et al. Prediction of the unconfined compressive strength of soft rocks: a PSO-based ANN approach[J]. Bulletin of Engineering Geology and the Environment, 2015, 74(3): 745-757. DOI:10.1007/s10064-014-0638-0 |
| [19] |
姚军, 刘磊, 杨永飞, 等. 基于多实验成像和机器学习的页岩多尺度孔隙结构表征新方法[J]. 天然气工业, 2023, 43(1): 36-46. YAO Jun, LIU Lei, YANG Yongfei, et al. A new method for characterizing multi-scale shale pore structure based on multi-experimental imaging and machine learning[J]. Natural Gas Industry, 2023, 43(1): 36-46. |
| [20] |
王斌, 魏柳斌, 于小伟, 等. 不同孔隙结构碳酸盐岩的岩石物理响应特征及储层预测新方法——以鄂尔多斯盆地奥陶系马家沟组四段为例[J]. 天然气工业, 2023, 43(3): 46-58. WANG Bin, WEI Liubin, YU Xiaowei, et al. Petrophysical response characteristics of carbonate rocks with different pore structures and new reservoir prediction method: A case study of the fourth member of Ordovician Majiagou Formation in the Ordos Basin[J]. Natural Gas Industry, 2023, 43(3): 46-58. |
| [21] |
陈超, 印兴耀, 陈祖庆, 等. 基于页岩岩石物理等效模型的地层压力系数预测方法[J]. 石油地球物理勘探, 2022, 57(2): 367-376, 394. CHEN Chao, YIN Xingyao, CHEN Zuqing, et al. Prediction for formation pressure coefficients based on an equivalent petrophysical model of shale[J]. Oil Geophysical Prospecting, 2022, 57(2): 367-376, 394. |
| [22] |
LI Z, ZHANG L, YUAN W, et al. Logging identification for diagenetic facies of tight sandstone reservoirs: A case study in the Lower Jurassic Ahe Formation, Kuqa Depression of Tarim Basin[J]. Marine and Petroleum Geology, 2022, 139: 105601. DOI:10.1016/j.marpetgeo.2022.105601 |
| [23] |
ASADI A. Application of artificial neural networks in prediction of uniaxial compressive strength of rocks using well logs and drilling data[J]. Procedia Engineering, 2017, 191: 279-286. DOI:10.1016/j.proeng.2017.05.182 |
| [24] |
MATIN S S, FARAHZADI L, MAKAREMI S, et al. Variable selection and prediction of uniaxial compressive strength and modulus of elasticity by random forest[J]. Applied Soft Computing, 2018, 70: 980-987. DOI:10.1016/j.asoc.2017.06.030 |
| [25] |
BARZEGAR R, SATTARPOUR M, NIKUDEL M R, et al. Comparative evaluation of artificial intelligence models for prediction of uniaxial compressive strength of travertine rocks, case study: Azarshahr area, NW Iran[J]. Modeling Earth Systems and Environment, 2016, 2(2): 76. DOI:10.1007/s40808-016-0132-8 |
| [26] |
HE M, ZHANG Z, LI N. Deep convolutional neural network-based method for strength parameter prediction of jointed rock mass using drilling logging data[J]. International Journal of Geomechanics, 2021, 21(7): 04021111. DOI:10.1061/(ASCE)GM.1943-5622.0002074 |
| [27] |
MAHMOODZADEH A, MOHAMMADI M, GHA FOOR SALIM S, et al. Machine learning techniques to predict rock strength parameters[J]. Rock Mechanics and Rock Engineering, 2022, 55(3): 1721-1741. DOI:10.1007/s00603-021-02747-x |
| [28] |
ZHANG Y, WANG J, YU L, et al. An extreme bias-penalized forecast combination approach to commodity price forecasting[J]. Information Sciences, 2022, 615: 774-793. DOI:10.1016/j.ins.2022.09.056 |
| [29] |
NASIRI H, HOMAFAR A, CHELGANI C. Prediction of uniaxial compressive strength and modulus of elasticity for Travertine samples using an explainable artificial intelligence[J]. Results in Geophysical Sciences, 2021, 8: 100034. DOI:10.1016/j.ringps.2021.100034 |
| [30] |
MARYAM M, MAHMOUD B. Comparison of LLNF, ANN, and COA-ANN techniques in modeling the uniaxial compressive strength and static Young's modulus of limestone of the Dalan Formation[J]. Natural Resources Research, 2019, 28: 223-239. DOI:10.1007/s11053-018-9383-6 |
| [31] |
张文扬, 汪凯, 袁宏俊. 安徽省城镇居民人均可支配收入组合预测[J]. 重庆工商大学学报(自然科学版), 2022, 39(5): 93-104. ZHANG Wenyang, WANG Kai, YUAN Hongjun. Combination forecast of per capita disposable income of urban residents in Anhui province[J]. Journal of Chongqing Technology and Business University (Natural Science Edition), 2022, 39(5): 93-104. |
| [32] |
唐小我. 最优组合预测方法及其应用[J]. 数理统计与管理, 1992, 11(1): 31-35. TANG Xiaowo. Optimal combination prediction method and its application[J]. Jouranl of Applied Statistics and Management, 1992, 11(1): 31-35. |
| [33] |
冯有良, 杨智, 张洪, 等. 咸化湖盆细粒重力流沉积特征及其页岩油勘探意义——以准噶尔盆地玛湖凹陷风城组为例[J]. 地质学报, 2023, 97(3): 839-863. FENG Youliang, YANG Zhi, ZHANG Hong, et al. Fine-grained gravity flow sedimentary features and their petroleum significance within saline lacustrine basins: A case study of the Fengcheng Formation in Mahu depression, Junnggar basin, China[J]. Acta Geologica Sinica, 2023, 97(3): 839-863. |
| [34] |
邹阳, 韦盼云, 曹元婷, 等. 碱湖型页岩油"甜点"分类与主控因素——以准噶尔盆地风城组为例[J]. 石油学报, 2023, 44(3): 458-470. ZOU Yang, WEI Panyun, CAO Yuanting, et al. Classification and main controlling factors of sweet spots of alkaline lake type shale oil: a case study of Fengcheng Formation in Junggar Basin[J]. Acta Petrolei Sinica, 2023, 44(3): 458-470. |
| [35] |
LIANG L, LIU X, XIONG J, et al. New model to evaluate the brittleness in shale formation[C]. SPG/SEG 2017 International Geophysical Conference, 2017, 1248-1251.
|



 熊健, 四川省成都市新都区新都大道8号西南石油大学油气藏地质及开发工程国家重点实验室,610500。Email:
熊健, 四川省成都市新都区新都大道8号西南石油大学油气藏地质及开发工程国家重点实验室,610500。Email: