2. 广东省地球物理高精度成像技术重点实验室, 广东深圳 518055;
3. 南方科技大学地球与空间科学系, 广东深圳 518055
2. Guangdong Provincial Key Laboratory of Geophysical High⁃resolution Imaging Technology, Shenzhen, Guangdong 518055, China;
3. Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China
电磁法是应用最早、应用最广的物探技术之一,经历了近百年的发展,在油气勘探、深部矿产资源与地热地下水勘查、城市环境监测与地下空间开发利用、地球深部结构成像及水下军事目标探测等方面都发挥着重要作用[1-3]。按照场源的不同,电磁勘探方法分为两类:一是天然场源电磁法,如大地电磁法[4](Magnetotelluric Method,MT);另一类是人工源电磁法,也称为可控源电磁(Controlled Source Electromagnetic,CSEM)法,主要包括人工源音频大地电磁法(Controlled Source Audio-frequency Magnetotelluric,CSAMT)[5]和人工源时间域电磁法(Time-domain Electromagnetic Method,TEM)[6]。在实际勘探、开发过程中,随着勘探目标深度不断加大、勘探地区的地质构造愈加复杂,常规的电磁方法已不能满足勘探需求,时频电磁法[7-8](Time-frequency Electromagnetic Method,TFEM)的提出有效改善了常规电磁方法勘探能力的不足。TFEM将频率域电磁勘探方法与时间域电磁勘探方法相结合,可同时获得时域和频域信号,改变了传统电磁法对时域和频域信息分别处理的方式,提高了采集效率和解释效果,广泛应用于深部资源勘查。不同电磁方法在工作原理和应用领域都具有自身局限性,除射频段地质雷达方法外,其他的电磁法都存在体积效应、静态位移等问题,且电磁场强度随着深度的增加呈指数级衰减,分辨率也呈指数级规律降低[1]。与地震方法相比,电磁法的垂向分辨率和分层能力也相差较大,为电磁数据处理和反演带来了困难。
地球物理反演是指基于观测物理场推断地下介质物理状态、空间分布和物性结构[9],反演通常包括单一物理量反演和多物理量联合反演[10]。非唯一性问题是地球物理反演固有且难以有效解决的难题,其主要原因有两点:其一,通过观测得到的资料是不完备的,每一种可能的解都满足不完备观测数据;其二,任何地球物理的观测数据都会受到外界干扰,导致反演结果与实际情况存在差异[10]。因此,对不同的地球物理数据采取联合反演策略,综合利用不同地球物理场或地球物理资料的优势以降低多解性是地球物理勘探发展的总趋势,也是发展的必然趋势[11]。
本文从先验信息约束下的电磁反演、天然源和人工源的联合电磁反演及电磁方法与地震方法联合反演的角度,分别介绍各自的研究现状,总结现有的问题并分析未来的发展方向。
1 多类型电磁方法联合反演方法研究现状 1.1 基于先验信息约束以减少电磁反演结果非唯一性研究现状基于已知资料的约束反演广泛应用于地震资料的处理和反演,且应用较早[12-17]。在电磁方法发展的早期,计算机技术处于初级阶段,直流电法和大地电磁法的数据处理均采用量板法求取目标深度,直到20世纪80年代才发展了一维反演和二维反演。但是,由于反演非唯一性造成的多解性极强,这一时期主要根据已知的地震、地质及重磁资料,采用交互对比的方法,优选符合地质构造特征的反演模型作为最终结果,这种处理方式很大程度上依赖于技术人员的经验,其结果的有效性和可靠性难以保证。此后,一些学者基于测井、地质、地震资料等先验信息建立约束模型[18-20],提出了模型约束反演方法,减少反演的非唯一性。对于不同的地质目标主要采取以下几种不同的方法:①对于盐岩构造,由于盐岩具有高速特性,利用地震方法无法获得下伏构造的有效反射,这时需要采用电磁方法辅助探测。为了减少电磁反演的非唯一性、提高探测精度,利用地震资料的反射界面构建盐层目标以上的几何模型,利用电测井资料构建电阻率变化范围,采用广义逆反演得到盐下构造,取得了较好效果[21]。②对于火成岩[20, 22],由于火成岩对地震反射有屏蔽作用,仅仅依靠地震方法难以厘清火成岩结构及储层信息。因此,可采用电磁方法,借助钻井、地震剖面资料对火成岩上覆电性层的结构进行建模约束,借助电测井资料对电性层电阻率进行建模约束,利用模拟退火法等方法对电磁数据进行约束反演,较好地克服了电磁勘探反演结果的多解性。
利用已知信息构建地层界面和地层电阻率约束模型[8, 23],其形式为
| $ {\boldsymbol{m}}_{j}^{{Q}_{0}}={\boldsymbol{m}}_{j}^{{Q}_{\mathrm{m}\mathrm{i}\mathrm{n}}}+{\beta }_{j}({\boldsymbol{m}}_{j}^{{Q}_{\mathrm{m}\mathrm{a}\mathrm{x}}}-{\boldsymbol{m}}_{j}^{{Q}_{\mathrm{m}\mathrm{i}\mathrm{n}}}) $ | (1) |
| $ {\boldsymbol{m}}_{i}^{{R}_{0}}={\boldsymbol{m}}_{i}^{{R}_{\mathrm{m}\mathrm{i}\mathrm{n}}}+{\lambda }_{i}({\boldsymbol{m}}_{i}^{{R}_{\mathrm{m}\mathrm{a}\mathrm{x}}}-{\boldsymbol{m}}_{i}^{{R}_{\mathrm{m}\mathrm{i}\mathrm{n}}}) $ | (2) |
式中:m代表模型;下标i、j表示地层界面编号;上标
对于下述不同的情况,分别采用不同的约束条件进行模型反演。
(1)油田开发区:利用电磁方法探测和监测油水分布,这样的研究区可为建模约束反演提供全方位的三维地震和钻孔资料。因此,由地层界面信息构成的几何模型可完全根据地震和钻孔资料进行构建,即
| $ {\boldsymbol{m}}_{i}^{{R}_{0}}=\frac{{S}_{\mathrm{B}}}{S}{\boldsymbol{m}}_{i}^{\mathrm{d}{R}_{\mu \pm {k}_{\mathrm{d}}\sigma }^{\mathrm{A}}}+\frac{S-{S}_{\mathrm{A}}}{S}{\boldsymbol{m}}_{i}^{\mathrm{d}{R}_{\mu \pm {k}_{\mathrm{d}}\sigma }^{\mathrm{B}}} $ | (3) |
式中:S为A井与B井间的距离;
(2)对于地震勘探困难区,主要利用电磁方法探测地震空白反射区的目标体,类似前面的火成岩发育区、盐岩构造区等。这类约束建模反演研究比较广泛[8, 23-24]。为了提高地震反射盲区的电磁反演效果,通常利用地震反射区域的地震资料构建约束模型,即式(1)中地层厚度模型
(3)对于无地震数据和钻孔数据的地区,可利用地质和重磁等资料构建约束模型,减少电磁反演的非唯一性。通常情况下,地表露头的地质结构是已知的,而深部的地质结构可以根据地质学家的推断建立多个模型,即基于式(1)、式(2)中可建立g个模型(包括几何模型
上述方法均是利用已知地质、物探资料作为先验信息对模型进行约束,本质上是通过构建较准确的初始模型减少反演的非唯一性。这种方法对已知资料的要求较高,对于成熟的开发区,已知资料比较多,该方法效果较好,而对于一些无先验资料或较少的地区,无法获得可靠的初始模型,无法实现有效约束,这类约束反演方法不可行。
除了上述模型约束反演,一些学者提出在反演目标函数中加入已知信息约束项,目的是提高反演精度。其反演目标函数的通用形式为
| $ F={F}_{\boldsymbol{d}}+{F}_{\boldsymbol{m}}+{F}_{\mathrm{r}} $ | (4) |
式中:F表示目标函数;下标d、m分别代表观测数据和模型,下标“r”代表正则化。F包括数据拟合项
第一种形式是构建参考模型约束项。王传武等[25]基于地质钻探得到的介质电阻率信息及地震反射法和地质雷达法得到的异常体界面信息构建参考模型约束,并将其添加到反演目标函数,其目标函数为
| $ \begin{array}{l}\varphi ={‖\mathrm{\Delta }\boldsymbol{d}-\boldsymbol{A}(\boldsymbol{m}-{\boldsymbol{m}}_{0})‖}^{2}+\lambda {‖\boldsymbol{C}(\boldsymbol{m}-{\boldsymbol{m}}_{0})‖}^{2}+\\ \eta {‖{\boldsymbol{F}}_{\mathrm{r}}(\boldsymbol{m}-{\boldsymbol{m}}_{\mathrm{r}})‖}^{2}\end{array} $ | (5) |
式中:
第二种形式是构建空间结构约束项。采用这种方式的前提是利用地震反射法、地质雷达法可以获得局部异常体确切的位置和形态信息,且异常区域中的介质电阻率分布相似。在反演过程中,不断迭代该区域内的网格电阻率,最终使得该区域所有网格电阻率值与区域内电阻率均值之差的平方和达到最小。这种方法的目标函数为
| $ \begin{array}{l}\varphi ={‖\mathrm{\Delta }\boldsymbol{d}-\boldsymbol{A}(\boldsymbol{m}-{\boldsymbol{m}}_{0})‖}^{2}+\lambda {‖\boldsymbol{C}(\boldsymbol{m}-{\boldsymbol{m}}_{0})‖}^{2}+\\ \ \ \ \ \ \ \ \ \eta \left({\boldsymbol{F}}_{\mathrm{s}}{\mathrm{\Delta }\boldsymbol{m})}^{\mathrm{T}}\right({\boldsymbol{F}}_{\mathrm{s}}\mathrm{\Delta }\boldsymbol{m})\end{array} $ | (6) |
式中:
上述两种形式均利用了地震反射数据和地质雷达数据对界面识别能力强及利用钻孔方法能直接得到地下介质物理性质的优势。但是,这一类反演方法的效果依赖于其他方法处理结果的准确性,特别是空间结构约束对于异常体的大小、位置和形态的先验刻画要求高。因此,这两类反演约束方法目前主要仅应用于工程勘察中浅部三维电阻率反演。
1.2 天然场源与人工源电磁方法联合反演不同的电磁方法对于地下电性结构的灵敏度和探测深度不同,如果能平衡不同电磁方法数据集的贡献,相对于单一电磁方法反演,不同电磁方法联合反演具有更高分辨率。MT数据对于区域性构造的电阻率变化较敏感,而利用CSEM数据则可较好地探测局部电性异常体,对薄层电性异常体的识别能力较强。因此MT和CSEM数据联合反演能够取长补短,提高反演精度。Da Silva Pinheiro等[27]计算了这两种方法联合反演过程中海塞矩阵的奇异值,得到了联合反演的零空间小于单独反演零空间的结论,从数理角度证明了MT和CSEM数据联合反演可在一定程度上减少反演的非唯一性。
早期关于这种方式的联合反演多为顺序联合反演,即以MT的反演结果作为CSEM数据反演的初始模型,其优点是克服了CSEM反演中初始模型对反演结果的影响,但这种顺序联合方式并未充分利用数据之间的约束关系,是一种伪联合。此后,陆续发展了真正意义上的联合反演,主流方法是基于非线性共轭梯度法[28]的联合反演。Commer等[29]在模型参数化的同时采用了单元约束和结构约束,利用非线性共轭梯度法进行三维同步反演,结果表明,若能恰当选取权重因子,联合反演结果可清晰地反映异常体的形态和位置。
MT与CSEM联合反演的效果主要表现在三个方面:①MT方法能弥补CSEM法深部信息不足的缺点。Mackie等[30]在海洋可控源理论数据中加入三个大地电磁台站的人工合成信号,利用非线性共轭梯度反演方法同步反演两个数据集,结果表明在CSEM数据频率难以达到的深度,反演得到的电阻异常体轮廓和深部界面清晰。②MT和CSEM在地震勘探困难区(盐岩及岩下构造、玄武岩及岩下构造)具有相互补充的作用。Gribenko等[31]构建了盐丘和储层模型,利用共轭梯度法比较了海洋大地电磁(Marine Magnetotelluric,MMT)和海洋可控源电磁(Marine Controlled Source Electromagnetic Method,MCSEM)数据单独反演和联合反演的结果。研究发现,MMT单独反演结果可以较好地反映盐丘位置,但对厚度很小的油气储层的刻画效果欠佳;MCSEM单独反演结果可以较好地恢复油气储层和盐丘的平面位置,但无法准确解释盐丘的深部界面;联合反演结果兼具MMT和MCSEM的优势,模型分辨率较高。Kumar等[32]研究发现,MT数据对于较厚的玄武岩层和其岩下构造识别能力较强,但对玄武岩薄层无法刻画;CSEM甚至可以恢复玄武岩薄层的横向长度。因而,联合MT和CSEM方法,可以准确地恢复玄武岩构造。③MMT有助于MCSEM压制空气波的影响[33]。受空气波的影响,MCSEM在对浅层油气目标进行探测时,数据反演误差大,联合反演MMT和MCSEM数据可以更准确确定目标位置,具有更高分辨率。
目前,CSEM和MT联合反演主要存在如下四个关键问题。
(1)非平面波效应与移动的多场源问题。人工源电磁法的应用包括陆上和海上。在陆上区域,地面可控源电磁勘探通常将发射源置于距离目标一定距离,如果源与接收点的距离不够远,CSAMT勘探会存在非平面波效应,对于面积较大的工区,基于平面波理论的解释结果会出现较大的误差[34],在构造比较复杂的情况下,会出现严重的阴影效应和复印效应,导致解释结果出现错误。目前地面电磁法已经发展了时频电磁法和广域电磁法,均不考虑非平面波校正问题,与此同时,移动源施工方法[35]也有助于有效克服CSAMT法的缺点。在MCSEM勘探中,发射与接收同线,移动的激发场源使得后续MT与MCSEM数据联合反演更为复杂。因此,开展CSEM与MT联合反演时,需充分考虑所用方法是否存在非平面波效应,以及如何处理多源移动的问题,才能确保反演结果的正确性。
(2)联合反演目标函数的构建和权重因子的选取。目前研究中对于CSEM和MT联合反演目标函数的构建大多沿用吉洪诺夫正则化的反演形式。虽然Liao等[36]在构建目标函数时将各个数据的目标函数做乘积处理,但这种构建方式的合理性尚存在争议。传统的构建形式时在目标函数中同时加入CSEM和MT的数据拟合项,这种方法依赖于两种方法数据权重因子的合理选取。联合反演目标函数为
| $ \varphi =\alpha {\varphi }_{{\boldsymbol{d}}_{\mathrm{M}\mathrm{T}}}^{\mathrm{M}\mathrm{T}}+\beta {\varphi }_{{\boldsymbol{d}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}}^{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}+{\lambda }_{\boldsymbol{m}}{\varphi }_{\boldsymbol{m}} $ | (7) |
式中:
第一种权重因子构建形式是Commer等[29]基于MT和CSEM的数据量提出的,这种构建形式无需确定式(7)中的
| $ \alpha =\sqrt{\frac{{N}_{\mathrm{M}\mathrm{T}}}{{N}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}}}\ \ \ \ {N}_{\mathrm{M}\mathrm{T}}\ge {N}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}} $ | (8) |
| $ \alpha =\sqrt{\frac{{N}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}}{{N}_{\mathrm{M}\mathrm{T}}}}\ \ \ \ {N}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}} > {N}_{\mathrm{M}\mathrm{T}} $ | (9) |
式中
对于MCSEM勘探,由于电性源是移动的,电磁场的振幅、相位随偏移距是变化的;MMT勘探利用的是与MCSEM相同的接收台站所采集的视电阻率和相位数据。因此,MCSEM的数据量远大于MMT的数据量,故式(9)的构建形式更常见。艾正敏等[34]采用这种构建方法取得了一定成效,但同时也发现这种加权系数的选择单纯基于数据量,没有考虑探测深度和探测精度及不同方法的分辨率存在差异等问题。
第二种权重因子构建形式也是Commer等[29]提出的,其依据是MT和CSEM数据拟合项对模型参数的梯度值
| $ \alpha =\sqrt{\frac{‖\nabla {\varphi }_{{\boldsymbol{d}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}}^{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}‖}{‖\nabla {\varphi }_{{\boldsymbol{d}}_{\mathrm{M}\mathrm{T}}}^{\mathrm{M}\mathrm{T}}‖}} $ | (10) |
这种权重因子考虑的是两种方法相对于初始模型的数据拟合项梯度,考虑了对整体数据拟合项的贡献,因而依赖于初始模型的选取。
上述两种构建形式均是在反演初始阶段就确定了,并不参与后续的反演迭代过程。
针对上述方法所构建的权重因子无法参与整个反演过程的问题,Meqbel等[35]提出了一种可以参与反演流程的权重因子,其计算公式为
| $ \left\{\begin{array}{l}\alpha =\frac{‖{\boldsymbol{J}}^{\mathrm{T}}\boldsymbol{r}‖}{‖{\boldsymbol{J}}_{\mathrm{M}\mathrm{T}}^{\mathrm{T}}{\boldsymbol{r}}_{\mathrm{M}\mathrm{T}}‖}\\ \beta =\frac{‖{\boldsymbol{J}}^{\mathrm{T}}\boldsymbol{r}‖}{‖{\boldsymbol{J}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}^{\mathrm{T}}{\boldsymbol{r}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}‖}\end{array}\right. $ | (11) |
| $ {\boldsymbol{J}}^{\mathrm{T}}\boldsymbol{r}={\boldsymbol{J}}_{\mathrm{M}\mathrm{T}}^{\mathrm{T}}{\boldsymbol{r}}_{\mathrm{M}\mathrm{T}}+{\boldsymbol{J}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}^{\mathrm{T}}{\boldsymbol{r}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}} $ | (12) |
| $ {\boldsymbol{r}}_{\mathrm{M}\mathrm{T}}={\boldsymbol{W}}_{\mathrm{M}\mathrm{T}}[{\boldsymbol{d}}_{\mathrm{M}\mathrm{T}}-\boldsymbol{f}{\left(\boldsymbol{m}\right)}_{\mathrm{M}\mathrm{T}}] $ | (13) |
| $ {\boldsymbol{r}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}={\boldsymbol{W}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}[{\boldsymbol{d}}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}-\boldsymbol{f}{\left(\boldsymbol{m}\right)}_{\mathrm{C}\mathrm{S}\mathrm{E}\mathrm{M}}] $ | (14) |
式中:
基于这种构建形式的反演思路是在每一次反演迭代时都要重新计算权重因子。Liao等[36]将这种构建形式应用于简化地热模型及实测数据,均得到了较好的反演结果。
(3)合理选择参与反演的数据。实际勘探中CSEM方法需要选取多个激发频率,获取由浅至深的电性结构,为了在联合反演中最大限度发挥MT和CSEM方法对深部、浅部成像的互补优势,CSEM数据频段的选取至关重要[37]。除此之外,选取CSEM的哪些电磁场分量参与反演也需慎重,关于这个问题相关的研究不多,同时讨论激发频率和参与反演电磁场分量选取的文献亦是鲜见。赵宁等[38]对不同激发频率下采集的CSEM数据与MT数据的反演结果进行对比,发现基于相对较低和较高发射频率得到的CSEM数据与MT数据的联合反演能够兼顾浅部和深部地层的成像,沿发射源极化方向的CSEM电场分量具有电场能量强的优势,反演结果的成像效果较好。但是,文献并未给出相应的理论解释及针对更复杂地质情况的选取依据和结论。
(4)提高联合反演计算效率。在反演问题中,特别是三维反演问题,需要进行大量的正演计算。现有的联合反演方法很少应用模拟退火法、遗传算法、粒子群算法等非线性反演方法,而这种全局最优化算法最关键的制约因素是计算消耗内存大、计算效率低。针对这种情况,Gribenko等[31]提出了一种“footprint”方法,并应用于CSEM和MT的联合反演。该方法在反演计算灵敏度矩阵时无需对整个目标域进行计算和存储,缩小了反演范围,一定程度上减少了运算时间。
1.3 地震数据与电磁数据联合反演电磁方法和地震方法对复杂或特殊地质构造成像时有各自的优点和局限性。与地震方法相比,利用电磁方法可以较好地识别目标的电阻率差异,对流体和岩性的辨识能力更强。但是,由于低频电磁波在地下的传播机制主要是波场的扩散和感应,对构造的分层识别效果不及地震方法。因此,电磁与地震数据的联合反演对于解决油气储层精细评估至关重要。
电磁—地震联合反演相关研究近年来得到广泛关注,但目前尚欠成熟。早期的地震—电磁联合反演研究主要有参考建模方面的联合和约束反演方面的联合。目前,参考建模已经进入实用阶段,主要做法是电磁参考地震建模,可明显提高反演结果的可靠性;地震解释过程中可参考电磁信息,对反射不清楚的地震模型进行修改,再进行偏移成像。关于约束反演方面的联合,则是利用地震剖面建立地层深度(厚度)模型,进行电阻率约束反演;另一方面,可利用电阻率剖面建立地震速度模型,为地震反射盲区成像提供依据。胡祖志等[39]结合上述思路构建了地震和电磁联合反演建模流程(图 1),反演流程主要分为两步:首先,以地震偏移结果得到的层位解释信息作为电磁数据反演的约束,进行电磁约束反演,得到符合地震解释的电阻率模型;然后,根据测井资料获得电阻率与速度之间的对应联系,通过电磁—地震约束反演得到电阻率剖面,修正速度模型,并进行迭代。当工区没有测井数据、无法获得较准确的物性关系时,则需基于速度与电阻率的经验公式[40-42]修正地震速度模型
| $ V=a{R}^{b} $ | (15) |

|
图 1 电磁与地震联合反演流程[39] |
式中:a、b为经验参数;R为电阻率;V为速度。显然这种方法要求电阻率与速度有较强的相关性,因此该方法只在特定的工区条件下适用,不是真正意义上的联合反演。
目前地震—电磁联合反演主要有两个方向:一是基于物理模型的联合反演;二是基于交叉梯度方法的联合反演。
基于物理模型的联合反演方法目前主要有两种。第一种是根据物性资料构建速度—电阻率相关的物理模型,进而构建岩石物理约束,为目标函数中的速度和电阻率拟合搭建一个桥梁,主要步骤如图 2所示。
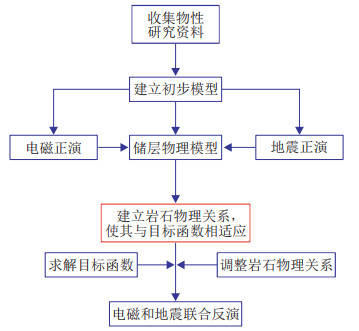
|
图 2 基于岩石物理约束的地震—电磁联合反演流程 |
图 2中关键步骤是利用物性的内在联系,实现相互补充、相互约束,降低反演的多解性。这类联合反演的目标函数通用形式为
| $ \varphi ({\sigma }_{2}, {V}_{\mathrm{P}})={\varphi }_{\mathrm{E}\mathrm{M}}\left({\sigma }_{2}\right)+{\varphi }_{\mathrm{s}\mathrm{e}\mathrm{i}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{c}}\left({V}_{\mathrm{P}}\right)+{\lambda }_{R}{\varphi }_{R}({\sigma }_{2}, {V}_{\mathrm{P}}) $ | (16) |
式中:
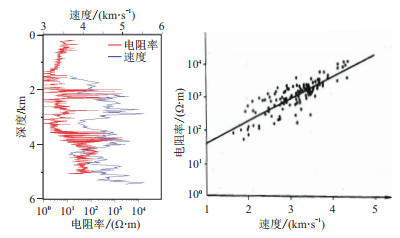
|
图 3 速度和电阻率测井曲线(左)及交会拟合曲线(右) |
基于物理模型的第二种联合反演方法是根据Archie公式和Gassmann公式构建地震和电磁数据与油气储层参数之间的关系[43-49],然后通过联合反演直接得到储层参数。这种方法的应用前提是目标工区已有比较完整的测井储层参数,能够为后续反演提供数据。这种联合反演的理论依据是:当研究对象为双相储层模型时,根据Archie公式,电导率对储层含水饱和度灵敏,对孔隙度则不甚灵敏;根据Gassmann公式,密度和纵波速度对孔隙度反应灵敏,但无法反映含水饱和度的变化[45]。因此,联合电磁数据和地震数据才能对油气储层参数做出合理的评估,这类问题的通用目标函数[46]为
| $ \varphi \left(\boldsymbol{m}\right)={\varphi }_{{\boldsymbol{d}}_{\mathrm{S}\mathrm{M}}}^{\mathrm{S}\mathrm{M}}\left(\boldsymbol{m}\right)+\gamma {\varphi }_{{\boldsymbol{d}}_{\mathrm{E}\mathrm{M}}}^{\mathrm{E}\mathrm{M}}\left(\boldsymbol{m}\right)+{\lambda }_{\mathrm{m}\mathrm{o}\mathrm{d}}{\varphi }_{\boldsymbol{m}}\left(\boldsymbol{m}\right) $ | (17) |
式中:上标/下标“SM”和“EM”分别代表地震方法和电磁方法;
| $ {\varphi }_{{\boldsymbol{d}}_{\mathrm{S}\mathrm{M}}}^{\mathrm{S}\mathrm{M}}\left(\boldsymbol{m}\right)=\frac{{{\eta }_{k}}^{2}}{2}\sum\limits_{k=1}^{{N}_{\mathrm{F}}^{\mathrm{S}\mathrm{M}}}\left\{\sum\limits_{i=1}^{{N}_{\mathrm{S}}^{\mathrm{S}\mathrm{M}}}\sum\limits_{j=1}^{{N}_{\mathrm{R}}^{\mathrm{S}\mathrm{M}}}{\left|{w}_{d;i, j, k}^{\mathrm{S}\mathrm{M}}[{\boldsymbol{d}}_{{}_{i, j, k}}^{\mathrm{S}\mathrm{M}}-{\boldsymbol{s}}_{{}_{i, j, k}}^{\mathrm{S}\mathrm{M}}(\boldsymbol{m}\left)\right]\right|}^{2}÷\right.\left.\sum\limits_{i=1}^{{N}_{\mathrm{S}}^{\mathrm{S}\mathrm{M}}}\sum\limits_{j=1}^{{N}_{\mathrm{R}}^{\mathrm{S}\mathrm{M}}}{\left|{w}_{d;i, j, k}^{\mathrm{S}\mathrm{M}}{\boldsymbol{d}}_{i, j, k}^{\mathrm{S}\mathrm{M}}\right|}^{2}\right\} $ | (18) |
| $ {\varphi }_{{\boldsymbol{d}}_{\mathrm{E}\mathrm{M}}}^{\mathrm{E}\mathrm{M}}\left(\boldsymbol{m}\right)=\frac{1}{2}\sum\limits_{k=1}^{{N}_{\mathrm{F}}^{\mathrm{E}\mathrm{M}}}\left\{\sum\limits_{i=1}^{{N}_{\mathrm{S}}^{\mathrm{E}\mathrm{M}}}\sum\limits_{j=1}^{{N}_{\mathrm{R}}^{\mathrm{E}\mathrm{M}}}{\left|{w}_{d;i, j, k}^{\mathrm{E}\mathrm{M}}[{\boldsymbol{d}}_{{}_{i, j, k}}^{\mathrm{E}\mathrm{M}}-{\boldsymbol{s}}_{{}_{i, j, k}}^{\mathrm{E}\mathrm{M}}(\boldsymbol{m}\left)\right]\right|}^{2}\right.÷\left.\sum\limits_{i=1}^{{N}_{\mathrm{S}}^{\mathrm{E}\mathrm{M}}}\sum\limits_{j=1}^{{N}_{\mathrm{R}}^{\mathrm{E}\mathrm{M}}}{\left|{w}_{d;i, j, k}^{\mathrm{E}\mathrm{M}}{\boldsymbol{d}}_{i, j, k}^{\mathrm{E}\mathrm{M}}\right|}^{2}\right\} $ | (19) |
式中:
| $ \gamma =\frac{{\varphi }_{\mathbf{d}}^{\mathrm{S}\mathrm{M}}\left({\boldsymbol{m}}_{0}\right)}{{\varphi }_{\mathbf{d}}^{\mathrm{E}\mathrm{M}}\left({\boldsymbol{m}}_{0}\right)} $ | (20) |
其中
杜润林等[42]和徐凯军等[46]利用上述方法构建储层理论模型,采用模拟退火并结合粒子群算法实现了一维MCSEM和地震数据的联合反演,无需计算繁琐的雅可比矩阵,反演结果较准确地预测了储层的孔隙度和饱和度;彭国民等[47]采用类似思路构建了归一化的联合反演目标函数,利用模拟退火法进行MCSEM与地震AVA(Amplitude Versus Angle)数据的联合反演,效果较好。
这类直接反演储层参数的联合反演严重依赖于稳定可靠的岩石物理关系,工业界广泛应用的Archie公式和Gassmann方程中的系数也需要根据实际测井资料确定,因而对于反演结果的准确性缺少评判依据。针对这个问题,Chen等[48-49]基于统计岩石物理模型和贝叶斯框架,利用马尔可夫链的蒙特卡洛抽样方法对储层参数预测值进行不确定性分析,结果表明联合CSEM数据和AVA数据可以降低对流体饱和度预测的不确定性,但这种方法对实测含噪数据的处理效果欠佳;同时,现有的大多数研究仅仅考虑了双相储层介质(油和水)情况,适用性差,对于同时含油、气和水的三相油气储层则需进一步讨论。
基于岩石物理关系的地震电磁联合反演存在很多问题,因此基于交叉梯度方法的联合反演自提出后就得到了广泛的应用和发展[50-59]。这种方法基于目标区域电导率剖面和地震剖面的结构相似性,即电导率变化与地震波速度变化方向是一致的。在联合反演的目标函数中引入交叉梯度函数来约束不同参数,相比岩石物理关系的耦合更普遍适用,反演效果良好,并形成了成熟的算法架构。图 4为体波走时与直流电阻率联合反演流程图。可见,交叉梯度方法在此流程中作用于地震速度模型和电磁电阻率模型,在反演中对模型值进行迭代更新。
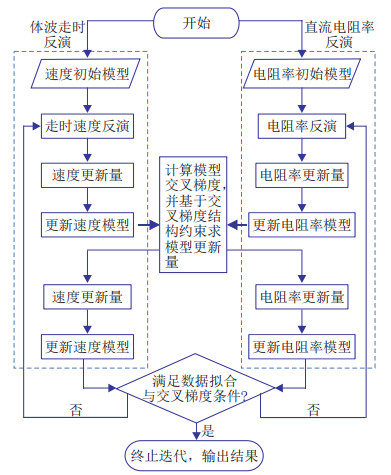
|
图 4 交叉梯度联合反演流程[60] |
交叉梯度函数的定义[52]为
| $ \boldsymbol{t}(x, y, z)=\nabla {\boldsymbol{m}}_{\mathrm{s}}(x, y, z)\times \nabla {\boldsymbol{m}}_{\mathrm{r}}(x, y, z) $ | (21) |
式中
(1)基于交叉梯度约束的联合反演的迭代流程。一种思路是将交叉梯度约束独立于地震和电磁各自的反演流程,只作用于整体的目标函数,其目标函数形式为
| $ \begin{array}{l}\varphi ({\boldsymbol{m}}_{\mathrm{s}}, {\boldsymbol{m}}_{\mathrm{r}})={\alpha }_{\mathrm{s}}{\varphi }_{\mathrm{s}}\left({\boldsymbol{m}}_{\mathrm{s}}\right)+{\beta }_{\mathrm{E}\mathrm{M}}{\varphi }_{\mathrm{E}\mathrm{M}}\left({\boldsymbol{m}}_{\mathrm{r}}\right)+\\ \ \ \ \ \ \ \ \ {\lambda }_{\mathrm{s}}{\varphi }_{{\boldsymbol{m}}_{\mathrm{s}}}\left({\boldsymbol{m}}_{\mathrm{s}}\right)+{\lambda }_{\mathrm{r}}{\varphi }_{{\boldsymbol{m}}_{\mathrm{r}}}\left({\boldsymbol{m}}_{\mathrm{r}}\right)+{\gamma }_{\mathrm{t}}‖\boldsymbol{t}({\boldsymbol{m}}_{\mathrm{s}}, {\boldsymbol{m}}_{\mathrm{r}})‖\end{array} $ | (22) |
式中:
这种约束方式真正实现了地震、电磁反演系统与交叉梯度结构约束的融合。高级等[58]基于阻尼最小二乘反演思路计算了含交叉梯度项的地震—电磁联合反演目标函数形式(式(22))下的灵敏度矩阵,该矩阵除了包括地震和电磁对应的灵敏度矩阵,还耦合了交叉梯度项,计算求解十分复杂,同时这种形式不利于选取合适的权重因子,很难平衡地震与电磁数据,甚至无法体现交叉梯度结构约束的作用。
之后,有学者提出了另一种思路,即交替式交叉梯度约束联合反演方法,其目标函数形式为
| $ {\varphi }_{\mathrm{s}\mathrm{e}\mathrm{i}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{c}}={\varphi }_{\mathrm{s}}\left({\boldsymbol{m}}_{\mathrm{s}}\right)+{\lambda }_{\mathrm{s}}{\varphi }_{{\boldsymbol{m}}_{\mathrm{s}}}\left({\boldsymbol{m}}_{\mathrm{s}}\right)+{\eta }_{\mathrm{s}\mathrm{e}\mathrm{i}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{c}}‖\boldsymbol{t}({\boldsymbol{m}}_{\mathrm{s}}, {\boldsymbol{m}}_{\mathrm{r}})‖ $ | (23) |
| $ {\varphi }_{\mathrm{E}}={\varphi }_{\mathrm{E}\mathrm{M}}\left({\boldsymbol{m}}_{\mathrm{r}}\right)+{\lambda }_{\mathrm{r}}{\varphi }_{{\boldsymbol{m}}_{\mathrm{r}}}\left({\boldsymbol{m}}_{\mathrm{r}}\right)+{\eta }_{\mathrm{E}\mathrm{M}}‖\boldsymbol{t}({\boldsymbol{m}}_{\mathrm{s}}, {\boldsymbol{m}}_{\mathrm{r}})‖ $ | (24) |
式中:
彭淼等[51]基于这种思路实现了大地电磁数据和地震走时资料的三维联合反演,并设计了单、双棱柱体模型进行理论模型测试,取得了较好的效果;齐嘉慧[52]利用交替交叉梯度反演实现了大地电磁与地震全波形数据的联合反演,讨论了权重系数的选取范围,获得了较单一类型数据反演更好的结果。
(2)交叉梯度约束的适用性。基于交叉梯度约束的联合反演研究大多是基于预构建的简单理论模型进行验证。当地质体的电阻率与速度的空间分布不一致时,基于交叉梯度的电磁—地震联合反演难以调整电阻率和速度模型的边界,使电阻率模型和速度模型有相似的物性结构[53]。针对这种情况,彭国民[53]提出了基于K均值聚类和回归分析技术的自适应修正方法,其本质是利用可信度高的物性模型修正另一种物性模型,可提高交叉梯度约束的准确度,但也存在一个问题,即K均值聚类算法依赖于聚类数目和初始聚类中心,因而该方法适应性不强。
综上所述,对于地震—电磁联合反演,无论是基于岩石物理模型约束还是基于交叉梯度约束都有其固有的限制条件,因此需要引入新思路和新方法进一步完善。
2 电磁联合反演的发展方向针对联合反演中对反演框架研究不足的问题,陈晓等[59]提出了一种新的联合反演框架:采用多次建模、综合约束和分步反演的策略,降低初始模型中人为因素的影响,一定程度上降低了反演结果对于初始模型的依赖性,但其方法仍局限于现有的反演研究思路。笔者认为未来电磁联合约束反演研究主要的发展方向包括以下几个方面。
(1)利用人工智能方法构建较精确的初始模型。人工智能方法在大地电磁反演中取得了一系列研究成果[60-69],但目前研究尚不成熟,对于联合反演而言,直接利用人工智能手段获取地层属性参数还为时尚早,但可以考虑结合人工智能手段获取更准确的初始模型。常规联合反演方法采用最优化方法寻找最优模型,例如高斯—牛顿法和非线性共轭梯度法,需要计算目标函数的梯度和灵敏度矩阵,同时依赖于初始模型的选取。如果初始模型选取不合理,得到的解往往只是局部最优解。而人工智能手段无需计算目标函数的梯度,对于大地电磁法而言,输入大地电磁的视电阻率和相位信息即可得到电阻率值。相对于传统反演方法,该方法在计算精度和稳定性上表现较好[63],可以很好地估计异常体的位置、横向维度和电阻率特征。人工智能方法可以为联合反演提供更准确的初始模型,进而提高联合反演的精度和可靠性。
(2)引入聚类分析和岩石物理信息构建约束模型。近二十年来,现有的正则化约束方法主要局限于先验测井资料约束、结构约束和岩石物理约束,这种全局的约束手段过于粗糙,特别是目标地域不适合采用结构约束方法、物性参数变化方向没有明显的相关性。岩石物性关系不明显时,现有约束方式的作用有限,甚至对反演结果造成误判,无法得到准确的地球物理剖面。Sun等[64]另辟蹊径,利用模糊C均值聚类方法将岩石物理资料看成模型参数域中的不同聚类单元,这样可以对特殊区域利用特定的岩石物理信息进行约束,提高精度的同时也在一定程度上减少了运算量。相对于传统的岩石物理约束,这种约束方式更适用于不同的岩性目标,能够改善现有岩石物理约束的经验公式准确度有限的问题。
(3)充分利用GPU并行计算进行联合反演。非线性的全局优化算法,例如模拟退火法、蒙特卡洛法、粒子群算法和量子遗传算法等,虽然无需依赖于初始模型的选取,也无需求解繁杂的敏感度矩阵,但往往占用计算内存巨大,在计算效率和收敛速度方面不占优势。研究[64]表明,随着模型复杂度的增加,内存和时间消耗呈指数级增长,因而复杂模型不适用于大规模的三维联合反演。杜润林等[65]基于并行计算、模拟退火法提出了MCSEM和地震数据联合反演方法,反演结果可以收敛到全局最优解,算法具有很好的并行性,明显提高了反演速度和精度。
(4)引入三维可视化与人机交互结合的反演思路。传统的联合反演流程大多采用迭代循环方式,程序开始运行后,直到整个反演流程结束才能恢复用户响应,无法实现用户对于可视化交互操作和反演进程的掌握和控制[66]。张晨[67]利用可拓展拓扑结果的模型构建技术和模型体可视化交互编辑技术,提出了一种三维可视化与人机交互结合的反演思路,不但可以实时查看反演的中间结果,根据结果的好坏实时地调整权重值等反演参数,还可在反演过程中对待反演的模型实时改变形状、大小和位置,实现了反演流程的人机交互性和实时性。对于联合反演,通过上述思路可以实时调整不同方法之间的权重,进而控制整个联合反演进程。
(5)发展基于多物理场同步采集数据仪器的联合反演。国内外关于联合采集技术方面的研究,特别是海洋环境下地球物理数据联合采集几乎为空白,故联合反演研究对于实测资料的应用有限,仅在理论层面上论述联合反演的可能性。资源勘探的重点逐渐转向海洋,这是一个必然的趋势。海洋环境为多物理场一体化采集仪器及方法的发展提供了有利条件。多物理场传感器可搭载在一套水下采集系统中,但目前电磁—地震一体化仪器处于研发阶段。这种基于多物理场同步采集的数据必然为电磁—地震联合反演提供最佳的数据基础。同时,基于电磁—地震一体化仪器的数据采集可保证不同地球物理数据的信息同步及噪声类型和量级的一致性,这为震电效应嵌入电磁效应与振动波机理相结合的耦合方程、进而联合利用电磁、地震方法解决深层次地质问题提供了数据基础。
3 认识与展望综上所述,由于不同的地球物理方法都有其优、缺点,所以应尽可能收集多种地球物理信息,从不同角度研究地质目标,联合多种方法进行反演,最终获得地下结构更客观、更准确的地质特征,减少反演的多解性。因此,多信息、多方法结合的电磁联合约束反演受到业内学者的关注和重视,相关研究取得长足进步。从最初结合地震和测井信息的建模约束,到天然源与人工源、电磁数据与地震数据的多方法联合反演,推进了电磁探测方法走向全面应用。但无论是何种约束联合反演方法,其解决地质问题的能力都是有限的,需结合实际需求合理选择约束联合方法,冗余的约束联合反演方法往往起不到最佳的成像效果。因而,需充分发挥先验信息,挖掘各种地球物理数据的优势,利用先进的数据处理方法和手段,结合现有的高性能计算方法,才能让联合反演真正为生产实践赋能,充分发挥其方法优势。
| [1] |
何展翔. 电磁勘探技术的机遇与挑战及发展方向[J]. 物探化探计算技术, 2019, 41(4): 433-447. HE Zhanxiang. Opportunities, challenges and development directions of electromagnetic exploration today[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2019, 41(4): 433-447. DOI:10.3969/j.issn.1001-1749.2019.04.01 |
| [2] |
赵国泽, 何展翔, 魏文博. 地球电磁学科的发展现状和展望[M]. 北京: 中国科学技术出版社, 2009.
|
| [3] |
赵国泽, 陈小斌, 汤吉. 中国地球电磁法新进展和发展趋势[J]. 地球物理学进展, 2007, 22(4): 1171-1180. ZHAO Guoze, CHEN Xiaobin, TANG Ji. Advanced geo-electromagnetic methods in China[J]. Progress in Geophysics, 2007, 22(4): 1171-1180. |
| [4] |
CAGNIARD L. Basic theory of the magnetotelluric method of geophysical prospecting[J]. Geophysics, 1953, 18(3): 605-635. DOI:10.1190/1.1437915 |
| [5] |
SANDBERG S K, HOHMANN G W. Controlled-source audiomagnetotellurics in geothermal exploration[J]. Geophysics, 1982, 47(1): 100-116. DOI:10.1190/1.1441272 |
| [6] |
薛国强, 李貅, 底青云. 瞬变电磁法理论与应用研究进展[J]. 地球物理学进展, 2007, 22(4): 1195-1200. XUE Guoqiang, LI Xiu, DI Qingyun. The progress of TEM in theory and application[J]. Progress in Geophysics, 2007, 22(4): 1195-1200. |
| [7] |
中国石油天然气集团公司. 人工源时间频率电磁测深方法[P]. CN200310050098.3, 2003.
|
| [8] |
何展翔, 胡祖志, 王志刚, 等. 时频电磁(TFEM)技术: 数据联合约束反演[J]. 石油地球物理勘探, 2020, 55(4): 898-905. HE Zhanxiang, HU Zuzhi, WANG Zhigang, et al. Time-frequency electromagnetic (TFEM) technique: step-by-step constraint inversion based on artificial fish swarm algorithm[J]. Oil Geophysical Prospecting, 2020, 55(4): 898-905. |
| [9] |
敬荣中. 地球物理非线性联合反演方法研究[D]. 湖南长沙: 中南大学, 2002.
|
| [10] |
杨文采. 地球物理反演的理论与方法[M]. 北京: 地质出版社, 1997.
|
| [11] |
王家映. 地球物理反演理论[M]. 湖北武汉: 中国地质大学出版社, 1998.
|
| [12] |
厉波. 测井约束反演中利用声波测井进行精确时深转换[J]. 内蒙古石油化工, 2005, 31(11): 114-115. LI Bo. Accurate time-depth transformation using sonic logging in log-constraint inversion[J]. Inner Mongolia Petrochemical Industry, 2005, 31(11): 114-115. |
| [13] |
谢万学, 王永刚, 邢文军. 井孔与地面地震数据联合反演方法综述[J]. 勘探地球物理进展, 2006, 29(1): 1-6. XIE Wanxue, WANG Yonggang, XING Wenjun. Review of joint inversion methods for borehole and surface seismic data[J]. Progress in Exploration Geophysics, 2006, 29(1): 1-6. |
| [14] |
聂凯轩, 陆正元, 冯斌. 测井约束反演技术在LZ21-4构造带储盖层综合分析中的应用[J]. 石油地球物理勘探, 2007, 42(1): 98-101. NIE Kaixuan, LU Zhengyuan, FENG Bin. Application of log-constraint inversion technique in comprehensive analysis of reservoir and cap in LZ21-4 structural belt[J]. Oil Geophysical Prospecting, 2007, 42(1): 98-101. |
| [15] |
谭荣彪, 李瑞, 李珂泂, 等. 井—震约束反演在薄互层复杂构造地区的应用[J]. 物探化探计算技术, 2008, 30(1): 52-57. TAN Rongbiao, LI Rui, LI Kejiong, et al. The Application of logging-seismic constrained inversion in thin interbed complex structure area[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2008, 30(1): 52-57. |
| [16] |
连太炜, 樊洪海, 于玲玲. 测井约束地震反演在地层孔隙压力预测中的应用[J]. 西部探矿工程, 2009, 21(6): 64-65. LIAN Taiwei, FAN Honghai, YU Lingling. Application of the formation pore pressure prediction by log-constraint seismic inverison[J]. West-China Exploration Engineering, 2009, 21(6): 64-65. |
| [17] |
史小东. 基于高频重建的井电匹配, 震电约束反演研究[D]. 北京: 中国地质大学(北京), 2010.
|
| [18] |
孟翠贤, 宋景明, 王永涛, 等. 电法约束反演在目标勘探中的应用[C]. 中国地球物理学会第二十一届年会论文集, 2005, 632.
|
| [19] |
杨辉, 王永涛, 王家林, 等. 大地电磁测深拟二维模拟退火约束反演[J]. 海相油气地质, 2001, 6(1): 47-52. YANG Hui, WANG Yongtao, WANG Jialin, et al. Magnetotelluric sounding restriction inversion using 2-D simulated annealing method[J]. Marine Origin Petroleum Geology, 2001, 6(1): 47-52. |
| [20] |
杨辉, 王永涛, 戴世坤, 等. 带地形的MT多参量二维快速模拟退火约束反演[J]. 石油地球物理勘探, 2003, 38(2): 213-217. YANG Hui, WANG Yongtao, DAI Shikun, et al. 2-D inversion of magnetotelluric (MT) multi-parameters with topography using fast simulated annealing[J]. Oil Geophysical Prospecting, 2003, 38(2): 213-217. DOI:10.3321/j.issn:1000-7210.2003.02.023 |
| [21] |
中国石油天然气集团公司. 一种减小电磁测深反演结果非唯一性的方法[P]. CN201310397390.6, 2013.
|
| [22] |
石艳玲, 魏强, 胡祖志, 等. 井震约束下的电磁反演技术在深层勘探中应用初探[C]. 2016中国地球科学联合学术年会论文集, 2016, 2192-2194.
|
| [23] |
王有涛, 何展翔, 陈学国, 等. 基于物性分析建模的时频电磁反演及储层评价——以准北缘石北构造带为例[J]. 石油地球物理勘探, 2022, 57(6): 1489-1497. WANG Youtao, HE Zhanxiang, CHEN Xueguo, et al. Time-frequency electromagnetic data inversion and reservoir evaluation based on physical property analysis modeling: a case study of the Shibei structural belt on the northern margin of the Junggar Basin[J]. Oil Geophysical Prospecting, 2022, 57(6): 1489-1497. |
| [24] |
石艳玲, 黄文辉, 魏强, 等. 电磁井震约束反演识别川中深层裂谷[J]. 石油地球物理勘探, 2016, 51(6): 1233-1240. SHI Yanling, HUANG Wenhui, WEI Qiang, et al. Deep rift identification with MT inversion constrained by shallow logging and seismic data[J]. Oil Geophysical Prospecting, 2016, 51(6): 1233-1240. |
| [25] |
王传武, 李术才, 刘斌, 等. 基于参考模型的三维电阻率约束反演方法研究[J]. 岩土工程学报, 2016, 38(9): 1685-1694. WANG Chuanwu, LI Shucai, LIU Bin, et al. 3D constrained electrical resistivity inversion method based on reference model[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(9): 1685-1694. |
| [26] |
刘斌, 聂利超, 李术才, 等. 三维电阻率空间结构约束反演成像方法[J]. 岩石力学与工程学报, 2012, 31(11): 2258-2268. LIU Bin, NIE Lichao, LI Shucai, et al. 3D electrical resistivity inversion tomography with spatial structural constraint[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(11): 2258-2268. |
| [27] |
DA SILVA PINHEIRO J L, SILVA M W C, DA PIEDADE A A, et al. 3D joint inversion of MMT and MCSEM data[C]. 17th International Congress of the Brazilian Geophysical Society, Rio de Janeiro, Brazil, 16-19 August 2021, 1-7.
|
| [28] |
RODI W, MACKIE R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 66(1): 174-187. |
| [29] |
COMMER M, NEWMAN G A. Three-dimensional controlled-source electromagnetic and magnetotelluric joint inversion[J]. Geophysical Journal International, 2009, 178(3): 1305-1316. |
| [30] |
MACKIE R, DONALD WATTS M, RODI W. Joint 3D inversion of marine CSEM and MT data[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 574-578.
|
| [31] |
GRIBENKO A V, ZHDANOV M S. Joint 3D inversion of marine CSEM and MT data[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 552-556.
|
| [32] |
KUMAR K, BORGOHAIN D, MORTEN J P, et al. Offshore sub-basalt exploration using CSEM and MT[C]. International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 2014, IPTC-17917-MS.
|
| [33] |
SASAKI Y. 3D inversion of marine CSEM and MT data: an approach to shallow-water problem[J]. Geophysics, 2013, 78(1): E59-E65. |
| [34] |
艾正敏, 叶益信, 汤文武, 等. 基于非结构三角网格的海洋CSEM和MT二维联合反演研究[J]. 物探与化探, 2021, 45(1): 149-158. AI Zhengmin, YE Yixin, TANG Wenwu, et al. A test study of 2D joint inversion of marine CSEM and MT based on unstructured triangular grid[J]. Geophysical and Geochemical Exploration, 2021, 45(1): 149-158. |
| [35] |
MEQBEL N, RITTER O. Joint 3D inversion of multiple electromagnetic datasets[J]. Geophysical Prospecting, 2015, 63(6): 1450-1467. |
| [36] |
LIAO W, PENG R, HU X, et al. 3-D joint inversion of MT and CSEM data for imaging a high-temperature geothermal system in Yanggao region, Shanxi province, China[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-13. |
| [37] |
ABUBAKAR A, LI M, LIU J, et al. Simultaneous joint inversion of MT and CSEM data using a multiplicative cost function[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 719-723.
|
| [38] |
赵宁, 王堃鹏, 秦策. 海洋CSEM和MT一维联合反演研究[J]. 物探化探计算技术, 2014, 36(2): 148-151. ZHAO Ning, WANG Kunpeng, QIN Ce. Research on 1-D joint inversion of marine CSEM and MT[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2014, 36(2): 148-151. |
| [39] |
胡祖志, 刘雪军, 杨利根, 等. 电磁与地震联合反演改善高陡构造成像[C]. 中国石油学会2019年物探技术研讨会论文集, 2019, 1012-1015.
|
| [40] |
DE STEFANO M, GOLFRE ANDREASI F, RE S, et al. Multiple-domain, simultaneous joint inversion of geophysical data with application to subsalt imaging[J]. Geophysics, 2011, 76(3): R69-R80. |
| [41] |
GAO G, ABUBAKAR A, HABASHY T M. Joint petrophysical inversion of electromagnetic and full-waveform seismic data[J]. Geophysics, 2012, 77(3): WA3-WA18. |
| [42] |
杜润林, 张晓波, 刘李伟, 等. 海洋可控源电磁和地震联合反演储层参数研究[C]. 中国石油学会2019年物探技术研讨会论文集, 2019, 1009-1011.
|
| [43] |
HOVERSTEN G M, CASSASSUCE F, GASPERIKOVA E, et al. Direct reservoir parameter estimation using joint inversion of marine seismic AVA and CSEM data[J]. Geophysics, 2006, 71(3): C1-C13. |
| [44] |
ABUBAKAR A, GAO G, HABASHY T M, et al. Joint inversion approaches for geophysical electromagnetic and elastic full-waveform data[J]. Inverse Problems, 2012, 28(5): 055016. |
| [45] |
DU Z, MACGREGOR L M. Reservoir characterization from joint inversion of marine CSEM and seismic AVA data using genetic algorithms: a case study based on the Luva gas field[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 737-741.
|
| [46] |
徐凯军, 杜润林, 刘展. 海洋可控源电磁与地震一维联合储层参数反演[J]. 石油地球物理勘探, 2016, 51(1): 197-203. XU Kaijun, DU Runlin, LIU Zhan. Joint reservoir parameter inversion of 1D marine controlled source electromagnetic and seismic data[J]. Oil Geophysical Prospecting, 2016, 51(1): 197-203. |
| [47] |
彭国民, 徐凯军, 杜润林, 等. MCSEM和地震AVA数据联合反演储层物性[J]. 石油地球物理勘探, 2018, 53(5): 1110-1116. PENG Guomin, XU Kaijun, DU Runlin, et al. Reservoir petrophysical parameter estimation with joint inversion of MCSEM and seismic AVA data[J]. Oil Geophysical Prospecting, 2018, 53(5): 1110-1116. |
| [48] |
CHEN J, HOVERSTEN G M, VASCO D, et al. A Bayesian model for gas saturation estimation using marine seismic AVA and CSEM data[J]. Geophysics, 2007, 72(2): WA85-WA95. |
| [49] |
CHEN J, HOVERSTEN G M. Joint inversion of marine seismic AVA and CSEM data using statistical rock-physics models and Markov random fields[J]. Geophysics, 2012, 77(1): R65-R80. |
| [50] |
GALLARDO L A, MEJU M A. Joint two‐dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints[J]. Journal of Geophysical Research (Solid Earth), 2004, 109(B3): B03311. |
| [51] |
彭淼, 谭捍东, 姜枚, 等. 基于交叉梯度耦合的大地电磁与地震走时资料三维联合反演[J]. 地球物理学报, 2013, 56(8): 2728-2738. PENG Miao, TAN Handong, JIANG Mei, et al. Three-dimensional joint inversion of magnetotelluric and seismic travel time data with cross-gradient constraints[J]. Chinese Journal of Geophysics, 2013, 56(8): 2728-2738. |
| [52] |
齐嘉慧. 基于交叉梯度结构约束的大地电磁和地震全波形数据交替联合反演[D]. 吉林长春: 吉林大学, 2020. QI Jiahui. Joint Iinversion of Alternating Magnetotelluric and Full-waveform Seismic Data Based on Cross-gradient Structure Constraints[D]. Jilin University, Changchun, Jilin, 2020. |
| [53] |
彭国民. 基于交叉梯度的CSEM和地震联合反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2019.
|
| [54] |
恩和得力海, 冯晅, 孙成城, 等. 大地电磁与地震联合反演在深部金属矿模型中的应用[C]. 2017中国地球科学联合学术年会论文集(五十)——专题104: 深部矿产资源评价理论方法, 2017, 15-16.
|
| [55] |
GALLARDO L A, MEJU M A. Joint two-dimensional cross-gradient imaging of magnetotelluric and seismic traveltime data for structural and lithological classification[J]. Geophysical Journal International, 2007, 169(3): 1261-1272. |
| [56] |
GALLARDO L A. Multiple cross-gradient joint inversion for geospectral imaging[J]. Geophysical Research Letters, 2007, 34(19): L19301. |
| [57] |
GALLARDO L A, MEJU M A. Characterization of heterogeneous near‐surface materials by joint 2D inversion of DC resistivity and seismic data[J]. Geophysical Research Letters, 2003, 30(13): 1658. |
| [58] |
高级, 张海江. 基于交叉梯度交替结构约束的二维地震走时与全通道直流电阻率联合反演[J]. 地球物理学报, 2016, 59(11): 4310-4322. GAO Ji, ZHANG Haijiang. Two-dimensional joint inversion of seismic velocity and electrical resistivity using seismic travel times and full channel electrical measurements based on alternating cross-gradient structural constraint[J]. Chinese Journal of Geophysics, 2016, 59(11): 4310-4322. |
| [59] |
陈晓, 于鹏, 邓居智, 等. 地球物理联合反演新框架研究[J]. 石油地球物理勘探, 2017, 52(4): 851-858, 883. CHEN Xiao, YU Peng, DENG Juzhi, et al. A new framework for geophysical joint inversion[J]. Oil Geophysical Prospecting, 2017, 52(4): 851-858, 883. |
| [60] |
ISAEV I, OBORNEV E, OBORNEV I, et al. Neural network recognition of the type of parameterization scheme for magnetotelluric data[C]. Advances in Neural Computation, Machine Learning, and Cognitive Research Ⅱ, Springer, Cham, 2018, 176-183.
|
| [61] |
CONWAY D, ALEXANDER B, KING M, et al. Inverting magnetotelluric responses in a three-dimensional earth using fast forward approximations based on artificial neural networks[J]. Computers & Geosciences, 2019, 127: 44-52. |
| [62] |
LIU W, XI Z, WANG H, et al. Two-dimensional deep learning inversion of magnetotelluric sounding data[J]. Journal of Geophysics and Engineering, 2021, 18(5): 627-641. |
| [63] |
ALYOUSUF T, YAOGUO L. Inversion using adaptive physics-based neural network: application to magnetotelluric inversion[C]. International Petroleum Technology Conference, Riyadh, Saudi Arabia, 2022, IPTC-22504-EA.
|
| [64] |
SUN J, LI Y. Joint inversion of multiple geophysical data using guided fuzzy C-means clustering[J]. Geophysics, 2016, 81(3): ID37-ID57. |
| [65] |
杜润林, 刘李伟, 孙建伟. 基于GPU的海洋可控源电磁和地震联合反演[C]. 2020年中国地球科学联合学术年会论文集, 2020, 1566-1566.
|
| [66] |
郑元满, 姚长利, 张晨. 重磁三维自动反演软件系统的分析与设计[J]. 现代地质, 2012, 26(6): 1225-1230. ZHENG Yuanman, YAO Changli, ZHANG Chen. Design a software for 3-D automatic gravity and magnetic inversion[J]. Geoscience, 2012, 26(6): 1225-1230. |
| [67] |
张晨. 磁异常及其梯度多参量联合反演及三维人机交互建模研究[D]. 北京: 中国地质大学(北京), 2013.
|
| [68] |
杨大方, 翁爱华, 杨悦, 等. 一个CSAMT非平面波效应的实例及数值分析[J]. 地质与勘探, 2015, 51(1): 151-156. YANG Dafang, WENG Aihua, YANG Yue, et al. An example of non-plane wave effect in CSAMT and numerical analysis[J]. Geology and Exploration, 2015, 51(1): 151-156. |
| [69] |
徐凤姣, 严良俊, 谢兴兵, 等. 移动可控源电磁法成像方法与应用[C]. 2014年中国地球科学联合学术年会论文集, 2014, 302-305.
|



 何展翔,广东省深圳市南山区学苑大道1088号南方科技大学地球与空间科学系,518055。Email:
何展翔,广东省深圳市南山区学苑大道1088号南方科技大学地球与空间科学系,518055。Email: