水力压裂指石油和天然气开发过程中利用水压力在岩层中压开新的裂缝或者对原有裂缝形态进行改造[1]。油气井的产能一般由储集层体积(SRV)决定,SRV主要取决于裂缝的数量及裂缝形态。因此,了解水力裂缝形态对于非常规油田开发非常关键,是评估压裂、完井及最大产量油藏管理最佳配置的关键因素。同时,可根据水力裂缝形态观测结果评估油气产能设计,进一步规划加密井轨迹、缩小井间距离。
随着油气勘探和开发的深入,了解地下油气储层详细结构的需求也越来越迫切。水力压裂使油气勘探和生产扩展到页岩储层及致密地层,建立油气从页岩及致密地层流向井筒的通道,为油气资源的开发提供必要的条件。压裂技术日新月异,但这一过程中还有很多信息未知,其中最主要的是水力裂缝中支撑剂的分布。支撑剂是一种抗压性足够大的球形颗粒,其作用是形成支撑覆盖层,阻止裂缝的闭合。通常情况下,支撑剂选用石英颗粒(砂子),其电导率可以忽略。应用电磁法监测支撑裂缝分布的前提是使用导电支撑剂替代传统支撑剂填充裂缝区域,以产生导电裂缝。导电支撑剂可有效提升电磁参数对比度,有利于对支撑裂缝几何形状进行监测。对于水力压裂裂缝,其监测系统由发射线圈和接收线圈组成(可以是单发—单收、单发—多收或多发—多收)。发射线圈所发射的电磁场在通过填充导电支撑剂的裂缝时,会产生次生(感应)电磁场,利用接收线圈可获取目标区域的电磁场信息。通过分析该电磁场可深入了解裂缝内总传导体的具体电磁表征,进而确定水力压裂裂缝的几何形态。
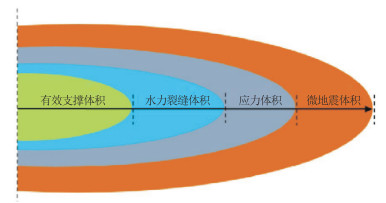
目前,微地震是水力压裂监测的另一项重要手段,其原理是通过在地面或者邻井中布置检波器,监测压裂过程中岩石剪切破裂诱发的地震波,据此分析、描述压裂过程中裂缝的几何形状和空间分布。但是,该技术成本高,后续数据处理复杂[2-3]。由于水力压裂诱导的微地震能量较小,其高频成分极易衰减,因此水力压裂诱导的微地震波在地层中的传播距离很大程度依赖于监测地区的岩石性质。为了对微地震震源进行精确定位,需要对压裂井和监测井所在空间建立准确的地层速度模型。然而,每个压裂阶段都会发生应力重新定向,压裂作业期间的速度分布特征也会随之发生变化,影响震源定位的精度[4-6]。由于记录到的地震事件来源于岩石破碎区域,微地震监测技术只能模拟水力压裂网络和储层改造后的SRV,其值远大于有效支撑体积EPV(图 1和图 2)。微地震监测记录中的无效信息来源于不含支撑剂的裂缝和非水力连接区域的岩石应力释放,在返排之后,这两个因素引起的地震事件不会促成烃的流动[7]。因此,迫切需要一种新方法,为水力裂缝监测提供更准确和可靠的技术支持。电磁监测技术凭借成本低、应用条件广泛等优势,成为水力裂缝监测的重要手段之一。
|
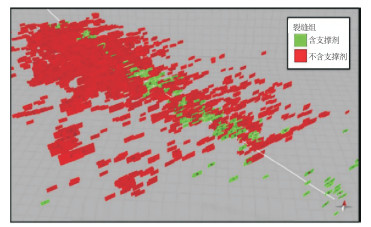
图 2 模拟裂缝斜视图[10] 裂缝方位根据震源机制获得。 |
水力裂缝电磁模拟在地球物理勘探中发挥着重要的作用。电法是种类最多、应用最广的地球物理探测方法之一,主要方法分支包括交流电法(也称电磁法)和直流电法两大类[11-12]。电磁方法利用交变电磁场对具有导电性或导磁性的物体产生感应作用或辐射作用,形成二次电磁(感应)场,通过观测二次电磁场分析被感应的或被辐射的物体。
本文首先介绍水力裂缝电磁探测技术的基本原理和方法,再对水力裂缝主要几何形态进行分类和总结,并简要分析水力裂缝电磁数值分析方法和监测仪器的优势和不足,最后对国内外基于电磁方法开展的水力裂缝探测技术进行总结分析。
2 水力裂缝电磁探测技术概述 2.1 电磁感应探测原理基于交流电的互感原理,发射线圈中的交变电流会在接收线圈中产生感应电动势,电磁感应测井利用的即是此原理[11, 13]。感应测井法将发射线圈和接收线圈都置于井中,发射线圈中的交变电流必然会在井周地层中产生感应涡流,这个涡流又会对接收线圈的感应电动势产生影响,因此感应电动势与涡流的强度有关,即与地层的电导率有关,其原理见图 3。发射线圈T和接收线圈R共同组成线圈系,线圈轴与井轴方向一致,即沿z轴。T与R的距离L称为线圈距。假定井周介质的岩性以z轴为旋转轴对称,则井周介质可看做由多个截面积为drdz的单元环组成,这里r表示介质单元环半径。令
| $ \mathrm{d}{U}_{\mathrm{R}}=-\frac{{\omega }^{2}{\mu }^{2}{n}_{\mathrm{T}}{n}_{\mathrm{R}}{S}_{\mathrm{R}}^{2}I}{4\mathrm{{\rm{ \mathsf{ π} }} }L}\cdot \frac{L}{2}\cdot \frac{{r}^{3}}{{R}_{\mathrm{T}}^{3}{R}_{\mathrm{R}}^{3}}\sigma \mathrm{d}r\mathrm{d}z $ | (1) |

|
图 3 电磁感应测井原理示意图 |
式中:
电磁感应探测方法的数据基础是均匀导电介质中的感应探头所记录的数据。如图 4所示,感应探头由两个线圈构成,一个线圈是初级交变磁场的发射源,另一个线圈是测量电动势和磁场的接收器。多数情况下,线圈的尺寸
| $ \left\{\begin{array}{l}\boldsymbol{{M}}={\boldsymbol{{M}}}_{0}{\mathrm{e}}^{-\mathrm{i}\omega t}\\ {\boldsymbol{{M}}}_{0}={S}_{\mathrm{R}}{n}_{\mathrm{R}}I\\ \omega =2\mathrm{{\rm{ \mathsf{ π} }} }f\end{array}\right. $ | (2) |

|
图 4 感应探头示意图 |
式中:M0表示磁矩;f表示频率。
在均匀介质条件下,令球坐标
| $ \boldsymbol{E}_{\varphi }=\frac{\mathrm{i}\omega \mu \boldsymbol{{M}}}{4\mathrm{{\rm{ \mathsf{ π} }} }{R}^{2}}{\mathrm{e}}^{\mathrm{i}kR}(1-\mathrm{i}kR)\mathrm{s}\mathrm{i}\mathrm{n}\theta $ | (3) |
| $ \boldsymbol{H}_{R}=\frac{2\boldsymbol{{M}}}{4\mathrm{{\rm{ \mathsf{ π} }} }{R}^{3}}{\mathrm{e}}^{\mathrm{i}kR}(1-\mathrm{i}kR)\mathrm{c}\mathrm{o}\mathrm{s}\theta $ | (4) |
| $ \boldsymbol{H}_{\theta }=\frac{\boldsymbol{{M}}}{4\mathrm{{\rm{ \mathsf{ π} }} }{R}^{3}}{\mathrm{e}}^{\mathrm{i}kR}(1-\mathrm{i}kR-{k}^{2}{R}^{2})\mathrm{s}\mathrm{i}\mathrm{n}\theta $ | (5) |
式中波数
采用双线圈仪器监测裂缝时,接收器记录的感应电动势U在实际计算中可通过对穿透线圈的磁场进行面积分求得
| $ {U}_{\mathrm{R}}=-{\int }_{{S}_{\mathrm{R}}}\mathrm{R}\mathrm{e}\left(\mathrm{i}\omega {\mu }_{0}{n}_{R}{\boldsymbol{H}}_{R}\right)\mathrm{d}S $ | (6) |
式中
| $ \nabla \times \nabla \times \boldsymbol H+\mathrm{i}\omega {\mu }_{0}\sigma \boldsymbol H=\nabla \times \boldsymbol{J}_{\mathrm{s}} $ | (7) |
式中
| $ \widehat{\boldsymbol{n}}\times \boldsymbol H=0 $ | (8) |
根据问题约束,可以进一步获得式(7)的解。
以上介绍的感应测井理论主要是确定由发射器—接收器测量的准静态电磁场与裂缝介质的基本关系[18-20],场问题可用以下方式来表述。
频域中,假设介电常数为
| $ \begin{array}{l}\nabla \times \boldsymbol E+\mathrm{i}\omega \mu \boldsymbol H=0\\ \nabla \times \boldsymbol H-\left(\sigma +\mathrm{i}\omega \varepsilon \right)\boldsymbol E=\boldsymbol{J}_{\mathrm{s}}\end{array} $ | (9) |
对含导电支撑剂裂缝的目标体引入等效电流源,根据电磁场理论,总场等于入射场与散射场之和,目标边界上总场是连续的这一边界条件,建立频域相关电磁方程求解裂缝区域的电磁场
| $ \boldsymbol{H}_{\mathrm{总}\mathrm{场}}=\boldsymbol{H}_{\mathrm{i}\mathrm{n}\mathrm{c}}^{\mathrm{T}}+{\boldsymbol{H}}_{\mathrm{s}\mathrm{c}\mathrm{a}}^{\mathrm{b}}+\boldsymbol{H}_{\mathrm{s}\mathrm{c}\mathrm{a}}^{\mathrm{f}} $ | (10) |
式中:
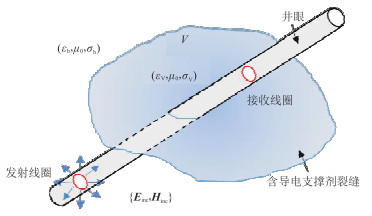
基于电磁方法探测含导电支撑剂水力裂缝的装置见图 5[22-23]。该装置沿井筒移动,发射信号的同时接收电磁场。发射器(线圈)可建模为一个外加源,用于激发时谐电磁场;接收器(线圈)记录的电磁场主要是发射器产生的入射场
| $ \boldsymbol{E}_{\mathrm{s}\mathrm{c}\mathrm{a}}\left(\boldsymbol{a}\right)=\underset{V}{\overset{}{\iiint }}-\mathrm{i}\omega {\mu }_{0}g\left(L\right)\boldsymbol{J}_{V}\left({\boldsymbol{a}}_{\mathrm{S}}\right)+\frac{\nabla g\left(L\right)}{\mathrm{i}\omega {\tilde{\varepsilon }}_{\mathrm{b}}}\nabla \text{'}\cdot \boldsymbol{J}_{V}\left({\boldsymbol{a}}_{\mathrm{S}}\right)\mathrm{d}{v}_{\mathrm{S}} $ |
| $ \boldsymbol{H}_{\mathrm{s}\mathrm{c}\mathrm{a}}\left(\boldsymbol{a}\right)=\nabla \times \underset{V}{\overset{}{\iiint }}g\left(L\right)\cdot \boldsymbol{J}_{V}\left({\boldsymbol{a}}_{S}\right)\mathrm{d}{v}_{\mathrm{S}} $ | (11) |
|
图 5 均匀页岩地层中水力裂缝电磁探测示意图 下标“b”和“v”分别表示背景和含导电支撑剂的空间。 |
式中:
| $ \boldsymbol{J}_{V}\left(\boldsymbol{a}\right)=\mathrm{i}\omega ({\tilde{\varepsilon }}_{V}-{\tilde{\varepsilon }}_{\mathrm{b}})\left[{\boldsymbol{E}}_{\mathrm{i}\mathrm{n}\mathrm{c}}\right(\boldsymbol{a})+{\boldsymbol{E}}_{\mathrm{s}\mathrm{c}\mathrm{a}}(\boldsymbol{a}\left)\right] \boldsymbol{a}\in V $ | (12) |
基于水力压裂裂缝的散射场,探测装置可设计多种接收方式,分析裂缝的方位、长度、宽度、有效支撑体积、倾斜角度或旋转角度等空间信息。
2.2 水力裂缝主要几何形态水力裂缝电磁探测方法的工作基础是含有导电支撑剂的裂缝与周围介质存在电性、磁性差异,因而可利用电导率、磁化率、介电常数等物理参数表征裂缝的几何特征。目前,主要有以下三类裂缝模型。
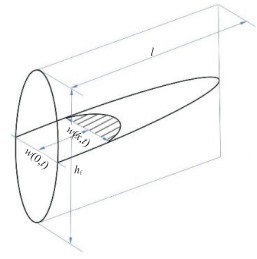
2.2.1 二维水力裂缝模型Zheltov[24]和Geertsma等[25]提出了KGD(Khristianovich,Geertsma & De Klerk)水力裂缝模型(图 6)。该模型假设水力裂缝高度hf确定不变(等于储层厚度),其水平截面满足弹性力学平面应变条件,即裂缝宽度沿垂直方向是固定的,令l表示水力裂缝半长,w表示裂缝宽度,此模型适合模拟裂缝hf > l的情况。
Perkins等[26]和Nordgren[27]提出了PKN(Perkins,Kern & Nordgren)水力裂缝模型(图 7),该模型同样假设水力裂缝高度hf不变,水力裂缝垂直截面为椭圆,且满足平面应变条件,但w沿垂直方向是变化的,此模型适合模拟hf≪l的情况。
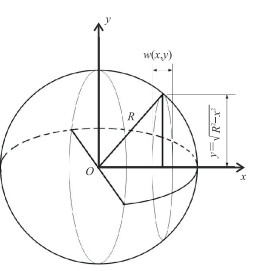
Green等[28]和Nikolski等[29]提出饼状水力裂缝模型(图 8)。此模型可模拟垂直井的水平裂缝,也可模拟水平井的垂直裂缝。
二维裂缝模型因计算效率高、物理机理清晰,得到广泛使用。二十世纪九十年代以前,二维裂缝模型占据主流,之后被逐步新发展的拟三维裂缝模型和三维裂缝模型取代。
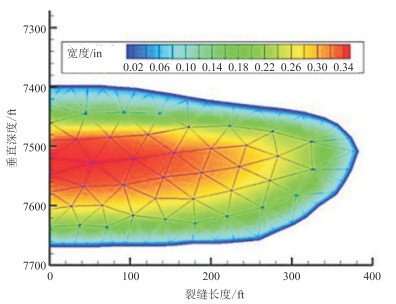
2.2.2 三维水力裂缝模型裂缝高度概念的引入使二维裂缝模型扩展到拟三维裂缝模型,某些情况下拟三维模型的hf计算值严重偏离真实值,存在一定的局限性。因此,进一步提出了平面三维水力裂缝模型,典型模型见图 9所示三维复合带电流体水力裂缝模型[30],即泵送通电支撑剂流体结束时的裂缝宽度剖面。假定裂缝为垂直的面裂缝,垂直剖面以井筒为对称轴。与hf和l相比,w可忽略不计(以颜色标识)。可见,其精度较拟三维水力裂缝模型更高,但运算量大,耗时长。
|
图 9 三维水力裂缝模型[30] |
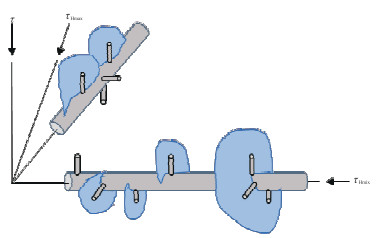
水平井分段多簇压裂技术是实现页岩高效生产的一项关键技术。单条水力裂缝模型已难以满足工业生产和学术研究需求。同时形成多条并排的水力裂缝并发生扩展,裂缝间会产生应力干扰作用,且不同裂缝所获得的压裂支撑剂的流量也不相同。在射孔引发多个起始裂缝后,裂缝尺寸会很快增大,使这些裂缝相互作用。图 10为几种常见的多裂缝模型[31]。
|
图 10 多条不同水力裂缝模型[31] |
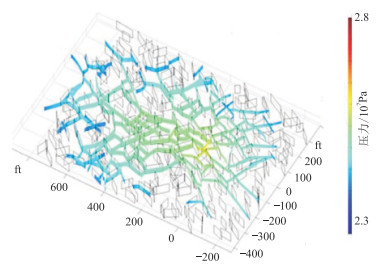
天然裂缝性地层水力裂缝的模型可能出现非平面形态,进而出现复杂的水力裂缝网络[32],典型模型见图 11。这类多裂缝模型更接近油气生产中的真实地层情况,多裂缝的随机性和复杂性给模拟研究带来很大困难。
|
图 11 水力裂缝网络模型[32] |
综上,水力裂缝的几何形态研究经历了从低维度到高维度,从二维到三维,从单条水力裂缝到多条水力裂缝,目前发展到地层水力裂缝网络。研究趋势从理论结构逐步转向实际地层真实情况,为油气勘探和生产提供更加可靠的工程应用和评价。
2.3 水力裂缝电磁数值分析方法电磁法作为一种重要的地球物理表征手段,可用于地下裂缝检测,特别是非常规石油勘探开发中的水力裂缝评价,具有重要意义。电磁场数值分析问题包含电磁场的正问题、逆问题及电磁场与其他物理场或系统的耦合问题。电磁场数值分析方法是计算电磁学重要组成部分,就已知给定区域内的几何结构与物理参数,求解一个电磁场定解问题,得到研究区域的电场或磁场的空间分布和时间变化,这属于电磁场的正问题。
目前,可进行电磁表征水力裂缝的数值分析方法主要有有限差分法、有限元法和边界元法。电磁场分析中最早应用的方法是有限差分法,这也是最早的离散数值方法。其原理是直接从微分方程出发,近似地用差分、差商代替微分、微商,研究规则边界非常方便,且容易实现,但数值解的稳定性难以保证。经典有限差分法的规则网格不能很好地模拟电磁场中复杂的几何形体及不同介质的物理参数特征,即便引入泰勒级数的高阶项也难以提高算法精度。因此,对于电磁场分析,有限差分法逐渐被有限元法替代。有限元法是目前应用最广泛的电磁场数值解法,其原理是从微分方程对应的泛函出发,利用变分原理结合区域离散得到方程组。该方法的优点是适用于具有复杂边界形状或边界条件、含有复杂介质的定解问题。这种方法的各个计算环节可以实现标准化,通过通用计算程序实现,且计算精度较高,对于水力裂缝电磁建模研究便于实现,不足之处是计算量较大。边界元法是另一种应用较广的电磁场数值分析方法,该方法是在经典积分方程的基础上,采用有限元的离散技术,利用边界积分方程求解微分方程。有限差分法和有限元法的剖分对象为整个求解场域,而边界元法的剖分对象为场域边界,对于模拟裂缝变形具有独特优势[33-34]。
另外,水力裂缝的电磁分析方法还有可控源电磁法、无限元法及近几年发展起来的无网格法等[35]。水力裂缝电磁数值模拟的难题在于长而薄的三维裂缝具有多尺度的特性,很难用传统的某种电磁建模方法进行数值模拟,因而采用多种数值分析方法模拟水力裂缝成为必然趋势。
电磁法正演模拟研究经历了从简单的一维、二维模型到复杂的三维模型、从场源总场到二次场、从节点有限元到矢量有限元、从规则结构化网格到多变的非结构化网格、从常规有限元到自适应有限元、从迭代求解到直接求解的发展过程。基于裂缝模型的电磁数值求解器的研究意义在于能够节省计算成本,更高效地利用资源,或对资源进行更合理的配置,对几亿甚至上百亿产值的国家油气相关企业来说都是非常有意义的。
2.4 水力裂缝诊断工具性能水力压裂过程是一个“黑匣子”,一是因为很难获得有关裂缝几何结构的信息,裂缝生长在地表以下数千英尺,要得到相关几何信息非常困难,二是因为压裂过程远比想象的复杂得多[36-38]。
尽管水力压裂工具采用最先进的技术进行设计,裂缝模型的几何信息仍然很难验证。为了填补这一空白,近几十年来,开发了多种裂缝探测技术,提高了对水力裂缝形态的认识[39-42]。Cipolla等[43]评估了裂缝监测中不同方法的能力和局限性(表 1)。根据其调查深度,这些方法大致可以分为三组:压裂中的远场监测;近井筒监测;间接测试模型。前两种是直接方法,而最后一种方法可开展裂缝尺寸的推断或间接测量。
|
|
表 1 裂缝诊断工具的能力和局限性[43] |
虽然远场监测手段在实际生产中应用广泛,但仍不能兼顾裂缝的多参数特征信息;近井筒方法可监测近距离裂缝比较单一的参数特征信息,但不能确定远井裂缝形态;间接模型监测结果存在多解性,裂缝特征参数不确定因素较多。电磁法压裂监测技术与电法测井研究机理相似,且均为近井探测,可以参考电法测井的研究方法进行裂缝监测。常规电法测井的局限性是探测深度有限,无法对长裂缝实现有效监测。针对裂缝方位识别,测井方法中有基于地层边界和倾角识别的随钻方位电阻率测井法,其理论也不能直接应用于压裂裂缝监测,但可借鉴此理论,对其进行进一步的修改和完善。
3 水力裂缝电磁探测技术研究进展 3.1 垂直井水力裂缝电磁探测技术及研究进展以LaBrecque等[44]为代表的Multi-Phase Technologies公司和Duke大学Qing Huo Liu团队,通过向浅层注入导电和介电支撑剂,监测形成的水力裂缝。研究提供了一种高度可控、可重复的方法确定拟用支撑剂的总体性质,并将这些体积特性集成到数值模型,研究支撑剂对地球物理场的响应特征。提出的垂直电极阵列本身没有足够的垂直范围(孔径)对井间配置的支撑剂进行精确成像,但利用此造影支撑剂进行井间裂缝表征是可行的,可用于井间裂缝探测可能性研究。Ahmadian等[45]将造影剂辅助电磁层析成像方法应用于水力诱导裂缝网络精确成像的有效性验证,对目前多种水力裂缝成像方法(微地震,示踪剂,倾斜计,及分布式声学和温度传感器)进行对比,提出一套完整的电磁主动支撑剂(EAP)辅助断层扫描方法,并在德克萨斯大学奥斯汀分校经济地质局的Devine试验场进行了现场试验,钻探了8口垂直井,并通过钻井结果验证该模型在EAP填充裂缝空间的物理边缘5 ft范围内的准确性。
近年来,中南大学、桂林理工大学和中国地质大学等高校的一些团队针对井筒电磁监测和数值模拟算法展开了研究[46-51]。何继善院士团队[46]提出的“广域电磁法”统一了频率域电磁法全区电阻率的定义和算法,构建了包括广域三维电磁场全波形数据采集、分析、处理和信号提取、三维电磁场张量的全波形正、反演理论技术体系,并成功研制了广域电磁法的仪器和装备,在油气勘查、固体矿产勘探、工程勘察等领域得到广泛应用,取得了很好的地质效果和经济效益。汤井田[48]在地电场勘探方法中进行了无限元正反演数值模拟研究,利用无限元代替不同的传统边界条件,极大缩小了计算区域,提高了计算速度和精度。汤文武等[49]通过引入频率适应网格,对多频点三维可控源电磁法进行正演模拟,分别对二次电场及二次耦合式的正演方式进行探索,在保证精度的同时提高了正演效率,优化了正演方案。李静和[51]提出了三维井地电磁两步快速反演算法,并给出了复杂油气藏建模方法,实现了多场源、多频率地—井垂直电磁剖面法快速正反演算法,为油气藏勘探应用的实用化奠定了坚实的理论基础。但是,监测压裂裂缝为电磁勘探中较新的研究领域,目前仍存在很多问题亟待解决。
研究人员在电磁探测水力裂缝方面也开展了有效研究。孙雨[52]和谢媛等[53-54]基于空间电磁场理论,采用有限元法对多种特定形状和不规则形状的垂直井水力裂缝模型进行了正演模拟,模拟结果可识别裂缝的位置信息,判断裂缝与地层位于不同区域,对含导电支撑剂的水力裂缝形态(大小、角度等)如何影响监测响应结果进行了具体分析,获得良好的效果。刘家琳[55]利用可控源电磁法对裂缝参数进行敏感性分析,对水力压裂过程中的大尺度地质模型及裂缝厚度与长度的多尺度建模问题进行了深入研究,结果表明可控源电磁法对压裂裂缝监测具有可行性,能有效确定裂缝参数信息。
垂直井水力裂缝电磁探测技术在油气探测方面拥有丰富的经验积累,而利用电磁法探测水力裂缝的相关技术还有待进一步探讨。随着非常规井(如水平井、斜井或多分支井)在石油工业领域的应用日渐广泛,相关研究也逐步转向非常规井的水力裂缝探测领域。
3.2 水平井水力裂缝电磁探测技术研究进展在过去20年中,随着水平井以及多分支井技术的快速发展,储层与井之间的暴露量急剧增加,达到了前所未有的数量级[56]。与储层中的垂直井相比,水平井得到更多的关注,促使水平井水力裂缝电磁探测研究迅速展开。
3.2.1 水平井水力裂缝电磁探测模型研究Pardo等[57-58]利用井孔电阻率测量值对裸眼井和钢套管井进行水力压裂监测,从数值上评估了使用电磁方法监测水平井人工水力裂缝的可能性。建模过程中,水力裂缝被导电支撑剂填充,可不垂直于井,其形态为薄圆盘状,该研究对利用电阻率测量方法判断水力裂缝的存在标准进行了量化,并评估了该方法对裂缝厚度、长度和倾角(相对于井)的敏感性。对环形线圈发射器与接收器之间的空间进行低频测量,以表征裸眼井中的水力压裂裂缝。传统的低频、短间距的穿套管测量也适用于钢套管井中水力裂缝的表征。研究表明,对于水平井的水力裂缝特征的量化,长间距、低频电极的效果通常优于螺线管系统。进一步检测并量化单条水力裂缝的厚度和长度,对于长达150 m的水力裂缝仍可精确评估,但前提是背景与裂缝的电导率差异足够大。
得克萨斯大学的Yang等[23, 59-62]提出了一种新的积分方程法,可有效识别复杂背景下多条水力裂缝的长度。分别在垂直井和水平井进行低频钻孔电阻率测量,检测并评估了低频钻孔电阻率测量对水力裂缝识别的适用性,量化了多分量低频钻孔电阻率测量对三维水力裂缝的形状、面积和倾角的敏感性分析,然后进行了三维参数反演,证实了该反演方案可以有效估计复杂三维裂缝的几何形状。
韩国汉阳大学的Noh等[63-64]开发了一种粒子映射(PM)方法,用于监测磁增强支撑剂水力压裂裂缝的可控源电磁(CSEM)数据反演,并将该方法应用于磁力增强支撑剂的成像及水力压裂裂缝的监测。此外,他们还采用模糊聚类方法的正则化方法,结合微震裂缝组几何结构进行PM反演,为支撑体积提供了清晰且可解释的成像结果。
Wang等[65]和Huang等[66]开发了基于积分方程组的求解器,用于层状薄介质片(TDS)表面积分方程(SIE)的求解,模拟水力裂缝横跨层状介质情况下的电磁散射。与传统的有限元法和体积积分方程法相比,TDS-SIE算法利用了裂缝的多尺度特性,不受体积网格的限制,具有很高的计算效率。
Zhai等[17]提出将三轴感应测量和扇形线圈轴向旋转测量(TIM-SCARM)相结合的方法表征水力裂缝。该方法将薄裂缝近似为一个曲面,以提高计算效率。研究重点是定量分析水力裂缝的导流能力、横截面形状、半长和方位,以评估这些参数对TIM-SCARM仪器结构的影响,研究多分量信号与裂缝特征的相关性。Li等[67]对含支撑剂水力压裂裂缝的多频电磁响应进行了短距离收发正演模型研究,基于磁偶极子激发裂缝的特殊响应特性,首次提出应关注有限信号,并讨论了裂缝附近信号的跳跃变化现象及相关参数的变化规律。
3.2.2 水平井水力裂缝电磁探测方法与仪器研究Wu等[68]开发了垂直裂缝指示器(VFIND) 和裂缝方向指示器(FOI),检测近似垂直裂缝并估计其走向。在此基础上,Omeragic等[69]利用三轴感应对水平井边界进行绘制,描述介质的各向异性,并对裂缝进行解释,检测近似垂直裂缝并估计其走向。研究表明,开展三轴感应测量与新的油基泥浆成像仪数据的联合解释,可确定与轨迹相交的裂缝方向,更好地表征水平井中的裂缝性储层,并提供有关裂缝范围和远离井眼区域的有效倾角信息(裂缝方向场景的变化等)。
得克萨斯大学Sharma课题组提出了一种新技术,研究低频电磁感应和导电性压裂支撑剂对水力压裂裂缝的影响[70-72]。此项研究由美国得克萨斯大学和E能谱技术公司(E-Spectrum Technologies)/吉尔哈特有限责任公司(Gearhart Companies Inc)联合开展。监测仪器包括三组三向发射器和接收器,通过检测导电支撑剂颗粒的位置,不仅可以确定水力裂缝的长度、高度和方向,还可获得裂缝中支撑剂的垂直分布。结合实际数据的反演结果和2D地震、3D地震等地球物理数据,还可以判断裂缝与天然水层是否连通。Zhang等[73-76]提出了一种利用井下电测量方法绘制水力压裂中导电支撑剂分布的方法。该方法直接对套管进行激发,可克服套管井中由于感应工具引起的限制。Shiriyev等[77]设计并制造了一台原型感应测井仪,由同轴、共面和交叉极化配置的三轴发射器和接收器线圈组成,利用不同大小、形状和方向的薄(高导电性)金属靶模拟各种裂缝,可用来检测和提取导电支撑剂的裂缝参数。
在中国,长江大学的Yan等[78]利用时域电磁法对中国南方涪陵页岩气田压裂过程进行了连续监测,采用大功率发射机和多通道瞬变电磁接收机阵列,通过监测电场水平分量的变化,构建电阻率动态图像,成功地对压裂液的空间分布进行成像,验证了电磁示踪剂监测技术在水力压裂监测中的应用是可行的。
中国石油大学(华东)的Zhang等[79]基于三轴电磁感应原理对水力压裂参数进行了正演模拟,成功地监测了裂缝方位和倾角的变化。研究发现,当发射源垂直于z轴时,可监测裂缝的长度和高度;发射源垂直于x轴时,发现观测信号峰值只对裂缝的方位敏感,对裂缝的长度不敏感,可根据信号峰值大小反演裂缝方位角。
中国石油大学(北京)的李洋[80]和Li等[81]针对油气井多级压裂过程中裂缝非对称生长问题,设计了一种基于电磁散射信号非对称收发线圈,对压裂裂缝发育走向进行有效监测,还讨论了电磁接收信号与不对称水力裂缝的方位参数(如裂缝发育方向和倾角)之间的关系。通过分析从旋转的接收器扇面获得的三维信号,可以确定多个不对称压裂裂缝的空间形态,解决了如何用电磁监测方法确定裂缝生长的三维方向的问题,为探测仪器的开发及数据反演提供了理论参考。吴世伟等[82]建立了多地层水力裂缝模型,对多层介质条件下裂缝的感应电动势进行了模拟,分析了对称裂缝和非对称裂缝在不同地层结构中的裂缝夹角、旋转角和展宽角等裂缝形态电磁测井响应特征,表明利用电磁法探测不同地层结构水力裂缝具有较高的准确性。
近年来,关于通过压裂监测开展近井筒水力裂缝直接探测的研究进展迅速,主要研究结论包括:①在单井中完成压裂裂缝监测,可以提高监测数据的可靠性;②仪器可以在油气井的生命周期(压裂中或压裂后)中的任意时刻提供裂缝数据分析,有效降低了作业成本,减小压裂作业的设备负担,同时可降低对环境的影响。在近井电磁探测的基础上,因迫切的实际需要,远井监测研究也得到了更多关注,通过井间电磁探测进行跨井水力裂缝监测逐渐成为另一研究热点,已获得一些初步研究成果和经验。
3.3 井间电磁探测在水力裂缝监测中的应用非常规油藏中,大部分钻井都是水平井或近水平井[83],单水平井完井工艺相对简单,而多分支井[84]的设计相对更复杂。因此,针对多井情况下,利用电磁方法监测裂缝的研究也越来越重要。对于油气储层,当井间距较大,存在高电导层时,以及多数油井具有金属套管,对高频电磁信号产生严重衰减和相移,因此利用高频电磁成像技术难以实现储层电性结构研究[85-87]。近年来的相关理论研究和实验结果表明,数十赫兹到十几千赫兹范围的低频电磁波可在数百米范围内进行有效探测[88],特别是对于多井油藏开发,通过远场电磁方法探测水力裂缝具有重要意义。
20世纪90年代开始,美国加利福尼亚大学伯克利分校与美国劳伦斯—伯克利(LBL)及劳伦斯—利沃莫(LLNL)、桑地亚(SNL)等国家实验室的学者先后完成了井间电磁测量系统的方法原理、数值模拟和现场可行性试验的系统论证工作,设计并制造了相应的测量仪器系统,开展了一系列卓有成效的现场模拟试验[89-90]。21世纪初,美国Utah大学地质与地球物理学专家Zhdanov等[91-93]提出了一种基于电磁测量的三维井间电磁层析成像技术,应用局部拟线性(LQL)方法对三维井间电磁数据进行正演模拟和聚焦反演,较好地恢复了导电岩层的电阻率分布,准确地判断其位置和形状。
沈金松等[94]和魏宝君等[95]针对重建地下介质电阻率分布的问题,提出了一种井间低频电磁波测量方法,并将三维问题简化成二维问题。利用该方法对金属套管井中有限尺寸线圈的电磁响应特征进行了研究,分析了金属套管中电磁测井对地层电阻率变化的灵敏度,分析了井眼泥浆参数、套管参数和不同线圈尺寸对电磁测井响应的影响。研究认为,采用非磁性或弱磁性套管的效果优于一般的铁磁性套管,增大线圈直径有助于增强有效电磁响应信号,为大井间距电磁测量提供了可行性分析。
Heagy等[96]将高导电性颗粒融入支撑剂,基于有效介质理论建立了岩石裂隙体有效电导率模型,并利用跨井电磁测量方法对导电支撑剂填充的水力裂缝组进行成像,裂缝获得了有效的电磁表征。Hoversten等[97]对六口水平套管井开展了时域电磁(TDEM)井—地系统正演模拟。模拟过程考虑了多套管井的真实井眼轨迹,使用时间域中的八叉树有限差分模型模拟多个具有复杂截面几何图案的水平套管井。此外,还利用压裂前TDEM数据估计了井区背景和井筒的电导率分布,并对此流程进行了演示和详尽阐述;对压裂后的双差TDEM数据进行反演,生成了表征水力裂缝薄层体的参数。根据反演结果,效果最好的是水力裂缝的长度和电导率,这对于指导井下进行分离和研究导电增强型支撑剂的分布很重要。Mishra等[98]基于井间电磁理论对水力裂缝几何形状进行了精确估计,利用二维解释成果可对三维非结构水力裂缝模型进行校准,引入了可靠的校准输入。这样的二维解释平面可以有多个,因此可在多口井中放置信号接收器开展多井监测,使三维水力裂缝模型更精确。
中国石油大学(华东)的Liu等[99]测量了水力裂缝中填充的磁性支撑剂被激活前、后的磁场,获得了填充有磁性支撑剂的裂缝引起的磁异常。该磁异常反映了水力裂缝的特征,可以通过数值反演获得水力裂缝的大致几何形态和方位。研究认为,除了地面监测外,至少应对两口相邻井进行井中磁场参数监测,以获得更准确的裂缝信息。
西安石油大学的仵杰等[100-102],采用多分量电磁远程探测仪对井旁裂缝特征进行了研究,模拟了发射频率、裂缝张开度、裂缝空间位置、裂缝方位角和俯仰角的响应特性,分析了多分量电磁远程探测仪对井旁裂缝响应的敏感性。
近年来,井间电磁监测技术开始应用于水力裂缝的研究,但以电磁感应或散射为主的井间低频电磁测量方法及相关的、成熟的成像处理技术还比较缺乏。应用井间电磁法对储层裂缝进行成像,必将成为研究地质储层非均匀性、评价储层流体动态特性的有效手段之一。
4 结束语无论在中国还是在国外,对水力压裂裂缝的电磁探测研究尚处于初步阶段,与之相关的一系列理论和技术问题,都需要进行系统和深入的研究。这些问题主要包括水力裂缝模型的建立、电磁数值求解器的开发、电磁场多尺度的理论研究和计算、分析仪器参数差异的对比度及其分布规律并进行设计优化、提高压裂裂缝关键参数电磁表征的精准度,以及对裂缝性储层非均质条件下油气藏资源的评估等。这些问题中,精确的水力裂缝模型和有效的电磁求解器是水力裂缝电磁研究的关键,这两点都属于地球物理电磁正演的正解问题,求解过程十分复杂,因此要力求通过优化地下裂缝模型的布局结构,基于裂缝自身特点使电磁多尺度计算方法简洁合理,从而使整个数值计算模型的求解简单化,再充分利用本构方程和边界条件等约束,使得求解问题逐一对应。由于裂缝识别和探测的复杂性,任何一种单一方法都不可能很好地解决这些问题,针对不同的裂缝问题需综合多学科、多属性的探测技术,尽量降低解释的多解性。
本文从电磁测井的角度出发,对水力压裂裂缝电磁研究现状进行了详细调研,其发展趋势主要为:以电磁学为基础,对孔隙、流体、固体力学等进一步耦合;从裸眼井到套管井,从单井到多分支井,从人工裂缝到天然裂缝,从单一裂缝到复杂多裂缝形态,从不考虑支撑剂状态到基于感应测井理论对电性或磁性支撑剂水力压裂裂缝进行电磁表征和评估,从均匀介质中的水力裂缝到非均匀介质中的水力裂缝,这些水力裂缝电磁监测技术的发展为更真实地推断水力裂缝形态及分布起到了重要作用。然而,水力压裂裂缝的电磁探测技术尚有很多问题需要解决,非均质性对于非常规储集层是普遍存在的,多级水力压裂的相互作用复杂,地下复杂裂缝的形成和分布规律很难掌握,多种因素如何共同影响、相互作用仍不清楚,这些都制约了研究方法的设计和创新。随着人工智能的迅速发展,将其应用于水力裂缝的电磁研究,改善裂缝油藏描述能力,为裂缝油藏高效开发提供有效参考,必将为地球物理测井应用研究带来更多的关注和挑战。
| [1] |
DONALDSON E C, ALAM W, BEGUM N. Hydraulic Fracturing Explained[M]. Gulf Publishing Company, Houston, TX, 2013.
|
| [2] |
蔡志东. 井中地震技术: 连接多种油气勘探方法的桥梁[J]. 石油地球物理勘探, 2021, 56(4): 922-934. CAI Zhidong. Borehole seismic: A bridge connecting multiple oil and gas exploration methods[J]. Oil Geophysical Prospecting, 2021, 56(4): 922-934. |
| [3] |
刘卫东, 刘腾蛟, 纪拥军, 等. 利用微地震监测成果判断砂砾岩油藏压裂裂缝井间连通性——以准噶尔盆地玛湖油田为例[J]. 石油地球物理勘探, 2022, 57(2): 395-404. LIU Weidong, LIU Tengjiao, JI Yongjun, et al. Determination of inter-well connectivity of fractured fractures in glutenite reservoirs by microseismic monitoring results: a case study of Mahu Oilfield in the Junggar Basin[J]. Oil Geophysical Prospecting, 2022, 57(2): 395-404. |
| [4] |
WARPINSKI N R, DU J. Source-mechanism studies on microseismicity induced by hydraulic fracturing[C]. SPE Annual Technical Conference and Exhibition, Florence, Italy, September 2010, SPE-135254-MS.
|
| [5] |
张晓林, 张峰, 李向阳, 等. 水力压裂对速度场及微地震定位的影响[J]. 地球物理学报, 2013, 56(10): 3552-3560. ZHANG Xiaolin, ZHANG Feng, LI Xiangyang, et al. The influence of hydraulic fracturing on velocity and microseismic location[J]. Chinese Journal of Geophy-sics, 2013, 56(10): 3552-3560. |
| [6] |
杨瑞召, 李德伟, 庞海玲, 等. 页岩气压裂微地震监测中的裂缝成像方法[J]. 天然气工业, 2017, 37(5): 31-37. YANG Ruizhao, LI Dewei, PANG Hailing, et al. Fracture imaging of the surface based microseismic monito-ring in shale gas fracking: methods and application[J]. Natural Gas Industry, 2017, 37(5): 31-37. |
| [7] |
XUE D, RABINOVICH M, BESPALOV F, et al. Characterization of fracture length and formation resistivity from array induction data[C]. SPWLA 49th Annual Logging Symposium, Austin, Texas, May 2008, SPWLA-2008-Ⅲ.
|
| [8] |
赵争光. 水力裂缝表征的电磁方法[R]. 北京: 中国矿业大学(北京), 2015.
|
| [9] |
MAXWELL S C, CIPOLLA C. What does microseismicity tell us about hydraulic fracturing?[C]. SPE Annual Technical Conference and Exhibition, Denver, Colorado, USA, October 2011, SPE-146932-MS.
|
| [10] |
MCKENNA J P. Where did the proppant go?[C]. SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, Colorado, USA, August 2014, URTEC-1922843-MS.
|
| [11] |
张庚骥. 电法测井 上册[M]. 北京: 石油工业出版社, 1984.
|
| [12] |
张庚骥. 电法测井 下册[M]. 北京: 石油工业出版社, 1986.
|
| [13] |
张意, 冯宏, 韩雪, 等. 石油电磁测井技术发展中的一些关键问题[J]. 石油地球物理勘探, 2021, 56(6): 1430-1447. ZHANG Yi, FENG Hong, HAN Xue, et al. Key problems in the development of petroleum electromagnetic logging[J]. Oil Geophysical Prospecting, 2021, 56(6): 1430-1447. |
| [14] |
NABIGHIAN M N. Electromagnetic Methods in Applied Geophysics[M]. Tulsa, Okla: Society of Exploration Geophysics, 1988.
|
| [15] |
KONG J A. Electromagnetic Wave Theory[M]. New York: Wiley, 1986.
|
| [16] |
NOTAROS B M. Electromagnetics[M]. Prentice Hall, Upper Saddle River, 2011.
|
| [17] |
ZHAI Y, LIU D J, POTTER D K, et al. Characterization of hydraulic fractures with triaxial electromagnetic induction and sector coil rotation measurement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-11. |
| [18] |
KAUFMAN A A. DASHEVSKY Y A. Principles of Induction Logging[M]. Boston: Elsevier, 2003.
|
| [19] |
KAUFMAN A. ITSKOVICH G. Basic Principles of Induction Logging[M]. Amsterdam: Elsevier, 2017.
|
| [20] |
刘国兴. 电法勘探原理与方法[M]. 北京: 地质出版社, 2005.
|
| [21] |
FLEISCH D. A student's guide to Maxwell's Equations[M]. Cambridge: Cambridge University Press, 2008.
|
| [22] |
SCHAUBERT D, WILTON D, GLISSON A. A tetrahedral modeling method for electromagnetic scatte-ring by arbitrarily shaped inhomogeneous dielectric bodies[J]. IEEE Transactions on Antennas and Propagation, 1984, 32(1): 77-85. DOI:10.1109/TAP.1984.1143193 |
| [23] |
YANG K, TORRES-VERDÍN C, YILMAZ A E. Detection and quantification of three-dimensional hydraulic fractures with horizontal borehole resistivity measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4605-4615. DOI:10.1109/TGRS.2015.2402656 |
| [24] |
ZHELTOV A K. Formation of vertical fractures by means of highly viscous liquid[C]. 4th World Petroleum Congress, Rome, Italy, June 1955, WPC-6132.
|
| [25] |
GEERTSMA J, DE KLERK F. A rapid method of predicting width and extent of hydraulically induced fractures[J]. Journal of Petroleum Technology, 1969, 21(12): 1571-1581. DOI:10.2118/2458-PA |
| [26] |
PERKINS T K, KERN L R. Widths of hydraulic fractures[J]. Journal of Petroleum Technology, 1961, 13(9): 937-949. DOI:10.2118/89-PA |
| [27] |
NORDGREN R P. Propagation of a vertical hydraulic fracture[J]. Society of Petroleum Engineers Journal, 1972, 12(4): 306-314. DOI:10.2118/3009-PA |
| [28] |
GREEN A E, SNEDDON I N. The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1950, 46(1): 159-163. DOI:10.1017/S0305004100025585 |
| [29] |
NIKOLSKI D V, MOGILEVSKAYA S G, LABUZ J F. Three-dimensional boundary element modeling of fractures under gravity load[C]. The 46th U. S. Rock Mechanics/Geomechanics Symposium, Chicago, Illinois, 2012, ARMA-2012.
|
| [30] |
RIBEIRO L H, SHARMA M M. A new Three-Dimensional, compositional, model for hydraulic fractu-ring with energized fluids[C]. SPE Annual Technical Conference and Exhibition, San Antonio, Texas, USA, 2012, SPE-159812-MS.
|
| [31] |
YEW C H, WENG X. Mechanics of Hydraulic Fracturing[M]. Amsterdam: Elsevier/GPP, 2015.
|
| [32] |
李亚龙, 刘先贵, 胡志明, 等. 页岩储层压裂缝网模拟研究进展[J]. 石油地球物理勘探, 2019, 54(2): 480-492. LI Yalong, LIU Xiangui, HU Zhiming, et al. Research progress on fracture network simulation in shale reservoirs[J]. Oil Geophysical Prospecting, 2019, 54(2): 480-492. |
| [33] |
覃新川. 电磁理论中的边界元方法探索[M]. 北京: 科学出版社, 2017.
|
| [34] |
程万, 金衍. 基于边界元法的水力压裂数值模拟技术[M]. 北京: 科学出版社, 2018.
|
| [35] |
谢德馨, 杨仕友. 工程电磁场数值分析与优化设计[M]. 北京: 机械工业出版社, 2017.
|
| [36] |
WRIGHT C A, DAVIS E J, WEIJERS L, et al. Horizontal hydraulic fractures: oddball occurrences or practical engineering concern?[C]. SPE Western Regional Meeting, Long Beach, California, 1997, SPE-38324-MS.
|
| [37] |
WRIGHT C A, MINNER W A, WEIJERS L, et al. Wellbore-to-Fracture communication problems pose challenges in California diatomite horizontal wells[C]. SPE Annual Technical Conference and Exhibition, San Antonio, Texas, October 1997, SPE-38632-MS.
|
| [38] |
WRIGHT C A, WEIJERS L, DAVIS E J, et al. Understanding hydraulic fracture growth: tricky but not hopeless[C]. SPE Annual Technical Conference and Exhibition, Houston, Texas, 1999, SPE-56724-MS.
|
| [39] |
WARPINSKI N R. Hydraulic fracturing in tight, fissured media[J]. Journal of Petroleum Technology, 1991, 43(2): 146-209. DOI:10.2118/20154-PA |
| [40] |
WRIGHT C A, DAVIS E J, MINNER W A, et al. Surface tiltmeter fracture mapping reaches new depths-10, 000 feet and beyond?[C]. SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium, Denver, Colorado, 1998, SPE-39919-MS.
|
| [41] |
WRIGHT C. Tiltmeter fracture mapping: from the surface and now downhole[J]. Petroleum Engineer International, 1998, 71(1): 611551. |
| [42] |
WRIGHT C A, DAVIS E J, GOLICH G M, et al. Downhole tiltmeter fracture mapping: finally measu-ring hydraulic fracture dimensions[C]. SPE Western Regional Meeting, Bakersfield, California, 1998, SPE-46194-MS.
|
| [43] |
CIPOLLA C L, WRIGHT C A. Diagnostic techniques to understand hydraulic fracturing: What? Why? And how?[J]. SPE Production & Facilities, 2002, 17(1): 23-35. |
| [44] |
LABRECQUE D, BRIGHAM R, DENISON J, et al. Remote imaging of proppants in hydraulic fracture networks using electromagnetic methods: results of small-scale field experiments[C]. SPE Hydraulic Fracturing Technology Conference, The Woodlands, Texas, USA, February 2016, SPE-179170-MS.
|
| [45] |
AHMADIAN M, LABRECQUE D, LIU Q H, et al. Validation of the utility of the Contrast-Agent-Assisted electromagnetic tomography method for precise ima-ging of a hydraulically induced fracture network[C]. SPE Annual Technical Conference and Exhibition, Calgary, Alberta, Canada, 2019, SPE-196140-MS.
|
| [46] |
何继善, 李帝铨. 深地探测尖兵——广域电磁法[J]. 国土资源科普与文化, 2019(3): 4-9. |
| [47] |
何展翔. 电磁勘探技术的机遇与挑战及发展方向[J]. 物探化探计算技术, 2019, 41(4): 433-447. HE Zhanxiang. Opportunities, challenges and development directions of electromagnetic exploration today[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2019, 41(4): 433-447. DOI:10.3969/j.issn.1001-1749.2019.04.01 |
| [48] |
汤井田. 基于有限元—无限元的电磁法正演与反演[M]. 湖南长沙: 中南大学出版社, 2019.
|
| [49] |
汤文武, 柳建新, 李耀国. 频率域可控源电磁法三维有限元正演[M]. 湖南长沙: 中南大学出版社, 2017.
|
| [50] |
李静和. 用于油气藏勘探的井筒电磁法反演算法研究[D]. 湖北武汉: 中国地质大学(武汉), 2015.
|
| [51] |
李静和. 用于油气藏勘探的井筒电磁法成像技术[M]. 湖南长沙: 中南大学出版社, 2019.
|
| [52] |
孙雨. 基于低频电磁感应方法的水力压裂裂缝长度诊断研究[D]. 北京: 中国石油大学(北京), 2019.
|
| [53] |
谢媛. 利用电磁波测井探测直井水力裂缝的正演模拟[D]. 北京: 中国石油大学(北京), 2019.
|
| [54] |
谢媛, 刘得军, 李彩芳, 等. 利用随钻电磁波测井探测直井水力裂缝的正演模拟[J]. 石油钻探技术, 2020, 48(2): 123-129. XIE Yuan, LIU Dejun, LI Caifang, et al. Forward modeling in hydraulic fracture detection by means of electromagnetic wave logging while drilling in vertical wells[J]. Petroleum Drilling Techniques, 2020, 48(2): 123-129. |
| [55] |
刘家琳. 基于可控源电磁法的垂直井水力压裂裂缝正演研究[D]. 北京: 中国石油大学(北京), 2021.
|
| [56] |
HILL A D, ZHU D, ECONOMIDES M J. Multila-teral Wells[M]. Society of Petroleum Engineers, Richardson, TX, 2008.
|
| [57] |
PARDO D, TORRES-VERDIN C. Hydrofracture diagnosis in open-hole and steel-cased wells using borehole resistivity measurements[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 180-184.
|
| [58] |
PARDO D, TORRES-VERDÍN C. Sensitivity analysis for the appraisal of hydrofractures in horizontal wells with borehole resistivity measurements[J]. Geophysics, 2013, 78(4): D209-D222. |
| [59] |
YANG K, CELIK E, TORRES-VERDIN C, et al. Detection and quantification of 3D hydraulic fractures with multi-component low-frequency borehole resisti-vity measurements[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 1213-1217.
|
| [60] |
YANG K, TORRES-VERDÍN C, YILMAZ A E. Detection and quantification of 3D hydraulic fractures with vertical borehole induction resistivity measurements[J]. Geophysics, 2016, 81(4): E259-E264. |
| [61] |
YANG K, YILMAZ A, TORRES-VERDÍN C. Efficient 3D parametric inversion of hydraulic fractures with low-frequency borehole triaxial electromagnetic measurements[C]. SEG Technical Program Expanded Abstracts, 2016, 35: 954-958.
|
| [62] |
YANG K. FFT and Multigrid Accelerated Integral Equation Solvers for Multi-Scale Electromagnetic Analysis in Complex Backgrounds[D]. The University of Texas at Austin, Texas, 2014.
|
| [63] |
NOH K, OH S, SEOL S J, et al. Analysis of anomalous electrical conductivity and magnetic permeability effects using a frequency domain controlled-source electromagnetic method[J]. Geophysical Journal International, 2016, 204(3): 1550-1564. |
| [64] |
NOH K, LEE K H, OH S, et al. Location-based parameterization of CSEM data inversion for the monito-ring of hydraulic fracturing with magnetically enhanced proppants[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 924-928.
|
| [65] |
WANG H, HUANG W F, FANG Y, et al. Efficient and accurate electromagnetic modeling of triaxial induction responses from multiscale fractures for well-logging applications[J]. IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2019, 4: 20-28. |
| [66] |
HUANG W F, WANG H, ZHAN Q, et al. Thin dielectric sheet-based surface integral equation for the scattering simulation of fractures in a layered medium[J]. IEEE Transactions on Geoscience and Remote Sen-sing, 2019, 57(10): 7606-7612. |
| [67] |
LI Y, LIU D J, ZHAI Y, et al. Study on multifrequency electromagnetic response of hydraulic fractu-ring fracture with proppant based on a forward model of short distance receiving and transmitting[C]. 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 2021, 1931-1941.
|
| [68] |
WU P, BARBER T, WANG G L, et al. Fracture characterization using triaxial induction tools[C]. SPWLA 54th Annual Logging Symposium, New Orleans, Louisiana, 2013, SPWLA-2013-CC.
|
| [69] |
OMERAGIC D, BAYRAKTAR Z, THIEL M, et al. Triaxial induction interpretation in horizontal wells: mapping boundaries, and characterizing anisotropy and fractures[C]. SPWLA 56th Annual Logging Symposium, Long Beach, California, USA, 2015, SPWLA-2015-I.
|
| [70] |
BASU S, SHARMA M M. A new method for fracture diagnostics using low frequency electromagnetic induction[C]. SPE Hydraulic Fracturing Technology Confe-rence, The Woodlands, Texas, USA, 2014, SPE-168606-MS.
|
| [71] |
BASU S. Fracture Diagnostics Using Low Frequency Electromagnetic Induction[D]. University of Texas, Austin, TX, 2014.
|
| [72] |
PALISCH T, AL-TAILJI W, BARTEL L, et al. Recent advancements in far-field proppant detection[C]. SPE Hydraulic Fracturing Technology Conference, The Woodlands, Texas, USA, 2016, SPE-179161-MS.
|
| [73] |
ZHANG P, SHIRIYEV J, TORRES-VERDÍN C, et al. Fracture diagnostics using a low-frequency electromagnetic induction method[C]. 50th U. S. Rock Mechanics/Geomechanics Symposium, Houston, Texas, 2016, ARMA-2016.
|
| [74] |
ZHANG P, BRICK Y, SHARMA M M. Numerical study of an electrode-based resistivity tool for fracture diagnostics in steel-cased wellbores[J]. Geophysics, 2018, 83(2): D41-D48. |
| [75] |
ZHANG P, SEN M K, SHARMA M M, et al. Mapping proppant distribution in hydraulic fractures in cased wellbores using low frequency downhole electrical measurements[C]. SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, Texas, USA, 2018, SPE-189884-MS.
|
| [76] |
ZHANG P. Low Frequency Downhole Electrical Measurements for Mapping Proppant Distribution in Hydraulic Fractures in Cased-Hole Wells[D]. The University of Texas, Austin, Texas, 2018.
|
| [77] |
SHIRIYEV J, BRICK Y, ZHANG P, et al. Experiments and simulations of a prototype triaxial electromagnetic induction logging tool for open-hole hydraulic fracture diagnostics[J]. Geophysics, 2018, 83(3): D73-D81. |
| [78] |
YAN L J, CHEN X X, TANG H, et al. Continuous TDEM for monitoring shale hydraulic fracturing[J]. Applied Geophysics, 2018, 15(1): 26-34. |
| [79] |
ZHANG L, QI J, LI L, et al. A forward modeling method based on electromagnetic theory to measure the parameters of hydraulic fracture[J]. Fuel, 2019, 251: 466-473. |
| [80] |
李洋. 基于电磁探测法的水力压裂裂缝空间方位正演研究[D]. 北京: 中国石油大学(北京), 2020.
|
| [81] |
LI Y, LIU D, ZHAI Y, et al. 3-D FEM azimuth forward modeling of hydraulic fractures based on electromagnetic theory[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(2): 246-250. |
| [82] |
吴世伟, 刘得军, 赵阳, 等. 层状介质水力裂缝电磁响应的有限元正演模拟[J]. 石油钻探技术, 2022, 50(2): 132-138. WU Shiwei, LIU Dejun, ZHAO Yang, et al. Finite-Element forward modeling of electromagnetic response of hydraulic fractures in layered medium[J]. Petroleum Drilling Techniques, 2022, 50(2): 132-138. |
| [83] |
WOLFSTEINER C, DURLOFSKY L J, AZIZ K. Approximate model for productivity of nonconventional wells in heterogeneous reservoirs[J]. SPE Journal, 2000, 5(2): 218-226. |
| [84] |
SALAS J R, CLIFFORD P J, JENKINS D P. Multilateral well performance prediction[C]. SPE Western Regional Meeting, Anchorage, Alaska, 1996, SPE-35711-MS.
|
| [85] |
曾文冲, 赵文杰, 臧德福. 井间电磁成像系统应用研究[J]. 地球物理学报, 2001, 44(3): 411-420. ZENG Wenchong, ZHAO Wenjie, ZANG Defu. Application research of crosshole electromagnetic tomography[J]. Chinese Journal of Geophysics, 2001, 44(3): 411-420. |
| [86] |
魏宝君. 井间电磁成像方法研究[D]. 北京: 中国石油大学(北京), 2003.
|
| [87] |
沈金松, 王志刚, 马超, 等. 井间电磁油气储层监测技术的发展和应用[J]. 石油地球物理勘探, 2014, 49(1): 213-224. SHEN Jinsong, WANG Zhigang, MA Chao, et al. Application of the cross-hole electromagnetic method(CHEM) in hydrocarbon reservoir monitoring[J]. Oil Geophysical Prospecting, 2014, 49(1): 213-224. |
| [88] |
WILT M, SCHENKEL C, DALEY T, et al. Mapping steam and water flow in petroleum reservoirs[J]. SPE Reservoir Engineering, 1997, 12(4): 284-287. |
| [89] |
WILT M J, ALUMBAUGH D L, MORRISON H F, et al. Crosswell electromagnetic tomography: System design considerations and field results[J]. Geophysics, 1995, 60(3): 871-885. |
| [90] |
WILT M, MORRISON H F, BECKER A, et al. Crosshole electromagnetic tomography: A new technology for oil field characterization[J]. The Leading Edge, 1994, 14(3): 173-177. |
| [91] |
ZHDANOV M S. Geophysical Inverse Theory and Regularization Problems[M]. Amsterdam: Elsevier, 2002.
|
| [92] |
ZHDANOV M S, YOSHIOKA K. Cross-well electromagnetic imaging in three dimensions[J]. Exploration Geophysics, 2003, 34(1/2): 34-40. |
| [93] |
ZHDANOV M S, YOSHIOKA K. Three-dimensional cross-well electromagnetic tomography[C]. SEG Technical Program Expanded Abstracts, 2003, 23: 526-529.
|
| [94] |
沈金松, 佟文琪, 房德斌. 用跨井电磁波资料重现地下介质的电阻率分布[J]. 石油地球物理勘探, 2000, 35(6): 741-750. SHEN Jinsong, TONG Wenqi, FANG Debin. Reappearance of resistivity distribution over subsurface medium using crosshole electromagnetic data[J]. Oil Geophysical Prospecting, 2000, 35(6): 741-750. |
| [95] |
魏宝君, 李晓强, 任广强, 等. 金属套管对多分量井间电磁响应的影响[J]. 中国石油大学学报(自然科学版), 2018, 42(5): 65-74. WEI Baojun, LI Xiaoqiang, REN Guangqiang, et al. Effects of metal casing on multi-component cross-hole electromagnetic responses[J]. Journal of China University of Petroleum (Edition of Natural Science), 2018, 42(5): 65-74. |
| [96] |
HEAGY L J, OLDENBURG D W, CHEN J. Where does the proppant go? Examining the application of electromagnetic methods for hydraulic fracture characterization[C]. GeoConvention 2014 Focus.
|
| [97] |
HOVERSTEN G M, SCHWARZBACH C, BELLIVEAU P, et al. Borehole to surface electromagnetic monitoring of hydraulic fractures[C]. Extended Abstracts of 79th EAGE Conference and Exhibition, 2017, 1-5.
|
| [98] |
MISHRA S, REDDY V. High accuracy estimation of hydraulic fracture geometry using crosswell electromagnetics[C]. SPE Annual Technical Conference and Exhibition, Dubai, UAE, 2021, SPE-206266-MS.
|
| [99] |
LIU J, CAO S, WU X, et al. Detecting the propped fracture by injection of magnetic proppant during fracturing[J]. Geophysics, 2019, 84(3): JM1-JM14. |
| [100] |
仵杰, 任垚煜, 贺秋利, 等. 电磁远探测仪器参数设计[J]. 西安石油大学学报(自然科学版), 2021, 36(1): 105-112, 120. WU Jie, REN Yaoyu, HE Qiuli, et al. Parameter design of remote detection tool with electromagnetic method[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2021, 36(1): 105-112, 120. |
| [101] |
仵杰, 云腾, 胡静. 基于多分量电磁远探测仪的井旁裂缝特性研究[J]. 西安石油大学学报(自然科学版), 2022, 37(1): 122-128. WU Jie, YUN Teng, HU Jing. Research on characte-ristics of crack beside well based on multi-component electromagnetic remote detector[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2022, 37(1): 122-128. |
| [102] |
仵杰, 胡静, 云腾. 基于COMSOL软件的半线圈电磁远探测响应特性分析[J]. 西安石油大学学报(自然科学版), 2022, 37(2): 95-101, 124. WU Jie, HU Jing, YUN Teng. Analysis of response characteristics of half-coil electromagnetic remote detection based on COMSOL software[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2022, 37(2): 95-101, 124. |



 刘得军,北京市昌平区府学路18号中国石油大学(北京)信息科学与工程学院,102249。Email:
刘得军,北京市昌平区府学路18号中国石油大学(北京)信息科学与工程学院,102249。Email: