2. 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
3. 中国石化胜利油田分公司物探研究院, 山东东营 257022
2. School of Geosciences, China University of Petroleum (East China), Qingdao, Shandong 266580, China;
3. Geophysical Research Institute, Shengli Oilfield Company, SINOPEC, Dongying, Shandong 257022, China
近年来,随着非常规油气勘探力度加大,其产量占比越来越高。非常规资源勘探与传统油气勘探的主要区别体现在确立甜点区与油气边界方面,而“脆性”对甜点范围预测、水力压裂具有重要作用[1]。普遍认为岩石弹性参数反映了岩石在外界应力作用下发生破坏、产生裂缝的能力,常用杨氏模量和泊松比表征岩石脆性。杨氏模量越大,泊松比越小,岩石脆性特征越明显,越容易压裂[2-4]。此外,力学实验参数及其组合也可表征岩石脆性[5]。
基本的岩石物性参数(压缩性、不可压缩性、体积模量、剪切模量等)较声波速度和波阻抗具有更明确的物理含义[6-7]。通常以拉梅参数λ、μ表示岩石的弹性性质。λ表征岩石的不可压缩性,对孔隙流体的体积变化更敏感,而μ表征岩石的刚性特征(或剪切特征),又称剪切模量,仅受骨架连通性的影响[8]。因此,为更好地描述地下储层信息,可直接从地震数据体中提取拉梅参数。
在岩石力学的定义中,脆性指物体受力变形很小时发生破裂的性质,与之相对应的延性则指物体承受较大塑性变形而不丧失其承载力的性质。脆性、延性与弹性、塑性均为岩石的变形特征。上述定义因为不易定量表征并未被广泛使用,为此人们提出了新的脆性定义[9]。
前人[10-11]利用岩石破裂时的总应变表征脆性,工程上多采用这一标准,即总应变大于5%时岩石呈塑性,反之呈脆性。也有人认为脆性是岩石破裂时黏聚力转化为内摩擦力的能力或者岩石本征内聚力与岩石在某种应力作用下破裂时的裂纹扩展阻力的比值[12]。脆性地层的主要特征为:高脆性岩层受力破裂后,往往裂缝较发育,对压裂作业非常敏感,能迅速形成复杂网状裂缝;脆性指数低的储集层一般形成简单的双翼型裂缝[13-15]。高脆性岩石具有低应变即发生破坏、低延性、内摩擦角大、硬度测试时裂纹发育完全、单轴抗压强度与劈裂试验抗拉强度比值大等特征。
1 岩石脆性影响因素影响岩石脆性的因素较多,包括岩石组分、层理和损伤等先存弱面结构、孔隙流体及其压力、围压、温度、岩体测量尺度以及受力演化过程等[5]。
岩性和矿物成分是岩石脆性的影响因素。一般来说,含有黏土矿物或亲水性较强矿物的岩石,如云母、绿泥石、角闪石等,容易表现出较强的塑性。相反,含有石英等亲水性较弱矿物的岩石则通常表现出较强的脆性。对于变质岩,由于其在高温、高压下形成,晶体结构通常会发生改变,因此可能会表现出塑性。凝灰岩在形成过程中受火山喷发物的压实和胶结作用,因此也有可能表现出一定的塑性。对于花岗岩、长英质岩屑等颗粒较大、结晶度高的岩石,由于晶体结构较完整,则表现为脆性。岩石含脆性矿物越多则脆性越大,反之亦然。不同岩石中脆性矿物含量与岩石脆性的定量关系及其影响机理仍是目前有待明确的问题。
在沉积地层和变质岩中,往往沿着层理面或先存软弱面脆性较大。这些结构使岩石的抗剪强度以及脆性产生各向异性[16-18]。如层状砂岩脆性与层理夹角呈幂指数关系,页岩脆性随层理倾角增大呈先减小后增加的趋势[19]。
岩石孔隙中的流体会降低孔隙可压缩性,为岩石提供附加刚度,并改变应力—应变曲线形态,增大岩石的有效模量[20-22]。这也是导致岩石动态杨氏模量大于静态杨氏模量的一个原因[23-25],甚至影响工程中的岩爆发生区域。但在泥页岩和黏土骨架中发生的水化作用反而降低岩石脆性、杨氏模量和抗压强度。进一步研究表明:岩石的弹性性质取决于围压与孔隙流体压力之差,即有效围压[26];脆性岩石强度随地层压力呈非线性增加、线性增加、降低三个阶段[27],或者脆性是孔隙度的线性函数[28]。显然,由于岩性和孔隙流体压力差异,孔隙流体对脆性的影响不是简单的线性关系。
围压也是影响岩石脆性的因素之一。围压多指周围岩体对岩石施加的压力,在岩石力学实验中指施加于柱样圆周上的环向压力。实验发现随着围压增大,岩石脆性不断降低。真三轴覆压实验表明,中间主应力和最小主应力也会影响岩石脆性[29],且关系较复杂,表现为多区间、多种函数关系[30]。
温度对岩石力学性质的影响较复杂,很难用线性关系概括。一般情况下,围压约50 MPa、温度从25℃增加到200℃的实验过程中,砂岩弹性模量约降低20%。
2 脆性计算方法当外力作用撤销后,物体的应力、应变状态立刻消失,并恢复其原有形状,这样的物体称为弹性体。脆性的定义和弹性参数在本质上存在一定关系,人们通过岩石的弹性参数表征岩石脆性。在地震勘探中,广泛应用弹性参数表示脆性指数。
Rickman等[4]研究了Barnnet页岩,认为岩石的脆性指数(Brittleness Index, BI)与杨氏模量呈正相关、与泊松比呈负相关,利用归一化杨氏模量和泊松比平均值表示BI
| $ \mathrm{B}{\mathrm{I}}_{1}=\frac{1}{2}\left(\frac{E-{E}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{E}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{E}_{\mathrm{m}\mathrm{i}\mathrm{n}}}+\frac{\sigma -{\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{\sigma }_{\mathrm{m}\mathrm{i}\mathrm{n}}-{\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right) $ | (1) |
式中:E为测定的杨氏模量,
Goodway等[30]认为最易破碎的区域位于低
| $ \mathrm{B}{\mathrm{I}}_{2}=\mu =\frac{E}{2(1+\sigma )} $ | (2) |
表达脆性。Guo等[31]在式(1)和式(2)的基础上,提出用拉梅常数
| $ \mathrm{B}{\mathrm{I}}_{3}=\frac{\lambda +2\mu }{\lambda }=\frac{1-\sigma }{\sigma } $ | (3) |
式(3)的结构较为单一,只用
Zhang等[32]在研究脆性各向异性时,采用杨氏模量和泊松比的比值表达脆性指数
| $ \mathrm{B}{\mathrm{I}}_{4}=\frac{E}{\sigma } $ | (4) |
| $ \mathrm{B}{\mathrm{I}}_{5}=\frac{E\rho }{\sigma } $ | (5) |
式(4)、式(5)表明:杨氏模量越大、泊松比越小、脆性越强;由于没有采用归一化,脆性指数具有量纲,且岩石的杨氏模量一般较大,所以脆性指数值也较大,不便于对比[33]。在此基础上,刘致水等[34]采用归一化杨氏模量和泊松比的比值表达脆性指数
| $ \mathrm{B}{\mathrm{I}}_{6}=\left(\frac{E-{E}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{E}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{E}_{\mathrm{m}\mathrm{i}\mathrm{n}}}\right)/\left(\frac{\sigma -{\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{\sigma }_{\mathrm{m}\mathrm{i}\mathrm{n}}-{\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right) $ | (6) |
式(6)结合了式(1)和式(4)的特点,不同的是对泊松比采用了正归一化,提高了结果的稳定性而且敏感度较高。
Chen等[35]认为杨氏模量对于石英含量高、有机质含量低、孔隙度低以及流体含量低的致密脆性岩石敏感。然而,对于含气脆性岩石(具有高石英含量、高有机质含量、高孔隙度和高含气饱和度的岩石),他们提出了一种新的脆性指示因子
| $ \mathrm{B}{\mathrm{I}}_{7}=\frac{E}{\lambda } $ | (7) |
该指标在分析和预测页岩脆性时表现出更好的敏感性,更适用于页岩脆性分析和预测。
利用弹性参数计算脆性指数的公式众多,基本以杨氏模量、泊松比以及拉梅常数等相关性较大的弹性参数组合表达脆性指数,无论计算公式如何变化和组合,都是基于脆性与杨氏模量呈正相关、与泊松比呈负相关的基本认识出发的。此外,可以结合岩石组分和弹性参数或者利用测井曲线拟合估计脆性指数[36]。
3 脆性预测新方法目前岩石脆性的预测方法基本分为两大类:Ⅰ基于传统方法的地震脆性反演方法;Ⅱ基于深度学习技术的脆性预测方法。两类方法各有千秋,优、缺点分述如下。
方法Ⅰ的优点:①在地震勘探中得到广泛应用,被用于预测地下地层性质、油气储层等;②算法相对成熟,具有较高的稳定性和可靠性;③可以利用物理模型和地质模型进行模拟和分析,有助于更好地了解油气资源的分布和可采性与地震数据的关系。
方法Ⅰ的缺点:①需要大量的先验知识和经验,对数据和模型的要求较高;②无法挖掘和利用大量地震数据中的非线性关系和隐含的规律;③难以处理复杂地质情况和非线性问题,预测效果受限。
方法Ⅱ的优点:①可以挖掘和利用大量的地震数据,对非线性关系和隐含规律具有较强的适应性;②无需先验知识和经验,可自动提取地震数据中的有效特征;③预测效果好于传统方法。
方法Ⅱ的缺点:①对数据的标注和质量要求较高,需要准确的地震数据和地质信息;②训练需要大量的计算资源和时间;③模型的可解释性有限,难以解释和分析预测结果。
下面选取几种最新的方法进行介绍。
3.1 振幅随入射角与方位角变化的新脆性指数公式及裂缝密度的贝叶斯直接反演方法Li等[37]提出了一种振幅随入射角和方位角变化(AVAZ)的贝叶斯反演方法,通过分析不同方位地震数据的振幅变化估计地下岩石的脆性和裂缝密度,充分考虑了地震噪声和不确定性。数值模拟和实际地震数据分析表明,该方法提高了脆性指标和裂缝密度的估计精度,有望在油气勘探和地质灾害预测中得到广泛应用。同时,该方法也为地震数据贝叶斯反演[38]提供了新的思路和方法。
Li等[37]提出新的脆性指数公式
| $ \mathrm{B}\mathrm{I}=\frac{\left(1+\sigma \right)\left(1-2\sigma \right)}{\sigma } $ | (8) |
| $ \frac{\mathrm{\Delta }\mathrm{B}\mathrm{I}}{\mathrm{B}\mathrm{I}}=\left(\frac{2\sigma }{2\sigma -1}-\frac{1}{1+\sigma }\right)\frac{\mathrm{\Delta }\sigma }{\stackrel{-}{\sigma }} $ | (9) |
式中
| $ \begin{aligned} R_{\mathrm{PP}}(\theta, \phi)= & a_E(\theta) R_E+a_{\mathrm{BI}}(\theta) R_{\mathrm{BI}}+ \\ & a_\rho(\theta) R_\rho+a_e(\theta, \phi) \Delta e \end{aligned} $ | (10) |
式中:
图 1
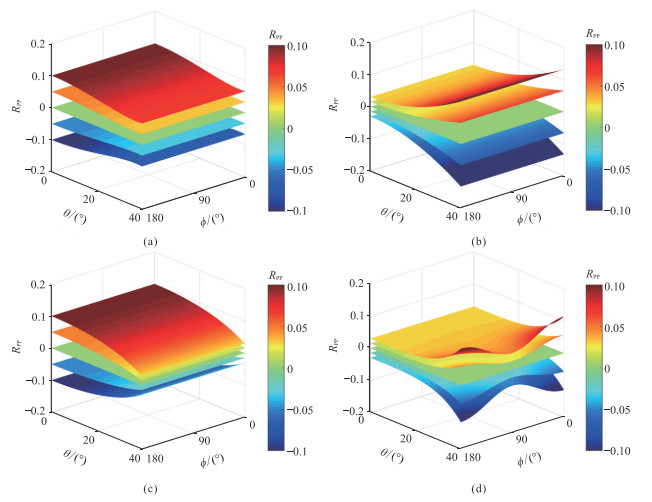
|
图 1 |
(1)在建模中假定页岩储层具有HTI对称性。由于背景岩石可能呈VTI对称性,忽略VTI背景容易导致AVAZ反演的弹性参数和各向异性参数不可靠。因此,由嵌入在VTI背景中的旋转不变的垂直裂缝系统形成的正方体模型可能更适合于描述典型的含裂缝页岩储层[41]。
(2)裂缝和背景岩石被气体和水的均匀混合流体饱和填充。
(3)界面呈弱各向异性。
(4)高质量的大入射角和宽方位地震反射数据是准确估计脆性指数和断裂密度的关键因素。模型参数的敏感性分析表明,入射角大于25°时,脆性指数反射率和裂缝密度对反射系数更敏感。
将脆性预测新方法应用于南四川盆地的二维数据。图 2为E、BI、ρ、Δe反演结果。由图可见,在储层周围E较小,而BI和Δe则较大,说明BI表征页岩气储层脆性的效果好于E。图 3为反演结果与测井数据(真值)的对比。由图可见,反演数据与测井数据之间的匹配度很高,说明该方法可以准确反演BI和Δe,更适合于描述天然裂缝或水力压裂的易裂脆性页岩。
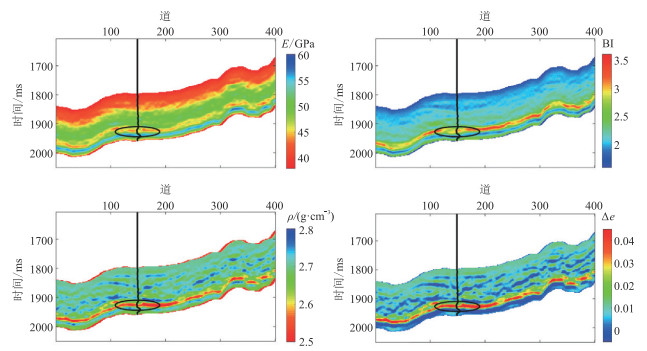
|
图 2 E、BI、ρ、 |
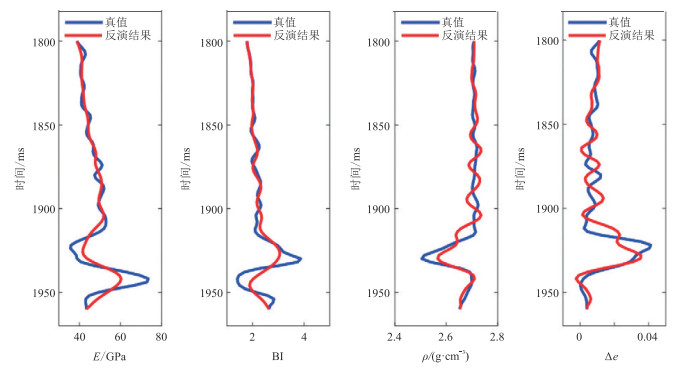
|
图 3 反演结果与测井数据的对比 |
Wood[42]通过稀疏测井数据集预测页岩的脆性指数,结合导数和波动率属性增强数据集,从而提高预测结果的准确性。结果表明,使用导数和波动率属性可以提高预测精度,在数据集较小的情况下尤为明显。此外还分析了模型的敏感性,以评估输入特征的重要性,表明导数属性明显影响模型性能,可以提高模型的预测精度。该方法可用于其他类型的机器学习模型,并且对于石油和天然气勘探领域有着较好的应用价值。
首先计算每条测井曲线(如伽马测井GR、体积密度测井PB和声波测井DT)的6种属性,即测井曲线一阶导数(属性1)、一阶导数的算术平均(属性2)、测井曲线二阶导数(属性3)、瞬时深度变化率的自然对数(属性4,即第N+1个深度点与第N个深度点的属性比值再取自然对数)、属性4在指定时间区间内的标准差(属性5,即L波动率)、L波动率的算术平均(属性6)。
完成测井数据集处理后,使用线性回归(LR)、弹性网络(ElasticNet)、K近邻算法(K-Nearest Neighbors,KNN)、支持向量回归(SVR)、自适应增强(ADA)、随机森林(RF)和极限梯度提升(XGB)预测BI。前两种方法假设每个自变量和因变量之间为线性关系,并利用经典的最小二乘回归使预测误差最小化。后五种方法能够处理自变量和因变量之间的非线性关系,即数据匹配、SVR和树集成回归。图 4为由KNN模型评估的示例验证子集的BI预测值与测量值。由图可见,包含特征选择属性的案例2的预测精度明显高于案例1。

|
图 4 由KNN模型(基于90%的数据记录)评估的示例验证子集(数据记录的10%)的BI预测值与测量值[44] (a)A井(案例1);(b)B井(案例1);(c)A井(案例2);(d)B井(案例2) 案例1包括3个变量(GR0、PB0、DT0),案例2包括9个变量(GR1、GR4、PB0、PB1、PB4、DT0、DT1、DT4、DT5),数字0表示原始测井数据,其余数字代表前述的属性号,如DT4代表声波测井的属性4。R为相关系数,MAE为平均绝对误差,RMSE为均方根误差。 |
Zhang等[43]提出了一种使用卷积神经网络(CNN)和长短期记忆网络(LSTM)的深度学习模型,通过学习不同测井曲线之间的关系生成缺失的DT曲线,并评估页岩脆性。首先,利用CNN提取测井曲线的特征;然后使用LSTM模型预测时间序列,从而生成缺失的DT曲线;最后,使用生成的DT曲线评估页岩的脆性指数。他们利用Permian盆地的测井数据集评估模型的性能,结果表明,使用CNN-LSTM模型生成的DT曲线可以在一定程度上提高脆性评估精度。此外,还分析了模型的敏感性,以评估不同的输入特征对模型性能的影响。总的来说,该方法可以在缺少测井数据的情况下,生成缺失的DT曲线并提高脆性评估精度。虽然该方法在实验中取得了一定效果,但是还需要实际数据的进一步验证和优化[43]。
图 5为CNN-LSTM网络结构图。由图可见,以GR、PB和补偿中子测井曲线为输入,数据经过CNN模块和LSTM模块,然后输出DT数据。与地质学思想类似,在LSTM生成DT曲线的过程中,整合了测井曲线之间的内在联系和不同测井曲线随深度变化的趋势。图 6为基于CNN-LSTM、LSTM和CNN的DTC(P-wave travel time)以及DTS(S-wave travel time)预测结果。由图可见:①CNN-LSTM模型精度最高(图 6a上、图 6b上)。②CNN-LSTM模型的DTC的R为0.90,RMSE为11.11

|
图 5 CNN-LSTM网络结构图[43] CNN的特征提取部分由一个卷积层和一个ReLU层组成。在序列学习模块中有两个LSTM层,其中每个有30个神经元。 |
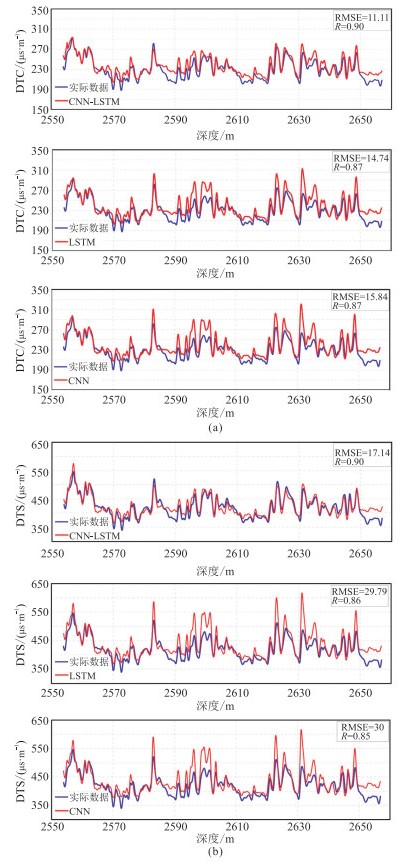
|
图 6 基于CNN-LSTM(上)、LSTM(中)和CNN(下)的DTC(a)以及DTS(b)预测结果 |
本文总结了岩石脆性的影响因素,汇总了主要的脆性计算方法。脆性预测目前主要有传统方法和基于人工智能的方法,两种方法各有优、缺点,在实际应用中可综合使用两种方法以达到更好的效果。脆性预测技术的发展方向涉及以下几个方面。
(1)更多的脆性属性研究。目前对于脆性属性的研究主要集中于岩石的物理和力学属性,未来可能还需要研究其他影响脆性的因素,如地史、化学成分等。
(2)精确的预测模型。脆性属性预测和模拟是地震勘探和地质勘查中重要的应用之一,未来对预测模型的精度要求可能更高,期待集成更多的技术手段,如人工智能等,以提高预测精度。
(3)应用领域的扩展。脆性属性除了用于地震勘探和地质勘查之外,也可用于其他领域,如地质灾害预测和土地利用规划等。未来可能会有更多的学科、领域将脆性属性引入研究范畴。
(4)更多地震数据的获取和处理。随着勘探深度增大和新兴技术的应用,将获得更多高质量的地震数据。同时,借助人工智能等新技术,可以更好地处理和解释这些数据。
(5)更精细的脆性评价方法。除了现有的地震属性、地震反演和岩石物理等方法外,还可能出现更精确的脆性评价方法,如基于声波谱的评价方法,可提供更多岩石的本质特征信息。
(6)深入研究脆性与油气藏的关系。未来将更深入地研究脆性与油气藏之间的关系,以更好地预测油气藏分布和储量、指导油气勘探。
总之,储层脆性的研究趋向于多元化和精细化,以满足不同领域的需求,并为相关领域研究提供更可靠的支持和指导。
| [1] |
张丰麒, 金之钧, 盛秀杰, 等. 基于基追踪-BI_Zoeppritz方程广义线性脆性指数直接反演方法[J]. 地球物理学报, 2017, 60(10): 3954-3968. ZHANG Fengqi, JIN Zhijun, SHENG Xiujie, et al. A direct inversion for brittleness index based on GLI with basic-pursuit decomposition[J]. Chinese Journal of Geophysics, 2017, 60(10): 3954-3968. DOI:10.6038/cjg20171023 |
| [2] |
秦晓艳, 王震亮, 于红岩, 等. 基于岩石物理与矿物组成的页岩脆性评价新方法[J]. 天然气地球科学, 2016, 27(10): 1924-1932, 1941. QIN Xiaoyan, WANG Zhenliang, YU Hongyan, et al. A new shale brittleness evaluation method based on rock physics and mineral compositions[J]. Natural Gas Geoscience, 2016, 27(10): 1924-1932, 1941. DOI:10.11764/j.issn.1672-1926.2016.10.1924 |
| [3] |
MAKOWITZ A, MILLIKEN K L. Quantification of brittle deformation in burial compaction, Frio and Mount Simon Formation sandstones[J]. Journal of Sedimentary Research, 2003, 73(6): 1007-1021. DOI:10.1306/051003731007 |
| [4] |
RICKMAN R, MULLEN M, PETRE E, et al. A practical use of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett Shale[C]. SPE Annual Technical Conference and Exhibition, 2008, doi: 10.2118/115258-MS.
|
| [5] |
曹东升, 曾联波, 吕文雅, 等. 非常规油气储层脆性评价与预测方法研究进展[J]. 石油科学通报, 2021, 6(1): 31-45. CAO Dongsheng, ZENG Lianbo, LYU Wenya, et al. Progress in brittleness evaluation and prediction me-thods in unconventional reservoirs[J]. Petroleum Science Bulletin, 2021, 6(1): 31-45. DOI:10.3969/j.issn.2096-1693.2021.01.003 |
| [6] |
GRAY D, Andersen E. The application of AVO and inversion to the estimation of rock properties[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 549-552.
|
| [7] |
GRAY D, GOODWAY B, CHEN T. Bridging the gap: Using AVO to detect changes in fundamental elastic constants[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 852-855.
|
| [8] |
DUFOUR J, GOODWAY B, SHOOK I, et al. AVO analysis to extract rock parameters on the Blackfoot 3C-3D seismic data[C]. SEG Technical Program Expanded Abstracts, 1998, 17: 174-177.
|
| [9] |
李庆辉, 陈勉, 金衍, 等. 页岩脆性的室内评价方法及改进[J]. 岩石力学与工程学报, 2012, 31(8): 1680-1685. LI Qinghui, CHEN Mian, JIN Yan, et al. Indoor evaluation method for shale brittleness and improvement[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(8): 1680-1685. |
| [10] |
徐开礼, 朱志澄. 构造地质学(第二版)[M]. 北京: 地质出版社, 1993.
|
| [11] |
陈国文, 覃素华, 刘雷颂, 等. 辽河坳陷大民屯凹陷沙四段页岩油"甜点"预测及评价[J]. 石油地球物理勘探, 2022, 57(增刊1): 145-153. CHEN Guowen, QIN Suhua, LIU Leisong, et al. Prediction and evaluation of sweet spots for shale oil in Es4 of Damintun Sag, Liaohe Depression[J]. Oil Geophysical Prospecting, 2022, 57(S1): 145-153. |
| [12] |
SCHOLZ C H. The Mechanics of Earthquakes and Faulting(3rd ed.)[M]. Cambridge University Press, 2019.
|
| [13] |
KAHRAMAN S, ALTINDAG R. A brittleness index to estimate fracture toughness[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(2): 343-348. DOI:10.1016/j.ijrmms.2003.07.010 |
| [14] |
李华阳, 周灿灿, 李长喜, 等. 致密砂岩脆性指数测井评价方法——以鄂尔多斯盆地陇东地区长7段致密砂岩储集层为例[J]. 新疆石油地质, 2014, 35(5): 593-597. LI Huayang, ZHOU Cancan, LI Changxi, et al. Logging evaluation and application of brittleness index in tight sandstone reservoir: A case study of Chang-7 tight sandstone reservoir in Longdong area of Ordos basin[J]. Xinjiang Petroleum Geology, 2014, 35(5): 593-597. |
| [15] |
戴世立, 王力娟, 辛朝坤. 松辽盆地北部古中央隆起带基底岩石弹性参数测试及特征分析[J]. 石油地球物理勘探, 2023, 58(2): 443-453. DAI Shili, WANG Lijuan, XIN Zhaokun. Testing and characteristic analysis of elastic parameters of basement rock in the paleo-central uplift belt in the nor-thern Songliao Basin[J]. Oil Geophysical Prospecting, 2023, 58(2): 443-453. |
| [16] |
HUCKA V, DAS B. Brittleness determination of rocks by different methods[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1974, 11(10): 389-392. |
| [17] |
FEI G, ZENG L, DI B, et al. The effect of stress on brittleness of synthetic shale with different types of clay minerals[C]. Extended Abstracts of 79th EAGE Conference & Exhibition, 2017, 1-5.
|
| [18] |
李远, 程飞, 雷栋, 等. 基于页岩岩石物理分析技术的TOC和脆性预测[J]. 石油地球物理勘探, 2018, 53(增刊2): 204-210. LI Yuan, CHENG Fei, LEI Dong, et al. TOC and brittleness prediction based on shale rock physical analysis[J]. Oil Geophysical Prospecting, 2018, 53(S2): 204-210. |
| [19] |
蔡国刚, 童亨茂. 太古宇潜山不同岩石类型裂缝发育潜力分析——以辽河西部凹陷为例[J]. 地质力学学报, 2010, 16(3): 260-270. CAI Guogang, TONG Hengmao. Analysis on fracture potential for different types of rocks in Archean Buried hill: A case study of Liaohe western sag[J]. Journal of Geomechanics, 2010, 16(3): 260-270. DOI:10.3969/j.issn.1006-6616.2010.03.004 |
| [20] |
张军, 艾池, 李玉伟, 等. 基于岩石破坏全过程能量演化的脆性评价指数[J]. 岩石力学与工程学报, 2017, 36(6): 1326-1340. ZHANG Jun, AI Chi, LI Yuwei, et al. Brittleness evaluation index based on energy variation in the whole process of rock failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1326-1340. |
| [21] |
MARTIN C D. Brittle failure of rock materials: test results and constitutive models[J]. Canadian Geotechnical Journal, 1996, 33(2): 378-378. DOI:10.1139/t96-901 |
| [22] |
任岩, 曹宏, 姚逢昌, 等. 岩石脆性评价方法进展[J]. 石油地球物理勘探, 2018, 53(4): 875-886. REN Yan, CAO Hong, YAO Fengchang, et al. Review of rock brittleness evaluation methods[J]. Oil Geophysical Prospecting, 2018, 53(4): 875-886. |
| [23] |
路保平, 林永学, 张传进. 水化对泥页岩力学性质影响的实验研究[J]. 地质力学学报, 1999, 5(1): 65-70. LU Baoping, LIN Yongxue, ZHANG Chuanjin. Laboratory study on effect of hydration to shale mechanics[J]. Journal of Geomechanics, 1999, 5(1): 65-70. |
| [24] |
葛洪魁, 陈颙, 林英松. 岩石动态与静态弹性参数差别的微观机理[J]. 石油大学学报(自然科学版), 2001, 25(4): 34-36. GE Hongkui, CHEN Yong, LIN Yingsong. Microscopic mechanism of difference between static and dynamic elastic parameters of rock[J]. Journal of the University of Petroleum, China, 2001, 25(4): 34-36. |
| [25] |
HANDIN J, HAGER R V Jr, FRIEDMAN M, et al. Experimental deformation of sedimentary rocks under confining pressure: Pore pressure tests 1[J]. AAPG Bulletin, 1963, 47(5): 717-755. |
| [26] |
黄书岭. 高应力下脆性岩石的力学模型与工程应用研究[D]. 北京: 中国科学院研究生院, 2008.
|
| [27] |
JIN X, SHAH S N, ROEGIERS J C, et al. An integrated petrophysics and geomechanics approach for fracability evaluation in shale Reservoirs[J]. SPE Journal, 2015, 20(3): 518-526. DOI:10.2118/168589-PA |
| [28] |
MOGI K. Effect of the intermediate principal stress on rock failure[J]. Journal of Geophysical Research, 1967, 72(20): 5117-5131. DOI:10.1029/JZ072i020p05117 |
| [29] |
杨继华, 刘汉东. 岩石强度和变形真三轴试验研究[J]. 华北水利水电学院学报, 2007, 28(3): 66-68. YANG Jihua, LIU Handong. True triaxial experimental study on rock strength and deformation[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2007, 28(3): 66-68. |
| [30] |
GOODWAY B, PEREZ M, VARSEK J, et al. Seismic petrophysics and isotropic-anisotropic AVO me-thods for unconventional gas exploration[J]. The Lea-ding Edge, 2010, 29(12): 1500-1508. |
| [31] |
GUO Z, CHAPMAN M, LI X. A shale rock physics model and its application in the prediction of brittleness index, mineralogy, and porosity of the Barnett Shale[C]. SEG Technical Program Expanded Abstracts, 2012, 31, SEG-2012-0777.
|
| [32] |
ZHANG B, ZHAO T, JIN X, et al. Brittleness evaluation of resource plays by integrating petrophysical and seismic data analysis[J]. Interpretation, 2015, 3(2): T81-T92. |
| [33] |
LUAN X, DI B, WEI J, et al. Laboratory measurements of brittleness anisotropy in synthetic shale with different cementation[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 3005-3009.
|
| [34] |
刘致水, 孙赞东. 新型脆性因子及其在泥页岩储集层预测中的应用[J]. 石油勘探与开发, 2015, 42(1): 117-124. LIU Zhishui, SUN Zandong. New brittleness indexes and their application in shale/clay gas reservoir prediction[J]. Petroleum Exploration and Development, 2015, 42(1): 117-124. |
| [35] |
CHEN J, ZHANG G, CHEN H, et al. The construction of shale rock physics effective model and prediction of rock brittleness[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 2861-2865.
|
| [36] |
MARTIN J. A Geomechanical Approach to Evaluate Brittleness Using Well Logs: Mississippian Limestone, Northern Oklahoma[D]. The University of Texas at Arlington, Texas, 2015.
|
| [37] |
LI L, ZHANG G, PAN X, et al. Bayesian amplitude variation with angle and azimuth inversion for direct estimates of a new brittleness indicator and fracture density[J]. Geophysics, 2022, 87(5): M189-M197. |
| [38] |
DAUBECHIES I, A DEVORE R, FORNASIER M, et al. Iteratively reweighted least squares minimization for sparse recovery[J]. Communications on Pure and Applied Mathematics, 2010, 63(1): 1-38. |
| [39] |
ZONG Z, YIN X, WU G. AVO inversion and poroelasticity with P- and S-wave moduli[J]. Geophysics, 2012, 77(6): N17-N24. |
| [40] |
PAN X, LI L, ZHOU S, et al. Azimuthal amplitude variation with offset parameterization and inversion for fracture weaknesses in tilted transversely isotropic media[J]. Geophysics, 2021, 86(1): C1-C18. |
| [41] |
SCHOENBERG M, HELBIG K. Orthorhombic media: Modeling elastic wave behavior in a vertically fractured earth[J]. Geophysics, 1997, 62(6): 1954-1974. |
| [42] |
WOOD D A. Predicting brittleness indices of prospective shale formations from sparse well‑log suites assisted by derivative and volatility attributes[J]. Advances in Geo-Energy Research, 2022, 6(4): 334-346. |
| [43] |
ZHANG F, DENG S, WANG S, et al. Convolutional neural network long short-term memory deep learning model for sonic well log generation for brittleness evaluation[J]. Interpretation, 2002, 10(2): T367-T378. |



 张军华,山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email:
张军华,山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院,266580。Email: