塔里木盆地碳酸盐岩油气藏主要分布于裂缝—孔洞型储层中[1],该类储层具有埋藏深、横向变化快和非均质性强的特点,利用地震资料精细预测较为困难,制约了缝洞型油气藏的进一步勘探与开发。碳酸盐岩缝洞型储层预测的一个重要手段就是寻找并确定这类缝洞连通体的地震反射特征,并借助地球物理手段精细预测断裂、溶洞和裂缝,再对缝洞系统及其空间接触关系进行综合表征与评价。
对于断裂和溶洞的识别与刻画,叠后地震数据仍是最常用且有效的基础资料。现阶段,人们通常提取一些边缘检测类的地震属性(相干、曲率和结构张量等)用于地下断裂和溶洞的识别,并且在简单构造区都取得了较好的应用效果[2-5]。叠后地震属性中应用最为广泛的是相干体技术[6-8],通过计算相邻地震道间的相似性来衡量地下构造的不连续程度。近年来发展了许多改进的相干体算法[9-11],特别是分频相干技术[12-14]进一步提高了相干分析的计算效率或断裂识别的分辨率。基于相位信息对地下弱构造有更高的敏感性,Wang等[15]提出一种基于分频相位的地质导向相干算法(后文统称为分频导向相干),将谱分解得到的谱相位有效地融入到地质导向相干算法中,更好地用于地下深层弱反射背景下异常构造的识别与刻画。相比于常规地震属性,该方法的识别结果横向分辨率更高,细节更为丰富,可作为叠后地震资料断裂溶洞识别的一种有效手段。
相比于大断裂,裂缝作为一种小尺度的不连续异常体,用叠后地震属性预测的结果精度较低,为此发展了基于叠前地震资料的各种裂缝预测方法。人们对水平横向各向同性介质(也被称为HTI介质)的地震反射各向异性特征进行了研究,并将其成功用于裂缝分布特征和裂缝介质弹性参数的预测中[16]。随着Ruger方程的提出以及宽方位地震资料采集和处理技术的发展,人们开始利用纵波反射振幅随入射角和炮检距的变化关系(AVAZ)来预测地下的裂缝分布情况[17-19],且已成为现阶段最有效、应用最广泛的预测方法。此外,研究表明,裂缝引起的各向异性不仅表现为方位振幅的差异,纵波速度、频率、衰减等地震属性也会存在方位上的差异,因此,一些基于方位地震属性各向异性的方法也被用于表征地下的裂缝发育强度[20-21]。相比于振幅,基于相位的信息对地下弱构造具有更高的敏感性。Yuan等[22]提出一种新属性——地质导向相位属性(后文统称为导向相位属性),同样能够反映地下构造的不连续,而且与相干属性相比,检测小尺度异常构造的潜力更大。基于此,本文尝试提取不同方位数据的导向相位属性进行差异性分析,发展一种基于宽方位导向相位属性的各向异性强度表征方法,以用于地下裂缝的预测。
本文研究基于叠后—叠前多属性分析的缝洞型储层地震综合预测方法。首先基于叠后地震资料的属性优选,将分频导向相干属性作为断裂及溶洞的识别结果,再基于本文提出的叠前宽方位各向异性强度表征方法,通过奇异值分解(SVD)计算不同方位导向相位属性的最大奇异值与奇异值之和的比值,用于预测地下裂缝的分布。最后将该流程应用于某区块碳酸盐岩的缝洞型储层预测,通过叠前、叠后多属性预测结果对缝洞体系进行综合表征与评价,用钻井结果验证了方法的有效性。
1 方法原理地下发育的裂缝能够诱导地层介质产生各向异性,而各向异性不仅能够引起方位振幅的差异,同样也会引起不同方位的其他地震属性之间的差异,由此发展了多种基于方位属性各向异性的裂缝预测方法[16-17]。Yuan等[22]提出的地质导向相位属性,可以用于检测地下的不连续异常体,并且对地下裂缝等弱构造具有比其他属性更高的敏感性。因此,本文尝试通过量化方位数据导向相位属性之间的这种差异性,发展一种宽方位导向相位属性各向异性强度表征方法,进而预测地下裂缝的分布。
该方法的整个处理解释流程如图 1所示,主要包括以下几个关键步骤:
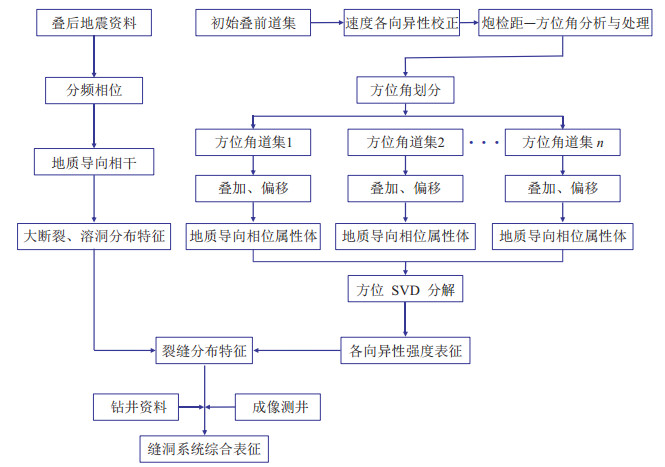
|
图 1 宽方位导向相位属性各向异性强度表征流程 |
(1)对拉平处理后的初始叠前道集进行速度各向异性校正,一方面消除速度各向异性对后续方位各向异性分析的影响,另一方面将叠前道集进一步拉平,从而为分方位叠加及层位解释提供高质量的基础数据;
(2)对优化后的叠前道集进行信噪比和炮检距—方位角分布等方面的分析,以寻找最佳分方位策略,并叠加得到不同方位的叠加数据体;
(3)设置相干道数和时窗等计算参数,对各方位叠加数据体采用相同参数处理之后,提取导向相位属性体;
(4)设置纵向滑动时窗,对各方位导向相位属性体进行方位奇异值分解,计算最大奇异值与奇异值之和的比值,表征地下的各向异性强度,作为地下裂缝的预测结果;
(5)提取目标储层处的裂缝预测结果,并与叠后断裂溶洞识别结果、已钻井数据等资料进行对比,进而分析缝洞型储层的缝洞接触关系及连通情况。
其中,步骤(4)中利用奇异值分解来量化不同方位属性之间差异性的计算流程如图 2所示,其具体原理如下:
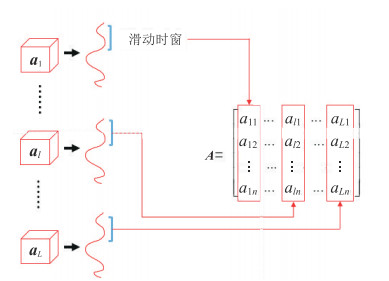
|
图 2 方位奇异值分解原理 |
首先定义一个n×L大小的矩形分析时窗,该窗口内的数据由包含n个采样点的L个地震道组成,这L道地震数据分别来自于不同方位导向相位属性体的相同位置。将该时窗内的数据定义为矩阵A,其中元素
| $ \boldsymbol{A}=\left[\begin{array}{cccc}{a}_{11}& {a}_{21}& \cdots & {a}_{L1}\\ {a}_{12}& {a}_{22}& \cdots & {a}_{L2}\\ \vdots & \vdots & \vdots & \vdots \\ {a}_{1n}& {a}_{2n}& \cdots & {a}_{Ln}\end{array}\right] =[{\boldsymbol{a}}_{1}, {\boldsymbol{a}}_{2}, \cdots , {\boldsymbol{a}}_{L}] $ | (1) |
随后,对矩阵A进行奇异值分解并得到L个非零的奇异值。设λj (j = 1, 2, …, L)是矩阵A的第j个奇异值,计算最大奇异值与奇异值之和的比值来表征地下的各向异性强度
| $ \sigma =\frac{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\sum\limits _{j=1}^{L}{\lambda }_{j}} $ | (2) |
式中
为了验证所提方法在裂缝预测中的应用效果,选取塔里木盆地某三维地震资料进行测试。该地区主要发育碳酸盐岩缝洞型储层,横向变化快、非均质性较强。已钻井表明该区高产井主要分布在断裂系统周边,目前主干断裂大体明晰,但次生断裂解释精度较低,特别是裂缝发育和分布特征刻画不清晰。因此,准确刻画断裂及裂缝分布特征,对于该地区油气勘探与开发具有非常重要的意义。
为更好刻画目标储层不连续异常体的分布特征,将从叠后地震、叠前地震和钻井资料三个方面进行综合分析。首先提取有效的叠后地震属性预测该区的大断裂和溶洞,再基于叠前地震资料开展AVAZ反演和宽方位导向相位属性各向异性强度表征,用于地下裂缝的预测,厘清裂缝与断裂溶洞系统的关系,并与实钻井资料进行对比分析,进而评价该区缝洞型储层发育情况。
2.1 叠后大断裂及溶洞预测基于叠后三维地震资料,提取三种常规地震属性以及分频导向相干属性,并通过不同属性识别效果的对比分析,最终优选出一种叠后大断裂预测的敏感属性。该工区共有主测线550条、联络线751条,工区覆盖面积为100 km2,道间距为15 m×15 m,采样间隔为2 ms。图 3a展示了其中一条地震剖面及目标储层位置(图中黑色线条处),从中可以看出该区断裂较为发育,溶洞的串珠状反射特征明显,目标储层处反射特征比较杂乱、信噪比较低。目标层原始振幅切片(图 3b)显示工区东部发育一条明显的大断裂,且断裂周边发育溶洞,这些都为地下储层中裂缝的形成创造了有利条件。

|
图 3 叠后地震资料分析 (a)地震剖面;(b)沿层振幅切片 |
随后,提取目标储层处的倾角属性、曲率属性和瞬时振幅属性,分别如图 4a~图 4c所示。倾角属性能够体现因发育断层或裂缝所引起的构造变化;曲率属性能够反映构造应力作用导致的地层形变特征,通常是裂缝发育的重要标志;而瞬时振幅属性能够有效地刻画地震数据中与围岩振幅差异较大且具有“串珠状”反射特征的溶洞系统。从各属性识别结果对比中可知,倾角属性和曲率属性预测断裂效果整体上相近,预测断裂比较离散、连续性较差;瞬时振幅属性只能够反映出溶洞信息;而分频导向相干属性[15](图 4d,低频、中频和高频结果RGB融合显示)能够检测更多的地质细节特征且连续性较好,能刻画溶洞的分布特征。因此,选取分频导向相干属性作为叠后大断裂和溶洞预测的敏感属性。
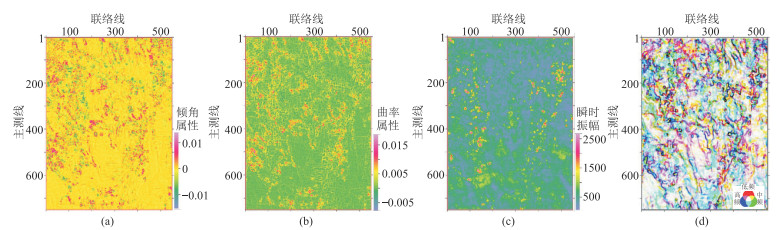
|
图 4 叠后沿层地震属性对比 (a)倾角;(b)曲率;(c)瞬时振幅;(d)分频导向相干 |
该工区已进行了宽方位地震资料的采集和处理。为进一步满足叠前属性处理的需求,在常规处理流程基础上,开展了精细的深度域速度建模和OVT域处理等工作,工区面元大小为15 m×15 m,平均覆盖次数为175。随后,根据叠前地震道集(图 5a)品质和方位角—炮检距分布情况(图 5c,图中正北方向为0°方位,且顺时针指示增大方向),将叠前炮检距道集按方位角划分为4组(图 5d),并进行分方位叠加处理,以各组中心方位角作为该组叠加数据的方位角(中心方位角分别为45°、135°、225°和315°)。图 5b展示了某位置处的分方位叠前道集,可以看到每个方位内的炮检距分布较为均匀,且各方位都存在大炮检距数据,道集数据经部分叠加后的信噪比也有所提升。图 5e中不同方位叠加数据的振幅谱显示,各方位叠加数据的振幅谱较为相近且存在细微差异。数据主频约为22 Hz、频带范围大致为5~50 Hz,地震资料整体分辨率不高。
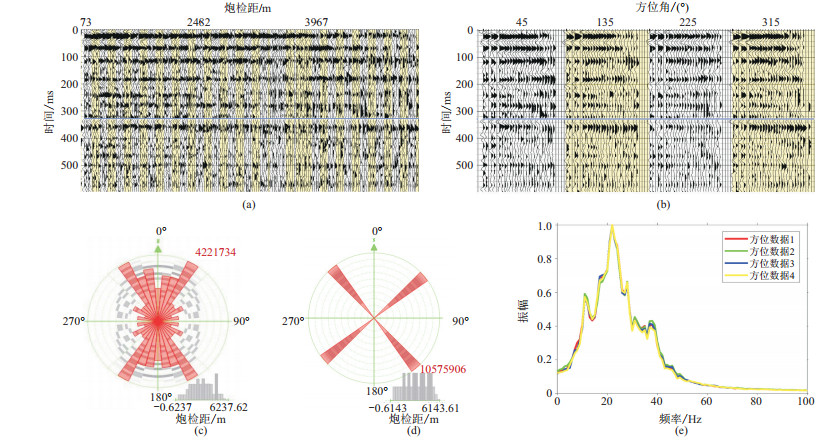
|
图 5 叠前道集分析与处理 (a)叠前道集;(b)分方位道集;(c)原始道集方位角—炮检距分布;(d)分方位后道集方位角—炮检距分布;(e)分方位叠加数据频谱 |
首先,提取不同方位叠加数据体的原始振幅切片(图 6),可以看出各方位数据在平面上的振幅强弱变化关系整体相似,且都揭示工区东部发育一条较大断裂带,但局部位置仍存在一些微弱差异(图中绿色椭圆所示),比如断裂在45°和225°方位数据中较为清晰,而在其他两个方位模糊。此外,受强振幅异常的影响,工区内小断裂和裂缝在原始振幅切片中都不能被很好识别。
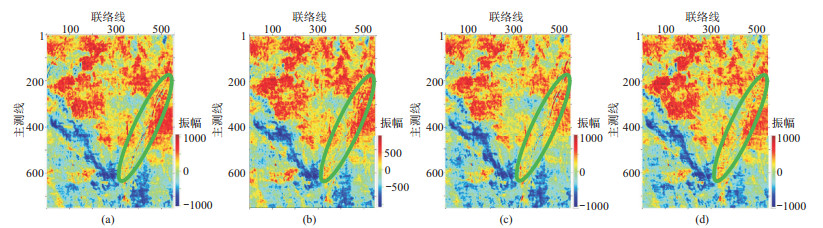
|
图 6 不同方位数据体沿层振幅切片对比 (a)45°;(b)135°;(c)225°;(d)315° |
随后,基于不同方位数据体,进一步计算并提取导向相位属性切片(图 7)。受部分叠加数据品质的限制,各方位导向相位属性容易受到随机噪声的影响,但分方位处理能够保留更多微构造细节,并且能够用导向相位属性较好地识别出来。同时,在不同方位导向相位属性体计算参数相同的条件下,不同属性结果仍存在微弱的差异,那么该差异可能是由于各向异性引起不同方位数据在构造上的差异所造成的。因此,可基于不同方位导向相位属性结果之间的差异,进一步分析目标储层的各向异性强度。

|
图 7 不同方位导向相位属性沿层切片对比 (a)45°;(b)135°;(c)225°;(d)315° |
通过图 1b中解释流程对不同方位导向相位属性体进行方位奇异值分解,计算得到最大奇异值与奇异值之和的比值,进一步提取沿层结果用于指示目标储层的各向异性强度分布情况,如图 8c所示。结果显示叠前裂缝预测结果与分频导向相干属性预测的断裂分布(图 4d)整体较为吻合,裂缝主要集中分布于断裂和溶洞附近,裂缝预测结果相对可靠。
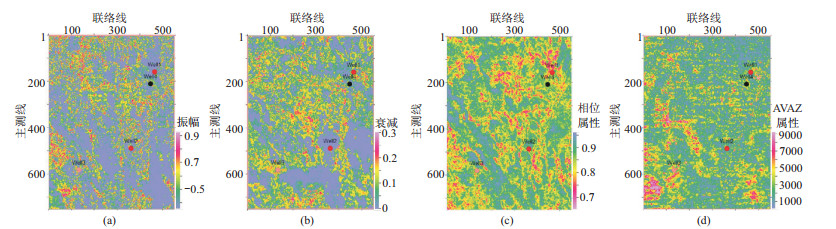
|
图 8 不同属性裂缝预测结果对比(层段T~T+30ms) (a)振幅各向异性;(b)衰减各向异性;(c)宽方位导向相位属性;(d)叠前AVAZ反演 |
此外,通过叠前角道集进一步开展基于精确Ruger方程的叠前AVAZ反演[18]和方位衰减各向异性的裂缝预测,并进行对比(图 8)。从目标储层横向展布特征来看,方位振幅各向异性(图 8a)、方位衰减各向异性(图 8b)和方位导向相位属性(图 8c)得到的裂缝预测结果整体上具有一定的相似性,并且与叠后断裂预测结果也存在一定的相关性,预测裂缝集中分布在断裂带周边,而叠前AVAZ反演结果却表现出较大的差异。从预测结果的裂缝分布形态来看,基于振幅类的预测裂缝(图 8a和8d)平面分布相对离散且连续性较差,而基于其他属性类的预测裂缝(图 8b和8c)平面分布比较自然,表现出较好的横向连续性。
2.3 缝洞系统综合表征为进一步对比不同裂缝预测方法的应用效果,从叠后断裂溶洞识别、叠前裂缝预测和已钻井情况三方面进行综合分析。该研究区共有4口井,各井油气产能情况为:Well 1井和Well 2井累计产油分别为36.18×104 t和30.81×104 t,均为高产井;Well 3井累计产油3.39×104 t,为低产井;Well 4井累计产油800 t,产量极低。同时钻井显示Well 2和Well 3井在目标层处存在放空、漏失现象。
图 9展示了4口井附近的预测结果放大显示,从左到右依次为叠后断裂溶洞识别、方位振幅各向异性、方位衰减各向异性、宽方位导向相位属性和叠前AVAZ反演结果。
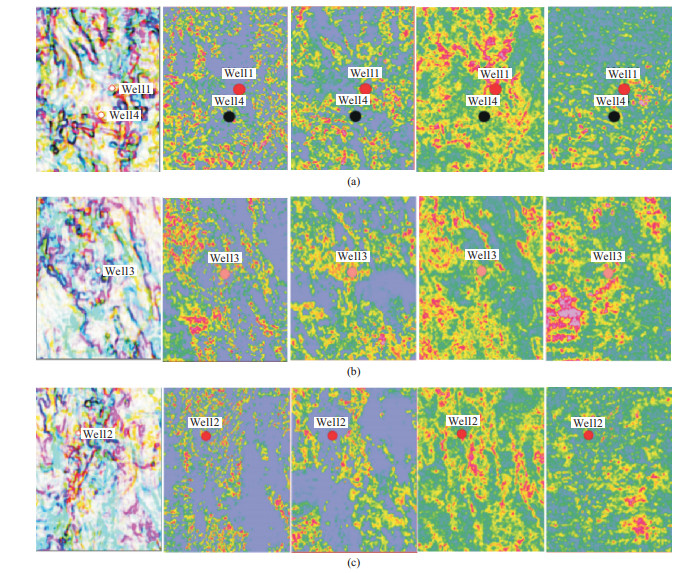
|
图 9 井周不同预测结果对比 (a)Well 1和Well 4;(b)Well 3;(c)Well 2 从左到右依次为叠后断裂溶洞识别、方位振幅各向异性、方位衰减各向异性、宽方位导向相位属性和叠前AVAZ反演结果。 |
从图 9a可以看出,叠后断裂预测结果显示Well 1井东部广泛发育大断裂和溶洞,方位衰减各向异性、宽方位相位属性和叠前AVAZ反演结果都显示该井周边发育有高密度裂缝区,从而使得大断裂与裂缝形成较好的连通性,该井获得高产能。Well 4井周边大断裂欠发育,而裂缝在该井周边不发育,并且大断裂与裂缝两者之间的连通程度也较差,导致该井产量极低。
从图 9b可见,Well 3井在钻井过程中有放空和漏失现象发生,说明该井周边孔洞发育,这在叠后断裂预测结果有所显示。叠前裂缝预测结果显示该井周边发育有少量裂缝,钻井资料表明该井初期产油量高,而后期产量明显降低,则可能与溶洞—裂缝的连通性较差有关。
从图 9c可见,钻井显示Well 2井也存在放空、漏失现象,叠后相干属性检测出该井周边发育有溶洞,且大断裂也较为发育。宽方位相位属性显示该井周边发育高密度裂缝区,且与大断裂的连通使得该井产量较高,而其他三种预测结果显示裂缝发育较差。
3 结论针对塔里木盆地深层碳酸盐岩缝洞型储层横向变化快、非均质性强的特点,本文研究了基于叠前—叠后地震多属性分析的缝洞型储层综合预测方法,并应用于塔河地区深层碳酸盐岩缝洞型储层的预测中,得到以下认识:
(1)在断裂和溶洞识别方面,基于叠后地震资料,通过多属性对比分析,优选分频导向相干结果作为一种敏感属性。
(2)在裂缝预测方面,基于叠前方位属性各向异性理论,提出了一种基于宽方位导向相位属性的各向异性强度表征方法,通过奇异值分解(SVD)计算不同方位导向相位属性的最大奇异值与奇异值之和的比值,用于表征目标储层的各向异性强度,从而作为裂缝的预测结果。
(3)三维实际资料测试结果表明,本方法能够更好地表征缝洞型储层的发育情况,预测裂缝分布特征连续性好且集中分布在断裂周边,综合预测结果与已钻井情况较为吻合,提升了缝洞型储层的预测精度,为后期油气勘探提供更有力的指导。
| [1] |
马艺璇, 李慧莉, 刘坤岩, 等. 基于分频相干体的蚂蚁追踪技术在塔河油田断裂刻画中的应用[J]. 石油物探, 2020, 59(2): 258-266. MA Yixuan, LI Huili, LIU Kunyan, et al. Application of an ant-tracking technique based on spectral decomposition to fault characterization[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 258-266. |
| [2] |
崔正伟, 程冰洁, 徐天吉, 等. 基于构造导向滤波与梯度结构张量相干属性的储层裂缝预测方法及应用[J]. 石油地球物理勘探, 2021, 56(3): 555-563. CUI Zhengwei, CHENG Bingjie, XU Tianji, et al. Reservoir fracture prediction method and application based on structure-oriented filtering and coherent attributes of gradient structure tensor[J]. Oil Geophysical Prospecting, 2021, 56(3): 555-563. |
| [3] |
闫家伟, 王文庆, 吕芳芳, 等. 复杂碳酸盐岩储层多数据融合预测技术——以千米桥潜山奥陶系为例[J]. 石油地球物理勘探, 2021, 56(3): 583-592. YAN Jiawei, WANG Wenqing, LYU Fangfang, et al. Fusion of multiple data for predicting complex carbonate reservoirs and its application: a case study on Ordovician of Qianmiqiao buried hills[J]. Oil Geophysical Prospecting, 2021, 56(3): 583-592. |
| [4] |
王静, 张军华, 芦凤明, 等. 构建三维深度监督网络的断层检测方法[J]. 石油地球物理勘探, 2021, 56(5): 947-957. WANG Jing, ZHANG Junhua, LU Fengming, et al. Research on fault detection method based on 3D deeply supervised network[J]. Oil Geophysical Prospecting, 2021, 56(5): 947-957. |
| [5] |
陈俊安, 陈海东, 龚伟, 等. 深度学习与边缘增强相结合的断裂综合检测技术——顺北地区超深走滑断裂检测应用实例[J]. 石油地球物理勘探, 2022, 57(6): 1304-1316. CHEN Jun'an, CHEN Haidong, GONG Wei, et al. Application of comprehensive fault detection technology combining deep learning with edge enhancement in detecting ultra-deep strike-slip faults in Shunbei block[J]. Oil Geophysical Prospecting, 2022, 57(6): 1304-1316. |
| [6] |
BAHORICH M, FARMER S. 3-D seismic discontinuity for faults and stratigraphic features; the coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. |
| [7] |
MARFURT K J, KIRLIN R L, FARMER S L, et al. 3-D seismic attributes using a semblance-based coherency algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. |
| [8] |
GERSZTENKORN A, MARFURT K J. Eigenstruc- ture-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. |
| [9] |
YAN B, YUAN S, WANG S, et al. Improved eigenvalue-based coherence algorithm with dip scanning[J]. Geophysics, 2017, 82(2): V95-V103. |
| [10] |
QI J, LI F, MARFURT K. Multiazimuth coherence[J]. Geophysics, 2017, 82(6): O83-O89. |
| [11] |
WANG S, YUAN S, WANG T, et al. Three-dimensional geosteering coherence attributes for deep-formation discontinuity detection[J]. Geophysics, 2018, 83(6): O105-O113. |
| [12] |
曾凡盛, 王兴春, 陈同俊. 谱分解和C3相干联合识别煤层小断层研究[J]. 地球物理学进展, 2013, 28(1): 462-467. ZENG Fansheng, WANG Xingchun, CHEN Tongjun. Joint technique of spectral decomposition and C3 coherence to detect fine faults of coal bed[J]. Progress in Geophysics, 2013, 28(1): 462-467. |
| [13] |
LI F, LU W. Coherence attribute at different spectral scales[J]. lnterpretation, 2014, 2(1): SA99-SA106. |
| [14] |
LI F, QI J, LYU B, et al. Multispectral coherence[J]. Interpretation, 2018, 6(1): T61-T69. |
| [15] |
WANG T, YUAN S, GAO J, et al. Multispectral phase-based geosteering coherence attributes for deep stratigraphic feature characterization[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1309-1313. |
| [16] |
RÜGER A. Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media[M]. Society of Exploration Geophysicists, Oklahoma, 2002.
|
| [17] |
于晓东, 桂志先, 汪勇, 等. 叠前AVAZ裂缝预测技术在车排子凸起的应用[J]. 石油地球物理勘探, 2019, 54(3): 624-633. YU Xiaodong, GUI Zhixian, WANG Yong, et al. Prestack AVAZ fracture prediction applied in Chepaizi Uplift[J]. Oil Geophysical Prospecting, 2019, 54(3): 624-633. |
| [18] |
WANG T, YUAN S, SHI P, et al. AVAZ inversion for fracture weakness based on three-term Rüger equation[J]. Journal of Applied Geophysics, 2019, 162: 184-193. |
| [19] |
PEREZ M A, GIBSON R L, NAFI TOKSOZ M. Detection of fracture orientation using azimuthal variation P-wave AVO responses[J]. Geophysics, 1999, 64(4): 1253-1265. |
| [20] |
GRIMM R E, LYNN H B, BATES C R, et al. Detection and analysis of naturally fractured gas resservoirs: multiazimuth seismic surveys in the Wind River Basin, Wyoming[J]. Geophysics, 1999, 64(4): 1277-1292. |
| [21] |
CLARK R A, BENSON P M, CARTER A J, et al. Anisotropic P-wave attenuation measured from a multi-azimuth surface seismic reflection survey[J]. Geophysical Prospecting, 2009, 57(5): 835-845. |
| [22] |
YUAN S, SU Y, WANG T, et al. Geosteering phase attributes: a new detector for the discontinuities of seismic images[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(1): 145-149. |



 王铁一, 北京市海淀区学院路31号中国石化石油勘探开发研究院,100083。Email:
王铁一, 北京市海淀区学院路31号中国石化石油勘探开发研究院,100083。Email: