2. 成都理工大学地球探测与信息技术教育部重点实验室, 四川成都 610059
2. Key Laboratory of Earth Exploration and Information Techniques, Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
断层和裂缝的连通网络影响地下地层的形态及地震资料处理、解释结果,要获得精确的地质模型,特别是在逆掩断层及相关褶皱带,需要精确检测、解释断层与裂缝。
存在复杂断层地区的三维地震数据质量受采集、处理等环节的多种因素影响。在地下地质结构较复杂地区的地震资料往往信噪比较低,需要压制随机噪声、提高地震数据的质量,以有效实现可视化和属性提取。通过应用不同的滤波器、数据转换和属性组合技术,可以增强断层与裂缝的地震响应特征。Marr[1]、Witkin[2]、Koenderink[3]阐述了多尺度图像分析的重要性,并在数字图像处理中引入尺度空间理论;伍鹏等[4]将二维高斯迭代平滑滤波用于曲率属性分析,但是没有考虑裂缝方向,不能突显不同方向的异常信息;在前人研究[5-7]的基础上,Cho等[8]、Park等[9]应用自适应Gabor滤波强化手指静脉图像并取得了不错的效果;Chen等[10-12]提出了一种多尺度曲率计算方法及地震定向滤波新算法,为结合裂缝方向选取最佳滤波器提供了理论基础;周元茂等[13-14]结合地震体曲率与各向异性高斯滤波方法,形成了组合型方向体曲率分析方法,可以突显不同方向的异常信息,但是缺少自适应性,需要人为提取裂缝方向;徐赫等[15]将旋转窗加入希尔伯特变换,以提取地震资料中不同方向的有效信息;Jabar等[16]引入一种综合属性和图像的分析技术增强地震断层图像。
本文结合前人方法,提出地震不连续信息的自适应方向增强方法,根据裂缝方向选取高斯滤波器方向对地震数据二次迭代滤波,可有效压制干扰、突出地震数据的有效信息,从而增强特定方向的不连续信息并提取高精度地质异常信息。
1 方法原理本文提出的地震不连续信息的自适应方向增强方法,根据裂缝走向不断地更换各向异性高斯滤波器的方向,使数据所受的异常干扰小,同时保留更多有效信息。具体操作分为五个步骤(图 1)。

|
图 1 不连续信息增强流程 |
(1)在0°~180°范围的所有给定方向的高斯窗扫描输入地震数据,在每个位置分别选取窗内振幅之和的最大值方向的处理结果;
(2)选定时窗扫描处理数据,将处理数据映射为
(3)求取时窗内数据特定方向的共生矩阵纹理参数,并判断处理数据的特定方向;
(4)将判断的裂缝方向代入各向异性高斯滤波方向矩阵进行二次迭代;
(5)对处理数据采用各向异性体曲率属性分析方法得到增强的最终图像。
1.1 灰度共生矩阵1973年,Haralick等[17]提出了灰度共生矩阵模型(GLCM),随后被用于揭示图像的纹理特征[18-22]。
其方法流程为,首先确定时窗宽度,扫描地震数据并进行灰度处理而构建灰度共生矩阵,设最大灰度级为
| $ \boldsymbol{R}\left(l, \theta \right)=\\\left[\begin{array}{ccc}P\left(\mathrm{0, 0}, l, \theta \right)& \cdots & P\left(0, L-1, l, \theta \right)\\ \vdots & \vdots & \vdots \\ P\left(L-\mathrm{1, 0}, l, \theta \right)& \cdots & P\left(L-1, L-1, l, \theta \right)\end{array}\right] $ | (1) |
式中L为最大灰度级。由于l、θ的选择不同,会导致不同的统计结果,如当
| $ \begin{array}{r}P\left(i, j, l, 0°\right)=\sum \left\{\left[\left(m, n\right), \left(p, q\right)\supset \left(x, y\right)\right]\left|m-p\right|\right.\\ =l, n-q=0, g\left(m, n\right)=i, \left.g\left(p, q\right)=j\right\}\\ \end{array} $ | (2) |
| $ \begin{array}{l}P\left(i, j, l, 90°\right)=\sum \left\{\left[\left(m, n\right), \left(p, q\right)\supset \left(x, y\right)\right]m-p\right.\\ =0, \left|n-q\right|=l, g\left(m, n\right)=i, \left.g\left(p, q\right)=j\right\}\end{array} $ | (3) |
选取最常用的能量E、相关性C、熵H及对比度I等4个纹理参数判断裂缝及突出蜿蜒通道的方向,即
| $ \left\{\begin{array}{l}\begin{array}{l}E\left(l, \theta \right)=\sum\limits_{i}\sum\limits_{j}P{\left(i, j, l, \theta \right)}^{2}\\ C\left(l, \theta \right)=\frac{\sum\limits_{i}\sum\limits_{j}\left[\left(ij\right)P\left(i, j, l, \theta \right)\right]-{\mu }_{x}{\mu }_{y}}{{\delta }_{x}{\delta }_{y}}\end{array}\\ \begin{array}{l}H\left(l, \theta \right)=\sum\limits_{i}\sum\limits_{j}P\left(i, j, l, \theta \right)\mathrm{l}\mathrm{g}P\left(i, j, l, \theta \right)\\ I\left(l, \theta \right)=\sum\limits_{i}\sum\limits_{j}{\left(i-j\right)}^{2}P\left(i, j, l, \theta \right)\end{array}\end{array}\right. $ | (4) |
其中
| $ \left\{\begin{array}{l}\begin{array}{c}{\delta }_{x}=\sum\limits_{i}{\left(i-{\mu }_{x}\right)}^{2}\sum\limits_{j}P\left(i, j, l, \theta \right)\\ {\delta }_{y}=\sum\limits_{i}{\left(j-{\mu }_{y}\right)}^{2}\sum\limits_{j}P\left(i, j, l, \theta \right)\end{array}\\ \begin{array}{c}{\mu }_{x}=\sum\limits_{i}i\sum\limits_{j}P\left(i, j, l, \theta \right)\\ {\mu }_{y}=\sum\limits_{i}j\sum\limits_{j}P\left(i, j, l, \theta \right)\end{array}\end{array}\right. $ | (5) |
通过时窗扫描地震数据,每扫描一次便计算一次灰度共生矩阵,并得到共生矩阵的4个纹理参数,通过
| $ \mathrm{m}\mathrm{a}\mathrm{x}\left[\frac{\left(\sum\limits_{i}{C}_{{\theta }_{i}}\right){E}_{{\theta }_{j}}+\left(\sum\limits_{i}{E}_{{\theta }_{i}}\right){C}_{{\theta }_{j}}}{2\left(\sum\limits_{i}{C}_{{\theta }_{i}}\right)\left(\sum\limits_{i}{E}_{{\theta }_{i}}\right)}\right]\to \theta $ | (6) |
| $ \mathrm{m}\mathrm{i}\mathrm{n}\left[\frac{\left(\sum\limits_{i}{H}_{{\theta }_{i}}\right){I}_{{\theta }_{j}}+\left(\sum\limits_{i}{I}_{{\theta }_{i}}\right){H}_{{\theta }_{j}}}{2\left(\sum\limits_{i}{H}_{{\theta }_{i}}\right)\left(\sum\limits_{i}{I}_{{\theta }_{i}}\right)}\right]\to \theta $ | (7) |
判断时窗位置的方向。如果满足式(6)或式(7),则输出时窗的数据方向;如果式(6)和式(7)所得时窗方向不同或

|
图 2 数据点对之间的关系 |
图 3为一个正十六边形模型,其中每一边的内角均为22.5°。使用20个采样点的时窗扫描图 3,分别计算θ为0°、22.5°、45°、67.5°、90°、112.5°、135°、157.5°的共生矩阵,通过共生矩阵得到各方向的纹理参数。将不同方向的4个纹理参数代入式(6)、式(7),选取式(6)、式(7)对应的角度作为该处纹理的方向。

|
图 3 正十六边形模型 |
图 4为判断纹理方向的模拟测试结果。由图可见,准确判断了正十六边形的各个方向,表明了方法的可行性。
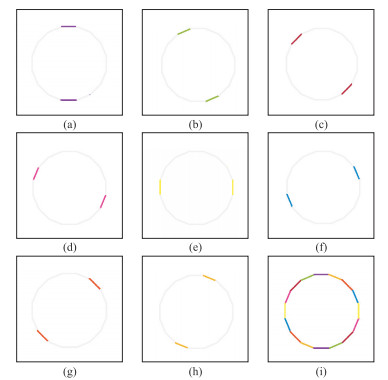
|
图 4 判断纹理方向的模拟测试结果 (a)突出0º方向;(b)突出22.5º方向;(c)突出45º方向;(d)突出67.5º方向;(e)突出90º方向;(f)突出112.5º方向;(g)突出135º方向;(h)突出157.5º方向;(i)突出上述8个方向 |
传统高斯函数滤波的基本原理是将高斯核函数与原始信号卷积,以二维高斯滤波为例,滤波器表达式为
| $ G\left(x, y, \sigma \right)=\frac{1}{2\mathrm{\pi }{\sigma }^{2}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}\left(\frac{{x}^{2}+{y}^{2}}{{\sigma }^{2}}\right)\right] $ | (8) |
式中:

|
图 5 二维高斯滤波器 |
将传统高斯滤波器中的
| $ {G}_{\theta }\left({x}_{\theta }, {y}_{\theta }, {\sigma }_{x}, {\sigma }_{y}, \theta \right)=\frac{1}{2\mathrm{\pi }{\sigma }_{x}{\sigma }_{y}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}\left(\frac{{x}_{\theta }^{2}}{{\sigma }_{x}^{2}}+\frac{{y}_{\theta }^{2}}{{\sigma }_{y}^{2}}\right)\right] $ | (9) |
| $ \left(\begin{array}{c}{x}_{\theta }\\ {y}_{\theta }\end{array}\right)=\left(\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}\theta & \mathrm{s}\mathrm{i}\mathrm{n}\theta \\ -\mathrm{s}\mathrm{i}\mathrm{n}\theta & \mathrm{c}\mathrm{o}\mathrm{s}\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right) $ | (10) |
式中
(a)各向同性高斯滤波(
为了利用各向异性高斯滤波描述地震数据中的蜿蜒河道、裂缝和其他地质不连续点,需要考虑σx、σy和θ的变化(图 6)。文中提出了一个基于各向异性高斯滤波方法的工作流程突出地震数据中的蜿蜒通道和其他地质不连续点。

|
图 6 各向异性高斯滤波器 (a) |
根据实际地震资料中的裂缝尺度,给定各向异性高斯滤波器
| $ F\left(\tau , {x}_{i}, {y}_{j}, {\theta }_{k}\right)={G}_{\theta }\left(x, y, {\sigma }_{x}, {\sigma }_{y}, {\theta }_{k}\right)S\left(\tau , {x}_{i}, {y}_{j}\right) $ | (11) |
式中:
对于0º~180º范围内所有给定的滤波方向
| $ F\left(\tau , {x}_{i}, {y}_{j}\right)=\underset{{\theta }_{k}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left[\left|F\left(\tau , {x}_{i}, {y}_{j}, {\theta }_{k}\right)\right|\right] $ | (12) |
其中
然后,定义地震方向滤波算子,得到时窗位置
| $ Z\left(\tau , {x}_{i}, {y}_{j}, {\theta }_{k}\right)=\frac{\sum\limits_{M=-w}^{w}{\left|F\left(\tau -M, {x}_{i}, {y}_{j}\right)\right|}^{2}}{\sum\limits_{M=-w}^{w}{\left|S\left(\tau -M, {x}_{i}, {y}_{j}\right)\right|}^{2}} $ | (13) |
式中:w为时窗窗口长度的一半;M为时窗尺度。
1.3 三维各向异性体曲率分析在三维地震数据中,一般需要将三维地震数据体先转化为倾角数据体,再根据倾角数据体计算任意点的曲率。可以根据复数道分析中的瞬时频率和瞬时波数计算三维地震数据体的视倾角
| $ \left\{\begin{array}{c}{p}_{x}=\frac{{k}_{x}}{\omega }\\ {q}_{y}=\frac{{k}_{y}}{\omega }\end{array}\right. $ | (14) |
式中:
在此基础上,构造新的方位视倾角分量
| $ \left\{\begin{array}{c}{p}_{\beta }={p}_{x}\mathrm{c}\mathrm{o}\mathrm{s}\beta =\frac{{k}_{x}\mathrm{c}\mathrm{o}\mathrm{s}\beta }{\omega }\\ {q}_{\beta }={q}_{y}\mathrm{s}\mathrm{i}\mathrm{n}\beta =\frac{{k}_{y}\mathrm{s}\mathrm{i}\mathrm{n}\beta }{\omega }\end{array}\right. $ | (15) |
式中
根据最小二乘逼近原理,得到二次曲面方程
| $ Q\left(x, y\right)=a{x}^{2}+b{y}^{2}+cxy+dx+ey+f $ | (16) |
其中
| $ \left\{\begin{array}{l}\begin{array}{c}a=\frac{1}{2}\frac{{\partial }^{2}F}{\partial {x}^{2}}=\frac{1}{2}\frac{\partial {p}_{\beta }}{\partial x}\\ b=\frac{1}{2}\frac{{\partial }^{2}F}{\partial {y}^{2}}=\frac{1}{2}\frac{\partial {q}_{\beta }}{\partial y}\end{array}\\ c=\frac{{\partial }^{2}F}{\partial x\partial y}=\frac{1}{2}\left(\frac{\partial {p}_{\beta }}{\partial x}+\frac{\partial {q}_{\beta }}{\partial y}\right)\\ d=\frac{\partial F}{\partial x}={p}_{\beta }\\ e=\frac{\partial F}{\partial y}={q}_{\beta }\end{array}\right. $ | (17) |
式中f为常数。最大正曲率
| $ \left\{\begin{array}{c}{K}_{\mathrm{p}\mathrm{o}\mathrm{s}}=a+b+{\left[{\left(a-b\right)}^{2}+{c}^{2}\right]}^{\frac{1}{2}}\\ {K}_{\mathrm{n}\mathrm{e}\mathrm{g}}=a+b-{\left[{\left(a-b\right)}^{2}+{c}^{2}\right]}^{\frac{1}{2}}\end{array}\right. $ | (18) |
为了验证本文方法在LH地区的应用效果,分别利用一次方向各向异性高斯滤波和本文方法对三维叠后地震数据体进行0°、90°方向的滤波。图 7为LH地区地震振幅沿层切片。由图可见,在多个方向存在强噪声,从而难以识别有效的不连续地质信息,也难以辨识各种尺度裂缝的空间走向。

|
图 7 LH地区地震振幅沿层切片 |
图 8为一次方向的各向异性高斯滤波与本文方法得到的最大正曲率属性。由图可见:①90°一次方向的各向异性高斯滤波(图 8a的红色、绿色方框处)及本文方法(图 8b的红色、绿色方框处)明显增强了纵向不连续性信息及构造异常特征,且图 8b更明显;0°一次方向的各向异性高斯滤波(图 8c的红色、黄色方框处)及本文方法(图 8d的红色、黄色方框处)则着重突出了横向构造特征,明显增强了断层及裂隙连续性,且图 8d更明显。②与一次方向各向异性高斯滤波(图 8a绿色箭头处、图 8c红色箭头处)相比,本文方法(图 8b绿色箭头处、图 8d红色箭头处)明显突出了指定方向的地质异常构造。

|
图 8 一次方向的各向异性高斯滤波与本文方法得到的最大正曲率属性 (a)一次方向的各向异性高斯滤波(90°);(b)本文方法(90°);(c)一次方向的各向异性高斯滤波(0°);(d)本文方法(0°) |
为了突出裂缝及断层走向,使用灰度共生矩阵对一次方向的各向异性高斯滤波结果提取

|
图 9 地震数据的裂缝方向图 不同颜色表示各种地质异常构造的走向。 |
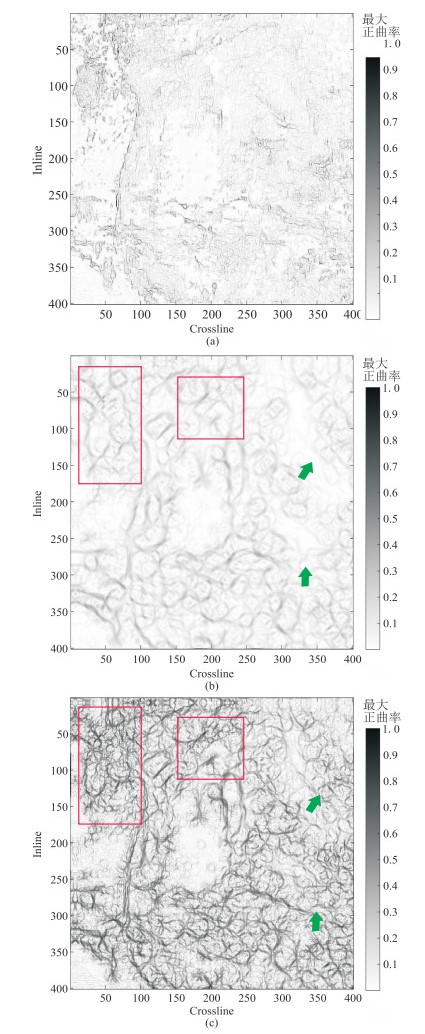
|
图 10 不同方法得到的实际地震数据的最大正曲率属性 (a)原始最大正曲率属性;(b)一次方向的各向异性高斯滤波;(c)本文方法 |
本文提出了一种地震不连续信息的自适应方向增强方法,在常规高斯滤波算法的基础上,推导了各向异性方向迭代高斯平滑滤波公式。该方法对地震数据进行两次时窗扫描,自适应地判断裂缝等异常信息的方向,再根据判断的方向选取匹配该方向的最优滤波器进行二次迭代处理,有效地压制与裂缝等方向不同的干扰信息,极大突出了地质构造特征,更好地反映了特定方向的构造细节和不连续性。同时该方法也可自行选取一个或多个特定方向,只展现所选方向的构造信息。该方法可为构造解释、了解断裂展布规律、储层预测等提供技术支持,体现了算法的可行性和优越性。
| [1] |
MARR D. A Computational Investigation into the Human Representation and Processing of Visual Information[M]. The MIT Press, 2010: 41-98.
|
| [2] |
WITKIN A P. Scale-Space Filtering[M]. San Francisco: Morgan Kaufmann Publishers Inc., 1987: 329-332.
|
| [3] |
KOENDERINK J J. The structure of images: 1984-2021[J]. Biological Cybernetics, 2021, 115(4): 117-120. |
| [4] |
伍鹏, 贺振华, 陈学华, 等. 二维高斯迭代平滑滤波曲率属性及其应用[J]. 地球物理学进展, 2010, 25(6): 2144-2149. WU Peng, HE Zhenhua, CHEN Xuehua, et al. Curvature attribute of two-dimensional Gaussian iterative smoothing filtering and applications[J]. Progress in Geophysics, 2010, 25(6): 2144-2149. |
| [5] |
YU C, QIN H, ZHANG L, et al. Finger-vein image recognition combining modified hausdorff distance with minutiae feature matching[J]. Journal of Biomedical Science & Engineering, 2009, 2(4): 261-272. |
| [6] |
YANG J F, YANG J L. Multi-channel Gabor filter design for finger-vein image enhancement[C]. Procee-dings of the Fifth International Conference on Image and Graphics, 2009, doi: 10.1109/icig.2009.170.
|
| [7] |
LEE E C, LEE H, PARK K R. Finger vein recognition using minutia-based alignment and local binary pattern-based feature extraction[J]. International Journal of Imaging Systems & Technology, 2009, 19(3): 179-186. |
| [8] |
CHO S R, PARK Y H, NAM G P, et al. Enhancement of finger-vein image by vein line tracking and adaptive Gabor filtering for finger-vein recognition[J]. Applied Mechanics & Materials, 2012. DOI:10.4028/www.scientific.net/AMM.145.219 |
| [9] |
PARK Y H, PARK K R. Image quality enhancement using the direction and thickness of vein lines for finger-vein recognition[J]. International Journal of Advanced Robotic Systems, 2012, 9(4): 154-163. DOI:10.5772/53474 |
| [10] |
CHEN X, JIANG W, JIANG S, et al. A new seismic directional filtering operator to directly highlight meandering channel deposits[C]. SEG Technical Program Expanded Abstracts, 2017, 36, SEG-2017-17676852.
|
| [11] |
CHEN X, YANG W, HE Z, et al. The algorithm of 3D multi-scale volumetric curvature and its application[J]. Applied Geophysics, 2012, 9(1): 65-72. DOI:10.1007/s11770-012-0315-7 |
| [12] |
陈学华, 贺振华, 杨威. 地震资料的三维多尺度体曲率分析及应用[C]. 中国地球物理2010——中国地球物理学会第二十六届年会、中国地震学会第十三次学术大会论文集, 2010, 584.
|
| [13] |
周元茂, 陈学华, 徐咪, 等. 地震资料的组合型方向体曲率分析方法[C]. SPG/SEG北京2016国际地球物理会议电子文集, 2016, 161-164.
|
| [14] |
周元茂, 陈学华, 罗鑫, 等. 组合型方位体曲率分析方法[J]. 石油地球物理勘探, 2017, 52(6): 1253-1260. ZHOU Yuanmao, CHEN Xuehua, LUO Xin, et al. An integrated volumetric curvature analysis[J]. Oil Geophysical Prospecting, 2017, 52(6): 1253-1260. |
| [15] |
徐赫, 陈学华, 吕丙南, 等. 任意旋转加窗希尔伯特变换的地震资料体边缘检测方法[J]. 石油地球物理勘探, 2021, 56(3): 536-542. XU He, CHEN Xuehua, LYU Bingnan, et al. Volumetric edge detection of seismic data base on arbitrarily rotaed windowed Hilbert transform[J]. Oil Geophysical Prospecting, 2021, 56(3): 536-542. |
| [16] |
JABAR M, MOHAMMAD R, MEHRDAD S M, et al. Fault enhancement in seismic images by introducing a novel strategy integrating attributes and image analysis techniques[J]. Pure and Applied Geophysics, 2022, 179(5): 1645-1660. DOI:10.1007/s00024-022-03014-y |
| [17] |
HARALICK R M, SHANMUGAM K, DINSTEIN I H. Texture features for image classification[J]. IEEE Transactions on Systems, Man and Cybernetics, 1973, SMC-3(6): 610-621. DOI:10.1109/TSMC.1973.4309314 |
| [18] |
CHOPRA S, ALEXEEV V. Applications of texture attribute analysis to 3D seismic data[J]. The Leading Edge, 2006, 25(8): 934-940. DOI:10.1190/1.2335155 |
| [19] |
GAO D. Volume texture extraction for 3D seismic visualization and interpretation[J]. Geophysics, 2003, 68(4): 1294-1302. DOI:10.1190/1.1598122 |
| [20] |
胡英, 陈辉, 贺振华, 等. 基于地震纹理属性和模糊聚类划分地震相[J]. 石油地球物理勘探, 2013, 48(1): 114-120. HU Ying, CHEN Hui, HE Zhenhua, et al. Seismic facies classification based on seismic texture attributes and fuzzy clustering[J]. Oil Geophysical Prospecting, 2013, 48(1): 114-120. |
| [21] |
王治国, 尹成, 雷小兰, 等. 河道纹理属性分析中的灰度共生矩阵参数研究[J]. 石油地球物理勘探, 2012, 47(1): 100-106. WANG Zhiguo, YIN Cheng, LEI Xiaolan, et al. GLCM parameters in fluvial texture analysis[J]. Oil Geophysical Prospecting, 2012, 47(1): 100-106. |
| [22] |
朱石磊, 段林娣, 林畅松, 等. 基于灰度共生矩阵的地震数据空间结构属性分析技术[J]. 石油地球物理勘探, 2012, 47(6): 951-957, 972. ZHU Shilei, DUAN Lindi, LIN Changsong, et al. Seismic structural properties analysis based on GLCM in Damintun Sag[J]. Oil Geophysical Prospecting, 2012, 47(6): 951-957, 972. |



 陈学华,四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室,610059。Email:
陈学华,四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室,610059。Email: