0 引言

孔隙度和饱和度是描述油藏的两个重要储层参数，精确地预测这两个参数可以有效指导油气勘探、开发。目前有三类常用的孔隙度和饱和度预测方法。第一类是基于岩石物理的方法^[1-3]，通过岩石物理方法确定弹性参数与储层参数之间的关系，基于叠前反演结果预测储层参数。该类方法应用广泛且物理意义明确，但受岩心、测井和地震数据之间尺度不匹配影响以及理论模型参数与实际介质参数差异影响，预测结果具有一定的局限性。第二类是基于地质统计学的方法^[4-6]，基于随机模拟方法预测储层参数。该类方法可以较好地融合多元信息，且可以获得较常规方法分辨率更高的预测结果，但受变差函数^[4]的影响，在构造复杂区域预测储层参数存在一定困难。第三类是基于地震多属性的方法^[7-9]，通过建立地震属性和储层参数之间的映射关系预测储层参数。该类方法伴随着机器学习理论和方法的快速发展，在储层参数预测领域的作用越来越重要。其中，支持向量机算法^[10]（Support Vector Machine，SVM）是利用结构风险最小化原理的监督学习方法，对小样本问题具有很好的适应性。赵学松等^[11]基于SVM建立了多种属性与储层参数之间的映射关系，可有效预测河道砂体分布特征。王维强^[12]利用SVM预测储层参数，模型数据和实际数据均表明该方法预测精度高。SVM的数学理论依据明确，但计算复杂度随着样本增加而增加，当数据量较大时，算法性能较差，且SVM不能提供后验概率分布，难以评估预测结果的不确定性。Tipping^[13]将贝叶斯理论引入SVM参数估计，提出了相关向量机算法（Relevance Vector Machine，RVM），数值试验证明RVM的预测结果较SVM更稀疏，泛化能力更强，同时可以给出预测结果的后验概率。Ji等^[14]基于RVM恢复低频地震数据，在模型和实际数据中均取得了较好效果。Pilikos^[15]有效地利用RVM稀疏重构地震数据，并根据预测结果的方差量化重构结果的不确定性。Dai等^[16]首次运用RVM预测储层参数，并取得了良好的应用效果，展示了在储层预测领域的巨大潜力。然而，RVM中的核参数对其性能影响很大，目前没有明确的理论指导核参数选取。

粒子群算法（Particle Swarm Optimization，PSO）可同时利用粒子局部信息和种群全局信息指导搜索，进而达到全局最优。为此，本文利用PSO指导核参数选取，在获取最优核参数基础上定量预测储层参数；同时考虑到变异系数可消除量纲的影响，引入变异系数评估预测结果的不确定性，并提出了一种新的基于粒子群优化的相关向量机算法（PSO-RVM）的孔隙度与饱和度定量预测方法。数值模拟和实际数据应用结果表明，所提方法可以定量预测孔隙度与饱和度，预测结果与钻测井吻合度高，且可操作性强，具有一定借鉴意义。

1 技术方法 1.1 RVM

RVM是一种基于贝叶斯理论的数学模型，其数学表达式为

$ {y}^{\left(i\right)}=\sum\limits _{j=1}^{M}{\omega }_{j}{\boldsymbol{\phi }}_{j}\left[{K}^{\left(i\right)}\right]+{\varepsilon }^{\left(i\right)}={\boldsymbol{\omega }}^{\mathrm{T}}\boldsymbol{\varPhi }\left[{K}^{\left(i\right)}\right]+{\varepsilon }^{\left(i\right)} $

(1)

式中：$ {y}^{\left(i\right)} $为第$ i $个样本的输出变量；$ \boldsymbol{\omega }=({\omega }_{1}, {\omega }_{2}, \cdots , {\omega }_{M}{)}^{\mathrm{T}} $为权系数，$ j\in (1, M) $表示第$ j $个输入变量，M为输入变量个数；$ {\varepsilon }^{\left(i\right)}\in N(0, {\sigma }^{2}) $为第$ i $个样本的随机噪声，$ {\sigma }^{2} $为噪声方差；$ \boldsymbol{\varPhi }\left[{K}^{\left(i\right)}\right]={\left\{{\boldsymbol{\phi }}_{1}\left[{K}^{\left(i\right)}\right], \cdots , {\boldsymbol{\phi }}_{M}\left[{K}^{\left(i\right)}\right]\right\}}^{\mathrm{T}} $，$ K $为核函数，$ {\boldsymbol{\phi }}_{j}\left[{K}^{\left(i\right)}\right]={\left\{K[{x}_{j}^{\left(i\right)}, {x}_{1}^{\left(i\right)}], \cdots , K[{x}_{j}^{\left(i\right)}, {x}_{M}^{\left(i\right)}]\right\}}^{\mathrm{T}} $为核函数矩阵，$ {x}_{j}^{\left(i\right)} $为第$ i $个样本的第$ j $个变量。

假设$ \boldsymbol{y}=({y}_{1}, {y}_{2}, \cdots , {y}_{M}{)}^{\mathrm{T}} $的每个样本独立同分布，可得其概率

$ p\left(\boldsymbol{y}\left|\boldsymbol{\omega }, {\sigma }^{2}\right.\right)=(2\mathrm{\pi }{\sigma }^{2}{)}^{-\frac{M}{2}}\mathrm{e}\mathrm{x}\mathrm{p}{-\frac{1}{2{\sigma }^{2}}{‖\boldsymbol{y}-\boldsymbol{\varPhi }\boldsymbol{\omega }‖}^{2}} $

(2)

若基于最大似然估计^[13]直接求解式（2）可能造成过拟合（即模型在训练集上性能较好，在验证集上表现一般，模型泛化能力较弱），为约束参数定义零均值高斯先验分布

$ p\left(\boldsymbol{\omega }\left|\boldsymbol{\alpha }\right.\right)=\prod \limits_{j=1}^{M}\sqrt{\frac{{\alpha }_{j}}{2\mathrm{\pi }}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{\alpha }_{j}}{2}{{\omega }_{j}}^{2}\right) $

(3)

式中α为超参数，$ {\alpha }_{j} $是与$ {\omega }_{j} $一一对应的超参数^[13]。

基于贝叶斯公式，可得未知参数后验概率

$ p(\boldsymbol{\omega }, \boldsymbol{\alpha }, {\sigma }^{2}\left|\boldsymbol{y}\right.)=\frac{p\left(\boldsymbol{y}\left|\boldsymbol{\omega }, \boldsymbol{\alpha }, {\sigma }^{2}\right.\right)p(\boldsymbol{\omega }, \boldsymbol{\alpha }, {\sigma }^{2})}{p\left(\boldsymbol{y}\right)} $

(4)

则未知输出值$ {\boldsymbol{y}}^{\mathrm{*}} $为

$ p\left({\boldsymbol{y}}^{\mathrm{*}}\left|\boldsymbol{y}\right.\right)=\int p\left({\boldsymbol{y}}^{*}\left|\boldsymbol{\omega }, \boldsymbol{\alpha }, {\sigma }^{2}\right.\right)p(\boldsymbol{\omega }, \boldsymbol{\alpha }, {\sigma }^{2}\left|\boldsymbol{y}\right.)\mathrm{d}\boldsymbol{\omega }\mathrm{d}\boldsymbol{\alpha }\mathrm{d}{\sigma }^{2} $

(5)

由贝叶斯推理^[15]，可得参数后验概率

$ \begin{array}{l}p\left(\boldsymbol{\omega }\left|\boldsymbol{y}, \boldsymbol{\alpha }, {\sigma }^{2}\right.\right)=\frac{p\left(\boldsymbol{y}\left|\boldsymbol{\omega }, {\sigma }^{2}\right.\right)p\left(\boldsymbol{\omega }\left|\boldsymbol{\alpha }\right.\right)}{p\left(\boldsymbol{y}\left|\boldsymbol{\alpha }, {\sigma }^{2}\right.\right)}\\ ={\left(2\mathrm{\pi }\right)}^{-\frac{M+1}{2}{\left|\boldsymbol{\varSigma }\right|}^{-\frac{1}{2}}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{{(\boldsymbol{\omega }-\boldsymbol{\mu })}^{\mathrm{T}}{\boldsymbol{\varSigma }}^{-1}(\boldsymbol{\omega }-\boldsymbol{\mu })}{2}\right]\end{array} $

(6)

式（6）中后验分布的方差Σ和期望μ分别为

$ \boldsymbol{\varSigma }=({\sigma }^{-2}{\boldsymbol{\varPhi }}^{\mathrm{T}}{\boldsymbol{\varPhi }+\boldsymbol{A})}^{-1} $

(7)

$ \boldsymbol{\mu }={\sigma }^{-2}\boldsymbol{\varSigma }{\boldsymbol{\varPhi }}^{\mathrm{T}}\boldsymbol{y} $

(8)

式中$ \boldsymbol{A}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\alpha }_{1}, {\alpha }_{1}, \cdots , {\alpha }_{M}) $为对角阵。大部分$ {\alpha }_{j} $在计算过程中趋于无穷大，即相应的系数$ {\omega }_{j} $为零，其余的非零权系数对应的样本即为相关向量。

由式（5）和式（6），可得

$ \begin{align}p\left(\boldsymbol{y}\left|\boldsymbol{\alpha }, {\sigma }^{2}\right.\right)=&\int p\left(\boldsymbol{y}\left|\boldsymbol{\omega }, {\sigma }^{2}\right.\right)p\left(\boldsymbol{\omega }\left|\boldsymbol{\alpha }\right.\right)\mathrm{d}\boldsymbol{\omega }\\ =&{\left(2\mathrm{\pi }\right)}^{-\frac{M}{2}}{\left|{\sigma }^{2}\boldsymbol{I}+\boldsymbol{\varPhi }{\boldsymbol{A}}^{-1}{\boldsymbol{\varPhi }}^{\mathrm{T}}\right|}^{-\frac{1}{2}}\times \\ &\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}{\boldsymbol{y}}^{T}({\sigma }^{2}\boldsymbol{I}+\boldsymbol{\varPhi }{\boldsymbol{A}}^{-1}{\boldsymbol{\varPhi }}^{T}{)}^{-1}\boldsymbol{y}\right]\end{align} $

(9)

由迭代法求解式（9），$ {\alpha }_{j} $和$ {\sigma }^{2} $的更新形式为

$ {\alpha }_{j}^{\mathrm{n}\mathrm{e}\mathrm{w}}=\frac{{\gamma }_{j}}{{\mu }_{j}^{2}} $

(10)

$ ({\sigma }^{2}{)}^{\mathrm{n}\mathrm{e}\mathrm{w}}=\frac{{‖\boldsymbol{y}-\boldsymbol{\phi }\boldsymbol{\mu }‖}^{2}}{M-\sum\limits _{j=0}^{M}{\gamma }_{j}} $

(11)

式中：$ {\gamma }_{j}=1-{\alpha }_{j}{\varSigma }_{jj} $，$ {\varSigma }_{jj} $为$ \boldsymbol{\varSigma } $的第$ j $个对角线元素；$ {\mu }_{j} $为第$ j $个权值的均值。

对于新样本，其预测分布满足高斯分布$ p\left({\boldsymbol{y}}^{\mathrm{*}}\left|\boldsymbol{y}\right.\right)\in N\left[{\boldsymbol{\mu }}^{\mathrm{T}}\boldsymbol{\varPhi }\right({K}^{\mathrm{*}}), ({\sigma }^{2}{)}^{\mathrm{*}}] $，其中

$ {\boldsymbol{y}}^{\mathrm{*}}={\boldsymbol{\mu }}^{\mathrm{T}}\boldsymbol{\varPhi }\left({K}^{\mathrm{*}}\right) $

(12)

$ ({\sigma }^{2}{)}^{\mathrm{*}}={\sigma }_{\mathrm{M}\mathrm{P}}^{2}+{\boldsymbol{\varPhi }}^{\mathbf{T}}({K}^{\mathrm{*}}{)}^{}\boldsymbol{\varSigma }\boldsymbol{\varPhi }\left({K}^{\mathrm{*}}\right) $

(13)

式中$ {\sigma }_{\mathrm{M}\mathrm{P}}^{2} $为式（10）、式（11）迭代结束时的噪声方差。

综上所述，RVM是通过核函数考察输入变量与输出变量之间的非线性关系，核参数对RVM性能影响很大，目前尚没有解决核参数选择难题的理论依据。

1.2 PSO-RVM

PSO是一种模拟鸟类觅食的全局寻优算法^[17]。假设问题的可能解均对应搜索空间中的粒子（每个粒子代表一只鸟），所求问题的最优解是食物的位置。在迭代过程中，以适应度函数（衡量粒子优劣性的函数，通常为误差函数）作为评价标准，每个粒子都在搜索空间搜索最优解，并通过自己和全体种群的移动经验调整下一步的移动方向和距离，从而实现解空间的全局寻优。

假设种群中有N个粒子，每个粒子在任意时刻的位置为$ {Z}_{i}=({z}_{i1}, \cdots , {z}_{id}, \cdots , {z}_{iD}) $，粒子的速度为$ {\boldsymbol{V}}_{i}=({v}_{i1}, {v}_{i2}, \cdots , {v}_{in}) $，其中$ i\in (1, N) $，$ d\in (1, D) $（D为解空间维数）。记粒子个体的历史最优位置（粒子个体适应度函数最优）为个体极值$ {\boldsymbol{p}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}i} $，种群中所有粒子的历史最优位置（种群所有粒子适应度函数最优）为种群极值$ {\boldsymbol{g}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $，则每个粒子位置和速度的迭代公式为

$ {v}_{id}^{k+1}=w{v}_{id}^{k}+{\lambda }_{1}{r}_{1}({p}_{id}^{k}-{z}_{id}^{k})+{\lambda }_{2}{r}_{2}({g}_{d}^{k}-{z}_{id}^{k}) $

(14)

$ {z}_{id}^{k+1}={v}_{id}^{k+1}+{z}_{id}^{k} $

(15)

式中：$ {v}_{id}^{k} $和$ {z}_{id}^{k} $分别为第i个粒子在d维空间的速度和位置，k为迭代次数；$ {\lambda }_{1} $和$ {\lambda }_{2} $为学习常系数；$ {r}_{1} $和$ {r}_{2} $为随机数；$ w $为惯性权重；$ {p}_{id}^{k} $与$ {g}_{d}^{k} $分别为在d维空间第i个粒子的个体极值和种群极值。

由式（14）和式（15）可知，粒子的移动方向由上一次的速度$ {v}_{id}^{k} $、粒子“个体认知”$ ({p}_{id}^{k}-{z}_{id}^{k}) $和“社会认知”$ ({g}_{d}^{k}-{z}_{id}^{k}) $三项决定，$ w $、$ {\lambda }_{1} $和$ {\lambda }_{2} $决定了三个系数的重要程度。图 1为粒子位置和移动方向示意图。

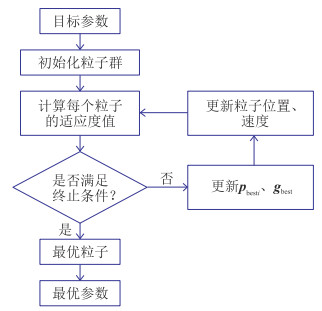
PSO是一种启发式算法，可以同时搜索解空间的不同区域，有效避免陷入局部极小值，进而求得全局最优解（图 2）。PSO不依赖于梯度的求取，只需选择合适的适应度函数即可全局搜索，广泛用于系统控制、动态规划等领域。

针对RVM的不足，采用PSO指导核参数选择，实施流程如表 1所示。

1.3 数值模拟测试

鉴于地震属性与孔隙度、饱和度之间复杂的非线性关系，设计

$ f\left(x\right)=(1+2x+0.5{x}^{2})\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{x}^{2}}{4}\right) $

(16)

测试SVM、RVM与PSO-RVM的优劣性。式中$ x\in \left[-\mathrm{5, 5}\right] 。$

为避免初始化参数对算法的影响，三种算法均选用高斯核函数，且初始核参数均为3。分别选择$ x\in \left[-\mathrm{3, 3}\right] $、$ x\in \left[-\mathrm{1, 3}\right] $为训练样本集，其余数据为验证集，测试不同训练样本集对算法性能的影响。

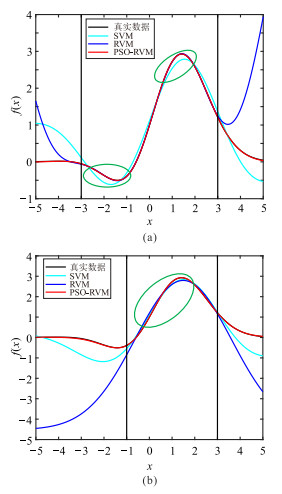
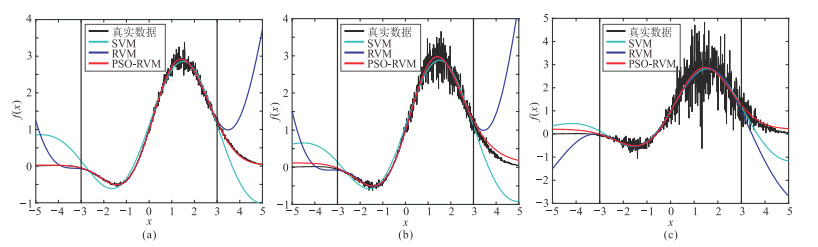
图 3为无噪情况下SVM、RVM与PSO-RVM预测结果。由图可知：三种算法在训练样本集范围内的学习效果均很理想，但整体来看，PSO-RVM的学习效果更优（绿色圈内）；在验证样本集范围，PSO-RVM的预测结果良好，而SVM和RVM的预测结果均出现不同程度的偏差。说明当核参数不合适时，RVM易造成过拟合，而PSO可以有效指导核参数选择，使PSO-RVM既有很强的学习能力，又有极佳的泛化能力。图 4为不同信噪比条件下SVM、RVM与PSO-RVM预测结果。由图可知，PSO-RVM均表现出更好的学习性能和泛化能力，但随着信噪比降低，PSO-RVM预测结果也出现一定偏差。表 2为不同信噪比条件下三种算法的预测性能指标。由表可知：在同一信噪比条件下，PSO-RVM预测结果与实际值相关系数更高，均方根误差更小，预测精度更高，抗噪能力更优；随着信噪比降低，PSO-RVM预测结果与实际值相关系数降低，均方根误差增大，证明预测精度随着信噪比降低而降低。

2 实际应用与效果分析

以中国西部M气田实际数据为例，定量预测储层孔隙度与含气饱和度。研究区目的层系为飞仙关组一段与二段，优质储层为鲕粒溶孔白云岩，整体厚度大，孔隙度为0~15%，储层物性较好但横向变化快，因此定量预测孔隙度难度大。同时研究区气、水关系复杂，含气地震响应特征不明显，利用常规方法难以精确预测含气饱和度。以井震数据为基础，基于PSO-RVM定量预测孔隙度和含气饱和度并评估不确定性。

2.1 孔隙度预测

研究区7口井资料包含孔隙度和含气饱和度解释成果，基于现有的地震、层位等资料，提取地震反演结果（由叠前地震反演获取）、衰减梯度、瞬时相位和振幅包络等28种地震属性，以井旁道地震属性和测井孔隙度为数据基础制作样本集，随机选择其中5口井作为训练井，剩余2口井（W1井和W2井）作为验证井。

基于逐步回归算法^[18]优选地震属性，其基本思想是：将属性逐个引入回归模型，每引入一个新属性，需要检验现有模型的显著性，并剔除不显著的属性，重复此过程，直到不再有新属性加入，即可得到最终的回归模型。随着属性数目增加，训练误差减小，但易造成过拟合，因此需结合验证误差确定最优属性组合，当验证误差最小时对应的属性组合即为最优属性组合。表 3为目标变量为孔隙度时的地震属性优选结果。由表可知，当输入属性为四种属性（纵波阻抗、振幅包络、相位余弦和正交道）时，验证均方根误差最小，该四种属性即为孔隙度预测最优属性组合。

基于地震属性优选结果，分别利用构建的RVM与PSO-RVM预测孔隙度。图 5为W1井、W2井孔隙度预测结果。由图可见，两种算法均有一定效果，但RVM在局部区域预测效果不理想，而PSO-RVM预测结果与测井孔隙度更接近，对细节的把控更优（图中绿色圈内）。

表 4为验证井孔隙度预测性能指标。由表可知，2口验证井的PSO-RVM预测孔隙度与测井孔隙度的相关系数（0.933、0.961）明显高于RVM（0.824、0.948），PSO-RVM预测孔隙度的均方根误差（0.972、0.752）也低于RVM（1.599、0.814），证明PSO-RVM预测精度高于RVM。

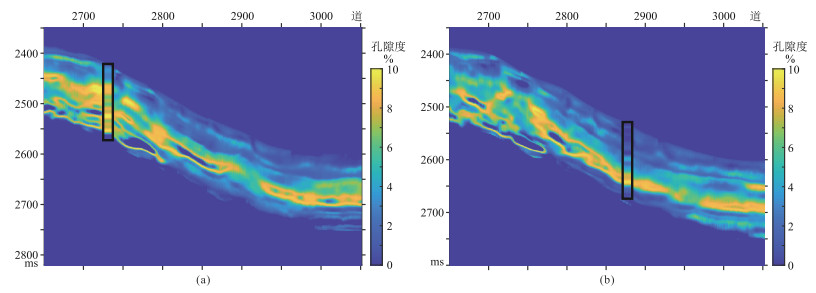
图 6为过W1井、W2井PSO-RVM孔隙度预测剖面。由图可见，PSO-RVM孔隙度预测结果与测井孔隙度解释结果吻合度较高。为量化预测结果的不确定性，引入变异系数（标准差和期望的比值）。图 7为过W1井和W2井PSO-RVM孔隙度预测变异系数剖面。由图可见：在局部区域（红色圈内）变异系数高值（大于0.4）集中在高孔隙度与低孔隙度分界，说明在分界处预测稳定性较差，与实际认识相符；总体来看，预测结果变异系数大多低于0.2，说明不确定性低，预测结果稳定。

2.2 含气饱和度预测

综合已提取的28种地震属性，以井旁道地震属性和测井含气饱和度为数据基础制作样本集，并保持与孔隙度数据集划分一致。

基于逐步回归算法优选含气饱和度敏感属性。表 5为目标变量为含气饱和度时的地震属性优选结果。由表可知，当输入属性为五种属性（绝对振幅、衰减梯度、纵波阻抗、横波阻抗和20~25 Hz滤波因子）时，验证均方根误差最小，该五种属性即为含气饱和度预测最优属性组合。

基于地震属性优选结果，分别利用构建的RVM与PSO-RVM预测含气饱和度。图 8为W1井、W2井含气饱和度预测结果。由图可见，两种预测算法均有一定效果，但RVM在局部区域预测效果不理想，而PSO-RVM预测结果与测井含气饱和度吻合度更高（绿色圈内）。

表 6为验证井含气饱和度预测性能指标。由表可知，两口验证井的PSO-RVM预测结果与测井含气饱和度相关系数均高于RVM预测结果，且均方根误差更小，证明了PSO-RVM预测精度更高。

图 9为过W1井、W2井含气饱和度预测剖面。由图可知，PSO-RVM预测结果与测井数据一致性更高。图 10为过W1井、W2井PSO-RVM含气饱和度预测变异系数剖面。由图可见，在预测含气饱和度时在局部区域（红色圈内）也存在变异系数值高（大于0.4）、稳定性差的问题。

综上所述，PSO-RVM孔隙度和含气饱和度预测精度较高。两口验证井的孔隙度与含气饱和度预测结果相关系数平均值相近（孔隙度：0.947；含气饱和度：0.957），而孔隙度预测结果均方根误差平均值更小（孔隙度：0.862；含气饱和度：3.251），预测效果更好；孔隙度预测结果变异系数大多低于0.2，含气饱和度预测结果变异系数大多低于0.3，说明孔隙度预测结果更稳定，这与地震数据蕴含更丰富的孔隙度信息有关。

3 结论

本文提出了一种基于PSO-RVM的储层参数定量预测与不确定性评估方法，数值模拟测试和实际数据应用表明：

（1）PSO-RVM具有较好的学习性能和泛化能力，且具备一定的抗噪能力；

（2）PSO-RVM预测结果的均方根误差低于RVM，预测精度更高，说明PSO可以有效指导RVM核参数选择，进而提高算法性能；

（3）PSO-RVM给出了预测结果后验概率，通过引入变异系数可以量化不确定性，便于解释人员评估不确定性；

（4）以井震数据为基础，基于PSO-RVM定量预测了孔隙度与含气饱和度，预测精度较高，且孔隙度预测精度更高，不确定性更低。在实际应用中，利用PSO-RVM预测不同储层参数的效果存在差异，通过变异系数评估不确定性可以明确预测风险程度，提高决策优化度。