2. 东华理工大学地球物理与测控技术学院, 江西南昌 330013;
3. 东华理工大学核资源与环境国家重点实验室, 江西南昌 330013;
4. 大庆油田勘探开发研究院, 黑龙江大庆 163712;
5. 东华理工大学核科学与工程学院, 江西南昌 330013
2. School of Geophysics and Measurement-Control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China;
3. State Key Laboratory of Nuclear Resources and Environment, East China University of Technology, Nanchang, Jiangxi 330013, China;
4. Exploration and Development Research Institute of Daqing Oilfield Company, Daqing, Heilongjiang 163712, China;
5. School of Nuclear Science and Engineering, East China University of Technology, Nanchang, Jiangxi 330013, China
现今油气勘探目标日益复杂,对地震勘探提出了更高要求。实际地下介质是黏弹性介质,地震波在其中传播将发生两类衰减:一类是与地层吸收性质相关的衰减,称为本征衰减;另一类是与地震波传播性质有关的衰减,称为非本征衰减,如球面扩散、透射损失等[1]。
品质因子Q值作为描述本征衰减的关键参数,在提高岩性预测精度及地震资料纵向分辨率方面具有重要作用。一方面,Q值与地层岩性、饱和度及渗透率等参数密切相关,可用于储层预测和油气识别[2-5];另一方面,Q是能量补偿反Q滤波方法的必要参数,可间接提高地震资料成像精度[6-8]。
自20世纪70年代起,Q值估计方法备受人们关注。其中,对数谱比(LSR)法是常用的传统算法,具有广泛的适用性,可估计透射波数据(如VSP资料[9-11])及地面反射波数据(如叠后地震资料[12-13]和叠前CMP数据[14])的Q值。但LSR法受频段、子波干涉和噪声等因素的影响较大[15-17],限制了其在实际地震资料中的应用。
为了克服这些因素的影响,人们一直在寻求优化算法。Wang等[17]基于积分运算弱化噪声的思想,利用对数谱面积差(LSAD)线性拟合对数谱斜率求取Q值,提高了算法的抗噪性,但Q值估计结果受非本征衰减的影响,仅适用于VSP数据。为消除非本征衰减的影响,An等[18]、Cheng等[19]利用高、低参考频段对数谱面积差(LSAD_LH)法及分段频率对数谱面积双差值(LSADD)法求取Q值,进一步改善了算法的实用性。许李囡等[20]在S变换域利用变分法估计Q值,受震源子波类型及时窗宽度的影响较小。杨登峰等[21]基于LSR法加入高斯函数权重算子求取斜率,降低了Q值估计算法对频段选择的依赖性。Zhang等[22-23]基于振幅谱积分差和振幅谱积分比值稳定地估计Q值。
目前,Q值估计方法发展迅速,但易受频段选择及非本征衰减等因素影响,Q值估计精度及稳定性不高。为此,本文提出基于不同阶次泰勒级数展开的含非本征衰减频域振幅比平均的Q值估计方法。首先,利用高、低双参考频段消除非本征衰减因素对Q值估计的影响,提出考虑非本征衰减的1~4阶频域振幅比单频点(FARS)Q值估计算法。在此基础上,采用频点平均模式构建多频点平均(FARA)Q值估计方法。最后通过模型试验和实例应用测试方法的效果和精度。
1 方法原理 1.1 FARS法的基本原理基于常Q值的Futterman体波衰减模型[24],在考虑非本征衰减影响时,地震波在黏弹性介质中的传播规律可用不同时刻的振幅变化表述[25]
| $ A(t, f)=P\left(t\right)A(0, f)\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{\mathrm{\pi }t}{Q}f\right] $ | (1) |
| $\begin{align} A(t+\mathrm{\Delta }t, f)=&P(t+\mathrm{\Delta }t)A(0, f)\times \\&\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{\mathrm{\pi }(t+\mathrm{\Delta }t)}{Q}f\right] \end{align}$ | (2) |
式中:P(t)为t时刻的非本征衰减项[17-18];Δt为时间延迟;A(0, f)为震源子波的振幅,f为频率。将式(1)与式(2)相比,得
| $ \begin{align}R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.&=\frac{A(t, f)}{A(t+\mathrm{\Delta }t, f)}\\ &=\frac{P\left(t\right)}{P(t+\mathrm{\Delta }t)}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{\mathrm{\pi }\mathrm{\Delta }t}{Q}f\right)\end{align} $ | (3) |
为了消除非本征衰减对Q值估计的影响,定义一个相对参考频段内振幅比的连乘,即
| $ \begin{align}R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.&={\left[\prod _{k=\mathrm{I}\mathrm{n}}^{\mathrm{I}\mathrm{n}+K-1}R\left({f}_{k}\right)\right]}^{\frac{1}{K}}\\ &={\left[\prod _{k=\mathrm{I}\mathrm{n}}^{\mathrm{I}\mathrm{n}+K-1}\frac{A(t, {f}_{k})}{A(t+\mathrm{\Delta }t, {f}_{k})}\right]}^{\frac{1}{K}}\\ &=\frac{P\left(t\right)}{P(t+\mathrm{\Delta }t)}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{\mathrm{\pi }\mathrm{\Delta }t}{Q}\frac{\sum\limits _{k=\mathrm{I}\mathrm{n}}^{\mathrm{I}\mathrm{n}+K-1}{f}_{k}}{K}\right)\end{align} $ | (4) |
令fc=
| $ \begin{align}\frac{R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}&=\mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{\mathrm{\pi }\mathrm{\Delta }t}{Q}(f-{f}_{c})\right]\\ &=\mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{\mathrm{\pi }\mathrm{\Delta }t}{Q}\left(f-\frac{\sum\limits _{k=\mathrm{I}\mathrm{n}}^{\mathrm{I}\mathrm{n}+K-1}{f}_{k}}{K}\right)\right]\end{align} $ | (5) |
令
| $ \frac{R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}\approx 1+x $ | (6) |
| $ \frac{R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}\approx 1+x+\frac{1}{2}{x}^{2} $ | (7) |
| $ \frac{R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}\approx 1+x+\frac{1}{2}{x}^{2}+\frac{1}{6}{x}^{3} $ | (8) |
| $ \frac{R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}\approx 1+x+\frac{1}{2}{x}^{2}+\frac{1}{6}{x}^{3}+\frac{1}{24}{x}^{4} $ | (9) |
求解以上四式,分别得到x在1~4阶泰勒级数展开的正解
| $ {x}_{1}=\frac{R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}-1 $ | (10) |
| $ {x}_{2}=-1+\sqrt{\frac{2R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}-1} $ | (11) |
| $ \begin{array}{c}{x}_{3}=\sqrt[3]{C(t+\mathrm{\Delta }t, f)+\sqrt{{C}^{2}(t+\mathrm{\Delta }t, f)+1}}-\\ \sqrt[3]{-C(t+\mathrm{\Delta }t, f)+\sqrt{{C}^{2}(t+\mathrm{\Delta }t, f)+1}}-1\end{array} $ | (12) |
其中
| $ C(t+\mathrm{\Delta }t, f)=\frac{3R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}-1 $ |
| $ {x}_{4}=-1-\frac{1}{2}\sqrt{\varDelta -4}+\frac{1}{2}\sqrt{\frac{16}{\sqrt{\varDelta -4}}-\varDelta -8} $ | (13) |
而
| $ \begin{array}{l}\varDelta =\frac{8\sqrt[3]{2}{\varDelta }_{1}}{\sqrt[3]{{\varDelta }_{2}+\sqrt{-4{\varDelta }_{1}^{3}+{\varDelta }_{2}^{2}}}}+\frac{8\sqrt[3]{{\varDelta }_{2}+\sqrt{-4{\varDelta }_{1}^{3}+{\varDelta }_{2}^{2}}}}{\sqrt[3]{2}} \\ {\varDelta }_{1}=\frac{1}{4}-\frac{R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{2R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}\\ {\varDelta }_{2}=\frac{3R\left(f\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}{4R\left({f}_{\mathrm{c}}\right)\left|{}_{t+\mathrm{\Delta }t}^{t}\right.}-\frac{1}{8}\end{array} $ |
则不同阶次i(i=1, 2, 3, 4)泰勒级数展开的Q值为
| $ {Q}_{i}\left(f\right)=\frac{\mathrm{\pi }\mathrm{\Delta }t}{{x}_{i}\left(f\right)}(f-{f}_{\mathrm{c}}) $ | (14) |
式(14)为不同阶次FARS法估计Q值基本公式。为削弱参考频段选取的影响,可选取低参考频段(如10~20 Hz)和高频段(如(2fm-10)~2fm,fm为地震子波的主频)的组合模式求取Q值。
1.2 FARA法的基本原理由于本文研究不随频率变化的Q估计值,因此可在振幅谱主值频段[fmin,fmax]采用FARA法提高Q值估计的稳定性
| $ {Q}_{i}=\frac{\mathrm{\pi }\mathrm{\Delta }t}{\overline{{x}_{i}}\left|\begin{array}{c}{f}_{\mathrm{m}\mathrm{a}\mathrm{x}}\\ {f}_{\mathrm{m}\mathrm{i}\mathrm{n}}\end{array}\right.}\overline{(f-{f}_{\mathrm{c}})}\left|\begin{array}{c}{f}_{\mathrm{m}\mathrm{a}\mathrm{x}}\\ {f}_{\mathrm{m}\mathrm{i}\mathrm{n}}\end{array}\right. $ | (15) |
一般情况下,起始频率fmin≥10 Hz,而fmax ≤ 2fm,10~2fm常被看作振幅谱的主值频段[22-23]。
| $ \frac{\overline{R\left(f\right)}}{R\left({f}_{\mathrm{c}}\right)}=\overline{\left[\frac{A(t+\mathrm{\Delta }t, f)}{A(t, f)}\right]}\cdot {\left[\prod\limits _{k=\mathrm{I}\mathrm{n}}^{\mathrm{I}\mathrm{n}+K-1}\frac{A(t+\mathrm{\Delta }t, {f}_{k})}{A(t, {f}_{k})}\right]}^{-1/K} $ | (16) |
图 1为两层介质模型在200、300 ms时刻的含非本征衰减地震记录。鉴于本文算法由子波振幅谱获取Q估计值,故展示图 1中4个衰减地震子波的振幅谱(图 2)。可以看出,随着旅行时间增加及Q值减小,主频向低频方向移动,不同时刻衰减子波的振幅关于主频呈近似对称分布。基于这一思想,本文将在主值频段[22]估计Q值。

|
图 1 两层介质模型在200、300 ms时刻的含非本征衰减地震记录 震源为主频50 Hz的Ricker子波,由上层介质垂直界面入射,将200、300 ms时刻的信号在同一地震道显示。上层介质密度为2.1 g/cm3,速度为2000 m/s;下层介质密度为2.2 g/cm3,速度为3000 m/s。 |

|
图 2 图 1中4个衰减地震子波的振幅谱 |
选取不同参考频段,利用FARS法估计Q值(图 3)。由图可见:①在低参考频段,随着频率增加,Q估计值先迅速增大,后缓慢下降,在20 Hz之后Q估计值逐渐趋于真值;在参考频段出现突变(图 3a的14 Hz处)。②在高参考频段,在超低频率处Q估计值随着频率增加迅速增大,随后趋于平缓;在参考频段也存在突变(图 3b的88 Hz及70 Hz处)。因此,图 3a、图 3b的Q估计值在大部分频段分布在真实Q值两侧,其中Q1估计值最明显。③将低、高参考频段组合,提高了Q值估计精度(图 3c),Q估计值在大部分频段更接近真值。

|
图 3 真实Q值为160(左)、40(右)的Q值估计结果 (a)低参考频段(10~20 Hz);(b)高参考频段((2fm-10)~2fm);(c)高、低参考频段组合 |
为了探究参考频段、时差、时窗、噪声等因素对FARA法的影响,进行了相应的测试分析。此外,LSADD法[19]可直接由含非本征衰减的地震记录估计Q值,与FARA方法的理论基础较相似。因此,对比、分析了FARA法与LSADD法的效果。
2.2.1 参考频段的影响FARA法在估计Q值时需给定参考频段,基于图 1,分别对不同衰减子波(Q =160、120、80、40)由FARA法估计Q值。鉴于FARA法在高、低参考频段附近的Q估计值不稳定,故在利用FARA法计算Q值时,选择主值频段为计算频段。如:在低参考频段10~(10+K)(模型中频率采样率为1 Hz,为简便表达,下文直接将与参考频点K有关的频率值表示为K),计算频段为(10+K)~2fm[22];在高参考频段(2fm-K)~2fm,计算频段为10~(2fm-K)。这里选取低参考频段10~20 Hz及其计算频段20~2fm、高参考频段(2fm-10)~2fm及其计算频段10~(2fm-10)估计高、低参考频段Q值,并求高、低频段Q估计值的平均值(表 1)。可见:①在低参考频段,只有1阶FARA法的Q估计值明显低于理论值,2~4阶FARA法的Q估计值与理论值相差不大。②在高参考频段,只有1阶FARA法的Q估计值明显偏大,2~4阶FARA法的Q估计值基本上都略大于理论值,相对误差(估计值和真值之差与真值的比值)略高于低参考频段。③高、低频段Q估计值的平均值表明,1阶FARA法有效提高了Q值估计精度;无论是低参考频段、还是高参考频段,由于2~4阶FARA法的Q估计值均略大于理论值,因此高、低频段Q估计值的平均值不能明显提高Q值估计精度。不同阶次FARA法获得的高、低频段Q估计值的平均值最大相对误差约为3%(Q = 40,1阶FARA法),说明由FARA法求取Q值的精度较高。需要说明的是,下文均采用高、低频段Q估计值的平均值作为FARA法的Q估计值。
|
|
表 1 不同参考频段的FARA法Q估计值 |
为了探究参考频带宽度(即参考频点个数K)对FARA法的影响,基于图 1采用FARA法获取Q估计值,并将高、低频的K均从1增至40,由此得到Q估计值随K的变化曲线(图 4)。可见:随着K增加,所有阶次的Q估计值基本呈现先逐渐下降再缓慢上升的趋势;虽然不同K的Q估计值都大于理论值,但最大偏差均未超过3%,可见选取不同的K基本不影响Q值估计精度,但适当增加K,可提高Q值估计的稳定性。

|
图 4 Q估计值随K的变化曲线 (a)Q=160;(b)Q=40 |
试验结果表明:对于FARA法来说,选择低参考频段计算Q值的精度高于高参考频段,采用高、低频段Q估计值的平均值可以提高Q值的估计精度,对于低阶次Q值更是如此;参考频点个数K对Q值估计结果影响不大,但适当增加K可以在一定程度上提高算法的稳定性。
2.2.2 旅行时差的影响由于FARA法是一种基于泰勒级数展开的近似算法,其误差将随着旅行时与Q的比值增大而增大。为了测试FARA法对旅行时差的敏感程度,基于图 1,固定参考子波的旅行时为200 ms,选择衰减子波的旅行时为250、300、400 ms,子波截取的时窗宽度为50 ms,高、低频的K均为40。图 5为不同旅行时差的LSADD法和FARA法的Q值估计结果。可见:无论Q值大小,LSADD法的Q估计值均大于理论值,且随着旅行时差的增加而增大;不同阶次FARA法的Q估计值基本也随旅行时差的增加而增大,但增大幅度整体小于LSADD法;无论旅行时差大小,各阶次FARA法的Q值估计精度均高于LSADD法。

|
图 5 不同旅行时差的LSADD法和FARA法的Q值估计结果 (a)Q=160;(b)Q=40 |
试验结果表明:FARA法由于采用高、低频段Q估计值的平均值,即使1阶Q估计值的精度也较高,但误差随着旅行时差的增大而略微增大,且任意阶次的Q值估计精度均高于LSADD法。
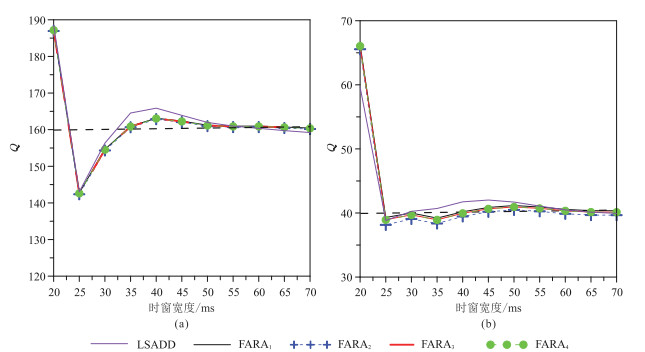
2.2.3 时窗宽度的影响为测试截取子波时窗宽度(子波不完整性)对FARA法的影响,基于图 1,得到Q估计值随时窗宽度的变化曲线(图 6)。可见,LSADD法、各阶次FARA法的Q估计值随时窗宽度的变化曲线基本一致,即随着时窗宽度增加先迅速降低、再逐渐增大、再缓慢下降并逐渐趋于真值。显然,当旅行时差较小时,Q估计值波动较大,明显偏离真值。当截取子波宽度大于25 ms(完整子波延续宽度约为50 ms)时,FARA法的Q估计值的波动小于LSADD法,估计精度更高。
|
图 6 Q估计值随时窗宽度的变化曲线 (a)Q=160;(b)Q=40 |
试验结果表明,FARA法和LSADD法在一定程度上均受子波不完整性的影响,但当时窗宽度大于子波宽度一半时,两种方法均能获得稳定、准确的Q估计值,但FARA法的Q估计值受时窗宽度影响更小。
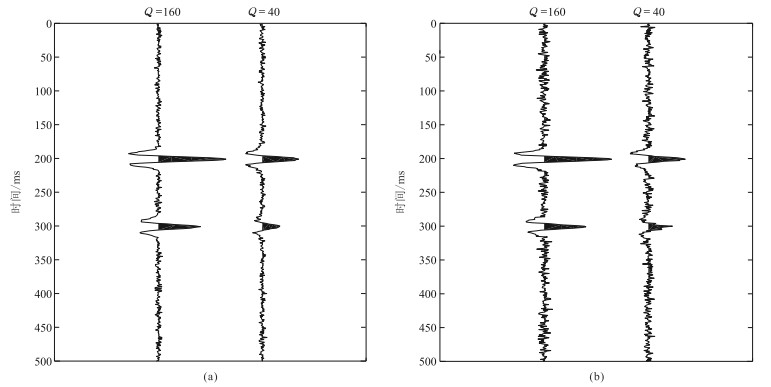
2.2.4 噪声的影响为测试FARA法的抗噪性,将图 1数据添加随机噪声(图 7),图 8为加噪前、后衰减地震子波的振幅谱。可见,加噪前、后振幅谱的主要能量均集中于2倍主频之内;且在主值频段(10~2fm),加噪前、后子波的整体一致性较好,说明选取主值频段估计Q值更合理。
|
图 7 图 1数据添加噪声 (a)信噪比=10 dB;(b)信噪比=5 dB |

|
图 8 加噪前、后衰减地震子波的振幅谱 (a)Q=160、t=200 ms;(b)Q=40、t=200 ms;(c)Q=160、t=300 ms;(d)Q=40、t=300 ms |
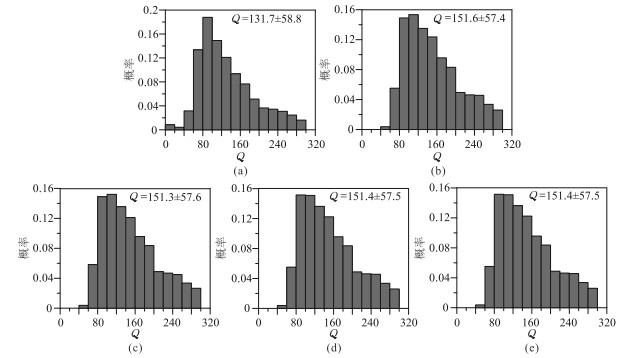
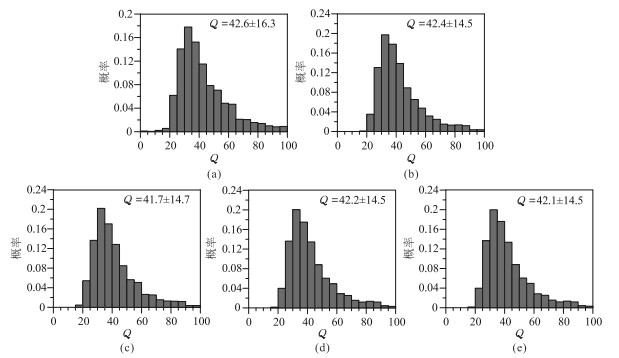
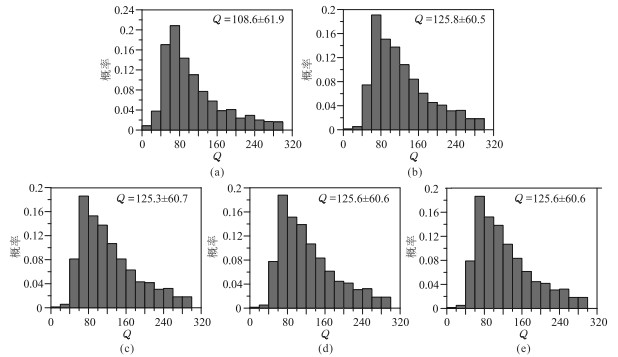
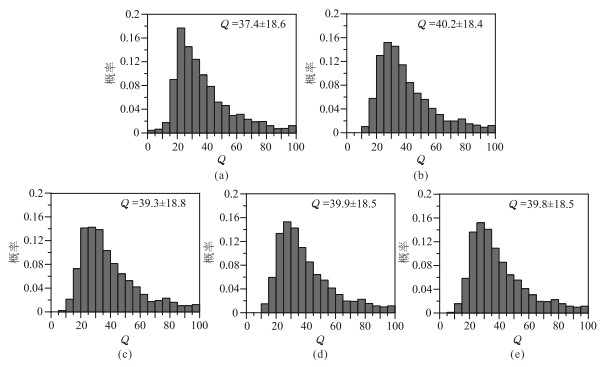
图 9~图 12为不同Q值、噪声的LSADD法和FARA法的Q估计值概率分布图。由图可见:①当理论Q值较大且噪声较弱时(图 9),不同阶次的FARA法的Q估计值几乎完全吻合,较LSADD法的Q估计值更接近真值(LSADD法、FARA法的Q估计值相对误差分别为17.7%、小于5.5%)。②当理论Q值较小且噪声较弱时(图 10),LSADD法与FARA法均能获得准确的Q估计值,但后者的精度更高。③当噪声较强时(图 11、图 12),无论理论Q值大小,两种算法的Q估计值波动均增大(LSADD法、FARA法的Q估计值相对误差分别为32%、21%),且在理论Q值较大时(图 11)得到的Q估计值明显偏小,在理论Q值较小时(图 12)得到的Q估计值精度较高,但FARA法的Q值估计精度更高。④不同阶次FARA法的Q估计值离散性更小,稳定性更强。
|
图 9 LSADD法和FARA法的Q估计值概率分布图(理论Q值为160,信噪比为10 dB) (a)LSADD法;(b)FARA1;(c)FARA2;(d)FARA3;(e)FARA4 将Q=160、40的Q估计阈值分别设定为0~300、0~100。选取时窗宽度为50 ms,计算频段均为10~2fm,FARA法的参考频点个数为40。图a中“Q=131.7±58.8”表示Q值估计的均值为131.7,均方差为58.8,后同。 |
|
图 10 LSADD和FARA法的Q估计值概率分布图(理论Q值为40,信噪比为10dB) (a)LSADD法;(b)FARA1;(c)FARA2;(d)FARA3;(e)FARA4 |
|
图 11 LSADD和FARA法的Q估计值概率分布图(理论Q值为160,信噪比为5 dB) (a)LSADD法;(b)FARA1;(c)FARA2;(d)FARA3;(e)FARA4 |
|
图 12 LSADD和FARA法的Q估计值概率分布图(理论Q值为40,信噪比为5 dB) (a)LSADD法;(b)FARA1;(c)FARA2;(d)FARA3;(e)FARA4 |
试验结果表明,FARA法的效果在一定程度上受噪声影响,Q值估计误差随着理论Q值的增大、噪声强度的增加而增大。由于FARA法采用高、低频段Q估计值的平均值作为FARA法的Q估计值,因此FARA法受噪声的影响程度低于LSADD法,且稳定性更高。
2.2.5 理论Q值与时差的综合影响由于FARA法是一种估计Q值的近似算法,其精度受
|
|
表 2 不同理论Q值、不同时差的FARA法Q估计值 |
为了测试新算法的实际应用效果,选取中国南海A区海洋叠前地震数据进行测试。图 13为中国南海A区CMP道集、第1道振幅谱及第1段截取的不同道地震子波的振幅谱。由图可见:由于不同主频子波的振幅相互叠加,CMP道集(图 13a)的第1道振幅谱(图 13b)曲线波动较大,但振幅谱能量主要集中分布在10~47 Hz范围。根据子波分布特征,在旅行时分别为532、744、936、1188、1356、1800及1976 ms处,将整个地震记录道分割为7段,然后利用LSADD法和本文提出的FARA法求取Q值,再求取Q估计值的平均值作为该段的平均等效Q值[17, 19]。在计算过程中选用的时窗宽度为48 ms,主值频段仍为10~2fm,FARA法参考频段的频点数K为40。为了了解处理流程,以第1段(起点为图 13a红色箭头处)为例详述实际资料处理过程。由第1段截取的不同道地震子波的振幅谱(图 13c)可见:①第1道子波主频约为29 Hz,其余各道子波主频均降低,由于旅行时差较小,因此主频降低不明显。②随着旅行时间增加,整体上振幅最大值不断减小,所有子波的振幅谱分布于10 Hz至2倍主频之间,与图 2相似。③第1道~第5道子波主频分别为28.9、26.8、26.4、26.4及28.6 Hz,说明由于激发、接收条件等因素的影响,导致部分接收子波的主频并没有随着传播时间增加而降低,若采用的参考子波振幅(或主频)小于衰减子波,则Q估计值会出现负值[26-27]。因此在计算平均等效Q值时,需要剔除负值。

|
图 13 中国南海A区CMP道集(a)、第1道振幅谱(b)及第1段截取的不同道地震子波的振幅谱(c) 图a的采样间隔为4 ms,已进行非本征衰减补偿 |
图 14为由不同方法估计的平均等效Q值。由图可见:①整体上,不同阶次的FARA法Q估计值的一致性较好,可相互印证,从而提高Q值估计精度;②FARA法得到的等效Q值整体上大于LSADD法,这与由图 9~图 12所得认识一致,表明实际地震记录中的噪声导致LSADD法Q估计值整体偏小。

|
图 14 由不同方法估计的平均等效Q值 |
准确估计品质因子Q值对提高岩性预测及地震成像精度均具有重要作用。本文从含非本征衰减的地震波振幅表达式出发,利用参考频段内振幅比的连乘消除非本征衰减对Q估计值的影响,然后在参考频点处再对振幅衰减因子进行1~4阶泰勒级数展开,由此推导不受非本征衰减影响的振幅比单频点Q值计算公式。此外,利用高、低频段Q估计值的平均值削弱参考频段的影响,并提高算法的稳定性。由模型试验及实例应用得到以下认识:
(1)本文提出的FARA法可在主值频段内稳定估计Q值,与LSADD法相比,具有受时差及时窗等因素影响小和抗干扰能力强的优点;
(2)选取主值频段估计Q值,可有效降低计算频段对Q估计值的影响,从而提高小Q值估计的稳定性;
(3)FARA法包含1~4阶的Q值估计结果,这些结果互为印证,进一步提高了方法的实用性;
(4)实例应用中,不同阶次FARA法获得的等效Q值一致性较好,整体上大于LSADD法的Q估计值,因此由FARA法得到的Q值更可靠;
(5)FARA法不仅适用于叠前CMP道集、VSP数据,同时也适用于叠后地震记录,而且无需事先进行非本征衰减补偿,具有较强的适用性和实用性。
| [1] |
李生杰, 施行觉, 王宝善, 等. 地层衰减在地震记录上的特征分析[J]. 石油地球物理勘探, 2002, 37(3): 248-253. LI Shengjie, SHI Xingjue, WANG Baoshan, et al. Analyzing characters of formation attenuation on seismic records[J]. Oil Geophysical Prospecting, 2002, 37(3): 248-253. DOI:10.13810/j.cnki.issn.1000-7210.2002.03.009 |
| [2] |
KLIMENTOS T, MCCANN C. Relationships among compressional wave attenuation, porosity, clay content, and permeability in sandstones[J]. Geophysics, 1990, 55(8): 998-1014. DOI:10.1190/1.1442928 |
| [3] |
BEST A I. The effect of pressure on ultrasonic velo-city and attenuation in near-surface sedimentary rocks[J]. Geophysical Prospecting, 1997, 45(2): 345-364. DOI:10.1046/j.1365-2478.1997.00344.x |
| [4] |
PINSION L J W, HENSTOCK T J, DIX J K, et al. Estimating quality factor and mean grain size of sediments from high resolution marine seismic data[J]. Geophysics, 2008, 73(4): G19-G28. DOI:10.1190/1.2937171 |
| [5] |
MULLER T M, GUREVICH B, LEBEDEV M. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks: A review[J]. Geophysics, 2010, 75(5): 75A147-75A164. DOI:10.1190/1.3463417 |
| [6] |
ZHANG J, WANG Y, NOBES D C, et al. Deep seismic reflection data interpretation using balanced filte-ring method[J]. Geophysics, 2017, 82(5): N43-N49. DOI:10.1190/geo2016-0061.1 |
| [7] |
马凯, 彭玉林, 张欣吉, 等. 近地表Q补偿技术在准噶尔盆地南缘山前带的应用[J]. 石油地球物理勘探, 2022, 57(增刊1): 1-5. MA Kai, PENG Yulin, ZHANG Xinji, et al. Application of near-surface Q compensation technology in piedmont zone of southern margin of Junggar Basin[J]. Oil Geophysical Prospecting, 2022, 57(S1): 1-5. |
| [8] |
程万里, 王守东, 孟巾钰, 等. 基于L1范数正则化约束的叠前数据衰减补偿方法[J]. 石油地球物理勘探, 2023, 58(3): 567-579. CHENG Wanli, WANG Shoudong, MENG Jinyu, et al. Prestack data attenuation compensation based on L1-norm regularization constraint[J]. Oil Geophysical Prospecting, 2023, 58(3): 567-579. DOI:10.13810/j.cnki.issn.1000-7210.2023.03.008 |
| [9] |
HAUGE P S. Measurements of attenuation from vertical seismic profiles[J]. Geophysics, 1981, 46(11): 1548-1558. DOI:10.1190/1.1441161 |
| [10] |
STAINSBY S D, WORTHINGTON M H. Q estimation from vertical seismic profile data and anomalous variations in the central North Sea[J]. Geophysics, 1985, 50(4): 615-626. DOI:10.1190/1.1441937 |
| [11] |
PUJOL J, SMITHSON S. Seismic wave attenuation in volcanic rocks from VSP experiments[J]. Geophy-sics, 1991, 56(9): 1441-1455. |
| [12] |
HACKERT C L, PARRA J O. Improving Q estimation from seismic reflection data using well-log-based localized spectral correction[J]. Geophysics, 2004, 69(6): 1521-1529. DOI:10.1190/1.1836825 |
| [13] |
郝亚炬, 黄捍东, 文晓涛, 等. 广义S域Q值估计方法及其在油气检测中的应用[J]. 石油地球物理勘探, 2017, 25(5): 1059-1066. HAO Yaju, HUANG Handong, WEN Xiaotao, et al. Q estimation in the generalized S domain and its application in the hydrocarbon detection[J]. Oil Geophysical Prospecting, 2017, 25(5): 1059-1066. DOI:10.13810/j.cnki.issn.1000-7210.2017.05.020 |
| [14] |
DASGUPTA R, CLARK R A. Estimation of Q from surface seismic reflection data[J]. Geophysics, 1998, 63(6): 2120-2128. DOI:10.1190/1.1444505 |
| [15] |
TONN R. The determination of the seismic quality factor Q from VSP data: A comparison of different computational methods[J]. Geophysical Prospecting, 1991, 39(1): 1-27. DOI:10.1111/j.1365-2478.1991.tb00298.x |
| [16] |
CASTRO NUNES B I, MEDEIROS W E, NASCI- MENTO A F, et al. Estimating quality factor from surface seismic data: A comparison of current approaches[J]. Journal of Applied Geophysics, 2011, 75(2): 161-170. DOI:10.1016/j.jappgeo.2011.07.003 |
| [17] |
WANG S, YANG D, LI J, et al. Q factor estimation based on the method of logarithmic spectral area diffe-rence[J]. Geophysics, 2015, 80(6): V157-V171. DOI:10.1190/geo2014-0257.1 |
| [18] |
AN Y, WANG X. Q estimation based on logarithmic spectral areas with different high and low frequencies[J]. Applied Geophysics, 2021, 18(1): 75-84. DOI:10.1007/s11770-021-0862-x |
| [19] |
CHENG W, WANG S, ZHOU C, et al. Q estimation based on the logarithmic spectral area double difference[J]. Geophysics, 2022, 87(2): V155-V167. DOI:10.1190/geo2021-0040.1 |
| [20] |
许李囡, 高静怀, 杨阳, 等. 基于S变换和变分法的品质因子Q估计方法[J]. 石油地球物理勘探, 2022, 57(1): 82-90. XU Linan, GAO Jinghuai, YANG Yang, et al. Qua-lity factor Q estimation based on S transform and variational method[J]. Oil Geophysical Prospecting, 2022, 57(1): 82-90. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.009 |
| [21] |
杨登锋, 刘军, 吴静, 等. 加权谱比法Q值估计[J]. 石油地球物理勘探, 2022, 57(3): 593-601. YANG Dengfeng, LIU Jun, WU Jing, et al. Q factor estimation by weighted spectral ratio method[J]. Oil Geophysical Prospecting, 2022, 57(3): 593-601. DOI:10.13810/j.cnki.issn.1000-7210.2022.03.010 |
| [22] |
ZHANG J, WANG Y, ZHANG G, et al. Q estimation using multifrequency point average method based on the Taylor series expansion with a different order[J]. Applied Geophysics, 2021, 18(4): 557-568. DOI:10.1007/s11770-021-0918-y |
| [23] |
张瑾, 张国书, 王彦国, 等. 利用泰勒级数展开的振幅谱积分差值的Q值估计方法[J]. 石油地球物理勘探, 2022, 57(2): 320-330. ZHANG Jin, ZHANG Guoshu, WANG Yanguo, et al. Amplitude spectral integral difference method for Q estimation based on Taylor series expansion[J]. Oil Geophysical Prospecting, 2022, 57(2): 320-330. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.009 |
| [24] |
FUTTERMAN W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [25] |
ZHANG C, ULRYCH T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(5): 1542-1547. DOI:10.1190/1.1512799 |
| [26] |
李伟娜, 云美厚, 党鹏飞, 等. 基于微测井资料的双线性回归稳定Q估计[J]. 石油物探, 2017, 56(4): 483-490. LI Weina, YUN Meihou, DANG Pengfei, et al. Stabi-lity Q estimation by dual linear regression based on uphole survey data[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 483-490. |
| [27] |
翟桐立, 马雄, 彭雪梅, 等. 基于井地一体化测量的近地表品质因子Q值估算与应用[J]. 石油物探, 2018, 57(5): 685-690. ZHAI Tongli, MA Xiong, PENG Xuemei, et al. Near- surface Q factor measurements by combining surface and cross-hole seismic surveys[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 685-690. |



 王彦国,江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
王彦国,江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email: