0 引言

东海深层低渗气藏主要分布在3500 m以下^[1]，资源量巨大^[2]。为了实现深层低渗气藏的高效开发，准确预测“甜点”具有重要的意义。

目前对“甜点”的预测主要集中在非常规储层方面，如页岩气^[3]、页岩油^[4]、煤层气^[5]、致密油^[6]、致密气^[7-12]等。对于致密气的“甜点”预测，应用的地球物理方法主要包括：①地震资料优化处理，如保真、保幅宽频、高分辨率地震资料叠前成像等；②储层反演，如叠前AVO反演、岩相约束的孔隙度(Φ)反演、密度反演等；③地震沉积学技术，如利用地层切片对岩相开展“甜点”垂向分布规律分析。总体上，不同地区“甜点”的地震响应特征不同，地球物理预测方法虽有差异，但研究思路相似。具体而言，“甜点”类型的划分是“甜点”预测的基础，岩石物理敏感参数的识别是“甜点”预测的关键，储层反演是“甜点”预测的核心。因此，在地质特征定性分析、划分“甜点”类型的基础上，寻找不同“甜点”的岩石物理敏感参数，应用合适的反演技术，可以预测“甜点”的空间展布特征。

西湖凹陷Z气田是近期东海陆架盆地发现的大型低渗气田之一，储层非均质性强，“甜点”的空间展布规律直接影响开发井位的设计方案。前人研究主要集中在“甜点”的地质特征^[13-16]、储层分类^[17]、地质成因^[18]、测井评价^[19]等方面。在利用地球物理技术预测“甜点”方面 ^[20-21]，尚未进一步开展不同类型“甜点”的精细预测。

为此，本文在划分“甜点”类型的基础上，分析不同类型“甜点”的岩石物理特征及变化规律；然后建立合适的地质—地球物理模型，模拟储层的地震反射特征；通过叠前弹性反演，实现厚储层内部“甜点”的精细表征，为大型低渗气田的有效开发提供地球物理技术支持。

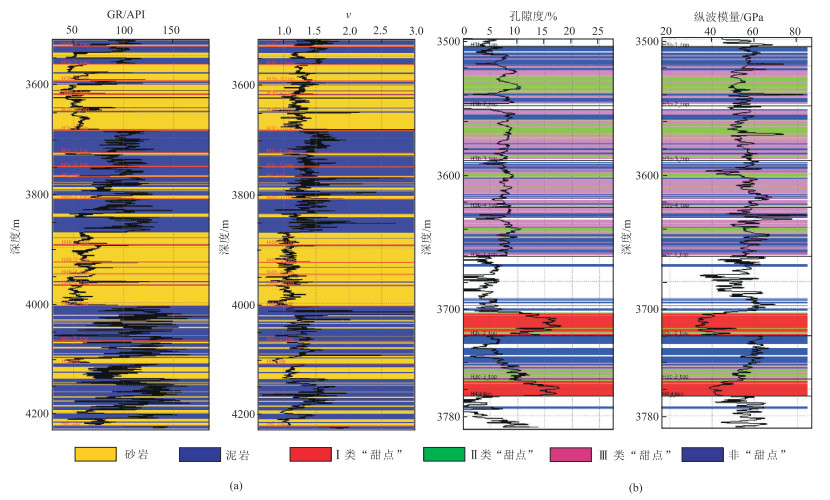
1 甜点储层特征

Z气田位于西湖凹陷中央反转构造带中北部，主要开发层系为H3(花港组三段)，发育河流—三角洲相沉积^[22-23]。砂体储层厚度约为200 m，非均质性强，埋深大于3500 m，一般具有低孔、低渗特征。H3进一步可以细分为H3a、H3b、H3c三个小层^[24]。其中，H3a储层为特低孔、特低渗，H3b、H3c储层均以中低孔、中低渗为主，但是在局部发育物性相对较好的“甜点”。

1.1 “甜点”分类及地质特征

在前人研究成果^[25-30]的基础上，综合考虑产能、物性、孔隙结构等因素，同时将控制上述参数的沉积相和成岩相及相关参数纳入“甜点”评价标准。据此，研究区“甜点”可进一步划分为三类(表 1)，即Ⅰ类、Ⅱ类和Ⅲ类。Ⅰ类和Ⅱ类“甜点”为高产层段，具有自然产能；Ⅲ类需要进行储层压裂改造。

由表 1可见，Ⅰ类和Ⅱ类“甜点”差异较大。Ⅰ类“甜点”孔隙度(Φ)大于11%，渗透率大于10 mD，孔隙结构以大孔喉道型为主；Ⅱ类“甜点”孔隙度为9%~11%，渗透率为3~10 mD，孔隙结构以中孔喉道型为主。

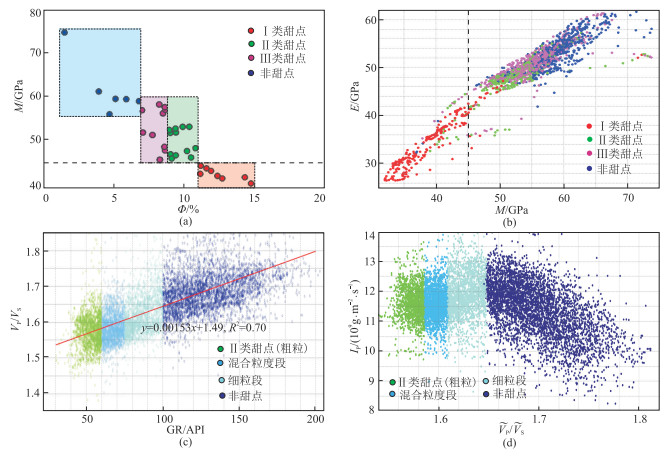
1.2 “甜点”敏感地球物理参数分析

通过岩石孔隙度Φ与岩石物理实验实测纵波模量(M)交会分析(图 1a)、测井数据计算的纵波模量与杨氏模量(E)交会分析(图 1b)，可以发现：相对于非“甜点”储层，“甜点”储层具有低M、低E的特征；Ⅰ类“甜点”的M低于45GPa，区分度较高，但是M较难用于区分Ⅱ类“甜点”。

Ⅱ类“甜点”主要为中粗砂岩，自然伽马(GR)较低(图 1c)，对Ⅱ类“甜点”有一定区分度。当GR≤60 API时，大部分为含砾砂岩和粗砂岩；当GR > 60 API时，各粒度砂岩叠置，无法区分。为了实现Ⅱ类“甜点”可预测的目的，采用GR划分储层类型，即当GR≤60 API时，为Ⅱ类“甜点”砂岩；当60 API < GR≤75 API时，为各粒度叠置混合砂岩；当75 API < GR≤100 API时，为细砂岩；当GR > 100 API时，为泥岩。因此，Ⅱ类“甜点”预测时只考虑GR≤60 API的储层。

利用地震资料直接预测GR难度较大，但V_P/V_S(纵横波速度比)与GR相关性较高(图 1c)，相关度R²达到0.7。因此，可以利用V_P/V_S与GR的相关性，将GR转换成$ {\tilde{V}}_{\mathrm{P}}/{\tilde{V}}_{\mathrm{S}} $(拟纵横波速度比)，与纵波阻抗I_P交会分析可实现对Ⅱ类“甜点”的识别(图 1d)。

1.3 “甜点”地震响应特征

由图 2可见，对储层地震反射特征影响较大的两个因素分别是孔隙类型和孔隙度。随着泥质含量的增加，砂岩底面的地震反射AVO曲线的截距为正且增加，但是梯度逐渐减小，曲线趋于平缓(图 2a)。随着含气饱和度的增加，砂岩底面的地震反射AVO曲线的截距为正且增加，但是当含气饱和度超过50%后，AVO曲线无明显变化(图 2b)。随着原生孔隙占比降低、砂岩孔隙连通性的变好，砂岩底面的地震反射AVO曲线的截距逐渐减小，由正变负，但是梯度逐渐增大(图 2c)。随着孔隙度的增加，砂岩底面的地震反射AVO曲线的截距增加，由负变正，但是梯度逐渐减小，由正变负(图 2d)。

为了对比“甜点”与非“甜点”的AVO响应特征，分别将研究区Z1井Ⅰ类和Ⅱ类“甜点”的速度、密度设置与围岩一致，实现非“甜点”储层替换，具体参数见表 2。

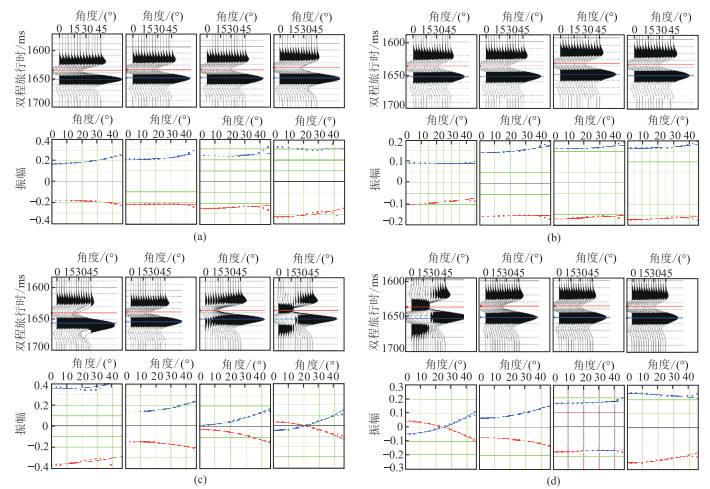
从图 3可以看出，Ⅰ类“甜点”是引起AVO异常的主要原因，Ⅰ类“甜点”替换为非“甜点”后反射振幅明显减弱。Ⅱ类“甜点”与非“甜点”的物性差异不大，所以替换前、后的AVO响应没有明显的变化。由此可见，Ⅰ类“甜点”在叠后地震资上表现为强振幅特征，而Ⅱ类“甜点”振幅无明显异常。

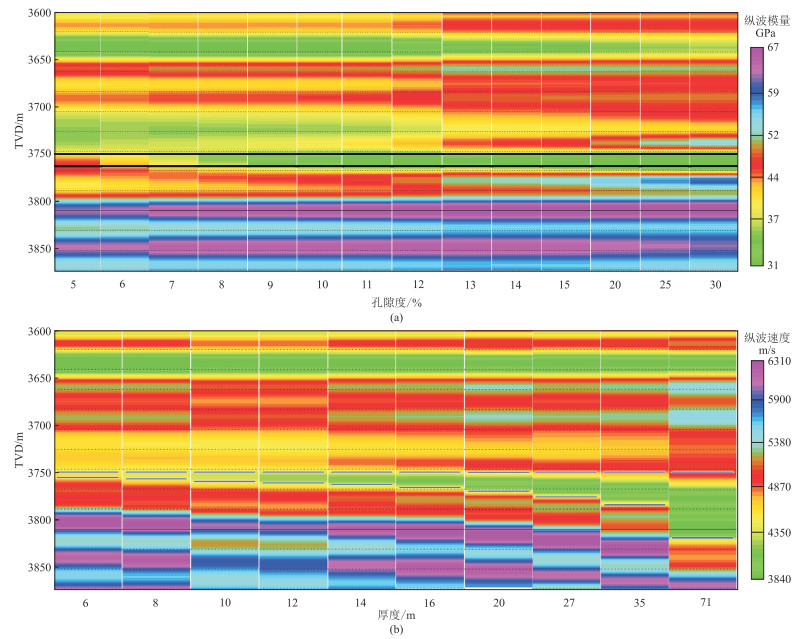
影响“甜点”识别精度的因素主要为孔隙度和厚度。通过AVO正演模拟不同孔隙度和不同厚度甜点的AVO响应特征(图 4)可以看到，Ⅰ类“甜点”在叠前地震正演中得到的纵波模量为异常低值，同时随着孔隙度的增大，纵波模量变小。

随着孔隙度的变化，地震反演方法对甜点的预测精度规律如下(图 4a)：当孔隙度＜9%时，无法准确预测“甜点”的位置和厚度；当孔隙度 > 15%时，“甜点”预测厚度要大于真实厚度；当孔隙度在10%~15%时，“甜点”预测厚度与真实厚度基本一致。

随着厚度的变化，地震反演对甜点的预测精度规律如下(图 4b)：当厚度 < 12 m时，反演结果无法同时准确地确定“甜点”的位置和厚度；当厚度范围在12~35 m时，“甜点”预测厚度与真实厚度基本吻合；当厚度 > 35 m时，可以确定“甜点”的位置但预测厚度存在一定偏差。因此，对于孔隙度 > 10%、厚度 > 12 m的“甜点”，反演预测结果的可靠性较高，即采用叠前反演方法可较好地表征厚度 > 12 m的Ⅰ类“甜点”。

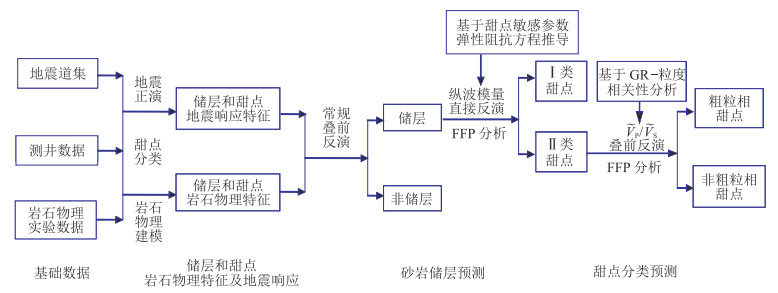
2 “甜点”地震预测方法 2.1 技术流程

在“甜点”分类、岩石物理分析及地震响应特征分析的基础上，采用基于“甜点”敏感参数弹性阻抗方程推导的纵波模量可以直接反演以表征Ⅰ类“甜点”，基于GR—粒度相关分析的$ {\tilde{V}}_{\mathrm{P}}/{\tilde{V}}_{\mathrm{S}} $叠前反演可以间接表征Ⅱ类“甜点”。“甜点”地震预测的关键技术与流程如图 5所示。

2.2 关键技术 2.2.1 Ⅰ类“甜点”纵波模量直接反演技术

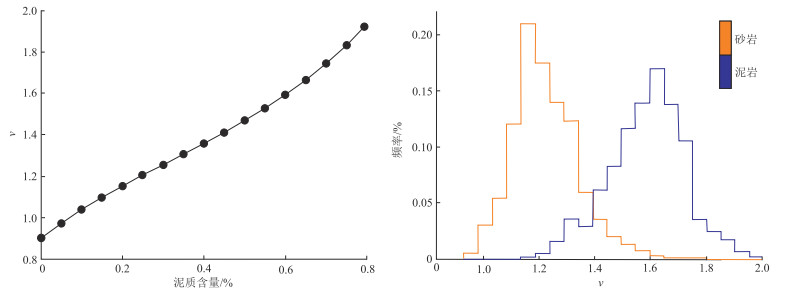
由图 6a可见，随着泥质含量的增加，ν (纵横波模量比)增大，二者之间相关性较高，这表明ν可作为储层预测的敏感参数。

由图 6b可见，砂岩与泥岩ν范围存在一定的差异，砂岩ν ≤1.4，泥岩ν＞1.4。

由图 7a可见，砂岩ν值低，泥岩ν值高，这表明利用ν可较好地区分砂岩与泥岩。由图 7b可见，砂岩区域Ⅰ类“甜点”存在低纵波模量值的特征，这更进一步验证了纵波模量用于区分Ⅰ类“甜点”的可行性。

Ⅰ类“甜点”的敏感弹性参数为M，而储层敏感参数为ν。为消除间接反演所导致的累计误差，需要构建M、ν的平面波反射特征方程。

Zeoppritz方程的近似公式为

$ \begin{array}{l}R\left(\theta \right)\approx \frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta \frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{V_\mathrm{P}}}-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{V_\mathrm{S}}}+\\ \;\;\;\;\;\;\;\; \frac{1}{2}(1-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta )\frac{\mathrm{\Delta }\rho }{\overline{\rho }}\end{array} $

(1)

式中：$ \gamma ={V}_{\mathrm{S}}/{V}_{\mathrm{P}} $，$ {V}_{\mathrm{P}} $、$ {V}_{\mathrm{S}} $、$ \rho $分别为纵波速度、横波速度、密度；$ \overline{V_\mathrm{P}} $、$ \overline{V_\mathrm{S}}、\overline{\rho}$分别为平均纵波速度、平均横波速度、平均密度；$ \mathrm{\Delta }{V}_{\mathrm{P}} $、$ \mathrm{\Delta }{V}_{\mathrm{S}} $、$ \mathrm{\Delta }\rho $分别为纵波速度变化量、横波速度变化量、密度变化量。

纵波模量反射系数$ \frac{\mathrm{\Delta }M}{\overline{M}} $、ν反射系数$ \frac{\mathrm{\Delta }\nu }{\overline{\nu }} $与纵波速度反射系数$ \frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{V_\mathrm{P}}} $、横波速度反射系数$ \frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{V_\mathrm{S}}} $及密度反射系数$ \frac{\mathrm{\Delta }\rho }{\overline{\rho }} $的关系为

$ \frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{V_\mathrm{P}}}=\frac{1}{2}\left(\frac{\mathrm{\Delta }M}{\overline{M}}-\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{V_\mathrm{S}}}\right) $

(2)

$ \frac{\mathrm{\Delta }\nu }{\overline{\nu }}=\frac{6}{3-4{\gamma }^{2}}\left(\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{V_\mathrm{P}}}-\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{V_\mathrm{S}}}\right) $

(3)

将式(2)、式(3)代入式(1)，可得到基于$ M $、$ \nu $、$ \rho $的平面波反射特征方程，具体形式为

$\begin{gathered} R\left(\theta \right)\approx \left(\frac{1}{4}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -2{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right)\frac{\mathrm{\Delta }M}{\overline{M}}+\\ \frac{(6{\gamma }^{2}-8{\gamma }^{4})\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{3}\frac{\mathrm{\Delta }\nu }{\overline{\nu }}+(\frac{1}{2}-\frac{1}{4}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta )\frac{\mathrm{\Delta }\rho }{\overline{\rho }} \end{gathered} $

(4)

式中：$ \overline{\nu } $、$ \overline{M} $分别为平均纵横波模量比、平均纵波模量；$ \mathrm{\Delta }\nu $、$ \mathrm{\Delta }M $分别为纵横波模量比变化量、纵波模量变化量。

相比于叠前AVO反演及叠后反演，叠前弹性阻抗反演利用了叠前部分叠加道集资料，综合利用了叠后反演与叠前反演的优点，不仅可以反演对储层较为敏感的弹性参数和物性参数，而且具有较强的抗噪能力。因此，本文在Connolly弹性阻抗方程的基础上，提出了基于M、$ \nu $及$ \rho $的弹性阻抗公式

$ \mathrm{E}\mathrm{I}\left(\theta \right)={\left({M}_{0}{\rho }_{0}\right)}^{\frac{1}{2}}{\left(\frac{M}{{M}_{0}}\right)}^{a}{\left(\frac{\nu }{{\nu }_{0}}\right)}^{b}{\left(\frac{\rho }{{\rho }_{0}}\right)}^{c} $

(5)

式中：$ {M}_{0} $、$ {\nu }_{0} $和$ {\rho }_{0} $分别表示纵波模量、$ \nu $和密度的平均值，一般可以通过测井资料统计获得；$ a=\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta $；$ b=\frac{(12{\gamma }^{2}-16{\gamma }^{4})\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta }{3} $；$ c=1-\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta $。

由式(5)可知，为了获得纵波模量、$ \nu $及密度，必须从反演中得到至少三个不同角度的弹性阻抗体，即$ \mathrm{E}\mathrm{I}\left({\theta }_{1}\right) $、$ \mathrm{E}\mathrm{I}\left({\theta }_{2}\right) $、$ \mathrm{E}\mathrm{I}\left({\theta }_{3}\right) $。

为了简化计算，可将式(5)模型进行线性变换，方程两边取对数，可以得到模型

$ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left(\theta \right)}{{A}_{0}}=a\;\mathrm{l}\mathrm{n}\frac{M}{{M}_{0}}+b\;\mathrm{l}\mathrm{n}\frac{\nu }{{\nu }_{0}}+c\;\mathrm{l}\mathrm{n}\frac{\rho }{{\rho }_{0}} $

(6)

式中$ {A}_{0}={\left({M}_{0}{\rho }_{0}\right)}^{1/2} $。将三个角度值分别代入理论模型表达式（6），可以得到方程组

$ \left\{\begin{array}{c}\mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{1}\right)}{{A}_{0}}=a\left({\theta }_{1}\right)\mathrm{l}\mathrm{n}\frac{M}{{M}_{0}}+b\left({\theta }_{1}\right)\mathrm{l}\mathrm{n}\frac{\nu }{{\nu }_{0}}+c\left({\theta }_{1}\right)\mathrm{l}\mathrm{n}\frac{\rho }{{\rho }_{0}}\\ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{2}\right)}{{A}_{0}}=a\left({\theta }_{2}\right)\mathrm{l}\mathrm{n}\frac{M}{{M}_{0}}+b\left({\theta }_{2}\right)\mathrm{l}\mathrm{n}\frac{\nu }{{\nu }_{0}}+c\left({\theta }_{2}\right)\mathrm{l}\mathrm{n}\frac{\rho }{{\rho }_{0}}\\ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{3}\right)}{{A}_{0}}=a\left({\theta }_{3}\right)\mathrm{l}\mathrm{n}\frac{M}{{M}_{0}}+b\left({\theta }_{3}\right)\mathrm{l}\mathrm{n}\frac{\nu }{{\nu }_{0}}+c\left({\theta }_{3}\right)\mathrm{l}\mathrm{n}\frac{\rho }{{\rho }_{0}}\end{array}\right. $

(7)

方程组(7)表达成矩阵的形式为

$ \left[\begin{array}{ccc}\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}{\theta }_{1}-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1}& \frac{1}{3}(12{\gamma }^{2}-16{\gamma }^{4})\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{1}& 1-\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}{\theta }_{1}\\ \frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}{\theta }_{2}-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{2}& \frac{1}{3}(12{\gamma }^{2}-16{\gamma }^{4})\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{2}& 1-\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}{\theta }_{2}\\ \frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}{\theta }_{3}-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{3}& \frac{1}{3}(12{\gamma }^{2}-16{\gamma }^{4})\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\theta }_{3}& 1-\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}{\theta }_{3}\end{array}\right]\left[\begin{array}{c}\mathrm{l}\mathrm{n}\frac{M}{{M}_{0}}\\ \mathrm{l}\mathrm{n}\frac{\nu }{{\nu }_{0}}\\ \mathrm{l}\mathrm{n}\frac{\rho }{{\rho }_{0}}\end{array}\right]=\left[\begin{array}{c}\mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{1}\right)}{{A}_{0}}\\ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{2}\right)}{{A}_{0}}\\ \mathrm{l}\mathrm{n}\frac{\mathrm{E}\mathrm{I}\left({\theta }_{3}\right)}{{A}_{0}}\end{array}\right] $

(8)

式（8）是一个线性方程组，只需知道三个相互独立的弹性阻抗数据体，用常规的求解方法便可以求得M、$ \nu $和$ \rho $。与基于纵波速度、横波速度及密度弹性阻抗方程反演的间接计算相比，该方法误差更小。

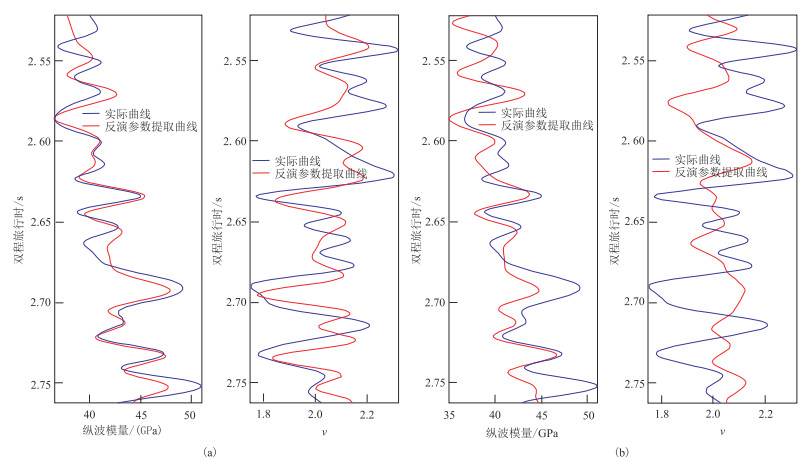
图 8为纵波模量直接提取与间接提取的反演结果对比，可以发现直接提取的反演结果误差更小、更加准确。

2.2.2 Ⅱ类“甜点”拟纵横波速度比反演技术

$ {\tilde{V}}_{\mathrm{P}}/{\tilde{V}}_{\mathrm{S}} $对于Ⅱ类“甜点”区分度较高，且能参与叠前反演生成拟纵横波速度比数据体。Ⅱ类“甜点”具低V_P/V_S、较高阻抗(图 1c、图 1d)，因此要实现Ⅱ类“甜点”的预测需要同时得到纵波阻抗及$ {\tilde{V}}_{\mathrm{P}}/{\tilde{V}}_{\mathrm{S}} $两个反演结果，并构建两者的联合概率分布。MCMC(马尔科夫链蒙特卡洛)概率反演利用反演参数之间的相关性实现特定岩相及流体类型的有效识别。可以利用基于$ {I}_{\mathrm{P}} $、$ \gamma $与$ \rho $的AVO近似公式计算反射系数，即

$\begin{align} R\left(\theta \right)&\approx \left(\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta -4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right)\frac{\mathrm{\Delta }{I}_{\mathrm{P}}}{\overline{I_\mathrm{P}}}+\\&4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }\tau }{\overline{\tau }}+\left(2{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta -\frac{1}{2}\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\theta \right)\frac{\mathrm{\Delta }\rho }{\overline{\rho }} \end{align} $

(9)

式中：$ \overline{I_\mathrm{P}} $、$ \overline{\tau } $分别为平均纵波阻抗、平均剪应力；$ \mathrm{\Delta }{I}_{\mathrm{P}} $、$ \mathrm{\Delta }\tau $分别为纵波阻抗变化量、剪应力变化量。

MCMC算法通过构建一条乃至若干条平稳分布与后验概率分布特征相同的马尔科夫链以实现对贝叶斯公式的求解。根据贝叶斯定理，后验概率分布正比于先验分布与似然函数的乘积。因此，首先利用测井数据建立不同类型“甜点”的$ {I}_{\mathrm{P}} $、$ {\tilde{V}}_{\mathrm{P}}/{\tilde{V}}_{\mathrm{S}} $及$ \rho $的先验联合概率分布，假设$ {I}_{\mathrm{P}} $、$ {\tilde{V}}_{\mathrm{P}}/{\tilde{V}}_{\mathrm{S}} $在每种“甜点”类型及非“甜点”下均满足高斯分布，因此参数先验分布可以假设为混合高斯分布，则可表示为

$ P\left(\boldsymbol{m}\right)~\underset{}{\sum\limits _{k=1}^{h}{\lambda }_{k}\mathrm{N}\left(\boldsymbol{m};{\overline{\boldsymbol{m}}}_{k}, {\sigma }_{{\boldsymbol{m}}_{k}}^{2}\right)} $

(10)

式中：$ \boldsymbol{m}=({I}_{\mathrm{P}}, {\tilde{V}}_{\mathrm{P}}/{\tilde{V}}_{\mathrm{S}}, \rho ) $；k表示当前甜点相；h是不同“甜点”类型及非“甜点”的个数；N表示正态分布；$ {\overline{\boldsymbol{m}}}_{k} $、$ {\sigma }_{{\boldsymbol{m}}_{\mathrm{k}}}^{2} $分别表示反演参数$ {\boldsymbol{m}}_{k} $在某一“甜点”类型(或非“甜点”)的均值、方差；$ {\lambda }_{k} $为不同“甜点”类型及非“甜点”之间的权重值。

对于似然函数$ p\left(\boldsymbol{d}\left|\boldsymbol{m}\right.\right) $，假设地震噪声满足均值为0、方差为$ {\sigma }_{\mathrm{n}}^{2} $的高斯分布，则可表征为

$ \begin{array}{l}p\left(\boldsymbol{d}\left|\boldsymbol{m}\right.\right)=\frac{1}{(2\mathrm{\pi }{\sigma }_{\mathrm{n}}^{2}{)}^{\frac{G}{2}}}\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left\{-\sum \frac{[\boldsymbol{d}-f{\left(\boldsymbol{m}\right)]}^{\begin{array}{l}2\\ \end{array}}}{2{\sigma }_{\mathrm{n}}^{2}}-\sum \frac{[\boldsymbol{d}-f{\left(\boldsymbol{m}\right)]}^{\begin{array}{l}2\\ \end{array}}}{2{\sigma }_{\mathrm{n}}^{2}}\right\}\end{array} $

(11)

式中：$ G $为反演参数的样点数；$ f $为地震正演算子；$ \boldsymbol{d} $为实际地震记录。因此，反演参数的后验概率分布为

$ p\left(\boldsymbol{m}\left|\boldsymbol{d}\right.\right)\hspace{0.33em}\propto \underset{k=1}{\sum\limits _{}^{h}}\left\{\frac{{\lambda }_{k}}{(2\mathrm{\pi }{\sigma }_{{\boldsymbol{m}}_{k}}^{2}{)}^{\frac{{G}_{k}}{2}}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{({\boldsymbol{m}}_{k}-{\overline{\boldsymbol{m}}}_{k}{)}^{\begin{array}{l}2\\ \end{array}}}{2{\sigma }_{{\boldsymbol{m}}_{k}}^{2}}\right.-\\ \left.\frac{({\boldsymbol{m}}_{k}-{\overline{\boldsymbol{m}}}_{k}{)}^{\begin{array}{l}2\\ \end{array}}}{2{\sigma }_{{\boldsymbol{m}}_{k}}^{2}}\right]\right\}\times \frac{1}{(2\mathrm{\pi }{\sigma }_{\mathrm{n}}^{2}{)}^{\frac{G}{2}}}\mathrm{e}\mathrm{x}\mathrm{p}\left\{-\sum\limits _{}^{}\frac{[\boldsymbol{d}-f{\left(\boldsymbol{m}\right)]}^{\begin{array}{l}2\\ \end{array}}}{2{\sigma }_{\mathrm{n}}^{2}}\right\} $

(12)

式中$ {G}_{k} $是当前甜点的反演参数样点数。反演的目标函数为

$ \begin{array}{l}J\left(\boldsymbol{m}\right)=-\sum \frac{[\boldsymbol{d}-f{\left(\boldsymbol{m}\right)]}^{\begin{array}{l}2\\ \end{array}}}{2{\sigma }_{\mathrm{n}}^{2}}-\\ \;\;\;\;\mathrm{l}\mathrm{n}\underset{k=1}{\sum\limits _{}^{h}}\left\{\frac{{\lambda }_{k}}{(2\mathrm{\pi }{\sigma }_{{\boldsymbol{m}}_{k}}^{2}{)}^{\frac{{G}_{k}}{2}}}\mathrm{e}\mathrm{x}\mathrm{p}[-\frac{({\boldsymbol{m}}_{k}-{\overline{\boldsymbol{m}}}_{k}{)}^{\begin{array}{l}2\\ \end{array}}}{2{\sigma }_{{\boldsymbol{m}}_{k}}^{2}}]\right\}\end{array} $

(13)

在反演过程中，针对反演参数值，可利用以下概率公式进行反演值的优选，即

$ \alpha ({\boldsymbol{m}}^{\boldsymbol{\text{'}}}, {\boldsymbol{m}}^{\boldsymbol{*}})=\mathrm{m}\mathrm{i}\mathrm{n}\left[1, \frac{\pi \left({\boldsymbol{m}}^{\boldsymbol{*}}\right)}{\pi \left({\boldsymbol{m}}^{\text{'}}\right)}\right] $

(14)

式中：$ \pi $为平稳后验概率分布；$ {\boldsymbol{m}}^{*} $为更新解；$ {\boldsymbol{m}}^{\text{'}} $为原有解。

将式(11)代入式(14)并简化常数项，即可得到接受概率表达式

$\begin{array}{l} \alpha \left({\boldsymbol{m}}^{\boldsymbol{*}}, {\boldsymbol{m}}^{\boldsymbol{\text{'}}}\right)=\\ \left\{\begin{array}{l}1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({\boldsymbol{m}}^{\boldsymbol{*}}\right)-J\left({\boldsymbol{m}}^{\text{'}}\right)\ge 0\\ \mathrm{e}\mathrm{x}\mathrm{p}\left[J\right({\boldsymbol{m}}^{\boldsymbol{*}})-J({\boldsymbol{m}}^{\boldsymbol{\text{'}}}\left)\right]\hspace{0.33em}\hspace{0.33em}\;\;\;J\left({\boldsymbol{m}}^{\boldsymbol{*}}\right)-J\left({\boldsymbol{m}}^{\boldsymbol{\text{'}}}\right) < 0\end{array}\right. \end{array}$

(15)

考虑到反演参数之间存在一定的相关性，在采样过程中，不再对反演参数的全局概率分布采样，而是在联合分布约束下的条件概率分布中采样，以此缩小解空间，即$ {\tilde{V}}_{\mathrm{P}}/\tilde{V} $$ {}_{\mathrm{S}} $的采样区间可表示为

$ \begin{array}{l}P\left(\frac{{{\tilde{V}}_{\mathrm{P}}}^{\boldsymbol{*}}}{{{\tilde{V}}_{\mathrm{S}}}^{\boldsymbol{*}}}\left|{I}_{\mathrm{P}}={{I}_{\mathrm{P}}}^{*}\right.\right)\\ \;\;\;\;\;\;=P\left[\frac{{{\tilde{V}}_{\mathrm{P}}}^{\boldsymbol{*}}}{{{\tilde{V}}_{\mathrm{S}}}^{\boldsymbol{*}}}\left|\left({{I}_{\mathrm{P}}}^{*}-{\psi }_{\mathrm{P}}\right)\right. < {I}_{\mathrm{P}} < \left({{I}_{\mathrm{P}}}^{*}+{\psi }_{\mathrm{P}}\right)\right]\end{array} $

(16)

式中：$ {{\tilde{V}}_{\mathrm{P}}}^{\boldsymbol{*}}/{{\tilde{V}}_{\mathrm{S}}}^{\boldsymbol{*}} $为更新的拟纵横波速比；$ {{I}_{\mathrm{P}}}^{*} $为更新的纵波阻抗；$ {\psi }_{\mathrm{P}} $为纵波阻抗区间长度的一半。

利用“甜点”敏感参数在不同“甜点”类型(或非“甜点”)的分布特征，估算不同类型“甜点”概率。假设其在Ⅱ类“甜点”的条件概率服从高斯分布，则Ⅱ类“甜点”概率可以表示为

$\begin{align} p\left({\rm I}={T}_{2}\left|{I}_{\mathrm{P}}\right., \frac{{\tilde{V}}_{\mathrm{P}}}{{\tilde{V}}_{\mathrm{S}}}\right)=&\left[1-\frac{p\left(I={T}_{1}\left|{I}_{P}\right.\right)}{\underset{}{\sum\limits _{k=1}^{h}p\left(I={T}_{1}\left|{I}_{\mathrm{P}}\right.\right)}}\right]\times \\& \frac{p\left(I={T}_{2}\left|\frac{{\tilde{V}}_{\mathrm{P}}}{{\tilde{V}}_{\mathrm{S}}}\right.\right)}{\underset{}{\sum\limits _{k=1}^{h}p\left(I={T}_{2}\left|\frac{{\tilde{V}}_{\mathrm{P}}}{{\tilde{V}}_{\mathrm{S}}}\right.\right)}} \end{align} $

(17)

式中：$ {T}_{2} $是指Ⅱ类“甜点”; $ {T}_{1} $是指Ⅰ类“甜点”。利用式(17)即可计算得到Ⅱ类“甜点”的概率体。

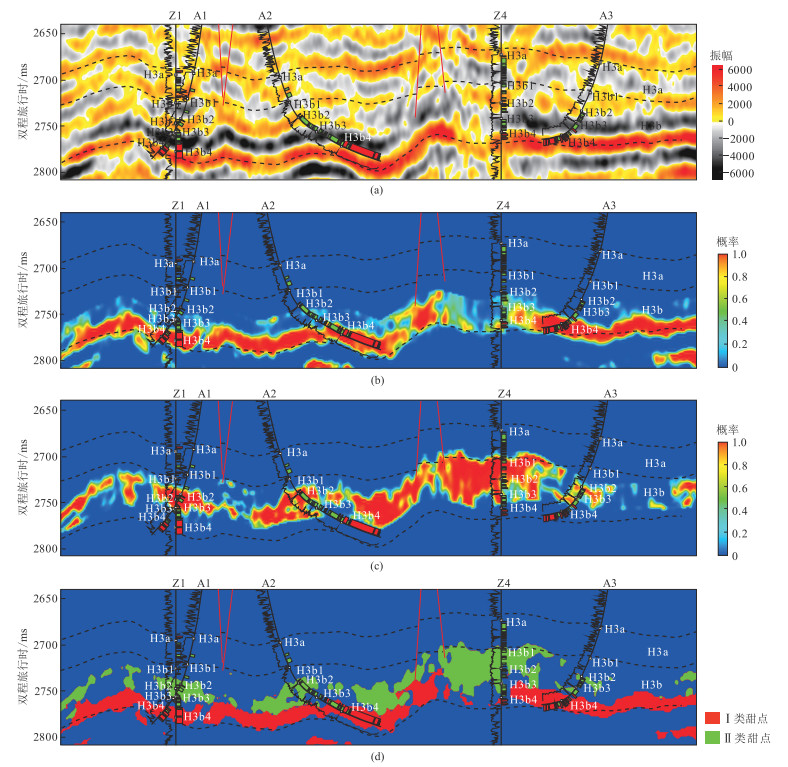
在Ⅰ类“甜点”和Ⅱ类“甜点”分布特征预测的基础上，采用FFP技术，定义各类“甜点”的概率密度函数(PDFs)；然后对反演结果的每一样本点应用贝叶斯模糊判别分析(Bayesian Inference)计算各种“甜点”类型的空间分布概率(图 9b、图 9c)，最后叠加就可以形成各类“甜点”的概率体(图 9d)。

3 应用效果

应用本文方法预测H3b“甜点”分布特征(图 9), 发现Ⅰ类“甜点”主要分布在中下部(H3b3、H3b4小层)，Ⅱ类“甜点”主要分布中部(H3b2小层)。

钻井资料揭示：“甜点”垂向分布主要受控于沉积环境，H3b早期以高能辫状水道沉积为主，在单期水道中部的中—粗砂岩发育Ⅰ类“甜点”；H3b中晚期以中低能水道沉积为主，Ⅱ类“甜点”主要发育在单期水道下部的中粗砂岩，少量发育在水道中部的中细砂岩。

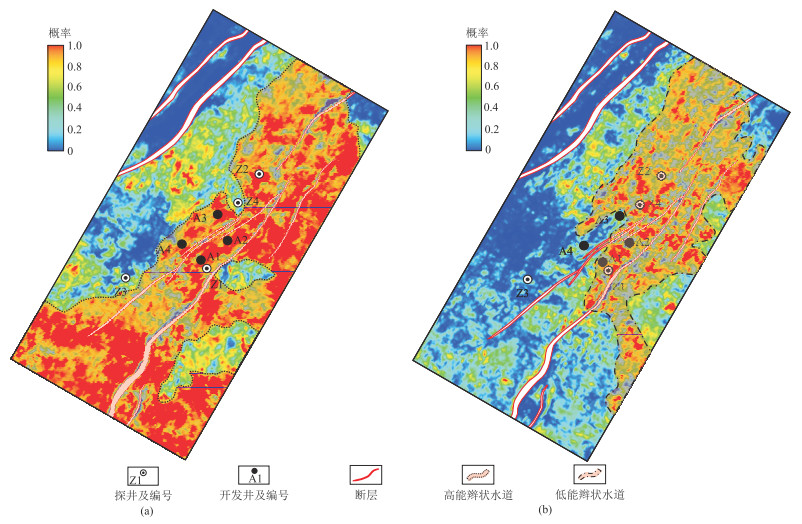
由图 10可见，Ⅰ类“甜点”主要分布在研究区中南部和西南部，多发育在高能辫状水道中；Ⅱ类“甜点”主要从东北方向沿着南部方向广泛分布，主要发育在中低能辫状水道中。据此，设计、部署井位11口，目前已完钻4口(A1~A4井)。新钻井结果表明本文研究预测的“甜点”是可靠的, Ⅰ类“甜点”厚度吻合率高达80%以上，Ⅱ类达70%以上(表 3)。该成果指导了气田井位的部署，实现了高效开发。

4 结论

(1) 针对东海厚层低渗气藏不同类型“甜点”，采用不同地球物理预测方法，即：Ⅰ类“甜点”采用纵波模量直接反演；Ⅱ类“甜点”采用拟纵横波速度比反演。

(2) 本文方法“甜点”预测厚度结果准确率高，Ⅰ类“甜点”吻合率达80%以上，Ⅱ类“甜点”吻合率70%以上。该方法可对其他类似低渗气藏的勘探具有参考价值。