2. 成都理工大学地球物理学院, 四川成都 610059;
3. 中海石油国际能源服务(北京)有限公司, 北京 100010
2. College of Geophysics, Chengdu University of Technology, Chengdu, Sichuan 610059, China;
3. CNOOC International Energy Services (Beijing) Co., Ltd., Beijing 100010, China
与叠后地震反演方法相比,叠前地震反演方法可获得更多的弹性参数,能更有效地进行储层预测和流体识别[1-3]。为了提高叠前地震反演结果的准确性,可通过约束方法[4-6]将先验信息引入反演。Berkhout[7]利用反射系数的稀疏信息和初始模型的趋势信息,应用L2范数约束添加先验约束信息,提高了反演结果的准确性。然而,Zhang等[8]发现采用L2范数约束先验信息会出现低稀疏性,导致反演结果分辨率变低,相邻岩层边界位置呈现非聚焦性平滑过渡。由于地层反射系数向量通常具有稀疏性,向量中存在稀疏非零值,因此在稀疏表示过程中如何提高先验约束信息的稀疏性非常重要。
Taylor等[9]提出了利用L1范数稀疏约束地震反演方法,随后Thueune等[10]、Kong等[11]、Zhang等[12]均验证了L1范数的稀疏性优于L2范数。Guitton等[13]优化了L1范数,提出了结合柯西约束的混合范数。李昕洁等[14]将该方法用于全波形反演,取得了较好的效果。Zhang等[8]提出了基于L1范数优化方法的基追踪反演(BPI)算法,传统叠前AVO反演边界尖锐问题得到一定程度的解决,同时证实了L1范数约束的稀疏性更好。张雨强等[15]、Sun等[16]在地球物理反演中引入了自适应Lp范数稀疏表示方法,可反演出“块状”地层,反演结果比L1范数纵向分辨率更高。Pérez等[17]提出了一种加权混合L2, 1范数的叠前AVO反演方法,优化了反演函数约束项的稀疏性,可获得更多的块状解。王治强等[18]采用了全变分(TV)约束波阻抗的方法,既可以有效压制随机噪声,还能较好地刻画地层边界。Li等[19]基于分裂Bregman迭代算法,将L1范数与全变分正则化结合,实现了更高横向分辨率的叠前地震多道同时反演。Huang等[20]、Wang等[21]、耿伟恒等[22]将非凸L1-2正则化方法拓展到叠前AVO反演,证明了L1-2范数比L1范数更稀疏。然而,上述稀疏约束忽略了岩层边界中的地震反射振幅信息,导致反演结果出现速度伪层,为后续参数预测积累了误差。
为此,本文提出了一种叠前重加权L1范数稀疏约束的地震反演方法(简称“本文方法”),在反演目标函数稀疏项的构建中引入了基于反射系数表示的重加权矩阵,即“重加权L1范数”。相比L1范数稀疏约束(简称“传统方法”),重加权L1范数的优越性主要体现在:其稀疏约束表示可以通过重加权矩阵补充地层边界信息。加权地层反射边界信息的引入能够提高L1范数约束的稀疏性,本文将重加权L1范数稀疏约束和初始低频模型约束同时用于构造反演目标函数,采用交替方向乘子法(ADMM)和软阈值收缩算法(ISTA)进行迭代求解[23-25]。理论模型测试和实际工区应用结果均表明,本文方法明显提高了叠前多参数同时反演的分辨率,对层速度边界刻画更清晰,极大减弱了速度伪层和密度伪层现象。
1 方法原理 1.1 正演模拟地震信号一般可以表示为
| $ \boldsymbol{S}=\boldsymbol{\omega }\mathrm{*}\boldsymbol{R}+\boldsymbol{N} $ | (1) |
式中:S为地震记录;
引入子波卷积矩阵
| $ \boldsymbol{W}=\left[\begin{array}{cccc}\begin{array}{l}\omega \left(1\right)\\ \omega \left(2\right)\end{array}& & & \\ ⋮& \begin{array}{l}\omega \left(1\right)\\ \omega \left(2\right)\end{array}& \ddots & \\ \omega \left(m\right)& ⋮& \ddots & \\ & \omega \left(m\right)& \ddots & \begin{array}{l}\omega \left(1\right)\\ \omega \left(2\right)\end{array}\\ & & \ddots & ⋮\\ & & & \omega \left(m\right)\end{array}\right] $ | (2) |
式中m为地震子波的长度。式(1)可简化为
| $ \boldsymbol{S}=WR+\boldsymbol{N} $ | (3) |
基于Aki和Richard反射系数近似公式[26]
| $\begin{gathered} R\left(\theta \right)=\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{2}\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}-4\frac{{\overline{V_\mathrm{S}}}^{2}}{{\overline{{V}_{\mathrm{P}}}}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{{\overline{V_\mathrm{S}}}_{}}+\\\frac{1}{2}(1-4\frac{{\overline{V\mathrm{S}}}^{2}}{{\overline{{V}_{\mathrm{P}}}}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta )\frac{\mathrm{\Delta }\rho }{\overline{\rho }} \end{gathered}$ | (4) |
其中
| $ \left\{\begin{array}{l}{V}_{\mathrm{P}}=\frac{{V}_{\mathrm{P}1}+{V}_{\mathrm{P}2}}{2}\\ \overline{{V}_{\mathrm{s}}}=\frac{{V}_{\mathrm{S}1}+{V}_{\mathrm{S}2}}{2}\\ \overline{\rho }=\frac{{\rho }_{1}+{\rho }_{2}}{2}\\ \mathrm{\Delta }{V}_{\mathrm{P}}={V}_{\mathrm{P}2}-{V}_{\mathrm{P}1}\\ \mathrm{\Delta }{V}_{\mathrm{s}}={V}_{\mathrm{S}2}-{V}_{\mathrm{S}1}\\ \mathrm{\Delta }\rho ={\rho }_{2}-{\rho }_{1}\end{array}\right. $ | (5) |
式中:
针对式(5),定义变量
| $ \left\{\begin{array}{l}{R}_{{V}_{\mathrm{P}}}=\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}\\ {R}_{{V}_{\mathrm{S}}}=\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}\\ {R}_{\mathrm{\rho }}=\frac{\mathrm{\Delta }\rho }{\overline{\rho }}\\ a\left(\theta \right)=\frac{\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta }{2}\\ b\left(\theta \right)=4\frac{{\overline{{V}_{\mathrm{S}}}}^{2}}{{\overline{{V}_{\mathrm{P}}}}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \\ c\left(\theta \right)=\frac{1}{2}(1-\frac{{\overline{{V}_{\mathrm{S}}}}^{2}}{{\overline{{V}_{\mathrm{P}}}}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta )\end{array}\right. $ | (6) |
式中:
近似地将
| $ {R}_{{V}_{\mathrm{P}}}=\frac{2({V}_{\mathrm{P}2}-{V}_{\mathrm{P}1})}{{V}_{\mathrm{P}2}+{V}_{\mathrm{P}1}}=\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}\approx \mathrm{\Delta }\mathrm{l}\mathrm{n}{V}_{\mathrm{P}} $ | (7) |
将
| $ {\boldsymbol{M}}_{{V}_{\mathrm{P}}}=\mathrm{l}\mathrm{n}{\boldsymbol{V}}_{\mathrm{P}}^{} $ | (8) |
根据式(7)、式(8),将纵波的反射系数表示成矩阵形式
| $ {\boldsymbol{R}}_{{V}_{\mathrm{P}}}={\boldsymbol{D}}_{0}{\boldsymbol{M}}_{{V}_{\mathrm{P}}} $ | (9) |
式中
| $ {\boldsymbol{D}}_{0}=\left[\begin{array}{ccccc}-1& 1& & & \\ & -1& 1& & \\ & & \ddots & \ddots & \\ & & & -1& 1\end{array}\right] $ | (10) |
同理可得
| $ {\boldsymbol{R}}_{{V}_{\mathrm{S}}}={\boldsymbol{D}}_{0}{\boldsymbol{M}}_{{V}_{\mathrm{S}}} $ | (11) |
| $ {\boldsymbol{R}}_{\rho }={\boldsymbol{D}}_{0}{\boldsymbol{M}}_{\rho } $ | (12) |
式中:
最终推导出正演模型的矩阵表达式为
| $ \boldsymbol{S}=\boldsymbol{W}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}+\boldsymbol{N} $ | (13) |
式中:
| $ \boldsymbol{M}={\left[\begin{array}{ccc}{\boldsymbol{M}}_{{V}_{\mathrm{P}}}& {\boldsymbol{M}}_{{V}_{\mathrm{S}}}& {\boldsymbol{M}}_{\rho }\end{array}\right]}^{\mathrm{T}} $ | (14) |
| $ \boldsymbol{D}=\left[\begin{array}{ccc}{\boldsymbol{D}}_{0}& 0& 0\\ 0& {\boldsymbol{D}}_{0}& 0\\ 0& 0& {\boldsymbol{D}}_{0}\end{array}\right] $ | (15) |
用于反演纵波速度、横波速度和密度的自然对数与地震记录之间的关系为
| $ J\left(\boldsymbol{M}\right)=\underset{\boldsymbol{M}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|\right|\boldsymbol{W}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}-\boldsymbol{S}|{|}_{2}^{2} $ | (16) |
式中
基于传统L1范数稀疏约束包含低频背景约束项,传统方法的反演目标函数为
| $ \begin{align}J\left(\boldsymbol{M}\right)=&\underset{\boldsymbol{M}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|\right|\boldsymbol{W}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}-\boldsymbol{S}|{|}_{2}^{2}+\\ &\lambda \left|\right|\boldsymbol{M}-{\boldsymbol{M}}_{0}|{|}_{2}^{2}+\alpha |\left|\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}\right|{|}_{1}\end{align} $ | (17) |
式中:
重加权矩阵数学表示形式[27]为
| $ \left|\right|\boldsymbol{Q}\boldsymbol{R}|{|}_{1}=\sum\limits _{i=1}^{N-1}\left|{q}_{i}{r}_{i}\right| $ | (18) |
式中:
| $ \boldsymbol{Q}=\left[\begin{array}{cccc}{q}_{1}& & & \\ & {q}_{2}& & \\ & & \ddots & \\ & & & {q}_{N-1}\end{array}\right] $ | (19) |
为了将重加权矩阵元素大小与反射系数建立联系,利用边界反射振幅信息将
| $ {q}_{i}=\frac{1}{\left|{r}_{i}\right|+\xi } $ | (20) |
式中
参照张雨强等[15]对比范数稀疏性的方法,将本文重加权L1范数和传统L1范数的稀疏问题分别表示为
| $ L\left(\boldsymbol{H}\right)=\underset{\boldsymbol{H}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|\right|\boldsymbol{H}|{|}_{1}^{}\;\mathrm{s}.\mathrm{t}.\mathrm{ }||\boldsymbol{H}-{\boldsymbol{H}}_{\mathrm{R}}|{|}_{2}^{2} < \eta $ | (21) |
| $ L\left(\boldsymbol{H}\right)=\underset{\boldsymbol{H}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|\right|QH|{|}_{1}^{}\;\mathrm{s}.\mathrm{t}.\mathrm{ }||\boldsymbol{H}-{\boldsymbol{H}}_{\mathrm{R}}|{|}_{2}^{2} < \eta $ | (22) |
式中:
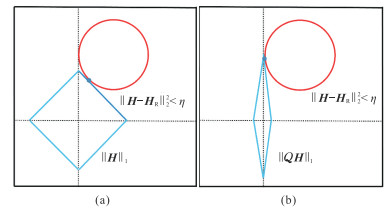
由图 1可见,交点位置即为问题的最优解,图 1b交点(蓝点)位置比图 1a更趋近坐标纵轴,这说明重加权L1范数比传统L1范数更具稀疏性,可获得更稀疏的反演结果。因此,本文构建的反演目标函数为
| $ J\left(\boldsymbol{M}\right)=\underset{\boldsymbol{M}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|\right|\boldsymbol{W}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}-\boldsymbol{S}|{|}_{2}^{2}+\lambda ||\boldsymbol{M}-{\boldsymbol{M}}_{0}|{|}_{2}^{2}+\alpha \left|\right|Q\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}|{|}_{1} $ | (23) |
|
图 1 L1范数(a)与重加权L1范数(b)的稀疏性对比 蓝线为范数的稀疏约束项,红线为反演值与真实值残差的二范数,交点为反射系数的解。 |
对于传统方法的目标函数(式(17))和本文方法的目标函数(式(23)),本文采用交替方向乘子方法(ADMM)将含多个未知参数的目标函数分解成多个单一参数的子问题进行求解。
以本文方法为例,首先采用拉格朗日乘子P代替L1范数中的QBDM矩阵进行运算,将上述非线性问题转化为有约束的线性问题,得到目标函数
| $ \begin{array}{l}{J}_{2}(\boldsymbol{M}, \boldsymbol{P})=\underset{\boldsymbol{M}, \boldsymbol{P}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|\right|\boldsymbol{W}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}-\boldsymbol{S}|{|}_{2}^{2}+\lambda ||\boldsymbol{M}-{\boldsymbol{M}}_{0}|{|}_{2}^{2}+\alpha \left|\right|\boldsymbol{P}|{|}_{1}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{s}.\mathrm{t}.\boldsymbol{P}=\boldsymbol{Q}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}\end{array} $ | (24) |
进一步引入二次惩罚项和对偶项[28],将式(24)有约束的目标函数转化为无约束的目标函数,得到
| $ \begin{align}{J}_{3}(\boldsymbol{M}, \boldsymbol{P}, \boldsymbol{C})=&\underset{\boldsymbol{M}, \boldsymbol{P}, \boldsymbol{C}}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|\right|\boldsymbol{W}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}-\boldsymbol{S}|{|}_{2}^{2}+\lambda ||\boldsymbol{M}-{\boldsymbol{M}}_{0}|{|}_{2}^{2}+\\ &\alpha \left|\right|\boldsymbol{P}|{|}_{1}+\mu ||\boldsymbol{P}-\boldsymbol{Q}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}-\boldsymbol{C}|{|}_{2}^{2}\end{align} $ | (25) |
于是,将式(25)拆解成分别关于
① 与
| $ \begin{aligned} K_1(\boldsymbol{M}) & =\min _{\boldsymbol{M}}\|\boldsymbol{W B D} \boldsymbol{M}-\boldsymbol{S}\|_2^2+\lambda\left\|\boldsymbol{M}-\boldsymbol{M}_0\right\|_2^2 \\ & +\mu\|\boldsymbol{P}-\boldsymbol{Q B D} \boldsymbol{M}-\boldsymbol{C}\|_2^2 \end{aligned} $ | (26) |
② 与P相关的目标函数为
| $ {K}_{2}\left(\boldsymbol{P}\right)=\underset{\boldsymbol{P}}{\mathrm{m}\mathrm{i}\mathrm{n}}\;\alpha \left|\right|\boldsymbol{P}|{|}_{1}+\mu ||\boldsymbol{P}-\boldsymbol{Q}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}-\boldsymbol{C}|{|}_{2}^{2} $ | (27) |
③ 与
| $ {K}_{3}\left(\boldsymbol{C}\right)=\underset{\boldsymbol{C}}{\mathrm{m}\mathrm{i}\mathrm{n}}\;\mu \left|\right|\boldsymbol{P}-\boldsymbol{Q}\boldsymbol{B}\boldsymbol{D}\boldsymbol{M}-\boldsymbol{C}|{|}_{2}^{2} $ | (28) |
针对式(26)采用函数梯度方法求解,可得
| $ \begin{array}{l}{\boldsymbol{M}}^{(k+1)}=[{\boldsymbol{D}}^{\mathrm{T}}{\boldsymbol{B}}^{\mathrm{T}}{\boldsymbol{W}}^{\mathrm{T}}\mathbf{W}\mathbf{B}\mathbf{D}+\lambda \boldsymbol{I}+\mu {\boldsymbol{D}}^{\mathrm{T}}{\boldsymbol{B}}^{\mathrm{T}}{{\boldsymbol{Q}}^{\left(k\right)}}^{\mathrm{T}}{\boldsymbol{Q}}^{\left(k\right)}{\mathbf{B}\mathbf{D}]}^{-1}·\\ \;\;\;\;\;\;\;\;\left\{\boldsymbol{D}^{\mathrm{T}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{W}^{\mathrm{T}} \boldsymbol{S}+\lambda \boldsymbol{M}_0+{\mu} \boldsymbol{D}^{\mathrm{T}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{Q}^{(k) \mathrm{T}}\left[\boldsymbol{P}^{(k)}-\boldsymbol{C}^{(k)}\right\}\right.\end{array} $ | (29) |
式中:“
针对式(27),引入软阈值收缩算法求解同时含有L1范数和L2范数的目标函数,可得
| $ \begin{gathered} {\boldsymbol{P}}^{(k+1)}=\mathrm{m}\mathrm{a}\mathrm{x}\left[|{\boldsymbol{Q}}^{\left(k\right)}\boldsymbol{B}\boldsymbol{D}{\boldsymbol{M}}^{(k+1)}+{\boldsymbol{C}}^{\left(k\right)}|-\frac{\alpha }{\mu }, 0\right]· \\ \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}[{\boldsymbol{Q}}^{\left(k\right)}\boldsymbol{B}\boldsymbol{D}{\boldsymbol{M}}^{(k+1)}+{\boldsymbol{C}}^{\left(k\right)}] \end{gathered}$ | (30) |
式中
| $ \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(y\right)=\left\{\begin{array}{cc}1& y > 0\\ 0& y=0\\ -1& y < 0\end{array}\right. $ | (31) |
针对式(28),可根据式(26)相同的求解方法,得到
| $ {\boldsymbol{C}}^{(k+1)}={\boldsymbol{C}}^{\left(k\right)}+[{\boldsymbol{Q}}^{\left(k\right)}\boldsymbol{B}\boldsymbol{D}{\boldsymbol{M}}^{(k+1)}-{\boldsymbol{P}}^{(k+1)}] $ | (32) |
基于式(20),本文引入的重加权矩阵对角线元素的迭代表达式为
| $ {q}_{i}^{(k+1)}=\frac{1}{\left|{r}_{i}^{(k+1)}\right|+\xi } $ | (33) |
式中:
通过对目标函数的详细求解,本文方法的地震反演流程框架如表 1所示。
|
|
表 1 叠前重加权L1范数的反演流程 |
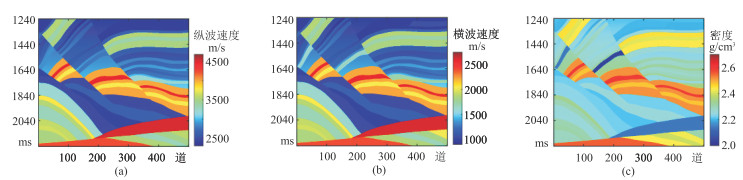
选择经典Marmousi Ⅱ模型测试本文方法和传统方法。该模型为横向500道、纵向500个采样点,其纵波速度、横波速度和密度的剖面分别如图 2所示。该模型中包含多种不同厚度、不同形状的砂岩地层,其中多组薄层将作为验证本文算法的重要地层。该模型还发育边界清晰的断层和背斜构造,适合验证本文方法在刻画地层边界、减弱伪层现象方面的优越性。
|
图 2 不同参数的理论模型 (a)纵波速度;(b)横波速度;(c)密度 |
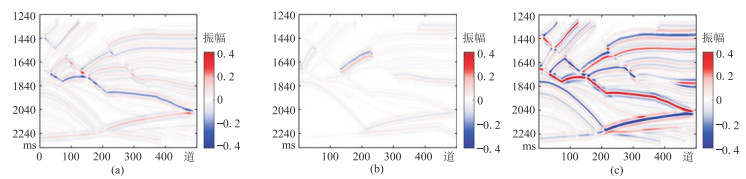
首先基于式(4),利用理论模型数据计算入射角为10°、20°和30°的地层反射系数;然后分别与频率为30 Hz的雷克子波褶积合成对应的近、中、远角度的地震记录(图 3)。
|
图 3 无噪情况下不同角度数据的合成地震记录 (a)近角度;(b)中角度;(c)远角度 |
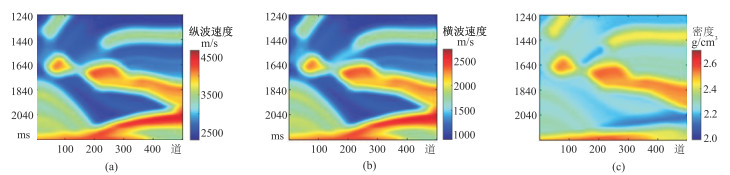
对反演目标函数添加可以补充背景信息的低频模型,对理论模型的纵波速度、横波速度和密度数据进行高斯低通滤波,即可获得叠前纵波速度、横波速度和密度的低频模型(图 4)。
|
图 4 不同参数低频初始模型 (a)纵波速度;(b)横波速度;(c)密度 |
由式(23)可知,正则化参数
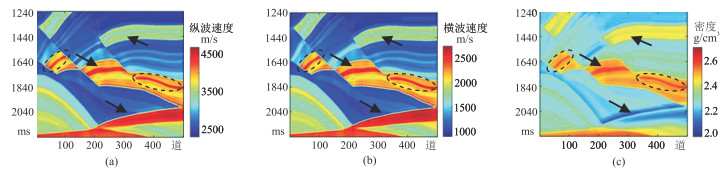
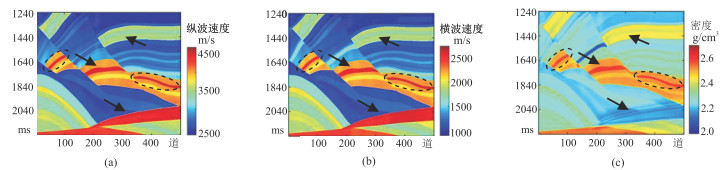
分别采用传统方法与本文方法对纵波速度、横波速度和密度进行同时反演。对比图 5与图 6可知,本文方法反演的地层边界更清晰,纵向分辨率明显更高(黑色箭头处),尤其针对薄气砂岩储层刻画能力更强(黑色虚线圆圈)。
|
图 5 无噪情况下传统方法不同参数的反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
|
图 6 无噪情况下本文方法不同参数的反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
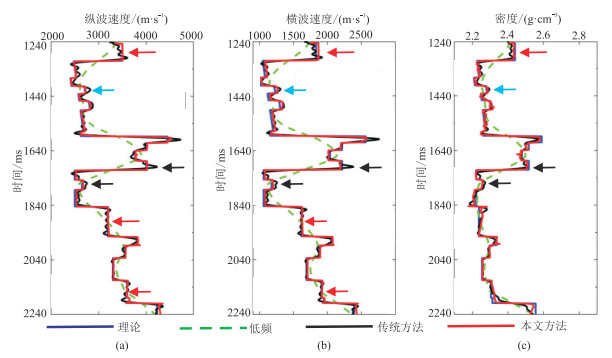
为了更准确地分析两种方法的反演效果,图 7展示了无噪情况下第100道(单道)不同参数反演结果。由图可见,在传统方法的反演结果中,同一地层出现较强的“正弦形”扰动(红色箭头处),导致同层中产生许多伪速度层和伪密度层(小波浪状),反演结果不够准确;而在本文方法反演结果中,边界更清晰,很大程度地减弱了伪层现象,保证了同层反演的稳定性。传统方法反演整体呈脉冲式(黑色箭头处),局部平滑了相邻地层边界,这是降低纵向分辨率的主要原因,而本文方法的反演结果与理论模型吻合度更高。传统方法识别薄层的分辨率低、精度低(蓝色箭头处),而本文方法通过加权反射系数的稀疏性,对薄层的识别能力明显提高,同时也在一定程度上降低了密度反演结果的不稳定性。
|
图 7 无噪情况下不同方法、不同参数第100道反演结果对比 (a)纵波速度;(b)横波速度;(c)密度 |
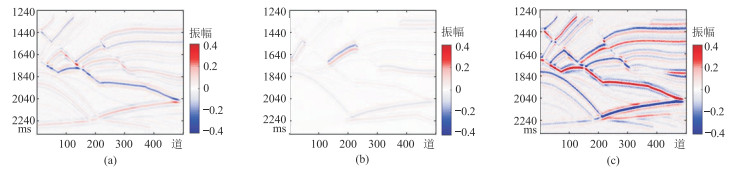
为测试本文方法的抗噪性,对远、中、近角度的地震记录添加20%的高斯白噪声(图 8),再分别采用传统方法和本文方法反演。在调参数过程中,随着加噪程度的增大,建议适当增大加权因子
|
图 8 添加20%的高斯白噪声的不同角度的地震记录 (a)近角度;(b)中角度;(c)远角度 |
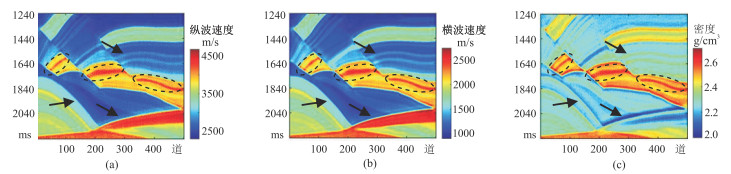
对比图 9与图 10可知,本文方法反演的地层边界分辨率更高(黑色箭头处);薄气砂岩储层边界更清晰,伪层现象大幅减少(黑色虚线圈处)。由此证明,在加噪情况下本文方法仍然能够获得比传统方法分辨率更高的纵波速度、横波速度和密度剖面。
|
图 9 添加20%的高斯白噪声的传统方法不同参数反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
|
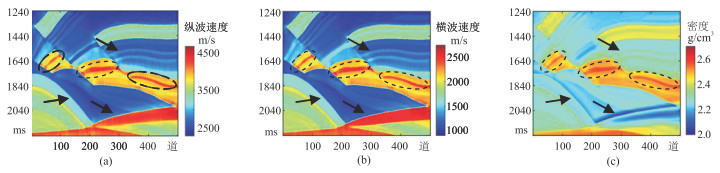
图 10 添加20%的高斯白噪声的本文方法不同参数反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
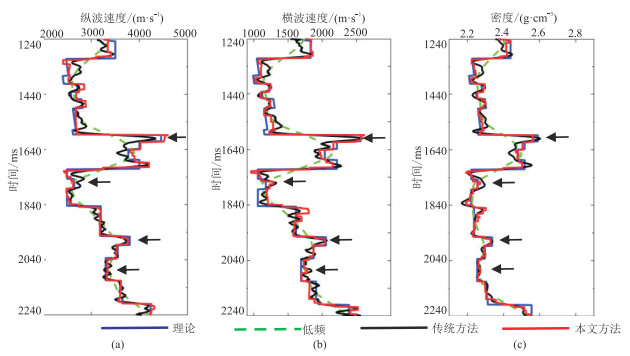
图 11展示了加噪情况下第100道(单道)反演效果对比。由图可见,相比传统方法,本文方法反演的纵波速度、横波速度和密度边界更清晰,且对薄层反演精度更高,识别更准确(黑色箭头处)。
|
图 11 添加20%的高斯白噪声的第100道不同参数反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
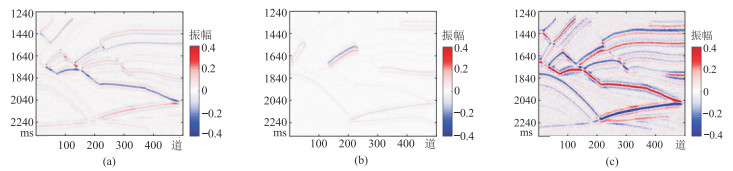
为了进一步测试本文方法的抗噪性,对地震记录加50%的高斯白噪声,得到的地震记录如图 12所示。分别采用本文方法与传统方法反演,通过启发式确定传统方法的最优参数为
|
图 12 添加50%的高斯白噪声的不同角度的地震记录 (a)近角度;(b)中角度;(c)远角度 |
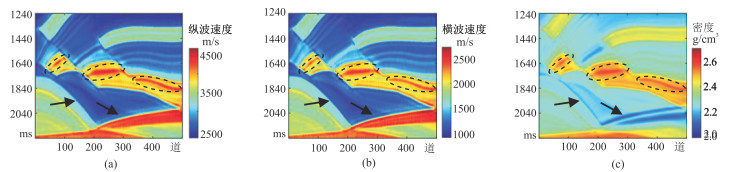
传统方法和本文方法得到的反演结果分别如图 13和图 14所示。由图可见,本文方法对细薄气砂岩储层的形态刻画更清晰,识别能力更强(黑色虚线圈内);同时,本文方法对地层边界刻画更清晰,而传统方法模糊了地层边界。
|
图 13 添加50%的高斯白噪声的传统方法不同参数反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
|
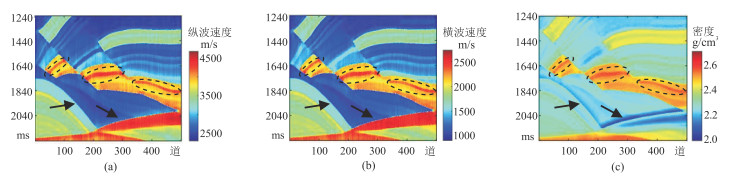
图 14 添加50%的高斯白噪声的本文方法不同参数反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
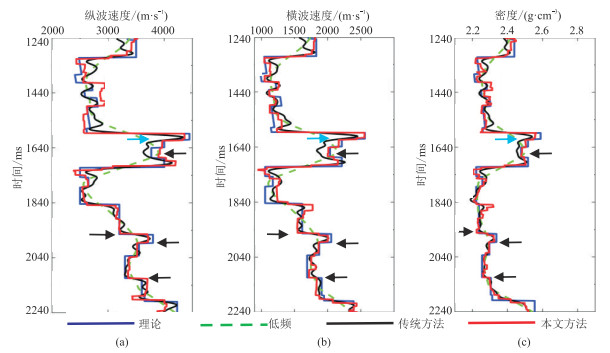
通过对比第100道(单道)不同参数反演结果(图 15),本文方法对边界刻画能力更强(黑色箭头处),反演结果更准确(蓝色箭头处)。
|
图 15 添加50%的高斯白噪声的第100道不同参数反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
综上所述,通过添加不同的噪声,本文方法仍然能够获得比较合理、可靠的反演结果。
2.3 鲁棒性测试为测试本文算法的鲁棒性,对地震记录添加大小为地震振幅一半的异常值,异常值数量为地震信号长度的3%。此时,传统方法的最优参数为
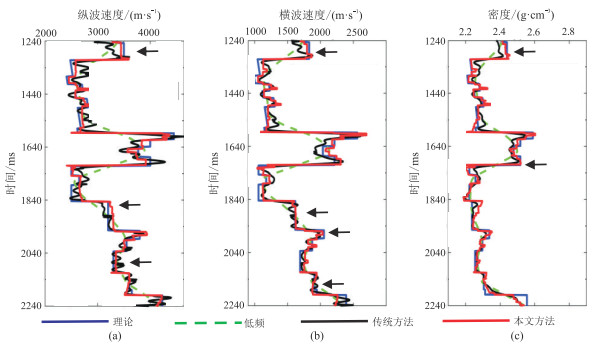
分别采用本文方法和传统方法对第100道进行单道反演,结果如图 16所示。由图可见,两种方法均受到异常值的较大影响,传统方法产生大量不准确的脉冲解,伪层现象和非聚焦平滑过渡现象加重(黑色箭头);而本文方法表现出更强的稳定性,边界刻画更准确,这说明本文方法鲁棒性更强,反演结果更加稳定、可靠。
|
图 16 添加3%数量异常值的第100道不同参数反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
引入信噪比(SNR)和归一化均方根误差(NRMSE)[30]用于评价反演效果。与均方根误差(RMSE)相比,NRMSE更能反映出反演结果与理论模型之间的平均差异(或偏差)和差异的可变性,以从横向和纵向的角度更直观、准确地对比两种方法的反演效果。它们表达式分别为
| $ \mathrm{S}\mathrm{N}\mathrm{R}=10\mathrm{ }\mathrm{l}\mathrm{g}\frac{\sum\limits _{i=1}^{\mathrm{T}\mathrm{r}}\sum\limits _{j=1}^{N}({Y}_{i, j}{-\overline{Y})}^{2}}{\sum\limits _{i=1}^{\mathrm{T}\mathrm{r}}\sum\limits _{j=1}^{N}({Y}_{i, j}-{X}_{i, j}{)}^{2}} $ | (34) |
| $ \mathrm{N}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\frac{\sqrt{\frac{\sum\limits _{i=1}^{\mathrm{T}\mathrm{r}}\sum\limits _{j=1}^{N}({Y}_{i, j}-{X}_{i, j}{)}^{2}}{\mathrm{T}\mathrm{r}\times N}}}{{Y}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{Y}_{\mathrm{m}\mathrm{i}\mathrm{n}}} $ | (35) |
式中:Y为理论参数值;
由表 2可知,本文方法反演的纵波速度、横波速度和密度的信噪比均高于传统方法;从纵向分析,本文方法的归一化均方根误差均低于传统方法;从横向分析,本文方法与传统方法获得的纵波速度、横波速度和密度中,纵波速度、横波速度的归一化均方根误差均小于密度,说明纵波速度、横波速度与模型差异的可变性更小,反演能力更强,反演结果质量更高。
|
|
表 2 无噪情况下不同方法反演结果评价 |
表 3和表 4分别为加噪20%和50%的评价结果。与表 2相似,均证明了本文方法比传统方法反演精度更高,抗噪性更强。
|
|
表 3 加噪20%情况下不同方法反演结果评价 |
|
|
表 4 加噪50%情况下不同方法反演结果的定量评价 |
实际资料来源于中国西部地区,目的层储层主要为页岩。选择A井(直井)测井数据参与实际应用。
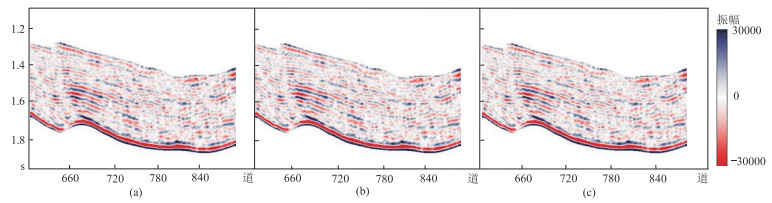
首先,对1.770 s处目的层按优势响应角度筛选出三组中心入射角的地震数据(图 17),并用于纵波速度、横波速度和密度的叠前三参数反演,它们依次为3°(1°~5°)、15°(13°~17°)、27°(25°~29°)。然后,对A井的纵波速度、横波速度和密度井数据进行内插、外推和低通滤波,构建出各参数的低频模型。再分别采用传统方法和本文方法进行反演,此时传统方法的最优参数为
|
图 17 过A井的共角度叠加地震剖面 (a)3°(近角度);(b)15°(中角度);(c)27°(远角度) |
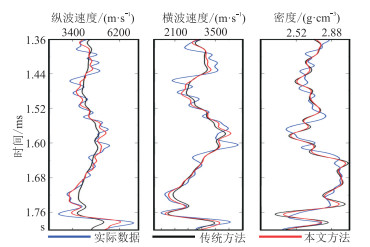
图 18为过A井的单道反演结果,可见本文方法比传统方法与实际数据吻合得更好。
|
图 18 过A井的单道不同方法、不同参数反演结果 |
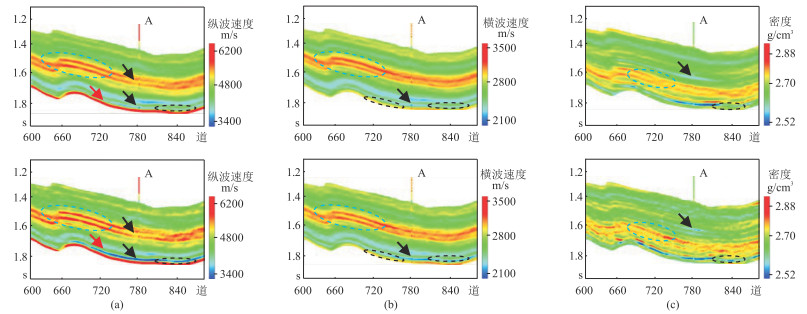
同样,由图 19可见,本文方法反演结果与实际数据吻合较好(黑色箭头处)。对于纵波速度反演结果来说,传统方法受伪层干扰,导致地层分辨率低(蓝色虚线圈内),出现混层现象;本文方法对薄层识别能力明显增强(红色箭头处),地层的横向连续性更好(黑色虚线圈内),对地层边界刻画更清晰(蓝色虚线圈内),纵向分辨率明显提高。类似地,横波速度和密度反演结果也能证明以上结论,这表明本文方法在实际应用中的可行性和优越性。
|
图 19 过A井传统方法(上)与本文方法(下)的不同参数反演结果 (a)纵波速度;(b)横波速度;(c)密度 |
本文提出的叠前重加权L1范数稀疏约束的地震反演方法,充分利用了叠前地震记录的边界振幅信息。通过理论模型测试和实际工区应用,与传统基于L1范数稀疏约束的叠前反演方法对比,得出如下结论:
(1) 本文方法能产生更多稀疏解,提高了反演结果的稀疏性,有利于刻画地层边界,弥补了L1范数在地层边界非聚焦平滑过渡的缺陷;
(2) 本文方法加权利用了地震反射系数的稀疏性,反演结果分辨率更高,减弱了L1范数约束反演中严重的伪层现象,使叠前地震反演结果更加准确;
(3) 本文方法具有较强的抗噪性,可为后续参数预测奠定更准确的基础。
由于本文方法采用的是单道反演形式,后续可以研究如何实现叠前重加权L1范数稀疏约束的多道同时反演,以进一步提升预测地层的横向连续性。
| [1] |
印海燕. AVO叠前反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2008. YIN Haiyan. The Study on Methods of AVO Prestack Inversion[D]. China University of Petroleum(East China), Qingdao, Shandong, 2008. |
| [2] |
李建华, 刘百红, 张延庆, 等. 叠前AVO反演在储层含油气性预测中的应用[J]. 石油地球物理勘探, 2016, 51(6): 1180-1186. LI Jianhua, LIU Baihong, ZHANG Yanqing, et al. Oil-bearing reservoir prediction with prestack AVO inversion[J]. Oil Geophysical Prospecting, 2016, 51(6): 1180-1186. |
| [3] |
WANG L, ZHOU H, WANG Y, et al. Three-parameter prestack seismic inversion based on L1-2 minimization[J]. Geophysics, 2019, 84(5): R753-R766. DOI:10.1190/geo2018-0730.1 |
| [4] |
WANG D, GAO J, SUN F, et al. An improved TV-type variational regularization method for seismic impedance inversion[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 7505205. |
| [5] |
ZHANG Y, WU W, ZHANG M, et al. Multitrace impedance inversion based on structure-oriented regularization[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 7503805. |
| [6] |
蔺营. 基于混合先验信息的随机反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2020. LIN Ying. Study of Stochastic Inversion Method Based on Mixed Prior Information[D]. China University of Petroleum(East China), Qingdao, Shandong, 2020. |
| [7] |
BERKHOUT A J. Least-squares inverse filtering and wavelet deconvolution[J]. Geophysics, 1977, 42(7): 1369-1383. DOI:10.1190/1.1440798 |
| [8] |
ZHANG R, SEN M K, SRINIVASAN S. A prestack basis pursuit seismic inversion[J]. Geophysics, 2013, 78(1): R1-R11. |
| [9] |
TAYLOR H L, BANKS S C, MCCOY J F. Deconvolution with the L1 norm[J]. Geophysics, 1979, 44(1): 39-52. DOI:10.1190/1.1440921 |
| [10] |
THEUNE U. JENSAS I Ø, EIDSVIK J. Analysis of prior models for a blocky inversion of seismic AVA data[J]. Geophysics, 2010, 75(3): C25-C35. DOI:10.1190/1.3427538 |
| [11] |
KONG D, PENG Z, FAN H, et al. Seismic random noise attenuation using directional total variation in the shearlet domain[J]. Journal of Seismic Exploration, 2016, 25(4): 321-338. |
| [12] |
ZHANG F, DAI R, LIU H. Seismic inversion based on L1-norm misfit function and total variation regularization[J]. Journal of Applied Geophysics, 2014, 109: 111-118. DOI:10.1016/j.jappgeo.2014.07.024 |
| [13] |
GUITTON A. Blocky regularization schemes for full-waveform inversion[J]. Geophysical Prospecting, 2012, 60(5): 870-884. DOI:10.1111/j.1365-2478.2012.01025.x |
| [14] |
李昕洁, 王维红, 郭雪豹, 等. 全波形反演正则化方法对比[J]. 石油地球物理勘探, 2022, 57(1): 129-139. LI Xinjie, WANG Weihong, GUO Xuebao, et al. Comparison of regularization methods for full-waveform inversion[J]. Oil Geophysical Prospecting, 2022, 57(1): 129-139. |
| [15] |
张雨强, 文晓涛, 吴昊, 等. 基于Lp拟范数稀疏约束和交替方向乘子算法的波阻抗反演[J]. 石油物探, 2022, 61(5): 856-864. ZHANG Yuqiang, WEN Xiaotao, WU Hao, et al. Seismic acoustic impedance inversion using Lp quasi-norm sparse constraint and alternating direction multiplier algorithm[J]. Geophysical Prospecting for Petroleum, 2022, 61(5): 856-864. |
| [16] |
SUN J, LI Y. Adaptive Lp inversion for simultaneous recovery of both blocky and smooth features in a geophysical model[J]. Geophysical Journal International, 2014, 197(2): 882-899. DOI:10.1093/gji/ggu067 |
| [17] |
PÉREZ D O, VELIS D R, SACCHI M D. Three-term inversion of prestack seismic data using a weighted l2, 1 mixed norm[J]. Geophysical Prospec-ting, 2017, 65(6): 1477-1495. DOI:10.1111/1365-2478.12500 |
| [18] |
王治强, 曹思远, 陈红灵, 等. 基于TV约束和Toeplitz矩阵分解的波阻抗反演[J]. 石油地球物理勘探, 2017, 52(6): 1193-1199, 1245. WANG Zhiqiang, CAO Siyuan, CHEN Hongling, et al. Wave impedance inversion based on TV regularization and Toeplitz-sparse matrix factorization[J]. Oil Geophysical Prospecting, 2017, 52(6): 1193-1199, 1245. |
| [19] |
LI S, PENG Z M, WU H. Prestack Multi-Gather simultaneous inversion of elastic parameters using multiple regularization constraints[J]. Journal of Earth Science, 2018, 29(6): 1359-1371. DOI:10.1007/s12583-017-0905-7 |
| [20] |
HUANG G, CHEN X, LUO C, et al. Pre‐stack seismic inversion based on L1-2-norm regularized logarithmic absolute misfit function[J]. Geophysical Prospec-ting, 2020, 68(8): 2419-2443. DOI:10.1111/1365-2478.13012 |
| [21] |
WANG G, CHEN S. Pre-Stack seismic inversion with L1-2-Norm regularization via a proximal DC algorithm and adaptive strategy[J]. Surveys in Geophysics, 2022, 43(6): 1817-1843. |
| [22] |
耿伟恒, 陈小宏, 李景叶, 等. 基于L1-2正则化的地震波阻抗"块"反演[J]. 石油地球物理勘探, 2022, 57(6): 1409-1417. GENG Weiheng, CHEN Xiaohong, LI Jingye, et al. Seismic"blocky"acoustic impedance inversion based on L1-2 regularization[J]. Oil Geophysical Prospecting, 2022, 57(6): 1409-1417. |
| [23] |
BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3(1): 1-122. |
| [24] |
GHADIMI E, TEIXEIRA A, SHAMES I, et al. Optimal parameter selection for the alternating direction method of multipliers (ADMM): quadratic problems[J]. IEEE Tran- sactions on Automatic Control, 2015, 60(3): 644-658. |
| [25] |
唐超, 文晓涛, 王文化. 基于最小范数优化交错网格有限差分系数的波动方程数值模拟[J]. 石油地球物理勘探, 2021, 56(5): 1039-1047. TANG Chao, WEN Xiaotao, WANG Wenhua. Numerical simulation of wave equations based on minimum-norm optimization of staggered-grid finite-difference coefficients[J]. Oil Geophysical Prospecting, 2021, 56(5): 1039-1047. |
| [26] |
AKI K, RICHARDS P G. Quantitative Seismology: Theory and Methods[M]. W. H. Freeman & Co., San Franciso, 1980.
|
| [27] |
CANDÈS E J, WAKIN M B, BOYD S P. Enhancing sparsity by reweighted ℓ1 minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 877-905. |
| [28] |
吴昊. 基于压缩感知的地震波成像及反演方法研究[D]. 四川成都: 电子科技大学, 2020. WU Hao. Research on Seismic Imaging and Inversion Based on Compression Sensing[D]. University of Electronic Science and Technology of China, Chengdu, Sichuan, 2020. |
| [29] |
HANSEN P C. Analysis of discrete illposed problems by means of the Lcurve[J]. SIAM Review, 1992, 34(4): 561-580. |
| [30] |
RANATUNGA T, TONG S T Y, YANG Y J. An approach to measure parameter sensitivity in watershed hydrological modelling[J]. Hydrological Sciences Journal, 2017, 62(1): 76-92. |



 文晓涛,四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院,610059。Email:
文晓涛,四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院,610059。Email: