2. 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580
2. School of Geoscienes, China University of Petroleum (East China), Qingdao, Shandong 266580, China
砂砾岩体是一种广泛存在于中国东部的碎屑岩储集体,主要发育于陆相断陷湖盆地中的陡坡带[1]。由于其侧向上紧邻深洼烃源岩,油气成藏条件优越,可发育岩性油气藏、构造―岩性油气藏和构造油气藏等[2-3],勘探潜力巨大[4],一直以来都是常规油气藏勘探的重要领域之一[5-6],同时也是非常规油气勘探的重要研究方向[7]。但砂砾岩体主要由多期砂砾沉积物滑塌、搬运、快速堆积和叠置而成[8],其沉积厚度大,埋深跨度大[9],横向变化快,沉积类型多样,空间展布及叠置关系复杂,具有强非均质性特征。与此对应,砂砾岩体成像结果的分辨率和信噪比偏低,顶、底界面之间的地震反射能量较弱,对内部结构特征认识不清[10],所以地震资料解释和储层预测难度较大,严重制约了砂砾岩体油气藏的勘探与开发。
除上述问题以外,砂砾岩体的岩性致密,粒度较粗,整体速度普遍较高,且明显不同于围岩的速度,而在地震数据处理过程中容易忽视砂砾岩体速度的空间变化,尤其是时间域砂砾岩体成像结果普遍存在构造假象[11],油水关系不清,圈闭难以落实。前人分析了时间域假象的成像机理,并对比了时、深域的成像差异,认为与时间域成像相比,深度域成像能够更好地刻画砂砾岩体产状[12]。总体而言,为提高砂砾岩体的速度模型精度,需要将处理技术与解释信息相结合,开展有针对性的处理工作[13]。
位于济阳凹陷的BS工区构造特征复杂,其中的陡坡带发育砂砾岩体,岩体与围岩速度差异较大,常规网格层析反演的结果很难反应出这种速度差异。本文在常规网格层析反演的基础之上,引入解释所得的砂砾岩体信息,通过施加约束条件控制岩体速度和空间分布,提高反演速度模型的精度,进而提高该工区砂砾岩体的成像质量。
1 成像域网格层析反演如何精确计算地震波速度,一直是地震资料处理和解释中的难题。当前生产应用的主流深度域建模方法是成像域网格层析反演方法[14-16]。该方法主要由构造倾角扫描、剩余曲率分析、反向射线追踪、构建方程组并求解更新量等步骤构成。对应的目标函数为
| $ O=\frac{1}{2}\left({‖{\Delta }\boldsymbol{T}-\boldsymbol{G}{\Delta }\boldsymbol{m}‖}_{2}^{2}+{\varepsilon }_{\mathrm{s}}{‖\boldsymbol{L}{\Delta }\boldsymbol{m}‖}_{2}^{2}\right) $ | (1) |
式中:ΔT表示由成像道集拾取的剩余深度差转化得到的走时残差;G为由射线路径构建的敏感度矩阵;Δm表示待求解的慢度更新量;εs为平滑项权重系数;L表示由拉普拉斯算子构成的平滑矩阵,实际中可结合构造倾角使用[17]。式(1)对应的反演方程组为
| $ \left[\begin{array}{c}\boldsymbol{G}\\ \sqrt{{\varepsilon }_{\mathrm{s}}}\boldsymbol{L}\end{array}\right]{\Delta }\boldsymbol{m}=\left[\begin{array}{c}{\Delta }\boldsymbol{T}\\ 0\end{array}\right] $ | (2) |
该方程组可应用最小平方正交分解(LSQR)算法求解[18]。配合叠前深度偏移使用,通过迭代更新可拉平成像道集,聚焦反射波能量,提高成像质量。
2 砂砾岩体特征约束层析反演式(1)对应方法所得的速度模型较为平滑,分辨率低。引入倾角约束后,分辨率有所提高,结果与构造趋势更一致,但仍无法适用于岩体或地层速度突变的情况。对岩体速度建模的实现方法以融合建模[19-20]和层位约束层析反演[21-24]为主。前者直接向模型中引入岩体空间分布和速度信息,但难以拉平成像道集;后者可更新速度,但只引入岩体空间分布信息,没有对速度进行限制。
借鉴层位约束的思想,本文进一步在速度变化范围和空间分布区域两方面添加约束条件,以控制反演过程,获得符合砂砾岩体特征的速度模型。
在速度变化范围方面,本文在层析反演过程中应用不等式约束,将砂砾岩体的成像速度限制在测井速度的预设区间之内,以提高速度层析建模的精度和稳定性。罚函数法[25]是目前实施不等式约束的常用方法之一,通过向目标函数中引入罚函数项,可将原有问题转化为无约束问题。本文采用内罚函数法,通过向目标函数中引入对数型障碍函数,实现不等式约束层析。在实施反演之前,需要通过融合建模方法将岩体速度赋值为测井速度,以保证速度在预设区间内。
在空间分布区域方面,层析反演的重点控制在砂砾岩体所在区域之内。对于岩体以外的区域,应减小反演对围岩速度的改变。为实现上述目的,需要对当前的成像剖面进行解释,提取砂砾岩体空间分布区域并引入到反演之中,对区域内施加不等式约束,对区域外施加正则化约束,使外部的更新量趋于0。
基于以上分析,将式(1)的目标函数拓展为
| $ \begin{align}O=&\frac{1}{2}\left[{‖{\Delta }\boldsymbol{T}-\boldsymbol{G}{\Delta }\boldsymbol{m}‖}_{2}^{2}+{\varepsilon }_{\mathrm{s}}{‖\boldsymbol{L}{\Delta }\boldsymbol{m}‖}_{2}^{2}+\right.\\ &\left.{\varepsilon }_{\mathrm{c}}{‖\left(\boldsymbol{I}-\boldsymbol{C}\right){\Delta }\boldsymbol{m}‖}_{2}^{2}\right]-{\varepsilon }_{\mathrm{p}}\sum _{i\in \boldsymbol{\varOmega }}\left[\mathrm{l}\mathrm{n}\left({m}_{i}+{\Delta }{m}_{i}-{m}_{i, \mathrm{m}\mathrm{i}\mathrm{n}}\right)+\right.\\ &\left.\mathrm{l}\mathrm{n}\left({m}_{i, \mathrm{m}\mathrm{a}\mathrm{x}}-{m}_{i}-{\Delta }{m}_{i}\right)\right] \end{align} $ | (3) |
式中:I为单位矩阵;εc为正则化系数;Ω表示砂砾岩体的空间分布区域;C为与Ω区域相对应的对角矩阵,由0或1构成,在区域之内的元素为1,之外的元素为0,该项约束岩体外的区域;对数函数项为施加的罚函数,εp为其权重系数;mi为模型当前值,mi, min、mi, max分别为设置的下限和上限。对式(3)求导,并对结果中的罚函数部分作一阶近似,可得相应的最小二乘解
| $ \begin{align}{\Delta }\boldsymbol{m}=&\left[{\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{G}+{\varepsilon }_{\mathrm{s}}{\boldsymbol{L}}^{\mathrm{T}}\boldsymbol{L}+{\varepsilon }_{\mathrm{c}}{\left(\boldsymbol{I}-\boldsymbol{C}\right)}^{\mathrm{T}}\left(\boldsymbol{I}-\boldsymbol{C}\right)\right.+\\& {\begin{array}{cc}& \left.{\varepsilon }_{\mathrm{p}}\boldsymbol{C}\left({\boldsymbol{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{T}}{\boldsymbol{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}+{\boldsymbol{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{T}}{\boldsymbol{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)\right]\end{array}}^{-1}\times \\& \begin{array}{cc}& \left[{\boldsymbol{G}}^{\mathrm{T}}{\Delta }\boldsymbol{T}+{\varepsilon }_{\mathrm{p}}\boldsymbol{C}\left({\boldsymbol{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}+{\boldsymbol{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)\right]\end{array}\end{align} $ | (4) |
式中Rmin、Rmax为与所设的下限、上限有关的对角矩阵,即
| $ \left\{\begin{array}{l}{\boldsymbol{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\frac{1}{{m}_{i}-{m}_{i, \mathrm{m}\mathrm{i}\mathrm{n}}}\right)\\ {\boldsymbol{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\frac{1}{{m}_{i}-{m}_{i, \mathrm{m}\mathrm{a}\mathrm{x}}}\right)\end{array}\right. $ | (5) |
在应用LSQR算法求解时,要输入的反演方程组为
| $ \left(\begin{array}{c}\boldsymbol{G}\\ \sqrt{{\varepsilon }_{\mathrm{s}}}\boldsymbol{L}\\ \sqrt{{\varepsilon }_{\mathrm{c}}}\left(\boldsymbol{I}-\boldsymbol{C}\right)\\ \sqrt{{\varepsilon }_{\mathrm{p}}}\boldsymbol{C}{\boldsymbol{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\\ \sqrt{{\varepsilon }_{\mathrm{p}}}\boldsymbol{C}{\boldsymbol{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\end{array}\right){\Delta }\boldsymbol{m}=\left(\begin{array}{c}{\Delta }\boldsymbol{T}\\ 0\\ 0\\ \sqrt{{\varepsilon }_{\mathrm{p}}}\boldsymbol{C}\\ \sqrt{{\varepsilon }_{\mathrm{p}}}\boldsymbol{C}\end{array}\right) $ | (6) |
由式(6)可知,当模型当前值逐步趋于区间边界时,R矩阵中对应元素的值将急剧增大,从而减小模型更新的步长,并会产生反向改变的效果;当模型当前值远离区间边界时,R矩阵中对应元素的值将减小,结合较小的权重系数,则不会对问题的解产生显著影响。
3 实际应用BS工区位于东营凹陷北部,含油层系多,油气藏类型丰富,有较大的勘探潜力。该地区构造特征较为复杂,浅部地层平缓且发育多条断层,深部为太古界潜山,地震速度高,内幕不清晰。潜山侧壁的陡坡带有砂砾岩体发育,其分布形态不规则,沉积较为杂乱。该工区地震数据经过常规处理,有声波测井、地震成果剖面、速度模型等资料,其中速度模型由常规网格层析反演获得,道集中岩体上覆地层的同相轴已基本拉平。通过分析测井数据得知砂砾岩体速度较为稳定,整体在4.6±0.4 km/s内变化,而其上覆地层的速度小于3.7 km/s,下伏潜山的速度超过5.5 km/s,均与砂砾岩体有较大速度差异。
为提取到较准确的岩体空间分布信息,本文基于原有成果资料开展测试应用工作,并采用原有成果资料作参照,以便对比分析。具体采用的技术流程如图 1所示。首先对地震资料进行偏移前的预处理工作,并基于原有成果剖面识别刻画砂砾岩体空间分布,通过填充、融合方式建立初始速度模型;然后进行叠前深度偏移,生成新的成像剖面和道集;之后基于成像道集拾取剩余曲率,基于成像剖面开展倾角分析,并识别、刻画出剖面中的砂砾岩体边界,再进行反向射线追踪,构建方程组;基于测井分析结果设置速度区间,基于识别、刻画结果设置约束区域,向原方程组中添加平滑约束、正则化约束、不等式约束等条件方程组,最后统一求解并更新速度模型,再进行下一次深度偏移,直到道集拉平、成像结果改善为止,输出最终结果。本文此次应用中,速度区间设为[4.2 km/s, 5 km/s],整个过程进行1次反演计算。
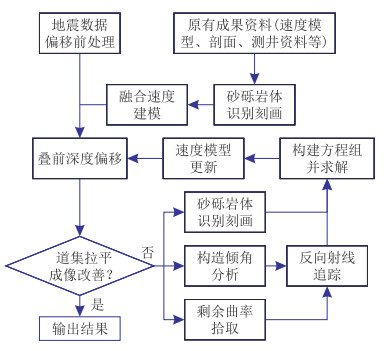
|
图 1 砂砾岩体特征约束层析建模技术流程 |
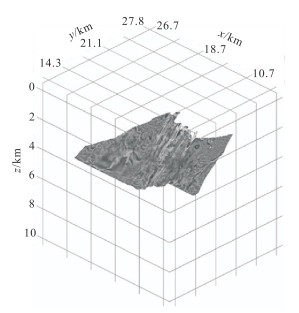
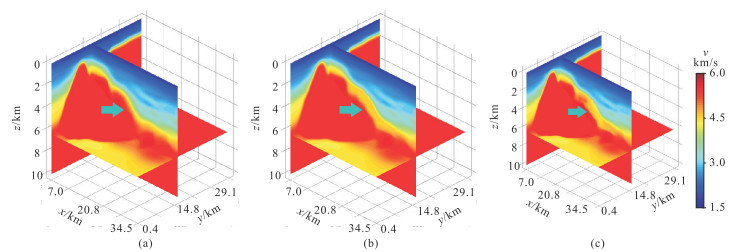
图 2为解释人员从成像剖面中刻画的砂砾岩体三维空间分布,岩体深度范围为[1.2 km, 5.6 km],x方向跨度超过20 km,y方向跨度接近10 km,最大厚度近2 km。图 3为原有速度模型、融合速度模型、反演速度模型的对比。由图可见,三个模型整体上没有明显差别,差别主要存在于砂砾岩体区域(图中箭头所指位置)。与原有速度模型(图 3a)相比,反演速度模型(图 3c)中的砂砾岩体速度与前者有明显不同,速度突变更为清晰;与融合速度模型(图 3b)相比,反演速度模型能够一定程度上反映出砂砾岩体内部的速度变化。通过对比分析可知,反演中引入的砂砾岩体信息起到了局部约束的效果。
|
图 2 拾取的砂砾岩体空间分布 |
|
图 3 不同速度模型的对比 (a)原有速度模型;(b)融合速度模型;(c)反演速度模型。箭头所指处为砂砾岩体位置。 |
图 4为不同速度模型和成像剖面的叠合显示。对比可知,原有速度模型(图 4a)与剖面中的砂砾岩体(蓝色虚线所示位置)分布并不吻合,而反演速度模型(图 4b)的吻合程度更高,且其中的岩体速度、上覆地层速度、潜山速度与测井分析结果基本一致。上述对比结果说明与常规网格层析的结果相比,本文结果更符合地质认识,证明了约束反演的有效性。

|
图 4 不同速度模型与成像剖面的叠合显示对比 (a)原有速度模型;(b)反演速度模型。蓝色虚线表示砂砾岩体范围。 |
为进一步验证反演的效果,图 5对比了融合速度模型与反演速度模型的偏移结果。与融合速度模型的成像剖面(图 5a)相比,反演速度模型的成像剖面(图 5b)整体质量相当,但对比箭头所指之处,反演速度模型的成像剖面中的砂砾岩体底界面反射更连续。以上结果证明,与融合建模技术相比,本文结果在一定程度上提高了砂砾岩体的成像精度。

|
图 5 不同模型的偏移成像剖面对比 (a)融合速度模型;(b)反演速度模型。阴影区域为砂砾岩体范围;箭头所指处为成像改善位置。 |
本文应用约束层析反演技术解决砂砾岩体速度建模问题,实际应用的结果表明:
与原有速度模型相比,结合砂砾岩体特征的约束层析反演结果与成像剖面的构造吻合程度更高,砂砾岩体速度与测井资料更符合,反演计算并未对其他区域的速度产生显著影响。
与融合速度模型相比,反演速度模型能在一定程度上反映出砂砾岩体内部的速度变化,二者的成像剖面质量整体相当,但后者的砂砾岩体底界成像连续性有所提高。
约束层析反演技术可以有效提高砂砾岩体速度模型的精度,本文处理流程有望推广应用到其他地质体的地震速度建模。
| [1] |
王鸿升, 胡天跃. 地震层速度在碎屑岩储层预测中的应用——以滨南—利津地区沙四段滩坝砂岩和砂砾岩体为例[J]. 石油地球物理勘探, 2014, 49(3): 538-545. WANG Hongsheng, HU Tianyue. Clasolite reservoir prediction with seismic interval velocity: an example in beach bar sandstones and sandstone-conglomerate bodies, Binnan-Lijin area[J]. Oil Geophysical Prospec-ting, 2014, 49(3): 538-545. DOI:10.13810/j.cnki.issn.1000-7210.2014.03.018 |
| [2] |
胡阳, 刘惠民, 郝雪峰. 断陷盆地陡坡带砂砾岩油气分布有序性及富集差异性——以东营凹陷为例[J]. 地质论评, 2021, 67(增刊1): 95-96. HU Yang, LIU Huimin, HAO Xuefeng. The orderly distribution and difference enrichment of glutenite oil and gas in steep slope zone of rift basin: A case study of Dongying Sag, Jiyang Depression, Bohai Bay Basin[J]. Geological Review, 2021, 67(S1): 95-96. |
| [3] |
高阳, 王永诗, 杜振京. 东营凹陷沙四下亚段砂砾岩致密化过程与油气成藏[J]. 地质论评, 2021, 67(增刊1): 93-94. GAO Yang, WANG Yongshi, DU Zhenjing. Densification process and hydrocarbon accumulation of deep burial sandy conglomerate in the Dongying Depression[J]. Geological Review, 2021, 67(S1): 93-94. |
| [4] |
刘建伟. 济阳坳陷东营凹陷北带砂砾岩扇体沉积相井震联合地震精细描述[J]. 特种油气藏, 2021, 28(1): 18-25. LIU Jianwei. Accurate description by well-to-seismic integration of glutenite fan sedimentation in the northern Dongying sag, Jiyang sub-basin[J]. Special Oil & Gas Reservoirs, 2021, 28(1): 18-25. DOI:10.3969/j.issn.1006-6535.2021.01.003 |
| [5] |
孔凡仙. 东营凹陷北部陡坡带砂砾岩体的勘探[J]. 石油地球物理勘探, 2000, 35(5): 669-676. KONG Fanxian. Prospecting for sand-gravel body in northern steep slope of Dongying depression[J]. Oil Geophysical Prospecting, 2000, 35(5): 669-676. DOI:10.3321/j.issn:1000-7210.2000.05.016 |
| [6] |
闫建平, 言语, 李尊芝, 等. 砂砾岩储层物性演化及影响因素研究——以东营凹陷北部陡坡带为例[J]. 岩性油气藏, 2016, 28(2): 1-6. YAN Jianping, YAN Yu, LI Zunzhi, et al. Physical property evolution of glutenite reservoir and its influencing factors: A case study from northern steep slope zone in Dongying sag[J]. Lithologic Reservoirs, 2016, 28(2): 1-6. DOI:10.3969/j.issn.1673-8926.2016.02.001 |
| [7] |
张云银, 刘海宁, 李红梅, 等. 应用微地震监测数据估算储层压裂改造体积[J]. 石油地球物理勘探, 2017, 52(2): 309-314. ZHANG Yunyin, LIU Haining, LI Hongmei, et al. Reservoir fracturing volume estimation with micro-seismic monitoring data[J]. Oil Geophysical Prospec-ting, 2017, 52(2): 309-314. |
| [8] |
张红贞, 孟恩, 孟东岳. 盐家油田巨厚砂砾岩体精细地层划分与对比[J]. 石油地球物理勘探, 2010, 45(1): 110-114. ZHANG Hongzhen, MENG En, MENG Dongyue. Fine stratigraphic classification and correlation for extremely thick glutenite in Yanjia Oilfield[J]. Oil Geophysical Prospecting, 2010, 45(1): 110-114. |
| [9] |
高阳. 东营凹陷北部陡坡带沙四下亚段砂砾岩储集层物性下限[J]. 新疆石油地质, 2017, 38(5): 559-566. GAO Yang. Lower limits of physical properties of glutenite reservoir in lower section of the 4th member of Shahejie formation in steep slope zone of Northern Dongying sag[J]. Xinjiang Petroleum Geology, 2017, 38(5): 559-566. |
| [10] |
雷蕾, 韩宏伟, 于景强. 近岸水下扇沉积样式及地震响应特征新认识[J]. 石油地球物理勘探, 2019, 54(5): 1151-1158. LEI Lei, HAN Hongwei, YU Jingqiang. New understandings of near-shore subaqueous fan sedimentary styles and its seismic responses[J]. Oil Geophysical Prospecting, 2019, 54(5): 1151-1158. |
| [11] |
宋亮, 张营革, 苏朝光, 等. 断陷湖盆陡坡带砂砾岩体构造恢复与内幕旋回划分——车镇凹陷北部陡坡带中浅层近岸扇体实例[J]. 石油地球物理勘探, 2010, 45(增刊1): 117-120. SONG Liang, ZHANG Yingge, SU Chaoguang, et al. True structure recovery and internal cycle division for glutenite bodies in the steep slop zone of faulting-depression basin: a middle-shallow near-shore fan example in the northern Chezhen sag[J]. Oil Geophysical Prospecting, 2010, 45(S1): 117-120. |
| [12] |
王惠勇, 韩宏伟, 张云银, 等. 东营北带东段胜坨—盐家地区砂砾岩扇体地层产状研究[J]. 石油物探, 2015, 54(2): 203-209. WANG Huiyong, HAN Hongwei, ZHANG Yunyin, et al. Study on the occurrence of glutenite fans in Shengtuo-Yanjia area, the east section of Northern Dongying sag[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 203-209. |
| [13] |
曹忠祥, 张宇, 蔡攀, 等. 济阳坳陷精细勘探新成果与启示[J]. 中国石油勘探, 2016, 21(3): 14-23. CAO Zhongxiang, ZHANG Yu, CAI Pan, et al. New achievements and recognitions of fine exploration in Jiyang depression[J]. China Petroleum Exploration, 2016, 21(3): 14-23. |
| [14] |
STORK C. Reflection tomography in the postmigrated domain[J]. Geophysics, 1992, 57(5): 680-692. |
| [15] |
WOODWARD M, NICHOLS D, ZDRAVEV A O, et al. A decade of tomography[J]. Geophysics, 2008, 73(5): VE5-VE11. |
| [16] |
秦宁, 王延光, 杨晓东, 等. 基于角道集剩余曲率分析的层析速度建模[J]. 石油地球物理勘探, 2015, 50(1): 61-66. QIN Ning, WANG Yanguang, YANG Xiaodong, et al. Tomography velocity model building based on ADCIGs residual curvature[J]. Oil Geophysical Prospecting, 2015, 50(1): 61-66. |
| [17] |
CLAPP R G, BIONDI B L, CLAERBOUT J F. Incorporating geologic information into reflection tomography[J]. Geophysics, 2004, 69(2): 533-546. |
| [18] |
PAIGE C C, SAUNDERS M A. LSQR: An algorithm for sparse linear equations and sparse least squares[J]. ACM Transactions on Mathematical Software, 1982, 8(1): 43-71. |
| [19] |
WANG B, KIM Y, MASON C, et al. Advances in velocity model-building technology for subsalt imaging[J]. Geophysics, 2008, 73(5): VE173-VE181. |
| [20] |
王延光, 尚新民, 赵胜天, 等. 山前带联合层析反演地震成像[J]. 石油地球物理勘探, 2021, 56(4): 782-791. WANG Yanguang, SHANG Xinmin, ZHAO Shengtian, et al. Joint tomography for foothills seismic imaging[J]. Oil Geophysical Prospecting, 2021, 56(4): 782-791. |
| [21] |
GUILLAUME P, MONTEL J P, HOLLINGWORTH S, et al. Seismic imaging with multi-layer tomography[J]. First Break, 2012, 30(10): 85-90. |
| [22] |
管文胜, 段文胜, 查明, 等. 利用基于模型的层析速度反演进行低幅度构造成像[J]. 石油地球物理勘探, 2017, 52(1): 87-93. GUAN Wensheng, DUAN Wensheng, ZHA Ming, et al. Low-relief structural imaging with model-based tomographic velocity inversion[J]. Oil Geophysical Prospecting, 2017, 52(1): 87-93. |
| [23] |
徐嘉亮, 周东红, 贺电波, 等. 高精度深度域层析速度反演方法[J]. 石油地球物理勘探, 2018, 53(4): 737-744. XU Jialiang, ZHOU Donghong, HE Dianbo, et al. High-precision velocity tomography inversion in the depth domain[J]. Oil Geophysical Prospecting, 2018, 53(4): 737-744. |
| [24] |
孟会杰, 徐兴荣, 王艳香, 等. 层位约束网格层析速度建模方法在尼日尔AG区块的应用[J]. 石油地球物理勘探, 2022, 57(增刊2): 58-63. MENG Huijie, XU Xingrong, WANG Yanxiang, et al. Application of horizon-constrained grid tomography-based velocity modeling method in Block AG, Niger[J]. Oil Geophysical Prospecting, 2022, 57(S2): 58-63. |
| [25] |
刘玉柱, 董良国, 夏建军. 初至波走时层析成像中的正则化方法[J]. 石油地球物理勘探, 2007, 42(6): 682-685, 698. LIU Yuzhu, DONG Liangguo, XIA Jianjun. Normalized approach in tomographic imaging of first breaks travel time[J]. Oil Geophysical Prospecting, 2007, 42(6): 682-685, 698. |



 金昌昆,山东省东营市东营区北一路210号胜利油田物探研究院,257022。Email:
金昌昆,山东省东营市东营区北一路210号胜利油田物探研究院,257022。Email: