0 引言

地下广泛存在方位各向异性介质，常与定向发育的裂缝相关。虽然方位各向异性不一定是裂缝导致的，本文仍基于裂缝方向来定义方位各向异性相关方向，即快横波的偏振方向。当横波斜交穿过裂缝介质(方位各向异性介质)时，会分裂为平行于裂缝方向偏振的快横波和垂直于裂缝方向偏振的慢横波(双折射)。三分量检波器接收到的是快、慢横波混叠在一起的信号(检波器水平分量摆置方向恰好与上行快、慢横波偏振方向一致或横波震源水平激发方向恰好与下行快、慢横波偏振方向一致除外)，直接对这些信号进行处理会导致成像质量降低，甚至出现假构造^[1]。此时需要进行横波分裂分析求取裂缝方向，并根据裂缝方向进行快、慢横波分离，或者进行横波分裂校正(根据裂缝方向和快慢波时差)。

纯横波地震勘探早于转换波。早在20世纪80年代，地球物理学家在纯横波地震勘探过程中观察到了横波分裂现象。Lynn等^[2]沿两条大致垂直的测线分别观测到了快横波和慢横波。Alford^[3]采集了两条十字交叉线的2C×2C横波数据，提出了Alford旋转法求取裂缝方向，将由横波分裂导致的原本分布在四个分量的反射能量旋转到主对角线两个分量，成功分离出快横波和慢横波。Li等^[4]提出线性变换法，根据四分量横波数据求取裂缝方向并对VSP横波地震数据进行了快、慢横波分离。对于纯横波分裂分析而言，以上方法均为单层裂缝算法，仅适用于裂缝方向不随深度变化情况，不能通过层剥离方式适应多层裂缝(裂缝方向随深度变化)情况。为解决这一问题，Yue等^[5]提出了多层裂缝反射纯横波分裂校正公式，提出了相应的裂缝参数求取方法，并应用模型数据进行了验证。

近三十年来，由于勘探成本的优势，PS转换横波地震勘探技术得到快速发展，PS转换横波分裂分析方法日趋成熟，常用的方法包括各种扫描算法，如快、慢横波互相关法^[6]和切向能量最小化法^[7]，这些方法同时计算裂缝方向和快、慢波时差。Bale等^[8]提出用最小二乘法计算裂缝方向，该方法要求两个或多个方位的地震数据，是一种适用于三维数据的横波分裂分析方法。对于多层裂缝情况的横波分裂处理，转换波比纯横波简单，上述单层裂缝转换横波分裂分析算法无需任何修改即可通过层剥离的方式逐层应用于多层裂缝，依次求取各层裂缝方向。

目前，PS转换波资料比较多，上述PS横波分裂分析和处理方法在工业应用中常常可以获得明显的应用效果，相关文献层出不穷^[9-14]。SP波横波分裂处理实例在业界却极为罕见，SP和PS两种转换波的横波分裂过程是相似的，唯一的区别是横波分裂发生在向下或向上的传播路径上。Yue等^[15]验证了最小二乘法^[8]对SP波数据的适应性，说明PS横波分裂分析方法可应用于SP波地震数据。本文采用切向能量最小化法^[7]对SP波合成数据进行测试，求得的裂缝方向与模型的裂缝方位一致，并将该方法应用于经过预处理的SP实际地震数据，逐个共转换点(CCP)求取裂缝方向。通过该三维九分量(3D9C)工区的四分量纯横波已判断该工区地下裂缝方向不随深度变化^[16]，因此，在求得裂缝方向后，只经过一步旋转运算便可实现从浅到深的快、慢横波转换纵(S1P、S2P)波分离。

对比分离后的S1P波和S2P波可见：虽然该工区裂缝方向不随深度变化，但是S1P波和S2P波的时差随深度增加逐渐增大。对于横波分裂校正，如果使用传统的转换横波分裂层剥离策略，需要划分多个时窗，并对每个时窗内的数据进行横波分裂分析，以获得每个时窗对应的裂缝方向和时差，在裂缝方向不随深度变化的情况下，这种重复多次计算裂缝方向的方式中很多计算是多余的。此外，层剥离的方式会将浅层裂缝方向计算误差传递到深层。为了避免上述问题，本文提出了一种横波分裂校正策略：在求取裂缝方向并进行、快慢波分离后，对S1P波和S2P波分别进行叠加，在S1P波和S2P波叠加剖面上分别拾取对应的层位以获取不同深度的时差，根据不同深度的时差以及不随深度变化的裂缝方向对SP地震数据进行横波分裂校正，校正后横波转换纵(SVP)波成像结果得到了进一步的改善。

1 SVP横波分裂分析和校正方法

3D9C地震数据的每一个分量都包含不同比例的纵波、横波和转换波。大致说来，PP波主要分布在垂直激发和垂直接收的分量，记为SzRz分量；PS转换波主要分布在垂直激发和两个水平方向接收的SzRx和SzRy分量，SS波主要分布在两个水平方向激发和两个水平方向接收的4分量地震数据，记为SxRx、SxRy、SyRx和SyRy分量；SP转换波主要分布在两个水平方向激发和垂直方向接收的SxRz和SyRz分量。常用的PS横波分裂分析算法都是基于SzRx和SzRy两个水平分量地震数据的。类似地，本文介绍的SP横波分裂处理也是基于SxRz和SyRz两分量地震数据的。也就是说，要求横波震源在每个炮点激发两次，才能获取本方法所需的地震数据。在数据处理方面，SP与PS转换波有所不同，可以通过SP数据炮、检点互换的方式借鉴PS波地震数据处理方法。

将SxRz和SyRz两分量地震数据的激发方向旋转到径向(R)和切向(T)，记为SVP_R和SVP_T分量，是本文SP波横波分裂分析算法的输入数据。类似地，后续将激发方向旋转到快、慢横波偏振方向后，记为S1P(快横波转换纵波)和S2P(慢横波转换纵波)分量。采用切向能量最小法^[7]计算地下裂缝方向。

将没有受到横波分裂效应影响的SP波记为u₀，分别记径向分量和切向分量为u_0R、u_0T。事实上，横波在进入方位各向异性介质界面且偏振方向与裂缝方位斜交时发生分裂，记裂缝方向为θ，地震道方位角为φ，S2P分量相对于S1P分量到达时间延迟(快、慢波时差)为Δt，检波器记录的反射SP波为u(径向分量u_R即SVP_R，切向分量u_T即SVP_T)。u与u₀的关系在频率域可以表示为

$ \boldsymbol{U}\left(\omega \right)={\boldsymbol{R}}^{-1}\boldsymbol{D}\boldsymbol{R}{\boldsymbol{U}}_{0}\left(\omega \right) $

(1)

式中

$ \boldsymbol{R}=\left[\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}(\theta -\varphi )& \mathrm{s}\mathrm{i}\mathrm{n}(\theta -\varphi )\\ -\mathrm{s}\mathrm{i}\mathrm{n}(\theta -\varphi )& \mathrm{c}\mathrm{o}\mathrm{s}(\theta -\varphi )\end{array}\right] $

(2)

$ \boldsymbol{D}=\left[\begin{array}{cc}1& 0\\ 0& {\mathrm{e}}^{-\mathrm{i}\omega \mathrm{\Delta }t}\end{array}\right] $

(3)

已知u，则u₀可表示为

$ {\boldsymbol{U}}_{0}\left(\omega \right)={\boldsymbol{R}}^{-1}{\boldsymbol{D}}^{{'}}\boldsymbol{R}\boldsymbol{U}\left(\omega \right) $

(4)

式中

$ {\boldsymbol{D}}^{{'}}=\left[\begin{array}{cc}1& 0\\ 0& {\mathrm{e}}^{\mathrm{i}\omega \mathrm{\Delta }t}\end{array}\right] $

(5)

R的物理含义为两个分量数据的坐标旋转，D和D$ {}^{{'}} $的物理含义分别为第二个分量数据的向后和向前时移。在时间域实现以上算法，并建立如下目标函数

$ A(\theta , \mathrm{\Delta }t)={\int }_{{\varphi }_{min}}^{{\varphi }_{max}}{\int }_{{t}_{\mathrm{s}}}^{{t}_{\mathrm{e}}}{u}_{0\mathrm{T}}^{2}(t, \varphi , \theta , \Delta t)\mathrm{d}t\mathrm{d}\varphi $

(6)

同时扫描裂缝方向和快慢波时差两个参数，当目标函数达到最小值，可以求得裂缝方向θ和快慢波时差Δt。式中：φ_min为最小方位角；φ_max为最大方位角；t_s为时窗的起始时间，t_e为时窗的结束时间。根据所求θ将横波震源的激发方向旋转到裂缝方向及其垂向，也就是快横波偏振方向和慢横波偏振方向，可实现$ \mathrm{S}1\mathrm{P} $和S2P波的分离，即

$ \begin{array}{l}\left[\begin{array}{c}\mathrm{S}1\mathrm{P}(t, \varphi )\\ \mathrm{S}2\mathrm{P}(t, \varphi )\end{array}\right]=\left[\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}(\theta -\varphi )& \mathrm{s}\mathrm{i}\mathrm{n}(\theta -\varphi )\\ -\mathrm{s}\mathrm{i}\mathrm{n}(\theta -\varphi )& \mathrm{c}\mathrm{o}\mathrm{s}(\theta -\varphi )\end{array}\right]\times \\ \begin{array}{cc}& \end{array}\left[\begin{array}{c}\mathrm{S}\mathrm{V}\mathrm{P}\_\mathrm{R}(t, \varphi )\\ \mathrm{S}\mathrm{V}\mathrm{P}\_\mathrm{T}(t, \varphi )\end{array}\right]\end{array} $

(7)

在获得的第j个时间样点(t_j时刻)快慢波时差Δt_j后，对慢波进行时差校正

$ \mathrm{S}2{\mathrm{P}}^{{'}}({t}_{j}, \varphi )=\mathrm{S}2\mathrm{P}({t}_{j}+\mathrm{\Delta }{t}_{j}, \varphi ) $

(8)

最后，将S2P$ {}^{{'}} $与S1P一起旋转回到径向和切向，得到横波分裂校正后结果SVP_R$ {}^{{'}} $和SVP_T$ {}^{{'}} $分量

$ \begin{array}{l}\left[\begin{array}{c}\mathrm{S}\mathrm{V}\mathrm{P}\_{\mathrm{R}}^{{'}}(t, \varphi )\\ \mathrm{S}\mathrm{V}\mathrm{P}\_{\mathrm{T}}^{{'}}(t, \varphi )\end{array}\right]=\left[\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}(\theta -\varphi )& -\mathrm{s}\mathrm{i}\mathrm{n}(\theta -\varphi )\\ \mathrm{s}\mathrm{i}\mathrm{n}(\theta -\varphi )& \mathrm{c}\mathrm{o}\mathrm{s}(\theta -\varphi )\end{array}\right]\times \\ \begin{array}{cc}& \end{array}\left[\begin{array}{c}\mathrm{S}1\mathrm{P}(t, \varphi )\\ \mathrm{S}2{\mathrm{P}}^{{'}}(t, \varphi )\end{array}\right]\end{array} $

(9)

2 模型数据测试

为了验证以上方法对SP波的适用性，本文设计了一个四层水平层状模型，每一层均为HTI各向异性，每层参数由相应的VTI各向异性介质参数(表 1)通过旋转获得，如此产生等效垂直裂缝的方位各向异性介质。业界已证实单层裂缝转换横波分裂分析方法可以通过层剥离的方式应用于多层裂缝情况^[10-11]，因此，只需要测试单层裂缝分析方法求取裂缝方向和快慢波时差精度，不需要重复测试层剥离过程。另外，本文实际3D9C工区的地下裂缝方向不随深度变化^[16]，为贴近实际数据情况，本文设计的理论模型每一层裂缝方向都为150°，即裂缝方向不随深度变化(这代表了一类地下介质情况，近年东方公司施工的一个3D9C^[17-18]和一个2D9C工区均属于这种情况)。如此设计模型，可以验证PS横波分裂分析方法应用于SP波地震数据求取裂缝方向的精度，同时又可以验证本文提出的横波分裂校正策略的可行性。该校正策略是针对裂缝方向不随深度变化情况提出的。

需要补充说明的是，当裂缝方向随深度变化时(多层裂缝情况)，可采用层剥离的方式实现多层裂缝转换横波分裂分析和校正，即从浅到深逐层应用单层裂缝横波分裂分析和校正方法，上一层横波分裂校正的结果作为下一层横波分裂分析和校正的输入数据，逐层类推。

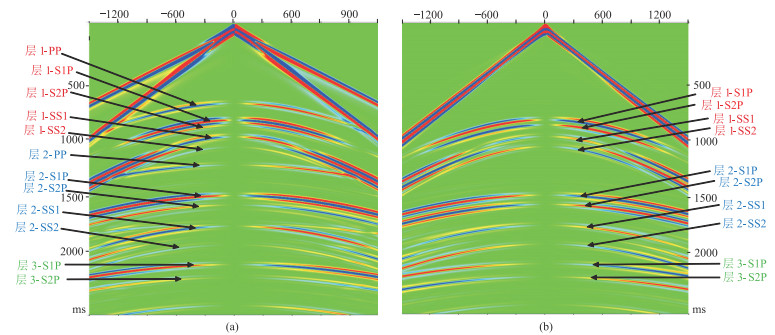
在模型表面选取一个炮点位置，在该炮点分别沿x方向和y方向加载水平集中力源，模拟横波可控震源。三分量检波器的z分量垂直向下，均匀分布在炮点四周的各条Inline线上。采用有限差分进行正演模拟，得到SxRz和SyRz两分量模型数据。图 1为过炮点测线的两分量单炮记录，该图对每个分量记录的来自各反射界面的不同类型波的强能量反射同相轴做了相应标记。水平力源的激发能量主要以横波形式向地下传播，下行横波遇到反射界面产生SP和SS两种反射波。SxRz分量和SyRz分量主要接收SP转换波，同时还接收SS波（传播方向非垂直）。由于水平集中力源不是纯剪切波震源，因此合成记录中可见PP波。图 1表明，SS和SP反射波均受到了横波分裂的影响，并且SS1与SS2波的时差是S1P与S2P波时差的2倍。

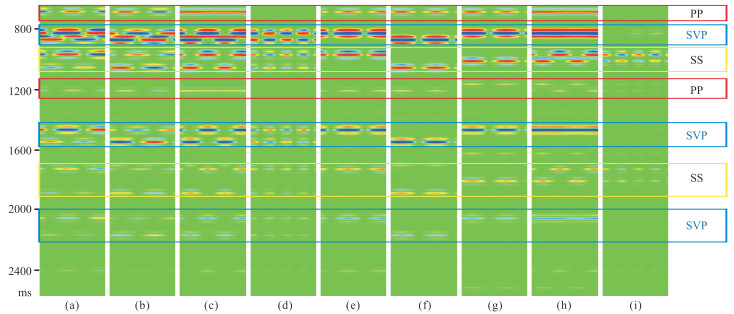
抽取炮检距为50 m的SxRz和SyRz分量合成数据，分别按照0°~360°方位角排序，如图 2a和图 2b所示，蓝色矩形框内的同相轴为SP反射波，其他为PP波和SS波。

将两个水平激发方向旋转到径向和切向，得到径向和切向激发的SVP_R(图 2c)和SVP_T分量(图 2d)，两图蓝色方框内SP转换波表现出明显的横波分裂特征，如SVP_T分量(图 2d)同相轴在裂缝方向及其垂向四个方位发生极性反转，这些横波分裂特征与PS横波分裂的表现特征相同。

以第一个蓝色矩形框的时间作为时窗进行横波分裂分析，求得裂缝方向为150°，与模型参数一致，验证了该转换横波分裂分析方法对SP两分量地震数据的适用性。根据裂缝方向进行快慢波分离，结果见图 2e和图 2f，三个蓝色矩形框的SP转换波都已经分离为S1P和S2P波，每种波的反射同相轴到达时间基本不随方位发生变化，可保障来自不同方位数据的同相叠加。对比三个蓝色矩形框的S1P和S2P波，可见快、慢波时差随时间增大而逐渐增加。

分别确定3个蓝色矩形框的快、慢波时差后，对S2P分量进行时差校正，得到S2P$ {}^{{'}} $分量(图 2g蓝框所示)，与S1P分量反射同相轴时间一致，消除了横波分裂或者方位各向异性对SP波的影响。最后，将S1P分量和S2P$ {}^{{'}} $分量的激发方向旋转回到径向和切向, 得到SVP_R$ {}^{{'}} $分量(图 2h)和SVP_T$ {}^{{'}} $分量(图 2i)，可见，SVP_T$ {}^{{'}} $分量反射能量基本消失，SVP_T分量减少的那些能量已校正到SVP_R$ {}^{{'}} $分量。SVP_R$ {}^{{'}} $比SVP_R分量能量增强的同时，来自同一个反射界面的同相轴时间不再随方位角发生变化，为后续叠加成像提供了保障。

3 实际数据应用

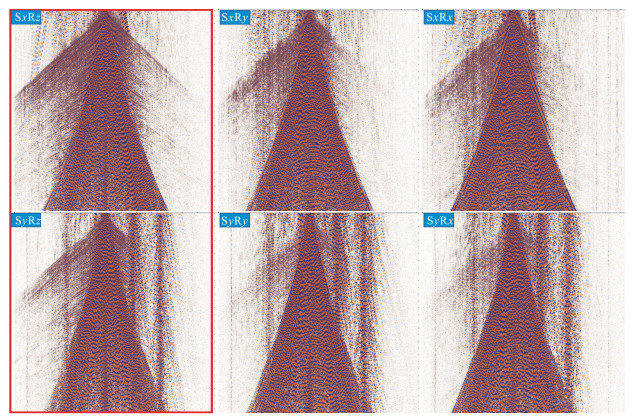
该实际数据取自一个3D9C工区。可控震源分别在每个炮点激发三次：垂直方向激发一次(z源)；水平方向激发两次，其中一次平行测线方向(x源)，另一次垂直测线方向(y源)。该工区施工质量很高，x源激发方向与测线方向基本保持平行，y源激发方向与测线方向基本保持垂直。需要指出的是：当震源车移动时，如果因为调头导致激发方向与预设方向相反，则对该激发相关的三个分量地震记录分别进行反极性处理。图 3为单炮点x源和y源激发的六分量横波源地震数据。在SxRz和SyRz两个分量上可见清晰的SP反射同相轴，主要分布在单炮中心强能量三角区以外。其余四个分量以纯横波能量为主。

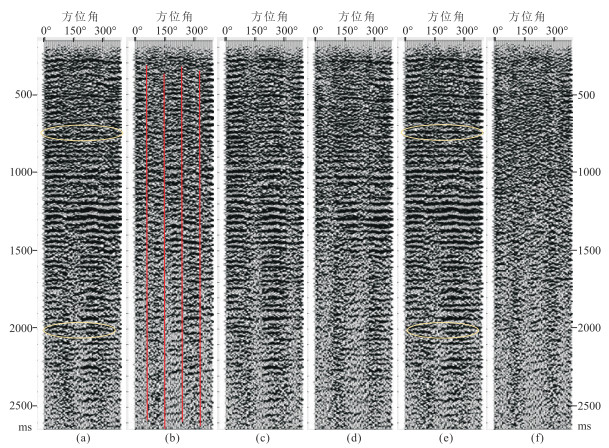
取SxRz和SyRz两分量地震数据，经过极性调整、水平分量旋转、静校正^[19]、去噪、抽CCP道集、动校正等预处理，再对两分量地震数据分别进行分方位叠加(间隔30°)得到SVP_R、SVP_T分量CCP大道集，按方位角排序结果如图 4a和图 4b所示。选取一个时窗，输入图 4a和图 4b所示的两分量CCP道集，计算该CCP点对应的地下裂缝方向。需要说明的是，为了保障裂缝方向的求取精度，要求以上预处理均为保持振幅处理，并且两分量应采用相同的处理流程和尽可能相同的处理参数(静校正量和动校正速度应完全相同)。动校正过程选用SP波速度，分方位叠加过程可以压制多数SS波和PP波能量。图 4b可见SVP_T分量具有较强的反射能量，表明地下介质存在方位各向异性。该图红线对应的四个方位可见同相轴极性反转现象，极性反转发生的方位指示了裂缝方向。该工区四分量纯横波处理结果表明，裂缝方向不随深度变化，这一结论可以从SP波同相轴极性反转发生的方位(红线处)不随时间或深度变化的现象得到进一步证实。

通过本文介绍的SP横波分裂分析方法计算每个CCP对应的地下裂缝方向和分析时窗内的时差。根据裂缝方向将激发方向旋转到裂缝方向及其垂向实现S1P和S2P波分离，结果见图 4c和图 4d。对比图 4c与图 4d可见，S1P波与S2P波反射同相轴存在明显时差，并且该时差随时间增加逐渐增大。

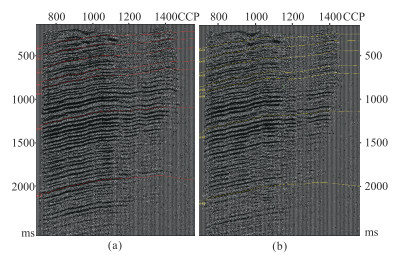
如果采用传统的层剥离方式做横波分裂校正，从浅到深将输入数据划分为多个时窗，逐个求取裂缝方向和快慢波时差。由于时差随深度增加逐渐增大，所以需要划分多个时窗，进行多次横波分裂分析，而且逐层计算会导致累计误差。为了避免以上问题，本文将分离后的S1P、S2P分量分别进行叠加，在两个叠加剖面上(图 5所示)分别拾取多个相互对应的层位，并计算所拾取层位对应的时差。层位之间的时差通过线性插值获取，如此便可获得快、慢波时差场。

得到时差场后，根据式(7)对慢横波S2P进行时差校正得到S2P$ {}^{{'}} $。时差$ \Delta {t}_{j} $常常不是时间采样间隔的整数倍，为保证时差校正精度，采用sinc函数插值计算样点值。将时差校正后S2P$ {}^{{'}} $与S1P分量一起旋转回到径向和切向，得到横波分裂校正后的SVP_R$ {}^{{'}} $和SVP_T$ {}^{{'}} $ (图 4e和图 4f)。SVP_T$ {}^{{'}} $反射能量基本消失，对比图 4e与图 4a黄色椭圆处，可见SVP_R$ {}^{{'}} $比SVP_R分量反射同相轴能量增强，并且不同方位同相轴的同相性也得到了改善。

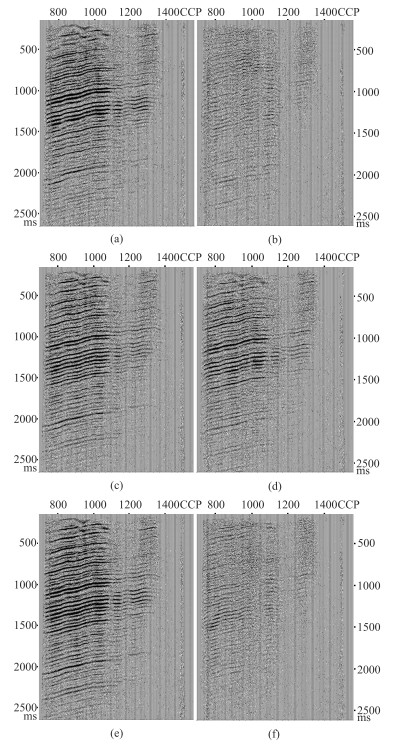
图 6a和图 6b分别为横波分裂处理前SVP_R和SVP_T分量叠加剖面。剖面右端对应地层含气，对上行纵波产生严重影响，导致SP转换波成像质量明显下降，只有纯横波成像不受气云影响，可以恢复地下真实构造^[20]。由于SVP_T分量反射同相轴间隔90°发生极性反转(图 4b)，SP波能量在叠加过程中相互抵消，导致该分量叠加剖面能量较弱。由此可见，在三维多分量数据处理过程中，切向分量总叠加/偏移剖面能量弱有时只是一种假象，并不能真实反映SP波能量在切向分量的分布状况。快、慢波分离后，S1P分量叠加剖面(图 6c)和S2P分量叠加剖面(图 6d)的成像效果比SVP_R(图 6a)明显改善。横波分裂校正后SVP_R$ {}^{{'}} $叠加剖面(图 6e)的同相轴时间与S1P(图 6c)相同，其能量比S1P更强(图 6c和图 6d展示的叠加数据与图 5展示的叠加剖面完全相同，二者的区别仅为显示参数不同)，与横波分裂处理前SVP_R(图 6a)相比，成像质量得到明显提高。由于SVP_T叠加剖面看起来比真实的反射能量弱了很多，所以SVP_T$ {}^{{'}} $ (图 6f)比SVP_T(图 6b)能量减弱的效果从叠加剖面上看起来并不明显。但是，SVP_R$ {}^{{'}} $ (图 6e和图 4e)较SVP_R(图 6a和图 4a)能量增强的现象可以说明，切向分量的反射能量已经基本被校正到径向分量上。切向分量SVP_T$ {}^{{'}} $存在少部分残留能量，原因主要是快、慢波时差求取精度不足，该校正结果有待后续的精细处理进一步提升。

4 结论

在实际3D9C地震勘探数据中能够观察到SP波的横波分裂现象，本文给出了有效的S1P和S2P波分离及SP波横波分裂校正方法。通过模型数据的验证及实际数据的应用，取得了以下几点认识：

(1) PS转换横波分裂分析方法可应用于SP转换波地震数据，并能获得地下介质的方位各向异性方向和强度，可对后续解释及储层预测提供参考；

(2) 首次在实际地震数据中成功分离出S1P波和S2P波，二者均可取得良好的成像结果；

(3) 在横波分裂校正过程中，提出了一种适用于裂缝方向不随深度变化而快慢波时差随深度变化的横波分裂校正策略，并在实际SP地震数据中应用，取得了显著的应用效果，表明了该策略的实用性。