0 引言

基于高频震源的海洋小道距、高分辨率多道地震探测方法^[1-2]具有主频高、频带宽的特点，是近海底地层层序及精细结构研究、天然气水合物资源勘查等的重要手段^[3-4]。这种采集技术在垂直与横向勘探分辨率上优势明显^[5-6]，但因其方法的特殊性和电缆本身的问题，导致在后期处理环节中地震资料的成像效果受到一定影响。主要表现为：为了提高原始资料的信噪比，电缆的深度平衡没有水鸟的控制，受其本身重力的作用，不同炮检距的位置入水深度表现出“远深近浅”的情况；同时采集过程中受风浪和海流运动以及电缆拖曳拉力变化的影响。这些因素综合引起电缆不等浮问题，在地震数据上反射同相轴呈现非双曲线时距关系，动校正之后地震道集存在剩余时差，从而影响速度分析的准确性，导致难以达到同相叠加的成像效果^[7-10]，降低了有效地层反射的信噪比和振幅能量，最终地震剖面的分辨率和成像精度受到影响。因此解决电缆不等浮问题是高分辨、小道距地震处理的重要环节^[11]。

电缆剩余时差校正方法分为三类：①交互拾取海底反射和虚反射走时以拟合方式求取时差。主要思路是根据电缆姿态变换特点，通过拾取实际虚反射的时间位置，通过近炮检距拟合获得理想的虚反射周期，二者的差值即为电缆的剩余时差。在资料处理过程中，该类方法缺点在于手动拾取工作量较大^[2]，所有地震记录均需拾取虚反射及海底反射时间。通常为减少人工工作量，需按一定间隔的炮距进行拾取，所有炮集数据的时差通过插值的方式获得。实测数据表明，当海底崎岖不平、炮间隔选择不当、缆深变换较快时，时差求取会有误差，校正后存在同相轴错位的现象。因此，这类方法在实际资料处理中有一定的局限性。②倾斜电缆处理中采用波场延拓缆深校正技术。但因采集过程中难以实时记录不同水听器位置的水深，故难以获得准确的时差^[12-13]。③道集剩余时差校正法，包括道集相干技术^[14-17]、统计法^[18-19]、相位匹配技术^[20-23]以及动态时间规整算法(DTW)^[24-25]等。首先以一定的技术手段形成模型参考道，然后对每道数据与参考道进行相关求取剩余时差校正量。但该类方法全程不受缆深数据约束，所求得的剩余时差量是电缆不等浮、速度求取不准确以及各向异性的综合体现。而且该类方法对道集的品质有一定要求^[26-30]，如：道集中多次波压制较彻底、信噪比较高，还要求相邻同相轴之间时差校正量较小、不存在相位反转的情况。而实际的高分辨、小道距地震资料，受噪声严重以及水听器响应弱的影响，数据信噪比往往较低，加上海况影响下电缆的不可控性，在不同炮检距处沉放深度差异明显，对应的校正量之间差别也较大，难以满足相应的假设要求。

针对上述方法存在的问题，本文提出一种基于虚反射走时和道集相干联合的电缆等浮校正方法。该方法综合利用虚反射走时方法和道集互相关方法的优势，通过相干函数控制，可实现非常规电缆等浮的时差校正。首先，分间隔在炮集上交互拾取海底反射和检波点的虚反射走时，所有炮相应的时间位置以拟合插值方法获取，通过二者的时差求出电缆的实时深度，转化到时间域获得初始的时差校正量；然后，通过基于模型道约束的二维相干算法获得参考的时差校正量；最后，根据二者互相关系数进行加权，得到修正的电缆不等浮剩余时差，应用后达到同相叠加的效果，从而实现地震资料成像品质的提升。

1 方法原理 1.1 基于虚反射走时的初始时差计算原理

在电缆等浮的情况下，不考虑虚反射时间随入射角不同造成的时差，地震记录上虚反射同相轴基本满足双曲线规律，延迟时间对应电缆沉放深度的双程旅行时，形态上与有效波一致。但在实际采集过程中由于各个位置的检波点存在沉放深度的差异，引起地震道集上海底反射同相轴呈明显的扭曲现象，即虚反射同相轴与一次波不完全平行。高分辨、小道距地震资料由于其特殊性，主要表现为主频较高、频带较宽的特点。一般而言，该类数据采样率为0.50或0.25 ms，对应的主频为100~200 Hz。因此，地震资料分辨率较高，在炮集上有效波和虚反射时间差较明显，在炮集上较容易识别。为保证较高的主频，震源沉放深度很小，虚反射基本表现为检波点的虚反射，因此影响虚反射延迟时间的关键是电缆的沉放深度。目前高分辨、小道距采集设备在中国尚处于技术不成熟阶段，实时电缆沉放深度无法准确获取，基于虚反射走时拾取方法可计算电缆深度，由时深转换可得到初始的时差校正量^[2]。

具体思路是：首先，采用人工交互拾取方法，抽取合适的炮距，拾取海底反射及虚反射波峰位置；然后，通过拟合插值获取所有炮的信息，炮距的选择主要考虑到海底的崎岖程度，当海底较平时，选择间隔较小的炮，海底较崎岖时，选择间隔较大的炮。总的来说，由中间炮插值出的海底和虚反射时间信息保证误差在15%以内，可有效保证时差加权选择的准确性。基于二者的时间差，通过公式推算对应炮的实际电缆沉放深度，以此计算电缆各个位置的初始剩余时差。

基于虚反射走时路径可以得到两者之间时差

$ \mathrm{d}T=\frac{1}{V}\left[\sqrt[]{(2{D}_{\mathrm{W}\mathrm{B}}+{D}_{\mathrm{R}}-{D}_{\mathrm{s}}{)}^{2}+{X}_{\mathrm{o}\mathrm{f}\mathrm{f}}^{2}}-\\\sqrt[]{(2{D}_{\mathrm{W}\mathrm{B}}-{D}_{\mathrm{R}}-{D}_{\mathrm{s}}{)}^{2}+{X}_{\mathrm{o}\mathrm{f}\mathrm{f}}^{2}}\right] $

(1)

式中：$ V $为海水速度；$ {D}_{\mathrm{W}\mathrm{B}} $为海底深度；$ {D}_{\mathrm{s}} $为震源深度；$ {D}_{\mathrm{R}} $为水听器沉放深度；$ {X}_{\mathrm{o}\mathrm{f}\mathrm{f}}{}^{} $为炮检距。

由式(1)可以反推各个水听器位置沉放深度

$ {D}_{\mathrm{R}}=\sqrt[]{\frac{(2{D}_{\mathrm{W}\mathrm{B}}-{D}_{\mathrm{s}}{)}^{2}+{X}_{\mathrm{o}\mathrm{f}\mathrm{f}}^{2}-\frac{{\left(V\mathrm{d}T\right)}^{2}}{4}}{\frac{4(2{D}_{\mathrm{W}\mathrm{B}}-{D}_{\mathrm{s}}{)}^{2}}{{\left(V\mathrm{d}T\right)}^{2}}-1}} $

(2)

此时，道集上对应的剩余时差$ \mathrm{d}{T}_{\mathrm{r}\mathrm{e}} $为

$ \mathrm{d}{T}_{\mathrm{r}\mathrm{e}}=\frac{{D}_{\mathrm{R}}-{D}_{\mathrm{s}}}{V} \times 1000 $

(3)

1.2 基于模型约束的绝对互相关参考时差计算原理

基于模型约束的绝对互相关算法求取剩余时差的主要理论基础是道集相干原理和模型道建立。通常动校正后共反射点道集上某一同相轴的数据是来自同一反射点的不同炮检距的信息，因此具有最大的相干性，处理过程中需要一个波组特征好、信噪比高的参考模型道进行控制。

合适的模型道对于道集的相干分析起着关键作用，单一的地震道集往往受多次波、噪声、反射能量弱等问题影响，达不到模型道的要求。一般而言，选择叠加剖面上对应的道集作为模型道，实际数据处理证明在剩余时差较大或相位反转的情况相干适配性较差；选定近炮检距内时差小的道参与同相叠加生成模型道，近道数据往往存在残余的多次波，模型道的准确性同样难以满足^[9]。理想的做法是根据地震道集情况，选择合适炮检距范围(1/6~4/6炮检距)信噪比较高的道进行部分叠加形成参考道，具体情况参考叠加后的剖面成像质量。叠加结果表示为

$ y\left(n\mathrm{\Delta }t\right)=\frac{1}{N}\sum\limits_{i=1}^{N}{x}_{i}\left(n\Delta t\right) $

(4)

式中：$ N $为道集内总道数；$ {x}_{i}(n\Delta t) $表示第i道数据，其中$ n $为对应道的振幅采样序号，$ \Delta t $为采样间隔。

获得模型道后，参考的剩余时差通过每道与模型道之间的互相关分析获得。处理过程中由于相关曲线存在多个极值，会导致相位串变。本文通过二维的相关函数同时求取时差和相位差，可有效解决相位问题。

设CMP道集中第i道数据$ {x}_{i} $对应模型道集为$ {y}_{i} $，假定$ {x}_{i} $和$ {y}_{i} $之间存在时差$ \Delta t $和相位差$ \theta $，因此剩余时差的确立本质是$ \Delta t $和$ \theta $的求取。给定一定长度时窗(至少涵盖2个波组)，对$ {x}_{i} $做相位$ \alpha $校正后，实部和虚部分别与$ {y}_{i} $的实部和虚部做互相关。互相关函数表示为

$ S\left(\alpha , \tau \right)=\mathrm{c}\mathrm{o}\mathrm{s}\alpha ·R\left(\tau \right)-\mathrm{s}\mathrm{i}\mathrm{n}\alpha ·I\left(\tau \right) $

(5)

式中：$ R\left(\tau \right) $为实部互相关道；$ I\left(\tau \right) $为虚部互相关道。$ S\left(\alpha , \tau \right) $是以时差$ \tau $和$ \theta $为自变量的二维函数。在有效的一个波长范围内，根据互相关函数的性质可知，$ (\theta , \Delta t) $对应$ S\left(\alpha , \tau \right) $的极值点。通过极值原理，将式(5)改写为

$ \frac{1}{2}\frac{\partial [{R}^{2}\left(\tau \right)+{I}^{2}\left(\tau \right)]}{\partial \tau }=0 $

(6)

于是，求取$ \Delta t $和$ \theta $转换为$ {R}^{2}\left(\tau \right)+{I}^{2}\left(\tau \right) $的极值问题。通过计算式(6)的极大值对应的点，即可获得$ \Delta t $和$ \theta $。相位的引入避免了剩余时差过大导致的相位串变问题。沿时间方向以固定的步长滑动时窗并计算时差量，直至完成一个地震道的计算。重复以上步骤，完成整个地震数据的处理，得到的时移量作为参考时差校正量。

1.3 剩余时差的加权选择

由前文分析可知，初始时差受炮插值的影响，在炮间隔选取不当、海底崎岖不平、缆深变换过快的情况下，插值后的CMP道集局部炮检距位置时差计算会产生误差。另外，由于海底反射和虚反射时间是由炮集拾取所得，通过转换应用到CMP道集上，可能会引起时差跳变。因此需要通过初始时差与参考时差的联合处理修正电缆时差。其思路是：在给定的时窗范围内，统计初始时差和参考时差之间异常位置的时间范围，选择二倍于最大时间作为滑动步长估算两个时差的互相关系数^[31]。考虑本文方法只针对缆深进行校正，参考时差量是综合时差量的体现，因为以初始时差量作为标准，如果超过90%，可认为初始时差量是正确的，低于90%，通过二者加权平均的方法进行计算。以此逐道进行处理，平滑后得到修正的电缆时差校正量。

相关系数计算公式如下

$ p=\frac{\mathrm{c}\mathrm{o}\mathrm{v}(x, y)}{{\sigma }_{x}{\sigma }_{y}}=\frac{\sum\limits_{i=1}^{N}({x}_{i}-\overline{x})({x}_{i}-\overline{y})}{\sqrt{\sum\limits_{i=1}^{N}({x}_{i}{-\overline{x})}^{2}}\sqrt{\sum\limits_{i=1}^{N}({y}_{i}{-\overline{y})}^{2}}} $

(7)

式中：$ \mathrm{c}\mathrm{o}\mathrm{v}(x, y)=\frac{\sum\limits_{i=1}^{N}({x}_{i}-\overline{x})({x}_{i}-\overline{y})}{N} $；$ {\sigma }_{x} $、$ {\sigma }_{x} $分别为$ x $、$ y $的标准差；$ \overline{x} $、$ \overline{y} $分别为x和y的平均值。

2 数据处理 2.1 模型数据处理

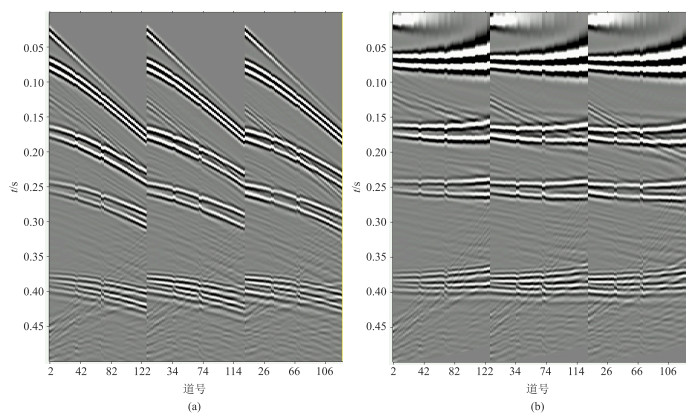
为了验证本文方法的有效性，首先对理论模型数据进行校正处理。本文选取主频为120 Hz的Ricker子波为震源，采用射线追踪方法构建一个高分辨率、小道距斜缆地震数据，共128道，炮距为12.5 m，道间距为3.125 m，每道有512个采样点，震源沉放深度为0。图 1a是模拟得到的地震记录，可见清晰的检波点虚反射；图 1b为经过动校正后的数据。可以看到，由于电缆设计深度不在一个平面上，地震记录上近道已经被拉平，远道未拉平，反射波时距曲线为非双曲线。随着炮检距的增大，虚反射和海底反射时差变大，局部位置由于电缆的沉放深度不连续，同相轴存在弯曲、抖动的情况。

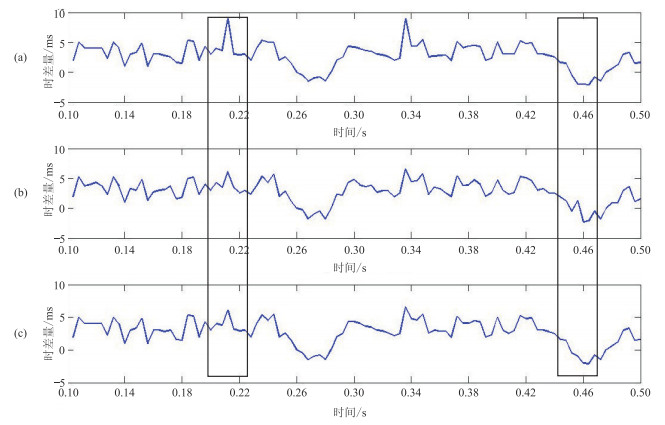
首先，拾取第一个炮集和第三个炮集的虚反射和海底反射时间，第二个炮集对应的时间通过二者插值获得，根据式（3）求得每一道的初始时差校正量。图 2a为炮集分选到CMP道集后某一道集第20道的初始校正量；然后，选择CMP道集中前20道叠加结果作为模型道，考虑模型数据波组特征较好，互相关系数的门槛值设为0.8，系数低于0.8的不做校正处理。为了包含整个未校平的同相轴范围，时窗长度设为60 ms，最大时差量为10 ms，每道与参考道进行相干计算，获得参考的时差校正量。图 2b为选择的CMP道集中第20道求得的参考校正量。可以看出，初始时差量和参考时差量在局部位置有一些相对异常的值，左边方框标识位置处初始时差校正量存在异常。右边方框标识位置处参考时差校正量存在异常。经互相关分析和加权，得到时差校正结果（图 2c），此时异常值得到消除，更符合剩余时差修正趋势。

把修正时差应用到整个CMP道集(经过虚反射压制处理)，并与常规互相关方法校正结果对比（图 3）。可以看出：常规互换方法在远炮检距位置上翘的同相轴基本被拉平，抖动现象有所改善，但在部分位置同相轴抖动现象未拉平(图 3b黑色箭头所示位置)，局部位置还出现了校正异常的现象(红色箭头所示位置)；本文方法很好地改善远炮检距动校不平和抖动现象(图 3c)。总体而言，本文方法比单纯的互相关方法的校正效果更好，达到了期望的处理效果。

2.2 实际数据处理

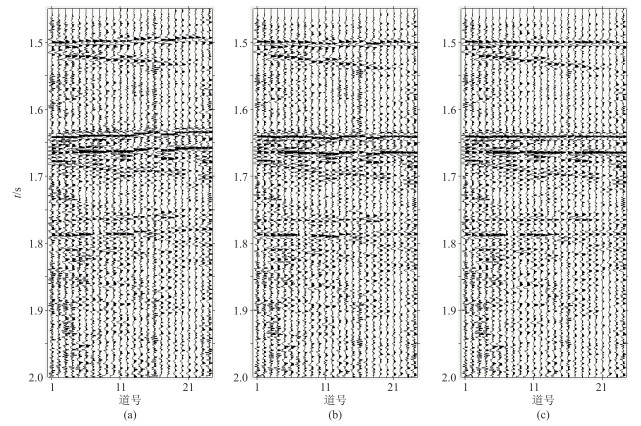
为了探讨本文方法在实际地震资料处理中的应用效果，选取某海域实际小道距地震资料进行处理分析。原始数据道数为120，炮间距为12.5 m，道间距3.125 m。为了保证数据的信噪比，先对道集进行各类噪声衰减预处理。图 4a为经过预处理后动校正的CMP道集，受电缆没有水鸟控制的影响，经过动校正后，中远炮检距存在动校不平的现象，剩余时差问题较严重，部分位置受不均匀海流的影响，有抖动的情况。受实际资料信噪比影响，在初始时差计算过程中，为了保证拾取的准确性，海底反射及虚反射的拾取炮间隔较小；参考时差计算过程中，考虑到无多次波的影响，选择叠加剖面作为模型参考道。图 4b和图 4c分别是常规的互相关方法和本文方法处理后的结果，可以看出，图 4c明显削弱了同相轴抖动现象，且在信噪比较低的位置效果更好。换言之，本文方法从二个维度对剩余时差进行识别，得到的剩余时差更加符合实际情况。从CMP道集效果来看，不同深度的同相轴被拉平，解决了电缆时差问题，提升了道集同相叠加的精度。

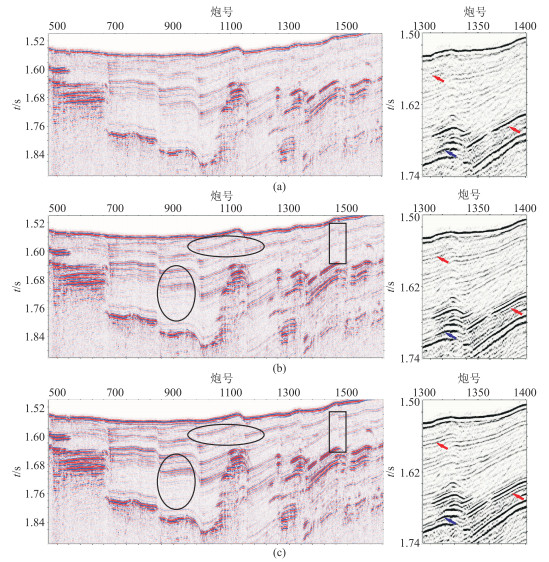
图 5a是时差校正前的叠加剖面，整体地震反射能量弱、信噪比低、地层连续性较差，同相轴存在抖动的现象，导致地质现象不明显，内幕反射不清晰。图 5b和图 5c分别是常规的互相关方法和本文方法处理后的结果，经二种方法电缆时差校正后，地层的连续性得到改善，剖面整体能量有了加强，尤其是弱反射区域，分辨率和信噪比得到提高。从解释角度分析，仔细对比可知，图 5c的波组特征更清楚，断层更清晰(方框位置所示)，在同相轴连续性和地层反射能量方面，改善更好(椭圆位置所示)，从而整体的剖面成像质量更高。

由图中局部位置的变密度显示放大图(图 5右)可以看出，由于小道距覆盖次数较低，电缆等浮情况对叠加剖面成像影响较大。从处理前、后剖面效果来看，弱反射轴以提升反射能量为主(红色箭头所示)，强反射轴以提升连续性为主(蓝色箭头所示)。总体而言，本文方法通过不同约束条件下的联合处理，处理效果优于常规的校正方法。

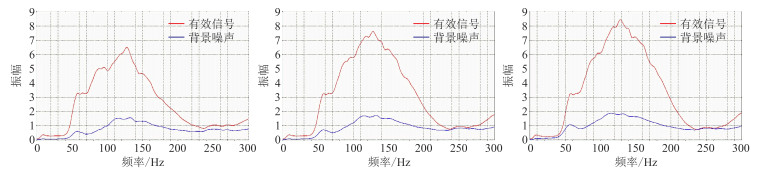
图 6为图 5的频谱。由图可见，噪声的频谱曲线基本保持不变，有效信号在振幅和频带宽度上都有明显改善。原始剖面频谱从130 Hz以后，整体振幅下降速度较快（图 6a），校正后，高频部分得到补偿。本文方法（图 6c）相比常规方法（图 6b）的优势在于，各个频段位置对应的振幅幅值更大，表明地震反射能量提升更多，校正后获得了更好同相叠加的效果。

3 结论与展望

(1) 小道距地震采集中由于国产电缆的不完善，往往存在电缆不等浮问题，严重影响地震数据的信噪比和成像精度。本文提出基于道集相干和虚反射走时联合的电缆等浮校正方法，能够实现对不同炮检距深度不一致引起的时差进行校正，应用后同相轴被拉平，同相轴连续性变好，剖面的成像品质得到提升。

(2) 本文方法从电缆深度计算和相干分析二个维度获得剩余时差校正量，保障了求取时差的准确性。

(3) 本文方法对数据有良好的适应性，在交互拾取的环节，可以根据海底的崎岖程度，对数据的拾取间隔进行选择，可实现生产化的处理，因此具有较好的适应性和推广价值。

(4) 本文方法主要针对的是可有效识别虚反射的高分辨率地震数据，对于常规多道地震处理中的电缆数据等浮校正，受分辨率的影响，有效波和虚反射难以准确分离，在应用上需做进一步的探索。