2. 中国石油集团东方地球物理公司, 河北涿州 072751
2. BGP Inc., China National Petroleum Corporation, Zhuozhou, Hebei 072751, China
近年来,中国进口油气资源总量居高不下,原油对外依存度高达72%,天然气对外依存度达44%,加大中国油气资源勘探力度、提升油气资源开发水平迫在眉睫[1-2]。油气资源开发水平的提高离不开勘探技术的进步。随着油气勘探的主战场逐步向深层、致密、隐蔽及非常规领域转移,勘探目标日趋复杂,发现难度不断增大,单独依靠传统纵波勘探存在地震分辨率低、地质目标成像精度不高等问题。与纵波相比,横波对介质的各向异性响应更敏感且传播速度更低,是提高构造成像精度与分辨率的勘探利器,更是气田勘探的最有效方法[3]。但横波激发难度大、传播稳定性差,长期以来难以获得品质高、频带宽、能量强的横波地震信号,是深层、非常规油气领域横波勘探的关键性难题。
可控震源是一种高效的地震勘探装备,其地震信号连续可控、激发能量密集且可任意分配,使高效激发横波成为可能[4-7]。横波可控震源的激发本质是通过振动器与大地之间的相互作用产生地震波,而振动器作为横波可控震源的关键执行部件,其与大地的耦合振动直接决定了横波的激发效果,是研究横波可控震源激发问题的基础。但目前横波可控震源尚未大规模投入使用,主要集中在现场测试、结构设计等方面,鲜有针对振动器—大地耦合振动的基础性研究[8-9]。
相对而言,对纵波可控震源振动器—大地耦合振动的研究较完善,研究方法及手段可为横波可控震源振动器的相关研究提供参考。1965年,Castanet等[10]最先提出了一种线性的弹簧—质量—阻尼模型,逐渐发展为纵波可控震源的主流控制模型[11]。由于该模型过于简化,忽略了振动器与大地之间的非线性作用,其局限性也日益显现。为此,Lebedev等[12-13]采用一组不同长度的弹簧模拟了在不同阶段由于接触不均造成的振动器—大地接触刚度的变化,建立了双线性刚度模型和双曲正切刚度模型。Wei[14]、黄志强等[15-16]、丁雅萍等[17]利用有限元方法建立了振动器—大地耦合振动模型,分析了耦合系统的固有频率、模态振型以及振动响应等,发现耦合系统参数显著影响振动器的动态响应。上述研究表明,合理地构建振动器—大地耦合振动模型是耦合振动的研究基础。横波可控震源与大地之间的耦合振动关系更复杂,涉及非均匀接触、土壤弹塑性、摩擦、埋深等多种非线性影响因素,但现阶段尚未见横波可控震源振动器—大地耦合振动实用模型及其响应特性的系统研究。此外,野外试验表明,横波可控震源的实际激发效果明显受地表条件参数影响,因此了解其影响机理必不可少[3, 18]。
针对以上问题,本文基于有限元法建立了考虑多种非线性影响因素的横波可控震源振动器—大地耦合振动三维数值仿真模型,从接触界面应力分布与变形、振动输出力、激发应力波传播以及能量传递特性等方面深入分析了振动器—大地耦合振动响应特性,同时研究了土壤类别、弹性模量、黏度等地表条件参数对响应特性的影响规律。本文的研究结果表明,利用数值模拟可有效分析振动器—大地耦合振动响应,可为横波可控震源振动器结构设计及优化等提供理论参考。
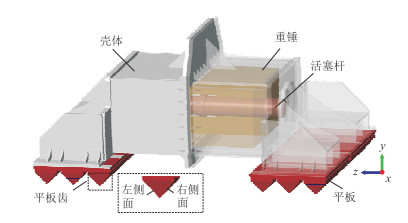
1 振动器—大地耦合振动数值仿真模型 1.1 振动器工作原理横波可控震源的核心部件为振动器,主要由壳体、重锤、活塞杆和平板组成(图 1)。在工作过程中,提升液压缸将可控震源运载底盘(震源车)微微顶起,使震源车车身重量压于振动器,从而建立振动器与大地的初始接触。随后,液压系统驱动重锤左、右运动,由此产生的反作用力作用于活塞杆,并由壳体传递给平板,最终通过平板与大地之间的相互作用输出信号和传递能量。值得一提的是,为提高横波的激发强度,要求横波可控震源振动器平板的结构为齿形,以便压入土壤从而增强平板—大地的相互作用。
|
图 1 横波可控震源振动器结构 |
为了还原横波可控震源的真实激发情况,本文基于有限元法建立了考虑非线性影响因素的横波可控震源振动器—大地耦合振动数值仿真模型。在保证仿真精度的前提下合理简化振动器的结构,简化的振动器—大地耦合振动模型由上部结构(包含壳体和活塞杆)、平板以及耦合大地三部分组成。确定耦合大地模型的尺寸是模拟振动器激发地震波传播特性的关键:尺寸过小,会产生边界效应、干涉等;尺寸过大,则会大幅增加计算量。因此,有必要分析大地模型尺寸无关性,以确定最合理的模型尺寸。经研究,最终确定的大地模型尺寸为:直径×深度=7000 mm×4000 mm[19]。
1.2.2 网格划分网格质量直接影响数值仿真分析的计算效率及可靠性,为了合理选择网格类型及尺寸,具体操作如下。
(1)振动器的网格划分。平板是振动器与大地之间相互作用的媒介,采用较小的网格单元可提高计算精度,选取单元尺寸为20 mm,单元类型为C3D8R(缩减积分六面体单元)。振动器上部结构复杂,尤其是当壳体为薄壁类零件时,网格划分容易造成单元过小、翘曲过高,因此将其定义为离散刚体并抽壳,通过设置集中质量分析上部结构对振动器动态响应的影响,再采用刚体单元类型R3D4划分网格,选取单元尺寸为50 mm。
(2)耦合大地的网格划分。仅细化平板与大地的接触界面,适当粗化其余部分,最大网格尺寸应小于激发应力波波长的1/5~1/4[20]。采用网格无关性分析合理选择接触界面的网格尺寸,保证大地模型最大网格尺寸不变。通过不断调整接触界面的网格尺寸,从而生成不同网格数量的大地网格模型。为方便比较,选取接触界面相同位置节点的振动位移幅值作为评判参数(表 1)。可见:当网格数量小于309520(Grid 3)时,增加网格数量,参考点的位移幅值变化较大;当网格数量达到309520时,继续增加网格数量对参考点位移幅值的影响很小,故确定大地网格数量为309520。
|
|
表 1 网格无关性分析结构 |
振动器的材料为45钢,采用线弹性材料模型。选取大地模型的土壤类别为黏土,考虑到工作过程中土壤的塑性变形,采用Drucker-Prager弹塑性本构关系描述土壤的非线性特性[21-23]。具体的材料参数设置如表 2所示。为真实反映平板与大地之间的相互作用情况,采用运动接触算法模拟平板与大地的接触,允许接触面存在有限滑移和接触分离,将平板与大地的法向接触属性设置为硬接触,切向接触属性采用库伦摩擦模型。
|
|
表 2 模型的材料参数 |
为避免耦合大地在振动过程中整体位移,约束其底面和四周表面的六个自由度。在实际工作过程中,振动器激发的应力波会向无穷远处传播,而仿真分析中大地模型的计算域有限,应力波会在人工截断边界产生反射,从而引入不真实的反射地震波。为模拟振动器激发地震波的真实传播特性,基于波动理论,采用黏弹性人工边界模拟地震波的远域能量传播效应。对于三维数值仿真模型,黏弹性人工边界节点的法向弹簧刚度和阻尼系数为[24]
| $ \left\{\begin{array}{l}{K}_{\mathrm{N}}=\frac{\lambda +2G}{r}\\ {C}_{\mathrm{N}}=\rho {v}_{\mathrm{P}}\end{array}\right. $ | (1) |
切向弹簧刚度和阻尼系数为
| $ \left\{\begin{array}{l}{K}_{\mathrm{T}}=\frac{G}{r}\\ {C}_{\mathrm{T}}=\rho {v}_{\mathrm{S}}\end{array}\right. $ | (2) |
式中:vP为介质的纵波波速;vS为介质的横波波速;
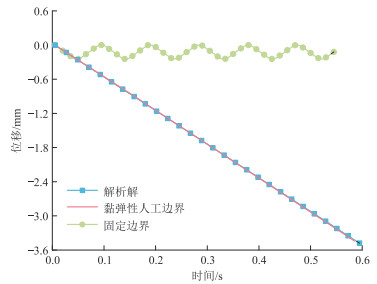
在Abaqus软件的基础上自行编程建立黏弹性人工边界,各边界节点的弹簧刚度和阻尼系数可以由式(1)、式(2)得到。根据文献[25]的方法验证建立的黏弹性人工边界,验证结果(图 2)表明,施加黏弹性人工边界的模型与解析法计算结果一致,证明黏弹性人工边界能够模拟地震波在无限域的传播特性。
|
图 2 黏弹性人工边界验证结果 |
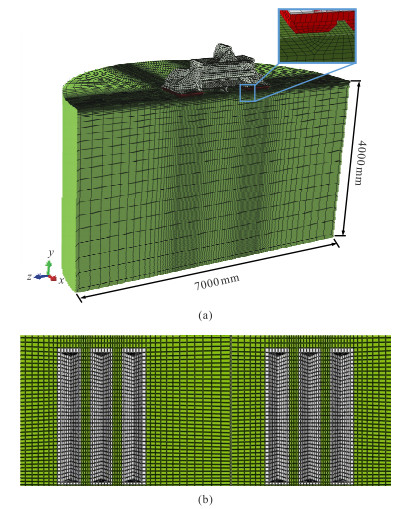
为充分还原横波可控震源的加载情况,通过地应力平衡、静态载荷加载以及动态载荷顺序加载。为保证初始接触的收敛性,静态载荷采用光滑幅值曲线,动态载荷是作用在活塞杆上的周期性液压力,峰值为1.7×107 Pa,激振频率为50 Hz,共加载10个周期。图 3为振动器—大地耦合振动数值仿真模型。由图可见,平板—大地接触界面由左、右两侧各三个不连续的齿坑组成(白色网格部分),对应振动器两侧平板的六个齿排。
|
图 3 振动器—大地耦合振动数值仿真模型 (a)整体模型;(b)接触区域放大图(白色网格部分) |
为有效研究横波可控震源振动器—大地耦合振动响应特性,需验证建立的仿真模型,其中验证大地模型的有效性是重点。横波在无限弹性均匀介质中的波速为
| $ {v}_{\mathrm{S}}=\sqrt{\frac{G}{\rho }}=\sqrt{\frac{E}{2\left(1+\nu \right)\rho }} $ | (3) |
式中:E为介质弹性模量;
为利用式(3)验证仿真模型的有效性,将大地模型设置为弹性土壤,其密度、弹性模量以及泊松比的取值与表 2一致。由式(3)求得的vS理论值为79.33 m/s,而仿真模型中横波可控震源振动器激发的剪切应力波从大地模型表面传播到模型底端(传播距离为3.6 m)所需时间为0.0453 s,对应vS=77.47 m/s。理论计算结果与数值仿真结果相差约2.34%,说明所建模型可以有效地模拟横波可控震源振动器的传播特性。
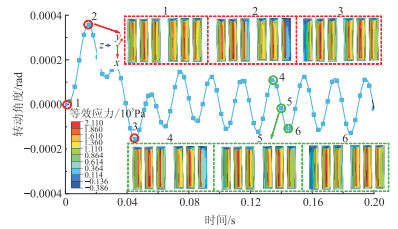
2 振动器—大地耦合振动响应特性分析 2.1 接触界面应力分布与变形振动器平板—大地接触界面的应力分布与平板和大地的相对运动紧密相关。图 4为振动器转动曲线与界面应力分布。由图可见:①在静态载荷的作用下,高应力区(红色)呈线性分布在接触界面的底端(时刻1);随着振动器在动态载荷的作用下向z轴正向运动(时刻2和时刻4),高应力区逐渐由接触界面的底端移向左侧面,而低应力区(蓝色)则出现在接触界面的右侧面。②同理,当振动器向z轴负向运动时,高、低应力区分别出现在接触界面的右侧、左侧。③振动器两侧平板与大地的接触应力并不对称,即一侧平板的接触应力明显小于另一侧(时刻2、时刻3、时刻4、时刻6)。上述现象与振动器所受力矩的不平衡有关,由于振动器所受驱动力与大地对平板的反作用力不在同一水平面上,由此产生的力矩使振动器绕x轴转动,造成平板被周期性地抬起、放下,进而导致平板与大地的不对称接触。④振动器绕x轴的转动角度随加载时间的变化曲线(图 4蓝色曲线)表明,振动器的转动角度在瞬态响应阶段(t = 0.012 s)达到最大值,随后进入较平稳的周期性转动,转动幅值约为1.14×10-4 rad。在仿真过程中,动态载荷的激发频率为50 Hz,理论上振动器应在t = 0.01 s达到最大转动角度,但实际上振动器在t = 0.012 s才达到最大转动角度,即振动器的实际运动稍晚于激发力(动态载荷),存在一定滞后。
|
图 4 振动器转动曲线与界面应力分布 1~6代表不同时刻,平板—大地接触界面的对应关系同图 3。 |
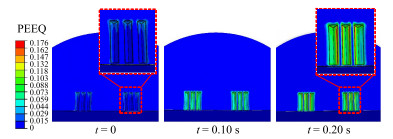
结合大地模型的等效塑性应变云图(图 5),进一步分析平板与大地接触界面的变形情况。在静态加载结束后(t = 0),大地模型的初始塑性变形主要集中在接触界面的两端以及外侧面的边缘处。随着动态载荷加载时间的增加,大地模型发生塑性变形的区域逐渐向整个接触界面扩散,并进一步蔓延至邻近接触界面的其余部分。平板与大地之间齿坑的尺寸也随着动态加载时间的增加而增大,在振动过程中,可能导致平板齿的某一侧面脱离与大地的接触——平板脱耦。脱耦将加剧平板与大地接触的不均匀性,降低横波可控震源的有效输出,不利于系统能量的传递。
|
图 5 大地模型的等效塑性应变云图 PEEQ表示等效塑性应变。 |
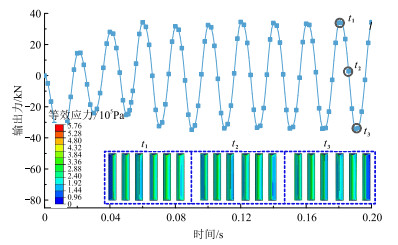
为研究横波可控震源振动器的输出强度,提取平板与大地之间沿水平方向的接触力——振动器的振动输出力(图 6)。受齿形结构的影响,平板与大地的接触面与水平方向存在夹角,其在水平方向的输出力仅为平板与大地接触力的一部分。图 6表明,平板与大地之间存在较明显的接触分布不均,同时由于最小接触压力为零,说明确有局部脱耦,可能引起平板与大地之间的冲击,产生“落重”脉冲,从而显著影响横波可控震源振动器激振性能及其能量传递特性。
|
图 6 振动器水平方向接触力曲线及接触压力分布 |
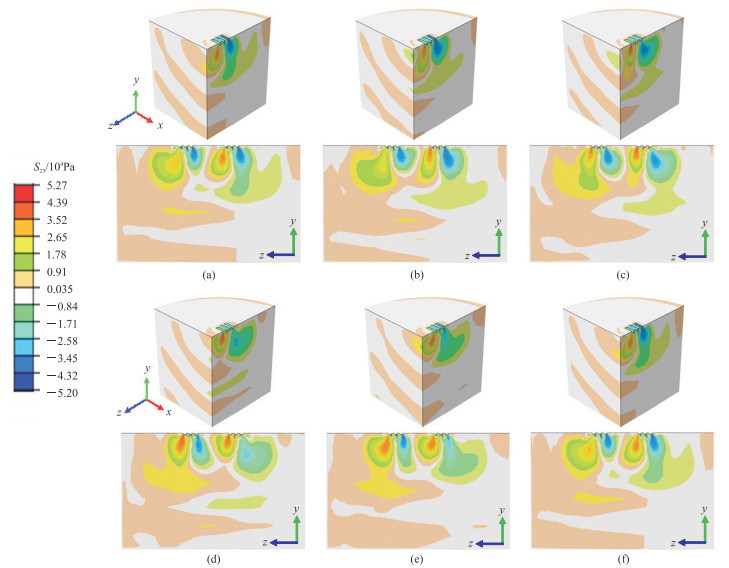
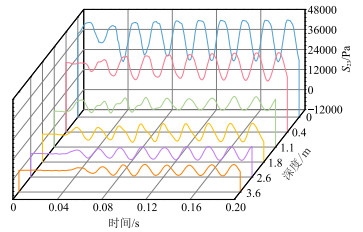
为分析横波可控震源振动器激发波的传播特性,提取大地模型的剪切应力云图(图 7)。可见:①高、低剪切应力区分别出现在平板—大地接触界面的两侧,伴随着振动器—大地耦合振动,高、低剪切应力区交替向大地模型底端传播。②在xOy平面内,由于激发波为SH波,波形较简单;在yOz平面内,激发波为SV波耦合纵波,因此波形更复杂。结合不同深度参考点剪切应力曲线(图 8)可知,振动器激发应力波的幅值随着传播深度的增加而降低,同时应力波曲线存在明显的波形畸变,畸变程度也随传播深度的增加而减弱。
|
图 7 大地模型剪切应力云图(S23为剪切应力) (a)t = 0.100 s;(b)t = 0.104 s;(c)t = 0.108 s;(d)t = 0.112 s;(e)t = 0.116 s;(f)t = 0.120 s |
|
图 8 不同深度参考点剪切应力曲线 |
工作过程中大地实际吸收能量决定了横波可控震源振动器激发地震波的传播深度。为进一步分析振动器—大地耦合振动系统的能量传递特性,计算了系统中各部分能量随动态加载时间的变化(图 9)。可见,系统的能量传递分为两个阶段:在第一阶段,外载荷做功迅速增加,同时土壤塑性变形造成的能量损失也迅速增加,但两者的增速存在差异,因此大地获得的有效能量先略微减小后增加;当系统的能量传递进入第二阶段后,外载荷做功以及塑性变形的能量耗散虽继续增加但增速放缓,振动器的输出与大地的消耗达到一种相对平衡的状态,因此该阶段大地获得的有效能量的变化量较小。此外,摩擦作用造成的能量损失在整个振动过程中也逐渐增大,但其能量耗散量远远小于塑性变形。此外,有效能量传递率表明,振动器输出能量的有效转化率随时间的增加先迅速增大后减小,但总体维持在一个较低的水平,系统的平均有效能量传递率不足10%。

|
图 9 耦合系统的能量传递特性 Ew为动态载荷做功,Ep为大地塑性变形造成的能量耗散,Ef为摩擦作用造成的能量耗散,Ee为大地获得的有效能量,η为有效能量传递率。 |
由上述分析可知,土壤塑性变形是造成能量耗散的主要原因,导致振动器的有效输出十分有限,系统的有效能量传递率很低。而增加振动器的工作时间,仅能增加振动器的总输出能量,无法明显提高大地获得的有效能量,也难以改善系统的有效能量利用率。
3 振动器—大地耦合振动影响机理分析 3.1 土壤类别的影响为模拟不同地表环境对振动器—大地耦合振动的影响机理,保持其他参数不变,选取松砂、紧砂、黏土等三种常见的土壤建立振动器—大地耦合振动模型,具体的材料参数如表 3所示。
|
|
表 3 不同土壤的材料参数 |
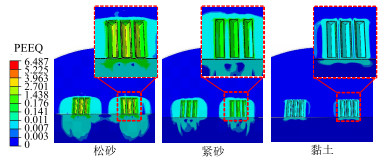
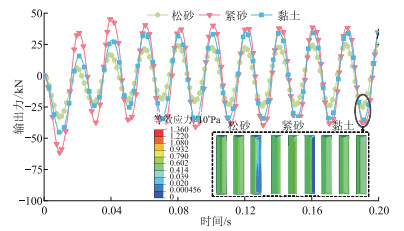
提取不同土壤的大地等效塑性应变云图(图 10),分析振动器在不同土壤环境的塑性变形情况。可见,砂土模型发生塑性变形的区域明显大于黏土模型,且砂土模型的最大等效塑性应变(6.4867)远大于黏土模型(0.1639),因此振动器在砂土环境工作时,平板与大地之间的挤压、剪切作用更易造成齿坑尺寸变大,进而影响振动器的输出精度。图 11为不同土壤的振动器接触力曲线。由图可知:①振动器在紧砂中输出力最大,在黏土中次之,在松砂中最小。②同一时刻振动器左侧平板与大地之间的接触压力分布云图表明,在砂土中平板—大地接触压力分布更不均匀,且不同砂土的不均匀程度也不一致,即振动器在紧砂和黏土中平板均会局部脱耦,但在紧砂中脱耦情况尤为严重。
|
图 10 不同土壤的大地等效塑性应变云图 |
|
图 11 不同土壤的振动器接触力曲线 |
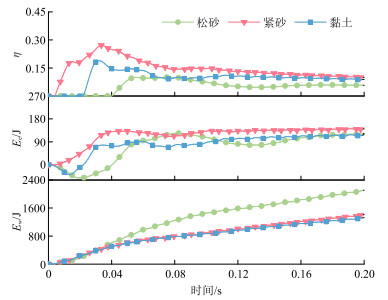
图 12为不同土壤的系统能量传递特性。由图可知:①在松砂中Ew最大,但相较而言,Ee却并未明显增加。②在紧砂或黏土中Ew相差无几,且前者的Ee略大于后者。③在松砂中耦合系统的η最低,在黏土中次之,在紧砂中最高。
|
图 12 不同土壤的系统能量传递特性 |
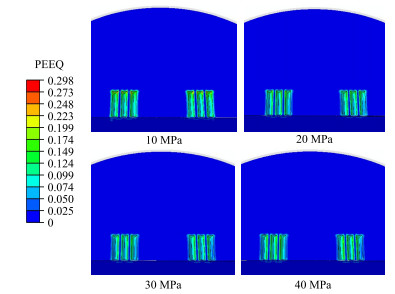
为研究土壤弹性模量对振动器—大地耦合振动响应的影响机理,保持其余参数不变,建立不同土壤弹性模量的振动器—大地耦合振动模型。图 13为不同弹性模量的大地等效塑性应变云图。由图可见,振动器在较大弹性模量的土壤中工作时,平板与大地接触界面的塑性变形更小,齿坑尺寸的变化幅度也更小。进一步提取不同弹性模量的振动器接触力曲线(图 14),可见:①振动器的输出力随着土壤弹性模量的增加而增大,但变化幅度减小。②同一时刻平板—大地接触压力分布云图表明,当土壤弹性模量分别为10、20、30、40 MPa时,最大接触压力分别为4.78×105、5.01×105、5.44×105、6.15×105 Pa,最小接触压力分别为2.52×102、1.89×102、0、0 Pa,因此随土壤弹性模量的增加,接触界面的最大接触压力增大、最小接触压力减小;当土壤弹性模量大于30 MPa时,接触界面的最小接触压力为0,说明平板与大地之间存在局部的接触脱耦。因此,土壤弹性模量的增加虽有助于提高振动器的输出强度,但过硬的土壤会造成平板脱耦,从而降低平板与大地的接触均匀性,进而影响振动器输出信号的精度。
|
图 13 不同弹性模量的大地等效塑性应变云图 |

|
图 14 不同弹性模量的振动器接触力曲线 |
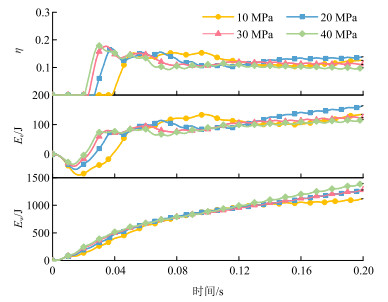
图 15为不同模量的系统能量传递特性。由图可知:①改变土壤的弹性模量对Ew的影响较小,Ew随土壤弹性模量的增加而略微增大。②Ee受土壤弹性模量的影响也较小,当t < 0.12 s时,Ee随土壤弹性模量的增加而略微减小;当t > 0.12 s、弹性模量为20 MPa时大地模型的Ee明显大于其他模型。③当土壤弹性模量分别为10、20、30、40 MPa时,η分别为9.78%、10.96%、10.62%、9.86%,因此在刚度适中的土壤中振动器的能量传递效果更好。
|
图 15 不同模量的系统能量传递特性 |
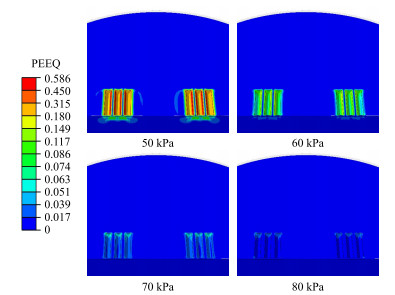
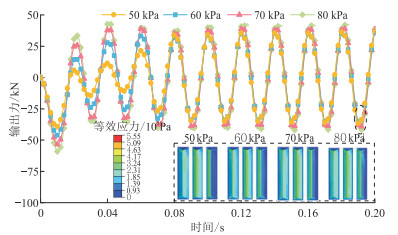
为探究土壤黏度对振动器—大地耦合振动响应的影响机理,保持其余参数不变,将土壤的黏聚力分别设置为50、60、70、80 kPa。图 16为不同土壤黏度的大地等效塑性应变云图。由图可见,耦合大地的最大等效塑性应变随土壤黏度的增加而显著降低,发生塑性变形的区域以及平板与大地之间齿坑尺寸的变化也明显减小,因此平板—大地相互作用更平稳、均匀。由不同土壤黏度的振动器接触力曲线(图 17)可知:①当土壤黏度取值为50、60、70、80 kPa时,最大接触压力分别为5.55×105、5.44×105、4.96×105、4.82×105 Pa,而最小接触压力均为0,说明接触界面的最大接触压力随土壤黏度的增加而减小,并且不同土壤黏度的平板均存在局部脱耦,但脱耦面积随黏度的增加而减小。②由于此时土壤弹性模量的取值均大于30 MPa,且平板均发生局部脱耦,说明土壤弹性模量才是决定平板是否脱耦的主控因素。③土壤黏度对振动器的输出强度影响不显著,整体而言,振动器的输出力随土壤黏度的增加而略微增大。
|
图 16 不同土壤黏度的大地等效塑性应变云图 |
|
图 17 不同土壤黏度的振动器接触力曲线 |
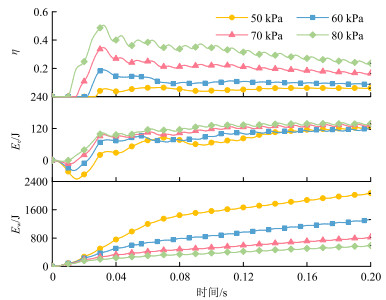
图 18为不同土壤黏度的系统能量传递特性。由图可知:①随土壤黏度的增加Ew显著减小、Ee、增大,因此η随土壤黏度的增加而明显增大。②当土壤黏度取值为50、60、70、80 kPa时,系统的η平均值分别为4.57%、9.68%、9.29%、30.44%,说明振动器在较大黏度的土壤中工作时,系统的能量利用率更高,有利于地震波向深层传播。
|
图 18 不同土壤黏度的系统能量传递特性 |
(1)由于不平衡力矩的存在,振动器两侧平板与大地的接触应力分布不对称;土壤的塑性变形会加剧平板与大地接触的不均匀性,造成平板与大地之间齿坑尺寸变大,引发平板局部脱耦。
(2)振动器激发剪切应力波的幅值随传播深度增加而降低,其谐波成分也随传播深度增加而逐渐耗散。
(3)横波可控震源振动器传递给大地的有效能量十分有限,导致耦合系统的有效能量传递率低,增加振动器工作时间也无法改善系统的能量转化情况,其平均能量传递率不足10%。
(4)不同土壤参数对振动器—大地耦合振动的影响各异,振动器在黏土中的激发效果更好,土壤弹性模量是振动器平板是否脱耦的主控因素,土壤黏聚力的增加能显著改善系统的能量传递特性。
综上所述,横波可控震源振动器的输出强度和精度还有待提高,在振动器的结构设计及优化过程中,应尽可能减小或消除不平衡力矩的影响,以增强平板与大地接触的均匀性。此外,通过优化平板齿结构(齿形、齿高、齿数等),可优化不同土壤参数的振动器响应特性,有助于在复杂勘探区推广、普及横波可控震源。
| [1] |
唐玮, 冯金德, 丁麟. 构建油气"双循环"发展格局的思考[J]. 石油科技论坛, 2020, 39(6): 13-17. TANG Wei, FENG Jinde, DING Lin. Thoughts on China's oil and gas "double-circulation" development pattern[J]. Petroleum Science and Technology Forum, 2020, 39(6): 13-17. |
| [2] |
王赟, 文鹏飞, 李宗杰, 等. 多分量油气地震勘探技术急需解决的几个问题[J]. 石油地球物理勘探, 2020, 55(6): 1395-1406. WANG Yun, WEN Pengfei, LI Zongjie, et al. Several urgent problems faced by muti-component seismic in oil and gas exploration[J]. Oil Geophysical Prospec-ting, 2020, 55(6): 1395-1406. |
| [3] |
苟量, 张少华, 李向阳. 提高横波勘探有效性引领物探技术创新[J]. 石油科技论坛, 2021, 40(4): 12-19. GOU Liang, ZHANG Shaohua, LI Xiangyang. Improving the effectiveness of shear-wave seismic exploration through geophysical technology innovation[J]. Petroleum Science and Technology Forum, 2021, 40(4): 12-19. DOI:10.3969/j.issn.1002-302x.2021.04.002 |
| [4] |
倪宇东, 王井富, 马涛, 等. 可控震源地震采集技术的进展[J]. 石油地球物理勘探, 2011, 46(3): 349-356. NI Yudong, WANG Jingfu, MA Tao, et al. Advances in vibroseis acquisition[J]. Oil Geophysical Prospec-ting, 2011, 46(3): 349-356. |
| [5] |
佟训乾, 林君, 姜弢, 等. 陆地可控震源发展综述[J]. 地球物理学进展, 2012, 27(5): 1912-1921. TONG Xunqian, LIN Jun, JIANG Tao, et al. Summary of development of land vibrator[J]. Progress in Geophysics, 2012, 27(5): 1912-1921. |
| [6] |
公亭, 王兆磊, 罗文山, 等. 横波源三维地震资料矢量横波四分量旋转和快慢波分离技术[J]. 石油地球物理勘探, 2022, 57(5): 1028-1034. GONG Ting, WANG Zhaolei, LUO Wenshan, et al. Four-component rotation and fast-slow wave separation techniques for 3D vector S-wave seismic data of S-wave sources[J]. Oil Geophysical Prospecting, 2022, 57(5): 1028-1034. |
| [7] |
张少华, 邓小江, 冯许魁, 等. 川南地区深层页岩气地球物理勘探技术新进展与攻关方向[J]. 石油地球物理勘探, 2023, 58(1): 238-248. ZHANG Shaohua, DENG Xiaojiang, FENG Xukui, et al. New progress and research direction of geophysical prospecting techniques for deep shale gas in southern Sichuan Basin[J]. Oil Geophysical Prospecting, 2023, 58(1): 238-248. |
| [8] |
王光德, 徐小刚. 横波可控震源应用浅析[J]. 物探装备, 2018, 28(3): 157-160. WANG Guangde, XU Xiaogang. Analysis of the application of shear-wave vibrator[J]. Equipment for Geophysical Prospecting, 2018, 28(3): 157-160. |
| [9] |
郝磊, 刘志刚, 黄玉峰, 等. 一种横波可控震源振动器结构及其性能分析[J]. 物探装备, 2021, 31(5): 311-313. HAO Lei, LIU Zhigang, HUANG Yufeng, et al. A kind of S-wave seismic vibrator shaker and its performance analysis[J]. Equipment for Geophysical Prospecting, 2021, 31(5): 311-313. |
| [10] |
CASTANET A, LAVERGNE M. Vibrator Contro-lling System: US, US3208550-A[P]. 1965-09-28.
|
| [11] |
SALLAS J J. Seismic vibrator control and the downgoing P-wave[J]. Geophysics, 1984, 49(6): 732-740. |
| [12] |
LEBEDEV A V, BERESNEV I A. Nonlinear distortion of signals radiated by vibroseis sources[J]. Geophysics, 2004, 69(4): 968-977. |
| [13] |
LEBEDEV A V, BERESNEV I A, VERMEER P L. Model parameters of the nonlinear stiffness of the vibrator-ground contact determined by inversion of vibrator accelerometer data[J]. Geophysics, 2006, 71(3): H25-H32. |
| [14] |
WEI Z. Modelling and modal analysis of seismic vibrator baseplate[J]. Geophysical Prospecting, 2010, 58(1): 19-31. |
| [15] |
黄志强, 李刚, 陶知非, 等. 可控震源振动器有限元模态分析与试验验证[J]. 工程设计学报, 2017, 24(5): 530-535. HUANG Zhiqiang, LI Gang, TAO Zhifei, et al. Finite element modal analysis and experimental verification of vibroseis vibrator[J]. Chinese Journal of Engineering Design, 2017, 24(5): 530-535. |
| [16] |
黄志强, 彭珣, 李刚. 可控震源振动器平板多频响应分析[J]. 工程设计学报, 2017, 24(6): 648-654. HUANG Zhiqiang, PENG Xun, LI Gang. Analysis of multi-frequency response of vibroseis vibrator baseplate[J]. Chinese Journal of Engineering Design, 2017, 24(6): 648-654. |
| [17] |
丁雅萍, 黄志强, 李刚. 基于有限元法的KZ-28型振动器平板结构优化与性能研究[J]. 机械设计与制造, 2016(11): 205-208. DING Yaping, HUANG Zhiqiang, LI Gang. Research on structure optimization on the performance of flat plate of KZ-28 type vibrator based on the finite element method[J]. Machinery Design & Manufacture, 2016(11): 205-208. |
| [18] |
DENG Z, LI C, CHEN G, et al. The application of pure shear wave seismic data for gas reservoir delineation[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2690-2694.
|
| [19] |
PENG X, HUANG Z, SUSANA L Q, et al. Nonlinear 3D finite element analysis of a shear-wave vibrator-ground interaction system[J]. Soil Dynamics and Earthquake Engineering, 2021. DOI:10.1016/j.soildyn.2020.106520 |
| [20] |
Kuhlemeyer R L, LYSMER J. Finite element method accuracy for wave propagation problems[J]. Journal of the Soil Mechanics and Foundation Division, 1973, 99(5): 421-427. |
| [21] |
肖晓春, 林皋, 迟世春. 桩—土—结构动力相互作用的分析模型与方法[J]. 世界地震工程, 2002, 18(4): 123-130. XIAO Xiaochun, LIN Gao, CHI Shichun. Analysis model and methods of pile-soil-structure dynamic inte- raction[J]. World Earthquake Engineering, 2002, 18(4): 123-130. |
| [22] |
NADERI-BOLDAJI M, ALIMARDANI R, HEMMAT A, et al. 3D finite element simulation of a single-tip horizontal penetrometer-soil interaction. Part Ⅰ: Deve-lopment of the model and evaluation of the model parameters[J]. Soil and Tillage Research, 2013, 134(11): 153-162. |
| [23] |
LUO C, YANG X, ZHAN C, et al. Nonlinear 3D finite element analysis of soil-pile-structure interaction system subjected to horizontal earthquake excitation[J]. Soil Dynamics and Earthquake Engineering, 2016, 84(5): 145-156. |
| [24] |
刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6): 46-51. LIU Jingbo, WANG Zhenyu, DU Xiuli, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J]. Engineering Mechanics, 2005, 22(6): 46-51. |
| [25] |
SUSANA L Q, JAIME P J, JUANA A T. Numerical modeling on vibroflotation soil improvement techniques using a densification constitutive law[J]. Soil Dynamics and Earthquake Engineering, 2014, 65(S1): 1-10. |



 彭珣, 四川省成都市新都区新都大道8号西南石油大学机电工程学院,610500。Email:
彭珣, 四川省成都市新都区新都大道8号西南石油大学机电工程学院,610500。Email: