2. 东北电力大学电气工程学院, 吉林吉林 132012;
3. 国网四川省电力公司资阳供电公司, 四川资阳 641300;
4. 中国石油勘探开发研究院西北分院, 甘肃兰州 730020;
5. 中山大学地球科学与工程学院, 广东广州 510275;
6. 吉林大学仪器科学与电气工程学院, 吉林长春 130026
2. College of Electrical Engineering, Northeast Electric Power University, Jilin, Jilin 132012, China;
3. Ziyang Electric Power Supply Company, State Grid Sichuan Electric Power Company, Ziyang, Sichuan 641300, China;
4. Research Institute of Petroleum Exploration & Development-Northwest, PetroChina, Lanzhou, Gansu 730020, China;
5. School of Earth Sciences and Engineering, SUN YAT-SEN University, Guangzhou, Guangdong 510275 China;
6. College of Instrumentation & Electrical Engineering, Jilin University, Changchun, Jilin 130026, China
分布式光纤声学传感(Distributed Optical Fiber Acoustic Sensing,DAS)是一种新型的地震资料采集技术,在VSP测量和微地震监测领域具有潜在应用前景[1]。区别于传统采集技术,DAS利用光纤中光散射信号的相位变化记录地震波场引起的应变信息,从而获得地震数据[2]。相较于电子检波器,DAS具有采集密度高、成本低和抗电磁干扰能力强等优势[3]。但是,DAS系统中微弱的光散射信号极易受到背景噪声的污染,导致接收信号畸变,严重影响地震记录质量[4]。DAS记录中的噪声主要以仪器噪声和采集噪声为主,包括衰落噪声、低频噪声、水平噪声和随机噪声等,且表现出较为复杂的特性。如何有效压制DAS资料噪声、提升记录质量,已成为地震资料处理领域研究热点之一[5]。
针对随机噪声消减问题,维纳滤波[6]、带通滤波、f-x反褶积[7]和中值滤波[8]等经典方法主要利用有效信号和背景噪声在物理特性或频带方面的差异实现信噪分离。但是上述方法通常是建立在一定先验假设基础上的,当实际噪声与先验假设存在差异时,去噪效果差[9]。以S变换[10]和时频峰值滤波[11]为代表的时频分析去噪方法利用信号和噪声在时频空间分布区域差异,结合合适的阈值函数,达到噪声成分的抑制和有效信号的恢复。类似地,小波变换[12]、曲波变换[13]、Seislet变换[14]和Shearlet变换[15]等基于稀疏变换的方法同样通过对含噪信号进行稀疏分解,结合有效信号和噪声的稀疏特征,选择合适的阈值函数,重构有效反射信息。但是,阈值函数的选取对于去噪效果影响极大,尤其是面对混叠噪声时,很难确定最优门限,无法有效重构反射信息[16]。此外,经验模态分解[17]和变分模态分解[18]等去噪方法可以将含噪信号分解为不同模态成分,结合信噪特征选择信号主导模态,完成地震信号恢复。但是,面对模态混叠问题[19],如何有效平衡信号恢复和噪声压制能力是需要进一步解决的关键问题之一。此外,以低秩矩阵分解[20]、奇异谱分析[21]、稳健主成分分析[5]和扩散滤波[22]等为代表的去噪方法也逐渐应用到实际地震数据去噪任务,但在处理性能方面仍有提升空间。上述方法虽然在传统地震噪声消减领域取得了效果,但是在面对低信噪比(Signal-to-Noise Ratio,SNR)、复杂地震资料时,去噪能力会明显下降。同时,由于缺乏对DAS噪声性质的可靠认知,目前仅有少量传统方法可用于DAS资料处理,代表性方法包括加权平均叠加[23]、线性滤波[24]和二维带通滤波[25]等,很难满足地震勘探的工业需求。因此,有必要开发智能消噪方法,持续提升DAS资料处理水平。
目前,基于深度学习的数据处理方法逐渐应用于地震资料处理领域[26-29]。相较于传统方法通过人工方式调节滤波参数,深度学习方法主要通过学习训练数据高维隐藏特征,自适应获得含噪数据和纯净记录之间的非线性映射关系,实现智能去噪[30]。针对地震勘探资料去噪问题,国内外研究人员进行了前期研究工作,前馈去噪卷积神经网络(Feed-forward Denoising Convolutional Neural Network, DnCNN)[31]和残差网络[32]等经典网络框架已经取得了成功应用。但是经典网络框架普遍结构比较简单,缺乏必要的信息交互和多尺度特征提取能力,在面对复杂的DAS噪声时,无法有效恢复被强光学噪声污染的弱上行反射信息[33]。后续提出的改进方法大致可以分为以下三类:一是与经典网络结合、改进的卷积神经网络(Convolutional Neural Network,CNN)去噪框架[34];二是自监督学习方法[35];三是基于生成对抗网络(Generative Adversarial Network,GAN)的去噪策略[33]。除此之外,陆续也有新的CNN去噪网络框架被提出及应用[36],取得了较传统网络方法更优的去噪结果。
上述人工智能方法无法充分利用DAS数据跨尺度的内在相关性,限制了对于精细特征的提取能力。本文提出了一种多尺度增强级联残差网络(Multiscale Enhanced Cascade Residual Network,MECRN),并将其应用到实际DAS资料处理。该网络引入一种基于空洞卷积的多尺度特征融合方案,对地震数据的不同尺度特征进行提取和组合,使得特征映射包含了原始数据更详细的信息,增强了网络对细节的恢复能力。另外结合浅层和深层特征的多尺度增强级联网络结构,能够促进特征和梯度的传播,避免了网络加深导致的浅层特征丢失问题。同时,MECRN采用双路径的增强残差结构,从给定的含噪资料中提取浅层信息,并通过多尺度残差块组实现多尺度特征提取,结合跳跃连接方式避免浅层信息丢失。在此基础上,通过残差学习方式整合全局和局部特征,提高重构特征的精度。合成数据和实际资料的去噪结果均表明,MECRN在压制DAS复杂背景噪声和恢复弱反射信号方面均取得了很好的效果。
1 MECRN的网络结构和去噪原理 1.1 MECRN的网络结构本文提出的MECRN基本结构如图 1所示。MECRN采用双路径的增强残差结构,分别通过级联结构和全局残差路径充分利用来自浅层的特征信息。其中级联机制不仅促进了特征和梯度的传播,还简化了模型训练。全局残差路径直接从原始含噪数据中捕获长距离空间特征,利用浅层特征提高去噪性能。

|
图 1 MECRN的网络结构 |
在MECRN中,上层支路利用多尺度残差块组实现地震记录特征的初步提取。多尺度残差块组由具有跳跃连接的多尺度特征提取块级联组成。堆叠多尺度特征提取块并在块间添加密集连接,保留了浅层特征的短期和长期记忆。每个多尺度特征提取块还包含四个空洞多尺度单元,结构如图 2a所示。空洞多尺度单元中利用了空洞卷积方式,结合具有不同扩张率(d)的并行卷积提取多尺度特征信息,在不改变特征图大小的同时扩大感受野,有效控制参数数量和计算成本。空洞多尺度单元将前段输入特征馈送到三个并行的空洞卷积中,以获取不同尺度的输出特征,进而将得到的输出特征一起发送到1×1卷积(Conv1×1)层,对不同尺度的特征进行整体压缩和融合,降低计算成本。在此基础上,再经过激活函数ReLU作用和普通3×3卷积(Conv3×3)压缩输出维度后,通过残差学习与并行卷积的输入特征融合,以此避免随网络加深造成浅层信息的丢失。

|
图 2 空洞多尺度单元(a)和多尺度特征融合模块(b)的网络结构 |
为了优化具有不同尺度的卷积模块中的稀疏局部特征,本文将多尺度特征融合模块用于直接提取初级特征,其输出通过长跳跃连接与多尺度残差块组的输出在重构块进行全特征融合。重构块通过残差学习和普通Conv3×3将全局特征和局部特征结合起来,将低频特征转化为高频特征,防止长期依赖问题。信息细化块通过四个级联的特征细化单元加一个卷积滤波器来细化特征,利用重构块提取的粗高频特征,学习更精确的高频特征,起到减小预测噪声与真实噪声之间差异的作用,并得到最终的去噪结果。
1.2 去噪原理本文使用MECRN压制DAS地震数据的背景噪声。地震数据
| $ \boldsymbol{y}=\boldsymbol{x}+\boldsymbol{n} $ | (1) |
MECRN的估计噪声与输入数据间的非线性映射关系可以表示为
| $ \widehat{\boldsymbol{n}}=R\left(\boldsymbol{y},\boldsymbol{\varTheta }\right) $ | (2) |
式中:Θ={w,b}为网络参数,其中w表示权重,b表示偏置;
| $ \widehat{\boldsymbol{x}}=\boldsymbol{y}-\widehat{\boldsymbol{n}} $ | (3) |
利用损失函数对网络参数进行优化训练。估计噪声与真实噪声之间的损失函数为
| $ L\left(\boldsymbol{\varTheta }\right)=\sum\limits_{i=1}^{K}{‖R({\boldsymbol{y}}_{i},\boldsymbol{\varTheta })-({\boldsymbol{x}}_{i}-{\boldsymbol{y}}_{i})‖}_{\mathrm{F}}^{2} $ | (4) |
式中:K为训练数据块数;
丰富且高质量的训练集可以增强有监督网络的学习能力,也可以提高数据处理的质量[37],训练集的真实性和完备性对网络的学习能力和去噪性能都有很大的影响。本文利用正演数据和实际勘探数据构建包含正演信号和实际噪声的高保真训练集。
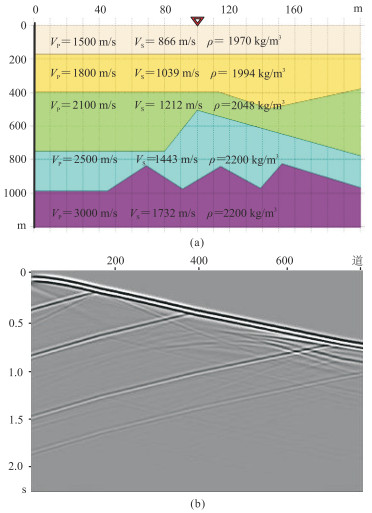
为保证正演数据的合理性,对实际DAS-VSP地震记录进行分析,构建二维地层模型(图 3a)。使用主频(15~120 Hz)变化的Ricker子波作为震源,利用弹性波方程模拟波场信息,获得用于构建信号训练集的模拟正演记录(图 3b)。为保证训练数据的泛化性,共模拟了200张不同地层结构下由不同主频激发得到的VSP记录,利用64×64的滑动窗截取模拟记录,共获得20000个信号片,构建了有效信号训练集。
|
图 3 地层模型(a)及其合成记录(b) 红三角表示震源位置,黑竖线表示接收井。 |
为了准确地估计DAS噪声、实现有效的噪声信号分离,有必要构造尽可能丰富的DAS噪声集训练MECRN。DAS噪声集主要是从无震源条件下获得的实际DAS-VSP噪声数据中提取。图 4为DAS噪声记录,包含的五种典型DAS噪声,包括随机噪声、水平噪声、衰落噪声、低频噪声和相干噪声。随机噪声是DAS数据中最常见的噪声,属于常规井下环境噪声干扰,可由机器运转、地下随机振动、电流干扰等原因产生。该类型噪声往往频带较宽、能量较强,在数据中分布较为均匀。水平噪声是由光学测量中耦合振动引起,大多由电子元件的潜在泄漏所产生,呈水平状分布,且频率较低。衰落噪声主要是由采集系统中后向散射光的破坏性干扰引起,包括干扰衰落和偏振衰落,通常表现为具有较高振幅的长周期噪声序列。低频噪声是由采集系统本身的硬件原因所致,该噪声主频相对较低、能量极强,在数据中表现为较大面积的黑色或白色区域,对DAS-VSP数据影响较大,尤其影响信号细节特征的恢复。相干噪声主要是因光纤与井壁耦合不好,在记录过程中由规则机械振动产生。与DAS信号集构建类似,利用64×64的滑动窗函数截取获得38625个64×64的DAS噪声片,经幅值归一化后得到DAS噪声训练集。图 5为典型信号片和噪声片。在此基础上,为保证MECRN的泛化能力,本文随机选择信号片和噪声片进行组合。将噪声片能量进行缩放后与信号片进行叠加,得到SNR随机分布在[-10 dB,0]范围内的含噪数据片,并与有效信号训练数据一起作为MECRN网络的输入,共同完成网络的训练。

|
图 4 DAS-VSP资料噪声记录 |

|
图 5 典型训练数据 (a)纯净信号片;(b)噪声片 |
本文使用软件平台为Matlab2017b,为满足网络训练需求,利用NVidia GeForce GTX 2026、CPU (Intel(R) Core(TM) i5-9400f和16-GB RAM组成硬件实验环境。在训练过程中,基于实验环境硬件条件,使用Adam优化器实现网络参数优化。另外,网络的初始学习率设置为1×10-3,随着迭代次数的增加逐渐降到1×10-5;批标准化大小设置为64。为了方便训练,对训练数据进行了归一化处理,训练周期设置为60。经过60个训练周期,损失函数也趋于稳定,选取性能最优模型用于处理模拟数据和实际DAS记录。
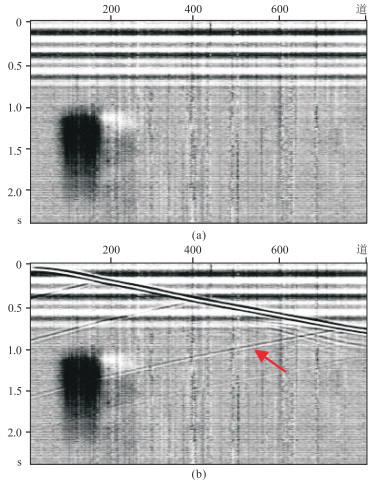
3 模拟数据处理结果分析为了验证MECRN网络的去噪性能,首先对模拟含噪DAS记录进行处理。对图 3b的模拟地震记录添加实际DAS噪声(图 6a),其中包括衰落噪声、水平噪声和时变光学噪声,获得SNR为-4 dB的含噪记录(图 6b)。由于强噪声的存在,反射信号被严重污染,特别是深层弱反射信息极难辨识(红色箭头所示)。
|
图 6 实际DAS噪声(a)及合成的含噪记录(b) |
为了准确反映MECRN网络的去噪性能,本文选用小波变换、带通滤波和DnCNN作为对比方法,对图 6b所示模拟含噪DAS数据进行处理,并对处理结果进行定性和定量分析。选择db4小波作为小波变换基函数,分解层数为15层,通过软阈值法实现噪声衰减。带通滤波频率范围设置为20~70 Hz,以实现信号的有效保留。DnCNN为20层网络结构,网络参数与参考文献[38]中一致。为保证去噪结果的客观性,DnCNN与MECRN使用相同的训练集和实验环境。
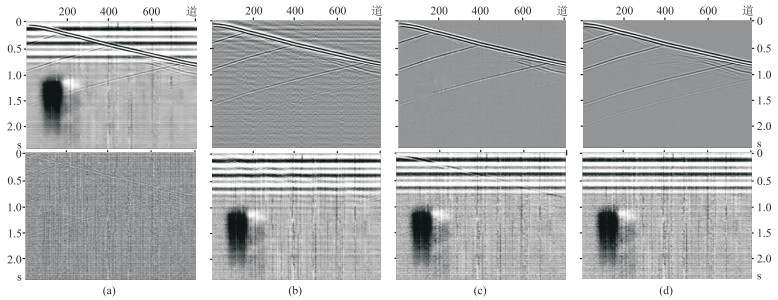
3.2 去噪结果比较利用MECRN和对比方法对模拟含噪DAS记录进行处理,去噪结果和滤除的噪声如图 7所示。小波变换法不能准确恢复出有效信号,对噪声压制效果不明显,只有部分高频噪声被滤掉(图 7a)。虽然带通滤波在一定程度上恢复了有效信号,但无法有效抑制同频噪声且有效信号失真(图 7b)。此外,这两种传统方法的滤除噪声中,具有明显信号成分残留。DnCNN和MECRN法对DAS噪声压制效果明显,恢复的有效反射同相轴清晰、连续,滤除的噪声同实际DAS噪声表现出相近的特征(图 7c、图 7d)。但是,DnCNN在压制DAS噪声的同时,对有效信号有损伤,去噪结果中仍有少量噪声残留(图 7c);MECRN表现出更强的去噪能力,恢复的同相轴更连续,去噪结果中无明显噪声残留(图 7d)。
|
图 7 四种方法的去噪结果(上)及滤除的噪声(下)对比 (a)小波变换;(b)带通滤波;(c)DnCNN;(d)MECRN |
合成含噪数据与四种方法去噪结果的局部放大对比如图 8所示。时变光学噪声导致反射同相轴受到严重污染(图 8a);小波变换法不能抑制强噪声干扰(图 8b);带通滤波虽然可以恢复同相轴信息,但噪声残留明显(图 8c);相较而言,DnCNN虽然可以有效抑制噪声,但是恢复的同相轴信息有明显缺失(图 8d);MECRN恢复的弱信号在连续性和清晰度方面都明显优于其他三种方法,并且噪声衰减更彻底(图 8e)。

|
图 8 四种方法的去噪结果局部放大对比 (a)含噪数据;(b)小波变换;(c)带通滤波;(d)DnCNN;(e)MECRN |
合成纯净记录及叠加噪声与四种方法去噪结果及去除的噪声的F-K谱的对比如图 9所示。首先,纯净信号和实际DAS背景噪声在频域存在明显混叠,消减难度较大(图 9a)。其次,如图 9b和图 9c所示,小波变换和带通滤波法不能有效去除混叠的DAS实际噪声,前者仅能滤除部分高频干扰,后者不能抑制通带内的噪声成分。相比来说,DnCNN和MECRN法可以有效实现混叠噪声的滤除,但是DnCNN结果中有明显噪声残留,MECRN恢复的信号同纯净信号最为接近(图 9d、图 9e),这也充分验证了MECRN法的有效性。

|
图 9 四种方法去噪结果(上)及滤除噪声(下)的F-K谱对比 (a)纯净记录(上)及叠加的噪声(下);(b)小波变换;(c)带通滤波;(d)DnCNN;(e)MECRN |
本文主要利用SNR和均方根误差(RMSE)对不同方法去噪结果进行量化分析。SNR用于表征噪声衰减能力,而RMSE侧重于反映信号保持能力。SNR和RMSE定义为
| $ \mathrm{S}\mathrm{N}\mathrm{R}=10\mathrm{ }\mathrm{l}\mathrm{g}\frac{\sum\limits_{i=1}^{M}\sum\limits_{j=1}^{N}{x}^{2}(i,j)}{\sum\limits_{i=1}^{M}\sum\limits_{j=1}^{N}{\left[\widehat{x}(i,j)-x(i,j)\right]}^{2}} $ | (5) |
| $ \mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{NM}\sum\limits_{i=1}^{M}\sum\limits_{j=1}^{N}{\left[\widehat{x}(i,j)-x(i,j)\right]}^{2}} $ | (6) |
式中:x为纯净信号;
应用四种方法对不同SNR的含噪记录进行处理,去噪结果的SNR和RMSE统计如表 1所示。以去噪前SNR为-2 dB的数据为例,MECRN法处理结果的SNR为20.97 dB,提升了约22 dB;DnCNN法处理结果的SNR为15.04 dB,提升约17 dB,表明MECRN法可以在提升弱反射信号的同时有效压制复杂DAS背景噪声,且去噪能力更强。
|
|
表 1 不同SNR数据四种方法去噪结果的SNR和RMSE统计 |
A井实际DAS-VSP记录(图 10)采集于中国东北地区,共由1372道记录组成,采样频率为2500 Hz。记录中噪声类型多样且性质复杂,如衰落噪声(黄色箭头所示)、水平噪声(红色箭头所示)、时变光学噪声(绿色箭头所示)和耦合噪声(蓝色箭头所示),严重影响了有效信息的提取。分别应用小波变换、带通滤波、DnCNN和MECRN法对实际DAS记录进行处理,结果如图 11所示。小波变换、带通滤波选取与合成记录处理时相同的滤波参数。由于无法利用实际记录构建信号训练集,DnCNN和MECRN则使用最优合成记录处理模型。

|
图 10 A井实际DAS-VSP记录 |

|
图 11 A井实际DAS-VSP数据四种方法去噪结果(上)及去除的噪声(下)对比 (a)小波变换;(b)带通滤波;(c)DnCNN;(d)MECRN |
小波变换法无法有效抑制DAS-VSP记录中的复杂噪声,去噪记录的反射信息并未得到有效恢复(图 11a)。带通滤波法虽然表现出一定的噪声消减能力,但去噪结果中仍然残留部分噪声,信号表现出过度平滑的特征,频率成分出现变化(图 11b)。由图 11c和图 11d可以发现:深度学习方法可以取得较传统方法更好的处理结果,与合成记录处理结果可相互验证;DnCNN对于衰落噪声抑制能力较弱,去噪结果中存在大量衰落噪声残留(红色箭头所示);MECRN可以更有效地抑制时变光学噪声,准确地恢复受噪声污染的弱反射信息(绿色方框所示)。
A井原始DAS-VSP记录及四种方法去噪结果的局部放大对比如图 12所示,可以看到:小波变换法处理之后,有效信号依然被强时变光学噪声掩盖(图 12b);带通滤波无法有效抑制同频噪声且恢复的有效信号存在频带展宽现象(图 12c);DnCNN法整体上对噪声压制效果良好,但针对光学噪声污染的弱同相轴信息恢复不佳,且在处理结果中还残留有部分光学噪声(图 12d);MECRN法处理结果中噪声得到了更彻底的压制,恢复的有效信号更加光滑、连续,同时还可重构出其他传统方法无法恢复的弱反射信息(图 12e)。

|
图 12 A井实际DAS-VSP数据与四种方法去噪结果的局部放大对比 (a)原始数据;(b)小波变换;(c)带通滤波;(d)DnCNN;(e)MECRN |
为验证模型的泛化能力,对不同工区B井的DAS-VSP数据(图 13)进行处理,结果如图 14所示。小波变换未能恢复隐藏在时变光学噪声中的反射同相轴信息(图 14a);同样,带通滤波的去噪能力表现出一定的局限性,无法重构弱反射信号(图 14b)。尽管DnCNN可以提供更好的去噪性能,但仍然可以直观地观察到残余噪声(图 14c)。相较而言,MECRN表现出了较好的去噪效果,在微弱信号恢复方面明显优于其他方法,恢复的同相轴更清晰、更连续(图 14d)。

|
图 13 B井实际DAS-VSP记录 |

|
图 14 B井实际DAS-VSP数据四种方法去噪结果(上)及去除的噪声(下)对比 (a)小波变换;(b)带通滤波;(c)DnCNN;(d)MECRN |
实验结果表明,在MECRN处理低SNR实际DAS记录时,仍然能够获得高精度的处理结果,拥有较强的去噪能力,验证了本文网络在去噪性能和信号恢复能力方面的优势,能满足DAS-VSP数据处理的要求。
5 结论针对实际DAS-VSP记录SNR低、噪声种类复杂且污染严重的问题,本文提出了一种基于多尺度的增强级联残差网络(MECRN)压制DAS地震数据中的背景噪声。MECRN采用双路径的增强残差结构,通过两种路径同时从给定的噪声图像中提取浅层信息,融合不同路径预测结果。此外,引入空洞卷积和多尺度模块提取不同尺度和级别的特征,并通过跳跃连接将浅层特征融入后续相邻块组,整合前期模块获取的特征,避免了浅层信息丢失。最后通过残差学习整合全局和局部特征,并对重建的特征细化,重构出高质量VSP数据。
为了证明网络的有效性,利用MECRN对合成含噪数据和实际DAS记录进行处理,并与传统方法和其他深度学习方法进行对比,结果表明MECRN可以有效抑制复杂DAS数据的背景噪声,恢复受噪声污染的弱反射信息,SNR提升超过了22 dB。因此,MECRN在DAS资料处理领域具有一定的应用前景,也可为后续高效消噪网络设计提供必要参考。
| [1] |
蔡志东. 井中地震技术: 连接多种油气勘探方法的桥梁[J]. 石油地球物理勘探, 2021, 56(4): 922-934. CAI Zhidong. Borehole seismic: A bridge connecting multiple oil and gas exploration methods[J]. Oil Geophysical Prospecting, 2021, 56(4): 922-934. |
| [2] |
EGOROV A, CORREA J, BÓNA A, et al. Elastic full-waveform inversion of vertical seismic profile data acquired with distributed acoustic sensors[J]. Geophysics, 2018, 83(3): R273-R281. DOI:10.1190/geo2017-0718.1 |
| [3] |
VERDON J P, HORNE S A, CLARKE A, et al. Microseismic monitoring using a fibre-optic distributed acoustic sensor (DAS) array[J]. Geophysics, 2020, 85(3): KS89-KS99. |
| [4] |
林融冰, 曾祥方, 宋政宏, 等. 分布式光纤声波传感系统在近地表成像中的应用Ⅱ: 背景噪声成像[J]. 地球物理学报, 2020, 63(4): 1622-1629. LIN Rongbing, ZENG Xiangfang, SONG Zhenghong, et al. Distributed acoustic sensing for imaging shallow structure Ⅱ: Ambient noise tomography[J]. Chinese Journal of Geophysics, 2020, 63(4): 1622-1629. |
| [5] |
DONG X, ZHONG T, LI Y. New suppression technology for low-frequency noise in desert region: The improved robust principal component analysis based on prediction of neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(7): 4680-4690. DOI:10.1109/TGRS.2020.2966054 |
| [6] |
MENDEL J. White-noise estimators for seismic data processing in oil exploration[J]. IEEE Transactions on Automatic Control, 1977, 22(5): 694-706. DOI:10.1109/TAC.1977.1101597 |
| [7] |
CHEN K, SACCHI M D. Robust F-x projection filtering for simultaneous random and erratic seismic noise attenuation[J]. Geophysical Prospecting, 2017, 65(3): 650-668. DOI:10.1111/1365-2478.12429 |
| [8] |
CHEN Y, ZU S, WANG Y, et al. Deblending of simultaneous source data using a structure oriented space-varying median filter[J]. Geophysical Journal International, 2020, 222(3): 1805-1823. DOI:10.1093/gji/ggaa189 |
| [9] |
LIU G, CHEN X. Noncausal F-x-y regularized nonstationary prediction filtering for random noise attenuation on 3D seismic data[J]. Journal of Applied Geophysics, 2013, 93: 60-66. DOI:10.1016/j.jappgeo.2013.03.007 |
| [10] |
PINNEGAR C R, EATON D W. Application of the S transform to prestack noise attenuation filtering[J]. Journal of Geophysical Research, 2003, 108(B9): 369-378. |
| [11] |
TIAN Y A, LI Y, YANG B J. Variable-eccentricity hyperbolic-trace TFPF for seismic random noise attenuation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6449-6458. DOI:10.1109/TGRS.2013.2296603 |
| [12] |
武国宁, 于萌萌, 王君仙, 等. 应用平稳小波变换与深度残差网络压制地震随机噪声[J]. 石油地球物理勘探, 2022, 57(1): 43-51. WU Guoning, YU Mengmeng, WANG Junxian, et al. Seismic random noise attenuation based on stationary wavelet transform and deep residual neural network[J]. Oil Geophysical Prospecting, 2022, 57(1): 43-51. |
| [13] |
ZHAO X, LI Y, ZHUANG G H, et al. 2-D TFPF based on contourlet transform for seismic random noise attenuation[J]. Journal of Applied Geophysics, 2016, 129: 158-166. DOI:10.1016/j.jappgeo.2016.03.030 |
| [14] |
DONG X T, JIANG H, ZHENG S, et al. Signal-to-noise ratio enhancement for 3C downhole microseismic data based on the 3D shearlet transform and improved backpropagation neural networks[J]. Geophysics, 2019, 84(4): V245-V254. DOI:10.1190/geo2018-0621.1 |
| [15] |
童思友, 高航, 刘锐. 基于Shearlet变换的自适应地震资料随机噪声压制[J]. 石油地球物理勘探, 2019, 54(4): 744-750. TONG Siyou, GAO Hang, LIU Rui. Seismic random noise adaptive suppression based on the Shearlet transform[J]. Oil Geophysical Prospecting, 2019, 54(4): 744-750. DOI:10.13810/j.cnki.issn.1000-7210.2019.04.003 |
| [16] |
KUTYNIOK G, LEMVIG J, LIM W Q. Optimally sparse approximations of 3D functions by compactly supported Shearlet frames[J]. SIAM Journal on Mathematical Analysis, 2012, 44(4): 2962-3017. DOI:10.1137/110844726 |
| [17] |
AMEZQUITA SANCHEZ J P, CHAVEZ ALEGRIA O, VALTIERRA RODRIGUEZ M, et al. Detection of ULF geomagnetic anomalies associated to seismic activity using EMD method and fractal dimension theory[J]. IEEE Latin America Transactions, 2017, 15(2): 197-205. DOI:10.1109/TLA.2017.7854612 |
| [18] |
YU S, MA J. Complex variational mode decomposition for slop-preserving denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 586-597. DOI:10.1109/TGRS.2017.2751642 |
| [19] |
BUSTOS A, RUBIO H, CASTEJÓN C, et al. EMD-based methodology for the identification of a high-speed train running in a gear operating state[J]. Sensors, 2018, 18(3): 793-800. DOI:10.3390/s18030793 |
| [20] |
LIU X, CHEN X, LI J, et al. Nonlocal weighted robust principal component analysis for seismic noise attenuation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(2): 1745-1756. DOI:10.1109/TGRS.2020.2996686 |
| [21] |
董烈乾, 张慕刚, 骆飞, 等. 应用SVD约束的迭代反演混叠噪声压制方法[J]. 石油地球物理勘探, 2021, 56(1): 57-61, 117. DONG Lieqian, ZHANG Mugang, LUO Fei, et al. Blended noise suppression based on SVD constrained iterative inversion[J]. Oil Geophysical Prospecting, 2021, 56(1): 57-61, 117. DOI:10.13810/j.cnki.issn.1000-7210.2021.01.006 |
| [22] |
严哲, 顾汉明, 蔡成国. 基于各向异性扩散滤波的地震图像增强处理[J]. 石油地球物理勘探, 2013, 48(3): 390-394. YAN Zhe, GU Hanming, CAI Chengguo. Seismic image enhancement based on anisotropic diffusion[J]. Oil Geophysical Prospecting, 2013, 48(3): 390-394. DOI:10.13810/j.cnki.issn.1000-7210.2013.03.009 |
| [23] |
YU G, CAI Z, CHEN Y, et al. Borehole seismic survey using multimode optical fibers in a hybrid wireline[J]. Measurement, 2018, 125: 694-703. DOI:10.1016/j.measurement.2018.04.058 |
| [24] |
SOTO M A, RAMÍREZ J A, THÉVENAZ L. Intensifying the response of distributed optical fibre sensors using 2D and 3D image restoration[J]. Nature Communications, 2016, 7(1): 10870. DOI:10.1038/ncomms10870 |
| [25] |
MARTINS H F, FERNÁNDEZ-RUIZ M R, COSTA L, et al. Monitoring of remote seismic events in metropolitan area fibers using distributed acoustic sensing (DAS) and spatiotemporal signal processing[C]. Optical Fiber Communication Conference and Exhibition (OFC), 2019, 1-3.
|
| [26] |
HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 |
| [27] |
ARUN P V, BUDDHIRAJU K M, PORWAL A, et al. CNN-based super-resolution of hyperspectral ima-ges[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6106-6121. DOI:10.1109/TGRS.2020.2973370 |
| [28] |
YU D, HINTON G, MORGAN N, et al. Introduction to the special section on deep learning for speech and language processing[J]. IEEE Transactions on Audio, Speech and Language Processing, 2012, 20(1): 4-6. DOI:10.1109/TASL.2011.2173371 |
| [29] |
JING Y, YANG Y, FENG Z, et al. Neural style transfer: A review[J]. IEEE Transactions on Visualization and Computer Graphics, 2020, 26(11): 3365-3385. DOI:10.1109/TVCG.2019.2921336 |
| [30] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [31] |
ZHANG K, ZUO W M, CHEN Y J, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
| [32] |
MA H, YAO H, LI Y, et al. Deep residual encoder-decoder networks for desert seismic noise suppression[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(3): 529-533. DOI:10.1109/LGRS.2019.2925062 |
| [33] |
DONG X, LI Y. Denoising the optical fiber seismic data by using convolutional adversarial network based on loss balance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(12): 10544-10554. |
| [34] |
FENG Q, LI Y. Denoising deep learning network based on singular spectrum analysis: DAS seismic data denoising with multichannel SVDDCNN[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5902911. |
| [35] |
VAN DEN ENDE M, LIOR I, AMPUERO J P, et al. A self-supervised deep learning approach for blind denoising and waveform coherence enhancement in distributed acoustic sensing data[J]. IEEE Transaction on Neural Networks and Learning Systems, 2023, 34(7): 3371-3384. |
| [36] |
ZHAO Y X, LI Y, WU N. Distributed acoustic sensing vertical seismic profile data denoiser based on convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-11. |
| [37] |
董新桐, 钟铁, 王洪洲, 等. 基于卷积对抗降噪网络的塔里木盆地沙漠地震资料消噪方法研究[J]. 地球物理学报, 2022, 65(7): 2661-2672. DONG Xintong, ZHONG Tie, WANG Hongzhou, et al. The denoising of desert seismic data acquired from Tarim basin based on convolutional adversarial denoising network[J]. Chinese Journal of Geophysics, 2022, 65(7): 2661-2672. |
| [38] |
ZHAO Y, LI Y, DONG X, et al. Low-frequency noise suppression method based on improved DnCNN in desert seismic data[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(5): 811-815. |



 董士琦, 吉林省吉林市船营区长春路169号东北电力大学电气工程学院通信工程系,132012。Email:
董士琦, 吉林省吉林市船营区长春路169号东北电力大学电气工程学院通信工程系,132012。Email: