0 引言

高分辨率的成像结果是后续地震资料解释、储层预测的基础。相比于常规的偏移方法，最小二乘偏移(Least Square Migration，LSM)法通过迭代反演的方式，可以较好地估计宽带反射系数而广泛应用于高分辨率成像^[1-3]，然而以数据拟合的方式迭代成像计算量较大，且在初始模型不准确或者数据质量差时迭代不收敛。

在LSM目标函数中，模型的二阶导数相对应的反演成像系统的Hessian矩阵包含了限制成像分辨率提高的多种因素，如带限子波、波场传播过程中的振幅衰减和观测系统的照明等^[4]。在理论上，消除Hessian矩阵的模糊效应是高分辨率LSM成像的关键。众多学者发展了非迭代的真振幅成像方法进行Hessian矩阵模糊效应的部分补偿^[5-7]。相比于数据域迭代的LSM法, 这些方法不存在不收敛的问题，且在照明补偿方面是十分有效的^[8-9]。Liu等^[10]利用局部支撑的点扩散函数(Point Spread Function，PSF)构造Hessian矩阵，通过基于PSF的照明补偿进行了像域的真振幅成像处理，补偿成像结果的振幅均匀性和分辨率都有所提高。然而，由子波引起的模糊效应并没有彻底消除，非迭代的真振幅成像仍然无法实现频带有效扩展的高分辨成像。

反褶积是一种通过压缩子波提高地震数据的时间分辨率的重要方法。在子波最小相位、子波时不变和噪声随机的假设条件下，经典的反褶积方法广泛应用于叠前、叠后地震数据的提高分辨率处理^[11]。为了克服最小相位的假设条件的缺陷, Oppenheim等^[12]最早进行了同态反褶积方法的研究；Rosa等^[13]首次将该方法应用于地震勘探领域的数据处理。然而，同态反褶积方法因为相位展开而导致其不稳定。最小熵反褶积(Minimum Entropy Deconvolution，MED)算法是另一种用于克服最小相位的假设条件的缺陷的方法，同时也是稀疏约束准则的首次应用^[14]。Gray^[15]假设反射系数具有稀疏性，提出了变量范数约束反褶积方法。针对子波时不变假设，Canadas^[16]提出了一种盲反褶积策略，可以同时反演反射系数与子波，这在一定程度上弥补了子波时变的不足。Zhang等^[17]利用改进的Cauchy分布进行盲反褶积，并且采用交替迭代的求解策略得到反射系数和混合相位子波。康治梁等^[18]在压缩感知框架下引入L_1/2范数进行稀疏约束反褶积。Wang等^[19]提出了基于Toeplitz稀疏矩阵分解的盲反褶积方法，将反射系数估计问题分解成为子波与反射系数的串联反演，可以较好地克服反褶积方法对初始子波的依赖性。在此基础上，Sui等^[20]将基于Toeplitz稀疏矩阵分解的反褶积扩展为具有非弹性衰减的非平稳稀疏脉冲反褶积。江雨濛等^[21]基于广义S变换，提出了子波时变盲反褶积方法。这些发展的反褶积方法，在一定程度上可以弥补经典反褶积方法的理论假设条件的不足，提高成像剖面的分辨率。然而，反褶积效果仍受子波的估计误差、噪声等影响。

一般来说，非迭代的保真成像结果经过较好的照明补偿，在一定程度上消除了子波的影响。基于此的反褶积处理通过压缩子波进行子波整形，提高了分辨率，这与经典褶积模型描述的正问题并不是严格对应的。从图像处理的角度看，反褶积前、后成像结果之间的关系隐含在带限子波与宽频理想子波之间，即常规的保真成像结果是带限子波与反射系数的褶积，而高分辨成像结果是理想宽频子波与反射系数的褶积。

深度学习在图像处理方面具有良好的性能和更高的效率。卷积神经网络(Convolutional Neural Network，CNN)常常用于挖掘隐藏在数据集之间的关系。经过良好训练的CNN往往无需人为调整参数，减轻了频繁的人机交互的负担。近年来，基于CNN学习类算法也广泛应用于地震数据处理，如插值、去噪、波阻抗反演、断层识别、全波形反演等。Chai等^[22]利用CNN进行反褶积，认为反褶积方法需要一个比较精确的初始子波。Gao等^[23]基于广义的褶积模型，利用深度学习技术对地震资料进行反褶积处理，在一定程度上提高了地震资料的垂向分辨率。黄颜茹等^[24]利用深度学习技术估计地震子波。Avila等^[25]利用多种网络在理论模型上进行了反褶积处理，认为U-Net比传统方法相对更高效。Liu等^[26]提出了一种基于CNN的点扩散函数反褶积方法，利用深度学习技术模拟基于Hessian滤波LSM法的偏移反褶积过程，并通过数值实验和实际数据验证了其有效性和优越性。

为了有效拓宽常规偏移结果的波数带，实现高分辨处理，本文首先从LSM反演成像的角度出发，对影响成像分辨率的重要因素进行了分析，指出Hessian矩阵中的观测系统照明和子波是影响成像精度的重要因素；然后从图像处理的角度指出反褶积的目标应当是具有宽频带的反射系数，然而常规偏移成像结果与地下宽带反射系数之间具强非线性关系，因此利用CNN对二者进行映射，同时引入宽频子波构建标签，发展基于卷积神经网络的子波整形反褶积方法；针对反褶积中初始子波估计不准确的问题，设计了子波和与反射系数串联、迭代、更新的实现方案；最后应用本文方法对层状模型资料和实际数据进行处理，两者结果均表明了该方法能够较好地压缩子波，可实现稳健宽频处理，获得宽带反射系数。

1 方法原理 1.1 地震资料成像分辨率分析

地震勘探的目的是利用观测的地震资料估计地下结构和其对应的模型参数。在Born近似假设下，地震记录与地下模型之间的关系表示为

$ \boldsymbol{d}=\boldsymbol{L}\boldsymbol{R} $

(1)

式中：$ \boldsymbol{d} $表示一阶地震反射波记录；$ \boldsymbol{R} $表示地下反射系数模型；$ \boldsymbol{L} $表示Born正演算子。给定地震观测数据估计反射系数模型是一个典型的地震反问题，可以通过如下目标泛函求解

$ J=\frac{1}{2}{‖\boldsymbol{d}-{\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}}‖}_{2}^{2} $

(2)

式中 $ {\boldsymbol{d}}_{\mathrm{o}\mathrm{b}\mathrm{s}} $为观测的地震反射数据。此目标泛函关于地下反射系数模型的一阶偏导为梯度。令目标函数的梯度为零，可得到其法线方程

$ {\boldsymbol{L}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{R}={\boldsymbol{L}}^{\mathrm{T}}\boldsymbol{d} $

(3)

式中：$ {\boldsymbol{L}}^{\mathrm{T}}\boldsymbol{d} $即为常规偏移结果，将其记为$ \boldsymbol{I} $；$ {\boldsymbol{L}}^{\mathrm{T}}\boldsymbol{L} $为Hessian算子，记为$ \boldsymbol{H} $。上述方程可以写为

$ \boldsymbol{I}=\boldsymbol{H}\boldsymbol{R} $

(4)

综上所述，常规偏移结果为真实反射系数经过Hessian算子滤波后的结果。Hessian算子也叫做模糊算子，它包含了观测系统、传播和子波等因素给真反射系数带来的模糊作用。梯度引导下的LSM可以修正上述Hessian算子引起的各种模糊效应并完成宽带反射系数估计。然而，实际应用中子波因素很难完全消除，即成像结果还是受子波频带限制。

1.2 成像域稀疏脉冲盲反褶积

基于图像反褶积理论，照明补偿后的成像结果可以表示为反射系数与子波褶积的结果，即

$ \boldsymbol{I}=\boldsymbol{R}\otimes \boldsymbol{S} $

(5)

式中：$ \boldsymbol{S} $为子波；$ \otimes $表示褶积运算。

在假设反射系数为高斯白噪、子波为最小相位的条件下，上述褶积模型对应的反问题的目标函数为

$ J=\underset{\boldsymbol{S},\boldsymbol{R}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{n}}\frac{1}{2}\left|\right|\boldsymbol{I}-\boldsymbol{S}\otimes \boldsymbol{R}|{|}_{2}^{2} $

(6)

由于子波与反射系数都是未知的，直接求解上式比较困难。为此，可以采用迭代优化方法求解，交替地估计子波和反射系数，即

$ {R}_{k+1}=\underset{\boldsymbol{R}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{n}}\frac{1}{2}\left|\right|\boldsymbol{I}-{S}_{k}\otimes \boldsymbol{R}|{|}_{2}^{2} $

(7)

$ {S}_{k+1}=\underset{\boldsymbol{S}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{n}}\frac{1}{2}\left|\right|\boldsymbol{I}-\boldsymbol{S}\otimes {R}_{\boldsymbol{k}+1}|{|}_{2}^{2} $

(8)

式中：$ {S}_{0} $为初始子波，可通过对振幅谱平均值的反傅里叶变换粗略估计；$ {R}_{k} $和 $ {S}_{k} $分别表示第 $ k $次迭代得到的反射系数和地震子波的估计值。

1.3 基于卷积神经网络的子波整形反褶积

CNN作为深度学习中具有代表性意义的网络，由于其强大的特征提取能力以及非线性特征映射能力，在地球物理领域得到了广泛的应用。

本文从图像处理角度引入深度学习技术，利用宽频子波构建宽频样本集，完成常规成像结果与地下模型之间的非线性映射，实现基于CNN的子波整形反褶积。反褶积过程包括训练和测试两个阶段，具体流程如图 1所示。

1.3.1 训练阶段

首先，利用已知模型构建训练集，通过最小化网络输入与标签之间的损失函数获得初始网络$ F({\boldsymbol{I}}^{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}};{\boldsymbol{\theta }}_{0}) $及初始网络参数 $ {\boldsymbol{\theta }}_{0} $，其表达式为

$ F({\boldsymbol{I}}^{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}},{\boldsymbol{R}}^{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}};{\boldsymbol{\theta }}_{0})=\left[{\boldsymbol{I}}^{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}\stackrel{\mathrm{映}\mathrm{射}}{\to }{\boldsymbol{R}}^{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}\right] $

(9)

$ {\boldsymbol{I}}^{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}=\boldsymbol{M}\otimes {S}_{0} $

(10)

式中 $ \boldsymbol{M} $为已知模型反射系数，将其与 $ {S}_{0} $的褶积结果 $ {\boldsymbol{I}}^{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}} $作为输入并对标签数据进行匹配。标签 $ {\boldsymbol{R}}^{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}} $由宽频子波和 $ \boldsymbol{M} $褶积获得。

将靶区数据的成像结果 $ {\boldsymbol{I}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}} $作为初始网络的输入，可以初步估计靶区数据宽带反射系数 $ {\boldsymbol{R}}^{\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}} $，即

$ {\boldsymbol{R}}^{\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}=F({\boldsymbol{I}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}};{\boldsymbol{\theta }}_{0}) $

(11)

据此可以进行子波更新，如

$ {S}_{k+1}=\underset{\boldsymbol{S}}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{n}}\frac{1}{2}\left|\right|{\boldsymbol{I}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}-{S}_{k}\otimes {\boldsymbol{R}}^{\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}}|{|}_{2}^{2}+{\lambda }_{2}|\left|{S}_{k}\right|{|}_{2}^{2} $

(12)

式中：$ {S}_{k} $为第 $ k $次估计得到的子波；$ {\lambda }_{2} $为加权系数。利用更新后的子波 $ {S}_{k+1} $，重复式(9)、式(11)和式(12)串联迭代子波和反射系数。

损失函数是衡量模型预测结果与真实标签之间的差异的函数。损失函数的值越小，说明模型的预测能力越强，反之则越弱。本文采用均方差(Mean Squared Error，MSE)损失作为评价参数，即

$ {L}_{\mathrm{M}\mathrm{S}\mathrm{E}}=\frac{1}{N}\sum\limits_{i=1}^{N}({\boldsymbol{y}}_{\boldsymbol{i}}-{\widehat{\boldsymbol{y}}}_{\boldsymbol{i}}{)}^{2} $

(13)

式中：$ {\boldsymbol{y}}_{\boldsymbol{i}} $为真实值；$ {\widehat{\boldsymbol{y}}}_{\boldsymbol{i}} $为模型输出；N为样本的数量。$ {L}_{\mathrm{M}\mathrm{S}\mathrm{E}} $的最小值为0（当预测等于真实值时），最大值为无穷大。本文通过Adam优化器最小化 $ {L}_{\mathrm{M}\mathrm{S}\mathrm{E}} $对参数进行优化，具体损失函数为

$ {L}_{\mathrm{M}\mathrm{S}\mathrm{E}}=\frac{1}{N}\sum\limits_{i=1}^{N}{‖F({\boldsymbol{I}}_{i}^{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}};\boldsymbol{\theta })-{\boldsymbol{R}}_{{}^{i}}^{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}}‖}_{\mathrm{F}}^{2} $

(14)

式中 $ \boldsymbol{\theta } $表示训练过程中的网络参数。

1.3.2 测试阶段

利用训练好的网络对成像结果进行高分辨处理，得到的反褶积结果为

$ {\boldsymbol{R}}^{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{i}\mathrm{r}\mathrm{m}}=F({\boldsymbol{I}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}};\widehat{\boldsymbol{\theta }}) $

(15)

式中：$ {\boldsymbol{R}}^{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{i}\mathrm{r}\mathrm{m}} $为测试阶段得到的宽频反射系数；$ \widehat{\boldsymbol{\theta }} $为最优网络参数。

1.4 网络模型

本文CNN结构如图 2所示。网络设计参考U-Net结构，将振幅谱的平均值做逆傅里叶变换估计得到的初始子波、叠后地震数据作为输入，输出为反射系数。网络主要由卷积核(Conv) + 批归一化(BN) + 激活函数(ReLU) 的模块堆叠组成。输入数据通道数为2，在两个Conv+BN+ReLU模块后变为64通道，卷积核尺寸为3×3。池化（尺寸为2×2）后特征图的尺寸减半，通道数不变。上采样由一个双线性插值和一个卷积层组成。上采样后特征图尺寸变为原来两倍，通道数不变。将左边特征图沿通道方向拼接到右边，实现不同尺度特征图的融合。在通道方向对特征图降维得到网络输出，最终的输出层卷积核尺寸为1×1。本文网络可在多尺度下融合图像特征，在小数据集的情况下能够充分提取隐含在成像结果与宽带反射系数之间的特征映射关系，以进行稳健的高分辨处理。

2 模型测试

本文采用Marmousi模型作为已知模型训练网络，并通过设计的薄层模型对网络进行测试。分别引入宽频子波和雷克子波构建不同的学习标签，以对比不同标签进行子波整形反褶积的效果。具体的学习标签分别采用理想的75 Hz主频的宽频子波和100 Hz主频的雷克子波与Marmousi模型的反射系数进行褶积获得(图 3)。

在训练阶段，提取靶区数据的子波和Marmousi模型的反射系数，二者褶积可得到成像剖面，并将它作为输入。其中初始子波可由靶区数据地震道的平均振幅谱估计而得。初始网络构建完成后，再根据式(11)、式(12)迭代更新反射系数和子波。

在训练过程中，利用90%的数据用作学习标签，另外10%的数据作为验证集。本文网络的训练采用Adam梯度下降法。设置批大小为20，共迭代3×10⁵次。初始学习率设为0.001，每迭代1.2×10⁵次学习率衰减90%。网络每训练3×10⁴次后，均需在验证集上评估模型的性能。

验证结果如图 4所示。由图可见，在验证集中，训练得到的网络的反演误差基本都在3%以内，最大误差不超过7%，这说明了本文方法的准确性。

本文设计了一个薄层模型，用于对比、测试训练得到的网络的泛化能力，并分别测试宽频子波与雷克子波作为标签情况下的方法的有效性。该薄层模型包含厚度为5~200 m的小层。

图 5a为该模型模拟的真振幅成像结果（通过37 Hz的宽频子波与反射系数褶积得到，作为网络测试的输入），图 5d为该模型理想反射系数剖面（为75 Hz宽频子波与薄层模型真反射系数褶积得到，在此不参与训练，只用作评价结果的标准）。利用Marmousi模型标签训练得到的两个CNN，分别对图 5a成像结果进行反褶积，最终结果分别如图 5b和图 5c所示。由图 5可见，通过雷克子波(图 5b)和宽频子波(图 5c)训练的网络都能有效拓宽成像结果的频带，薄层都能得到较好地分辨。二者与理想模型剖面之间的差距都很小。

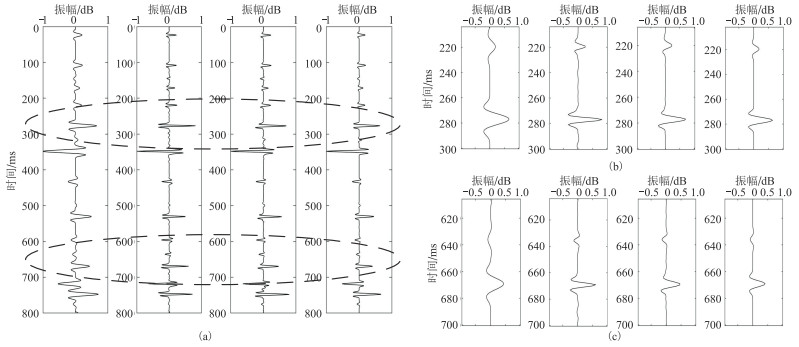
为了进一步验证宽频处理的必要性，分别抽取CDP为600的数据进行对比(图 6)。由图可见，利用宽频子波标签学习得到的网络进行反褶积得到的结果可以有效地压缩子波、提高分辨率。相比于利用雷克子波标签学习得到的结果，宽频子波标签的反褶积结果与宽带反射系数剖面吻合更好，其振幅也更加均衡。

3 实际资料应用

为了测试本文方法的应用效果，应用本文方法对中国东部M探区实际地震资料进行处理。

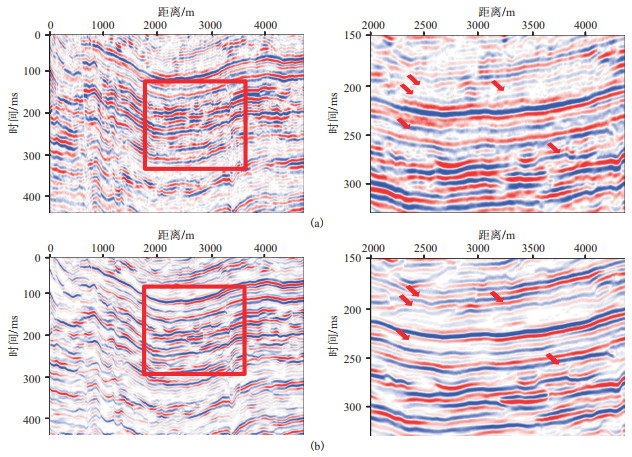
由图 7可见，经过反褶积处理后，分辨率明显提高，同相轴的横向连续性也得到提高，一些无法分辨的同相轴得到有效识别（红色箭头处）。

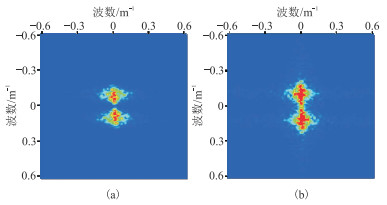
再分别对两个局部剖面(图 7a、图 7b)进行二维傅里叶变换，其二维波数谱如图 8所示。由图可见，经过反褶积处理后，局部剖面的波数带得到了有效拓宽，尤其是低波数部分。由此可以证明，本文方法在实际数据处理中具有较好的应用效果。

4 结束语

针对偏移后成像结果的分辨率提高问题，本文提出的基于CNN的深度学习子波整形反褶积方法，能充分利用已知模型数据，充分提取数据集的特征，建立成像结果与宽带反射系数的非线性映射关系，有效地实现目标数据的反褶积处理。薄层模型的测试结果表明，基于宽频子波褶积反射系数的标签进行训练，可以较好地压缩子波旁瓣，实现高分辨处理。子波和反射系数串联迭代反演，可以在一定程度上克服对固定子波假设的不利条件，但初始子波的准确性对反褶积过程还是有一定影响。中国东部M探区实际资料处理结果显示，本文方法能较好地拓展成像结果的波数带，同时保持和输入成像结果类似的波组特征，展示了该方法良好的应用效果。

然而，本文方法只是针对图像进行子波整形反褶积处理，将来可进一步利用模型测试分析低波数分量和与吸收衰减有关的高波数分量等恢复的有效性。