2. 中国石油勘探开发研究院, 北京 100083
2. Research Institute of Petroleum Exploration and Development, Beijing 100083, China
断层解释是地震资料解释的关键环节之一。早期的人工断层解释结果依赖于解释人员的专业知识及经验。三维地震数据的断层解释一般需要人工先对二维地震剖面进行标记[1],然后合成三维断层体。随着数据体越来越庞大、勘探区域越来越复杂,人工标记的效率和精度已无法满足实际生产需求[2]。计算机技术的进步使断层识别方法得到发展,如用于断层识别的地震属性技术(相干[3-5]、方差[6]、曲率[7]等)、蚁群算法[8]、最优曲面投票技术[9]等。但是,地震属性对噪声等非地质因素和其他地层不连续特征比较敏感[10],通常需要对断层识别结果进行人工干预或处理。
近年来,深度学习技术在图像分割、目标检测、图像识别等领域取得了显著进展。深度学习算法已应用于许多地球物理问题的解决,如断层解释[11-14]、地震数据插值[15-17]、阻抗反演[18-21]、地震数据去噪[22]、速度谱拾取[23]等。以人工解释成果或合成数据作为标签,深度神经网络可学习地震数据与断层之间的映射关系,实现二维或三维地震资料断层自动识别[24],大大减少人为干预,大幅度提高断层解释的效率和精度[25-26]。神经网络通过随机梯度下降优化训练,以损失函数衡量模型的误差,迭代更新网络模型参数。利用深度神经网络训练三维地震资料断层解释模型时,损失函数的选取对断层解释结果至关重要。
目前,已经有众多用于断层解释的损失函数和网络结构。Wu等[27]合成了带标签的三维地震数据体,利用平衡交叉熵(BCE)损失函数训练U-Net,最终将训练模型用于三维实际地震数据的断层解释。Wei等[28]使用焦点(Focal)损失函数训练CNN网络,在训练过程中对难、易样本使用不同权重。Dou等[29]提出Mask Dice损失函数指导Fault-Net训练,以解决人工解释标签的假阴性问题。为了在增强断层特征的同时抑制无关特征,何易龙等[30]引入Focal-Tversky损失函数训练3D U-Net++L3模型,使断层在地震数据体中的位置更准确、形态更清晰。Araya-Polo等[31]基于断层面的连续性,利用Wasserstein损失函数训练DNN,实现断层自动检测,该损失函数适用于解决输出结果具有空间依赖性的问题。
此外,一些在医学图像及自然图像语义分割任务中应用的损失函数同样适用于地震资料的断层解释。Salehi等[32]针对病灶数量远低于非病灶数量的数据不平衡问题,提出Tversky损失函数训练三维FCN,该损失函数在许多医疗图像分割任务中表现优异。Jadon[33]提出Log-Cosh Dice损失函数训练二维U-Net以用于医学图像分割,该损失函数封装了骰子(Dice)损失函数和双曲余弦函数的特性。Jakhetiya等[34]基于余弦相似度计算卷积神经网络深层特征之间的相似性,进而对三维合成图像的质量进行评估。Raj等[35]引入余弦(Cosine)损失函数解决医学图像分割常见的小数据集问题。
本文介绍了可用于三维地震资料断层解释的10种损失函数,即BCE、Dice、Focal、Cosine、Log-Cosh Dice、Tversky、Focal-Tversky、Wasserstein、BCE-Dice和BCE-Cosine损失函数等,以3D U-Net作为网络结构,以Adam(Adaptive Moment Estimation)作为优化器,用归一化和数据增强后的三维合成样本训练网络,比较各损失函数训练模型的收敛速度、计算效率和抗噪性能,分析网络层数变化对各损失函数训练模型的影响,对比、分析合成数据与实际数据断层解释的应用效果,以期为选取合适的损失函数进行地震资料的断层解释提供参考。
1 方法原理利用深度学习技术进行三维地震资料断层识别,是以三维地震数据体作为卷积神经网络的输入,对每个像素点进行语义判断,将分类问题转化为分割问题,通过学习训练数据的断层映射关系,从而预测实际工区的断层分布特征。
1.1 数据预处理首先,对输入网络的训练数据进行Min-Max归一化处理,使其取值范围为0~1,该操作在不改变结构信息的同时限制地震数据振幅的范围,从而减少由于地震数据振幅范围不一致造成的不确定性[36];其次,对归一化后的数据进行伽马变换[37],通过非线性变换对图像细节进行增强;最后,将12个不同尺度的噪声随机添加到合成数据中,以解决由于合成数据与实际数据分布之间差异较大而导致的预测结果不准确的问题。数据预处理前、后结果如图 1所示,预处理后地震数据(图 1b)振幅为0~1,且构造地质细节得到增强。

|
图 1 数据预处理前(a)、后(b)对比 |
U-Net架构起源于医学图像分割领域[38],经典结构为U型对称网络,由编码器、解码器和跳跃连接三部分构成。本文使用的3D U-Net将原U-Net的卷积层数从23减少到18,在保证断层识别精度的同时,实现节省内存、减少计算量、提高计算效率的目的。
本文3D U-Net网络结构如图 2所示。编码器包含卷积层、批归一化(BN)层、ReLU(Rectified Linear Units)激活函数、失活(Dropout)层和最大池化下采样层,可以有效地从三维地震数据中学习代表性特征。解码器包括卷积层、BN层、ReLU激活函数、Dropout层和上采样层,不断地将特征进行上采样操作以重构空间信息,从而恢复数据的分辨率。跳跃连接(图 2黄色箭头)用于拼接编码器与解码器中对应的特征,弥补下采样过程中丢失的信息。

|
图 2 地震资料断层解释3D U-Net网络结构 |
3D U-Net网络的输入、输出通道数依次为16、32、64、128,考虑到整体结构的对称性,该网络共设置四层结构。
1.3 损失函数本文介绍10种可用于3D U-Net训练而识别地震资料断层的损失函数,并利用各损失函数训练卷积网络(图 2),对比、分析合成数据训练与实际数据预测效果。
1.3.1 BCE损失函数交叉熵损失函数在图像分割问题中应用比较广泛。BCE损失函数是在交叉熵损失函数的基础上增加了样本的正例和负例的数量比例权重[39],在处理断层与非断层类别分布不平衡时可以使网络更倾向于预测结果为非断层。BCE损失函数可表示为
| $ {L}_{\mathrm{B}\mathrm{C}\mathrm{E}}=-\beta \sum\limits_{i=1}^{N}{y}_{i}\text{lg}{p}_{i}-(1-\beta )\sum\limits_{i=1}^{N}(1-{y}_{i})\text{lg}(1-{p}_{i}) $ | (1) |
式中:
BCE损失函数考虑两个分布之间的差异,然而基于分布的损失函数在分割任务中并不区分前景与背景,对假阴性标签非常敏感[1]。
基于区域的损失函数旨在最小化真值与预测结果之间的不匹配程度,代表性分割损失函数是Dice损失函数[40],可表示为
| $ {L}_{\mathrm{D}\mathrm{i}\mathrm{c}\mathrm{e}}=1-\frac{2\sum\limits_{i=1}^{N}{p}_{i}{y}_{i}+1}{\sum\limits_{i=1}^{N}{p}_{i}+\sum\limits_{i=1}^{N}{y}_{i}+1} $ | (2) |
Dice损失函数衡量神经网络预测值与真值之间的全局重叠程度。该损失函数广泛应用于医学图像分割任务,适用于解决数据不平衡问题[41]。在地震资料的断层解释中,断层与非断层数量的比例非常不均衡,类别分布不平衡的问题与医学图像分割任务类似,因此利用深度学习技术识别地震资料断层时,应用Dice损失函数训练模型预测断层效果较好[29, 36, 40, 42-43]。
1.3.3 Focal损失函数Focal损失函数[28]可看作二元交叉熵损失函数的变体,它在帮助深度模型解决难、易样本不平衡的分割任务时效果很好。该损失函数将样本分为难、易两类,引入调制因子调节难、易样本对整体损失的贡献权重,在模型学习过程中降低易样本的权重,从而使模型更专注于学习难样本。Focal损失函数定义为
| $ {L}_{\mathrm{F}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}=-{\alpha }_{t}(1-{p}_{t}{)}^{\gamma }\mathrm{l}\mathrm{g}{p}_{t} $ | (3) |
式中
| $ {p}_{t}=\left\{\begin{array}{cc}p& y=1\\ 1-p& y=0\end{array}\right. $ | (4) |
| $ {\alpha }_{t}=\left\{\begin{array}{cc}\alpha & y=1\\ 1-\alpha & y=0\end{array}\right. $ | (5) |
式中:
余弦相似度是通过标签向量与预测向量的夹角余弦值来衡量模型预测值与真实值之间的相似性。余弦距离更加注重两个向量在方向上的差异[45],而对绝对距离或位置不敏感。Cosine损失函数[34]可以表示为
| $ {L}_{\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{e}}=1-\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\boldsymbol{yp}}=1-\frac{\boldsymbol{y}\cdot \boldsymbol{p}}{‖\boldsymbol{y}‖‖\boldsymbol{p}‖} $ | (6) |
式中:
Log-Cosh Dice损失函数[46]是Dice损失函数的一种变体,它通过添加Log-Cosh平滑损失函数曲线而得。
双曲余弦函数定义为
| $ {L}_{\mathrm{L}\mathrm{C}\mathrm{D}}=\mathrm{l}\mathrm{g}\left(\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}{L}_{\mathrm{D}\mathrm{i}\mathrm{c}\mathrm{e}}\right) $ | (7) |
Log-Cosh Dice损失函数不仅封装了Dice损失函数的特点,而且因双曲余弦函数的特性而具有易于处理的性质。
1.3.6 Tversky损失函数Tversky损失函数可以看作Dice损失函数的推广形式[47]。它通过添加一个权重因子
| $ {L}_{\mathrm{T}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{k}\mathrm{y}}=1-\frac{1+\sum\limits_{i=1}^{N}{y}_{i}{p}_{i}}{1+\sum\limits_{i=1}^{N}{y}_{i}{p}_{i}+\lambda \sum\limits_{i=1}^{N}{y}_{i}(1-{p}_{i})+(1-\lambda )\sum\limits_{i=1}^{N}(1-{y}_{i}){p}_{i}} $ | (8) |
当
为了解决正、负样本高度不平衡和断层与背景难以区分的问题,何易龙等[30]结合Focal损失函数和Tversky损失函数的优点,提出Focal-Tversky损失函数,其表达式为
| $ {L}_{\mathrm{F}\mathrm{T}}=(1-{L}_{\mathrm{T}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{k}\mathrm{y}}{)}^{\tau } $ | (9) |
式中参数
Wasserstein距离作为距离衡量指标,可用于衡量两个概率分布之间的相似程度,它表示移动一个分布使其拟合另一个分布需要的最小代价[48]。KL散度(Kullback-Leibler Divergence)和JS散度(Jensen-Shannon Divergence)也可以用于衡量两个概率分布之间的差异[49]。不同的是,当两个分布完全没有重叠时,KL散度的值没有意义,JS散度的值是一个常数,而Wasserstein距离仍然可以有效地定量反映它们之间的距离。Wasserstein损失函数为[31]
| $ \left\{\begin{array}{l}{L}_{\mathrm{W}}=\underset{\boldsymbol{T}\in \prod (\boldsymbol{y},\boldsymbol{p})}{\mathrm{m}\mathrm{i}\mathrm{n}}〈\boldsymbol{T},\boldsymbol{M}〉\\ \prod (\boldsymbol{y},\boldsymbol{p})=\left\{\boldsymbol{T}\in {\mathbb{R}}_{+}^{K\times K}:\boldsymbol{T}\mathbf{1}=\boldsymbol{p},{\boldsymbol{T}}^{\mathrm{T}}\mathbf{1}=\boldsymbol{y}\right\}\end{array}\right. $ | (10) |
式中:
由于交叉熵损失函数并没有考虑预测断层结果的结构信息,所以它无法定量区分预测结果错误的偏离程度。Araya-Polo等[31]使用Wasserstein损失函数获取数据空间与断层之间的映射关系,基于该损失函数对结构化信息适当处理以获得断层网络的准确预测。
1.3.9 BCE-Dice损失函数Dice损失函数训练时更关注前景区域,这一特性可以解决样本中前景与背景不平衡的问题,从而保证有较低的假阴性。前景、背景不平衡问题是指图像中只有小部分区域包含目标、大部分区域不包含目标。BCE损失函数针对每个像素点计算损失,当前点的损失只和当前预测值与真实标签值的距离有关。BCE-Dice损失函数将BCE损失函数和Dice损失函数进行组合,其表达式为
| $ {L}_{\mathrm{B}\mathrm{C}\mathrm{E}\mathrm{-}\mathrm{D}\mathrm{i}\mathrm{c}\mathrm{e}}={w}_{\mathrm{B}}{L}_{\mathrm{B}\mathrm{C}\mathrm{E}}+{w}_{\mathrm{D}}{L}_{\mathrm{D}\mathrm{i}\mathrm{c}\mathrm{e}} $ | (11) |
式中
BCE损失和Dice损失的值相差一个数量级(BCE损失更小),若在BCE-Dice组合损失函数中Dice损失函数能够占据主导地位,就需要令
BCE损失函数通过计算真实标签与预测值的像素损失以衡量数据的预测分布与真实分布之间的差异,而Cosine损失函数通过计算夹角余弦值衡量标签向量与预测向量之间的差异。可以综合上述两种断层预测结果与真实值的差异衡量方式,使用BCE-Cosine损失函数训练断层预测模型,其函数形式为
| $ {L}_{\mathrm{B}\mathrm{C}\mathrm{E}\mathrm{-}\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{e}}={w}_{\mathrm{B}}{L}_{\mathrm{B}\mathrm{C}\mathrm{E}}+{w}_{\mathrm{C}}{L}_{\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{e}} $ | (12) |
式中
BCE损失和Cosine损失的值相差一个数量级(BCE损失更小),若Cosine损失函数能够作为主要因素影响BCE-Cosine组合损失函数的变化,则可以令
本文将Wu等[27]提供的合成数据集进行数据预处理后用于3D U-Net的网络训练。该数据集包含200个训练数据对和20个验证数据对,每个数据对由随机生成的128×128×128合成地震图像和对应的128×128×128断层标签组成。数据预处理后的合成地震数据及对应的标签如图 3所示。

|
图 3 训练使用的合成地震数据预处理后 结果(左)及断层标签(右) |
在实验中,使用NVIDIA GeForce RTX 3090训练神经网络,CPU配置为Intel(R) Xeon(R) Gold 6226R。网络训练在PyTorch框架下实现,采用Adam优化算法[50],学习率设置为1×10-4。为缓解过拟合现象,将模型权重衰减设置为1×10-6,编码器中Dropout层的随机丢弃率设置为0.5。由于本文使用的数据集中单个数据体较大,因此批大小设置为1。训练轮次设置为100,每轮训练结束后都进行精度和损失的计算,当验证集的损失在5轮内不再下降时停止训练,并且以验证损失最小作为网络模型输出。
2 数据实验设置相同的网络结构和训练参数,通过实验对比应用10种损失函数分别训练四层和五层(在图 2网络结构的基础上增加一层,通道数由[16,32,64,128]变为[16,32,64,128,256])3D U-Net的收敛速度和计算效率,并且在合成数据验证集和实际数据集展示断层识别效果。同时,测试各种损失函数对不同信噪比地震数据的抗噪性能。
2.1 训练效率对比利用各损失函数训练3D U-Net的停止轮次和训练时间如表 1所示。由表可知,应用Log-Cosh Dice损失函数的平均训练时间最短,应用BCE-Dice损失函数的平均训练时间最长,两者之间相差3.303 s。在10种损失函数中,有7种损失函数(Dice、Focal、Cosine、Log-Cosh Dice、Tversky、Focal-Tversky、Wasserstein损失函数)的每轮平均训练时间都在57 s左右,最长与最短的训练时间仅相差0.165 s,因此对于网络训练效率来说,平均训练时间并无显著差异。
|
|
表 1 各损失函数训练四层3D U-Net网络效率对比 |
针对训练轮次而言,应用Wasserstein损失函数只需要43轮就可以达到停止条件,而应用Focal损失函数则需要80轮。除了Focal损失函数,应用其他损失函数训练的网络都可以在60轮之内达到停止条件。正是由于应用Focal损失函数的停止轮次非常晚,从而导致应用该损失函数的总训练时间最长。
从总训练时间来看,应用Dice、Cosine、Focal-Tversky和Wasserstein损失函数训练3D U-Net均能够在3000 s内停止,训练效率较高。
2.2 断层预测效果对比应用各种损失函数在合成数据验证集上的断层预测结果如图 4所示。由图可知,应用Focal损失函数(图 4e)训练模型的预测结果整体连续性较差,应用Cosine (图 4f)、Tversky (图 4h)和Focal-Tversky(图 4i)损失函数对于临近断层(红色圆圈内)的识别效果较好;应用Dice (图 4d)、Cosine (图 4f)、Tversky (图 4h)和Focal-Tversky(图 4i)损失函数对于交叉结构断层部分(红色箭头处)识别效果较好,断层预测结果更加清晰、准确。

|
图 4 验证集中合成数据及不同损失函数断层预测结果 (a)合成地震数据;(b)断层标签;(c)BCE;(d)Dice;(e)Focal;(f)Cosine;(g)Log-Cosh Dice;(h)Tversky;(i)Focal-Tversky;(j)Wasserstein;(k)BCE-Dice;(l)BCE-Cosine。线号为25,道号为30,时间采样点为110。 |
为了更加客观地评价实验结果,在训练不同损失函数的模型后,应用图像分割中常用的几个评估指标[33],如交并比(IoU)、敏感性(Sensitivity)和特异性(Specificity),对合成数据验证集的效果进行评价。评估指标定义为
| $ \mathrm{I}\mathrm{o}\mathrm{U}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N}} $ | (13) |
| $ \mathrm{S}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{y}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}} $ | (14) |
| $ \mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}=\frac{\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}} $ | (15) |
式中:TP表示真实为断层且预测也为断层的像素数量;FP表示真实为非断层而预测为断层的像素数量;TN表示真实为断层而预测为非断层的像素数量;FN表示真实为非断层且预测也为非断层的像素数量。
交并比通过计算断层预测结果和真实值之间交集与并集的比值,衡量真实的断层结果与预测结果之间的重叠程度。敏感性是识别出的断层占所有断层的比例,值越高表示尽可能地将正例判断为正,即将断层判断为断层,而不出现漏判。特异性是识别出的非断层占所有非断层的比例,值越高表示尽可能地将负例判断为负,即将非断层判定为非断层,而不出现误判。被漏判的断层部分叫做假阴率,被误判的部分叫做假阳率,因此敏感性和特异性尽可能高,能够最大程度地避免假阴性和假阳性。合成数据验证集的断层预测效果的指标评价结果如表 2所示。
|
|
表 2 合成数据断层预测效果的评价指标 |
由表 2可见,应用Focal损失函数的交并比和敏感性最低、特异性最高,这表示利用该损失函数训练的模型能够保证不会把非断层预测为断层,但与此同时会以部分断层遗漏为代价,导致有效断层较少。应用Dice损失函数的指标评估结果与Focal损失函数的恰恰相反,敏感性最高而特异性最低,该结果表明利用Dice损失函数训练模型能够降低假阴性,使尽可能多的断层部分被预测出来。应用Tversky损失函数和Focal-Tversky损失函数的交并比都比较高,整体来看,漏判和误判都较少,这两个方法断层预测结果(图 4h、图 4i)和标签结果(图 4b)非常接近。此外,应用Cosine损失函数的三个指标评估结果均高于平均值,断层预测结果(图 4f)与标签结果(图 4b)也比较相近,对断层部分和非断层部分的预测都比较准确。预测效果最差的是应用Wasserstein损失函数,三个指标的值都非常低,由图 4j也可以看出,部分断层交叉区域混乱,且概率密度值较低。
综上所述,应用Cosine、Tversky和Focal-Tversky损失函数训练的3D U-Net在合成数据集识别断层效果较好。
2.3 不同网络层数训练效率对比本文选择的网络模型为四层3D U-Net结构(图 2),而断层解释任务中五层3D U-Net网络结构也是常用的基本模型[16, 51-52]。因此,本文在相同的实验配置下,利用各损失函数对五层3D U-Net模型也进行了训练,并记录了10种损失函数分别对四层和五层3D U-Net的训练效率(图 5、图 6和表 3)。
|
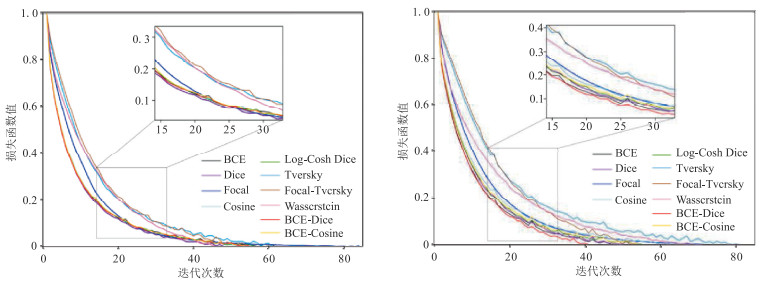
图 5 应用不同损失函数对四层(左)和五层(右)3D U-Net的训练损失变化曲线 图中方框内为局部放大显示。 |

|
图 6 不同损失函数对四层(左)和五层(右)3DU-Net的验证损失变化曲线 图中方框内为局部放大显示。 |
|
|
表 3 应用不同损失函数训练五层3D U-Net网络效率对比 |
本文将应用各损失函数训练四层、五层3D U-Net的训练损失(图 5)和验证损失(图 6)用最大值归一化,并且选出15个训练轮次进行局部放大展示。
由图 5、图 6可见,无论是四层还是五层3D U-Net,应用BCE、Dice、Cosine、Log-Cosh Dice、BCE-Dice和BCE-Cosine损失函数训练模型的训练损失和验证损失都下降较快,而且损失值较低。由局部放大图可以看到,在第15~第30轮的训练过程中,应用Dice损失函数训练四层3D U-Net能够达到较小的训练损失和验证损失,而训练五层3D U-Net时,应用BCE-Dice损失函数的训练损失和验证损失更小。此外,网络层数增多并不一定导致训练轮次增多,可以看到部分损失函数能够在更早的训练轮次达到停止条件。应用各损失函数训练四层和五层3D U-Net的详细训练时间和停止轮次分别见表 1和表 3。
由于网络层数增加,表 3展示的平均训练时间与表 1相比都增加了1 s左右。就训练时间而言,应用Focal-Tversky损失函数的平均训练时间最短,应用BCE-Dice损失函数的平均训练时间最长,二者之间相差2.615 s。相比表 1的结果来说,差值有所减小。在应用的10种损失函数中,有7种损失函数(Dice、Focal、Cosine、Log-Cosh Dice、Tversky、Focal-Tversky、Wasserstein损失函数)的平均训练时间都在58 s左右,这与表 1所示结果有相似的规律。对于表 3中的训练轮次来说,最早停止的是应用BCE-Dice损失函数,仅需要37轮训练,甚至比表 1中最少的43轮(Wasserstein损失函数)更早停止,最晚停止的是应用Tversky损失函数,且比表 1中最多的80轮(Focal损失函数)更早停止。对比表 1与表 3可知,部分损失函数(BCE、Focal、Log-Cosh Dice、Focal-Tversky、BCE-Dice等损失函数)在增加网络层数后反而能够减少训练轮次,这可能是由于增加网络层数,在训练集上越容易过拟合,因此停止迭代的轮数越早。
从总训练时间来看,使用BCE、Dice、Log-Cosh Dice、Focal-Tversky和BCE-Dice损失函数训练五层3D U-Net都能够在3000 s内停止,与表 1所示结果并不完全相同,只有应用Dice和Focal-Tversky损失函数能在网络层数变化后仍保持较高的训练效率。
2.4 抗噪性能对比当地震资料的信噪比存在显著差异时,应用不同的损失函数有可能会体现出不同的抗噪性能。因此,本文在合成数据训练集上选取一个数据样本,分别添加方差为0、0.005、0.02、0.05、0.09的高斯噪声,得到五个数据体。将噪声方差为0的数据(原始合成数据)作为干净数据,添加噪声后信噪比分别为16.637、10.900、7.480、5.606 dB。用10种损失函数训练的模型分别对上述五种信噪比数据体进行断层预测,结果如表 4所示。由表可见,随着数据噪声方差逐渐增加,敏感性、特异性和交并比都在逐渐下降,这说明应用各损失函数训练模型的预测效果都在不同程度地变差。
|
|
表 4 不同噪声方差地震数据断层预测结果评价指标 |
从整体来看,应用Focal损失函数的敏感性非常低,而特异性非常高,这说明利用该损失函数训练的模型能够避免把非断层预测为断层,但是同时会以部分断层遗漏为代价。在噪声方差从0增大到0.09的过程中,应用BCE、Focal、Focal-Tversky和Wasserstein损失函数预测结果的敏感性指标都有比较明显的下降,这说明对于信噪比越低的地震数据,应用上述损失函数训练模型预测的断层连续性越差。在这个过程中,应用Dice、Cosine、Log-Cosh Dice和BCE-Dice损失函数的敏感性指标值变化较小,对不同噪声数据适应性较好。噪声方差从0.05增大到0.09时,敏感性数值降低较小的是应用Cosine、Log-Cosh Dice、Tversky和BCE-Cosine损失函数,这说明当噪声增加到一定程度后,再继续增加噪声,应用上述损失函数仍然能够保持较好的断层预测效果。
应用各损失函数训练模型的预测结果特异性值都比较高,而且随着噪声逐渐增大,该值并没有显著降低,说明应用各损失函数在预测不同噪声数据的断层时只会产生较少的错误结果,对于主要断层的识别不会产生太大的影响。
就交并比而言,噪声方差从0提高到0.09时,下降较大的是应用Focal和Wasserstein损失函数,较小的是Dice和BCE-Dice损失函数。噪声方差从0.05到0.09时,交并比下降较大的是应用Focal、Tversky和Focal-Tversky损失函数,较小的是Cosine、Log-Cosh Dice和Wasserstein损失函数。由于交并比仅衡量预测结果中断层、非断层比例与真实结果的相似程度,所以需要与其他指标结合进行分析。
综上所述,利用Dice、Cosine、Log-Cosh Dice和BCE-Dice损失函数训练的模型具有较好的抗噪性能,能够适应不同噪声数据的断层解释。
3 实际数据应用效果实际数据为荷兰近海F3区块的部分地震数据,共512条测线,每条测线384道,时间采样间隔为4 ms,采样点数为128,数据尺寸为512×384×128。
首先利用各损失函数训练的3D U-Net对地震数据进行断层预测,选取切面(线号和道号均为29, 时间采样点为111)展示断层预测结果。FaultSeg3D网络[27]的断层预测结果以及应用本文10种损失函数训练3D U-Net得到的断层预测结果如图 7所示。

|
图 7 F3区块实际地震数据及不同方法断层预测结果 (a)地震数据;(b)FaultSeg3D网络;(c)BCE损失函数;(d)Dice损失函数;(e)Focal损失函数;(f)Cosine损失函数;(g)Log-Cosh Dice损失函数;(h)Tversky损失函数;(i)Focal-Tversky损失函数;(j)Wasserstein损失函数;(k)BCE-Dice损失函数;(l)BCE-Cosine损失函数 |
由图 7可见,红色方框中发育一条贯穿整个时间剖面的大断层,在FaultSeg3D网络预测结果(图 7b)中,该断层的连续性欠佳,而应用Tversky损失函数(图 7h)和Focal-Tversky损失函数(图 7i) 预测的该断层连续性较好。
在线方向上明显可见一条“Y”型断层(图 7b红色圆圈内),FaultSeg3D网络预测该断层及其相邻断层(图 7b)比较清晰、连续,同样有类似预测效果的是应用BCE损失函数(图 7c)和BCE-Cosine损失函数(图 7l)训练的模型。虽然利用Dice损失函数(图 7d)、Focal-Tversky损失函数(图 7i)和BCE-Dice损失函数(图 7k)的预测结果也展示出了该“Y”型断层的主要形态,但是其邻近断层却没有完全预测出来,出现了一定的不连续性。由于该区域存在特殊的断层形态以及邻近断层相互影响等原因,其他损失函数(图 7e、图 7f、图 7g、图 7h、图 7j)对该“Y”型断层的预测效果较差。
图 7中红色箭头所指的区域存在几条近似平行的邻近断层,由于距离较近,各断层相互影响,增加了模型预测的难度。应用BCE-Cosine损失函数的预测断层(图 7l)连续性较好,比较清晰、完整。
综上所述,当损失函数包含BCE损失时,训练的模型对“Y”型断层和距离较近的相邻断层的预测效果较好,断层边缘清晰且连续性较好,对于断层细节丰富或断层分布较复杂的区域,该类损失函数是模型训练的较好选择。对于独立大断层来说,加入Tversky损失的损失函数训练的模型在断层连续性方面预测效果更好。
4 讨论本文所述10种损失函数中,Focal损失函数、Tversky损失函数和Focal-Tversky损失函数存在超参数,不同的超参数取值会影响损失函数对网络训练的效果。对于BCE-Dice损失函数和BCE-Cosine损失函数这类混合损失函数,各损失函数的权重也会影响整个损失函数的效果。因此,可以通过调节损失函数的超参数或权重以获得更好的断层预测效果。
在3D U-Net的合成数据和实际数据应用中,Wasserstein损失函数预测断层效果均较差,该结论仅为本文在断层问题上应用3D U-Net的测试结论。有可能结合其他结构的网络,如主要由生成器和判别器构成的GAN(Generative Adversarial Networks)网络,该损失函数可能会表现出更佳性能。因此,可能存在一些损失函数,需要配合特定网络结构才能发挥其优势。此外,本文仅对比研究了10种用于深度神经网络识别三维地震资料断层的损失函数,可能存在其他文中未涉及到的损失函数,它们在断层解释方面也有优异表现。
5 结论损失函数在决定深度学习模型性能和预测效果方面有着至关重要的作用。对于三维地震资料断层解释这类复杂的任务,并没有一个通用的最优损失函数。本文总结了可用于三维地震资料断层解释的10种损失函数,在相同网络模型、训练参数以及停止准则的条件下,通过三维合成样本训练网络,对比各种损失函数训练3D U-Net的收敛速度、计算效率和抗噪性能,并在荷兰近海F3区块地震数据应用中展示了断层预测效果。
对于合成数据集来说,Cosine、Tversky和Focal-Tversky损失函数训练的3D U-Net断层预测效果较好。Dice、Cosine、Log-Cosh Dice和BCE-Dice损失函数训练的3D U-Net具有较好的抗噪性能,在地震资料断层解释任务中能够适应不同噪声的数据。
对于F3区块实际地震数据来说,Tversky和Focal-Tversky损失函数训练的3D U-Net预测的断层连续性较好。当交叉或平行断层分布密集、邻近断层互相影响时,BCE、BCE-Dice和BCE-Cosine损失函数训练的3D U-Net预测的断层完整、清晰,细节更丰富。
本研究可为相关工程人员在利用深度学习技术进行地震资料断层解释实践时提供参考。
| [1] |
DOU Y, LI K, ZHU J, et al. Attention-based 3-D seismic fault segmentation training by a few 2-D slice labels[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-15. |
| [2] |
张政, 严哲, 顾汉明. 基于残差网络与迁移学习的断层自动识别[J]. 石油地球物理勘探, 2020, 55(5): 950-956. ZHANG Zheng, YAN Zhe, GU Hanming. Automatic fault recognition with residual network and transfer learning[J]. Oil Geophysical Prospecting, 2020, 55(5): 950-956. |
| [3] |
BAHORICH M, FARMER S. 3-D seismic discontinuity for faults and stratigraphic features: the coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [4] |
MARFURT K J, KIRIN R L, FARMER S L, et al. 3-D seismic attributes using a semblance-based coherency algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [5] |
GERSZTENKORN A, MARFURT K J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [6] |
Van BEMMEL P P, PEPPER R E F. Seismic signal processing method and apparatus for generating a cube of variance values: US6151555[P]. 1999-08-19.
|
| [7] |
ROBERTS A. Curvature attributes and their application to 3D interpreted horizons[J]. First Break, 2001, 19(2): 85-100. DOI:10.1046/j.0263-5046.2001.00142.x |
| [8] |
PEDERSEN S I, SKOV T, RANDEN T, et al. Automatic fault extraction using artificial Ants[M]//ISKE A, RANDEN T. Mathematical Methods and Modelling in Hydrocarbon Exploration and Production. Springer, Berlin, Heidelberg, 2005, 107-116.
|
| [9] |
WU X, FOMEL S. Automatic fault interpretation with optimal surface voting[J]. Geophysics, 2018, 83(5): 067-082. DOI:10.1190/geo2018-0115.1 |
| [10] |
BI Z, WU X. Improving fault surface construction with inversion-based methods[J]. Geophysics, 2021, 86(1): IM1-IM14. DOI:10.1190/geo2019-0832.1 |
| [11] |
WANG Z, LI B, LIU N, et al. Distilling knowledge from an ensemble of convolutional neural networks for seismic fault detection[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [12] |
LIU N, HE T, TIAN Y, et al. Common azimuth seismic data fault analysis using residual UNet[J]. Interpretation, 2020, 8(3): SM25-SM37. DOI:10.1190/INT-2019-0173.1 |
| [13] |
JING J, YAN Z, ZHANG Z, et al. Fault detection using a convolutional neural network trained with point-spread function-convolution-based samples[J]. Geophy-sics, 2023, 88(1): IM1-IM14. |
| [14] |
何涛, 刘乃豪, 吴帮玉, 等. 基于ResU-Net的三维断层识别方法及应用[J]. 工程数学学报, 2023, 40(1): 1-19. HE Tao, LIU Naihao, WU Bangyu, et al. ResU-Net based three-dimensional fault identification method and application[J]. Chinese Journal of Engineering Mathematics, 2023, 40(1): 1-19. |
| [15] |
YU J, WU B. Attention and hybrid loss guided deep learning for consecutively missing seismic data Reconstruction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-8. |
| [16] |
LI X, WU B, ZHU X, et al. Consecutively missing seismic data interpolation based on coordinate attention Unet[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [17] |
HE T, WU B, ZHU X. Seismic data consecutively missing trace interpolation based on multistage neural network training process[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [18] |
WU B, MENG D, WANG L, et al. Seismic impedance inversion using fully convolutional residual network and transfer learning[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(12): 2140-2144. DOI:10.1109/LGRS.2019.2963106 |
| [19] |
ZHENG X, WU B, ZHU X. Multi-task deep learning seismic impedance inversion optimization based on homoscedastic uncertainty[J]. Applied Sciences, 2022, 12(3): 1200. DOI:10.3390/app12031200 |
| [20] |
WU B, MENG D, ZHAO H. Semi-supervised learning for seismic impedance inversion using generative adversarial networks[J]. Remote Sensing, 2021, 13(5): 909. DOI:10.3390/rs13050909 |
| [21] |
伊小蝶, 吴帮玉, 孟德林, 等. 数据增广和主动学习在波阻抗反演中的应用[J]. 石油地球物理勘探, 2021, 56(4): 707-715. YI Xiaodie, WU Bangyu, MENG Delin, et al. Application of data augmentation and active learning to seismic wave impedance inversion[J]. Oil Geophysical Prospecting, 2021, 56(4): 707-715. |
| [22] |
QIU C, WU B, LIU N, et al. Deep learning prior model for unsupervised seismic data random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [23] |
QIU C, WU B, MENG D, et al. Attention neural network semblance velocity auto picking with reference velocity curve data augmentation[C]. 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 2021, 4596-4599.
|
| [24] |
路鹏飞, 杜文龙, 李丽, 等. 基于VNet深度学习架构的低序级断层智能识别方法[J]. 石油地球物理勘探, 2022, 57(6): 1276-1286. LU Pengfei, DU Wenlong, LI Li, et al. Intelligent recognition method of low-grade faults based on VNet deep learning architecture[J]. Oil Geophysical Prospecting, 2022, 57(6): 1276-1286. |
| [25] |
陈俊安, 陈海东, 龚伟, 等. 深度学习与边缘增强相结合的断裂综合检测技术——顺北地区超深走滑断裂检测应用实例[J]. 石油地球物理勘探, 2022, 57(6): 1304-1316. CHEN Jun̓ an, CHEN Haidong, GONG Wei, et al. Application of comprehensive fault detection technology combining deep learning with edge enhancement in detecting ultra-deep strike-slip faults in Shunbei block[J]. Oil Geophysical Prospecting, 2022, 57(6): 1304-1316. |
| [26] |
杨平, 宋强功, 詹仕凡, 等. 基于深度学习的高效构造解释技术研发及工业化应用[J]. 石油地球物理勘探, 2022, 57(6): 1265-1275. YANG Ping, SONG Qianggong, ZHAN Shifan, et al. Research and industrial application of efficient structural interpretation technology based on deep learning[J]. Oil Geophysical Prospecting, 2022, 57(6): 1265-1275. |
| [27] |
WU X, LIANG L, SHI Y, et al. FaultSeg3D: using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. DOI:10.1190/geo2018-0646.1 |
| [28] |
WEI X L, ZHANG C X, KIM S W, et al. Seismic fault detection using convolutional neural networks with focal loss[J]. Computers & Geosciences, 2022, 158: 104968. |
| [29] |
DOU Y, LI K, ZHU J, et al. MD loss: efficient training of 3-D seismic fault segmentation network under sparse labels by weakening anomaly annotation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-14. |
| [30] |
何易龙, 文晓涛, 王锦涛, 等. 基于3D U-Net++L3卷积神经网络的断层识别[J]. 地球物理学进展, 2022, 37(2): 607-616. HE Yilong, WEN Xiaotao, WANG Jintao, et al. Fault recognition based on 3D U-Net++L3 convolutional neural network[J]. Progress in Geophysics, 2022, 37(2): 607-616. |
| [31] |
ARAYA-POLO M, DAHLKE T, FROGNER C, et al. Automated fault detection without seismic processing[J]. The Leading Edge, 2017, 36(3): 208-214. |
| [32] |
SALEHI S S M, ERDOGMUS D, GHOLIPOUR A. Tversky loss function for image segmentation using 3D fully convolutional deep networks[C]. Machine Learning in Medical Imaging, Cham, Switzer land, 2017, 379-387.
|
| [33] |
JADON S. A survey of loss functions for semantic segmentation[C]. 2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Via del Mar, Chile, 2020, 1-7.
|
| [34] |
JAKHETIVA V, CHAUDHARY S, SUBUDHI B N, et al. Perceptually unimportant information reduction and cosine Similarity-Based quality assessment of 3D-Synthesized images[J]. IEEE Transactions on Image Processing, 2022, 31: 2027-2039. |
| [35] |
RAJ A, TOLLENS F, HANSEN L, et al. Deep Learning-Based total kidney volume segmentation in autosomal dominant polycystic kidney disease using attention, cosine loss, and sharpness aware minimization[J]. Diagnostics, 2022, 12(5): 1159. |
| [36] |
ZHU D, ZHENG C, WANG W, et al. Rapid fault extraction from seismic images via deep learning[J]. Journal of Electronic Imaging, 2022, 31(5): 051423. |
| [37] |
JU M, DING C, GUO Y, et al. IDGCP: image dehazing based on gamma correction prior[J]. IEEE Transactions on Image Processing, 2020, 29: 3104-3118. |
| [38] |
RONNEBERGER O, FISCHER P, BROX T. U-Net: convolutional networks for biomedical image segmentation[C]. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015, Cham, Switzerland, 2015, 234-241.
|
| [39] |
XIE S, TU Z. Holistically-Nested edge detection[C]. 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 2015, 1395-1403.
|
| [40] |
GAO K, HUANG L, ZHENG Y, et al. Automatic fault detection on seismic images using a multiscale attention convolutional neural network[J]. Geophysics, 2022, 87(1): N13-N29. |
| [41] |
MILLETARI F, NAVAB N, AHMADI S A. V-Net: fully convolutional neural networks for volumetric medical image segmentation[C]. 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 2016 565-571.
|
| [42] |
唐杰, 孟涛, 韩盛元, 等. 基于多分辨率U-Net网络的地震数据断层检测方法[J]. 石油地球物理勘探, 2021, 56(3): 436-445. TANG Jie, MENG Tao, HAN Shengyuan, et al. A fault detection method of seismic data based on Multi ResU-Net[J]. Oil Geophysical Prospecting, 2021, 56(3): 436-445. |
| [43] |
GAO K, HUANG L, ZHENG Y. Fault detection on seismic structural images using a nested residual U-Net[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-15. |
| [44] |
LIN T Y, GOYAL P, GIRSHICK R, et al. Focal loss for dense object detection[C]. 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 2017, 2999-3007.
|
| [45] |
邓建国, 张素兰, 张继福, 等. 监督学习中的损失函数及应用研究[J]. 大数据, 2020, 6(1): 60-80. DENG Jianguo, ZHANG Sulan, ZHANG Jifu, et al. Loss function and application research in supervised learning[J]. Big Data Research, 2020, 6(1): 60-80. |
| [46] |
NANNI L, CUZA D, LUMINI A, et al. Deep ensembles in bioimage segmentation [EB/OL]. (2021-12-24)[2023-09-01]. https://arxiv.org/abs/2112.12955.
|
| [47] |
ABRAHAM N, KHAN N M. A novel focal tversky loss function with improved attention U-Net for lesion segmentation[C]. IEEE 16th International Symposium on Biomedical Imaging, Venice, Italy, 2018, 683-687.
|
| [48] |
FROGNER C, ZHANG C, MOBAHI H, et al. Learning with a Wasserstein loss[C]. Proceedings of the 28th International Conference on Neural Information Processing Systems-Volume 2, Cambridge, MA, USA, 2015, 2053-2061.
|
| [49] |
RUBNER Y, TOMASI C, GUIBAS L J. The earth mover̓ s distance as a metric for image retrieval[J]. International Journal of Computer Vision, 2000, 40(2): 99-121. |
| [50] |
KINGMA D P, BA J. Adam: A method for stochastic optimization[EB/OL]. (2017-01-30)[2023-09-01]. https://arxiv.org/abs/1412.6980.
|
| [51] |
BI Z, WU X, GENG Z, et al. Deep relative geologic time: a deep learning method for simultaneously interpreting 3‐D seismic horizons and faults[J]. Journal of Geophysical Research. Solid Earth, 2021, 126(9). DOI:10.1029/2021JB021882 |
| [52] |
ALFARHAN M, DERICHE M, MAALEJ A, et al. Multiple events detection in seismic structures using a novel U-Net variant[C]. 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 2020, 2900-2904.
|



 吴帮玉, 陕西省西安市咸宁西路28号西安交通大学数学与统计学院,710049。Email:
吴帮玉, 陕西省西安市咸宁西路28号西安交通大学数学与统计学院,710049。Email: