2. 中国石油大学(北京)CNPC物探重点实验室, 北京 102249;
3. 东方地球物理公司, 河北涿州 072750;
4. 油气勘探计算机软件国家工程研究中心, 北京 100088
2. CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum (Beijing), Beijing 102249, China;
3. BGP Inc., CNPC, Zhuozhou, Hebei 072750, China;
4. National Engineering Research Center for Oil and Gas Exploration Computer Software, Beijing 100088, China
目前,油气地震勘探主要利用了纵波(PP波)的信息。纵波对地层的声波速度、阻抗的变化最为敏感,在构造成像、断层解释等方面得到了广泛应用;结合岩石物理分析可以在一定程度上描述储层特征[1]、识别孔隙流体的变化[2-3]。油气藏的定量解释依赖于利用地震数据反演所获得的地层参数,而仅利用有限角度(炮检距)的纵波数据同步反演多个弹性参数比较困难[4-5]。其中,密度(
相比于纵波,横波(SV-SV波和SH-SH波)的动力学特征有着显著的差异。在同一频带、相同的吸收衰减条件下,横波数据的分辨率更高,对地层的横波速度(VS)、密度、剪切模量、各向异性参数等更为敏感,因此可以用来更好地反演以上参数。如图 1所示,相比纵波资料,横波资料在反演横波速度、密度等参数时不确定性更低,在描述油气藏的骨架性质、物性特征、裂缝、地应力等方面具有明显优势[12-16]。因此,将横波引入油气勘探能够弥补纵波勘探能力的不足,有助于提升复杂油气藏的储层预测精度和油气识别能力[17-19]。

|
图 1 PP波(a)与SH-SH波(b)反演纵波速度、横波速度、密度的后验概率密度分布 最大后验概率密度对应反演最优解。 |
为了明确横波的传播机理,诸多学者开展了理论研究[20-25]。横波曾在早期被应用于地震勘探[26-28],通过多分量地震采集得到的横波各向异性属性用于裂缝油气储层描述[29-30],但在较长的一段时期内,横波并没有在油气勘探中得到广泛应用,主要是因为传统的横波震源技术无法获得高品质数据。
转换横波不依赖于震源,可以通过爆炸源和垂直力源激发、三分量检波器接收,因此从20世纪90年代开始,它作为横波的替代应用于油气勘探。目前,业界已针对转换波数据的处理和成像开展了大量的研究工作[31-35]。实际应用结果表明,由于横波传播基本不受流体影响,转换横波在气云区成像方面具有一定的优势[36];联合反演纵波和转换横波数据有助于改善地层横波速度和密度的反演结果,提高了反演稳定性和精度[37-39]。然而,相比纵波,转换横波的数据品质往往较低,难以独立应用于储层的精细描述。纵波和转换波联合反演的效果在很大程度上依赖于纵、横波数据的匹配精度,这导致联合反演方法在实际应用中受到一定程度的制约。
近年来,大吨位、宽频横波可控震源技术在油气勘探行业中迅速发展,可以激发与纵波数据品质相当的SV-SV波和SH-SH波[40-44],为横波油气勘探技术的发展和广泛应用提供了良好的基础。但是,目前地震横波的反演理论尚不完善,有必要进一步开展纵波与横波的反演能力对比、分析,为横波反演方法研究提供理论依据。为此,本文首先介绍了不同类型地震波反射系数的近似式,并通过与精确反射系数对比分析近似式的精度;然后构建针对不同弹性参数的线性反演框架,计算不同待求参数组合的反演协方差矩阵,对比PP波、PSV波、PP波和PSV波联合、SH-SH波、SV-SV波在反演不同弹性参数时的不确定性;进而通过计算不同类型地震波反演的特征值和条件数,对比、分析反演问题的不适定性;最后以反演协方差矩阵和反演条件数为依据明确了不同类型地震波的反演能力及横波反演方法的应用潜力。
2 不同类型地震波反射系数近似公式不同弹性参数表示的反射系数近似式广泛应用于地震反演,因此在介绍PP波、PSV波、SH-SH波、SV-SV波反射系数近似式基础上,通过与精确反射系数对比分析其精度。
2.1 PP波| $ \begin{array}{l}{R}_{\mathrm{P}\mathrm{P}}^{}=\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\stackrel{-}{\theta }\frac{\mathrm{\Delta }{V}_{\mathrm{P}}}{\overline{{V}_{\mathrm{P}}}}-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\theta }\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}+\\ \,\,\,\,\,\,\,\,\,\, \frac{1}{2}\left(1-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\theta }\right)\frac{\mathrm{\Delta }\rho }{\overline{\rho }}\end{array} $ | (1) |
式中:
根据弹性参数之间的关系,可得到利用纵波阻抗
| $ {R}_{\mathrm{P}\mathrm{P}}^{}=\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\stackrel{-}{\theta }\frac{\mathrm{\Delta }{I}_{\mathrm{P}}}{\overline{{I}_{\mathrm{P}}}}-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\theta }\frac{\mathrm{\Delta }{I}_{\mathrm{S}}}{\overline{{I}_{\mathrm{S}}}}+ \\ \,\,\,\,\,\,\,\,\,\, \frac{1}{2}\left(4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\theta }-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\stackrel{-}{\theta }\right)\frac{\mathrm{\Delta }\rho }{\overline{\rho }} $ | (2) |
利用
| $ {R}_{\mathrm{P}\mathrm{P}}^{}=\frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\stackrel{-}{\theta }\frac{\mathrm{\Delta }{I}_{\mathrm{P}}}{\overline{{I}_{\mathrm{P}}}}-\frac{1}{2}\left(4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\theta }+\\ \,\,\,\,\,\,\,\,\,\, \mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\stackrel{-}{\theta }\right)\frac{\mathrm{\Delta }\mu }{\overline{\mu }}+\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\stackrel{-}{\theta }\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}} $ | (3) |
对比PP波反射系数近似式与精确公式,分析近似式在不同入射角的精度。采用的弹性界面参数如表 1所示,其中模型1和模型2均为弱阻抗差,模型3和模型4均为强阻抗差。
|
|
表 1 不同模型弹性参数 |
由图 2可见,式(1)~式(3)的精度基本相同。在弱阻抗差情况下(图 2a、图 2b),反射系数近似式在入射角50°以内保持较高的精度;在强阻抗差情况下(图 2c、图 2d),虽然在临界角附近的精度有所下降,但在入射角30°以内依然保持较高的精度。由此可以得出结论,PP波反射系数近似式可用于后续反演能力分析。
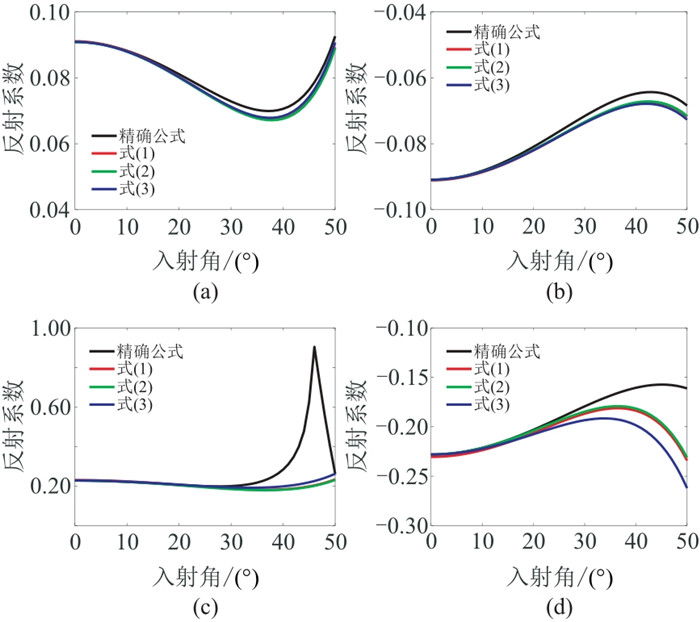
|
图 2 PP波反射系数近似式精度分析 (a)模型1;(b)模型2;(c)模型3;(d)模型4 |
PSV波的反射系数近似式为[48]
| $ {R}_{\mathrm{P}\mathrm{S}\mathrm{V}}=\frac{2\mathrm{s}\mathrm{i}\mathrm{n}\theta }{\mathrm{c}\mathrm{o}\mathrm{s}\phi }\left(\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\phi -\gamma \mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{c}\mathrm{o}\mathrm{s}\phi \right)\frac{\mathrm{\Delta }V\mathrm{s}}{\overline{V\mathrm{s}}}- \\ \,\,\,\,\,\,\, \frac{\mathrm{s}\mathrm{i}\mathrm{n}\theta }{2\mathrm{c}\mathrm{o}\mathrm{s}\phi }\left(1-2\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\phi +2\gamma \mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{c}\mathrm{o}\mathrm{s}\phi \right)\frac{\mathrm{\Delta }\rho }{\overline{\rho }} $ | (4) |
式中
在此基础上,根据弹性参数之间的关系可进一步整理得到
| $ {R}_{\mathrm{P}\mathrm{S}\mathrm{V}}=\frac{2\mathrm{s}\mathrm{i}\mathrm{n}\theta }{\mathrm{c}\mathrm{o}\mathrm{s}\phi }\left(\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\phi -\gamma \mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{c}\mathrm{o}\mathrm{s}\phi \right)\frac{\mathrm{\Delta }{I}_{\mathrm{S}}}{\overline{{I}_{\mathrm{S}}}}- \\ \,\,\,\,\,\,\, \frac{\mathrm{s}\mathrm{i}\mathrm{n}\theta }{2\mathrm{c}\mathrm{o}\mathrm{s}\phi }\left(1+2\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\phi -2\gamma \mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{c}\mathrm{o}\mathrm{s}\phi \right)\frac{\mathrm{\Delta }\rho }{\overline{\rho }} $ | (5) |
利用
| $ \begin{array}{l}{R}_{\mathrm{P}\mathrm{S}\mathrm{V}}=-\frac{\mathrm{s}\mathrm{i}\mathrm{n}\theta }{2\mathrm{c}\mathrm{o}\mathrm{s}\phi }\left(1-2\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\phi +2\gamma \mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{c}\mathrm{o}\mathrm{s}\phi \right)\times \\ \,\,\,\,\,\,\, \frac{\mathrm{\Delta }\mu }{\overline{\mu }}+\frac{\mathrm{s}\mathrm{i}\mathrm{n}\theta }{\mathrm{c}\mathrm{o}\mathrm{s}\phi }\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}\end{array} $ | (6) |
从式(4)~式(6)可以看出,PSV波的反射系数近似式虽然只含有2个待反演的模型参数,但是由于公式中还包含了
对比PSV波反射系数近似式与精确式,分析近似式在不同入射角的精度。同样采用表 1所示的弹性参数。
由图 3可见,式(4)~式(6)的精度基本相同。在弱阻抗差情况下,反射系数近似式在入射角50°以内保持较高的精度;在强阻抗差情况下,虽然在临界角附近的精度有所下降,但在入射角30°以内仍然保持较高的精度。

|
图 3 PSV波反射系数近似式精度分析 (a)模型1;(b)模型2;(c)模型3;(d)模型4 |
SH-SH波反射系数的精确式可表示为[49]
| $ {R}_{\mathrm{S}\mathrm{H}}=\frac{{\rho }_{1}{V}_{\mathrm{S}1}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{1}-{\rho }_{2}{V}_{\mathrm{S}2}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{2}}{{\rho }_{1}{V}_{\mathrm{S}1}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{1}+{\rho }_{2}{V}_{\mathrm{S}2}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{2}} $ | (7) |
式中
根据斯奈尔定律,并且基于弱阻抗差假设
| $ \frac{\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{2}}{\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{1}}\approx 1-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\phi \mathrm{\Delta }{V}_{\mathrm{S}}/\overline{{V}_{\mathrm{S}}} $ | (8) |
将式(8)代入式(7),忽略二阶以上高阶项,可推导出用
| $ {R}_{\mathrm{S}\mathrm{H}}=-\frac{1}{2}\left(1-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}{\phi }_{1}\right)\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}-\frac{1}{2}\frac{\mathrm{\Delta }\rho }{\overline{\rho }} $ | (9) |
在此基础上,可进一步推导得到利用
| $ {R}_{\mathrm{S}\mathrm{H}}=-\frac{1}{2}\frac{\mathrm{\Delta }{I}_{\mathrm{S}}}{\overline{{I}_{\mathrm{S}}}}+\frac{1}{2}\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}{\phi }_{1}\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}} $ | (10) |
利用
| $ {R}_{\mathrm{S}\mathrm{H}}=-\frac{1}{2}\frac{\mathrm{\Delta }\mu }{\overline{\mu }}+\frac{1}{2}\left(1+\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}{\phi }_{1}\right)\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}} $ | (11) |
从式(9)~式(11)可以看出,SH-SH波的反射系数方程都具有非常简单的表达形式,即每个方程只含有2个待反演的模型参数(如式(9)中的
对比SH-SH波反射系数近似式与精确公式,分析近似式在不同入射角的精度,同样采用表 1所示的弹性参数。
由图 4可见,式(9)~式(11)的精度基本相同。在弱阻抗差情况下,反射系数近似式在入射角50°以内保持较高的精度;在强阻抗差情况下,虽然由于临界角导致精度有所下降,但在入射角30°以内仍然保持较高的精度。
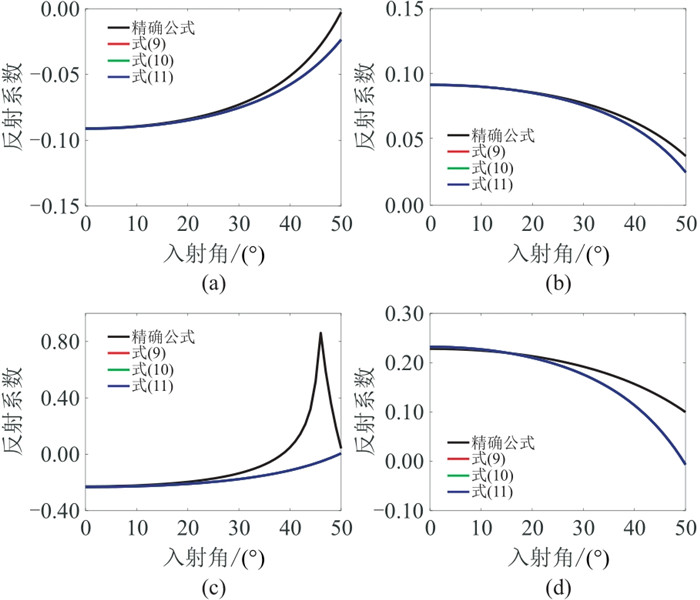
|
图 4 SH-SH波反射系数近似式精度分析 (a)模型1;(b)模型2;(c)模型3;(d)模型4 |
Zhang[51]推导了用
| $ \begin{array}{l}{R}_{\mathrm{S}\mathrm{V}}=-\frac{1}{2}\left(\frac{1}{\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\stackrel{-}{\phi }}-8\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\phi }\right)\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}}-\\ \frac{1}{2}\left(1-4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\phi }\right)\frac{\mathrm{\Delta }\rho }{\overline{\rho }}\end{array} $ | (12) |
式中
| $ \begin{array}{l}{R}_{\mathrm{S}\mathrm{V}}=-\frac{1}{2}\left(1-4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\phi }\right)\frac{\mathrm{\Delta }{I}_{\mathrm{s}}}{\overline{{I}_{\mathrm{s}}}}-\\ \frac{1}{2}\left(\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}\stackrel{-}{\phi }-4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\phi }\right)\frac{\mathrm{\Delta }{V}_{\mathrm{s}}}{\overline{{V}_{\mathrm{s}}}}\end{array} $ | (13) |
利用
| $ {R}_{\mathrm{S}\mathrm{V}}=-\frac{1}{2}\left(1-4\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\stackrel{-}{\phi }\right)\frac{\mathrm{\Delta }\mu }{\overline{\mu }}+\frac{1}{2}\frac{\mathrm{c}\mathrm{o}\mathrm{s}2\stackrel{-}{\phi }}{\mathrm{c}\mathrm{o}{\mathrm{s}}^{2}\stackrel{-}{\phi }}\frac{\mathrm{\Delta }{V}_{\mathrm{S}}}{\overline{{V}_{\mathrm{S}}}} $ | (14) |
从式(12)~式(14)可以看出,SV-SV波近似式中的
对比SV-SV波反射系数近似式与精确公式,分析近似式在不同入射角的精度,同样采用表 1所示的弹性参数。
由图 5可见,反射系数近似式式(12)~式(14)的近似精度基本相同。在弱阻抗差情况下,反射系数近似公式在入射角50°以内保持较高的精度;在强阻抗差情况下,多临界角现象导致近似式精度大幅下降(在模型3时,第一个临界角约为21°),仅在入射角20°以内保持较高精度。

|
图 5 SV-SV波反射系数近似式精度分析 (a)模型1;(b)模型2;(c)模型3;(d)模型4 |
综上所述,不同类型地震波反射系数近似式在弱阻抗差(模型1和模型2)的情况下,入射角50°以内均保持较高的近似;在强阻抗差(模型3和模型4)的情况下,近似式的精度出现了不同程度的下降,这是由于近似式的推导是基于弱阻抗假设条件的。因此,在后续的反演分析中,本文采用的最大入射角为50°,反射系数近似式的精度可满足理论分析的需求。
3 基于协方差矩阵的反演不确定性分析 3.1 方法原理根据不同类型地震波的反射系数近似式可以构建一个线性正演方程
| $ \boldsymbol{R}=\boldsymbol{F}\boldsymbol{m} $ | (15) |
式中
根据贝叶斯原理,待求参数的后验概率密度分布的最大值是其期望值,参数的方差可描述后验概率密度分布与期望之间的离散程度,因此方差可用于描述参数估计的不确定性。参数协方差矩阵的对角线元素表示每个参数估计的方差,而非对角元素表示不同变量之间的相关性,因此参数协方差矩阵可用于研究反演中的不确定性。本文采用Downton[8]和Zhang等[52]的方法,通过计算待求参数的协方差矩阵
| $ {\boldsymbol{C}}_{\boldsymbol{m}}={\sigma }_{n}^{2}{\left[\boldsymbol{F}^{\mathrm{T}}\boldsymbol{F}\right]}^{-1} $ | (16) |
式中:
利用不同弹性参数表示的反射系数近似式可得到对应的待求参数组合。本文分别计算了最大入射角度分别为30°、40°、50°时的反演协方差矩阵。协方差矩阵中某元素的数值越大,表明反演该元素对应的参数的不确定性越大。结合前人的研究成果,本文将反演协方差矩阵中元素值小于0.05作为反演不确定性较小的定量评价标准。
3.2 结果分析 3.2.1 PP波PP波在不同最大角度下的反演协方差矩阵如图 6所示。由图可见,对于所有的待求参数组合,反演协方差矩阵中各元素的数值都随着PP波数据的最大入射角度的增加而减小,这表明入射角度越大,反演各个参数的不确定性越小。当PP波数据的最大角度为30°时,只有

|
图 6 不同角度数据PP波反演不同弹性参数时的协方差矩阵 最大入射角度分别为30°(a)、40°(b)、50°(c)。左为反演 |
PSV波在不同入射角下的协方差矩阵如图 7所示。由图可见,当PSV波的最大角度为30°时,只有

|
图 7 不同角度PSV波反演不同弹性参数时的协方差矩阵 最大纵波入射角度分别为30°(a)、40°(b)、50°(c),对应的横波反射角分别为23.6°、30.9°、37.8° ( |
由于单独利用PP波反演
根据PP波和PSV波近似式(式(1)~式(6)),PP-PSV波联合反演不同参数的不确定性如图 8所示。由图可见,当最大角度(纵波入射角)为30°时,
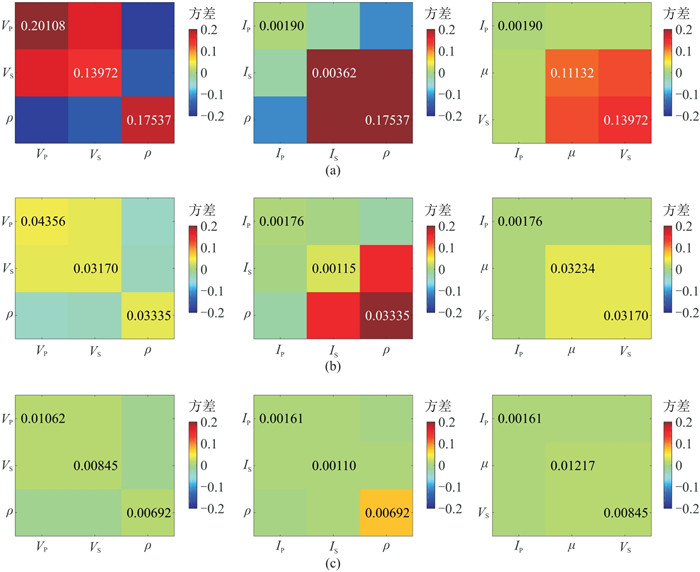
|
图 8 不同角度PP波和PSV波联合反演不同弹性参数时的协方差矩阵 最大纵波入射角度分别为30°(a)、40°(b)、50°(c),对应的横波反射角分别为23.6°、30.9°、37.8° ( |
SH-SH波反演不同弹性参数的不确定性如图 9所示。由图可见,即使使用小角度的数据(< 30°),SH-SH波反演

|
图 9 不同角度SH-SH波反演不同弹性参数时的协方差矩阵 最大入射角度分别为30°(a)、40°(b)、50°(c)。左为反演 |
SV-SV波的反演协方差矩阵如图 10所示。由图可见,与PP波相比,SV-SV波在反演
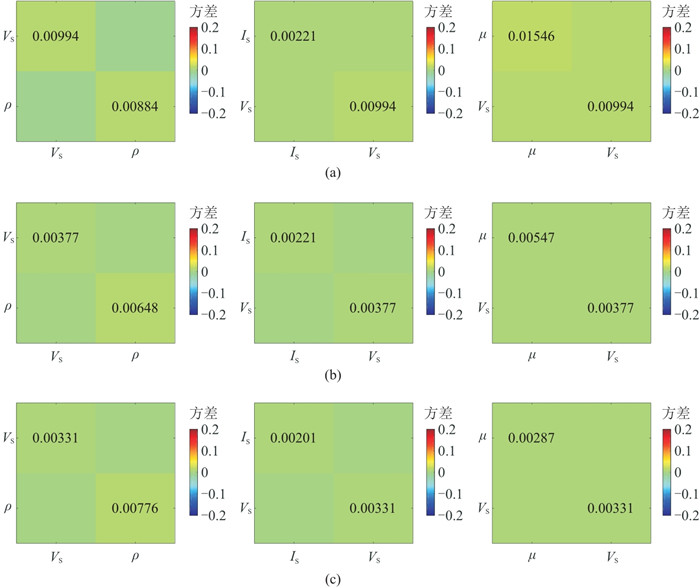
|
图 10 不同角度SV-SV波反演不同弹性参数时的协方差矩阵 最大入射角度分别为30°(a)、40°(b)、50°(c)。左为反演 |
综上所述,对于同一类型地震波的不同待求参数组合,反演的不确定性也存在一定差异。PP波及PP波与PSV波联合反演的最佳待求参数组合为
在数据空间和模型空间可以将
| $ \boldsymbol{F}=\boldsymbol{D}\mathit{\pmb{\Lambda }}{\boldsymbol{M}}^{\mathrm{T}} $ | (17) |
式中:
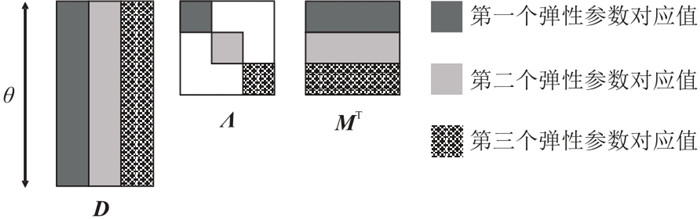
|
图 11 线性正演算子奇异值分解示意图[54] |
通常可以用条件数描述反演的不适定性,它为
| $ \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\left(\boldsymbol{F}\right)=‖\boldsymbol{F}‖\cdot ‖\boldsymbol{F}^{-1}‖ $ | (18) |
对于反演而言,条件数较大的反演称为病态,条件数较小的反演称为良态。因此,可进一步利用条件数随最大入射角的变化分析线性反演的不适定性。为便于直观显示,本文将特征值和条件数的单位均用dB(即
根据不同反射系数近似式构建
根据PP波反射系数近似式(式(1))构建
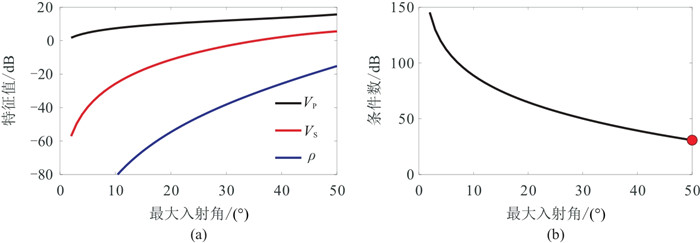
|
图 12 PP波反演的特征值(a)和条件数(b)随最大入射角的变化关系 |
PSV波反演的特征值及条件数随最大入射角的变化情况如图 13所示,PSV波反演仅有2个待反演参数,其中
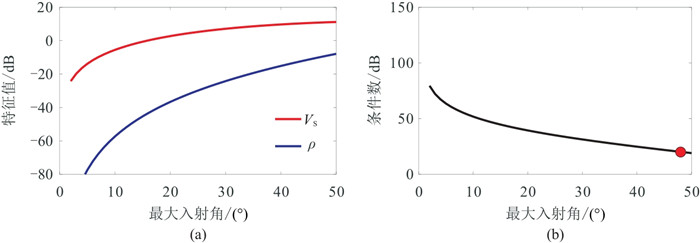
|
图 13 PSV波反演的特征值(a)和条件数(b)随最大入射角的变化关系 |
PP波和PSV波联合反演的特征值及条件数随最大入射角的变化情况如图 14所示。由图可见,在三个特征值中
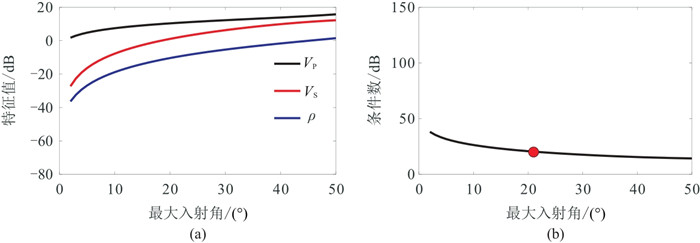
|
图 14 PP波和PSV波联合反演的特征值(a)和条件数(b)随最大入射角的变化关系 |
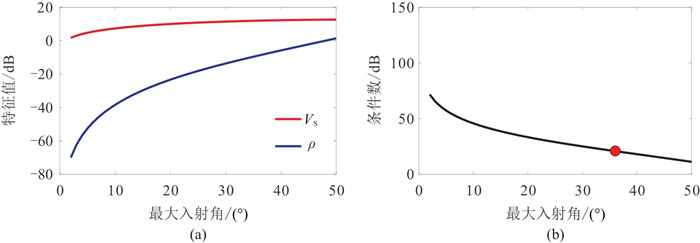
SH-SH反演的特征值及条件数随最大入射角的变化情况如图 15所示。与PSV波类似,SH-SH波反演仅有2个待反演参数,其中
|
图 15 SH-SH波反演的特征值(a)和条件数(b)随最大入射角的变化关系 |
SV-SV波反演的特征值及条件数随最大入射角的变化情况如图 16所示。SV-SV波反演仅有2个待反演参数,其中

|
图 16 SV-SV波反演的特征值(a)和条件数(b)随最大入射角的变化关系 |
综上所述,根据反演协方差矩阵和反演条件数可得到不同类型地震波反演弹性参数的反演能力如表 2所示。从表中可以看出,横波(SV-SV波和SH-SH波)在反演等横波阻抗
|
|
表 2 不同类型地震波反演弹性参数时的可行性分析 |
本文基于不同类型地震波反射系数近似式,构建线性反演框架,利用反演协方差矩阵和反演条件数对比、分析了地震纵、横波对不同弹性参数的反演能力。理论分析验证了横波在反演密度、剪切模量、横波速度等参数方面具有良好的应用潜力,可为横波反演方法研究提供有力的理论支撑。与转换横波相比,横波的处理过程更为简单,在弹性参数反演及储层预测方面具有良好的应用前景。
需要说明的是,以上理论分析并没有引入正则化,这是因为不同的正则化方法会不同程度地降低反演结果的不确定性和不适定性,不利于客观地分析不同类型地震波的反演能力。而在实际地震数据反演中,则需要合理使用正则化以降低反演结果的不确定性。另外,在分析中假设不同类型的地震波数据具有相同的信噪比,这一假设可能与应用中的实际情况并不一致。
附录A 不同类型地震波的线性正演算子F表达式根据PP波反射系数近似式(1),待求解参数为纵波速度VP、横波速度VS和密度ρ时,入射角度分别为
| $ \boldsymbol{F}=\left[\begin{array}{ccc} \frac{1}{2} \sec ^2 \theta_1 & -4 \gamma^2 \sin ^2 \theta_1 & \frac{1}{2}\left(1-4 \gamma^2 \sin ^2 \theta_1\right) \\ \frac{1}{2} \sec ^2 \theta_2 & -4 \gamma^2 \sin ^2 \theta_2 & \frac{1}{2}\left(1-4 \gamma^2 \sin ^2 \theta_2\right) \\ \,\,\,\,\,\,\,\,\,\,\,& \vdots & \\ \frac{1}{2} \sec ^2 \theta_N & -4 \gamma^2 \sin ^2 \theta_N & \frac{1}{2}\left(1-4 \gamma^2 \sin ^2 \theta_N\right) \end{array}\right] $ | (A-1) |
式中
根据PSV波反射系数近似式(式(4)),待求解参数为VS和ρ时,入射角度分别为
| $ \boldsymbol{F}=\left[\begin{array}{l}\frac{2\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}}{\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{1}}\left(\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\phi }_{1}-\gamma \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{1}\right)-\frac{\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{1}}{2\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{1}}\left(1-2\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\phi }_{1}+2\gamma \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{1}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{1}\right)\\ \frac{2\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{2}}{\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{2}}\left(\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\phi }_{2}-\gamma \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{2}\right)-\frac{\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{2}}{2\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{2}}\left(1-2\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\phi }_{2}+2\gamma \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{2}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{2}\right)\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots & \\ \frac{2\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{N}}{\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{N}}\left(\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\phi }_{N}-\gamma \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{N}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{N}\right)-\frac{\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{N}}{2\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{N}}\left(1-2\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\phi }_{N}+2\gamma \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{N}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_{N}\right)\end{array}\right] $ | (A-2) |
根据SH-SH波反射系数近似式(9),待求解参数为VS和ρ时,SH波入射角度分别为
| $ \boldsymbol{F}=\left[\begin{array}{l}-\frac{1}{2}\left(1-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}{\phi }_{1}\right)-\frac{1}{2}\\ -\frac{1}{2}\left(1-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}{\phi }_{2}\right)-\frac{1}{2}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, \vdots & \\ -\frac{1}{2}\left(1-\mathrm{t}\mathrm{a}{\mathrm{n}}^{2}{\phi }_{N}\right)-\frac{1}{2}\end{array}\right] $ | (A-3) |
根据SV-SV波反射系数近似式(式(12)),待求解参数为VS和ρ时,SV波入射角和透射角的平均值分别为
| $ \boldsymbol{F}=\left[\begin{array}{cc} -\frac{1}{2}\left(\frac{1}{\cos ^2 \bar{\phi}_1}-8 \sin ^2 \bar{\phi}_1\right) & -\frac{1}{2}\left(1-4 \sin ^2 \bar{\phi}_1\right) \\ -\frac{1}{2}\left(\frac{1}{\cos ^2 \bar{\phi}_2}-8 \sin ^2 \bar{\phi}_2\right) & -\frac{1}{2}\left(1-4 \sin ^2 \bar{\phi}_2\right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\, \vdots \\ -\frac{1}{2}\left(\frac{1}{\cos ^2 \bar{\phi}_N}-8 \sin ^2 \bar{\phi}_N\right) & -\frac{1}{2}\left(1-4 \sin ^2 \bar{\phi}_N\right) \end{array}\right] $ | (A-4) |
当待求解参数为其他弹性参数时,根据不同类型地震波的反射系数近似式即可得到对应的
| [1] |
郭强, 雒聪, 刘红达, 等. 自适应优化参数模拟退火的叠前地震联合反演方法[J]. 石油地球物理勘探, 2023, 58(3): 670-679. GUO Qiang, LUO Cong, LIU Hongda, et al. Prestack seismic hybrid inversion based on simulated annealing algorithm with adaptive optimization parameters[J]. Oil Geophysical Prospecting, 2023, 58(3): 670-679. DOI:10.13810/j.cnki.issn.1000-7210.2023.03.020 |
| [2] |
RUSSELL B H, HEDLIN K, HILTERMAN F J, et al. Fluid-property discrimination with AVO: A Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [3] |
RUSSELL B H, GRAY D, HAMPSON D P. Linearized AVO and poroelasticity[J]. Geophysics, 2011, 76(3): C19-C29. DOI:10.1190/1.3555082 |
| [4] |
DE NICOLAO A, DRUFUCA G, ROCCA F. Eigenvalues and eigenvectors of linearized elastic inversion[J]. Geophysics, 1993, 58(5): 670-679. DOI:10.1190/1.1443451 |
| [5] |
WANG Y. Simultaneous inversion for model geometry and elastic parameters[J]. Geophysics, 1999, 64(1): 182-190. DOI:10.1190/1.1444514 |
| [6] |
BLOM N, BOEHM C, FICHTNER A. Synthetic inversions for density using seismic and gravity data[J]. Geophysical Journal International, 2017, 209(2): 1204-1220. DOI:10.1093/gji/ggx076 |
| [7] |
ROY B, ANNO P, GURCH M. Imaging oil-sand reservoir heterogeneities using wide-angle prestack seismic inversion[J]. The Leading Edge, 2008, 27(9): 1192-1201. DOI:10.1190/1.2978982 |
| [8] |
DOWNTON J E. Seismic Parameter Estimation from AVO Inversion [D]. University of Calgary, Calgary, 2005.
|
| [9] |
曹俊兴, 薛雅娟, 田仁飞, 等. 深层碳酸盐岩储层含气性检测方法技术研究[J]. 石油物探, 2019, 58(1): 9-16. CAO Junxing, XUE Yajuan, TIAN Renfei, et al. Advances in hydrocarbon detection in deep carbonate reservoirs[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 9-16. |
| [10] |
GRANLI J R, ARNTSEN B, SOLLID A, et al. Imaging through gas-filled sediments using marine shear-wave data[J]. Geophysics, 1999, 64(3): 668-677. DOI:10.1190/1.1444576 |
| [11] |
AVSETH P, MUKERJI T, MAVKO G. Quantitative Seismic Interpretation: Applying Rock Physics Tools to Reduce Interpretation Risk[M]. Cambridge: Cambridge University Press, 2005.
|
| [12] |
CRAMPIN S. Evaluation of anisotropy by shear-wave splitting[J]. Geophysics, 1985, 50(1): 142-152. DOI:10.1190/1.1441824 |
| [13] |
DUFFAUT K, ALSOS T, ROGNØ H, et al. Shear-wave elastic impedance[J]. The Leading Edge, 2000, 19(11): 1222-1229. DOI:10.1190/1.1438510 |
| [14] |
GONG X, DU Q, ZHAO Q. SP-and SS-imaging for 3D elastic reverse time migration[J]. Geophysics, 2018, 83(1): A1-A6. DOI:10.1190/geo2017-0286.1 |
| [15] |
KAZEI V, ALKHALIFAH T. Scattering radiation pattern atlas: What anisotropic elastic properties can body waves resolve?[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(3): 2781-2811. DOI:10.1029/2018JB016687 |
| [16] |
王赟, 孙丽霞, 李栋青, 等. 勘探地震中的六分量观测[J]. 石油物探, 2021, 60(1): 13-24. WANG Yun, SUN Lixia, LI Dongqing, et al. Six-component observation for exploration seismology[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 13-24, 33. |
| [17] |
王波, 聂其海, 陈进娥, 等. 四维多波地震在油藏动态监测中的应用[J]. 石油地球物理勘探, 2021, 56(2): 340-345. WANG Bo, NIE Qihai, CHEN Jine, et al. Application of 4D multi-component seismic survey in dynamic reservoir monitoring[J]. Oil Geophysical Prospecting, 2021, 56(2): 340-345. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.016 |
| [18] |
代福材, 张峰, 李向阳, 等. 多波联合反演研究进展[J]. 石油物探, 2021, 60(1): 57-69. DAI Fucai, ZHANG Feng, LI Xiangyang, et al. Progress of multi-wave joint inversion[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 57-69. |
| [19] |
李向阳, 张少华. 勘探地震中横波分裂研究四十年回顾[J]. 石油物探, 2021, 60(2): 190-209. LI Xiangyang, ZHANG Shaohua. Forty years of shear-wave splitting in seismic exploration: An overview[J]. Geophysical Prospecting for Petroleum, 2021, 60(2): 190-209. DOI:10.3969/j.issn.1000-1441.2021.02.002 |
| [20] |
BHATTACHARYA S N. Exact solutions of SH wave equation for inhomogeneous media[J]. Bulletin of the Seismological Society of America, 1970, 60(6): 1847-1859. DOI:10.1785/BSSA0600061847 |
| [21] |
AKI K, RICHARDS P G. Quantitative Seismology: Theory and Methods[M]. San Francisco: W. H. Freeman and Co, 1980.
|
| [22] |
VIRIEUX J. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 1984, 49(11): 1933-1942. DOI:10.1190/1.1441605 |
| [23] |
姚振兴, 徐大方. 关于一种新型横波震源(SH型)的探讨[J]. 地球物理学报, 1986, 29(4): 382-389. YAO Zhenxing, XU Dafang. A pure shear wave source for reflection prospecting[J]. Chinese Journal of Geophysics, 1986, 29(4): 382-389. DOI:10.3321/j.issn:0001-5733.1986.04.008 |
| [24] |
FU L Y, BOUCHON M. Discrete wavenumber solutions to numerical wave propagation in piecewise heterogeneous media: I. Theory of two-dimensional SH case[J]. Geophysical Journal International, 2004, 157(2): 481-498. DOI:10.1111/j.1365-246X.2004.02135.x |
| [25] |
王美霞, 杨顶辉, 宋国杰. 二维SH波方程的半解析解及其数值模拟[J]. 地球物理学报, 2012, 55(3): 914-924. WANG Meixia, YANG Dinghui, SONG Guojie. Semi-analytical solutions and numerical simulations of 2D SH wave equation[J]. Chinese Journal of Geophysics, 2012, 55(3): 914-924. |
| [26] |
WON I J, CLOUGH J W. A new torsional shear-wave generator[J]. Geophysics, 1981, 46(11): 1607-1608. DOI:10.1190/1.1441168 |
| [27] |
詹正彬, 姚姚. 多波及横波地震勘探[M]. 北京: 地质出版社, 1994. ZHAN Zhengbin, YAO Yao. Multi Wave and Transverse Wave Seismic Prospecting[M]. Beijing: Geology Press, 1994. |
| [28] |
DASIOS A, MCCANN C, ASTIN T R, et al. Seismic imaging of the shallow subsurface: shear-wave case histories[J]. Geophysical Prospecting, 1999, 47(4): 565-591. DOI:10.1046/j.1365-2478.1999.00138.x |
| [29] |
BUSH I, CRAMPIN S. Paris Basin VSPs: case history establishing combinations of fine-layer (or lithologic) anisotropy and crack anisotropy from modelling shear wavefields near point singularities[J]. Geophysical Journal International, 1991, 107(3): 433-447. DOI:10.1111/j.1365-246X.1991.tb01405.x |
| [30] |
LI X, CRAMPIN S. Linear-transform techniques for processing shear-wave anisotropy in four-component seismic data[J]. Geophysics, 1993, 58(2): 240-256. DOI:10.1190/1.1443409 |
| [31] |
THOMSEN L. Converted-wave reflection seismo-logy over inhomogeneous, anisotropic media[J]. Geophysics, 1999, 64(3): 678-690. DOI:10.1190/1.1444577 |
| [32] |
LI X Y, YUAN J. Converted-wave moveout and conversion-point equations in layered VTI media: theory and applications[J]. Journal of Applied Geophysics, 2003, 54(3/4): 297-318. |
| [33] |
李录明, 罗省贤. 多波资料处理及解释方法的研究进展[J]. 石油地球物理勘探, 2006, 41(6): 663-671. LI Luming, LUO Shengxian. Progress in study of multi-wave data processing and interpretation[J]. Oil Geophysical Prospecting, 2006, 41(6): 663-671. DOI:10.3321/j.issn:1000-7210.2006.06.011 |
| [34] |
ZHANG F, WANG Y. Wavelet-preserved PP-and PS-wave registration[J]. Journal of Geophysics and Engineering, 2010, 7(4): 395-403. DOI:10.1088/1742-2132/7/4/006 |
| [35] |
WANG Y, WANG C, LI J, et al. Frequency-dependent S-wave splitting parameters analysis: A case study from azimuthal PS data, Sanhu area of the Qaidam Basin, China[J]. Geophysics, 2019, 84(6): B375-B386. DOI:10.1190/geo2018-0627.1 |
| [36] |
DAI H, LI X Y, CONWAY P. Imaging beneath gas clouds using 3D prestack Kirchhoff time migration of PS-converted waves: A case study from the North Sea[J]. The Leading Edge, 2007, 26(4): 522-529. DOI:10.1190/1.2723216 |
| [37] |
VEIRE H H, LANDRØ M. Simultaneous inversion of PP and PS seismic data[J]. Geophysics, 2006, 71(3): R1-R10. DOI:10.1190/1.2194533 |
| [38] |
ZHANG F. Joint Inversion of Seismic PP-and PS-Waves in the Ray Parameter Domain[D]. Imperial College London, London, 2010.
|
| [39] |
芦俊, 王赟, 石瑛. 利用多波地震与测井数据联合反演预测煤岩的坚固性[J]. 地球物理学报, 2011, 54(11): 2967-2972. LU Jun, WANG Yun, SHI Ying. Coal hardness prediction using joint inversion of multi-wave seismic data and logging[J]. Chinese Journal of Geophysics, 2011, 54(11): 2967-2972. DOI:10.3969/j.issn.0001-5733.2011.11.027 |
| [40] |
ALKAN E, HARDAGE B. Directs wave modes produced by vertical and horizontal vibrators[J]. Journal of Seismic Exploration, 2013, 22(2): 147-168. |
| [41] |
GUPTA M, DEANGELO M V, HARDAGE B. PP and SS wave interpretation of a carbonate formation: A case study from the Arbuckle interval in Wellington field, Kansas[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 2082-2087.
|
| [42] |
DENG Z, WU W, JING Y, et al. The joint PP and SH-SH data characterization of structures and reservoirs[C]. Extended Abstracts of 81st EAGE Conference and Exhibition, 2019, 1-5.
|
| [43] |
ZHANG F, LI X. Inversion of the reflected SV-wave for density and S-wave velocity structures[J]. Geophysical Journal International, 2019, 221(1): 1635-1639. |
| [44] |
王波, 张峰, 代福材, 等. VTI介质SH-SH波地震反演方法研究[J]. 地球物理学报, 2023, 66(5): 2112-2122. WANG Bo, ZHANG Feng, DAI Fucai, et al. Study on seismic inversion method of SH-SH wave in VTI media[J]. Chinese Journal of Geophysics, 2023, 66(5): 2112-2122. |
| [45] |
BORTFELD R. Approximations to the reflection and transmission coefficients of plane longitudinal and transverse waves[J]. Geophysical Prospecting, 1961, 9(4): 485-502. DOI:10.1111/j.1365-2478.1961.tb01670.x |
| [46] |
RICHARDS P G, FRASIER C W. Scattering of elastic waves from depth-dependent in homogeneities[J]. Geophysics, 1976, 41(3): 441-458. DOI:10.1190/1.1440625 |
| [47] |
FATTI J L, SMITH G C, VAIL P J, et al. Detection of gas in sandstone reservoirs using AVO analysis: A 3-D seismic case history using the Geostack technique[J]. Geophysics, 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [48] |
ZOU K. S-Zero Stack: A converted wave processing to extract subsurface density information[J]. Geophysics, 2014, 79(3): N1-N10. DOI:10.1190/geo2013-0029.1 |
| [49] |
周竹生. P-SV波和SH波的AVO分析[J]. 石油地球物理勘探, 1993, 28(4): 430-438. ZHOU Zhusheng. AVO analysis of P-SV and SH waves[J]. Oil Geophysical Prospecting, 1993, 28(4): 430-438. |
| [50] |
DAI F, ZHANG F, LI X. SH-SH wave inversion for S-wave velocity and density[J]. Geophysics, 2022, 87(3): A25-A32. |
| [51] |
ZHANG F. Simultaneous inversion for S-wave velocity and density from the SV-SV wave[J]. Geophysics, 2021, 86(2): R187-R195. |
| [52] |
ZHANG F, ZHANG T, LI X. Seismic amplitude inversion for the transversely isotropic media with vertical axis of symmetry[J]. Geophysical Prospecting, 2019, 67(9): 2368-2385. |
| [53] |
WEI Z T, TANG X M. Numerical simulation of radiation, reflection, and reception of elastic waves from a borehole dipole source[J]. Geophysics, 2012, 77(6): D253-D261. |
| [54] |
JIN S, CAMBOIS G, VUILLERMOZ C. Shear-wave velocity and density estimation from PS-wave AVO analysis: Application to an OBS dataset from the North Sea[J]. Geophysics, 2000, 65(5): 1446-1454. |



 张峰, 北京市昌平区府学路18号中国石油大学(北京)油气资源与探测国家重点实验室,102249。Email:
张峰, 北京市昌平区府学路18号中国石油大学(北京)油气资源与探测国家重点实验室,102249。Email: