2. 长江大学地球物理与石油资源学院, 湖北武汉 430100
2. School of Geophysics and Petroleum Resources, Yangtze University, Wuhan, Hubei 430100, China
伴随着石油勘探、开发技术的快速发展,高精度地震勘探要求地震资料的信噪比、分辨率和保真度更高,而高信噪比是高分辨率和高保真度的前提,也是地震资料精细处理和解释的必然要求。在野外地震数据采集过程中,由于地质条件复杂多变、环境噪声多样、设备损耗以及人为因素的干扰,检波器接收到的地震信号往往含有声波、面波、多次波等规则噪声和随机噪声,通过常规组合和叠加方法难以完全去除,导致地震资料信噪比达不到准确刻画地下地质构造的要求,对地震数据的偏移成像和反演等造成了消极影响,因此去除地震资料中的噪声至关重要。
人们提出了一系列传统的地震资料去噪方法:以数学变换为基础的方法,包括傅里叶变换[1]、小波变换[2-3]、Curvelet变换[4]和Seislet变换[5-6]等;基于滤波的方法[7];经验模态分解(Empirical Mode Decomposition,EMD)的方法[8];降秩方法[9-10];压缩感知和字典学习方法等[11-20]。
在基于数学变换的方法中,傅里叶变换具有非常重要的地位,是地震资料处理的基础,但傅里叶变换不能同时兼顾时间域和频率域分辨率。小波变换的提出进一步优化了时间域和频率域窗函数调节问题,具有时域和频域局部化性质,可较好地分析丰富的频率成分和非平稳信号。与小波变换相比,Curvelet变换在去除不规则噪声的同时有效信号的损失较小。Seislet变换可有效压缩含有空间假频的不完整地震数据,首次在地震数据分解和重构过程中预测并更新算子,可节省内存空间、提高运算速度[6]。耿瑜等[11]根据地震数据的频散关系提出了多尺度Dreamlet变换压缩方法,压缩比较Curvelet变换更高,并且在相同的压缩条件下,对压缩、重建后的数据成像,可更好地刻画重要构造。但是,由于地震信号的特征复杂、噪声和有效信号在变换域存在重叠,因此在变换域准确分离噪声而不损伤有效信号的难度较大。
在基于滤波的方法中,Porsani等[12]提出了修正Spitz方法,将全步长预测滤波器修改为半步长,大大提高了噪声压制效果。EMD方法根据数据本身的时间尺度特征分解信号,不需要预设任何基函数。在理论上该方法适用于所有信号分解,尤其在处理非平稳及非线性数据方面优势明显。但该方法存在较严重的端点效应,因此去噪效果不好。
奇异谱分析(Singular Spectrum Analysis,SSA)是经典的降秩方法,通过对由地震数据频率切片构造的Hankel矩阵降秩进行去噪。程文婷等[13]基于自相似性和低秩先验的地震数据去噪方法,通过块匹配算法搜索地震数据的自相似块,再以“自相似块组”为单元,利用低秩约束压制随机噪声。Donoho[14]提出了压缩感知(Compressed Sensing,CS)理论,充分利用信号稀疏性或可压缩性采集、编/解码信号,在降低信号取样要求的同时减少信号处理时间和降低成本。唐刚[15]将CS理论用于地震勘探领域,通过有机结合地震资料采集和数据重建,充分利用地震资料在字典变换域的稀疏化特征,在大幅降低采样率和节约成本的同时,获得了理想的处理效果。以上模型驱动去噪方法的优点是具有可解释性,算法过程中的每一步都具有数学或物理意义,缺点是需要根据某种数据类型设计对应的问题模型,需要更多的先验知识调整参数才能获得更好的效果,而且简单的物理模型往往不能描述高维度地震数据的复杂特征和细微差别。
模型驱动去噪方法较大地提高了地震资料信噪比,但以字典学习和深度学习为代表的数据驱动方法为压制地震数据的随机噪声提供了新思路。在CS理论基础上,Aharon等[16]提出了一种信号表示理论,使用字典代替传统变换域方法的基函数,通过在变换域中选择基函数的最佳组合分离噪声和有效信号。Tang等[17]将字典学习算法引入地震数据处理,有效去除了伪Gibbs现象。Beckouche等[18]通过MOD(Method of Optimal Direction)算法构造学习型字典,结合随机噪声压制过程和字典的训练压制随机噪声。宋维琪等[19]基于K-SVD(K-Singular Value Decomposition)字典学习,根据地震资料本身的特点训练稀疏表示地震资料的最优字典,从而分离噪声与有效信号达到去噪的目的。Wu等[20]利用SGK(Sequence Generalized K-means)算法代替K-SVD字典学习,提出同步随机噪声去除和重建三维地震数据的快速字典学习方法,显著提高了计算效率。
近年来,大数据、人工智能技术的飞速发展为短时间内处理海量数据提供了保障。目前,地震勘探正向超深层、复杂构造、岩性勘探和非常规方向发展,对地震资料的信噪比和保真度提出了更高要求,神经网络的出现为处理以上问题提供了新思路和途径。深度学习与传统的模型驱动方法相比,在给定先验信息的前提下,在应用过程中对参数的调节更少,对于初学者更友好。主要的神经网络结构,如卷积神经网络(Convolutional Neural Network,CNN)[21]、去噪卷积神经网络(Denoising Convolutional Neural Network,DnCNN)[22]、U-Net深度神经网络[23]、前反馈(Back Propagation,BP)神经网络[24]、空洞卷积神经网络[25](Dilated Convolutional Neural Network,DCNN)、残差网络(ResNet)[26]等,在地震随机噪声衰减领域已经取得了较好效果。
本文介绍了传统去噪方法及字典学习、深度学习等数据驱动学习方法,通过简述前人研究成果,展望了深度学习在地震去噪领域的发展前景。
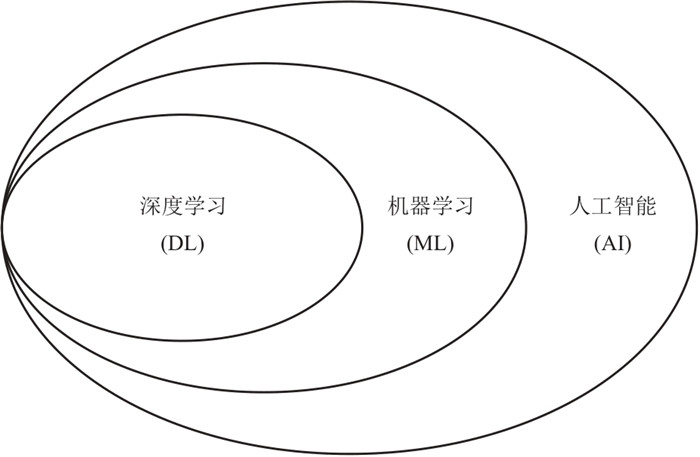
1 深度学习的发展历程20世纪50年代,Turing[27]首次提出了人工智能概念(图 1),机器学习是人工智能的核心,普遍用于人工智能的各个领域;深度学习是机器学习领域的重要组成部分,能够模仿人脑处理和解释数据。随着深度学习的进一步发展,神经网络作为一种机器学习算法出现在大众视野中,它是受人脑运行规律启发的一项技术,旨在从信息处理的角度抽象处理人脑神经元,通过建立模型模拟人脑神经元的运行规律。这些模型按照输入和输出的映射关系构成不同类型的神经网络,从而解决各类实际问题。神经网络建立了输入和输出的复杂映射关系,一般由输入层、输出层和众多隐藏层构成,输入特征通过隐藏层的复杂变换传递到输出层进而得到输出结果,深层节点可以会聚、合并、重组上一层的特征,从而识别复杂特征。因此各种具有独特神经处理单元和复杂层次结构的神经网络不断涌现,Lecun等[21]提出的LeNet在当时的学术界和工业界受到广泛关注,随后不断出现许多典型的神经网络结构,如AlexNet[28]、VGGNet[29]、U-Net、ResNet、循环神经网络(RNN)、生成对抗神经网络(Generative Adversarial Network,GAN)和深度置信等网络,这些网络在图像识别、医学成像、信号处理以及人工地震等领域发挥了巨大作用。
|
图 1 人工智能、机器学习与深度学习的关系 |
本文介绍几种典型的去噪神经网络结构,包括CNN、DnCNN、U-Net、BP、DCNN、ResNet等,并分析网络性能和随机噪声衰减结果。
2.1 CNN首先介绍CNN及其优点,其次阐述CNN的发展现状,再重点描述多粒度特征融合CNN(Multigranularity Feature Fusion CNN,MFFCNN)的网络结构与去随机噪声效果,并对比5种方法的去噪结果,最后总结了CNN的不足。
CNN已经成功用于地震资料随机噪声衰减领域。CNN具有局部连接、权值共享和池化操作的独特操作,大大减小了参数使用量,提高了网络运算效率,最先用于地震随机噪声衰减。
韩卫雪等[30]构建了一种适用于地震资料去噪的CNN,并成功用于海上叠前地震数据和陆地叠后地震数据随机噪声衰减,实验数据显示该方法的随机噪声去除效果优于小波变换、曲波变换等传统方法。针对利用CNN进行地震资料去噪的结构选择具有盲目性的问题,Zhang等[31]利用稀疏自动编码器有效衰减了地震数据随机噪声,并保留了数据的细微特征。Dong等[32]通过构建噪声集训练不同区域的去噪模型,有效抑制了不同地区的地震随机噪声。Yang等[33]提出了一种智能CNN降噪框架,可以自适应地捕捉地震资料中的有效信号,获得去噪信号。利用激活函数指数线性单元(Exponential Linear Units,ELU)和Adam优化算法训练网络,ELU能够缓解负区间的梯度消失,提高了网络对负尺度有效信息的提取能力,有效提升了随机噪声衰减效果。向奎[34]通过改进图像超分辨率重构领域的超分辨率CNN(Super Resolution Convolutional Neural Network,SRCNN)[35]衰减地震道集随机噪声。改进的SRCNN直接从输入图像和输出图像学习端到端的映射,可将含噪道集视为低分辨率图像,去噪道集视为高分辨率图像。该映射以从输入图片到输出图片的CNN的形式表示。SRCNN兼具结构简单和参数调整方便的优点,不仅图像处理水平很高,而且实现了即时可用的高速实用性。
大多数CNN采用监督学习方式衰减地震随机噪声,需要构建大量的无噪数据和含噪数据作为训练集,由于难以获得无噪数据,导致监督学习方法的去噪效果不佳,降低了网络的泛化性。使用合成地震数据训练网络时,由于合成地震记录与真实地震记录在结构上相差较大,大大降低了监督学习方法的实际地震数据去噪效果。
无监督学习克服了难以获得实际无噪地震数据的困难,基于概率密度和输入样本的相似性学习噪声数据和有效信号的相似性,达到压制随机噪声的目的。用于地震数据处理领域的无监督学习方法主要有三类:第一类是自动编码器(Autoencoder,AE),可以高效地处理含噪地震数据,并且非线性表示能力较好;第二类是深度图像先验(Deep Image Prior,DIP),此类方法需要满足两个前提,即噪声是独立分布的,且地震信号的自相关性更强。但是,在网络训练时必须要确定噪声衰减的最优迭代次数;第三类是自监督深度学习(Self-Supervised Learning),将含噪地震数据作为输入和标签训练神经网络,通过自监督损失函数去噪。自监督学习方法可以引入监督学习网络的训练模型权重训练初次全连接层,降低了网络模型的训练时间成本。
Fang等[36]提出了一种新型无监督学习的地震随机噪声衰减方法,可以直接使用含噪标签训练网络,有效提高了地震资料的信噪比。但该方法对非零均值噪声的衰减效果较差,需要进行零均值校正。Chen等[37]提出了一种新的自监督学习地震数据去噪方法,利用含噪数据训练网络,对丢弃层产生的原始噪声数据进行伯努利采样训练神经网络,在测试过程中采用蒙特卡罗(Monte Carlo)自积分法进一步提高了网络的去噪效果。Wang等[38]提出了一种基于模型的地震数据无监督深度学习的去随机噪声方法,在物理模型部分改进了迭代软阈值算法(Iterative Soft Threshold Algorithm,ISTA),并设计了一个平滑惩罚损失函数计算可训练参数的梯度;将由f-x反褶积处理的含噪地震数据作为网络输入,经过网络的进一步处理后输出去噪地震剖面,不需要地震数据的先验信息,具有良好的泛化性,去噪效果优于传统方法以及监督学习、无监督学习去噪方法。
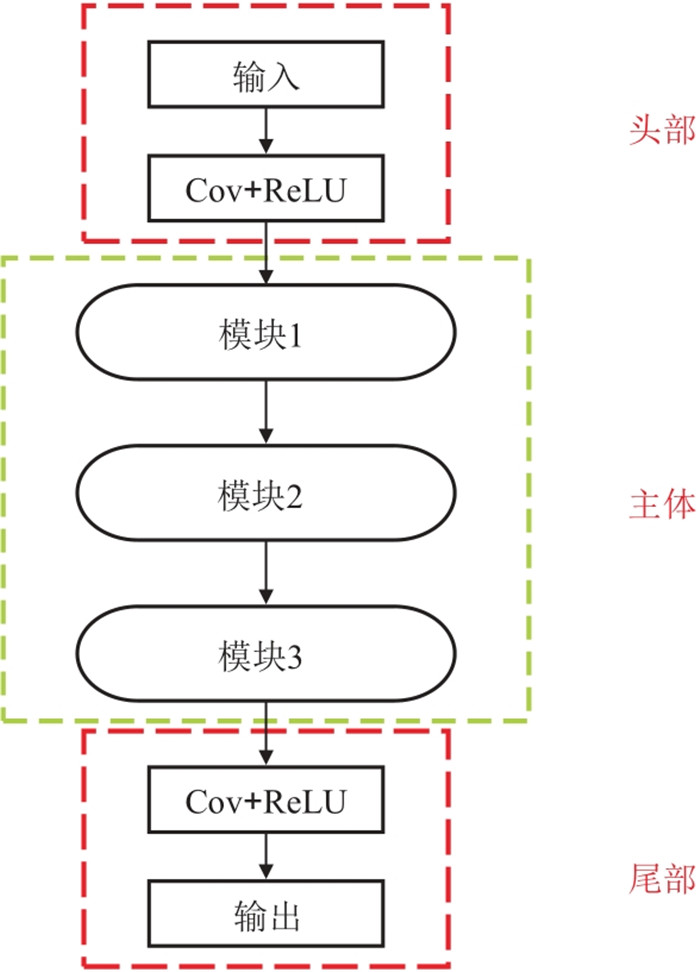
传统的基于CNN的地震随机噪声压制方法大多使用固定大小的卷积核,不能通过可变大小的卷积核提取不同尺度的地震信号特征。为了解决这一问题,Feng等[39]使用具有不同尺寸卷积核的多粒度特征融合模块(Multigranularity Feature Fusion,MFF)提取地震数据中不同尺度的波动特征,并利用特征融合结构的特征更好地处理地震数据的细节和纹理信息,提出了MFFCNN地震随机噪声衰减方法,提高了地震资料去噪效果。首先,MFFCNN的头部将输入数据经卷积层(Cov)和激活函数ReLU(Rectified Linear Unit)提取初步特征;然后,将获得的特征图送入网络结构主体,模块1、模块2、模块3分别采用3×3、5×5、7×7的卷积核分别从不同的粒度提取潜在特征;最后,经过尾部的卷积层和激活函数还原输出(图 2)。
|
图 2 MFCNN结构[39] |
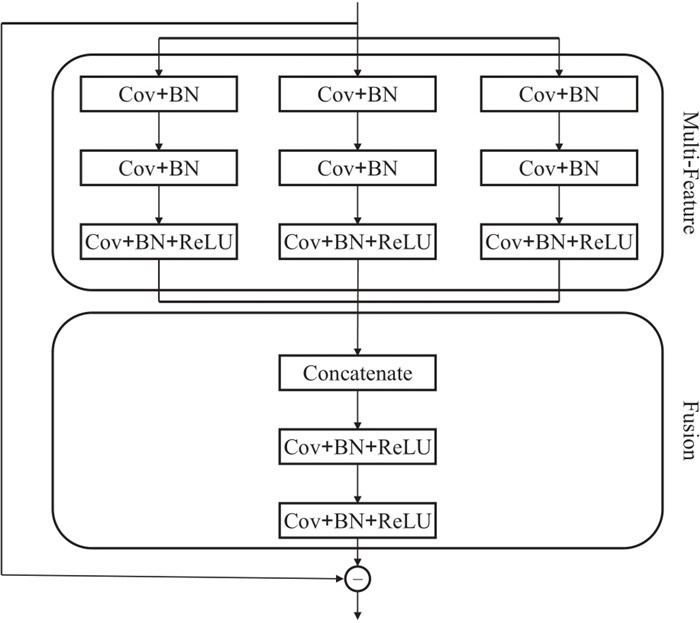
图 3为MFFCNN主体部分的三个MFF模块详细结构。由图可见,每个卷积层的卷积核数量为16,保证了输出图像的通道数与输入图像一致。通过不同尺寸的卷积核的模块输出16×3的通道数连接张量,通过卷积层融合成一个16×1的张量,使MFF模块的输出图像尺寸与输入保持一致。最后,将MFF模块输入与MFF模块的输出的残差作为网络输出。
|
图 3 MFFCNN主体部分的三个MFF模块详细结构[39] BN为批标准化(Batch Normalization)。 |
图 4为不同方法的去噪结果。由图可见:合成地震数据(图 4a)添加标准差σ=1.3的随机噪声后同相轴模糊不清(图 4b),经过6种方法压制噪声后信噪比都得到了相应提高(图 4c~图 4h),且都存在一定的有效信号损失和同相轴弯曲,但是MFFCNN处理结果的同相轴最清晰,波形畸变最小,在压制随机噪声的同时,更好地保证了地震信号的保真度(图 4h)。

|
图 4 不同方法的去噪结果[39] (a)合成地震记录;(b)图a添加随机噪声(σ=1.3);(c)块追踪三维滤波(BM3D);(d)非局部Haar变换(NLH);(e)加权核范数最小化(WNNM);(f)DnCNN;(g)注意力引导网络(ADNET);(h)MFFCNN |
表 1为不同去噪方法压制噪声后的峰值信噪比(PSNR)和结构相似度指数(Structural Similarity Index,SSIM),其中SSIM的值越接近1代表噪声压制前、后的地震剖面越相似、效果越好。由表可见,随着输入数据加入的随机噪声越大,各种方法去噪后的PSNR降低,但是MFFCNN的去噪效果始终优于其他方法,其PSNR、SSIM始终大于29.575 dB、0.9474。
|
|
表 1 不同去噪方法压制噪声后的PSNR(dB)/SSIM[39] |
CNN作为一种BP网络,自由参数的数量较少,可以提高训练效率,并且减少特征损失。但是,CNN在压制地震随机噪声时具有一定的盲目性,不同的CNN结构对地震随机噪声的压制效果不同。
2.2 DnCNNDnCNN在CNN的基础上使用了更深层次的网络结构、残差算法以及批标准化,噪声衰减效果更好。Xu等[40]首先在图像去噪领域提出了DnCNN。为了在CNN的基础上进一步压制地震随机噪声、提高地震数据的信噪比,Yu等[41]将DnCNN用于地震随机噪声衰减,分别使用不同的卷积层个数进行去噪试验,结果表明卷积层个数为17时随机噪声衰减效果最好。但是,DnCNN仍存在特征图利用不充分、细节特征丢失的缺点,导致去噪地震资料存在一定的波形失真。为此,张超铭等[42]进一步改进DnCNN,使网络更适用于地震数据去噪。改进模型Constrained-DnCNN在浅层网络引入约束卷积提取低层特征并传递到深层网络,因此能够自主学习噪声残差特征,并借鉴残差网络的结构设计,通过跳连接(Skip Connection)提高网络训练效果。结果表明,Constrained-DnCNN可以实现盲去噪,并进一步增强去噪效果,提高地震数据信噪比。针对DnCNN对复杂地震数据的去噪效果较差、存在波动特征损失的问题,钟铁等[43]提出了多分支去噪神经网络(Diverse Branch Block Convolutional Neural Networks,DBBCNN),对沙漠地区复杂地震数据的随机噪声衰减实验结果表明,DBCNN可以更好地压制随机噪声,去噪地震数据的信噪比较高。Zhong等[44]利用多尺度去噪卷积神经网络(Multiscale Denoising Convolutional Neural Network,MSDCNN)压制地震随机噪声,可在不同尺度提取地震数据特征,其跨尺度交互功能提高了去噪精度,特别对低信噪比地震资料的去噪效果更好,并在更大程度上保留了有效信号的振幅特性。
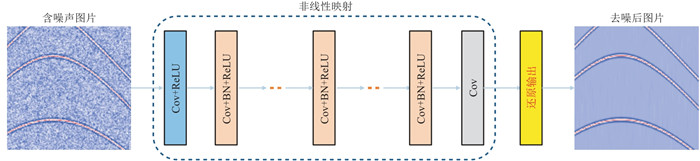
DnCNN的输入信号为含噪地震数据,网络共有17个卷积层,前16层的卷积核尺寸为3×3,步长为1,卷积核数量为64。为了使输出特征图的大小与网络输入匹配,在卷积后进行填充0操作,避免了图像的特征损失。该网络在第1个卷积层中使用激活函数ReLU对含噪数据归一化处理;第2~第16卷积层添加批归一化处理,加快网络收敛速度;第17卷积层通过卷积还原输出,网络的输出为预测的随机噪声,经过还原输出为去噪数据(图 5)。
|
图 5 DnCNN去噪网络结构[41] |
DnCNN是一种利用残差学习和BN进行去噪的CNN,由于DnCNN为没有池化层的全卷积网络结构,导致内部数据结构和空间层级化信息丢失,造成去噪地震数据的少部分纹理特征丢失、卷积核感受野较小以及捕获邻域信息能力不足的问题。
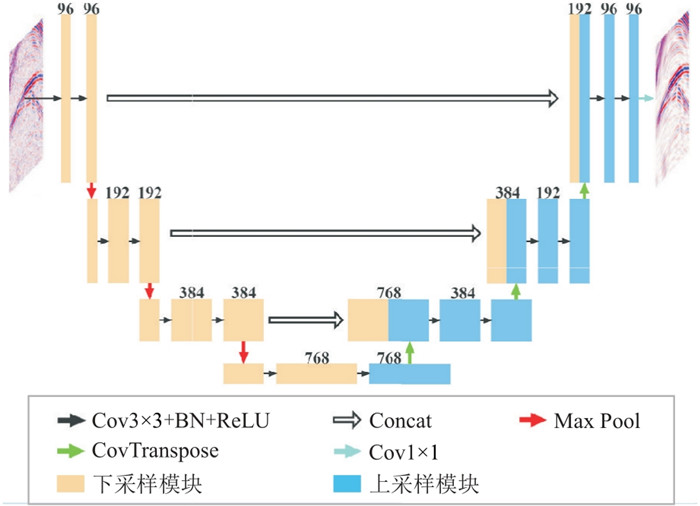
2.3 U-netU-Net是改进的全卷积网络,因其结构的形状类似于字母“U”而得名(图 6)。U-Net最早由Ronneberger等[23]提出,目前已成为深度学习领域最重要的方法之一,同时也普遍用于地震随机噪声衰减。
|
图 6 U-Net结构[48] U-Net主要结构包括压缩通道和扩展通道。首先在压缩通道中重复采用卷积、池化等不同操作,提取不同层次的输入图像特征,然后在扩展通道采用反卷积运算,再在压缩通道将相应的特征图像拼接,最终输出去噪地震数据(与输入图像尺寸相同)。 |
在U-Net结构的基础上,王钰清等[45]提出了一种以数据增广和CNN为基础的U型网络,为解决深度学习中的数据标签问题提供了新的途径和方法。罗仁泽等[46]构建了一种较U-Net更深的残差U型网络(RU-Net),该网络具有强大的特征捕获能力,引入残差块后,通过对提取的随机噪声进行二次消化、学习,尽量保留一次学习可能丢失的随机噪声特征,使学习到的噪声特征更接近噪声本质,因此随机噪声压制效果优于U-Net。Bai等[47]搭建了一种基于U-Net的深度学习网络压制地震随机噪声,与U-Net不同的是在编码器部分添加了Dropout防止网络过拟合,可以提高网络的运行效率,网络输出为含噪地震数据和去噪地震数据之间的残差。将余弦相似度指数作为损失函数,可更好地保持去噪地震数据同相轴的横向连续性。Liu等[48-49]在前人的基础上基于U-Net提出了融入自相似性的无监督地震数据噪声压制(Noise2Sim)方法,采用相似图像采样器生成训练对,提出了相似驱动的自监督学习(Similarity-informed Self-learning,SISL)模型。在训练过程中引入正则化约束的损失函数约束有效信号损失,有效提高了地震数据信噪比。
图 6为U-Net结构。由图可见,U-Net网络主要分为编码和解码两个部分,其中编码部分使用卷积核尺寸为3×3的卷积与BN和ReLU串联,使用最大池化(Max Pooling)压缩特征图尺寸,转置卷积(CovTranspose)的作用是重构特征图,使用Conat跳连接缓解网络训练过程的过拟合。
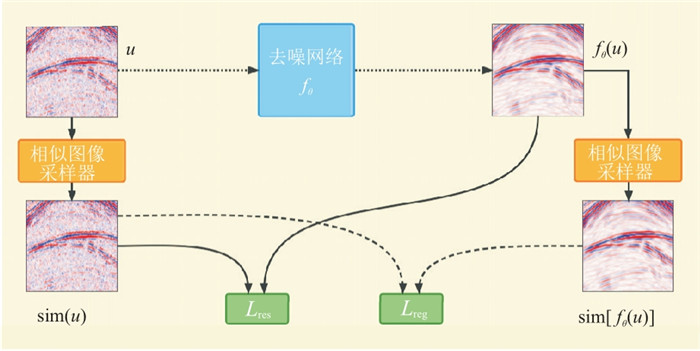
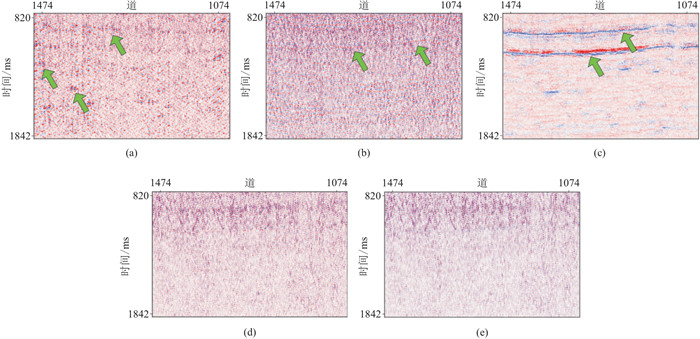
图 7为SISL结构图。由图可见:将原始含噪数据u送入相似图像采样器中生成相似噪声图像sim(u)。然后,将u作为去噪网络fθ的输入得到去噪后的数据fθ(u)。再将fθ(u)送入相似图像采样器得到sim[fθ(u)]。使用的混合损失函数由两部分组成:①fθ(u)与sim(u)之间的均方误差损失函数Lres;②考虑到sim[fθ(u)]和sim(u)之间的差异,引入正则化约束的均方误差损失函数Lreg,可以有效地减少有效信号的损失。图 8、图 9分别为不同算法的去噪结果、去除的噪声剖面。由图可见:①K-SVD(图 8b)和非局部均值(Nonlocal Means,NLM)(图 8c)方法去噪剖面信噪比较高,同相轴较清晰,但是相对于含噪地震数据(图 8a),图 8b、图 8c损失了部分波动特征,还存在一些条带噪声和剩余随机噪声(图 9a、图 9b),并使部分同相轴过于平滑;②由于图 8a中存在非零均值噪声,由噪声数据的无监督去噪方法(Noise2Void)虽然更好地保留了波动特征(图 8d),但噪声剖面残存有效信号(图 9c);③Noise2Sim(图 8e)和SISL(图 8f)方法较好地保护了有效信号并压制了随机噪声,二者总体上去噪效果接近,但图 8e左上角存在部分波形错乱,噪声剖面(图 9d、图 9e)的颜色指示SISL(图 9e)更好地保留了有效信号。因此,SISL方法可以有效地消除随机噪声,并较好地保留有效信号。U-Net通过独特的编码和解码操作,在地震随机噪声衰减领域已取得较好效果,但仍存在模型泛化性受限和地震数据局部细节丢失等问题。
|
图 7 SISL结构图[48] |

|
图 8 不同算法的去噪结果[48] (a)含噪地震数据;(b)K-SVD;(c)NLM;(d)Noise2void;(e)Noise2sim;(f)SISL |
|
图 9 不同算法去除的噪声剖面[48] (a)K-SVD;(b)NLM;(c)Noise2Void;(d)Noise2sim;(e)SISL |
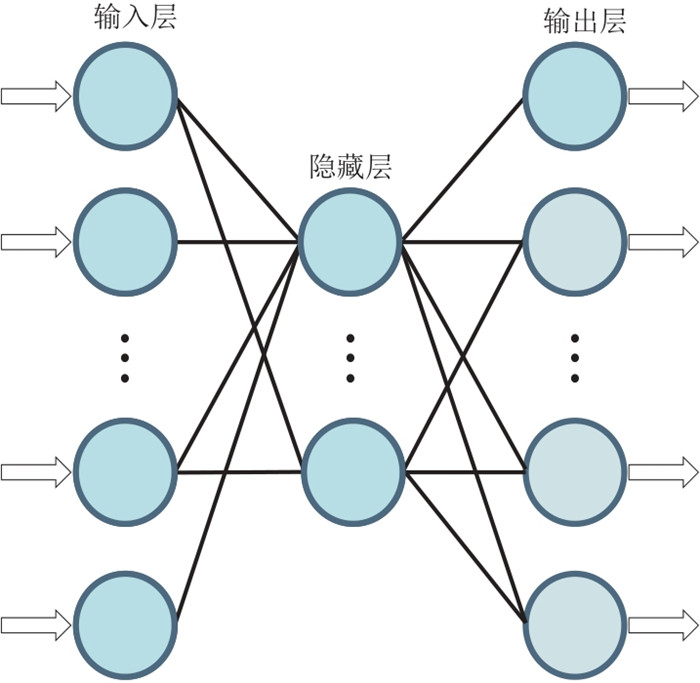
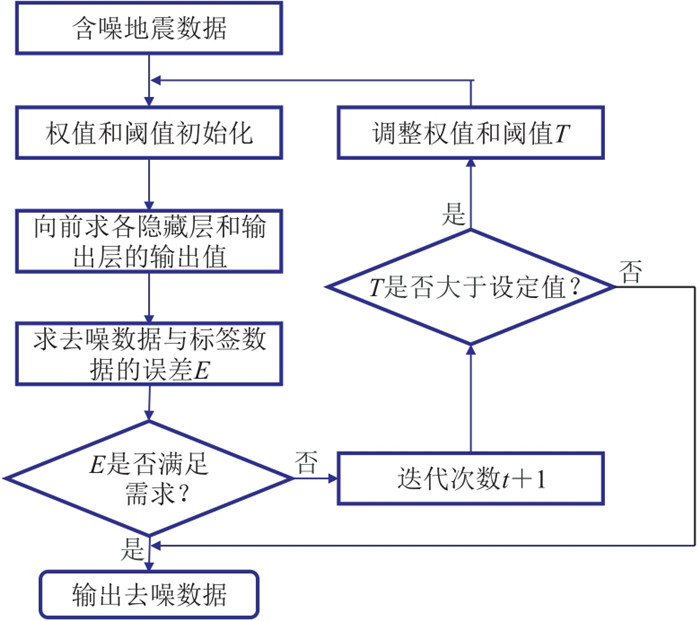
按误差反向传播训练的BP神经网络是一种多层前馈网络,最早由Rumelhart等[24]提出。图 10为BP神经网络结构。由图可见,网络结构主要包括输入层、复杂的隐藏层和输出层,神经元的作用是连接相邻的层并进行相关计算。图 11为BP神经网络工作流程。由图可见:噪声衰减原理是把含噪数据作为输入数据,然后通过隐藏层的处理和反向传播调整权值和参数,输入数据从输入层经过隐藏层逐层处理,然后转入输出层,每一层的神经元状态仅受上一层神经元状态的影响;如果输出结果不及预期,则转入反向传播,即将误差信号沿着连接通路原路返回,不断修改各神经元的权值,使误差信号逐渐降至最小。输出为去除的随机噪声,再用原始含噪数据减去BP神经网络输出的噪声剖面,即可得到去噪地震数据。
|
图 10 BP神经网络结构[24] |
|
图 11 BP神经网络地震数据去噪流程(据文献[24]修改) |
BP神经网络在去噪方面有独特优势,它能自动学习噪声和地震资料之间的函数关系,并且具有网络结构简单、效果好、普适性强等优点。但BP神经网络主要用于处理非线性问题,对于线性问题,噪声衰减效果并不理想。
2.5 DCNNDCNN在DnCNN的基础上扩大了卷积层的感受野,能够进一步缓解池化操作造成的特征细节丢失问题,用于地震随机噪声衰减可更有效地提取地震资料中的波动特征,保留更多细节。顾航[50]提出了一种基于DCNN的地震数据去噪算法解决DnCNN去噪后部分纹理信息丢失问题。将空洞卷积引入DnCNN结构,采用扩大感受野的方式获取更多的地震记录波动特征,以增强网络的特征学习能力。应用空洞卷积改进DnCNN结构构建地震数据去噪模型,通过优化网络扩展率、训练集、网络参数提高模型去噪能力。玉琨[51]基于DnCNN网络结构并结合空洞卷积的优势改进DnCNN算法:利用空洞卷积核代替传统的卷积核,并在不增加参数的情况下扩大CNN的感受野,设计了一个用于地震资料去噪的对称式空洞卷积神经网络(Symmetric Dilated Convolutional Neural Network,SDCNN)。
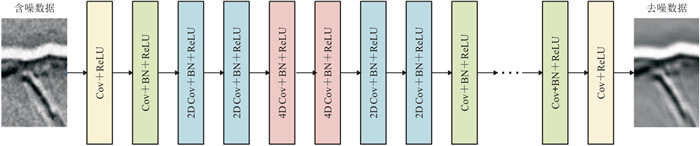
SDCNN将空洞卷积方法引入DnCNN框架,以空洞卷积代替部分传统卷积,为网络提供了更大的感受野,使地震数据的内部数据结构保留更多的有效信息,并避免了丢失大量有效信息的情况发生。SDCNN充分考虑了含噪地震记录与残差之间的关系,扩大了卷积视野,便于恢复地震记录的纹理信息,其结构如图 12所示。含噪数据作为网络结构的输入,经过多层1D、2D、4D卷积层、BN和ReLU激活函数,最终输出结果为去噪数据。
|
图 12 SDCNN结构[53] SDCNN主要包含Cov、BN和ReLU,其中2D Cov和4D Cov分别代表扩张率为2和4的二维卷积。 |
DCNN具有较大的感受野,在提取随机噪声特征时能利用更大范围的背景信息,大大增强了信息捕获能力,既能消除大量的随机噪声,又避免了有效信息的丢失。但由于空洞卷积在常规卷积核的相邻权重之间插入了“0”,因此损失了捕获信息的连续性。
2.6 ResNetHe等[26]提出的ResNet是改进的深层CNN,在图像处理领域引起了巨大反响。通过在卷积层之间添加快捷连接(Shortcut Connection)操作,解决了随着网络层数加深带来的梯度消失问题。何凯[52]提出基于双重残差结构的CNN地震随机噪声压制方法,缓解了CNN的梯度消失问题,可更好地提取地震数据特征。结果表明,该方法在保留有用信息的同时能够更好地压制随机噪声。在地震信号去噪问题中,ResNet通过逐层残差学习,可充分学习信号和噪声特征。在图像处理领域,研究表明重复的配对操作可以有效地提高网络性能。为了进一步提高去噪效果,方文倩等[53]将双重ResNet结构引入地震资料随机噪声衰减,该方法允许将不同层配对操作的两个算子任意组合,可提取丰富的地震数据和随机噪声特征,提高了网络的随机噪声衰减性能。武国宁等[54]结合ResNet的拓扑结构与平稳小波变换(Wavelet)压制地震随机噪声,避免了训练过程中的梯度消失问题,可获得信号低频以及不同方向的高频特征信息。
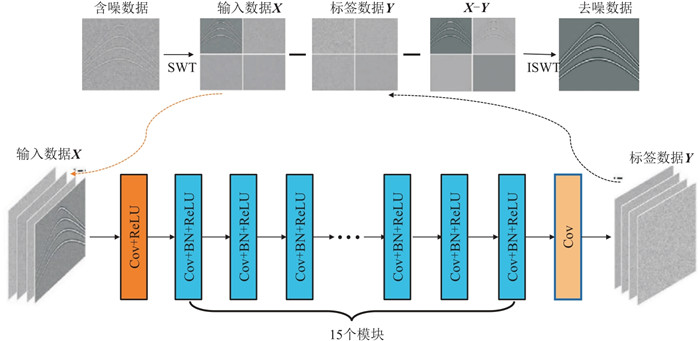
图 13为小波变换与深度ResNet结构。网络输入为一级平稳Haar小波变换(SWT)得到的低频以及不同方向的高频含噪数据。ResNet共有17层,其中第一层为卷积和激活函数层(Cov+ReLU),其他层为卷积、批量归一化和激活函数层(Cov+BN+ReLU),最后一层为卷积层(Cov)用于重建输出。输出为一级平稳Haar小波变换的四个分量。用输入数据X与标签数据Y相减得到的信号通过逆平稳小波变换(ISWT)得到去噪数据。
|
图 13 小波变换与深度ResNet结构[54] |
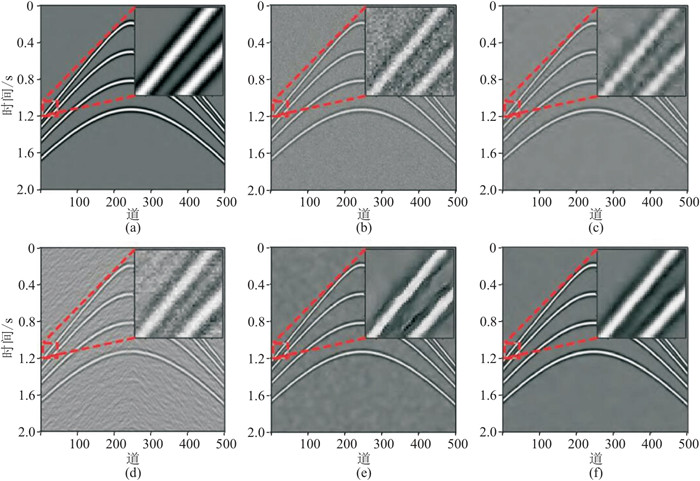
图 14为含有4个不同斜率的线性同相轴的模拟数据去噪效果对比。由图可见,文献[54]的方法对加噪地震数据的去噪效果(图 14f)优于小波阈值(图 14c)、f-x域反褶积(图 14d)、DnCNN(图 14e)、方法。
|
图 14 含有4个不同斜率的线性同相轴的模拟数据去噪效果对比[54] (a)干净数据;(b)含噪数据(σ=0.15);(c)小波阈值;(d)f-x域反褶积;(e)DnCNN;(f)文献[54]的方法红色方框区域放大显示在右上角。 |
ResNet的提出解决了由于网络层数过深带来的性能退化问题,可以反向更新解决梯度消失和梯度爆炸问题,打破了网络的不对称性,增强了网络的泛化性。
2.7 迁移学习目前,由于CNN等监督学习方法需要大量的标签数据,但野外地震数据量大、采集成本高以及地震资料保密机制的限制,难以获得高质量的标签数据,很难继续提高去噪效果。为了解决缺乏真实地震数据的问题,人们提出了GAN[55]用于生成数据集,但是将GAN生成的数据作为训练集处理结果可能不尽人意。
Sun等[56]提出了基于无监督迁移学习的地震随机噪声衰减方法,该方法在Batson等[57]提出的自监督盲去噪(Noise2self)的基础上加入迁移学习策略。假设真实地震信号是相关的、噪声是相互独立的,使用一个不变的值(J-invariant)用于估计降噪器的去噪性能。利用N2STL(Noise2self Transfer Learning)方法对含有不同高斯噪声的2D叠前和叠后合成地震记录、2D野外共反射点道集和3D叠后地震记录降噪,在增强地震资料信噪比的同时更好地保留了深部有效信号,取得了理想的去噪效果。另外,自注意力机制等网络结构的地震资料去噪效果较好。
2.8 不同网络模型噪声压制效果对比目前,利用神经网络压制地震随机噪声已成为研究热点,人们不断提出了新的网络模型、优化算法、学习策略以及数据集制作方式。CNN、DnCNN和U-Net都是利用卷积操作提取特征,但是它们的网络结构不同。DnCNN在CNN的基础上引入BN和残差学习策略,加快了网络的收敛速度;U-Net在CNN的基础上增加了编码和解码步骤,分别通过池化层或下采样和转置卷积或上采样实现,能够提取更高维度的复杂特征。文中对比、分析了不同的网络结构以及去噪效果(表 2)。
|
|
表 2 不同网络结构改进方式及去噪效果评价 |
采用2D开源数据集[41],将数据集划分为145631个标签数据,并对每个标签数据添加40%的随机噪声作为训练集(图 15)依次训练。初始学习率为0.0001,卷积核尺寸为3×3,步长为1,利用Adam优化算法自动调整学习率提高网络收敛速度。共迭代80次,每次送入神经网络的样本数设置为64。测试在Ubuntu操作系统下进行,内存为32 G,GPU型号为NVIDA GeForce RTX 3090。噪声压制效果(表 3)表明,随着噪声比例增加,原始地震数据的信噪比SNR不断降低,去噪地震数据的信噪比SNRCNN、SNRDnCNN显著提高,且DnCNN的噪声压制效果好于CNN。

|
图 15 随机抽取的训练数据和标签数据对 |
|
|
表 3 DnCNN和CNN的去噪前、后的信噪比 |
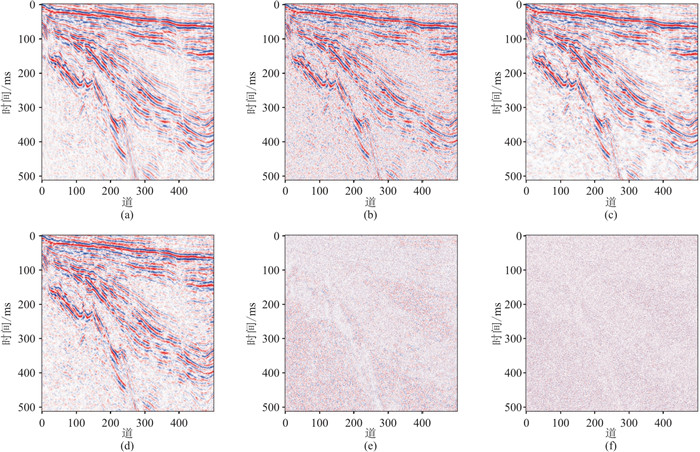
图 16为实际地震数据去噪结果。由图可见,对于原始地震数据(图 16a)的加噪数据(图 16b),DnCNN的噪声压制效果(图 16d、图 16f)好于CNN(图 16c、图 16e),能够更好地压制随机噪声并保留弱振幅地震信号,且图 16d的同相轴更清晰。
|
图 16 实际地震数据去噪效果 (a)原始地震数据;(b)图a添加40%随机噪声;(c)CNN去噪结果;(d)DnCNN去噪结果;(e)CNN去除的噪声;(f)DnCNN去除的噪声 |
以CNN、DnCNN、U-Net、BP、ResNet和迁移学习等为代表的深度学习方法的实际去噪效果优于传统方法和字典学习方法,且不需要设定结构模型,泛化性更强。利用训练好的网络结构去噪时,计算时间往往比模型驱动短且精度更高。
但是基于深度学习的地震去噪技术也存在诸多不足:实际数据的去噪效果往往差于合成数据;普适性不强;神经网络的“黑匣子”特性使其物理可解释性大大降低;网络性能与训练数据的泛化性密切相关,若训练集覆盖所有类型的解,则去噪效往往较好;用于训练网络的数据集因人而异,难以评价网络性能。
3.2 展望深度学习技术已经成功用于地震去噪领域,但也存在诸多问题,期待深度学习在以下方面取得进展和突破:
(1) 搭建适用于不同噪声的去噪神经网络结构,并将更优的网络结构引入地震随机噪声压制。目前基于深度学习的去噪方法中,大多针对去除地震随机噪声,而对于面波、声波、多次波、绕射波等相干噪声的压制方法较少,若能通过深度学习方法去除相干噪声,将会大幅提高地震资料处理效率及信噪比。将更多的神经网络模型引入地震资料去噪领域提高资料处理精度,将成为未来的研究方向。
(2) 将地震信号转换到变换域构造网络的损失函数。在变换域可在一定程度上分离噪声和有效信号,将变换域的地震信号作为网络损失函数可进一步加快网络收敛速度、提高网络的预测精度,但也存在多次变换的累计误差。
(3) 改进学习策略的同时制作更具代表性的数据集,尽可能地使训练数据覆盖所有类型的解,提高网络泛化性。对于基于监督学习的地震随机噪声衰减方法,训练结果与训练集的质量密切相关,因此制作更具代表性的数据集使训练集尽可能地覆盖所有解,可以提高网络的泛化性;采用基于无监督学习的方式可以摆脱对无噪数据的依赖,将含噪数据做为训练集也是发展趋势之一。
(4) 自动化的参数调优。神经网络依赖于大量的训练集,而地震数据量巨大,造成模型训练时间过长。因此期待自动改进网络参数的方法,在保证地震资料信噪比的同时,提高网络的训练速度。
(5) 结合模型驱动与数据驱动的方法。基于模型的方法并不依赖标记数据学习映射,但简单的模型往往不能描述高维复杂数据的细微差别和动态变化,而且每一步算法都需要对应的数学/物理模型,不具备泛化性。相比之下,基于数据驱动的方法不依赖于解析近似,从复杂数据中提取有效信息,但不具备数学可解释性。采用即插即用等方式,结合模型驱动与数据驱动的方法可以进一步探索数据驱动和模型驱动的优势。
| [1] |
陈旭. 分数傅里叶变换在地震资料处理中的应用初探[D]. 吉林长春: 吉林大学, 2009.
|
| [2] |
DEIGHAN A J, WATTS D R. Groun-roll suppression using the wavelet transform[J]. Geophysics, 1997, 62(6): 1896-1903. DOI:10.1190/1.1444290 |
| [3] |
王振国, 周熙襄, 李晶. 基于小波变换的最小光滑滤波去噪[J]. 石油地球物理勘探, 2002, 37(6): 594-600. WANG Zhenguo, ZHOU Xixiang, LI Jing. Noise attenuation using minimum smooth filter based on wavelet transform[J]. Oil Geophysical Prospecting, 2002, 37(6): 594-600. DOI:10.13810/j.cnki.issn.1000-7210.2002.06.008 |
| [4] |
李继伟, 臧殿光, 刁永波, 等. 自适应相减和Curvelet变换组合压制面波[J]. 石油地球物理勘探, 2020, 55(5): 1005-1015. LI Jiwei, ZANG Dianguang, DIAO Yongbo, et al. Combination of adaptive subtraction and Curvelet transform to suppress surface waves[J]. Oil Geophysical Prospecting, 2020, 55(5): 1005-1015. DOI:10.13810/j.cnki.issn.1000-7210.2020.05.009 |
| [5] |
FOMEL S. Towards the seislet transform[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2847-2851.
|
| [6] |
刘洋, FOMEL Sergey, 刘财, 等. 高阶seislet变换及其在随机噪声消除中的应用[J]. 地球物理学报, 2009, 52(8): 2142-2151. LIU Yang, FOMEl Sergey, LIU Cai, et al. High-order seislet transform and its application of random noise attenuation[J]. Chinese Journal of Geophysics, 2009, 52(8): 2142-2151. DOI:10.3969/j.issn.0001-5733.2009.08.024 |
| [7] |
邓心欢. 自适应时频峰值滤波压制地震勘探随机噪声[D]. 吉林长春: 吉林大学, 2016.
|
| [8] |
胡瑞卿, 何俊杰, 李华飞, 等. 时频域变分模态分解地震资料去噪方法[J]. 石油地球物理勘探, 2021, 56(2): 257-264. HU Ruiqing, HE Junjie, LI Huafei, et al. Seismic data de-noising method based on VMD in time-frequency domain[J]. Oil Geophysical Prospecting, 2021, 56(2): 257-264. DOI:10.13810/j.cnki.issn.1000-7210.2021.02.006 |
| [9] |
WANG C, ZHU Z, GU H, et al. Hankel low-rank approximation for seismic noise attenuation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(1): 561-573. DOI:10.1109/TGRS.2018.2858545 |
| [10] |
刘璐, 刘洋, 刘财, 等. 地震随机噪声压缩感知迭代压制方法[J]. 地球物理学报, 2021, 64(12): 4629-4643. LIU Lu, LIU Yang, LIU Cai, et al. Iterative seismic random noise suppression method based on compressive sensing[J]. Chinese Journal of Geophysics, 2021, 64(12): 4629-4643. DOI:10.6038/cjg2021P0045 |
| [11] |
耿瑜, 吴如山, 高静怀. 基于Dreamlet变换的地震数据压缩理论与方法[J]. 地球物理学报, 2012, 55(8): 2705-2715. GENG Yu, WU Rushan, GAO Jinghuai. Dreamlet compression of seismic data[J]. Chinese Journal of Geophysics, 2012, 55(8): 2705-2715. DOI:10.6038/j.issn.0001-5733.2012.08.023 |
| [12] |
PORSANI M J, URSIN B. Deconvolution and wavelet estimation by using a genetic algorithm[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 2185-2188.
|
| [13] |
程文婷, 方文倩, 付丽华. 基于自相似性和低秩先验的地震数据随机噪声压制[J]. 石油物探, 2020, 59(6): 880-889. CHENG Wenting, FANG Wenqian, FU Lihua. Seismic noise suppression via self-similarity and low-rank prior[J]. Geophysical Prospecting for Petroleum, 2020, 59(6): 880-889. DOI:10.3969/j.issn.1000-1441.2020.06.006 |
| [14] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [15] |
唐刚. 基于压缩感知和稀疏表示的地震数据重建与去噪[D]. 北京: 清华大学, 2010.
|
| [16] |
AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 |
| [17] |
TANG G, MA J, YANG H. Seismic data denoising based on learning-type overcomplete dictionaries[J]. Applied Geophysics, 2012, 9(1): 27-32. DOI:10.1007/s11770-012-0310-z |
| [18] |
BECKOUCHE S, MA J. Simultaneous dictionary learning and denoising for seismic data[J]. Geophysics, 2014, 79(3): A27-A31. DOI:10.1190/geo2013-0382.1 |
| [19] |
宋维琪, 弓震, 王超, 等. 基于K-SVD字典学习方法的地震资料去噪[J/OL]. 地球物理学进展, 2020(2020-06-08)[2022-05-03]. https://kns.cnki.net/kcms/detail/11.2982.P.20200608.1134.066.html.
|
| [20] |
WU J, CEHN Q, GUI Z, et al. Fast dictionary learning for 3D simultaneous seismic data reconstruction and denoising[J]. Journal of Applied Geophysics, 2021. DOI:10.1016/j.jappgeo.2021.104446 |
| [21] |
LECUN Y, BOTTOU L. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [22] |
ZHANG K, ZUO W, CHEN Y, et al. Beyond a Gaus-sian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2016, 26(7): 3142-3155. |
| [23] |
RONNEBERGER O, FISCHER P, BROX T. U-Net: convolutional networks for biomedical image segmentation[C]. Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, 2015, 234-241.
|
| [24] |
RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back propagating errors[J]. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0 |
| [25] |
LI Y, ZHANG X, CHEN D. CSRNET: Dilated convolutional neural networks for understanding the highly congested scenes[C]. Proceedings-2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, 1091-1100.
|
| [26] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]. Proceedings-2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016, 770-778.
|
| [27] |
TURING A M. Computing machinery and intelligence[J]. Mind, 1950. DOI:10.1093/mind/lix.236.433 |
| [28] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communication of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [29] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. 2014, doi: 10.48550/arXiv.1409.1556.
|
| [30] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869. HAN Weixue, ZHOU Yatong, CHI Yue. Deep learning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [31] |
ZHANG M, LIU Y, CHEN Y. Unsupervised seismic random noise attenuation based on deep convolutional neural network[J]. IEEE Access, 2019, 7: 179810-179822. DOI:10.1109/ACCESS.2019.2959238 |
| [32] |
DONG X, ZHONG T, LI Y. New suppression technology for low-frequency noise in desert region: The improved robust principal component analysis based on prediction of neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(7): 4680-4690. DOI:10.1109/TGRS.2020.2966054 |
| [33] |
YANG L, CHEN W, LIU W, et al. Random noise attenuation based on residual convolutional neural network in seismic datasets[J]. IEEE Access, 2020, 8: 30271-30286. DOI:10.1109/ACCESS.2020.2972464 |
| [34] |
向奎. 基于卷积神经网络的地震资料去噪方法研究[D]. 北京: 中国石油大学(北京), 2018.
|
| [35] |
DONG C, LOY C C, HE K, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transaction on Pattern Analysis Machine Intelligence, 2016, 38(2): 295-307. DOI:10.1109/TPAMI.2015.2439281 |
| [36] |
FANG W, FU L, LI H. Unsupervised CNN based on self-similarity for seismic data denoising[J]. IEEE Geoscience and Remote Sensing Letters, 2021. DOI:10.1109/LGRS.2021.3131046 |
| [37] |
CHEN G, LIU Y, ZHANG M, et al. Dropout-based robust self-supervised deep learning for seismic data denoising[J]. IEEE Geoscience and Remote Sensing Letters, 2022. DOI:10.1109/LGRS.2022.3167999 |
| [38] |
WANG F, YANG B, WANG Y, et al. Learning from noisy data: An unsupervised random denoising method for seismic data using model-based deep learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022. DOI:10.1109/TGRS.2022.3165037 |
| [39] |
FENG J, LI X, LIU X, et al. Multigranularity feature fusion convolutional neural network for seismic data denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 3123509. DOI:10.1109/TGRS.2021 |
| [40] |
XU Q, ZHANG C, ZHANG L. Denoising convolutional neural network[C]. 2015 IEEE International Conference on Information & Automation, 2015, 1184-1187.
|
| [41] |
YU S, MA J, WANG W. Deep learning for denoising[J]. Geophysics, 2019, 84(6): V333-V350. DOI:10.1190/geo2018-0668.1 |
| [42] |
张超铭, 文晓涛, 张晓琦, 等. 基于DnCNN与约束卷积的地震数据去噪方法[J/OL]. 地球物理学进展, 2022(2022-03-18)[2022-03-30]. https://kns.cnki.net/kcms/detail/11.2982.P.20220316.1806.032.html.
|
| [43] |
钟铁, 陈云, 董新桐, 等. 基于DBBCNN的沙漠区地震资料随机噪声衰减方法[J]. 石油地球物理勘探, 2022, 57(2): 268-278. ZHONG Tie, CHEN Yun, DONG Xintong, et al. Research on random noise attenuation method for seismic data from deserts based on DBBCNN[J]. Oil Geophysical Prospecting, 2022, 57(2): 268-278. DOI:10.13810/j.cnki.issn.1000-7210.2022.02.003 |
| [44] |
ZHONG T, CHENG M, DONG X, et al. Seismic random noise attenuation by applying multiscale denoising convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021. DOI:10.1109/TGRS.2021.3095922 |
| [45] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433. WANG Yuqing, LU Wenkai, LIU Jinlin, et al. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. |
| [46] |
罗仁泽, 李阳阳. 一种基于RUnet卷积神经网络的地震资料随机噪声压制方法[J]. 石油物探, 2020, 59(1): 51-59. LUO Renze, LI Yangyang. Random seismic noise attenuation based on RUnet convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 51-59. |
| [47] |
BAI T, ZHAO H, WANG Z. A U-Net based deep learning approach for seismic random noise suppression[C]. IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, 2022, 6165-6168.
|
| [48] |
LIU N, WANG J, GAO J, et al. Similarity-informed self-learning and its application on seismic image denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022. DOI:10.1109/TGRS.2022.3210217 |
| [49] |
LIU N, WANG J, GAO J, et al. NS2NS: Self-learning for seismic image denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022. DOI:10.1109/TGRS.2022.3217289 |
| [50] |
顾航. 基于卷积神经网络的地震数据去噪研究[D]. 黑龙江大庆: 东北石油大学, 2019.
|
| [51] |
玉琨. 基于对称式空洞卷积神经网络的地震资料去噪方法研究[D]. 四川成都: 成都理工大学, 2020.
|
| [52] |
何凯. 隔震结构地震响应分析及抗震性能研究[D]. 湖北武汉: 华中科技大学, 2015.
|
| [53] |
方文倩, 李志明. 基于双重残差网络的地震数据随机噪声压制[J]. 工程地球物理学报, 2021, 18(1): 44-50. FANG Wenqian, LI Zhiming. Random noise attenuation in seismic data based on dual residual networks[J]. Chinese Journal of Engineer Geophysics, 2021, 18(1): 44-50. |
| [54] |
武国宁, 于萌萌, 王君仙, 等. 应用平稳小波变换与深度残差网络压制地震随机噪声[J]. 石油地球物理勘探, 2022, 57(1): 43-51. WU Guoning, YU Mengmeng, WANG Junxian, et al. Seismic random noise attenuation based on stationary wavelet transform and deep residual neural network[J]. Oil Geophysical Prospecting, 2022, 57(1): 43-51. DOI:10.13810/j.cnki.issn.1000-7210.2022.01.005 |
| [55] |
GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[J]. Communications of the ACM, 2020, 63(11): 139-144. |
| [56] |
SUN H, YANG F, MA J. Seismic random noise attenuation via self-supervised transfer learning[J]. IEEE Geoscience and Remote Sensing Letters, 2022. DOI:10.1109/LGRS.2022.3146173 |
| [57] |
BATSON J, ROYER L. Noise2self: Blind denoising by self-supervision[C]. Proceedings of the 36th International Conference on MachineLearning, 2019, 524-533.
|
| [58] |
ZHANG M, LIU Y, CHEN Y. Unsupervised seismic random noise attenuation based on deep convolutional neural network[J]. IEEE Access, 2019, 7: 179810-179822. |
| [59] |
XU W, ZHOU Y, LIU D, et al. Seismic intelligent deblending via plug and play method with blended CSGs trained deep CNN Gaussian denoiser[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022. DOI:10.1109/TGRS.2022.3166029 |
| [60] |
SHAO D, ZHAO Y, LI Y, et al. Noisy2Noisy: Denoise pre-stack seismic data without paired training data with labels[J]. IEEE Geoscience and Remote Sen-sing Letters, 2022. DOI:10.1109/LGRS.2022.3145835 |



 白敏, 湖北省武汉市蔡甸区大学路111号长江大学武汉校区地球物理与石油资源学院,430100。Email:
白敏, 湖北省武汉市蔡甸区大学路111号长江大学武汉校区地球物理与石油资源学院,430100。Email: