2. 国家现代地质勘查工程技术研究中心, 河北廊坊 065000
2. National Center for Geological Exploration Technology, Langfang, Hebei 065000, China
重力勘探是一种传统的地球物理勘探方法,是对实测重力数据进行自由空气校正、中间层校正、地形校正、正常场校正等预处理获得布格重力异常[1-2],再用场分离技术和重力反演方法获得地下密度异常体的位置信息或者密度信息[3-4]的一种间接勘探方法。
在数据预处理阶段,为了消除起伏地形密度体的干扰,需要进行地形改正。它的计算过程主要考虑两个方面:第一,对起伏地形选择恰当的密度数值。既可选择能代表研究区地层特征的密度值,也可以按照有关规范设定岩石密度、海水密度、淡水密度[5-6]。第二,结合实际的地形改正范围选择合适的地形数据库。一般近区和中区地形改正范围为0~2000 m,采用空间分辨率和精度较高的地形数据库,如应用高精度差分卫星定位测地技术(GPS-RTK)或航摄获得的高精度数字高程模型(DEM)数据[7];远区地形改正范围为2000~166700 m,需要覆盖率较高的地形数据库,如航天飞机雷达地形测绘使命(SRTM)或高级星载热发射和反射辐射仪(ASTER)得到的DEM数据。
地形数据库的空间分辨率、精度、覆盖率都会影响计算结果,分析某单一变量难以清晰地论述这些关系。因此,地形数据库是全面、深入地研究地形改正的各种影响因素及其影响程度的关键要素。全站仪或GPS-RTK方式获取的高程数据精度最高,但成本高,工作效率低;航天遥感技术与空间测量分析技术的快速发展将地面测量获得DEM转变为由主动遥感方法自动生成DEM[8],其中激光雷达(LiDAR)在获取大范围、高精度、多种DEM方面的效率较高,明显提升了大比例尺地形测绘和勘察效率[9]。
一般假设地形体的密度为常数,基于DEM地形改正的主要研究内容包括地形数据水平分辨率与计算精度之间的关系[10-12]、不同数据源的地形改正精度要求[7]。由于单一源的高分辨率数据的覆盖范围有限,地形改正方法的精度评价都是基于某一个数学模型的假设条件,只能讨论高程测量误差对地形改正的影响,不能分析由扇形锥、扇形柱等数学模型近似实际地形产生的误差。目前,利用LiDAR数据分析陆地重力近区地形改正数学模型产生的近似误差以及中区地形改正的影响因素的文献较少。
本文采用美国地调局三维高程计划(3DEP)的LiDAR高程数据,选择12个数据区作为研究对象,利用LiDAR高程数据为参考数据,以直棱柱模型重力解析式计算结果为地形改正参考值,从统计角度对比近区和中区地形改正的数学模型和计算方法的精度,这是本文的主要创新点;在此基础上,分析不同计算方法、不同地形网格间距的差异,并且对比不同方法的计算效率。
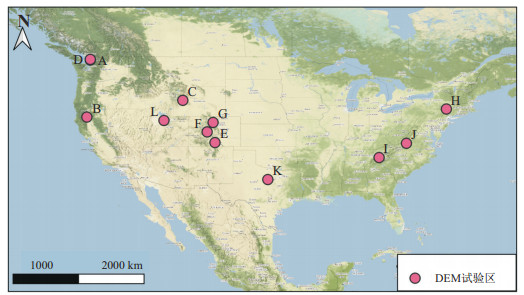
1 数据说明美国地质调查局从2016年至2023年实施3DEP,目前可公开访问的高程数据的最高精度为1 m×1 m,即栅格尺寸为1 m×1 m,数据维度为10012×10012,高程值为由机载LiDAR扫描获得的初始数据经滤波得到的裸露地表高程[13]。本文选用3DEP高程数据集中地形起伏特征明显的12个DEM为试验数据区,其地理位置分布见图 1。在生产过程中会融合其他数据,因此最终数据产品的精度并不统一。基于地貌划分原则,试验区的地貌包括丘陵(海拔 < 500 m,相对高度 < 200 m)、中山(海拔为800~3500 m,相对高度 > 500 m)、高山(海拔 > 3500 m,相对高度 > 500 m),详细的统计数据见表 1,数据下载网址为:https://www.usgs.gov/3d-elevation-program。
|
图 1 DEM试验区的地理位置分布图(背景地形图为Stamen Terrain地形图) 每个试验区对应的栅格数据的范围均为10012 m×10012 m,栅格像元尺寸均为1 m×1 m。后续数据处理中,将全部试验区数据的原始维度从10012×10012截断到10000×10000,经过粗网格处理获得较低分辨率的地形数据。 |
|
|
表 1 机载激光雷达DEM统计表 |
3DEP提供的原始数据的水平分辨率为1 m×1 m,为平面投影后数据,与ASTER GDEM(全球DEM)等以经纬度表示的数据不同,更适合作为重力近区和中区地形改正的试验参考数据。为分析不同网格间距对地形改正精度的影响,将1 m×1 m栅格数据进行“粗网格”处理,处理过程的本质是“平滑”原始数据,使地形更“平缓”。以栅格数据存储DEM的数据空间排列都是有规律的,有些情况需要平面坐标变换,如ASTER GDEM高程数据,具体方法见下文。每个栅格像元的数值表示该像元覆盖面积内的平均高程,这与节点高程数据只表示单一位置高程信息的本质不同。
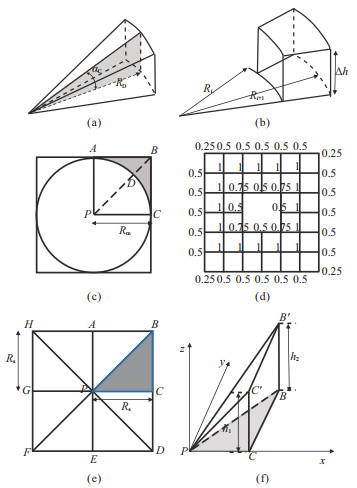
2 近区与中区地形改正方法 2.1 近区地形改正方法根据区域重力调查规范,1:5万比例尺近区地形改正半径为20 m,其他比例尺的近区地形改正半径为50 m[14-15]。采用八方位圆域法计算时,内环一般采用扇形锥模型(图 2a),外环采用扇形柱模型(图 2b)。扇形锥模型的地形改正为[16]
|
图 2 近区和中区地形改正采用的数学模型 (a)扇形锥模型;(b)扇形柱模型;(c)内接口(灰色充填部分);(d)梯形积分系数分布;(e)斜顶面三角棱柱模型平面投影;(f)斜顶面三角棱柱模型, |
| $ \mathtt{δ}{g}_{\mathrm{c}}=\frac{2\mathrm{\pi }G\sigma {R}_{\mathrm{D}}}{{n}_{\mathrm{c}}}\left(1-\mathrm{c}\mathrm{o}\mathrm{s}\;{\alpha }_{\mathrm{c}}\right) $ | (1) |
式中:
扇形柱模型的地形改正为
| $ \mathtt{δ}{g}_{\mathrm{p}}=\frac{2\mathrm{\pi }G\sigma }{{n}_{\mathrm{p}}}\left(\sqrt[]{{R}_{i}^{2}+{\Delta }{h}^{2}}+{R}_{i+1}-\\ \sqrt[]{{R}_{i+1}^{2}+{\Delta }{h}^{2}}-{R}_{i}\right) $ | (2) |
式中:
对于方域近区地形改正,重力规范中一般采用由测点P、角点B以及边长中点C构成的斜顶面三角棱柱模型(图 2e和图 2f)计算地形改正值,模型整体与扇形锥模型类似,不同的是该模型高度主要受角点和边长中点的控制。基于该模型的方域近区地形改正为
| $ \begin{array}{l}\mathtt{δ}{g}_{\mathrm{s}}=\sum\limits_{j=1}^{8}G\sigma {R}_{\mathrm{s}}\left[\mathrm{l}\mathrm{n}\left(1+\sqrt[]{2}\right)-\frac{1}{\sqrt[]{{b}_{j}^{2}+1}}\right.\times \\ \left.\mathrm{l}\mathrm{n}\frac{{a}_{j}{b}_{j}+{b}_{j}^{2}+1+\sqrt[]{\left({a}_{j}^{2}+1\right)\left({b}_{j}^{2}+1\right)+2{a}_{j}{b}_{j}\left({b}_{j}^{2}+1\right)+{\left({b}_{j}^{2}+1\right)}^{2}}}{{a}_{j}{b}_{j}+\sqrt[]{({a}_{j}{}^{2}+1)({b}_{j}^{2}+1})}\right]\end{array} $ | (3) |
其中
| $ {a}_{j}=\frac{{h}_{1, j}}{{R}_{\mathrm{s}}} $ |
| $ {b}_{j}=\frac{{h}_{2, j}-{h}_{1, j}}{{R}_{\mathrm{s}}} $ | (4) |
式中:
分环、分方位进行重力近区地形改正要将实际地形数据按照圆域数据处理,而高精度重力中区地形改正通常采用规则网格的高程数据。这些数据通常以附带平面投影坐标或者附带大地坐标信息的栅格数据存储,在平面上坐标数据通常以方域显示。在调用这些方域数据对某个测点进行中区地形改正时,还需要计算近区圆域数据与中区方域数据的间隙产生的地形改正值(图 2c的灰色充填部分),这一部分质量产生的地形改正值要累加到近区圆域地形改正值中——数据接口处理,在重力调查规范中也称为内接口补角计算。
区域重力调查规范给出的内接口补角地形改正的简化公式为
| $ \begin{array}{l}\mathtt{δ}{g}_{\mathrm{m}}=\frac{G\sigma \left(1-0.25\mathrm{\pi }\right){R}_{\mathrm{m}}}{1.105}\times \\ \left[1-\frac{1.105{R}_{\mathrm{m}}}{\sqrt[]{{\left({\Delta }{h}_{\mathrm{c}}\right)}^{2}+{\left(1.105{R}_{\mathrm{m}}\right)}^{2}}}\right]\end{array} $ | (5) |
式中
| $ {\Delta }{h}_{\mathrm{c}}=\frac{\sum\limits_{m=1}^{4}{w}_{m}{H}_{m}}{\sum\limits_{m=1}^{4}{w}_{m}}-{H}_{P} $ | (6) |
其中
| $ {w}_{m}=\frac{1}{{\left({x}_{m}-{x}_{P}\right)}^{2}+{\left({y}_{m}-{y}_{P}\right)}^{2}} $ | (7) |
为权重系数。式中:
夏江海[17]给出补角地形改正的修正公式
| $ \begin{array}{l}\mathtt{δ}{{g}_{\mathrm{m}}}^{{'}}=2G\sigma \left\{\frac{\mathrm{\pi }}{4}\left[\sqrt[]{{R}_{\mathrm{m}}^{2}+{\left({\Delta }{h}_{\mathrm{c}}\right)}^{2}}-{R}_{\mathrm{m}}\right]\right.+{R}_{\mathrm{m}}\mathrm{l}\mathrm{n}\left(\sqrt[]{2}+1\right)-\frac{{R}_{\mathrm{m}}}{2}\times \\ \mathrm{l}\mathrm{n}\frac{\sqrt[]{2{R}_{\mathrm{m}}^{2}+{\left({\Delta }{h}_{\mathrm{c}}\right)}^{2}}+{R}_{\mathrm{m}}}{\sqrt[]{2{R}_{\mathrm{m}}^{2}+{\left({\Delta }{h}_{\mathrm{c}}\right)}^{2}}-{R}_{\mathrm{m}}}+\mathrm{ }{\Delta }{h}_{\mathrm{c}}\times \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\left.\sqrt[]{\frac{2{R}_{\mathrm{m}}^{2}+{\left({\Delta }{h}_{\mathrm{c}}\right)}^{2}}{2\left[\left.{R}_{m}^{2}+{\left({\Delta }{h}_{\mathrm{c}}\right)}^{2}\right]\right.}}-\frac{\mathrm{\pi }}{2}{\Delta }{h}_{c}\right\}\end{array} $ | (8) |
中区地形改正方法的实现取决于采用的数学模型。通常采用直棱柱模型解析式求解,或采用二重梯形积分快速计算,还可以采用倾斜顶面棱柱模型,利用表面积分法近似计算。理想模型数值模拟表明,高斯表面积分法的计算精度高于二重梯形积分公式。可将棱柱体质量压缩至中心垂线上——质量线模型,这种简化模型的计算表达式简洁、计算速度较快。以下讨论直棱柱模型解析式的离散形式、质量线模型方法、直棱柱模型的二重梯形积分方法及基于三角面元的表面积分方法。
2.3.1 直棱柱模型解析式根据区域重力调查规范[14-15],中区地形改正采用平顶面棱柱模型计算公式,某点的水平坐标和高程为
| $ {\left.{\left.{\left.\begin{array}{l}\mathtt{δ}{g}_{\mathrm{t}\mathrm{p}}=\\ G\sigma \sum\limits_{k=0}^{I-1}\sum\limits_{q=0}^{J-1}\left\{x\mathrm{l}\mathrm{n}\left[y+r\left(x, y, z\right)\right]+y\mathrm{l}\mathrm{n}\left[x+r\left(x, y, z\right)\right]-z\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{xy}{zr\left(x, y, z\right)}\right\}\end{array}\right|}_{{x}_{P}-\left({x}_{k}-\frac{{\Delta }x}{2}\right)}^{{x}_{P}-\left({x}_{k}+\frac{{\Delta }x}{2}\right)}\right|}_{{y}_{P}-\left({y}_{q}-\frac{{\Delta }y}{2}\right)}^{{y}_{P}-\left({y}_{q}+\frac{{\Delta }y}{2}\right)}\right|}_{\Delta h}^{0} $ | (9) |
式中
应用上述公式计算测点的中区地形改正时,需要排除近区范围的直棱柱模型的影响,避免重复计算。
2.3.2 质量线模型方法基于质量线模型的计算是将三重积分进一步简化为离散的二重积分形式,即
| $ \mathtt{δ}{g}_{\mathrm{t}\mathrm{m}}=G\sigma \sum\limits_{k=0}^{I-1}\sum\limits_{q=0}^{J-1}\left[{\left(\Delta x\right)}_{kq}{\left(\Delta y\right)}_{kq}\left(\frac{1}{{r}_{kq}}-\frac{1}{\sqrt[]{{r}_{kq}^{2}+\Delta {h}^{2}}}\right)\right] $ | (10) |
式中:
利用高斯公式将地形质量引力场的三重积分转化为二重表面积分,在测点数千米范围内进行地形改正可忽略地球表面弯曲影响。由于地形体的外边界的侧面与高程基准面互相垂直,其法线与
| $ \begin{array}{l}\mathtt{δ}{g}_{\mathrm{t}\mathrm{p}}=G\sigma \iiint \frac{z\mathrm{d}x\mathrm{d}y\mathrm{d}z}{{\left({x}^{2}+{y}^{2}+{z}^{2}\right)}^{\frac{3}{2}}}\\ =G\sigma \left(\underset{\mathrm{S}\mathrm{d}}{\overset{}{\iint }}\frac{\mathrm{d}x\mathrm{d}y}{{r}_{kq}}-\underset{\mathrm{S}\mathrm{t}}{\overset{}{\iint }}\frac{\mathrm{d}x\mathrm{d}y}{\sqrt[]{{r}_{kq}^{2}+\Delta {h}^{2}}}\right)\end{array} $ | (11) |
式中:
| $ \mathtt{δ}{g}_{\mathrm{T}}\approx G\sigma \Delta x\Delta y\sum\limits_{k=0}^{I-1}\sum\limits_{q=0}^{J-1}\left\{\frac{{C}_{kq}}{{r}_{kq}}\left[1-{\left(\sqrt[]{1+{\left(\frac{\Delta h}{{r}_{kq}}\right)}^{2}}\right)}^{-1}\right]\right\} $ | (12) |
式中
基于散度定理,将式(11)的体积分转换为起伏地形和地形高程基准面包围区域的表面积分,这两部分通过三角面元离散,再利用高斯积分等数值积分方法估算每个三角面元的积分近似结果,最后累加求和。地形改正近似表示为[18]
| $ \mathtt{δ}{g}_{\mathrm{t}\mathrm{p}}\approx G\sigma \frac{{L}^{2}}{2}\sum\limits_{n=1}^{\mathrm{N}\mathrm{E}}\sum\limits_{u=1}^{\mathrm{N}\mathrm{Q}}\left(\frac{{W}_{u}}{{R}_{nu}^{\mathrm{{'}}}}-\frac{{W}_{u}}{{R}_{nu}}\right) $ | (13) |
其中
| $ {R}_{nu}^{\mathrm{{'}}}=\sqrt[]{{\left({x}_{n}^{u}\right)}^{2}+{\left({y}_{n}^{u}\right)}^{2}} $ | (14-1) |
| $ \left\{\begin{array}{l}{R}_{nu}=\sqrt[]{{\left({R}_{nu}^{\mathrm{{'}}}\right)}^{2}+{\left({z}_{n}^{u}\right)}^{2}}\\ {x}_{n}^{u}={x}_{\alpha }{\zeta }_{1}^{\left(u\right)}+{x}_{\beta }{\zeta }_{2}^{\left(u\right)}+{x}_{\eta }{\zeta }_{3}^{\left(u\right)}\\ {y}_{n}^{u}={y}_{\alpha }{\zeta }_{1}^{\left(u\right)}+{y}_{\beta }{\zeta }_{2}^{\left(u\right)}+{y}_{\eta }{\zeta }_{3}^{\left(u\right)}\\ {z}_{n}^{u}={z}_{\alpha }{\zeta }_{1}^{\left(u\right)}+{z}_{\beta }{\zeta }_{2}^{\left(u\right)}+{z}_{\eta }{\zeta }_{3}^{\left(u\right)}\end{array}\right. $ | (14-2) |
式中:
目前,公开访问的ASTER GDEM、SRTM等高程数据都采用WGS-84大地基准,由理论地球位场模型EGM96推导的大地水准面为高程基准,计算栅格像元的沿经线方向尺寸为
| $ \left\{\begin{array}{l}{\Delta }{M}_{\mathrm{x}}={r}_{\mathrm{e}}\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{\mathrm{e}}\Delta L\\ {\Delta }{M}_{\mathrm{y}}={r}_{\mathrm{e}}\Delta {\varphi }_{\mathrm{e}}\end{array}\right. $ | (15) |
式中:
| $ \left\{\begin{array}{l}{\Delta }{M}_{\mathrm{x}}\approx \left({r}_{\mathrm{E}}+{N}_{\mathrm{E}\mathrm{G}\mathrm{M}96}+{H}_{P}\right)\mathrm{c}\mathrm{o}\mathrm{s}{\varphi }_{\mathrm{e}}\Delta L\\ {\Delta }{M}_{\mathrm{y}}\approx \left({r}_{\mathrm{E}}+{N}_{\mathrm{E}\mathrm{G}\mathrm{M}96}+{H}_{P}\right)\Delta B\end{array}\right. $ | (16) |
式中:
| $ {r}_{\mathrm{E}}=\frac{a}{\sqrt[]{1+{e}^{\mathrm{{'}}2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}{\varphi }_{\mathrm{e}}}} $ | (17) |
式中
| $ {\varphi }_{\mathrm{e}}=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\left.\frac{{b}^{2}}{{a}^{2}}\mathrm{t}\mathrm{a}\mathrm{n}B\right)\right. $ | (18) |
综上所述,近区地形改正方法既可采用扇形锥与扇形柱的混合模型,也可仅采用扇形锥模型,而斜顶面三角棱柱模型可避免圆域与方域数据接口问题。中区地形改正方法中直棱柱模型解析式的精度最高;梯形积分与三角面元积分都是三维体积分的二维化简形式,其中三角面元积分通过调整积分阶数提高计算精度,是较灵活的计算方法;质量线模型方法是将模型化简的方法。
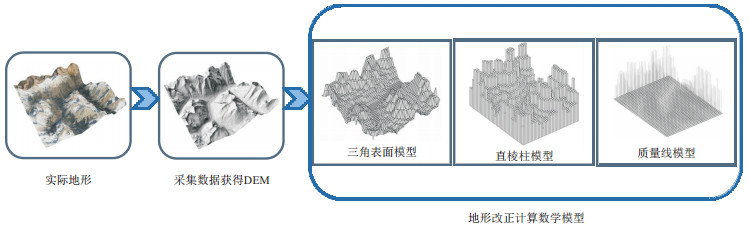
3 数值试验 3.1 误差分析与数值试验环境重力勘探近区和中区地形改正的计算精度及其改善方法一直以来都是关注重点。图 3为重力中区地形改正的工作流程。从实际地形通过某种测量手段(水准测量、机载激光雷达等)获得数字高程数据,或者直接从测绘局申请数字高程数据,该过程存在测量误差(包括点位误差和高程误差)和DEM处理误差。在获得研究区完整DEM后,利用某种数学模型进行重力近区和中区地形改正,该过程会引入模型近似误差及其计算误差,这两种误差通常难以分离。本文默认模型近似误差包括计算误差,作为主要研究对象。
|
图 3 重力中区地形改正的工作流程 |
区域重力规范[14-15]一般都假定密度为常数,基于某种数学模型及其公式讨论高程精度以及点位误差对重力地形改正精度的影响,如杨亚斌等[20]利用扇形、锥形和扇形柱公式计算理论误差。
本文以机载LiDAR高程数据为参考,衡量不同数学模型产生的模型近似误差以及网格间距对地形改正精度的影响。假定地形密度为常数,忽略实际地层密度不均匀产生的影响,全部数值试验均在Intel Core i7-11800H CPU(8核、基准频率为2.30 GHz)、64 GB RAM的移动工作站、Windows 10操作系统的计算环境下完成,采用基于MEX文件的Matlab 2020b并行计算方法。
3.2 近区地形改正的模型近似误差以往评价近区地形改正精度时以扇形锥、扇形柱以及三角棱柱等理论模型获得的地形改正值为参考值[20],忽略数学模型近似产生的差异。本文以1 m×1 m间距的高程数据为参考数据、直棱柱模型重力解析式计算结果为参考值,评价常用数学模型的近区地形改正精度。采用八方位圆域或者方域三角棱柱计算方法,近区地形改正的范围分为0~20 m与0~50 m两种,形成7种计算方案(表 2)。可见,既可以单独使用扇形锥或者三角棱柱单一模型进行近区地形改正(Ⅰ、Ⅱ、Ⅲ与Ⅳ),也可以内环采用扇形锥、中环和外环采用扇形柱的混合模型方案(Ⅴ、Ⅵ与Ⅶ)。为模拟野外情况做如下约定:基于1 m×1 m网格数据,以间隔45°读取1个高程数据。如方案Ⅶ中采用3环,环的外边缘到测点距离分别为10、25和50 m,利用计算机程序读取原始地形每个方位的半径为10、17.5、37.5 m圆上的高程节点值[21],内环利用扇形锥、中环和外环利用扇形柱模型计算后累加求和。
|
|
表 2 近区地形改正的七种计算方案 |
近区地形改正值试验设定如下:每个试验区中央6000 m×6000 m范围内,平均分布间距为100 m的
计算每种计算方案的计算值与参考值的差异,利用该差异的最大值(
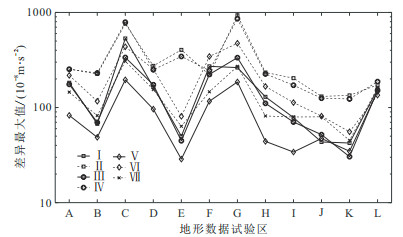
图 4为近区地形改正不同计算方案的差异最大值对数曲线。由图可见:①不同计算方案得到的差异最大值与近区地形改正半径有直接关系,差异最大值通常集中在Ⅱ和Ⅳ,即使八方位Ⅶ的最大差异值在某些试验区仍高于Ⅰ、Ⅲ和Ⅴ。②单一模型方案(Ⅰ、Ⅱ、Ⅲ和Ⅳ)的最大差异值较大,混合模型方案有效降低了最大差异值。③差异最大值与地貌密切相关,如Ⅱ、Ⅳ和Ⅵ中,大于
|
图 4 近区地形改正不同计算方案的差异最大值对数曲线 |
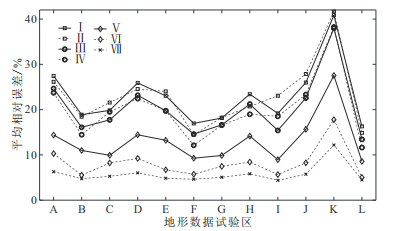
图 5为近区地形改正不同计算方案的平均相对误差曲线。由图可见:①Ⅰ、Ⅲ、Ⅴ的平均相对误差曲线的变化趋势一致,计算精度从高到低的排序为Ⅴ、Ⅲ、Ⅰ,特别是Ⅴ可以保证K区以外的11个试验区的平均相对误差小于20%。②Ⅱ、Ⅳ、Ⅵ、Ⅶ的平均相对误差曲线的变化趋势相近,计算精度从高到低的排序为Ⅶ、Ⅵ、Ⅳ、Ⅱ,其中八方位Ⅶ使全区的平均相对误差小于13%,计算精度最高。③在相同计算方案情况下,K区的平均相对误差高于其他区;L区的平均相对误差总体上小于15%。
|
图 5 近区地形改正不同计算方案的平均相对误差曲线 |
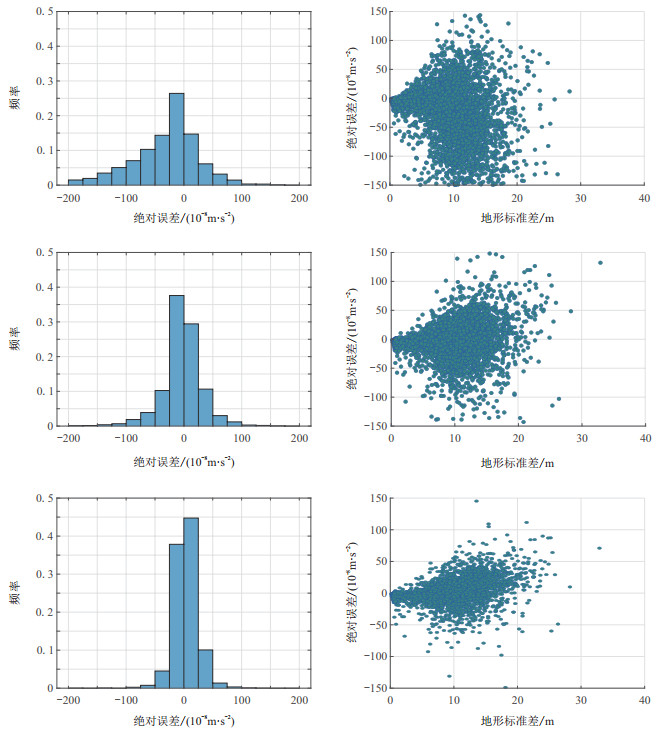
除了差异最大值和平均相对误差外,也可以使用绝对误差值小于
|
图 6 A区Ⅳ(上)、Ⅵ(中)和Ⅶ(下)的绝对误差直方图(左)及绝对误差—地形标准差散点图(右) 模型绝对误差分布直方图总测点数目为3721 |
|
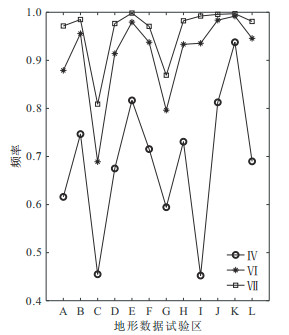
图 7 近区地形改正不同计算方案的频率 |
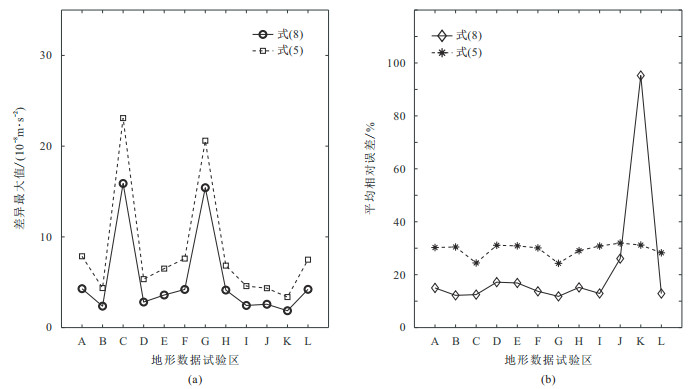
根据式(5)与式(8),对12个试验区的全部测点的东北补角进行计算,采用质量线公式计算补角地形改正的参考值。对比每个试验区3721个测点的计算结果与参考值,并统计每个试验区全部测点的差异最大值(
|
图 8 内接口补角地形改正的差异最大值(a)及平均相对误差(b) |
重力勘探中区地形改正主要分为圆域计算或方域计算,前者利用扇形柱体模型,多用于早期手工数据成图阶段或圆域电子量板地形改正,后者利用规则网格划分的直棱柱模型,便于计算机编程计算。当前,方域计算已成为主要方式。参考地质矿产行业标准[15],区域重力调查中区地形改正范围一般为50~2000 m,而1:5万比例尺的重力中区地形改正范围则为20~2000 m。
对12个试验区的原始
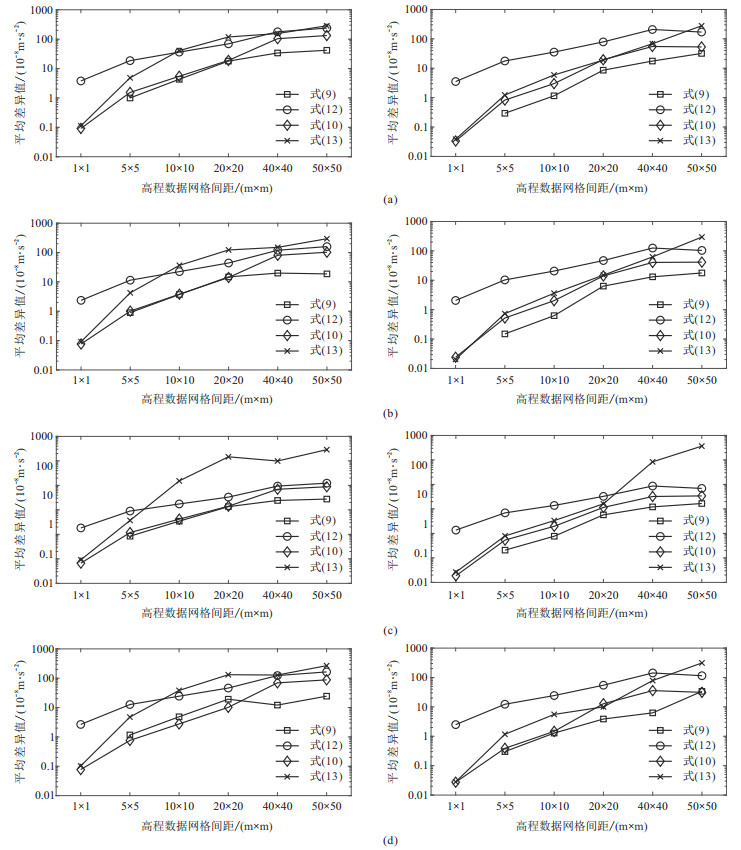
|
图 9 地形改正范围分别为20~2000 m(左)、50~2000 m(右)的不同中区地形改正方法的平均差异值 (a)C区;(b)I区;(c)K区;(d)L区 |
直棱柱模型解析式法、梯形积分法、质量线模型法以及三角面元表面积分法的计算时间分别为457.93、48.69、57.87和157.01 s,因此梯形积分法的计算效率最高,其中三角面元高斯积分法的计算时间和计算精度受高斯节点数量的影响(本文采用三个节点)。综合考虑计算效率和计算精度,认为质量线模型法可作为中区地形改正的首选方法,特别是当网格间距为5 m×5 m~20 m×20 m时,该方法的平均差异值与直棱柱模型解析式法相近。
对试验区统一采用质量线模型法进行中区地形改正,得到平均差异值统计数据(图 10)。可见:①当网格间距小于
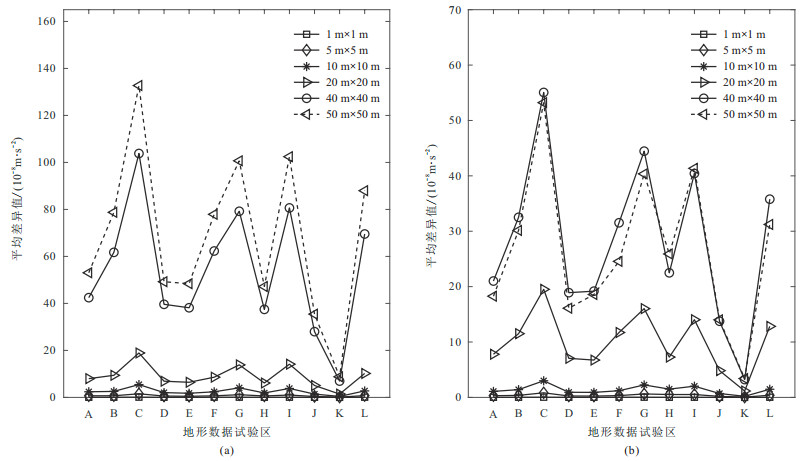
|
图 10 由质量线模型法得到的地形改正范围分别为20~2000 m(a)、50~2000 m(b)的中区地形改正平均差异值 |
综上所述:为了保证高山区中区地形改正精度,应采用较高水平分辨率的DEM,并设定地形改正范围的内边界为50 m;采用 网格间距为
本文基于包含美国典型地貌(喀斯喀特山脉、落基山脉、阿巴拉契亚山脉、德克萨斯丘陵、宾汉峡谷铜矿区)的1 m×1 m激光雷达DEM,以直棱柱模型解析式计算结果为地形改正参考值,对比、分析了重力勘探近区和中区地形改正的模型近似误差和计算方法误差;基于5种低分辨率网格高程数据和4种计算方法,分析了网格间距、中区地形改正内边界和计算方法对中区地形改正的影响。得到如下认识。
(1)采用八方位圆域、方域等7种计算方案的近区地形改正统计结果表明,近区地形改正范围与计算模型是影响计算结果的主要因素。使用混合模型方案可有效降低模型近似的计算误差,当近区地形改正半径为20 m时,采用混合模型的方案Ⅴ可以保证K区以外的11个区的平均相对误差小于20%;当近区地形改正半径为50 m时,采用八方位方案Ⅶ可以将全区的平均相对误差控制在13%以内,是计算精度最高的方案。
(2)近区地形改正计算结果表明,地形起伏较平缓的丘陵(K区)的差异最大值与中山(J区)相当;在复杂地表的露天铜矿区(L区),7种计算方案的差异最大值大致处于相同量级。
(3)补角地形改正的修正公式(式(8))不适用于丘陵。相比而言,区域重力调查规范给出内接口补角地形改正的简化公式(式(5))的平均相对误差约为30%,表达式简洁、计算稳定性更好,适用性更强。
(4)影响中区地形改正计算结果的因素包括高程数据网格间距、中区地形改正内边界和计算方法,其中网格间距是主要因素。当网格间距小于
(5)当中区地形改正范围为50~2000 m时,计算精度从高到低的排序为直棱柱模型解析式法、质量线模型法、三角面元高斯积分法、梯形积分法,计算时间分别为457.93、57.87、157.01、48.69 s。综合计算精度和计算时间两个因素,质量线模型法为首选计算方法。
| [1] |
KUHN M, FEATHERSTONE W E, KIRBY J F. Complete spherical Bouguer gravity anomalies over Australia[J]. Australian Journal of Earth Sciences, 2009, 56(2): 213-223. DOI:10.1080/08120090802547041 |
| [2] |
骆迪, 刘展, 李曼, 等. 重力校正中存在的若干问题[J]. 地球物理学进展, 2013, 28(1): 111-120. LUO Di, LIU Zhan, LI Man, et al. Several issues in gravity correction[J]. Progress in Geophysics, 2013, 28(1): 111-120. |
| [3] |
孟庆奎, 舒晴, 高维, 等. 一种用于重力场分离的约束插值切割方法[J]. 石油地球物理勘探, 2022, 57(5): 1204-1217. MENG Qingkui, SHU Qing, GAO Wei, et al. A constrained interpolation cut method for gravity field separation[J]. Oil Geophysical Prospecting, 2022, 57(5): 1204-1217. |
| [4] |
相鹏, 谭绍泉, 陈学国, 等. 利用高斯径向基函数的拟神经网络重力反演方法[J]. 石油地球物理勘探, 2021, 56(6): 1409-1418. XIANG Peng, TAN Shaoquan, CHEN Xueguo, et al. Gravity inversion method based on quasi-neural network featuring Gaussian radial basis function[J]. Oil Geophysical Prospecting, 2021, 56(6): 1409-1418. DOI:10.13810/j.cnki.issn.1000-7210.2021.06.023 |
| [5] |
HINZE W J. Bouguer reduction density, why 2.67[J]. Geophysics, 2003, 68(5): 1559-1560. DOI:10.1190/1.1620629 |
| [6] |
THOMAS G, KURT S, BERNHARD H. The rock water ice topographic gravity field model RWI_TOPO_2015 and its comparison to a conventional rock-equivalent version[J]. Surveys in Geophysics, 2016, 37(5): 937-976. DOI:10.1007/s10712-016-9376-0 |
| [7] |
刘生荣, 高鹏, 耿涛, 等. 不同源DEM数据在高山区重力中区地形改正中的适用性[J]. 物探与化探, 2019, 43(5): 1111-1118. LIU Shengrong, GAO Peng, GENG Tao, et al. The applicability of different sources DEM data in median region terrain correction of gravity in high mountain areas[J]. Geophysical & Geochemical Exploration, 2019, 43(5): 1111-1118. |
| [8] |
李志林, 朱庆, 谢潇. 数字高程模型[M]. 第三版. 北京: 科学出版社, 2018.
|
| [9] |
郭双建. 机载激光雷达测量技术在大比例地形测绘中的运用及优势[J]. 世界有色金属, 2020(8): 214-215. GUO Shuangjian. Application and advantages of airborne Lidar measurement technology in large scale topographic mapping[J]. World Nonferrous Metals, 2020(8): 214-215. DOI:10.3969/j.issn.1002-5065.2020.08.098 |
| [10] |
张俊, 张宝松, 邸兵叶, 等. 高程数据网格间距对重力中区地形改正精度的影响[J]. 物探与化探, 2014, 38(1): 157-161. ZHANG Jun, ZHANG Baosong, DI Bingye, et al. The effect of the grid spacing of elevation on the accuracy of median region terrain correction of gravity[J]. Geophysical & Geochemical Exploration, 2014, 38(1): 157-161. |
| [11] |
胡明科. 重力勘探中地形改正方法的研究及应用[D]. 四川成都: 成都理工大学, 2015, 14-16.
|
| [12] |
黎哲君, 周冬瑞, 张毅, 等. 基于DEM重力地形改正方法比较研究[J]. 海洋测绘, 2019, 39(1): 1-6. LI Zhejun, ZHOU Dongrui, ZHANG Yi, et al. Comparative study on several DEM-based strategies for terrain reduction of gravity[J]. Hydrographic Surveying and Charting, 2019, 39(1): 1-6. |
| [13] |
CALLAHAN D, BERBER M M. Vertical accuracy of the USGS 3DEP program data: study cases in Fresno County and in Davis, California[J]. Boletim de Ciências Geodésicas, 2022. DOI:10.1590/s1982-2170202200-0100004 |
| [14] |
中华人民共和国地质矿产行业标准. DZ/T 0004-2015. 重力调查技术规范(1: 50000)[S]. 北京: 中华人民共和国国土资源部, 2015, 6-7.
|
| [15] |
中华人民共和地质矿产行业标准. DZ/T 0082-2021. 区域重力调查规范[S]. 北京: 中华人民共和国自然资源部, 2021, 22-24.
|
| [16] |
孙刚. 重力勘探近区地形改正理论模型[J]. 煤田地质与勘探, 1993, 21(5): 45-49. SUN Gang. Theoretical model of short range terrain correction of gravity exploration[J]. Coal Geology & Exploration, 1993, 21(5): 45-49. |
| [17] |
夏江海. 重力测量中地形改正的一个问题[J]. 石油物探, 1986, 25(2): 81-86. XIA Jianghai. Problems concerning the terrain correction of gravity[J]. Geophysical Prospecting for Petroleum, 1986, 25(2): 81-86. |
| [18] |
ZHOU X, ZHONG B, LI X. Gravimetric terrain corrections by triangular-element method[J]. Geophysics, 1990, 55(2): 232-238. |
| [19] |
沈景刚. 基于三角剖分和高斯积分法的复杂表面热辐射计算[D]. 江苏徐州: 中国矿业大学, 2018, 30-34.
|
| [20] |
杨亚斌, 韩革命, 梁萌. 重力近区地形改正精度探讨[J]. 物探化探计算技术, 2011, 33(1): 92-96. YANG Yabin, HAN Geming, LIANG Meng. Gravity near zone terrain correction precision discussion[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2011, 33(1): 92-96. |
| [21] |
范祥发. 区域重力调查近区地形改正快速计算[J]. 工程地球物理学报, 2007, 4(6): 560-562. FAN Xiangfa. On fast calculation for the near region terrain correction of the regional gravity survey[J]. Chinese Journal of Engineering Geophysics, 2007, 4(6): 560-562. |



 孙诚业, 河北省廊坊市广阳区金光道84号中国地质科学院地球物理地球化学勘查研究所重磁探测研究室,065000。Email:
孙诚业, 河北省廊坊市广阳区金光道84号中国地质科学院地球物理地球化学勘查研究所重磁探测研究室,065000。Email: