2. 浙江省钱塘江管理局勘测设计院, 浙江杭州 310016;
3. 中南大学地球科学与信息物理学院, 湖南长沙 410083;
4. 湖南科技大学计算机科学与工程学院, 湖南湘潭 411201;
5. 国防科技大学气象海洋学院, 湖南长沙 410073
2. Survey and Design Institute of Zhejiang Qiantang River Administration Bureau, Hangzhou, Zhejiang 310016, China;
3. School of Geosciences and Info-physics, Central South University, Changsha, Hunan 410083, China;
4. School of Computer Science and Engineering, Hunan University of Science and Technology, Xiangtan, Hunan 411201, China;
5. College of Meteorology and Oceanography, National University of Defense Technology, Changsha, Hunan 410073, China
激发极化法(简称激电法)作为电法勘探重要的分支方法,通常情况下比电阻率法和大地电磁法更适用于目标体与围岩电阻率差异不大的浸染型金属矿床的勘探[1]。根据数据采集方式,激电法测量方式包括地—地、地—井、井—地、井—井[2],其中后三种方法是利用已有钻孔探测井旁盲矿或矿体空间分布,确定矿体埋深、方位,追踪并圈定矿化带。这些方法勘探成本较高。地—地测量是在地面发射和接收,无需钻孔,成本较低,但是不适用于深部矿产的勘测[3]。不同测量方法各有优缺点,因此开展激发极化法探测应根据矿区(工区)实际情况和地质任务选择合适的测量方法。
正演是反演的基础,为了能更好地进行精细反演,需开展激电法三维数值模拟方法研究。激电法数值模拟与电阻率法数值模拟具有相通性,即激电法正演需要进行两次直流电阻率法的正演计算[4]。目前三维数值模拟方法主要包括积分方程法[5-8]、有限单元法[9-15]及有限差分法[15-18],其他数值模拟方法均由这三种方法衍生得到。针对不同测量方法的激电三维数值模拟方法主要包括:Hohmann[19]和朴华荣等[20]基于积分方程法研究了地—地测量的三维极化体激发极化效应;张辉等[21]利用体积分方程法对同时存在激电效应和电磁效应的半空间三维体进行研究,并分析了激电效应和电磁效应并存对正演结果的影响;Tsourlos等[22]和黄俊革[23]利用有限单元法开展了地—地三维激电数值模拟,验证了采用偏导数矩阵与视极化率的关系式计算极化率的可行性;吕玉增[24]和王智[25]利用基于四面体网格交叉剖分的有限单元法开展了地—井、井—地三维激电数值模拟,系统分析了井旁不同形态矿体的激电异常特征;周峰等[26]利用有限差分法开展了井—井激电三维正演,并利用二次异常电位差曲线反演得到矿体的激发极化特征;李长伟[27]利用放射状三棱柱单元结构网格的有限单元法实现了井—井激电法三维数值模拟;高文龙等[28]利用变步长有限差分法实现了井—井激电法三维数值模拟,并分析了侵入带、井径、不同电极系装置及不同井液电阻率对激电效应结果的影响;李静和等[29]为了高效、高精度探测重金属污染的激发极化空间分布,提出了接触式供电—地面观测和接触式供电—直接观测两种观测系统,进行了接触式激发极化法渗漏型目标探测的应用研究,解决了复杂施工环境条件的限制问题,同时提高了观测信号的强度和观测精度。
以上传统的激电法三维数值模拟大多基于空间域,在计算复杂模型时存在计算量大、存储需求高、效率较低等问题。本文基于二维傅里叶变换,将激电法三维数值模拟问题转化为波数域一维数值模拟问题进行求解,可以避免大型稀疏线性方程组的求解,降低计算量和存储需求,明显提高计算效率。此外,传统激电测深装置主要为二极装置、三极装置、偶极装置等,这些装置对地下介质的分辨率有限。本文通过改善数据采集装置提高对地下电性异常体的分辨率,即引入差分装置[30]和积分装置。差分装置指的是以两组供电电流强度相等、方向相反的偶极发射装置并列或共线作为供电装置,利用偶极电极接收信号;积分装置以两组供电电流大小相等、方向相同的偶极发射装置并列或共线作为供电装置,也是利用偶极电极接收信号。本文基于井—井测量方式,对比传统测深装置、差分装置及积分装置对井旁极化矿体的分辨率。最后,对不同背景介质下二极装置和差分装置得到的视电阻率和视极化率响应特征进行分析,比较各自的优势。
1 理论方法 1.1 边值问题激发极化法中,地下点电流源产生的电位满足微分方程[9]
| $ \nabla \cdot \left(\sigma \nabla U\right)=-\frac{4\mathrm{\pi }}{\omega }I\mathrm{\delta }\left(A\right) $ | (1) |
式中:
| $ \begin{array}{l}\nabla \cdot \left({\sigma }_{\mathrm{a}}\nabla U\right)+\nabla \cdot \left({\sigma }_{\mathrm{b}}\nabla {U}_{\mathrm{a}}\right)+\nabla \cdot \left({\sigma }_{\mathrm{b}}\nabla {U}_{\mathrm{b}}\right)\\ =-\frac{4\mathrm{\pi }}{\omega }I\mathrm{\delta }\left(A\right)\end{array} $ | (2) |
其中
| $ \nabla \cdot \left({\sigma }_{\mathrm{b}}\nabla {U}_{\mathrm{b}}\right)=-\frac{4\mathrm{\pi }}{\omega }I\mathrm{\delta }\left(A\right) $ | (3) |
将式(3)代入式(2),可得
| $ \nabla \cdot \left({\sigma }_{\mathrm{b}}\nabla {U}_{\mathrm{a}}\right)=-\nabla \cdot \left({\sigma }_{\mathrm{a}}\nabla U\right) $ | (4) |
因电位U与电场E满足
| $ \nabla \cdot \left({\sigma }_{\mathrm{b}}\nabla {U}_{\mathrm{a}}\right)=\nabla \cdot \boldsymbol{J} $ | (5) |
对于水平层状介质模型,将式(5)沿三个方向展开,可得
| $ \begin{array}{l}\frac{\partial {\sigma }_{\mathrm{b}}}{\partial z}\frac{\partial {U}_{\mathrm{a}}}{\partial z}+{\sigma }_{\mathrm{b}}\left(\frac{{\partial }^{2}{U}_{\mathrm{a}}}{\partial {x}^{2}}+\frac{{\partial }^{2}{U}_{\mathrm{a}}}{\partial {y}^{2}}+\frac{{\partial }^{2}{U}_{\mathrm{a}}}{\partial {z}^{2}}\right)\\ =\frac{\partial {J}_{x}}{\partial x}+\frac{\partial {J}_{y}}{\partial y}+\frac{\partial {J}_{z}}{\partial z}\end{array} $ | (6) |
式中J=[Jx,Jy,Jz],Jx,Jy,Jz为空间域三个方向上的散射电流。
对式(6)沿水平方向进行二维傅里叶变换,可得
| $ \frac{\partial }{\partial z}\left({\sigma }_{\mathrm{b}}\frac{\partial {\tilde{U}}_{\mathrm{a}}}{\partial z}\right)-{k}^{2}{\sigma }_{\mathrm{b}}{\tilde{U}}_{\mathrm{a}}=\mathrm{i}{k}_{x}{\tilde{J}}_{x}+\mathrm{i}{k}_{y}{\tilde{J}}_{y}+\frac{\partial {\tilde{J}}_{z}}{\partial z} $ | (7) |
式中:
从式(7)可看出,方程右端
根据前述求解激电法三维数值模拟问题的思路,需给出方程组的边界条件、求解方程组的方法、背景场、波数域电场与电位的关系式、波数选取方法、迭代算子等。
因式(7)沿x和y方向为波数域,由傅里叶变换特性可知,x和y方向的边界条件自动满足,所以只需给出z方向的边界条件。假设z轴向下为正方向,地面为上边界
| $ {\left.\frac{\partial {\tilde{U}}_{\mathrm{a}}}{\partial z}\right|}_{z={z}_{\mathrm{m}\mathrm{i}\mathrm{n}}}=0 $ | (8) |
选取异常体下方某位置为下边界
| $ {\nabla }^{2}U=0 $ | (9) |
| $ {\nabla }^{2}{U}_{\mathrm{b}}=0 $ | (10) |
因此
| $ {\nabla }^{2}{U}_{\mathrm{a}}=0 $ | (11) |
对应的波数域异常电位
| $ \frac{{\partial }^{2}{\tilde{U}}_{\mathrm{a}}}{\partial {z}^{2}}-{k}^{2}{\tilde{U}}_{\mathrm{a}}=0 $ | (12) |
式(12)的通解为
| $ {\tilde{U}}_{\mathrm{a}}=C{\mathrm{e}}^{-kz}+D{\mathrm{e}}^{kz} $ | (13) |
式中C和D为常数。因无穷远处(
| $ {\left.{\tilde{U}}_{\mathrm{a}}\right|}_{z={z}_{\mathrm{m}\mathrm{a}\mathrm{x}}}=C{\mathrm{e}}^{-kz}\begin{array}{c}\end{array} $ | (14) |
对式(14)求导,下边界
| $ {\left.\frac{\partial {\tilde{U}}_{\mathrm{a}}}{\partial z}\right|}_{z={z}_{\mathrm{m}\mathrm{a}\mathrm{x}}}=-k{\tilde{U}}_{\mathrm{a}} $ | (15) |
式(7)、式(8)和式(15)即组成三维激电法的边值问题。
1.2 有限单元法对于三维激电法的边值问题,可采用基于二次插值的一维有限单元法求解。利用伽辽金法[8]得到边值问题等价有限单元方程
| $ \begin{array}{c}\sum\limits_{e=1}^{M}\underset{e}{\int }\left[{\sigma }_{\mathrm{b}}\frac{\partial {\tilde{U}}_{\mathrm{a}}^{e}}{\partial z}\frac{\partial {N}_{i}}{\partial z}+{k}^{2}{\sigma }_{\mathrm{b}}{\tilde{U}}_{\mathrm{a}}^{e}{N}_{i}+\right.\\ \left.\left(\mathrm{i}{k}_{x}{\tilde{J}}_{x}^{e}+\mathrm{i}{k}_{y}{\tilde{J}}_{y}^{e}+\frac{\partial {\tilde{J}}_{z}^{e}}{\partial z}\right){N}_{i}\right]\mathrm{d}z+\\ k{\left.\left({\sigma }_{\mathrm{b}}{\tilde{U}}_{\mathrm{a}}{N}_{i}\right)\right|}_{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}}=0\end{array} $ | (16) |
式中:M为垂向剖分单元总数;
| $ \boldsymbol{K}{\tilde{\boldsymbol{U}}}_{\mathrm{a}}=\tilde{\boldsymbol{P}} $ | (17) |
式中:
从求解三维激电异常电位边值问题的思路可看出,本文利用二维傅里叶变换对复杂数值模拟问题进行降维求解,即将三维数值模拟问题转换成为不同波数域中的一维数值模拟问题进行求解,可大幅度降低计算量及对存储的需求,提高计算效率。
1.3 关键环节分析 1.3.1 背景场求解思路本文算法基于异常场,因此需先确定背景场。在给出边值问题时,分别假设背景介质为均匀半空间、层状模型、电阻率随深度连续变化等不同情况。电阻率随深度连续变化的特殊情况就是层状介质,即垂向节点电阻率值连续变化。当背景为均匀半空间时,源在任意位置所产生的背景场的求解方法详见文献[1]。当背景为层状介质时,本文推导了点电流源在任意位置产生的背景场,详见附录B。
1.3.2 波数选取方法本文采用基于标准FFT法的二维傅里叶变换,波数的选取基于采样定理,具体方法详见文献[32-33]。需要说明的是,二维反傅里叶变换可以采用基于标准FFT法或高斯-FFT法[33-34]。
1.3.3 迭代算子和波数域电场的求解针对求解电位的边值问题,首先根据背景场求出电位和电场的近似解,然后利用算子进行迭代求解,最终获得高精度数值解。本文采用的迭代算子[35-36]为
| $ \left\{\begin{array}{c}{\boldsymbol{E}}^{\left(n\right)}=\alpha {\boldsymbol{E}}_{\mathrm{T}}^{\left(n\right)}+\beta {\boldsymbol{E}}^{\left(n-1\right)}\\ \alpha =\frac{2{\sigma }_{\mathrm{b}}}{2{\sigma }_{\mathrm{b}}+{\sigma }_{\mathrm{a}}}\\ \beta =\frac{{\sigma }_{\mathrm{a}}}{2{\sigma }_{\mathrm{b}}+{\sigma }_{\mathrm{a}}}\end{array}\right. $ | (18) |
式中:
| $ \left\{\begin{array}{l}{\tilde{E}}_{\mathrm{a}x}=\mathrm{i}{k}_{x}{\tilde{U}}_{\mathrm{a}}\\ {\tilde{E}}_{\mathrm{a}y}=\mathrm{i}{k}_{y}{\tilde{U}}_{\mathrm{a}}\\ {\tilde{E}}_{\mathrm{a}z}=\frac{\partial {\tilde{U}}_{\mathrm{a}}}{\partial z}\end{array}\right. $ | (19) |
本次三维数值模拟采用以下流程:
(1)对求解域采用均匀网格剖分,并利用采样定理得到波数域采样点。
(2)计算背景电场,并求出相应散射电流,利用二维傅里叶变换得到波数域散射电流。
(3)令边值问题式(7)等式右端的波数散射电流等于前一个步骤得到的值,求解方程组得到波数域异常电位,进而得到波数域异常电场。
(4)利用二维反傅里叶变换得到空间域异常电位和异常电场,加上背景场得到总场。
(5)将更新后的总电场与先前总电场进行对比,判断是否满足残差要求。若满足,则输出总电位和电场;否则,利用迭代算子修改总电场,并根据修改的总电场计算波数域散射电流,重复步骤(3)~步骤(5),直至满足残差要求。
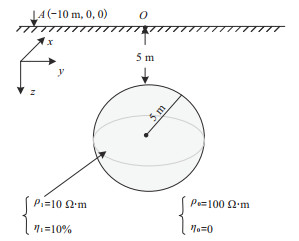
2 算例分析 2.1 算法正确性验证为了验证本文算法的正确性,利用均匀半空间背景下的低阻、高极化率球体模型进行测试。模型如图 1所示。采用均匀网格剖分计算区域,节点总数为101×101×81,水平方向剖分间隔为1 m,垂直方向剖分间隔为0.5 m。算法利用Gauss-FFT法进行二维傅里叶反变换。采用二极装置进行测量,电流强度为1 A,供电电极置于点A(-10 m,0,0)。测点沿地面x方向布设。
|
图 1 低阻、高极化球体模型示意图 |
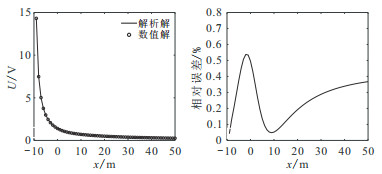
采用解析解[1]作为理论值,两种算法的总电位和相对误差如图 2所示。可以看出,两种算法得到的总电位曲线吻合较好,最大相对误差为0.54%,验证了本文算法的正确性。
|
图 2 图 1模型的电位解析解和数值解(左)及其相对误差(右) |
为了研究均匀半空间背景下激电差分装置对高极化率异常体的异常响应特征及不同背景条件下差分装置的异常响应特征,分别讨论以下两种情况。
2.2.1 高阻/低阻、高极化矿体模型对于井—井勘探,为了探测井旁盲矿,为了节约成本,通常在单孔井中进行测量,即供电电极和测量电极均放置在同一口井中[2]。在金属矿产勘探中,黄铁矿、黄铜矿、方铅矿等矿产多表现为低阻、高极化特性,铬铁矿、黑钨矿及侵染状硫化矿等通常表现为高阻、高极化特性[37]。为了研究高阻或低阻的高极化矿体在差分装置下的激发极化响应特征,不失一般性,可利用简化的金属矿模型——两个大小相同的棱柱异常体模型进行测试。
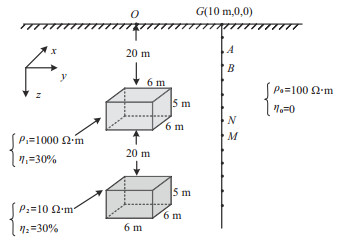
模型如图 3所示,两个异常体中心点在地面上的投影位于直角坐标系原点,钻孔井口G坐标为(10 m,0,0),其他参数详见图中标注。分别利用五种装置(二极装置、三极装置、偶极装置、积分装置、差分装置)沿井孔测量。采用均匀网格剖分计算区域,节点总数为61×51×81,水平方向剖分间隔为2 m,垂直方向剖分间隔为1 m。另外,为了分析电极位于不同位置时盲矿的激电异常特征,分别将供电电极对A-B置于井口(中间点坐标:(10.0 m,0,1.5 m))、井中(中间点坐标(10 m,0,50 m))和井底(中间点坐标(10 m,0,90 m)),使用极距为1 m的接收电极对M-N沿钻孔自上而下布设。
|
图 3 两个棱柱异常体模型示意图 |
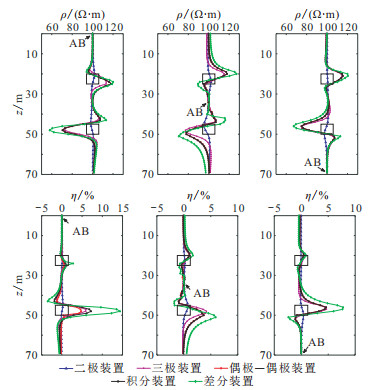
供电电极位于井口、井中和井底时得到的视电阻率和视极化率曲线如图 4所示。可以看出,供电电极放置于不同位置时,五种装置得到的极化体视电阻率和视极化率曲线形态大体相似,即矿体附近均出现异常。这种现象可依据“电偶极子”叠加原理进行分析,即矿体产生的异常场可近似等效为多个“电偶极子”组合叠加的结果[38]。此外,低阻异常体产生的异常远大于高阻异常体产生的异常,说明低阻异常体对电流更敏感。另外,从图中还看出,对于同一供电位置,差分装置测得的异常幅值远大于其他装置,积分装置和偶极装置产生的异常幅值次之,三极装置再次之,二极装置测得的异常幅值最小,说明通过物理差分可有效提高分辨率。因三极装置观测的是电位差,所以对介质的分辨率高于二极装置;积分装置和偶极装置相当于在三极装置的基础上对供电源进行了一次差分,所以它们的分辨率也高于三极装置。尽管积分装置和偶极装置的分辨率相同,但是积分发射装置是由两组偶极发射装置同向供电组合而成,所以供电电流更大,信噪比更高;差分装置则是在偶极装置的基础上对供电源再次进行差分计算,所以分辨率进一步提高。综上所述,差分装置勘探效果优于其他装置,可为野外勘探测量装置的选择提供参考。
|
图 4 供电电极AB位于不同位置时的电阻率(上)和极化率(下)曲线 左:井口;中:井中;右:井底 |
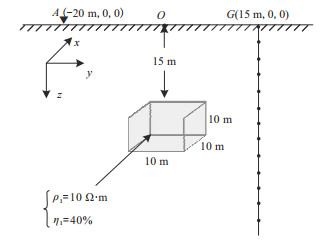
为了进一步研究不同背景下矿体的激发极化特征,建立图 5所示低阻、高极化异常体模型。异常体中心位置在地面的投影位于坐标原点。为了便于对比,对此模型分别利用二极装置和差分装置进行测量。点源(两组偶极源中心位置)位于(-20 m,0,0),接收电极M、N极距为1 m,沿钻孔向下布设。假设背景介质的极化率为0,电阻率分为三种情况:(a)均匀半空间,电阻率为
|
图 5 低阻、高极化异常体模型示意图 |
|
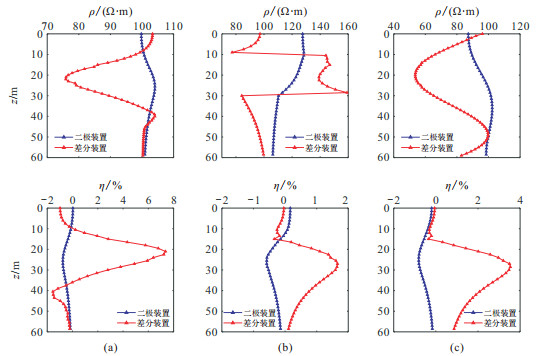
图 6 不同背景介质下的电阻率(上)和极化率(下)曲线 (a)均匀半空间;(b)三层水平介质;(c)纵向电阻率连续变化介质 |
对比不同背景介质下两种装置的视电阻率曲线,可见差分装置能更好地反映背景介质和异常体的垂向电性特征和激发极化特征。
需要说明的是,不同背景介质下同一种装置得到的视极化率曲线形态相似,说明无激电效应的背景介质对极化率影响较小。在实际生产中,对复杂背景介质下极化矿体的勘查可综合考虑电阻率和极化率两个参数,以便更好地分析矿体及围岩的空间分布。
3 结论(1)将空间域与波数域相结合能有效求解激电法三维数值模拟问题,为探索激电法数据的高效、高精度的数值模拟提供一条新思路。
(2)与其他装置相比,差分装置对异常体的视电阻率/视极化率异常响应更明显,分辨率更高。但因该装置是两组发射电流大小相同、方向相反的偶极发射装置组合而成,相对于其他装置,向地下供电能量更低,需增大供电电流,所以在实际应用中,需要综合考虑地质任务及经济成本,选择合适的测量装置及参数。
(3)视电阻率能有效反映目标体及围岩的电性特征,而视极化率能反映目标体的激电效应特征,综合分析这两个参数可更精确地解释异常体的空间分布及地电异常特征。
附录A 有限元单元分析z轴方向可利用节点二次插值函数表示单元e的电位、电流密度及电导率,其形函数表达式为
| $ \left\{\begin{array}{l}{\tilde{U}}_{\mathrm{a}}^{e}={U}_{\mathrm{a}j}^{e}{N}_{j}+{U}_{\mathrm{a}p}^{e}{N}_{p}+{U}_{\mathrm{a}m}^{e}{N}_{m}\\ {\tilde{j}}_{x}^{e}={j}_{xj}^{e}{N}_{j}+{j}_{xp}^{e}{N}_{p}+{j}_{xm}^{e}{N}_{m}\\ {\tilde{j}}_{y}^{e}={j}_{yj}^{e}{N}_{j}+{j}_{yp}^{e}{N}_{p}+{j}_{ym}^{e}{N}_{m}\\ {\tilde{j}}_{z}^{e}={j}_{zj}^{e}{N}_{j}+{j}_{zp}^{e}{N}_{p}+{j}_{zm}^{e}{N}_{m}\\ {\sigma }_{\mathrm{b}}^{e}={\sigma }_{\mathrm{b}j}^{e}{N}_{j}+{\sigma }_{\mathrm{b}p}^{e}{N}_{p}+{\sigma }_{\mathrm{b}m}^{e}{N}_{m}\end{array}\right. $ | (A-1) |
式中j、p、m表示单元内节点编号。因此,式(16)的积分项为
| $ \begin{array}{l}{\int }_{j}\left[{\sigma }_{\mathrm{b}}\frac{\partial {\tilde{U}}_{\mathrm{a}}^{e}}{\partial z}\frac{\partial {N}_{i}}{\partial z}+{k}^{2}{\sigma }_{\mathrm{b}}{\tilde{U}}_{\mathrm{a}}^{e}{N}_{i}+\right.\\ \left.\left(\mathrm{i}{k}_{x}{\tilde{J}}_{x}+\mathrm{i}{k}_{y}{\tilde{J}}_{y}+\frac{\partial {\tilde{J}}_{z}}{\partial z}\right){N}_{i}\right]\mathrm{d}z=\\ \left({\boldsymbol{K}}_{1}+{\boldsymbol{K}}_{2}\right){\tilde{\boldsymbol{U}}}_{\mathrm{a}}^{e}+{\boldsymbol{K}}_{3}{\tilde{\boldsymbol{J}}}_{x}^{e}+{\boldsymbol{K}}_{4}{\tilde{\boldsymbol{J}}}_{y}^{e}+{\boldsymbol{K}}_{5}{\tilde{\boldsymbol{J}}}_{z}^{e}\end{array} $ | (A-2) |
式中
| $ {\tilde{\boldsymbol{U}}}_{\mathrm{a}}^{e}=\left(\begin{array}{c}{\tilde{U}}_{\mathrm{a}j}\\ {\tilde{U}}_{\mathrm{a}p}\\ {\tilde{U}}_{\mathrm{a}m}\end{array}\right), {\tilde{\boldsymbol{J}}}_{x}^{e}=\left(\begin{array}{c}{\tilde{J}}_{xj}\\ {\tilde{J}}_{xp}\\ {\tilde{J}}_{x}\end{array}\right), {\tilde{\boldsymbol{J}}}_{y}^{e}=\left(\begin{array}{c}{\tilde{J}}_{yj}\\ {\tilde{J}}_{yp}\\ {\tilde{J}}_{ym}\end{array}\right), {\tilde{\boldsymbol{J}}}_{z}^{e}=\left(\begin{array}{c}{\tilde{J}}_{zj}\\ {\tilde{J}}_{zp}\\ {\tilde{J}}_{zm}\end{array}\right) $ | (A-3) |
| $ {\boldsymbol{K}}_{1}=\frac{1}{30l}\left(\begin{array}{ccc}37{\sigma }_{\mathrm{b}j}+36{\sigma }_{\mathrm{b}p}-3{\sigma }_{\mathrm{b}m}& -44{\sigma }_{\mathrm{b}j}-32{\sigma }_{\mathrm{b}p}-4{\sigma }_{\mathrm{b}m}& 7{\sigma }_{\mathrm{b}j}-4{\sigma }_{\mathrm{b}p}+7{\sigma }_{\mathrm{b}m}\\ -44{\sigma }_{\mathrm{b}j}-32{\sigma }_{\mathrm{b}p}-4{\sigma }_{\mathrm{b}m}& 48{\sigma }_{\mathrm{b}j}+6{\sigma }_{\mathrm{b}p}+48{\sigma }_{\mathrm{b}m}& -4{\sigma }_{\mathrm{b}j}-32{\sigma }_{\mathrm{b}p}-44{\sigma }_{\mathrm{b}m}\\ 7{\sigma }_{\mathrm{b}j}-4{\sigma }_{\mathrm{b}p}+7{\sigma }_{\mathrm{b}m}& -4{\sigma }_{\mathrm{b}j}-32{\sigma }_{\mathrm{b}p}-44{\sigma }_{\mathrm{b}m}& -3{\sigma }_{\mathrm{b}j}+36{\sigma }_{\mathrm{b}p}+37{\sigma }_{\mathrm{b}m}\end{array}\right) $ | (A-4) |
| $ {\boldsymbol{K}}_{2}=\frac{l{k}^{2}}{420}\left(\begin{array}{ccc}39{\sigma }_{\mathrm{b}j}+20{\sigma }_{\mathrm{b}p}-3{\sigma }_{\mathrm{b}m}& 20{\sigma }_{\mathrm{b}j}+16{\sigma }_{\mathrm{b}p}-8{\sigma }_{\mathrm{b}m}& -3{\sigma }_{\mathrm{b}j}-8{\sigma }_{\mathrm{b}p}-3{\sigma }_{\mathrm{b}m}\\ 20{\sigma }_{\mathrm{b}j}+16{\sigma }_{\mathrm{b}p}-8{\sigma }_{\mathrm{b}m}& 16{\sigma }_{\mathrm{b}j}+192{\sigma }_{\mathrm{b}p}+16{\sigma }_{\mathrm{b}m}& -8{\sigma }_{\mathrm{b}j}+16{\sigma }_{\mathrm{b}p}+20{\sigma }_{\mathrm{b}m}\\ -3{\sigma }_{\mathrm{b}j}-8{\sigma }_{\mathrm{b}p}-3{\sigma }_{\mathrm{b}m}& -8{\sigma }_{\mathrm{b}j}+16{\sigma }_{\mathrm{b}p}+20{\sigma }_{\mathrm{b}m}& -3{\sigma }_{\mathrm{b}j}+20{\sigma }_{\mathrm{b}p}+39{\sigma }_{\mathrm{b}m}\end{array}\right) $ | (A-5) |
| $ {\boldsymbol{K}}_{3}=\frac{\mathrm{i}{k}_{x}l}{30}\left(\begin{array}{ccc}4& 2& -1\\ 2& 16& 2\\ -1& 2& 4\end{array}\right) $ | (A-6) |
| $ {\boldsymbol{K}}_{4}=\frac{\mathrm{i}{k}_{y}l}{30}\left(\begin{array}{ccc}4& 2& -1\\ 2& 16& 2\\ -1& 2& 4\end{array}\right) $ | (A-7) |
| $ {K}_{5}=\frac{1}{6}\left(\begin{array}{ccc}-3& 4& -1\\ -4& 0& 4\\ 1& -4& 3\end{array}\right) $ | (A-8) |
其中l为单元长度。
式(16)中的最后一项表示
| $ k{\left({\sigma }_{\mathrm{b}}{\tilde{U}}_{\mathrm{a}}{N}_{i}\right)}_{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}}=k{\left({\sigma }_{\mathrm{b}}{\tilde{U}}_{\mathrm{a}}\right)}_{{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}}=B{\tilde{U}}_{\mathrm{a}{z}_{\mathrm{m}\mathrm{a}\mathrm{x}}} $ | (A-9) |
令笛卡尔坐标系原点位于地面,点电流源置于层状介质中任意位置,则源所在地层内测点和非源所在地层内测点的电位和电场分别为
| $ \left\{\begin{array}{l}{U}_{j}\left(r, z\right)=\frac{I}{4\mathrm{\pi }{\sigma }_{j}}\frac{1}{r}+{\int }_{0}^{\mathrm{\infty }}\left[{A}_{j}\left(\lambda \right){\mathrm{e}}^{-\lambda \left(z-{z}_{j}\right)}+{B}_{j}\left(\lambda \right){\mathrm{e}}^{\lambda \left(z-{z}_{j+1}\right)}\right]{J}_{0}\left(\lambda r\right)\mathrm{d}\lambda \\ {{E}_{x}}_{j}\left(r, z\right)=\frac{x-{x}_{\mathrm{s}}}{r}{\int }_{0}^{\mathrm{\infty }}\left[\frac{I}{4\mathrm{\pi }{\sigma }_{j}}{\mathrm{e}}^{-\lambda \left|z-{z}_{s}\right|}+{A}_{j}\left(\lambda \right){\mathrm{e}}^{-\lambda \left(z-{z}_{j}\right)}+{B}_{j}\left(\lambda \right){\mathrm{e}}^{\lambda \left(z-{z}_{j+1}\right)}\right]\lambda {J}_{1}\left(\lambda r\right)\mathrm{d}\lambda \\ {{E}_{y}}_{j}\left(r, z\right)=\frac{y-{y}_{\mathrm{s}}}{r}{\int }_{0}^{\mathrm{\infty }}\left[\frac{I}{4\mathrm{\pi }{\sigma }_{j}}{\mathrm{e}}^{-\lambda \left|z-{z}_{s}\right|}+{A}_{j}\left(\lambda \right){\mathrm{e}}^{-\lambda \left(z-{z}_{j}\right)}+{B}_{j}\left(\lambda \right){\mathrm{e}}^{\lambda \left(z-{z}_{j+1}\right)}\right]\lambda {J}_{1}\left(\lambda r\right)\mathrm{d}\lambda \\ {{E}_{z}}_{j}\left(r, z\right)={\int }_{0}^{\mathrm{\infty }}\left[\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(z-{z}_{\mathrm{s}}\right)\frac{I}{4\mathrm{\pi }{\sigma }_{j}}{\mathrm{e}}^{-\lambda \left|z-{z}_{\mathrm{s}}\right|}+{A}_{j}\left(\lambda \right){\mathrm{e}}^{-\lambda \left(z-{z}_{j}\right)}-{B}_{j}\left(\lambda \right){\mathrm{e}}^{\lambda \left(z-{z}_{j+1}\right)}\right]\lambda {J}_{0}\left(\lambda r\right)\mathrm{d}\lambda \end{array}\right. $ | (B-1) |
| $ \left\{\begin{array}{l}{U}_{i}\left(r, z\right)={\int }_{0}^{\mathrm{\infty }}\left[{A}_{i}\left(\lambda \right){\mathrm{e}}^{-\lambda \left(z-{z}_{i}\right)}+{B}_{i}\left(\lambda \right){\mathrm{e}}^{\lambda \left(z-{z}_{i+1}\right)}\right]{J}_{0}\left(\lambda r\right)\mathrm{d}\lambda \\ {E}_{xi}\left(r, z\right)=\frac{x-{x}_{0}}{r}{\int }_{0}^{\mathrm{\infty }}\left[{A}_{i}\left(\lambda \right){\mathrm{e}}^{-\lambda \left(z-{z}_{i}\right)}+{B}_{i}\left(\lambda \right){\mathrm{e}}^{\lambda \left(z-{z}_{i+1}\right)}\right]\lambda {J}_{1}\left(\lambda r\right)\mathrm{d}\lambda \\ {E}_{yi}\left(r, z\right)=\frac{y-{y}_{0}}{r}{\int }_{0}^{\mathrm{\infty }}\left[{A}_{i}\left(\lambda \right){\mathrm{e}}^{-\lambda \left(z-{z}_{i}\right)}+{B}_{i}\left(\lambda \right){\mathrm{e}}^{\lambda \left(z-{z}_{i+1}\right)}\right]\lambda {J}_{1}\left(\lambda r\right)\mathrm{d}\lambda \\ {E}_{zi}\left(r, z\right)={\int }_{0}^{\mathrm{\infty }}\left[{A}_{i}\left(\lambda \right){\mathrm{e}}^{-\lambda \left(z-{z}_{i}\right)}-{B}_{i}\left(\lambda \right){\mathrm{e}}^{\lambda \left(z-{z}_{i+1}\right)}\right]\lambda {J}_{0}\left(\lambda r\right)\mathrm{d}\lambda \end{array}\right. $ | (B-2) |
式(B-1)和式(B-2)中:j表示源所在地层序号;i表示非源层序号;系数A和B的表达式根据点电流源在不同位置分为五种情况。假设地下包含n层介质,则点电流源位于第1层、第2层、第3~第n-2层、第n-1层、第n层五种情况下A和B的取值分别见式(B-3)~式(B-7)。
| $ \left\{\begin{array}{l}{A}_{0}=0\\ {B}_{0}=P+{A}_{1}+{B}_{1}{\mathrm{e}}^{-\lambda {h}_{1}}\\ {A}_{1}=\frac{{J}_{1}+{T}_{1}{J}_{2}{\mathrm{e}}^{-\lambda {h}_{1}}}{1-{T}_{1}{T}_{2}{\mathrm{e}}^{-2\lambda {h}_{1}}}\\ {B}_{1}={J}_{2}+{T}_{2}{A}_{1}{\mathrm{e}}^{-\lambda {h}_{1}}\\ {A}_{2}=\frac{Q+{A}_{1}{\mathrm{e}}^{-\lambda {h}_{1}}+{B}_{1}}{1+{T}_{3}{\mathrm{e}}^{-2\lambda {h}_{2}}}\\ {B}_{2}={T}_{3}{A}_{2}{\mathrm{e}}^{-\lambda {h}_{2}}\\ {A}_{i}=\frac{{A}_{i-1}{\mathrm{e}}^{-\lambda {h}_{i-1}}+{B}_{i-1}}{1+{T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}\\ {B}_{i}={T}_{i+1}{A}_{i}{\mathrm{e}}^{-\lambda {h}_{i}}, i=3, \dots , n-1\\ {A}_{n}={A}_{n-1}{\mathrm{e}}^{-\lambda {h}_{n-1}}+{B}_{n-1}\\ {B}_{n}=0\end{array}\right. $ | (B-3) |
式中
| $ \left\{\begin{array}{l}P=\frac{I}{4\mathrm{\pi }{\sigma }_{1}}{\mathrm{e}}^{-\lambda {z}_{s}}\\ Q=\frac{I}{4\mathrm{\pi }{\sigma }_{1}}{\mathrm{e}}^{-\lambda \left({z}_{2}-{z}_{s}\right)}\\ {J}_{1}={T}_{1}P\\ {J}_{2}={T}_{2}Q\\ {T}_{1}=\frac{{\sigma }_{1}-{\sigma }_{0}}{{\sigma }_{1}+{\sigma }_{0}}\\ {T}_{n}=\frac{{\sigma }_{n-1}-{\sigma }_{n}}{{\sigma }_{n-1}+{\sigma }_{n}}\\ {T}_{i}=\frac{\left({\sigma }_{i-1}-{\sigma }_{i}\right)+\left({\sigma }_{i-1}+{\sigma }_{i}\right){T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}{\left({\sigma }_{i-1}+{\sigma }_{i}\right)+\left({\sigma }_{i-1}-{\sigma }_{i}\right){T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}\\ \begin{array}{cc}& {i}={n}-1, {n}-2, \dots , 2\end{array}\end{array}\right. $ |
| $ \left\{\begin{array}{l}{A}_{0}=0\\ {B}_{0}={A}_{1}+{B}_{1}{\mathrm{e}}^{-\lambda {h}_{1}}\\ {A}_{1}={T}_{1}{B}_{1}{\mathrm{e}}^{-\lambda {h}_{1}}\\ {B}_{1}=\frac{P+{A}_{2}+{B}_{2}{\mathrm{e}}^{-\lambda {h}_{2}}}{{T}_{1}{\mathrm{e}}^{-2\lambda {h}_{1}}+1}\\ {A}_{2}={J}_{2}+{T}_{2}{B}_{2}{\mathrm{e}}^{-\lambda {h}_{2}}\\ {B}_{2}=\frac{{J}_{3}+{J}_{2}{T}_{3}{\mathrm{e}}^{-\lambda {h}_{2}}}{1-{T}_{2}{T}_{3}{\mathrm{e}}^{-2\lambda {h}_{2}}}\end{array}\right. $ | (B-4a) |
| $ \left\{\begin{array}{l}{A}_{3}=\frac{Q+{A}_{2}{\mathrm{e}}^{-\lambda {h}_{2}}+{B}_{2}}{1+{T}_{4}{\mathrm{e}}^{-2\lambda {h}_{3}}}\\ {B}_{3}={T}_{4}{A}_{3}{\mathrm{e}}^{-\lambda {h}_{3}}\\ {A}_{i}=\frac{{A}_{i-1}{\mathrm{e}}^{-\lambda {h}_{i-1}}+{B}_{i-1}}{1+{T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}\\ {B}_{i}={T}_{i+1}{A}_{i}{\mathrm{e}}^{-\lambda {h}_{i}}, i=4, \dots , n-1\\ {A}_{n}={A}_{n-1}{\mathrm{e}}^{-\lambda {h}_{n-1}}+{B}_{n-1}\\ {B}_{n}=0\end{array}\right. $ | (B-4b) |
式中
| $ \left\{\begin{array}{l}P=\frac{I}{4\mathrm{\pi }{\sigma }_{2}}{\mathrm{e}}^{\lambda \left({z}_{2}-{z}_{s}\right)}\\ Q=\frac{I}{4\mathrm{\pi }{\sigma }_{2}}{\mathrm{e}}^{-\lambda \left({z}_{3}-{z}_{s}\right)}\\ {J}_{2}={T}_{2}P\\ {J}_{3}={T}_{3}Q\\ {T}_{1}=\frac{{\sigma }_{1}-{\sigma }_{0}}{{\sigma }_{1}+{\sigma }_{0}}\\ {T}_{2}=\frac{\left({\sigma }_{2}-{\sigma }_{1}\right)+\left({\sigma }_{2}+{\sigma }_{1}\right){T}_{1}{\mathrm{e}}^{-2\lambda {h}_{1}}}{\left({\sigma }_{2}+{\sigma }_{1}\right)+\left({\sigma }_{2}-{\sigma }_{1}\right){T}_{1}{\mathrm{e}}^{-2\lambda {h}_{1}}}\\ {T}_{i}=\frac{\left({\sigma }_{i-1}-{\sigma }_{i}\right)+\left({\sigma }_{i-1}+{\sigma }_{i}\right){T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}{\left({\sigma }_{i-1}+{\sigma }_{i}\right)+\left({\sigma }_{i-1}-{\sigma }_{i}\right){T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}\\ \begin{array}{cc}& {i}={n}-1, \dots , \mathrm{4, 3}\end{array}\\ {T}_{n}=\frac{{\sigma }_{n-1}-{\sigma }_{n}}{{\sigma }_{n-1}+{\sigma }_{n}}\end{array}\right. $ |
| $ \left\{\begin{array}{l}{A}_{0}=0\\ {B}_{0}={A}_{1}+{B}_{1}{\mathrm{e}}^{-\lambda {h}_{1}}\\ {A}_{i}={T}_{i}{B}_{i}{\mathrm{e}}^{-\lambda {h}_{i}}\\ {B}_{i}=\frac{{A}_{i+1}+{B}_{i+1}{\mathrm{e}}^{-\lambda {h}_{i+1}}}{{T}_{i}{e}^{-2\lambda {h}_{i}}+1}\\ \begin{array}{cc}& \mathrm{i}=1, \dots , \mathrm{j}-2\end{array}\\ {A}_{j-1}={T}_{j-1}{B}_{j-1}{\mathrm{e}}^{-\lambda {h}_{j-1}}\\ {B}_{j-1}=\frac{P+{A}_{j}+{B}_{j}{\mathrm{e}}^{-\lambda {h}_{j}}}{{T}_{j-1}{\mathrm{e}}^{-2\lambda {h}_{j-1}}+1}\\ {A}_{j}={J}_{j}+{T}_{j}{B}_{j}{\mathrm{e}}^{-\lambda {h}_{j}}\\ {B}_{j}=\frac{{J}_{j+1}+{J}_{j}{T}_{j+1}{\mathrm{e}}^{-\lambda {h}_{j}}}{1-{T}_{j}{T}_{j+1}{\mathrm{e}}^{-2\lambda {h}_{j}}}\\ {A}_{j+1}=\frac{Q+{A}_{j}{\mathrm{e}}^{-\lambda {h}_{j}}+{B}_{j}}{1+{T}_{j+2}{\mathrm{e}}^{-2\lambda {h}_{j+1}}}\\ {B}_{j+1}={T}_{j+2}{A}_{j+1}{\mathrm{e}}^{-\lambda {h}_{j+1}}\\ {A}_{i}=\frac{{A}_{i-1}{\mathrm{e}}^{-\lambda {h}_{i-1}}+{B}_{i-1}}{1+{T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}\\ {B}_{i}={T}_{i+1}{A}_{i}{\mathrm{e}}^{-\lambda {h}_{i}}, i=j+2, \dots , n-1\\ {A}_{n}={A}_{n-1}{\mathrm{e}}^{-\lambda {h}_{n-1}}+{B}_{n-1}\\ {B}_{n}=0\end{array}\right. $ | (B-5) |
式中
| $ \left\{\begin{array}{l}P=\frac{I}{4\mathrm{\pi }{\sigma }_{j}}{\mathrm{e}}^{\lambda \left({z}_{j}-{z}_{s}\right)}\\ Q=\frac{I}{4\mathrm{\pi }{\sigma }_{j}}{\mathrm{e}}^{-\lambda \left({z}_{j+1}-{z}_{s}\right)}\\ {J}_{j}={T}_{j}P\\ {J}_{j+1}={T}_{j+1}Q\\ {T}_{1}=\frac{{\sigma }_{1}-{\sigma }_{0}}{{\sigma }_{1}+{\sigma }_{0}}\\ {T}_{i}=\frac{\left({\sigma }_{i}-{\sigma }_{i-1}\right)+\left({\sigma }_{i}+{\sigma }_{i-1}\right){T}_{i-1}{\mathrm{e}}^{-2\lambda {h}_{i-1}}}{\left({\sigma }_{i}+{\sigma }_{i-1}\right)+\left({\sigma }_{i}-{\sigma }_{i-1}\right){T}_{i-1}{\mathrm{e}}^{-2\lambda {h}_{i-1}}}\\ \begin{array}{cc}& i=\mathrm{2, 3}, \dots , j\end{array}\\ {T}_{i}=\frac{\left({\sigma }_{i-1}-{\sigma }_{i}\right)+\left({\sigma }_{i-1}+{\sigma }_{i}\right){T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}{\left({\sigma }_{i-1}+{\sigma }_{i}\right)+\left({\sigma }_{i-1}-{\sigma }_{i}\right){T}_{i+1}{\mathrm{e}}^{-2\lambda {h}_{i}}}\\ \begin{array}{cc}& {i}={n}-1, \dots , {j}+1\end{array}\\ {T}_{n}=\frac{{\sigma }_{n-1}-{\sigma }_{n}}{{\sigma }_{n-1}+{\sigma }_{n}}\end{array}\right. $ |
| $ \left\{\begin{array}{l}{A}_{0}=0\\ {B}_{0}={A}_{1}+{B}_{1}{\mathrm{e}}^{-\lambda {h}_{1}}\\ {A}_{i}={T}_{i}{B}_{i}{\mathrm{e}}^{-\lambda {h}_{i}}\\ {B}_{i}=\frac{{A}_{i+1}+{B}_{i+1}{\mathrm{e}}^{-\lambda {h}_{i+1}}}{{T}_{i}{\mathrm{e}}^{-2\lambda {h}_{i}}+1}, i=\mathrm{1, 2}, \dots , n-3\\ {A}_{n-2}={T}_{n-2}{B}_{n-2}{\mathrm{e}}^{-\lambda {h}_{n-2}}\\ {B}_{n-2}=\frac{P+{A}_{n-1}+{B}_{n-1}{\mathrm{e}}^{-\lambda {h}_{n-1}}}{{T}_{n-2}{\mathrm{e}}^{-2\lambda {h}_{n-2}}+1}\\ {A}_{n-1}=\frac{{J}_{n-1}+{T}_{n-1}{J}_{n}{\mathrm{e}}^{-\lambda {h}_{n-1}}}{1-{T}_{n-1}{T}_{n}{\mathrm{e}}^{-2\lambda {h}_{n-1}}}\\ {B}_{n-1}={J}_{n}+{T}_{n}{A}_{n-1}{\mathrm{e}}^{-\lambda {h}_{n-1}}\\ {A}_{n}=Q+{A}_{n-1}{\mathrm{e}}^{-\lambda {h}_{n-1}}+{B}_{n-1}, {B}_{n}=0\end{array}\right. $ | (B-6) |
式中
| $ P=\frac{I}{4\mathrm{\pi }{\sigma }_{n-1}}{\mathrm{e}}^{\lambda \left({z}_{n-1}-{z}_{s}\right)} , Q=\frac{I}{4\mathrm{\pi }{\sigma }_{n-1}}{\mathrm{e}}^{-\lambda \left({z}_{n}-{z}_{s}\right)} $ |
| $ {J}_{n-1}={T}_{n-1}P , {J}_{n}={T}_{n}Q , {T}_{1}=\frac{{\sigma }_{1}-{\sigma }_{0}}{{\sigma }_{1}+{\sigma }_{0}} $ |
| $ {T}_{i}=\frac{\left({\sigma }_{i}-{\sigma }_{i-1}\right)+\left({\sigma }_{i}+{\sigma }_{i-1}\right){T}_{i-1}{\mathrm{e}}^{-2\lambda {h}_{i-1}}}{\left({\sigma }_{i}+{\sigma }_{i-1}\right)+\left({\sigma }_{i}-{\sigma }_{i-1}\right){T}_{i-1}{\mathrm{e}}^{-2\lambda {h}_{i-1}}} $ |
| $ \begin{array}{cc}& i=\mathrm{2, 3}, \dots , n-1\end{array} $ |
| $ {T}_{n}=\frac{{\sigma }_{n-1}-{\sigma }_{n}}{{\sigma }_{n-1}+{\sigma }_{n}} $ |
| $ \left\{\begin{array}{l}{A}_{0}=0\\ {B}_{0}={A}_{1}+{B}_{1}{\mathrm{e}}^{-\lambda {h}_{1}}\\ {A}_{i}={T}_{i}{B}_{i}{\mathrm{e}}^{-\lambda {h}_{i}}\\ {B}_{i}=\frac{{A}_{i+1}+{B}_{i+1}{\mathrm{e}}^{-\lambda {h}_{i+1}}}{{T}_{i}{\mathrm{e}}^{-2\lambda {h}_{i}}+1}i=2, \dots , n\\ {A}_{n-1}={T}_{n-1}{B}_{n-1}{\mathrm{e}}^{-\lambda {h}_{n-1}}\\ {B}_{n-1}=\frac{P+{A}_{n}}{{T}_{n-1}{\mathrm{e}}^{-2\lambda {h}_{n-1}}+1}\\ {A}_{n}={T}_{n}P, {B}_{n}=0\end{array}\right. $ | (B-7) |
式中
| $ \left\{\begin{array}{l}{T}_{1}=\frac{{\sigma }_{1}-{\sigma }_{0}}{{\sigma }_{1}+{\sigma }_{0}}\\ {T}_{i}=\frac{\left({\sigma }_{i}-{\sigma }_{i-1}\right)+\left({\sigma }_{i}+{\sigma }_{i-1}\right){T}_{i-1}{\mathrm{e}}^{-2\lambda {h}_{i-1}}}{\left({\sigma }_{i}+{\sigma }_{i-1}\right)+\left({\sigma }_{i}-{\sigma }_{i-1}\right){T}_{i-1}{\mathrm{e}}^{-2\lambda {h}_{i-1}}}\\ P=\frac{I}{4\mathrm{\pi }{\sigma }_{n}}{\mathrm{e}}^{\lambda \left({z}_{n}-{z}_{s}\right)}\end{array}\right. $ |
上面公式适用于地下介质至层数n > 5的情况。当n < 5时,可将某层分解为电导率相等的多层,即可采用以上公式。若需计算多源下任意位置的电位和电场,可分别计算每个点电流源产生的场值,进行矢量叠加即可。求解点源在层状介质任意位置产生的电位和电场可采用滤波法。传统的滤波法需要逐个测点递推计算层系数,对于层状和节点较多的情况,计算速度慢。因此,本文采用优化的滤波法求解,即先计算电位和电场表达式中与z轴深度方向的相关系数,然后计算所有波数下与z轴深度方向无关的层系数和某一平面节点的电场/电位系数并进行存储,后续计算任意深度上测点的场值时,只需调用存储数据,将其与z轴相关系数相乘并进行累加即可,如此可快速计算背景场值。模型测试结果表明,采用此方法比优化前计算速度提高约20倍。
| [1] |
李金铭. 地电场与电法勘探[M]. 北京: 地质出版社, 2005.
|
| [2] |
蔡柏林, 黄智辉, 谷守民. 井中激发极化法[M]. 北京: 地质出版社, 1983.
|
| [3] |
罗延忠, 张桂青. 频率域激电法原理[M]. 北京: 地质出版社, 1988.
|
| [4] |
宋滔, 白禹. 时间域激发极化法各向异性介质响应分析[J]. 贵阳学院学报(自然科学版), 2021, 16(4): 107-110, 114. SONG Tao, BAI Yu. Analysis of the response of anisotropic media in the time-domain induced polarization method[J]. Journal of Guiyang College (Natural Sciences), 2021, 16(4): 107-110, 114. DOI:10.16856/j.cnki.52-1142/n.2021.04.023 |
| [5] |
MICHALSKI K A, MOSIG J R. Multilayered media Green's functions in integral equation formulations[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(3): 508-519. DOI:10.1109/8.558666 |
| [6] |
MÉNDEZ-DELGADO S, GÓMEZ-TREVIÑO E, PÉREZ-FLORES M A. Forward modelling of direct current and low-frequency electromagnetic fields using integral equations[J]. Geophysical Journal International, 1999, 137(2): 336-352. |
| [7] |
郭飞, 马西奎, 邱关源. 一种适于直流电阻率正演模拟求解地表电位的积分方程法[J]. 西安交通大学学报, 1999, 33(10): 17-22. GUO Fei, MA Xikui, QIU Guanyuan. Integral equation applied to modeling of surface potential in DC resistivity[J]. Journal of Xi'an Jiaotong University, 1999, 33(10): 17-22. |
| [8] |
REN Z, CHEN H, TANG J, et al. A volume-surface integral approach for direct current resistivity problems with topography[J]. Geophysics, 2018, 83(5): E293-E302. DOI:10.1190/geo2017-0577.1 |
| [9] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [10] |
熊彬, 阮百尧, 罗延钟. 复杂地形条件下直流电阻率异常三维数值模拟研究[J]. 地质与勘探, 2003, 39(4): 60-64. XIONG Bin, RUAN Baiyao, LUO Yanzhong. 3-D numerical simulation study of DC resistivity anomaly under complicated terrain[J]. Geology and Prospecting, 2003, 39(4): 60-64. |
| [11] |
LI Y, SPITZER K. Finite element resistivity modelling for three-dimensional structures with arbitrary anisotropy[J]. Physics of the Earth and Planetary Interiors, 2005, 150(1-3): 15-27. DOI:10.1016/j.pepi.2004.08.014 |
| [12] |
强建科, 罗延钟. 三维地形直流电阻率有限元法模拟[J]. 地球物理学报, 2007, 50(5): 1606-1613. QIANG Jianke, LUO Yanzhong. The resistivity FEM numerical modeling on 3-D undulating topography[J]. Chinese Journal of Geophysics, 2007, 50(5): 1606-1613. |
| [13] |
殷长春, 杨志龙, 刘云鹤, 等. 基于环形扫面测量的三维直流电阻率法任意各向异性模型响应特征[J]. 吉林大学学报(地球科学版), 2018, 48(3): 872-880. YIN Changchun, YANG Zhilong, LIU Yunhe, et al. Characteristics of 3D DC resistivity response for arbitrary anisotropic models using circular scanning measurement[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(3): 872-880. |
| [14] |
赵宁, 黄明卫, 申亚行, 等. 高阶自适应有限元三维直流电阻率正演方法及其在沁水盆地煤气层压裂监测中的应用[J]. 石油地球物理勘探, 2021, 56(1): 209-216. ZHAO Ning, HUANG Mingwei, SHEN Yahang, et al. Forward modeling of 3D DC resistivity based on high-order adaptive finite element and its application in Qinshui Basin[J]. Oil Geophysical Prospecting, 2021, 56(1): 209-216. |
| [15] |
许巍, 魏然, 黄航, 等. 油气储层低频界面极化效应数值模型[J]. 石油地球物理勘探, 2022, 57(6): 1481-1488. XU Wei, WEI Ran, HUANG Hang, et al. Numerical simulation of polarization effect in low-frequency interface of oil-gas reservoirs[J]. Oil Geophysical Prospecting, 2022, 57(6): 1481-1488. |
| [16] |
LOKE M H, BARKER R D. Practical techniques for 3D resistivity surveys and data inversion[J]. Geophysical Prospecting, 1996, 44(3): 499-523. |
| [17] |
ZHOU B, GREENHALGH S A. Finite element three dimensional direct current resistivity modelling: accuracy and efficiency considerations[J]. Geophysical Journal International, 2010, 145(3): 679-688. |
| [18] |
马欢, 谭捍东, 林昌洪. 井地、地井、井间和地面激电资料三维共轭梯度反演研究[C]. 第十一届中国国际地球电磁学术讨论会论文集, 2013, 219-221. MA Huan, TAN Handong, LIN Changhong. Three-dimensional conjugate inversion of surface-borehole, borehole-surface, borehole-borehole and surface IP data[C]. Proceedings of the 11th China International Geoelectromagnetic Symposium, 2013, 219-221. |
| [19] |
HOHMANN G W. Three-dimensional induced polarization and electromagnetic modeling[J]. Geophysics, 1975, 40(2): 309-324. |
| [20] |
朴化荣, 薛爱民, 金东, 等. 积分方程法求解三度极化体的激发极化效应[J]. 物化探计算技术, 1985(4): 310-325. PIAO Huarong, XUE Aimin, JIN Dong, et al. Computation of the IP response of three-dimensional polarizable bodies using integral equation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1985(4): 310-325. |
| [21] |
张辉, 李桐林, 董瑞霞. 体积分方程法模拟复电阻率三维体电磁响应[J]. 煤田地质与勘探, 2006, 34(1): 70-74. ZHANG Hui, LI Tonglin, DONG Ruixia. Modeling electromagnetic responses of complex resistivity 3-D body using volume integral equation method[J]. Coal Geology & Exploration, 2006, 34(1): 70-74. |
| [22] |
TSOURLOS P I, OGILVY R D. An algorithm for the 3-D inversion of tomographic resistivity and induced polarization data: preliminary results[J]. Journal of the Balkan Geophysical Society, 1999, 2(2): 30-45. |
| [23] |
黄俊革. 三维电阻率/极化率有限元正演模拟与反演成像[D]. 湖南长沙: 中南大学, 2003. HUANG Junge. 3-D Resistivity/IP Modeling and Inversion Based on FEM[D]. Central South University, Changsha, Hunan, 2003. |
| [24] |
吕玉增. 地—井、井—地IP三维快速正反演研究[D]. 湖南长沙: 中南大学, 2008. LYU Yuzeng. The Research on 3-D Fast Forward and Inversion of Surface-borehole and Borehole-surface IP Methods[D]. Central South University, Changsha, Hunan, 2008. |
| [25] |
王智. 井中激电正反演及其应用研究[D]. 湖北武汉: 中国地质大学(武汉), 2015. WANG Zhi. Research on Forward and Inversion of Induced Polarization in Borehole and Application[D]. China University of Geosciences(Wuhan), Wuhan, Hubei, 2015. |
| [26] |
周峰, 潘和平, 文国军, 等. 基于有限差分的井中激发极化三维正演[J]. 电波科学学报, 2010, 25(4): 785-792. ZHOU Feng, PAN Heping, WEN Guojun, et al. Three-dimensional forward modeling of induced of polarization borehole using finite difference method[J]. Chinese Journal of Radio Science, 2010, 25(4): 785-792. |
| [27] |
李长伟. 井中激发极化法正反演及快速迭代求解技术研究[D]. 湖南长沙: 中南大学, 2012. LI Changwei. Study on Forward and Inversion of Induced-polarization Well Logging and Fast Iterative Solvers[D]. Central South University, Changsha, Hunan, 2012. |
| [28] |
高文龙, 严良俊, 周磊. 井中激电三维数值模拟及井眼影响因素分析[J]. 地球物理学进展, 2021, 36(3): 1257-1266. GAO Wenlong, YAN Liangjun, ZHOU Lei. 3D numerical simulation of in-hole IP and analysis of borehole influencing factors[J]. Progress in Geophysics, 2021, 36(3): 1257-1266. |
| [29] |
李静和, 何展翔, 杨俊, 等. 针对渗漏型目标的新型接触式激电法及应用[J]. 石油地球物理勘探, 2021, 56(3): 659-669. LI Jinghe, HE Zhanxiang, YANG Jun, et al. Contact-type induced polarization and its application for detecting leakage[J]. Oil Geophysical Prospecting, 2021, 56(3): 659-669. |
| [30] |
赵东东, 戴世坤, 张松宝, 等. 一种应用于直流电阻率法勘探的偶极差分装置及方法[P]. CN202011101478.5. 2021-04-09.
|
| [31] |
BOISVERT R F. Algorithms for special tridiagonal systems[J]. SIAM Journal on Scientific and Statistical Computing, 1991, 12(2): 423-442. |
| [32] |
柴玉璞. 偏移抽样理论及其应用[M]. 北京: 石油工业出版社, 1997.
|
| [33] |
陈龙伟, 戴世坤, 吴美平. 应用任意采样点数FFT算法时离散频率计算[J]. 地球物理学进展, 2016, 31(1): 164-169. CHEN Longwei, DAI Shikun, WU Meiping. Computation of discrete frequency when using FFT algorithm with random sampling points[J]. Progress in Geophysics, 2016, 31(1): 164-169. |
| [34] |
WU L, TIAN G. High-precision Fourier forward modeling of potential fields[J]. Geophysics, 2014, 79(5): G59-G68. |
| [35] |
戴世坤, 赵东东, 李昆, 等. 基于矢量位和标量位的空间波数混合域电磁三维正演模拟[J]. 地球物理学报, 2022, 65(1): 404-416. DAI Shikun, ZHAO Dongdong, LI Kun, et al. Forward modeling of 3D electromagnetic problems using vector and scalar potentials in a mixed space-wavenumber domain[J]. Chinese Journal of Geophysics, 2022, 65(1): 404-416. |
| [36] |
戴世坤, 陈轻蕊, 凌嘉宣, 等. 空间—波数域三维大地电磁场积分方程法数值模拟[J]. 地球物理学报, 2022, 65(6): 2294-2310. DAI Shikun, CHEN Qingrui, LING Jiaxuan, et al. Three-dimensional numerical simulation of magnetotelluric field in the space-wavenumber domain[J]. Chinese Journal of Geophysics, 2022, 65(6): 2294-2310. |
| [37] |
潘纪顺, 葛为中, 折京平. 地面/井地/井间超高密度电阻率成像技术[J]. 华北水利水电学院学报, 2010, 31(2): 74-78. PAN Jishun, GE Weizhong, SHE Jingping. High-density electrical resistivity imaging technique of ground/borehole-to-surface/inter-well[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2010, 31(2): 74-78. |
| [38] |
吕玉增, 阮百尧, 彭苏萍. 地—井方位激电观测异常特征研究[J]. 地球物理学进展, 2012, 27(1): 201-216. LYU Yuzeng, RUAN Baiyao, PENG Suping. A study on anomaly of surface-borehole direction induced polarization survey[J]. Progress in Geophysics, 2012, 27(1): 201-216. |



 周印明, 湖南省湘潭市雨湖区桃园路1号湖南科技大学计算机科学与工程学院,411201。Email:
周印明, 湖南省湘潭市雨湖区桃园路1号湖南科技大学计算机科学与工程学院,411201。Email: