2. 东华理工大学地球物理与测控技术学院, 江西南昌, 330013
2. School of Geophysics and Measurement-Control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China
基于岩(矿)石的密度、磁化率、电阻率及波阻抗等物性特点,地球物理方法可分为重、磁、电、震等不同勘探方法。由于观测数据体在空间上的局限性,单凭某一种地球物理方法很难准确推测复杂的地下地质结构[1]。但不同类型的地球物理数据间具有互补性,可联合多种地球物理数据进行综合解释,降低多解性,提高解释的可靠性[2-4]。重力场和磁场均是地下所有场源产生异常的总和,具有严重的体积效应,多解性明显。因而,利用重、磁异常进行综合分析与解释,有助于提高地质解释的准确性。
重磁对应分析法是重磁联合定性解释的一种常用方法,该方法基于重磁泊松定理,通过研究重力垂向一阶导数和化极磁异常的相关性开展岩性识别与构造划分[5]。Garland[6]首先提出了重磁对应分析方法,应用于计算单一地质体的磁化强度与剩余密度的比值(泊松比),从而确定场源性质;Cordell等[7]结合重力异常和磁源重力异常振幅谱,估计北极地区的柯尼希斯贝格比(即剩余磁化强度与感应磁化强度之比)及总磁化方向;Chandler等[8]利用滑动窗口实现了多源重磁场的相关性研究;Chandler等[9]应用滑动窗口下的重磁对应分析法对美国明尼苏达中东部至佩尼奥克统造山带前寒武系开展地质填图,取得了较好的应用效果。
刘心铸[10]将重磁对应分析法引入中国,并进行了单一和叠加异常体的模型试验及应用分析;黎益仕等[11]以重磁对应分析为约束,开展了重磁联合反演,获得了良好的应用效果;范正国等[12]分析了重磁对应分析法的局限性,提出了自适应重磁对应分析法,在一定程度上提高了方法的可靠性与实用性;宋景明[13]利用磁源重力异常剔除磁性体引起的重力异常,得到了反映沉积构造特征的剩余重力异常;在此基础上,颜廷杰等[14]利用多尺度窗口滑动线性回归修正方法将磁场换算为磁源重力异常,得到了纯粹由无磁性地质体产生的剩余重力异常;王彦国等[15]基于重磁泊松定理推导了总磁化方向的估计方法,并在相山铀矿田获得了良好的应用效果。一些学者还在不同地区开展了重磁对应分析法的应用,取得了很好的应用效果[16-19]。然而,常规重磁对应分析法需要进行化极处理,且仅适用于重磁异常高度相关的情况。此外,该方法易产生虚假信息,严重限制了该方法的实际应用[12, 18]。鉴于此,本文从重力二阶垂向导数与归一化磁源强度的表达式出发,推导出新形式下的重磁泊松公式。在此基础上,提出了基于重力二阶垂向导数与归一化磁源强度互相关系数的重磁相关性分析方法,并通过噪声扰动处理消除重磁同源体之外的虚假强相关信号。由于本方法使用了重力二阶导数,很大程度上削弱了区域重力场的影响;同时,归一化磁源强度基本不受磁化方向影响。因此,本文方法无需做化极处理,具有较强的适用性和实用性。通过模型试验验证了方法的可行性与优越性。最后,将该方法应用于相山铀矿田重磁资料处理,获得了良好的效果。
1 基本原理| $ g=\frac{G\mathrm{\Delta }\rho {k}_{\mathrm{g}}({z}_{0}-z)}{{\left[(x-{x}_{0}{)}^{2}+(y-{y}_{0}{)}^{2}+(z-{z}_{0}{)}^{2}\right]}^{({N}_{\mathrm{g}}+1)/2}} $ | (1) |
式中:G是万有引力常数;
对重力异常g求取z方向的二阶导数
| $ \begin{array}{l}{g}_{zz}=G\mathrm{\Delta }\rho {k}_{\mathrm{g}}({N}_{\mathrm{g}}+1)({z}_{0}-z)\times \\ \frac{{N}_{\mathrm{g}}({z}_{0}{-z)}^{2}-3\left[(x-{x}_{0}{)}^{2}+(y-{y}_{0}{)}^{2}\right]}{{\left[(x-{x}_{0}{)}^{2}+(y-{y}_{0}{)}^{2}+(z-{z}_{0}{)}^{2}\right]}^{({N}_{\mathrm{g}}+5)/2}}\end{array} $ | (2) |
| $ \begin{array}{l}{T}_{\mu }=\sqrt{-{\lambda }_{2}^{2}-{\lambda }_{1}{\lambda }_{3}}\\ =\frac{{\mu }_{0}M{k}_{\mathrm{M}}}{4\mathrm{\pi }{\left[(x-{x}_{0}{)}^{2}+(y-{y}_{0}{)}^{2}+(z-{z}_{0}{)}^{2}\right]}^{({N}_{\mathrm{M}}+1)/2}}\end{array} $ | (3) |
式中:
磁梯度张量
| $ \boldsymbol{\varGamma }={\mu }_{0}\left[\begin{array}{ccc}\frac{{\partial }^{2}U}{\partial {x}^{2}}& \frac{{\partial }^{2}U}{\partial x\partial y}& \frac{{\partial }^{2}U}{\partial x\partial z}\\ \frac{{\partial }^{2}U}{\partial y\partial x}& \frac{{\partial }^{2}U}{\partial {y}^{2}}& \frac{{\partial }^{2}U}{\partial y\partial z}\\ \frac{{\partial }^{2}U}{\partial z\partial x}& \frac{{\partial }^{2}U}{\partial z\partial y}& \frac{{\partial }^{2}U}{\partial {z}^{2}}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial {B}_{x}}{\partial x}& \frac{\partial {B}_{x}}{\partial y}& \frac{\partial {B}_{x}}{\partial z}\\ \frac{\partial {B}_{y}}{\partial x}& \frac{\partial {B}_{y}}{\partial y}& \frac{\partial {B}_{y}}{\partial z}\\ \frac{\partial {B}_{z}}{\partial x}& \frac{\partial {B}_{z}}{\partial y}& \frac{\partial {B}_{z}}{\partial z}\end{array}\right] $ | (4) |
式中:U表示磁位;
当观测点位于场源上方时,重力二阶垂向导数和归一化磁源强度公式可分别简化为
| $ \left\{\begin{array}{l}{g}_{zz}({x}_{0}, {y}_{0}, z)=G\mathrm{\Delta }\rho {k}_{\mathrm{g}}\frac{{N}_{\mathrm{g}}({N}_{\mathrm{g}}+1)}{({z}_{0}{-z)}^{{N}_{\mathrm{g}}+2}}\\ {T}_{\mu }({x}_{0}, {y}_{0}, z)=\frac{{\mu }_{0}M{k}_{\mathrm{M}}}{4\mathrm{\pi }}\frac{1}{({z}_{0}{-z)}^{{N}_{\mathrm{M}}+1}}\end{array}\right. $ | (5) |
从常规重磁泊松公式可知,对于重磁同源体,其磁异常与重力异常的一阶导数形式一致,因此
| $ {T}_{\mu }({x}_{0}, {y}_{0}, z)=\frac{{\mu }_{0}{k}_{\mathrm{M}}}{4\mathrm{\pi }G{k}_{\mathrm{g}}{N}_{\mathrm{g}}({N}_{\mathrm{g}}+1)}\cdot \frac{M}{\Delta \rho }\cdot {g}_{zz}({x}_{0}, {y}_{0}, z)\\ =k\frac{M}{\Delta \rho }\cdot {g}_{zz}({x}_{0}, {y}_{0}, z) $ | (6) |
上式即为基于重力二阶垂向导数与归一化磁源强度的重磁泊松公式。对于同一场源,记
依据式(6),可引入下面的互相关系数判断重磁的同源性
| $ C=\frac{\sum\limits_{i=1}^{W}{g}_{zz}({x}_{i}, {y}_{i}, z){T}_{\mu }({x}_{i}, {y}_{i}, z)}{\sqrt{\sum\limits_{i=1}^{W}{g}_{zz}^{2}({x}_{i}, {y}_{i}, z)\times \sum\limits_{i=1}^{W}{T}_{\mu }^{2}({x}_{i}, {y}_{i}, z)}} $ | (7) |
式中W表示滑动计算窗口的总点数。上式中包含重力二阶导数和磁场一阶导数,可大幅度降低重磁背景场的影响。
根据柯西不等式可得
| $ \begin{array}{l} {\left[\sum\limits_{i=1}^{{W}_{n}}{g}_{zz}({x}_{i}, {y}_{i}, z){T}_{\mu }({x}_{i}, {y}_{i}, z)\right]}^{2}\le \\ \sum\limits_{i=1}^{{W}_{n}}{g}_{zz}^{2}({x}_{i}, {y}_{i}, z)\sum\limits_{i=1}^{{W}_{n}}{T}_{\mu }^{2}({x}_{i}, {y}_{i}, z)\end{array} $ | (8) |
因此,相关系数C取值范围为[-1, 1]。
同样,依据式(6)可以计算包含场源几何形状影响因素的重磁泊松比
| $ k\frac{M}{\mathrm{\Delta }\rho }=\frac{\sum\limits_{i=1}^{W}{T}_{\mu }({x}_{i}, {y}_{i}, z)}{\sum\limits_{i=1}^{W}{g}_{zz}({x}_{i}, {y}_{i}, z)} $ | (9) |
直接使用重力二阶垂向导数和归一化磁源强度进行互相关计算时,效果并不理想,主要原因是远离场源时,归一化磁源强度太小且窗口内数值变化不明显,此时窗口内各点的
| $ \begin{array}{l}C=\frac{\overline{{T}_{\mu }^{}}\sum\limits_{i=1}^{{W}_{n}}{g}_{zz}({x}_{i}, {y}_{i}, z)}{\sqrt{\sum\limits_{i=1}^{{W}_{n}}{g}_{zz}^{2}({x}_{i}, {y}_{i}, z){\left(\overline{{T}_{\mu }^{}}\right)}^{2}}}\\ =\frac{\sum\limits_{i=1}^{{W}_{n}}{g}_{zz}({x}_{i}, {y}_{i}, z)}{\sqrt{\sum\limits_{i=1}^{{W}_{n}}{g}_{zz}^{2}({x}_{i}, {y}_{i}, z)}}\to \pm 1\end{array} $ | (10) |
根据上式可知,当远离磁源区且重力二阶垂向导数处于非零值区域时,系数C接近
为解决这一问题,对重力二阶垂向导数和归一化磁源强度添加两个不相关的噪声干扰,然后再进行互相关计算。虽然添加随机噪声会降低数据信噪比,但互相关系数计算是一个平均化处理过程,可有效削弱噪声对有效信号的干扰。在接近场源区内,场源的有用信号占比更大,互相关系数主要取决于重磁异常的相关性;在远离场源处,噪声占主导地位,且随机分布,此时互相关系数趋于零。由于归一化磁源强度具有非负性,因此互相关系数趋于1时,意味着高密度、强磁性场源的存在;接近-1时,表明场源具有低密度、强磁性的特点。
2 模型试验 2.1 单一异常体模型试验为了测试方法的可行性与有效性,首先建立一个单一异常体模型,分别模拟重磁完全同源、部分同源及完全不同源三种情况。
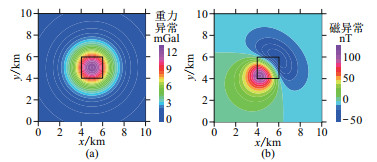
模型包含一个正方体异常体,异常体边长为2 km,上顶面埋深为1 km,剩余密度为1.0 g/cm3,磁化强度为1 A/m,磁倾角及磁偏角均为45°。图 1为该模型的重力异常与磁异常。
|
图 1 单一异常体模型的重力异常(a)和磁异常(b) 黑色方框表示异常体位置,下同。 |
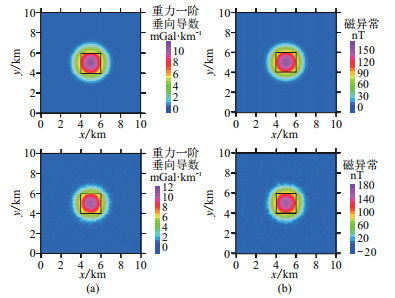
图 2是该模型的理论重力异常一阶垂向导数和理论垂直磁化磁异常,及含10%随机干扰的异常,以此数据计算常规重磁对应分析法的相关系数。需要指出的是,该模型是重磁完全同源,与重磁不同源的差别是仅异常位置发生偏移,异常形态是一致的,因此文中不对其进行展示。
|
图 2 单一异常体模型的重力一阶垂向导数(a)及垂直磁化磁异常(b) 上:理论值;下:含10%噪声 |
图 3(上)是基于图 2(上)数据,采用常规重磁分析法分别对重磁异常同源、部分同源、完全不同源三种情况下计算的系数C。可以看出,重磁异常完全同源时,C在整个测区都接近于1,这不利于确定重、磁源的真实位置;当重磁异常部分同源和完全不同源时,C在远离场源区存在大面积的正相关和负相关,在重力源与磁源质心连线上,则存在明显的负相关。这说明无论是重磁同源还是不同源,理论重力一阶垂向导数和垂直磁化磁异常的重磁对应分析法效果并不理想,均不能较准确地反映重磁场的相关性。范正国等[12]对常规重磁对应分析法开展了详细的模拟实验工作,得到了同样的结论,这也是该方法未能广泛应用的主要原因。

|
图 3 常规重磁对应分析法对无噪数据(上)和含噪数据(下)计算的互相关系数C(窗口大小5×5) (a)重磁异常同源;(b)重磁异常部分同源;(c)重磁异常不同源 |
图 3(下)是基于图 2(下)数据,分别对重磁异常同源、部分同源、完全不同源三种情况计算的C。可以看出,由于噪声干扰的引入,C值在远离场源区处于零值上下波动。在重磁完全同源的场源上方接近1,但重磁部分同源及完全不同源时,重磁源质心连线上仍存在明显的负相关。这表明,对重、磁场进行噪声扰动有助于提高重磁对应分析方法在重磁完全同源时的可靠性,但在其他情况(重磁部分同源及完全不同源)下仍不适用,易得到虚假信息,不利于重磁综合解释。
图 4是基于图 1中的重力异常和斜磁化磁异常换算得到的重力二阶垂向导数和归一化磁源强度,以及分别添加10%随机干扰的结果。图 5(上)是对图 4(上)数据分别计算重磁同源、部分同源及完全不同源时的无噪声重力二阶垂向导数与归一化磁源强度的互相关系数C。可以看出,无论重磁是否同源,在重力源内外均存在强相关性,这显然是不合理的。图 5(下)是基于图 4(下)计算的重力二阶垂向导数与归一化磁源强度的互相关系数C。可以看出:添加噪声干扰后,C在重磁同源位置上相关性较强,而在重磁场源外则相关性较弱;当重磁完全不同源时,整个测区内的相关系数基本在零值附近,即重磁完全不相关。显然,通过添加噪声扰动可显著提高方法的有效性与可靠性。相对于常规重磁对应分析法,本文方法能够更好地反映重磁同源体的真实位置。

|
图 4 单一异常体模型的重力二阶垂向导数(a)及归一化磁源强度(b) 上:无噪数据;下:含10%噪声 |
2.2 叠加模型试验
为了验证方法对复杂情况的应用效果,构建了一个多场源组成的叠加模型,模型参数见表 1。其中正方体与岩脉为重磁同源,棱柱体为部分同源,球体是无磁性的。由于常规重磁对应分析法需要将斜磁化磁异常转换成垂直磁化磁异常,而对于磁化方向不同的多场源,难以进行有效的化极处理,因此这里不再进行常规算法的试验。
|
|
表 1 组合模型参数 |
图 6a、图 6b是组合模型产生的重力异常和磁异常。可以看出,受规模较大的棱柱体异常的影响,岩脉上方的重力异常表现为等值线同行扭曲;受磁化方向影响,磁异常较复杂,难以直接识别磁源位置。

|
图 6 组合模型重磁异常 (a)重力异常;(b)磁异常;(c)无噪声重力二阶垂向导数;(d)无噪声归一化磁源强度;(e)添加10%噪声的重力二阶垂向导数;(f)添加10%噪声的归一化磁源强度。图中圈码代表异常体编号,黑色实线、虚线分别表示重力源和磁源位置,图 7同。 |
图 6c、图 6d是无噪声时重力二阶垂向导数及归一化磁源强度。可以看出,重力二阶垂向导数和归一化磁源强的极值均与自身场源位置对应很好。图 6e、图 6f是添加10%随机干扰后的重力二阶垂向导数和归一化磁源强度。
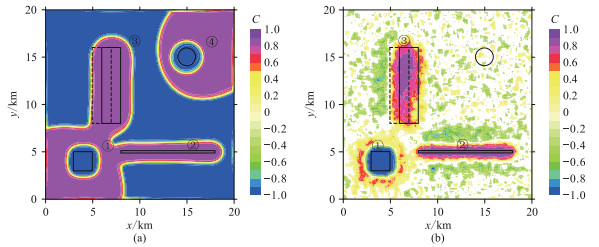
图 7a是利用无噪声时重力二阶垂向导数与归一化磁源强度(图 6c和图 6d)计算的互相关系数。可以看出,在重力场源分布区内存在明显的相关性,在场源外也呈现强相关性,尤其值得注意的是,球体本身是无磁性的,但也反映出明显的负相关,即表现为负密度、强磁性的特征,这显然会给解释带来不利影响。图 7b则是利用噪声扰动后重力二阶垂向导数与归一化磁源强度(图 6e和图 6f)计算的互相关系数。可以看出,互相关系数在正方体上方为明显的负相关(接近-1),在岩脉和棱柱体同源部位表现为强正相关(接近1),在球体上方则显示为完全不相关(接近0),除此之外的区域,互相关系数同样在零值附近波动。这也再次表明在进行重磁相关性计算时,添加噪声扰动有助于准确判断重磁异常是否同源。
|
图 7 本文算法基于叠加模型重磁异常计算的互相关系数C(窗口大小5×5) (a)无噪声;(b)含噪声。 |
为了检验算法对实际资料的应用效果,选取了江西相山铀矿田地区的地面重、磁数据(比例尺1:50000)进行测试。江西相山火山盆地是中国第一大、世界第三大火山岩型铀矿田[25]。
相山火山盆地位于华夏板块湘桂赣地块北东缘乐安—抚州断隆带上(图 8)。该区遭受了扬子—加里东期、海西—印支期造山作用,燕山期NEE向赣杭构造火山岩带西南端与近SN向赣中南花岗岩带的交接地带发生了强烈的构造—岩浆—成矿作用[26-27]。相山铀矿田中心区域出露大面积的下白垩统鹅湖岭组碎斑熔岩,向外依次分布着条带状的下白垩统打鼓顶组流纹英安岩、下白垩统花岗斑岩及青白口系变质岩,西北侧还发育上白垩统的沉积岩。相山地区铀矿化主要受断裂构造、火山构造、变质基底及岩石层间接触面控制,多控矿因素交汇更有利于富矿的形成[28-31]。因此,推断有利控矿因素的分布位置对相山地区铀矿勘查具有重要的研究意义。

|
图 8 江西相山地区地质图 |
为方便重、磁异常解释及其相关性分析,图 9给出了相山火山盆地主要岩石的密度、磁化率散点分布,其中碎斑熔岩、流纹英安岩、花岗斑岩及变质岩样品分别为822、353、101、75块。从图 9可以看出,碎斑熔岩和花岗斑岩密度均主要为2.60~2.65 g/cm3,均值分别为2.63、2.64 g/cm3,同属于低密度体;流纹英安岩密度主要为2.65~2.75 g/cm3,均值为2.69 g/cm3,为中—高密度体;变质岩密度主要为2.7~2.8 g/cm3,均值为2.76 g/cm3,为高密度体。部分碎斑熔岩岩样的磁化率为(10~100)×10-6 SI,属于低磁性,但大部分岩样的磁化率分布在(100~1000)×10-6 SI,相当于中强磁性;流纹英安岩岩样磁化率则多数为(10~100)×10-6 SI,部分为(100~1000)×10-6 SI,还有少量样本磁化率大于1000×10-6 SI,即流纹英安岩磁性变化较大,弱、中、强磁性样品均有;花岗斑岩约一半样品磁化率为(10~100)×10-6 SI,另一半为(100~1000)×10-6 SI,说明花岗岩表现为弱、中磁性;变质岩的磁化率分布较集中,多数为(20~30)×10-6 SI,表现为弱磁性。上述岩石密度、磁化率统计分析结果表明,碎斑熔岩、中—强度磁性花岗斑岩及中—强磁性流纹英安岩这三类岩石都可看作是重、磁同源体。

|
图 9 相山地区主要岩石密度(上)和磁化率(下)散点分布图 (a)碎斑熔岩;(b)流纹英安岩;(c)花岗斑岩;(d)变质岩。黑色横实线表示密度平均值或磁化率强度的分界线。 |
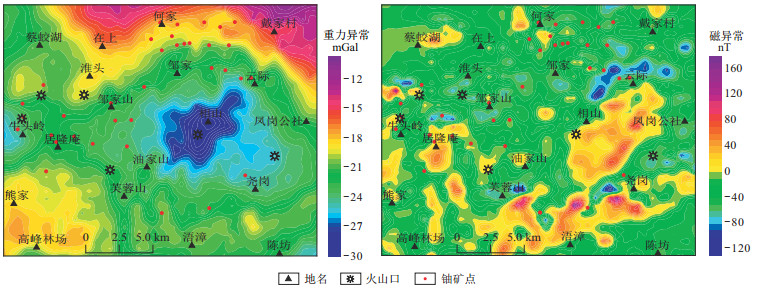
图 10是相山铀矿田的布格重力异常和总磁力异常图。布格重力异常整体表现为中心区域异常低、外围异常高,这样的分布特征主要与大面积的低密度碎斑熔岩和高密度变质岩有关。磁异常主要以局部异常为主,正磁异常主要分布在研究区的南侧与中东侧,以SN、NE、NEE向为主,这些正磁异常在近正北侧都可以寻找到相对应的负磁异常分布。然而,在邹家山—邹家一带,存在大面积的负磁异常,且这些负磁异常幅值明显大于周围的正异常幅值,表明该区域的岩石有可能具有与当代地磁场方向不一致的剩磁[15]。
|
图 10 相山地区布格重力异常(左)及地面磁异常(右) |
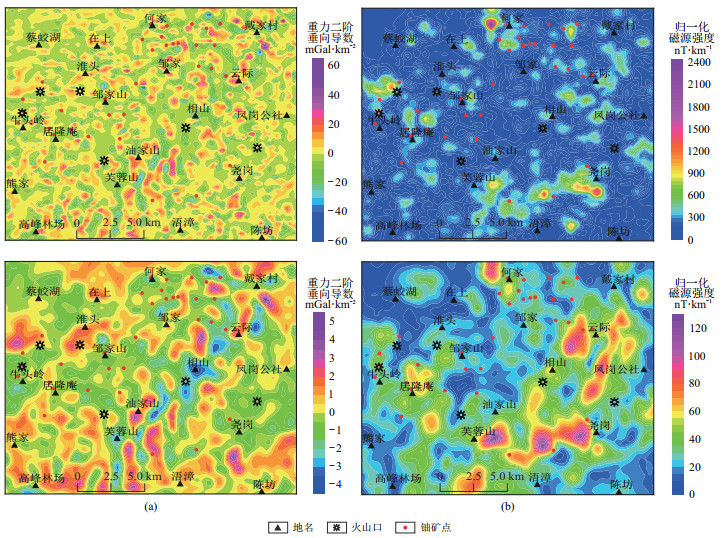
图 11(上)是研究区观测面上的重力二阶垂向导数和归一化磁源强度。可以看出,地面上的重力二阶垂向导数分布凌乱,以小规模条带状异常为主,各个方向异常相互切割严重;地面归一化磁源强度主要在中西部、中南部及西北部存在明显的异常,多数铀矿点位于异常高—低分界位置。
|
图 11 相山地区重力二阶垂向导数(a)和归一化磁源强度(b) 上:地面场值;下:向上延拓500 m场值。 |
图 11(下)是向上延拓500 m的重力二阶垂向导数和归一化磁源强度。可见此时重力导数及归一化磁源强度的局部异常规模较大,走向明显,均以NS、NE、NEE向为主。铀矿点主要位于重力导数梯度带(或零值线)附近,及归一化磁源强度异常高—低分界线位置这些位置往往与断裂带或岩性接触带关系密切。
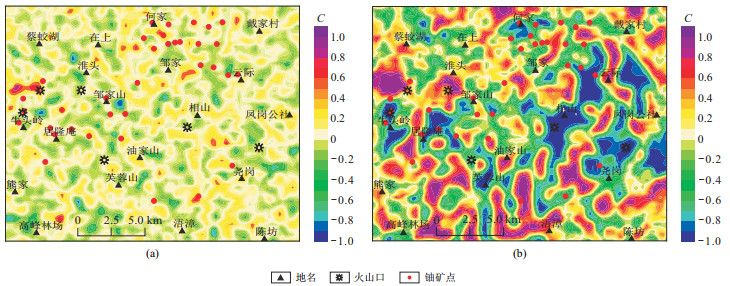
图 12是基于添加了10%噪声扰动下相山地区重力二阶垂向导数与归一化磁源强度计算的互相关系数。可以看出,地面上互相关系数C(图 12a)仅在牛头岭北侧存在一个呈近东西向展布的条带状高值区,该区对应大面积出露的流纹英安岩,其他位置基本都在-0.5~0.5,即大部分地区重磁相关性并不明显,这是由于对重力场进行了二阶导数计算,因而异常较为凌乱。向上延拓500 m后的互相关系数C(图 12b)的分布反映出多个重磁强相关区域:①牛头岭北侧、淮头南侧这两个正强相关区域反映了高密度、强磁性的流纹英安岩具有一定规模;②云际—尧岗西沿线、芙蓉山西侧、居隆庵西侧存在强正相关区,推测为碎斑熔岩之下存在一定规模的流纹英安岩,其中居隆庵地区的大量钻孔资料已证实了这一推测[32-33],这为相山地区在层间接触面寻找铀矿提供了参考,尤其相山铀矿田西部的云际—尧岗西沿线一带;③牛头岭、居隆庵、相山、尧岗北等地区存在大面积负强相关区域,应是低密度、强磁性碎斑熔岩的反映,何家—戴家村一带存在近东西向的条带状负相关区域,应与低密度的花岗斑岩有关,不过何家附近的负相关性更加显著,区域更大,表明这里的花岗斑岩应具有较大规模,而位于相山铀矿田北部的沙洲矿床产于花岗岩内外接触带[34-35],因此重磁相关性分析结果为沙洲矿床开展深部铀矿勘查也提供了依据;④云际东、凤岗南及芙蓉山等区域的强负相关性区域,可能反映了低密度、强磁性的花岗斑岩分布;⑤几乎所有的铀矿点都位于强正相关与强负相关的过渡带,反映了相山地区铀矿点与岩性接触面关系密切;⑥牛头岭、芙蓉山、相山、尧岗北分布的古火山口处于大面积的强负相关区域,表明这些火山口喷发的主要物质是碎斑熔岩[36],而牛头岭北、淮头南两地的火山口则以流纹英安岩喷出为主,另外居隆庵东侧大面积的负强相关则表明该区可能还存在一个碎斑熔岩的古火山口。显然,这些丰富的重磁相关性信息为相山铀矿田地质研究及铀矿勘查提供了一定参考依据。
|
图 12 基于10%噪声扰动下相山地区重力二阶垂向导数与归一化磁源强度的互相关系数C分布(窗口大小3×3) (a)未延拓;(b)上延500 m |
基于重力二阶垂向导数与归一化磁源强度表达式关系,本文提出了一种新的重磁相关分析方法,削弱了背景场与磁化方向的影响。为提高相关分析结果的可靠性,本文对重力二阶垂向导数和归一化磁源强度进行较强的随机噪声扰动。模型试验表明,此方法可以有效地识别重磁同源体的位置,且不存在虚假信息;同时,该方法适用于重磁场源位置不同、磁源磁化方向不一致的复杂环境。将本文方法应用于相山铀矿田,重磁相关性分析结果较好地揭示了鹅湖岭组碎斑熔岩、打鼓顶组流纹英安岩及花岗斑岩等重磁同源岩石的分布位置及规模,也反映了不同位置古火山喷出的主要岩石类型,同时揭示了铀矿与岩性接触面的密切关系。这些结论为研究相山地区深部铀矿成矿环境提供了数据基础。
| [1] |
张镕哲, 李桐林, 邓海, 等. 大地电磁、重力、磁法和地震初至波走时的交叉梯度二维联合反演研究[J]. 地球物理学报, 2019, 62(6): 2139-2149. ZHANG Rongzhe, LI Tonglin, DENG Hai, et al. 2D joint inversion of MT, gravity, magnetic and seismic first-arrival wave traveltime with cross-gradient constrai-nts[J]. Chinese Journal of Geophysics, 2019, 62(6): 2139-2149. |
| [2] |
GAO X, XIONG S, ZENG Z, et al. 3D inversion modeling of joint gravity and magnetic data based on a sinusoidal correlation constraint[J]. Applied Geophysics, 2019, 16(4): 519-529. DOI:10.1007/s11770-019-0792-z |
| [3] |
刘鹏, 陈康, 何青林, 等. 四川盆地二叠系火山岩裂隙式喷发模式探讨[J]. 石油地球物理勘探, 2021, 56(2): 389-397. LIU Peng, CHEN Kang, HE Qinglin, et al. Fissure erupting model of Permian volcanic rock in Sichuan Basin[J]. Oil Geophysical Prospecting, 2021, 56(2): 389-397. |
| [4] |
张振宇, 胡祥云, 王刚, 等. 内蒙古狼山成矿带深部地质结构特征[J]. 石油地球物理勘探, 2022, 57(4): 982-991. ZHANG Zhenyu, HU Xiangyun, WANG Gang, et al. Characteristics of deep geological structure of Lang-shan metallogenic belt in Inner Mongolia[J]. Oil Geophysical Prospecting, 2022, 57(4): 982-991. |
| [5] |
刘彦华, 陈宗刚, 欧阳长亮. 重磁异常对应分析在相山地区的应用[J]. 物探与化探, 2008, 32(6): 586-589. LIU Yanhua, CHEN Zonggang, OUYANG Changliang. The application of correspondence analysis of gravity and magnetic anomalies in Xiangshan area[J]. Geophysical and Geochemical Exploration, 2008, 32(6): 586-589. |
| [6] |
GARLAND G D. Combined analysis of gravity and magnetic anomalies[J]. Geophysics, 1951, 16(1): 51-62. DOI:10.1190/1.1437650 |
| [7] |
CORDELL L, TAYLOR P T. Investigation of magnetization and density of a north Atlantic seamount using Poisson's theorem[J]. Geophysics, 1971, 36(5): 919-937. DOI:10.1190/1.1440224 |
| [8] |
CHANDLER V W, KOSKI J S, BRAILE L W. Analysis of multisource gravity and magnetic anomaly data sets by moving‐window application of Poisson's theorem[J]. Geophysics, 1981, 46(1): 30-39. DOI:10.1190/1.1441136 |
| [9] |
CHANDLER V W, MALEK K C. Moving‐window Poisson analysis of gravity and magnetic data from the Penokean orogen, east-central Minnesota[J]. Geophysics, 1991, 56(1): 123-132. DOI:10.1190/1.1442948 |
| [10] |
刘心铸. 重磁异常对应分析——赴美学习重磁方法介绍之一[J]. 国外地质勘探技术, 1985(3): 1-8. LIU Xinzhu. The method of gravity and magnetic anomaly analysis, one of the introduction of gravity and magnetic method learned from America[J]. Foreign Geoexploration Technology, 1985(3): 1-8. |
| [11] |
黎益仕, 殷秀华, 刘占坡. 对应分析约束下的重磁联合反演及其在塔里木盆地的应用[J]. 地震地质, 1996, 18(4): 361-368. LI Yishi, YIN Xiuhua, LIU Zhanpo. Simultaneous inversion of gravimetric and magnetic data constrained with internal correspondence analysis and its application to the Tarim basin[J]. Seismology and Geology, 1996, 18(4): 361-368. |
| [12] |
范正国, 刘前坤, 黄旭钊, 等. 自适应重磁对应分析[J]. 吉林大学学报(地球科学版), 2012, 42(6): 1903-1911. FAN Zhengguo, LIU Qiankun, HUANG Xuzhao, et al. Adaptive correlative analysis between aeromagnetic and gravity anomaly[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(6): 1903-1911. |
| [13] |
宋景明. 基于对应分析的重力异常分离技术及应用[J]. 天然气工业, 2007, 27(增刊1): 318-319. SONG Jingming. Gravity anomaly separation technique based on gravity and magnetic correspondence analysis and its application[J]. Natural Gas Industry, 2007, 27(S1): 318-319. |
| [14] |
颜廷杰, 甘文龙, 管彦武. 非均匀物性条件下多尺度窗口修正法换算磁源重力异常及在寻找DSO的应用[J]. 地球物理学报, 2017, 60(12): 4840-4854. YAN Tingjie, GAN Wenlong, GUAN Yanwu. Magnetic fields reduction to pseudo-gravity anomalies using multi-scale windows in the condition of non-uniform property and its application to searching for DSO[J]. Chinese Journal of Geophysics, 2017, 60(12): 4840-4854. |
| [15] |
王彦国, 邓居智, 葛坤朋, 等. 基于重磁泊松定理的磁化方向估计及应用: 以相山铀矿田为例[J]. 地球物理学报, 2022, 65(12): 4914-4929. WANG Yanguo, DENG Juzhi, GE Kunpeng, et al. Estimating magnetization direction of field sources based on Poisson's theorem of gravity and magnetic anomaly and its application: a case study of Xiangshan uranium ore field[J]. Chinese Journal of Geophysics, 2022, 65(12): 4914-4929. |
| [16] |
楼海, 余钦范. 青藏高原亚东—格尔木地学断面重磁异常的对应分析[J]. 现代地质, 1991, 5(3): 338-346. LOU Hai, YU Qinfan. Quantitative correlation analysis of gravity and magnetic anomalies on the geoscience transect from Yadong to Golmud, Qinghai-Tibet Plateau[J]. Geoscience, 1991, 5(3): 338-346. |
| [17] |
刘沈衡, 朱春生. 重磁异常对应分析应用实例[J]. 有色金属矿产与勘查, 1998(3): 33-36. LIU Shenheng, ZHU Chunsheng. Correspondence analysis of gravitational and magnetic anomalies and its practical application[J]. Geological Exploration for Non-Ferrous Metals, 1998(3): 33-36. |
| [18] |
曾昭发, 吴燕冈, 郝立波, 等. 基于泊松定理的重磁异常分析方法及应用[J]. 吉林大学学报(地球科学版), 2006, 36(2): 279-283. ZENG Zhaofa, WU Yangang, HAO Libo, et al. The Poisson's theorem based analysis method and application of magnetic and gravity anomalies[J]. Journal of Jilin University (Earth Science Edition), 2006, 36(2): 279-283. |
| [19] |
刘燕戌, 李文勇, 徐剑春. 航空重、磁异常相关性分析方法及其应用[J]. 物探与化探, 2012, 36(5): 783-787. LIU Yanqu, LI Wenyong, XU Jianchun. Correlation analytical method and its application to airborne gravity and magnetic anomalies[J]. Geophysical and Geochemical Exploration, 2012, 36(5): 783-787. |
| [20] |
BLAKELY R J. Potential Theory in Gravity and Magnetic Applications[M]. Cambridge: Cambridge University Press, 1995.
|
| [21] |
马国庆, 孟庆发, 李丽丽, 等. 利用重/磁场梯度比值函数计算地质体深度[J]. 石油地球物理勘探, 2019, 54(1): 229-234. MA Guoqing, MENG Qingfa, LI Lili, et al. Gradient ratio function of gravity and magnetic data for geological body depth calculation[J]. Oil Geophysical Prospecting, 2019, 54(1): 229-234. |
| [22] |
WILSON H S. Analysis of the magnetic gradient tensor[J]. Canada Technical Memorandum, 1985, 8: 5-13. |
| [23] |
BEIKI M, CLARK D A, AUSTIN J R, et al. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data[J]. Geophysics, 2012, 77(6): J23-J37. |
| [24] |
PEDERSEN L B, RASMUSSEN T M. The gradient tensor of potential field anomalies: some implications on data collection and data processing of maps[J]. Geophysics, 1990, 55(12): 1558-1566. |
| [25] |
DAHLKAMP F J. Uranium Deposits of the World: Asia[M]. Berlin, Heidelberg: Springer, 2009.
|
| [26] |
毛景文, 陈懋弘, 袁顺达, 等. 华南地区钦杭成矿带地质特征和矿床时空分布规律[J]. 地质学报, 2011, 85(5): 636-658. MAO Jingwen, CHEN Maohong, YUAN Shunda, et al. Geological characteristics of the Qinhang (or Shihang) metallogenic belt in South China and spatial-temporal distribution regularity of mineral deposits[J]. Acta Geologica Sinica, 2011, 85(5): 636-658. |
| [27] |
郭福生, 林子瑜, 黎广荣, 等. 江西相山火山盆地地质结构研究: 来自大地电磁测深及三维地质建模的证据[J]. 地球物理学报, 2017, 60(4): 1491-1510. GUO Fusheng, LIN Ziyu, LI Guangrong, et al. Study on the geological structure of Xiangshan uranium-bearing volcanic basin: evidences from magnetotelluric sounding and GOCAD modeling[J]. Chinese Journal of Geophysics, 2017, 60(4): 1491-1510. |
| [28] |
陈柏林. 断裂构造发育过程与控矿构造形成演化——以邹家山铀矿床为例[J]. 地质力学学报, 2020, 26(3): 285-298. CHEN Bailin. Development process of fault structure and formation and evolution of ore-controlling structure: a case study of the Zoujiashan uranium deposit[J]. Journal of Geomechanics, 2020, 26(3): 285-298. |
| [29] |
林锦荣, 胡志华, 饶泽煌, 等. 相山火山盆地及邻区铀多金属成矿类型、成矿特征及控矿因素[J]. 铀矿地质, 2020, 36(6): 491-499. LIN Jinrong, HU Zhihua, RAO Zehuang, et al. Uranium-polymetallic mineralization types, metallogenic characteristics and ore-controlling factors in the Xiangshan Volcanic Basin and its adjacent areas[J]. Uranium Geology, 2020, 36(6): 491-499. |
| [30] |
孙会饶, 方启春, 魏欣, 等. 江西相山矿田邹家山铀矿床地质特征及外围找矿潜力[J]. 矿产勘查, 2021, 12(2): 235-239. SUN Huirao, FANG Qichun, WEI Xin, et al. Geological characteristics and prospecting potential of Zoujiashan uranium deposit in Xiangshan orefield, Jiangxi Province[J]. Mineral Exploration, 2021, 12(2): 235-239. |
| [31] |
姚亦军, 许芸芸. 江西相山铀矿田东部与西部地质特征对比及其意义[J]. 铀矿地质, 2022, 38(1): 58-65. YAO Yijun, XU Yunyun. Comparison and significance of geological characteristics between the east and west of Xiangshan uranium ore field in Jiangxi[J]. Uranium Geology, 2022, 38(1): 58-65. |
| [32] |
周玉龙, 高琰. 相山矿田居隆庵地区铀成矿条件及资源潜力[J]. 铀矿地质, 2010, 26(5): 271-276. ZHOU Yulong, GAO Yan. Uranium formation conditions and perspective potential of Julong'an area, Xiangshan uranium orefield[J]. Uranium Geology, 2010, 26(5): 271-276. |
| [33] |
谢琛, 艾成辉, 丁昊, 等. 居隆庵铀矿床找矿模式对相山矿田找矿的意义[J]. 东华理工大学学报(自然科学版), 2018, 41(4): 352-357. XIE Chen, AI Chenghui, DING Hao, et al. Significance of the prospecting pattern of Guelongan uranium deposit to the prospecting of Xiangshan ore field[J]. Journal of East China Institute of Technology (Natural Science Edition), 2018, 41(4): 352-357. |
| [34] |
张玉燕, 李子颖, 黄志章, 等. 江西相山沙洲矿床铀的存在形式和迁移特征探讨: 来自诱发裂变径迹的证据[J]. 高校地质学报, 2012, 18(4): 639-646. ZHANG Yuyan, LI Ziying, HUANG Zhizhang, et al. A study on existing forms and migration process of uranium at Shazhou deposit, Jiangxi Provinve, China: evidences from induced fission tracks[J]. Geological Journal of China Universities, 2012, 18(4): 639-646. |
| [35] |
吴志春, 郭福生, 李华亮, 等. 主成分分析法在相山火山盆地蚀变分带解译中的应用[J]. 大地构造与成矿学, 2020, 44(3): 385-403. WU Zhichun, GUO Fusheng, LI Hualiang, et al. Application of principal component analysis in interpretation of alteration zone in the Xiangshan volcanic basin[J]. Geotectonica et Metallogenia, 2020, 44(3): 385-403. |
| [36] |
郭福生, 黎广荣, 周万蓬, 等. 江西相山铀矿田古火山口探讨[J]. 大地构造与成矿学, 2019, 43(3): 528-541. GUO Fusheng, LI Guangrong, ZHOU Wanpeng, et al. Multidisciplinary study on the volcanic calderas in the Xiangshan uranium-bearing basin, Jiangxi[J]. Geotectonica et Metallogenia, 2019, 43(3): 528-541. |



 田野, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
田野, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院,330013。Email:
