0 引言

近年来，随着油气勘探的目标逐渐转向非常规储层，作为致密砂岩储层预测中至关重要的地质目标——甜点的识别越来越受到重视^[1]。甜点是非常规储层中一种重要的地质和产能概念，用于描述致密砂岩储层中相对高孔、高渗的区域^[2]。因此，要实现甜点预测，首先要获取砂体的空间展布特征，在砂体内部寻找甜点。然而，砂体及其内部甜点往往具有不同的敏感参数，因此通常需要进行反演参数之间的转换，这往往增加了累积误差，降低了反演结果的精度和效率。此外，致密砂岩内部甜点普遍厚度较小，传统的确定性反演难以满足预测精度的需求。因此，需要建立一种高分辨率且高效的致密砂岩甜点直接预测方法。

叠前地震反演技术是实现岩性和流体识别的一种重要手段^[3-9]。作为一种常用的地震反演方法，概率反演方法利用随机采样获得一系列关于后验概率分布的样本，充分利用测井数据所建立的先验模型约束，具有较高的垂向分辨率。马尔可夫链—蒙特卡洛（MCMC）算法^[10]是一种较为常用的概率反演算法，它通过构建若干条与后验概率分布相同的马尔科夫链实现对贝叶斯公式的求解^[11-12]。1970年，Hastings^[13]提出了最为常用的MCMC算法形式，即Metropolis-Hastings（MH）算法，并且广泛应用于地球物理反演领域。常规MH算法收敛速度较慢，且稳定性较差。在MH算法的基础上，许多学者提出了一系列改进措施^[14-19]。这些措施主要是通过改进搜索步长，充分利用多条马尔科夫链之间的交互性，提高了算法的收敛性和稳定性。然而，MH及其改进算法多依赖于参数先验采样空间的设置，对于一个较为复杂的参数采样空间，MH算法往往易陷入局部极值，影响了反演结果的精度与效率。

为此，本文利用叠前地震数据，提出了一种基于改进贝叶斯概率反演的致密砂岩甜点直接预测方法。以R实际工区为靶区，首先，选取岩性敏感参数和甜点敏感参数，推导基于两者的Zeoppritz近似方程，并结合地震褶积模型，建立敏感参数与地震数据的直接关系，避免反演结果因参数转换带来的累积误差；然后，在贝叶斯理论框架下，将统计混合高斯先验信息^[20]与平滑约束先验相结合，构建反演参数的后验概率表达式；最后，利用改进贝叶斯概率的反演方法实现岩性与甜点敏感参数的高精度预测。该方法建立反演参数之间的联合概率分布，计算参数的条件概率分布，并将它作为随机采样过程中的约束条件，减少了反演参数的采样空间，从而提高了反演的效率与精度。

1 方法原理 1.1 地震正演模型

地震正演模型是叠前概率反演的基础，它主要由Zeoppritz近似方程^[21]和褶积公式组成。R靶区岩性和甜点的敏感弹性参数分别为泊松比和纵波模量。为减少误差的累积，从Aki-Richards近似式出发，推导了基于泊松比、纵波模量和密度的Zeoppritz近似公式。

Aki-Richards近似式为

$ \begin{array}{l}R\left(\theta \right)\approx \frac{1}{2}\mathrm{s}\mathrm{e}{\mathrm{c}}^{2}\theta \frac{\mathrm{\Delta }\alpha }{\stackrel{-}{\alpha }}-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \frac{\mathrm{\Delta }\beta }{\stackrel{-}{\beta }}+\\ \frac{1}{2}\left(1-4{\gamma }^{2}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\theta \right)\frac{\mathrm{\Delta }\rho }{\stackrel{-}{\rho }}\end{array} $

(1)

式中：$ R\left(\theta \right) $为PP波反射系数；$ \theta $为入射角；$ \stackrel{-}{\alpha } $、$ \stackrel{-}{\beta } $、$ \stackrel{-}{\rho } $分别为地下纵波速度、横波速度和密度的平均值；$ \mathrm{\Delta }\alpha $、$ \mathrm{\Delta }\beta $、$ \mathrm{\Delta }\rho $分别代表地层分界面两侧的纵波速度、横波速度和密度的变化量；$ \gamma $为横波速度与纵波速度之比。

纵波模量反射系数$ \mathrm{\Delta }M/\overline{M} $、泊松比反射系数$ \mathrm{\Delta }\sigma/\stackrel{-}{\sigma } $分别为

$ \frac{\mathrm{\Delta }M}{\overline{M}}=2\frac{\mathrm{\Delta }\alpha }{\stackrel{-}{\alpha }}+\frac{\mathrm{\Delta }\rho }{\stackrel{-}{\rho }} $

(2)

$ \frac{\mathrm{\Delta }\sigma }{\stackrel{-}{\sigma }}=\frac{1}{\frac{3}{2}-{\gamma }^{2}-\frac{1}{2{\gamma }^{2}}}\left(\frac{\mathrm{\Delta }\alpha }{\stackrel{-}{\alpha }}-\frac{\mathrm{\Delta }\beta }{\stackrel{-}{\beta }}\right) $

(3)

式中：$ \stackrel{-}{\sigma } $、$ \overline{M} $分别代表地下泊松比、纵波模量的平均值；$ \mathrm{\Delta }\sigma $、$ \mathrm{\Delta }M $分别是地层分界面两侧的泊松比、纵波模量的变化量。

将式（2）、式（3）代入式（1），则可得到关于纵波模量$ M $、泊松比$ \sigma $及密度$ \rho $的新的近似公式，即

$ \begin{aligned} & R(\theta) \approx\left(\frac{1}{4} \sec ^2 \theta-2 \gamma^2 \sin ^2 \theta\right) \frac{\Delta M}{\bar{M}}+ \\ & \left(6 \gamma^2-4 \gamma^4-2\right) \sin ^2 \theta \frac{\Delta \sigma}{\bar{\sigma}}+\left(\frac{1}{2}-\frac{1}{4} \sec ^2 \theta\right) \frac{\Delta \rho}{\bar{\rho}} \end{aligned} $

(4)

给定子波$ W $，地震数据可以利用褶积模型表征^[22]，即

$ d(t, \theta )={\int }_{0}^{t}R(\tau , \theta )\mathrm{*}W(t-\tau )\mathrm{d}\tau $

(5)

式中$ :d(t, \theta ) $表征$ t $时刻的振幅；$ \tau \mathrm{为}\mathrm{临}\mathrm{近}\mathrm{点}\mathrm{的}\mathrm{时}\mathrm{间} $。

利用式（4）、式（5），可以得到敏感参数与地震记录之间的正演关系，这为贝叶斯概率反演中似然函数的构建奠定了基础。

1.2 贝叶斯概率反演

在贝叶斯理论基础上，贝叶斯概率反演根据先验分布构建反演参数的采样空间，利用似然函数对样本进行优选，构建若干条样本链以实现对后验概率的表征。因此，需要首先根据贝叶斯定理构建反演参数的后验概率分布表达式。

1.2.1 后验概率分布构建

由于反演具有多解性，因此概率反演的主要目标是获取反演参数的可能取值，即后验概率分布。根据贝叶斯定理，后验概率分布$ p\left({\boldsymbol{m}}\left|{\boldsymbol{d}}\right.\right) $主要包含先验概率分布$ p\left({\boldsymbol{m}}\right) $及似然函数$ p\left({\boldsymbol{d}}\left|{\boldsymbol{m}}\right.\right) $两部分，可以表征为

$ p\left({\boldsymbol{m}}\left|{\boldsymbol{d}}\right.\right)\propto p\left({\boldsymbol{d}}\left|{\boldsymbol{m}}\right.\right)\cdot p\left({\boldsymbol{m}}\right) $

(6)

式中：$ {\boldsymbol{m}}={(\mathit{M}, \mathit{\sigma }, \mathit{\rho })}^{\mathrm{T}} $是反演参数；$ {\boldsymbol{d}} $为观测地震记录。

$ p\left({\boldsymbol{m}}\right) $反映了利用测井数据统计的敏感参数概率分布特征。在实际地层中，不同岩性的弹性参数先验信息是不同的。假设不同岩相下反演参数满足不同的单一峰值高斯分布，则统计先验概率分布可以分解为多个高斯概率分布的叠加。因此，统计先验概率分布$ {p}_{\mathrm{s}}\left({\boldsymbol{m}}\right) $满足混合高斯分布。混合高斯分布主要通过不同高斯分量的均值、方差以及权重系数进行表征，可表示为

$ \begin{aligned} p_{\mathrm{s}}(\boldsymbol{m}) & =\sum\limits_{k=1}^h\left\{\lambda_{\mathrm{m}}^k \frac{1}{(2 {\rm{\mathsf{π}}})^{\frac{1}{2}}} \frac{1}{\left.\boldsymbol{C}_{\mathrm{m}}^k\right|^{\frac{1}{2}}} \times\right. \\ & \left.\exp \left[-\frac{1}{2}\left(\boldsymbol{m}-\boldsymbol{\mu}_{\mathrm{m}}^k\right)^{\mathrm{T}}\left(\boldsymbol{C}_{\mathrm{m}}^k\right)^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu}_{\mathrm{m}}^k\right)\right]\right\} \end{aligned} $

(7)

$ \sum\limits_{k=1}^{h}{\lambda }_{m}^{k}=1 $

(8)

式中：$ {\boldsymbol{\mu}}_{\mathrm{m}}^{k} $、$ {\boldsymbol{C}}_{\mathrm{m}}^{k} $、$ {\lambda }_{\mathrm{m}}^{k} $分别为反演参数$ {\boldsymbol{m}} $的第$ k $个高斯分量的均值、协方差矩阵、权重值；$ h $为高斯混合分布的峰态数量，即岩相类型数。

为提高概率反演的稳定性，通常需要引入先验平滑约束^[23]。假设平滑约束先验信息$ {p}_{\mathrm{l}}\left({\boldsymbol{m}}\right) $与实际模型之差满足高斯分布，则可以表征为

$ \begin{array}{l}{p}_{\mathrm{l}}\left({\boldsymbol{m}}\right)=\frac{1}{\left(2\mathrm{{\rm{\mathsf{π}}} }\right){}^{\frac{N}{2}}}\frac{1}{{\left|{\boldsymbol{C}}_{0}^{}\right|}^{\frac{1}{2}}}\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}({\boldsymbol{m}}-{\boldsymbol{m}}_{0}{)}^{\mathrm{{\rm T}}}({\boldsymbol{C}}_{0}^{}{)}^{-1}({\boldsymbol{m}}-{\boldsymbol{m}}_{0})\right]\end{array} $

(9)

式中：$ N $为样点数；$ {\boldsymbol{m}}_{0} $为平滑约束先验模型；$ {\boldsymbol{C}}_{0}^{} $是实际模型与平滑约束先验模型之差的协方差矩阵。

$ p\left({\boldsymbol{d}}\left|{\boldsymbol{m}}\right.\right) $表征反演参数所合成的地震记录与实际地震记录的相似程度，通常利用高斯分布进行表征，即

$ \begin{array}{l}p\left({\boldsymbol{d}}\left|{\boldsymbol{m}}\right.\right)=\frac{1}{\left(2\mathrm{{\rm{\mathsf{π}}} }\right){}^{\frac{N}{2}}}\frac{1}{\left|{\boldsymbol{C}}_{\mathrm{e}}^{}\right|{}^{\frac{1}{2}}}\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left\{-\frac{1}{2}{\left[{\boldsymbol{d}}-{\boldsymbol{f}}\left({\boldsymbol{m}}\right)\right]}^{\mathrm{{\rm T}}}({\boldsymbol{C}}_{\mathrm{e}}^{}{)}^{-1}\left[{\boldsymbol{d}}-{\boldsymbol{f}}\left({\boldsymbol{m}}\right)\right]\right\}\end{array} $

(10)

式中：$ {\boldsymbol{C}}_{\mathrm{e}}^{} $是地震噪声的协方差矩阵；$ {\boldsymbol{f}} $表征正演算子，即地震正演模型。

综上所述，后验概率分布可以表示为

$ \begin{array}{l}p\left({\boldsymbol{m}}\left|{\boldsymbol{d}}\right.\right)\propto {p}_{\mathrm{s}}\left({\boldsymbol{m}}\right)\cdot {p}_{\mathrm{l}}\left({\boldsymbol{m}}\right)\cdot p\left({\boldsymbol{d}}\left|{\boldsymbol{m}}\right.\right)\\ \propto c\cdot \sum\limits_{k=1}^{h}\frac{{\lambda }_{\mathrm{m}}^{k}}{{\left|{\boldsymbol{C}}_{\mathrm{m}}^{k}\right|}^{\frac{1}{2}}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{1}{2}J\left({\boldsymbol{m}}\right)-\frac{1}{2}{g}_{k}\left({\boldsymbol{m}}\right)\right]\end{array} $

(11)

式中：c为常数；

$ \begin{array}{l}J\left({\boldsymbol{m}}\right)={\left[{\boldsymbol{d}}-{\boldsymbol{f}}\left({\boldsymbol{m}}\right)\right]}^{\mathrm{{\rm T}}}({\boldsymbol{C}}_{\mathrm{e}}^{}{)}^{-1}\left[{\boldsymbol{d}}-{\boldsymbol{f}}\left({\boldsymbol{m}}\right)\right]+\\ \;\;\;\;\;\;({\boldsymbol{m}}-{\boldsymbol{m}}_{0}{)}^{\mathrm{T}}({\boldsymbol{C}}_{0}^{}{)}^{-1}({\boldsymbol{m}}-{\boldsymbol{m}}_{0})\end{array} $

(12)

$ {g}_{k}\left({\boldsymbol{m}}\right)=\frac{1}{2}({\boldsymbol{m}}-{\boldsymbol{\mu}}_{\mathrm{m}}^{k}{)}^{\mathrm{T}}({\boldsymbol{C}}_{\mathrm{m}}^{k}{)}^{-1}({\boldsymbol{m}}-{\boldsymbol{\mu}}_{\mathrm{m}}^{k}) $

(13)

$ J\left({\boldsymbol{m}}\right) $表征反演结果与平滑约束模型、合成地震记录与实际地震记录之间的相似程度；$ {g}_{k}\left({\boldsymbol{m}}\right) $表征反演结果在第$ k $个高斯分量下所满足的高斯分布特征。

1.2.2 Metropolis-Hastings（MH）算法

要实现敏感参数的反演，需要求解反演参数的后验概率分布。基于MH算法的概率反演方法可以避免贝叶斯公式中复杂的边缘积分计算问题，构建若干条平稳分布与后验概率分布特征相同的马尔科夫链可实现对贝叶斯公式的求解，马尔科夫链达到平稳状态下的一系列样本，即可表征反演结果的后验概率分布特征。

MH算法主要分为随机采样与样本优选两个部分^[24]：①根据参数先验分布构建反演参数的采样空间，通过对参数采样空间的抽样，获得来自参数先验分布的一系列样本；②利用观测数据与地震正演模型构建反演参数的似然函数，并利用似然函数与接受准则对马尔科夫链样本进行优选，使马尔科夫链逐渐收敛到平稳状态，即后验概率分布。

其中，接受概率可以表示为

$ \zeta ({\boldsymbol{m}}^{\text{'}}, {\boldsymbol{m}}^{\mathrm{*}})=\mathrm{m}\mathrm{i}\mathrm{n}\left[1, \frac{{\rm{\mathsf{π}}} \left({\boldsymbol{m}}^{\mathrm{*}}\right)q({\boldsymbol{m}}^{\mathrm{*}}, {\boldsymbol{m}}^{\text{'}})}{{\rm{\mathsf{π}}} \left({\boldsymbol{m}}^{\text{'}}\right)q({\boldsymbol{m}}^{\text{'}}, {\boldsymbol{m}}^{\mathrm{*}})}\right] $

(14)

式中：$ {\rm{\mathsf{π}}} (•) $为平稳分布，即后验概率分布$ p\left({\boldsymbol{m}}\left|{\boldsymbol{d}}\right.\right) $；$ q({\boldsymbol{m}}^{\text{'}}, {\boldsymbol{m}}^{\mathrm{*}}) $为模型$ {\boldsymbol{m}}^{\text{'}} $转移到模型$ {\boldsymbol{m}}^{\mathrm{*}} $的建议分布。

当$ q({\boldsymbol{m}}^{\text{'}}, {\boldsymbol{m}}^{\mathrm{*}}) $为对称分布时，式（14）可以改写为^[25]

$ \zeta ({\boldsymbol{m}}^{\text{'}}, {\boldsymbol{m}}^{\mathrm{*}})=\mathrm{m}\mathrm{i}\mathrm{n}\left[1, \frac{{\rm{\mathsf{π}}} \left({\boldsymbol{m}}^{\mathrm{*}}\right)}{{\rm{\mathsf{π}}} \left({\boldsymbol{m}}^{\text{'}}\right)}\right] $

(15)

平稳分布$ {\rm{\mathsf{π}}} \left({\boldsymbol{m}}\right) $即反演参数的后验概率分布。将式（11）代入式（15），并简化常数项，即可得到概率反演的接受概率表达式

$ \zeta ({\boldsymbol{m}}^{\text{'}}, {\boldsymbol{m}}^{\mathrm{*}})=\mathrm{m}\mathrm{i}\mathrm{n}\left\{1, \frac{r\left({\boldsymbol{m}}^{\mathrm{*}}\right)}{r\left({\boldsymbol{m}}^{\text{'}}\right)}\mathrm{e}\mathrm{x}\mathrm{p}\left[-J\left({\boldsymbol{m}}^{\mathrm{*}}\right)-J\left({\boldsymbol{m}}^{\text{'}}\right)\right]\right\} $

(16)

其中

$ r\left({\boldsymbol{m}}\right)=\sum\limits_{k=1}^{h}\frac{{\lambda }_{\mathrm{m}}^{k}}{\left|{\boldsymbol{C}}_{\mathrm{m}}^{k}\right|}\mathrm{e}\mathrm{x}\mathrm{p}\left[-{g}_{k}\left({\boldsymbol{m}}\right)\right] $

(17)

$ J(•) $为反演的目标函数，表征实际地震记录与合成地震记录、反演结果与先验约束模型之间的总体相似程度，可用来反映反演结果的收敛情况。

1.2.3 基于条件概率分布约束的MH算法

传统的MH方法一般是将测井资料所统计的全局累计概率分布作为反演参数的采样区间，通常采样区间范围较大而降低了反演结果的精度和效率。因此，本文充分考虑反演参数之间的相关性，通过建立反演参数的条件概率分布来减小采样空间。

针对不同的岩性（即统计先验概率分布中不同的高斯分量），构建泊松比的条件概率分布

$ {\boldsymbol{\sigma}}_{k}\sim N({\mu }_{\sigma }^{k}, {\boldsymbol{C}}_{\sigma }^{k}) $

(18)

式中$ {\mu }_{\sigma }^{k} $、$ {\boldsymbol{C}}_{\sigma }^{k} $分别表示泊松比第$ k $个高斯分量的均值、协方差矩阵。

根据上一次的迭代结果，计算当前岩相的估算结果；再根据估算结果分配每个样点的条件概率分布，即采样空间。通过对泊松比的条件概率分布进行抽样，获得泊松比模型$ {\boldsymbol{\sigma}}_{}^{\mathrm{*}} $。

在此基础上，可以用参数之间的联合概率密度函数计算纵波模量与密度的条件概率分布，即

$ p\left({\boldsymbol{M}}_{}^{\mathrm{*}}\left|\mathit{\sigma }={\boldsymbol{\sigma}}_{}^{\mathrm{*}}\right.\right)=p\left({\boldsymbol{M}}_{}^{\mathrm{*}}\left|{\boldsymbol{\sigma}}_{}^{\mathrm{*}}-{\boldsymbol{\psi}}_{\sigma }\le \mathit{\sigma }\le {\boldsymbol{\sigma}}_{}^{\mathrm{*}}+{\boldsymbol{\psi}}_{\sigma }\right.\right) $

(19)

$ p\left({\boldsymbol{\rho}}_{}^{\mathrm{*}}\left|\mathit{\sigma }={\boldsymbol{\sigma}}_{}^{\mathrm{*}}\right.\right)=p\left({\boldsymbol{\rho}}_{}^{\mathrm{*}}\left|{\boldsymbol{\sigma}}_{}^{\mathrm{*}}-{\boldsymbol{\psi}}_{\sigma }\le \mathit{\sigma }\le {\boldsymbol{\sigma}}_{}^{\mathrm{*}}+{\boldsymbol{\psi}}_{{}_{\sigma }}\right.\right) $

(20)

式中$ [{\boldsymbol{\sigma}}_{}^{\mathrm{*}}-{\boldsymbol{\psi}}_{\sigma }, {\boldsymbol{\sigma}}_{}^{\mathrm{*}}+{\boldsymbol{\psi}}_{{}_{\sigma }}] $表示当$ \mathit{\sigma }={\boldsymbol{\sigma}}_{}^{\mathrm{*}} $时泊松比的建议采样区间。通过对纵波模量及密度的条件概率分布抽样，即可获得新的纵波模量$ {\boldsymbol{M}}_{}^{\mathrm{*}} $及密度模型$ {\boldsymbol{\rho}}_{}^{\mathrm{*}} $。

相比传统MH反演，基于条件概率分布约束的MH反演不是对全局概率分布函数进行采样，而是通过对条件概率分布进行抽样以获得新的样本，从而减小了反演参数的采样空间，提高了算法的收敛性与稳定性。

1.3 岩相与甜点概率估计

在反演结果的基础上，根据不同岩相和甜点类型的弹性参数特征，利用贝叶斯分类方法估算岩相和甜点等离散相态的后验概率分布，进而得到岩相和甜点的预测结果。

给定岩性敏感参数泊松比预测结果$ \tilde{\sigma} $，砂体的后验概率分布可以表征为^[26]

$ p\left({I}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}\left|\tilde{\sigma}\right.\right)\propto p\left(\tilde{\sigma}\left|{I}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}\right.\right)\cdot p\left({I}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}\right) $

(21)

式中：$ p\left({I}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}\right) $为砂体的先验认知，即$ p\left({I}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}\right)={S}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}/\left({S}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}+{S}_{\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{l}\mathrm{e}}\right) $，其中$ {S}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}} $、$ {S}_{\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{l}\mathrm{e}} $分别代表训练数据中砂岩、泥岩的累计发生次数，两者均可通过统计测井数据和解释结果获得；$ p\left(\tilde{\sigma}\left|{I}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}\right.\right) $为砂岩所对应弹性敏感参数的概率。

给定$ \tilde{\sigma} $，依据最大后验概率原则，可利用以下公式判别离散岩相

$ \begin{gathered} I\mathrm{s}.\mathrm{t}.p\left({I}_{k}\left|\tilde{\sigma}\right.\right)\ge p\left({I}_{i}\left|\tilde{\sigma}\right.\right), 1\le i\le N, i\ne k\\\Rightarrow I={I}_{k}\end{gathered} $

(22)

同理，在岩相预测结果的基础上，给定甜点敏感参数预测结果$ \tilde{M} $，则甜点类型$ Q $可以利用下式判别

$ \begin{gathered} \mathrm{s}.\mathrm{t}.p\left({Q}_{\tau }\left|\tilde{M}, {I}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}\right.\right)\ge p({Q}_{j}\left|\tilde{M}\right., {I}_{\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{d}}), 1\le j\le A, \\ j\ne \tau \Rightarrow Q={Q}_{\tau }\end{gathered} $

(23)

式中$ A $表征甜点类型数目。

2 模型试算及实际数据应用 2.1 一维数据反演测试

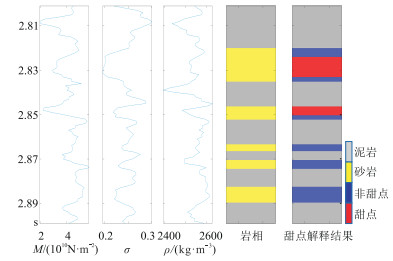
为了验证本文甜点预测方法的可行性，利用真实测井数据构建一维模型（图 1）进行叠前反演测试。给定35 Hz Ricker子波，利用正演模型计算合成角道集，并加入一定的随机噪声（SNR=10 dB），得到观测地震记录；再对一维模型进行平滑处理，得到反演初始模型；然后分别应用本文所提出的优化概率反演方法与传统概率反演方法获得敏感参数的反演结果及甜点估算结果。为提高反演的稳定性，同时运行3条马尔可夫链。

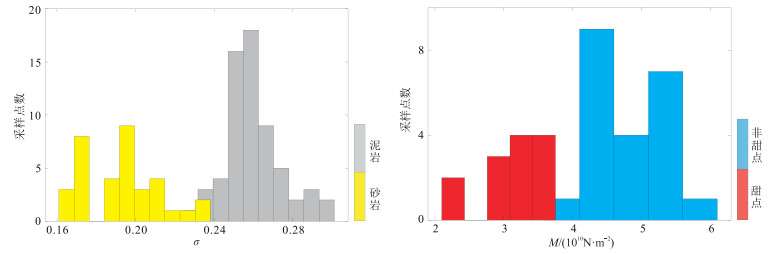
图 2是一维数据模型所统计的不同岩相及砂岩内部不同甜点类型的敏感参数分布直方图。由图 2可见，泊松比对岩性较为敏感，纵波模量对砂体内部的甜点较为敏感，且二者的参数先验概率分布满足高斯混合先验分布。

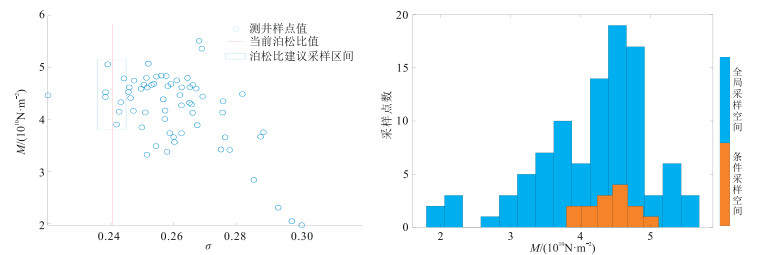
图 3是利用模型数据构建的泊松比与纵波模量的联合概率分布及纵波模量条件分布计算结果，可以发现条件概率分布的引入可以有效减小参数的采样空间。

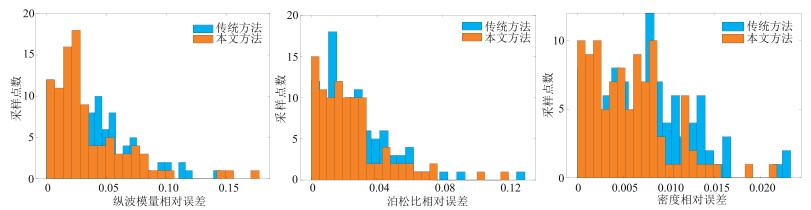
图 4是不同方法的敏感参数反演结果及岩相、甜点估算结果，图 5为统计的反演结果相对误差直方图。由图 4和图 5可以发现，相较于传统方法，本文方法的多个反演结果构成了更加稳定的后验概率分布特征，且相对误差略低，具有更高的精度与稳定性。

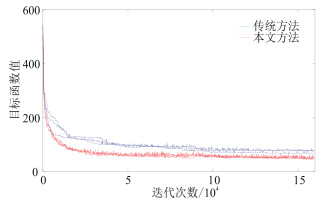
图 6为不同方法3条链目标函数值随迭代次数的变化。由图可见，相比传统概率反演方法，基于条件概率分布约束的反演方法的目标函数值在马尔科夫链达到平稳状态时更小，且收敛速度更快，前者需要25000次迭代，传统概率反演方法需要85000次迭代。

图 7是反演结果与实际模型参数分布直方图的对比，可以发现反演结果的参数分布与实际模型参数分布具有较高的相似性，这说明反演结果满足高斯混合先验分布假设。

模型测试表明本文方法可以有效识别岩相及砂体内部甜点。

2.2 实际数据测试

为了验证本文方法在实际应用中的可行性，利用中国北部R区块实际数据进行测试。R区块位于斜坡构造带，发育水下分流河道、河口坝砂体，其中高能、厚层河道砂体粒度粗、分选好，储层物性好，是致密砂岩甜点发育的主要区域；砂体内部，甜点具备相对较高的孔隙度与低弹性模量特征，因此叠前地震反演是实现该储层甜点预测的有效手段。由于叠前地震资料品质的限制，为了提高反演的稳定性，将叠前角度道集按2°~10°、10°~18°、18°~26°分别进行角度叠加，三个部分叠加数据的中心角度分别为6°、14°、22°。利用井数据提取地震子波，并对井插值数据进行平滑处理得到初始模型。

图 8为叠后与角度部分叠加地震剖面，可见研究层段地震分辨率较低，将会制约甜点的预测精度。

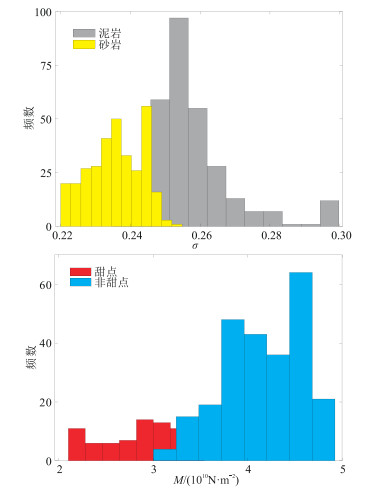
图 9为测井数据统计的不同岩相与砂体内部不同类型甜点泊松比、纵波模量的分布直方图，可以确定岩性与甜点敏感参数分别为泊松比与纵波模量。

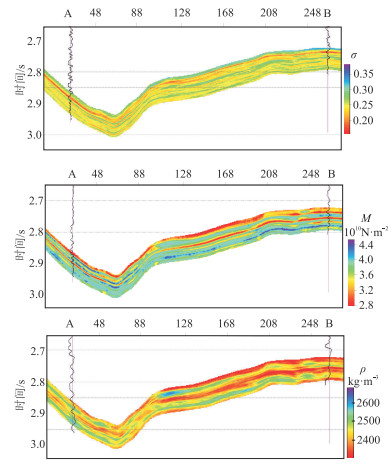
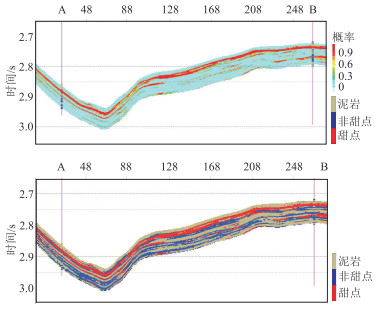
图 10与图 11分别为弹性参数反演剖面与甜点估算结果。与测井曲线对比可以发现，反演结果与井曲线吻合较好（图 10），且甜点估算结果符合测井解释结果（图 11）。

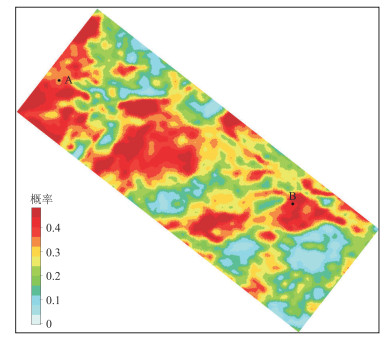
图 12为沿层的甜点概率平面属性。由图可见，甜点主要发育于区块西部与南部，这与地质认识相吻合，进一步验证了本文方法反演结果的合理性。

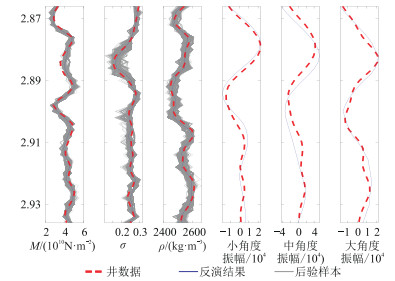
图 13为井旁道反演结果与实际井数据的对比，可以发现井旁道反演结果与井曲线吻合较好，且合成地震记录与实际地震记录相匹配，这说明了本文反演方法的有效性。

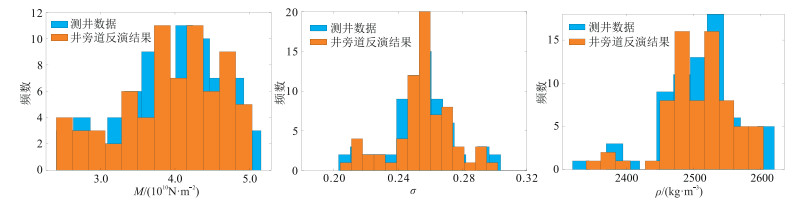
图 14为井旁道反演结果与测井数据分别统计的参数分布直方图。由图可见，本文方法反演结果的参数分布特征与统计参数先验一致，这说明了本文方法反演结果统计特征与先验假设一致。

综上所述，本文基于叠前概率反演的甜点直接估算方法可以有效应用于实际工区。

3 结束语

本文在Zoeppritz近似方程的基础上，推导了基于致密砂岩岩性与甜点敏感参数的反射系数方程，并将统计混合高斯先验与平滑约束先验相结合，建立反演参数的后验概率分布表达式，通过改进MH算法实现对后验概率分布的求解，从而建立基于叠前概率反演的甜点直接估算方法。在反演过程中，通过引入条件概率分布约束，减小反演参数的采样空间，不仅加快了算法的收敛，还提高了反演的稳定性。模型测试与实际数据应用均表明，基于叠前概率反演的甜点直接估算方法可以有效地实现甜点预测。