受地震资料主频和频带宽度限制,通常认为常规地震资料可识别的最小储层厚度为1/4波长。面对日益复杂的地质条件,尤其是复杂目标区小断层、小构造和小岩性体等小尺度开发目标的精细解释与地质刻画[1],常规地震资料的品质难以满足精细勘探的需求[2],需要对地震资料进行高分辨率处理。
高分辨率地震资料处理通过合理恢复地震记录的高、低频信息拓宽有效频带,在尽可能保持信噪比的前提下提高地震分辨率[3-4],从而改善薄层解释效果,提高储层预测精度。曹务祥[5]在小波包分解的基础上进行谱白化处理,解决了常规方法划分频带较粗的问题,提高了地震资料分辨率。章柯等[6]基于二进制小波变换提出了多分辨率反褶积方法,针对不同尺度信号的信噪比不同的特点,分别采用不同的反褶积预测步长有效压制噪声、提高分辨率。刁瑞[7]通过对比经验模态分解(EMD)与常规傅里叶滤波处理方法、小波包分解方法,证实EMD方法是较合理的地震资料分频方法,获得了较好的EMD反褶积效果。
本文结合EMD反褶积技术与构造导向约束滤波技术提高三维地震资料的分辨率,在JL地区的应用效果表明:EMD反褶积方法可提高地震数据的纵向分辨率,在实际构造条件约束下构造导向约束滤波可滤除高分辨率资料的部分噪声,从而提高资料信噪比;联合使用EMD反褶积与构造导向约束滤波,可提高长兴组生物礁储层预测精度。
1 EMD反褶积 1.1 EMD原理地震信号是一种非平稳信号,地震子波的时变性一直困扰地震数据处理,因此需要利用自适应性较强的分析方法提取非平稳地震信号的局部特征信息。Huang等[8]于1998年首次指出每一个信号都是由有限个固有本征函数(IMF)组成,每一个IMF都是单分量信号,满足希尔伯特变换要求。因此可对地震信号进行EMD,从而提取信号的局部特征信息。信号通过EMD得到的IMF不受外界影响,分解个数完全由原信号自身决定,因此EMD方法具有完全的自适应性[9],是分析非平稳地震信号的良好方法。
EMD可表示为
| $ x\left(t\right)=\sum \limits_{i=1}^{n}{f}_{i}\left(t\right)+r\left(t\right) $ | (1) |
式中:fi(t)为信号x(t)经EMD得到的第i个IMF,t为时间;n为IMF个数;r为EMD后的残差。根据文献[8]的定义,经过EMD的每一个IMF应该满足:
(1)当信号完成一次筛选后,出现在信号中的最大极值点和最小极值点个数之和与过零点的个数之差小于2;
(2)筛选的信号上、下包络线对应点的均值全部为0。
信号x(t)的EMD步骤如下:
(1)首先使用三次样条插值方法拟合x(t)的最大极值点、最小极值点的包络线,得到上包络线xmax(t)、下包络线xmin(t),即
| $ {m}_{1}\left(t\right)=\frac{{x}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(t\right)+{x}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(t\right)}{2} $ | (2) |
(2)筛选处理。求得第一个筛选分量f1(t)
| $ {f}_{1}\left(t\right)=x\left(t\right)-{m}_{1}\left(t\right) $ | (3) |
如果f1(t)同时满足IMF的两个假设条件,则f1(t)是第一个IMF,否则重复步骤(1),将f1(t)作为新信号继续进行EMD,直到新筛选分量同时满足两个假设条件。完成第一个IMF筛选后,残差为
| $ {r}_{1}\left(t\right)=x\left(t\right)-{f}_{1}\left(t\right) $ | (4) |
(3)将r1(t)作为下一次筛选的原函数,重复上述过程,直到所有满足两个假设条件的IMF全部分解,则完成x(t)的EMD全过程。
根据实际需要,当残差满足以下两个迭代条件,则视为EMD完成。第一,根据不同的信号设立相应的阈值,当残差小于阈值时迭代完成;第二,残差函数变成单调函数[9-10]。
1.2 EMD反褶积过程本文将地震信号视为含噪褶积模型信号,即
| $ x\left(t\right)=w\left(t\right)*R\left(t\right)+N\left(t\right) $ | (5) |
式中:w(t)为地震子波;R(t)为反射系数;N(t)为噪声。
x(t)经EMD得到的各IMF基本满足从高频到低频的分布,即通过EMD完成信号分频。由于EMD算法的完全自适应性,因此无需确定地震子波,仅通过信号自身便可完成分解。通过对不同分量进行预测反褶积,同时在分量信号合并成新的主信号时通过基于信噪比分析的加权重组,在提高分辨率的同时,使资料相对保幅。同时,由于在EMD过程中不能完全确定噪声是否分离,因此在分量信号反褶积及信号重组过程中不做信号筛选处理,而是对全分量信号重组。其优点是能更好地保持资料的相对振幅关系,而噪声则通过滤波方法去除。EMD反褶积的具体流程如下。
(1)x(t)经EMD得到多个IMF;
(2)对每一个IMF进行预测步长为l的预测反褶积,即
| $ \operatorname{IMF}\hat{_{i}}(t+l)=\xi(t) * f_i(t)=\sum\limits_{\tau=0}^{\infty} \xi(\tau) f_i(t-\tau) $ | (6) |
式中:ξ(t)为根据维纳滤波思想求得的原始信号满足最小均方误差的反褶积算子;
通过分析不同IMF的信噪比,依据信噪比高低选择不同的l,以拓宽高信噪比频带、压制低信噪比频带,从而提高信噪比。
(3)对
| $ X\left(t\right)=\sum \limits_{i=1}^{n}{\omega }_{i}\operatorname{IMF}\hat{_{i}}\left(t\right)+r\left(t\right) $ | (7) |
式中权重系数ωi为反褶积处理前单个IMF信噪比
| $ {\omega }_{i}=\frac{\mathrm{S}\mathrm{N}\mathrm{R}\left[{f}_{i}\left(t\right)\right]}{\frac{1}{n}\sum \limits_{i=1}^{n}\mathrm{S}\mathrm{N}\mathrm{R}\left[{f}_{i}\left(t\right)\right]} $ | (8) |
基于信噪比分析的预测反褶积和加权重组可基本实现地震数据的相对保幅处理。
1.3 效果对比分析为了说明EMD反褶积方法在提高地震分辨率方面的效果,分别使用理论数据和实际地震数据进行分析。
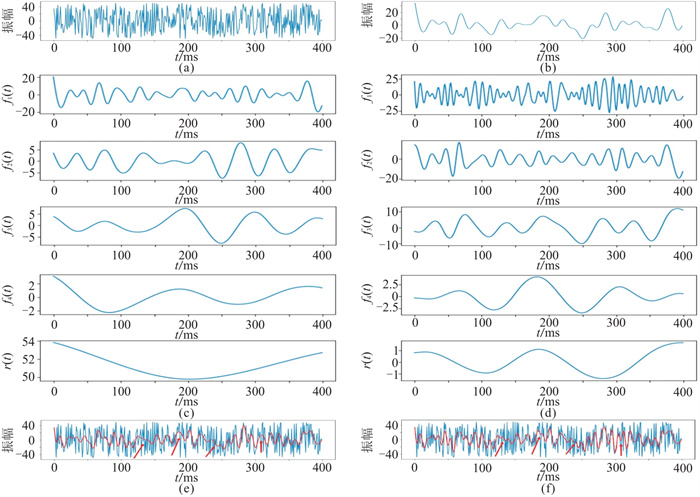
使用随机生成的长度为400 ms的信号作为原始地震信号(图 1a),并进行低通滤波以模拟经过大地滤波器的实际地震信号(图 1b)。将图 1b直接进行反褶积,信号分辨率得到一定恢复(图 1e的红色曲线)。将图 1b通过相同预测步长的EMD(图 1c)、反褶积(图 1d)及加权重组,得到的信号细节(图 1f红色箭头处)较图 1e的红色曲线更丰富,更接近图 1a。可见,相对于常规叠后反褶积,EMD反褶积能更好地恢复信号细节,提高薄层的分辨率。
|
图 1 基于理论数据的EMD反褶积与常规反褶积对比 (a)原始地震信号;(b)图a经过低通滤波;(c)图b经EMD得到的IMF及残差;(d)对图c反褶积;(e)图b直接反褶积与图a对比;(f)图d经加权重组与图a对比 |
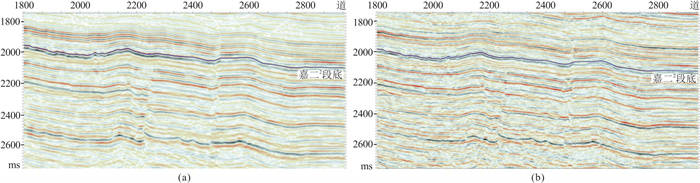
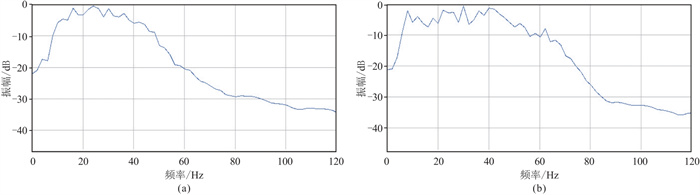
选取四川盆地JL地区的地震数据分析EMD反褶积方法的效果。图 2为叠后EMD反褶积前、后地震剖面。由图可见,经EMD反褶积的地震剖面的分辨率较高,波组特征清楚,构造、断层、断点清晰,层间信息更丰富(图 2b)。由叠后EMD反褶积前(图 3a)、后(图 3b)地震剖面的频谱可见:图 3a的主频约为23 Hz,频带为6~55 Hz;图 3b的主频约为29 Hz,频带为5~74 Hz,层间信息更丰富,在有效拓宽频带的同时,较好地保持了相对振幅关系与时频特性。
|
图 2 叠后EMD反褶积前(a)、后(b)地震剖面 |
|
图 3 叠后EMD反褶积前(a)、后(b)地震剖面频谱(2000~2500 ms) |
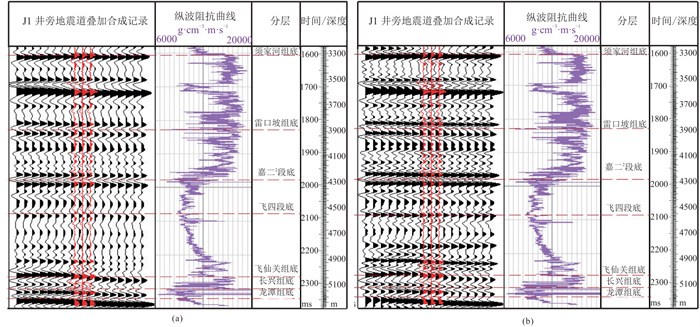
图 4为J1井EMD反褶积前、后合成记录标定。由图可见,EMD反褶积前(图 4a)、后(图 4b)的波组特征、反射层位一致,且图 4b的薄层和复波等信息与地震合成记录及阻抗曲线吻合良好,说明常规地震资料经过EMD反褶积得到的信息真实、可靠。
|
图 4 J1井EMD反褶积前(a)、后(b)合成记录标定(标定子波为对应的井旁道子波) |
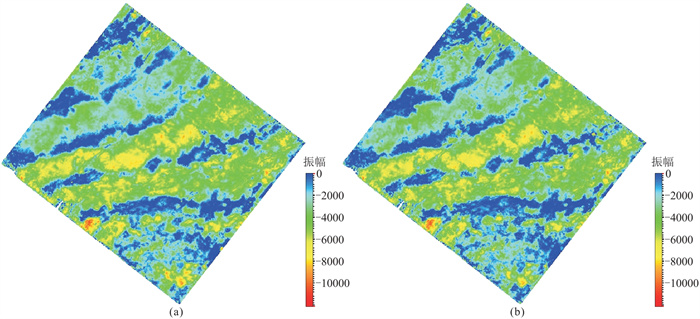
为研究EMD反褶积的保幅性,选择嘉二2段底为辅助层提取振幅属性进行对比、分析。嘉二2段为一套在JL地区稳定分布的泥质云岩夹泥质膏岩的薄层,厚度约为30 m,嘉二2段底在地震资料上对应一个容易对比、追踪的强波谷(图 2)。分别基于EMD反褶积前、后的资料提取沿嘉二2段底的最大波谷振幅属性(图 5)。可见,嘉二2段底的相对振幅关系在EMD反褶积前(图 5a)、后(图 5b)几乎一致,仅在个别局部小区域有轻微变化,说明EMD反褶积较好地保持了地震资料的相对振幅关系,为后续研究奠定了基础。
|
图 5 EMD反褶积前(a)、后(b)嘉二2段底最大波谷振幅属性 |
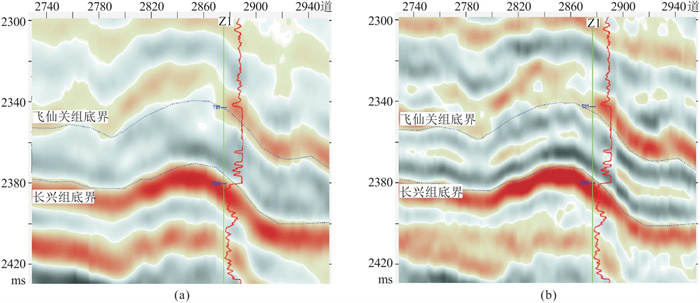
长兴组沉积时JL地区位于海槽相向台缘相过渡带,横向多井证实储层为生物礁,岩性主要为碎屑灰岩。生物礁主要发育在长兴组沉积晚期,极个别井在长兴组沉积早期也发现局部储层。测井曲线表明,长兴组早期沉积的曲线呈频繁变化特征,晚期沉积的曲线特征基本一致,生物礁储层多发育在晚期。图 6为EMD反褶积前、后过Z1井地震剖面。由图可见:原始地震资料无法分辨长兴组早、晚期沉积,对生物礁储层预测造成了一定困难(图 6a);图 6a经叠后EMD反褶积处理后,能明显看到长兴组内部基本分成了上、下两个同相轴(图 6b),分别对应测井曲线揭示的早、晚期沉积,说明EMD反褶积提高了地震资料分辨率,为研究长兴组晚期生物礁储层展布提供了可靠的资料。
|
图 6 EMD反褶积前(a)、后(b)过Z1井地震剖面 为方便对比井曲线,剖面均经过希尔伯特变换;测井曲线为纵波时差曲线。 |
反褶积常常带来一定噪声,通过滤波可以有效减小噪声。一般来说,对地震资料进行常规叠后滤波往往只是单纯的数学运算,很少受实际构造条件约束[11-13]。当地层水平时,常规叠后滤波的效果较好;当地层具有一定倾角时,可能出现分辨率降低、信噪比下降现象[14]。由于JL地区地层均具有一定倾角,因此本文采用构造导向约束滤波处理,可较好地去噪、提高信噪比。
2.1 构造导向约束滤波原理对于地层中的某点来说,由于不同方向具有不同的地层倾角,因此采用方位角、倾角数据组定量刻画任意点。目前在三维地震数据中,主要通过振幅数据梯度法和频率—波数域扫描法获得地层倾角和方位角信息,从而获得包含倾角和方位角信息的构造导向数据体,可以对数据体的其他运算约束。
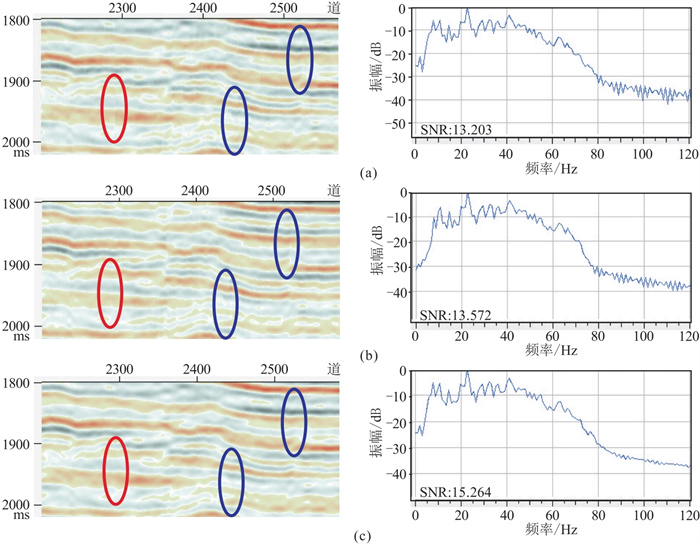
2.2 滤波效果分析中值滤波可以较好地压制反褶积引起的脉冲噪声并保护边缘信息,因此广泛用于地震资料处理[15-16]。图 7为滤波效果对比。由图可见:滤波前剖面存在噪声(图 7a);常规中值滤波剖面基本滤除了水平地层噪声(图 7b左红圈处),但仍然存在倾斜地层噪声(图 7b左蓝圈处),信噪比提升不大,频谱依然存在高频抖动(图 7b右);基于构造导向约束的中值滤波剖面较好地滤除了噪声,同时提高了信噪比(图 7c左),明显减弱了频谱的高频抖动(图 7c右),剖面特征基本与图 7a一致。
|
图 7 滤波效果对比 (a)滤波前剖面(左)及频谱(右);(b)常规中值滤波剖面(左)及频谱(右);(c)基于构造导向约束的中值滤波剖面(左)及频谱(右) |
对原始地震资料进行EMD反褶积和构造导向约束滤波联合处理,得到高分辨率地震资料。分别基于原始地震资料和高分辨率地震资料,利用J1、Z1、P4三口井的数据和1口盲井S1的数据进行稀疏脉冲反演,得到长兴组的储层预测结果。经对比发现,基于高分辨率资料的储层预测结果更符合地质认识,且与盲井更匹配。
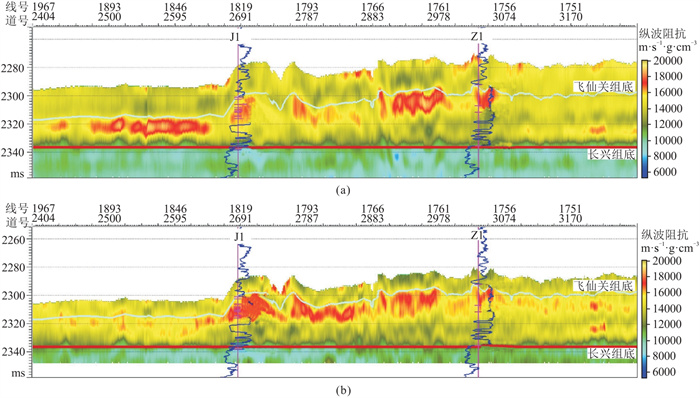
图 8为处理前、后过Z1-J1连井波阻抗反演剖面。由图可见,处理前、后反演剖面的储层大致形态一致,但细节处有差异:前者显示长兴组较厚处储层不连续,且较薄处储层品质很好(图 8a左侧);后者显示长兴组较厚处储层连续发育,较薄处储层相对不发育(图 8b左侧),与生物礁储层多发育在沉积厚度较大区域的地质认识相符。
|
图 8 处理前(a)、后(b)过Z1-J1连井波阻抗反演剖面 为了方便对比长兴组晚期生物礁储层,均对长兴组底界拉平处理;测井曲线为纵波阻抗曲线。图 9同。 |
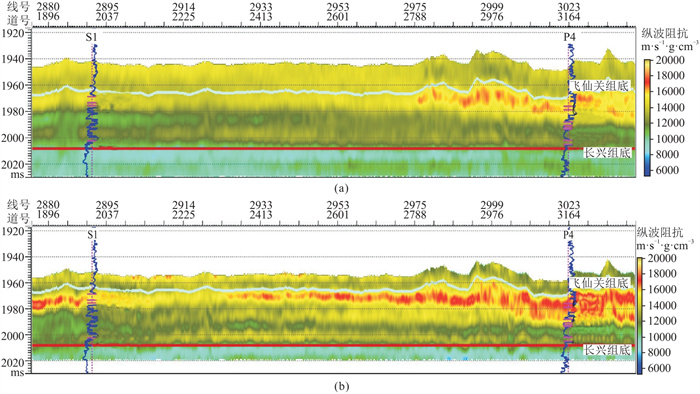
S1井在长兴组钻遇厚约17 m的生屑灰岩,最终解释差气层厚度为5.8 m;P4井钻遇4套长兴组早期和晚期储层,最终解释差气层累计厚度为27.5 m。图 9为处理前、后过S1-P4井连井波阻抗反演剖面。由图可见:处理前反演剖面(图 9a)在S1井处基本无储层,P4井处长兴组晚期储层较薄,早期基本无储层,预测厚度约为8 m,与实钻差异较大;处理后反演剖面(图 9b)在S1井处储层较薄,预测厚度为5 m,P4井处储层较发育,预测储层厚度为32 m,与实钻结果更匹配。
|
图 9 处理前(a)、后(b)过S1-P4井连井波阻抗反演剖面 |
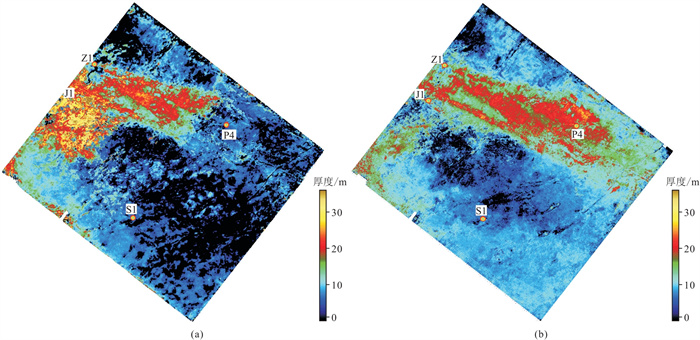
图 10为处理前、后长兴组储层厚度预测平面图。由图可见:①处理前长兴组储层厚度预测图(图 10a)显示,P4井储层厚度小于10 m,S1井储层厚度接近0,同时J1井南部有一偏厚滩体状有利储层,生物礁储层整体呈滩状分布。上述结果与周边及整体大区域的生物礁储层多呈条带状分布的地质认识存在偏差,生物礁储层厚度预测绝对误差平均值为8.2 m(表 1)。②处理后长兴组储层厚度预测图(图 10b)显示,P4井处储层相对发育,S1井处储层较薄,J1井、Z1井处储层厚度约为15~20 m,生物礁储层整体呈条带状分布。上述结果与区域上生物礁储层多呈条带状分布的地质认识一致,生物礁储层厚度预测绝对误差平均值为2.2 m(表 1)。
|
图 10 处理前(a)、后(b)长兴组储层厚度预测平面图 |
|
|
表 1 处理前、后井点储层预测厚度与实钻结果 |
综上所述,基于联合处理的地震资料的储层预测结果更符合整体地质认识,在井点处与实钻结果更匹配,储层预测精度更高。
4 结束语(1)联合叠后EMD反褶积与构造导向约束滤波的处理技术能有效提高地震分辨率,且地震资料的频带宽度较大,同时保持了较高的信噪比。
(2)采用所提技术进行储层预测,得到的储层信息与实钻结果更匹配,更符合地质认识,储层预测精度高于原始地震资料。
| [1] |
周宗良, 吴刚, 肖建玲, 等. 地震拓频处理技术在歧口深层气藏储层预测中的应用[J]. 工程地球物理学报, 2015, 12(5): 604-609. ZHOU Zongliang, WU Gang, XIAO Jianling, et al. The application of seismic frequency expanding processing technique to deep gas reservoir prediction in Qikou[J]. Chinese Journal of Engineering Geophysics, 2015, 12(5): 604-609. |
| [2] |
王江, 赵传军, 李国福, 等. 地震拓频处理技术在乌尔逊断陷北部储层预测中的应用[J]. 大庆石油地质与开发, 2021, 40(4): 125-131. WANG Jiang, ZHAO Chuanjun, LI Guofu, et al. Application of seismic frequency expanding processing technology in the reservoir prediction of North Wuerxun Rift[J]. Petroleum Geology & Oilfield Development in Daqing, 2021, 40(4): 125-131. |
| [3] |
高喜龙. 埕岛油田东斜坡地震资料特殊处理及储层预测[J]. 断块油气田, 2012, 19(1): 88-91. GAO Xilong. Reservoir prediction and special processing of seismic data in eastern slope area of Chengdao Oilfield[J]. Fault-Block Oil & Gas Field, 2012, 19(1): 88-91. |
| [4] |
云美厚, 赵秋芳, 李晓斌. 地震分辨率思考与高分辨率勘探对策[J]. 石油地球物理勘探, 2022, 57(5): 1250-1262. YUN Meihou, ZHAO Qiufang, LI Xiaobin. Thought about seismic resolution and countermeasures of high-resolution seismic exploration[J]. Oil Geophysical Prospecting, 2022, 57(5): 1250-1262. |
| [5] |
曹务祥. 利用小波包算法提高地震资料分辨率[J]. 石油地球物理勘探, 1996, 31(5): 704-711. CAO Wuxiang. Seismic resolution improvement using wavelet package algorithm[J]. Oil Geophysical Prospecting, 1996, 31(5): 704-711. |
| [6] |
章珂, 李衍达, 刘贵忠, 等. 多分辨率地震信号反褶积[J]. 地球物理学报, 1999, 42(4): 529-535. ZHANG Ke, LI Yanda, LIU Guizhong, et al. Multiresolution seismic signal deconvolution[J]. Chinese Journal of Geophysics, 1999, 42(4): 529-535. |
| [7] |
刁瑞. 分频带预测反褶积方法研究[J]. 断块油气田, 2015, 22(1): 53-57. DIAO Rui. Method of separate frequency predictive deconvolution[J]. Fault-Block Oil & Gas Field, 2015, 22(1): 53-57. |
| [8] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for non-stationary time series analysis[J]. Proceedings of the Royal Society A, 1998, 454(1971): 903-995. |
| [9] |
邬蒙蒙. 基于经验模态分解(EMD)的地震资料时频分析研究及应用[D]. 四川成都: 成都理工大学, 2020.
|
| [10] |
何富裕, 杨巍, 朱仕军. 改进的经验模态分解方法及在储层预测中的应用[J]. 化工设计通讯, 2021, 47(3): 184-186. HE Fuyu, YANG Wei, ZHU Shijun. Improved empirical mode decomposition method and its application in reservoir prediction[J]. Chemical Engineering Design Communications, 2021, 47(3): 184-186. |
| [11] |
罗焕章. 方向性滤波去噪方法及其应用[J]. 油气地质与采收率, 2011, 18(6): 50-52. LUO Huanzhang. Method and application of orientation filtering and noising cancelling[J]. Petroleum Geology and Recovery Efficiency, 2011, 18(6): 50-52. |
| [12] |
胡瑞卿, 何俊杰, 李华飞, 等. 时频域变分模态分解地震资料去噪方法[J]. 石油地球物理勘探, 2021, 56(2): 257-264. HU Ruiqing, HE Junjie, LI Huafei, et al. Seismic data de-noising method based on VMD in time-frequency domain[J]. Oil Geophysical Prospecting, 2021, 56(2): 257-264. |
| [13] |
徐彦凯, 刘曾梅, 薛亚茹, 等. 应用双通道卷积神经网络的地震随机噪声压制方法[J]. 石油地球物理勘探, 2022, 57(4): 747-756. XU Yankai, LIU Zengmei, XUE Yaru, et al. Suppression of seismic random noise using dualchannel convolutional neural network[J]. Oil Geophysical Prospecting, 2022, 57(4): 747-756. |
| [14] |
赵明章, 范雪辉, 刘春芳, 等. 利用构造导向滤波技术识别复杂断块圈闭[J]. 石油地球物理勘探, 2011, 46(增刊1): 128-133. ZHAO Mingzhang, FAN Xuehui, LIU Chunfang, et al. Complex fault-block traps identification with structure-oriented filter[J]. Oil Geophysical Prospecting, 2011, 46(S1): 128-133. |
| [15] |
孙宏琦, 施维颖, 巨永锋. 利用中值滤波进行图像处理[J]. 长安大学学报(自然科学版), 2003, 23(2): 104-106. SUN Hongqi, SHI Weiying, JU Yongfeng. Image processing with medium value filter[J]. Journal of Chang'an University(Natural Science Edition), 2003, 23(2): 104-106. |
| [16] |
王卫华. 利用中值相关滤波预测相干信号[J]. 石油地球物理勘探, 2000, 35(3): 273-282. WANG Weihua. Coherent signal prediction using mid-value correlative filtering[J]. Oil Geophysical Prospecting, 2000, 35(3): 273-282. |



 邵佳, 四川省成都市双流区华阳大道一段216号中国石油集团东方地球物理公司西南物探研究院,610213。Email:
邵佳, 四川省成都市双流区华阳大道一段216号中国石油集团东方地球物理公司西南物探研究院,610213。Email: