0 引言

微地震监测技术被广泛地应用于页岩层、致密层和干热岩等非常规资源的压裂开发，为评价压裂效果和调整压裂方案等提供了技术手段，从而为非常规资源的产能提高奠定了基础^[1-3]。在储层压裂监测资料处理中，微地震事件定位准确与否直接影响压裂裂缝形态的解释^[4]。但在实际储层压裂监测作业中，由于微地震资料信噪比可能较低或能量较弱，增加了准确拾取微地震事件初至的难度，初至拾取误差对基于旅行时的微地震事件定位方法的精度影响尤为显著^[5-6]。而基于波形叠加目标函数的微地震事件偏移定位不需要初至数据，定位精度不受初至拾取误差的影响，更适应井中低信噪比微地震资料反演处理，但其精度受波形叠加函数构造方法的影响^[7]。

前人提出了基于振幅^[7-8]、波形相似性^[9]和互相关^[10-13]的波形叠加成像函数构造方法。基于波形相似性和互相关的目标函数均用于衡量波形相干性，因此这两类方法的精度相差不大，但互相关方法在计算互相关系数时计算量更大，限制了该方法的实际应用^[14]。基于单一的振幅叠加或波形相似性构造方法的精度均不高，故一些学者认为将波形相似性及振幅叠加相结合可进一步提高成像函数的分辨率。Eaton等^[15]将波形相似性函数与振幅叠加函数相结合，提出了基于波形相似性加权振幅叠加的定位方法。随后一些学者对该经典算法进行了改进及深入分析，Zhang等^[16]基于三分量信息，提出了基于波形相似性加权振幅叠加的交叉分量互相关方法，在一定程度上提高了定位结果的分辨率；Zhao等^[17]分析了地面观测系统采集参数对波形相似性加权振幅叠加定位结果的影响，认为地面排列具有更多检波器和更小的检波器间距时，该方法可提高定位结果的纵向分辨率；Zhang等^[18]深入分析了波形相似性加权振幅叠加方法的分辨率，认为其相似性构造函数和振幅叠加构造函数的分辨率与检波器分布有关，不同方向的分辨率不同，在井中观测时，相似性构造函数在沿着检波器到震源方向上不确定性更大，而沿着其垂直方向上分辨率更高；振幅叠加构造函数在沿着检波器到震源方向上分辨率更高，而沿着其垂直方向上不确定性更大。此外，针对震源机制产生辐射花样后造成的极性变化，一些学者采用绝对值类处理方法规避了极性变化，虽然提高了解的稳定性，但以牺牲成像函数分辨率为代价^[14]。随后，Trojanowski等^[14]、Kim等^[19]和Xu等^[20-21]认为极性修正方法可改善波形一致性叠加效果，从而提高波形叠加函数分辨率。对原始波形进行极性修正处理后，常规波形叠加成像函数的分辨率仍有待于进一步提高。

基于前人的研究结果，为提高波形叠加成像函数的分辨率，本文提出一种优化波形相似性加权振幅叠加的成像函数构造方法，即先将纵、横波波形相似性基函数相乘，再将其振幅叠加基函数相乘，然后将两个积相乘，最后在整个时窗内对其求和。用理论模型和实际资料对常规方法与本文改进方法进行了效果测试和对比。

1 原理

波形叠加偏移定位方法首先利用射线追踪计算震源（事件）点到每一个接收点的时间，以其中一个为参考时间构建每个接收点的时移量；其次，应用时移量校正后，由同一个震源产生、不同接收点的记录必然同时具有强振幅，基于上述原理可用波形叠加为成像函数求得震源的时空参数^[22]。前人的研究成果表明，联合利用纵波和横波信息进行波形叠加可提高微地震事件偏移定位精度^{[16, 18, 23]}。根据研究目的，本文仅深入讨论基于纵、横波的成像函数构造方法。

1.1 成像函数

振幅叠加、互相关函数及相似性函数各自在提高成像函数分辨率上受到一定限制^[18]。而与互相关函数相比，相似性成像函数分辨率相差不大，且计算量更小，故本文仅讨论如何构造基于波形相似性和振幅叠加的成像函数。

1.1.1 基于波形相似性加权振幅叠加的成像函数

Zhang等^[18]发展了一种波形相似性加权振幅叠加的定位方法，为了消除震源机制辐射花样造成的极性变化，该方法的输入波形数据均采用振幅绝对值或平方。

针对同一个事件，通过主事件信息计算由速度模型误差造成的每个检波器的纵、横波旅行时校正量^[24]。以该事件的横波近似初至作为参考旅行时为例，假设震源点到第i个检波器应用旅行时校正量后纵、横波理论旅行时记为$ {t}_{i}^{k} $（k为P或S，表示纵波或横波），到第m个检波器应用旅行时校正量后横波理论旅行时记为$ {t}_{m}^{\mathrm{S}} $，则可构造第i个检波器的纵波或横波与第m个检波器的横波理论时差

$ \mathrm{\Delta }{t}_{i}^{k}={t}_{i}^{k}-{t}_{m}^{\mathrm{S}} $

(1)

则波形相似性函数定义为

$ S\left(t\right)=\sqrt{{S}_{\mathrm{P}}\left(t\right)\times {S}_{\mathrm{S}}\left(t\right)} $

(2)

$ {S}_{k}\left(t\right)=\frac{\sum \limits_{\tau =t-{w}_{1}}^{t+{w}_{1}}{\left[\sum \limits_{i=1}^{n}\left|{u}_{i}\right(\mathrm{\Delta }{t}_{i}^{k}+\tau \left)\right|\right]}^{2}}{n\sum \limits_{\tau =t-{w}_{1}}^{t+{w}_{1}}\sum \limits_{i=1}^{n}{\left|\left.{u}_{i}(\mathrm{\Delta }{t}_{i}^{k}+\tau )\right|\right.}^{2}} $

(3)

式中：t表示时间，范围为[$ {t}_{m\mathrm{F}\mathrm{A}}^{\mathrm{S}} $$ - $w₂，$ {t}_{m\mathrm{F}\mathrm{A}}^{\mathrm{S}} $+w₂]，其中$ {t}_{m\mathrm{F}\mathrm{A}}^{\mathrm{S}} $是该事件第m个检波器记录横波的近似初至估计值，2w₂为外时窗长度；n是检波器总数；u_i是第i检波器地震信号振幅；2w₁为内时窗长度。

振幅叠加函数为

$ \sigma \left(t\right)=\frac{1}{n}\sum \limits_{i=1}^{n}{\sigma }_{i}^\text{P}\left(t\right)\times {\sigma }_{i}^\text{S}\left(t\right) $

(4)

$ {\sigma }_{i}^{k}\left(t\right)=\frac{\sum \limits_{\tau =t-{w}_{1}}^{t+{w}_{1}}{V}_{i}(\mathrm{\Delta }{t}_{i}^{k}+\tau )}{2{w}_{1}+1} $

(5)

$ {V}_{i}\left({t}_{i}\right)=\frac{\mathrm{S}\mathrm{T}\mathrm{A}\left({t}_{i}\right)}{\mathrm{L}\mathrm{T}\mathrm{A}\left({t}_{i}\right)}=\frac{\frac{1}{{n}_{\mathrm{s}}}\sum \limits_{a=0}^{{n}_{\mathrm{s}}-1}{\left|{u}_{i}({t}_{i}-a\mathrm{\delta }t)\right|}^{2}}{\frac{1}{{n}_{\mathrm{l}}}\sum \limits_{a=0}^{{n}_{\mathrm{l}}-1}{\left|{u}_{i}({t}_{i}-a\mathrm{\delta }t)\right|}^{2}} $

(6)

式中：$ {\sigma }_{i}^{\mathrm{P}}\left(t\right) $、$ {\sigma }_{i}^{\mathrm{S}}\left(t\right) $分别为纵、横波的振幅叠加能量；V_i（t_i）为第i个检波器在时间t_i处能量比值；STA和LTA分别为短、长时窗内信号能量的平均值；$ \mathrm{\delta }t $为采样间隔；n_s、n_l分别是短、长时窗内样点数。

定义波形相似性加权振幅叠加成像函数为

$ I\left(t\right)=\sigma \left(t\right)\times {S}_{}^{2} \left(t\right) $

(7)

1.1.2 基于极性修正波形相似性加权振幅叠加的成像函数

式（4）的振幅叠加函数因采用长、短时窗平均能量作为输入，不适合应用极性修正，仅将式（3）的波形相似性函数的输入绝对值波形替换成极性修正后波形。

极性修正后波形相似性函数重写为

$ {S}^{\mathrm{p}\mathrm{c}}\left(t\right)=\sqrt{{S}_{\mathrm{P}}^{\mathrm{p}\mathrm{c}}\left(t\right)\times {S}_{\mathrm{S}}^{\mathrm{p}\mathrm{c}}\left(t\right)} $

(8)

$ {S}_{k}^{\mathrm{p}\mathrm{c}}\left(t\right)=\frac{\sum \limits_{\tau =t-{\mathrm{w}}_{1}}^{t+{\mathrm{w}}_{1}}{\left[\sum \limits_{i=1}^{n}\mathrm{s}\mathrm{g}{\mathrm{n}}_{{}_{i}}^{k}\times {u}_{i}(\mathrm{\Delta }{t}_{i}^{k}+\tau )\right]}^{2}}{n\sum \limits_{\tau =t-{\mathrm{w}}_{1}}^{t+{\mathrm{w}}_{1}}\sum \limits_{i=1}^{n}{\left[\mathrm{s}\mathrm{g}{\mathrm{n}}_{{}_{i}}^{k}\times {u}_{i}(\mathrm{\Delta }{t}_{i}^{k}+\tau )\right]}^{2}} $

(9)

式中$ \mathrm{s}\mathrm{g}{\mathrm{n}}_{{}_{i}}^{k} $是第i个检波器记录的纵或横波原始振幅u_i的对应极性修正符号，可通过互相关极性分析方法^{[19, 25]}求取。

式（7）重写整理为

$ {I}^{\mathrm{p}\mathrm{c}}\left(t\right)=\sigma \left(t\right)\times {\left[{S}^{\mathrm{p}\mathrm{c}}\left(t\right)\right]}^{2} $

(10)

式中$ {I}^{\mathrm{p}\mathrm{c}}\left(t\right) $是基于极性修正波形相似性加权振幅叠加的成像函数。

1.1.3 优化波形相似性加权振幅叠加的成像函数

为了提高波形叠加成像函数的分辨率，本文对常规方法的波形叠加函数进行综合优化改进。先将纵、横波波形相似性基函数相乘，再将其振幅叠加基函数相乘，然后将两个积相乘，最后在整个时窗内对其求和。优化波形叠加成像函数为

$ {I}_{\mathrm{S}\mathrm{W}\mathrm{S}}\left(t\right)=\sum \limits_{\tau =t-{w}_{1}}^{t+{w}_{1}}{L}_\text{P}\left(\tau \right)\times {L}_\text{S}\left(\tau \right)\times {G}_\text{P}\left(\tau \right)\times {G}_\text{S}\left(\tau \right) $

(11)

$ {L}_{k}\left(\tau \right)=\sum \limits_{i=1}^{n}\text{sgn}_{{}_{i}}^{k}\times {u}_{i}\left(\Delta \right.{t}_{i}^{k}+\tau ) $

(12)

$ {G}_{k}\left(\tau \right)=\frac{{\left[\sum \limits_{i=1}^{n}\mathrm{s}\mathrm{g}{\mathrm{n}}_{{}_{i}}^{k}\times {u}_{i}(\mathrm{\Delta }{t}_{i}^{k}+\tau )\right]}^{2}}{n\sum \limits_{i=1}^{n}{\left[\mathrm{s}\mathrm{g}{\mathrm{n}}_{{}_{i}}^{k}\times {u}_{i}(\mathrm{\Delta }{t}_{i}^{k}+\tau )\right]}^{2}} $

(13)

式中：$ {L}_{k}\left(\tau \right) $是纵波或横波振幅叠加基函数，其含义表示消除对应地震道正常时差（$ \mathrm{\Delta }{t}_{i}^{k} $）及应用极性修正处理后，检波器记录的纵波或横波在时间序列τ处波形叠加值；$ {G}_{k}\left(\tau \right) $经过极性修正后时间序列τ处纵波或横波的相似性基函数值。

1.2 定位步骤

（1）输入目标微地震事件中任意一个检波器记录纵、横波的粗略估计初至旅行时，该初至旅行时可通过能量比法获得，无需扫描整个时间轴，只需扫描粗略初至附近范围时间，以提高扫描效率；

（2）输入校正后速度模型及对目标区域网格化，再通过射线追踪方法计算所有网格点分别到所有检波器的纵、横波理论初至旅行时，并对上述初至旅行时应用旅行时校正量后建立其对应旅行时表；

（3）依据式（7）、式（10）或式（11）构造波形相似性加权振幅叠加成像函数；

（4）通过极化约束下网格搜索技术寻找上述目标函数成像最大值，并输出最大成像值所对应位置，即微地震事件位置。

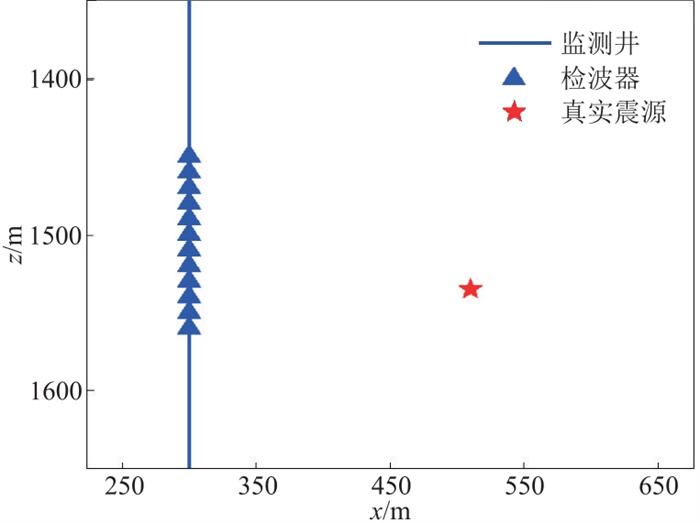
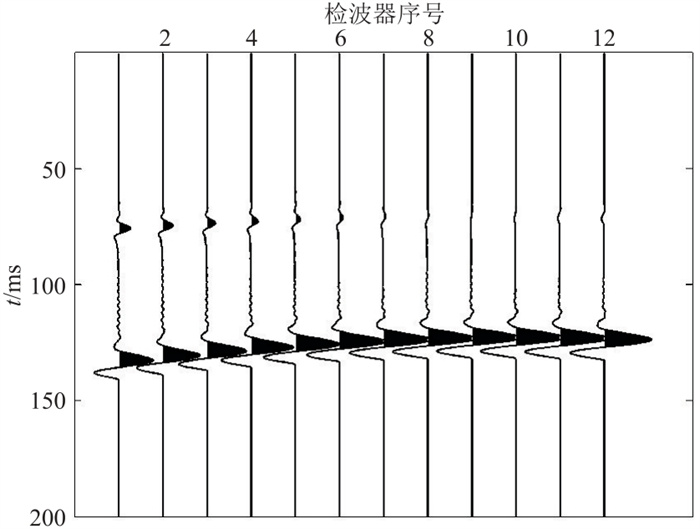
2 理论模型数据测试 2.1 模型及合成记录

为了对比基于常规波形叠加成像函数与基于优化波形叠加成像函数的井中微地震定位方法效果，本文采用简单的二维均匀模型，建立一个二维井中观测系统（图 1），其中纵波速度、横波速度和密度分别为3000 m/s、1700 m/s、2.1 g/cm³。在x=300 m处设置一口监测井（直井），在该井中设置12级检波器，其深度范围为1450~1560 m，检波器间距为10 m。设计微地震事件震源位置为（x，z）=（510 m，1535 m）。然后对上述模型应用二维弹性波动方程模拟了z分量微地震记录^[26]（图 2），震源是主频为60 Hz的Ricker子波，时间采样间隔为0.5 ms。

2.2 无噪声微地震数据的成像函数效果对比

对图 2无噪声数据分别应用式（7）、式（10）和式（11）构造的波形叠加成像函数进行微地震定位，结果如图 3所示。可以看出，优化后波形叠加成像函数的定位结果能量更聚焦、分辨率更高；基于优化波形叠加成像函数的定位结果更接近真实震源，定位精度更高。

统计学中峰度反映了总体数据取值分布形态陡缓的程度^[12]。为了定量评价三种成像函数的成像效果，计算三种成像函数的定位结果在震源处的峰度值，分别为22.0、26.7、45.4。可见，优化波形叠加成像函数的定位结果的峰度值最大，表明成像结果更聚焦、分辨率更高。

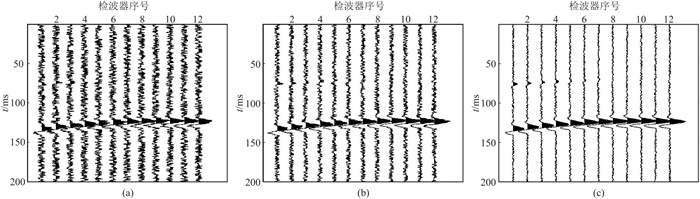
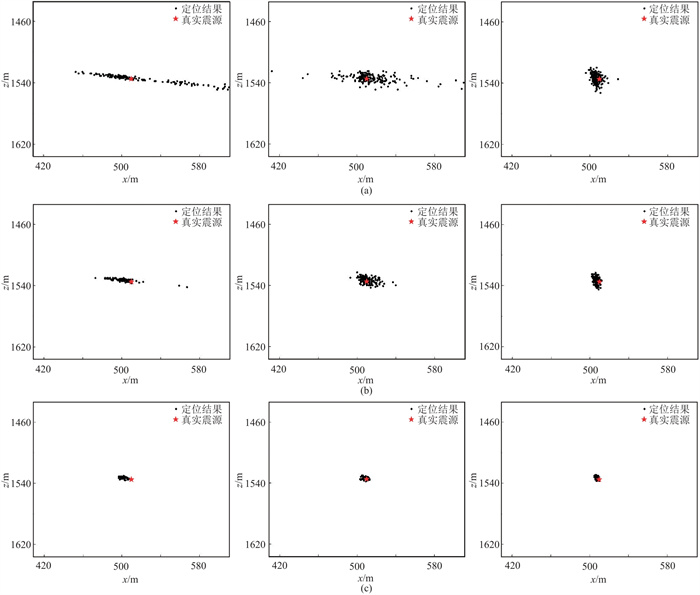
2.3 低信噪比微地震数据的定位效果对比

为了验证不同波形叠加成像函数的微地震定位方法的抗噪性，对图 2无噪声微地震数据加入不同强度随机噪声（以微地震数据中纵波信号为参考计算信噪比^[18]）。为了对比更直观，本文分别进行加入不同强度随机噪声的200次蒙特卡罗试验，分别生成信噪比为0.1、0.2及0.5的600个微地震记录，其中一次蒙特卡罗试验生成的含噪声地震记录称为一次实现^[7]（图 4）。然后对比三种方法在不同信噪比情况下的定位精度（图 5）。

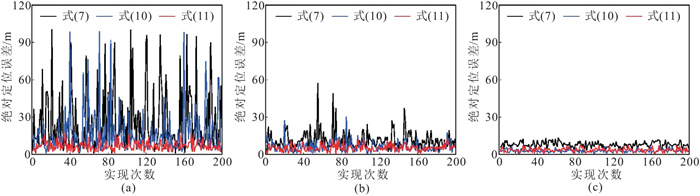
由图 5可以看出，随着信噪比增大，三种成像函数的蒙特卡罗重定位结果均逐渐收敛于真实震源位置，基于优化波形叠加成像函数的200次蒙特卡罗定位结果比其他两种成像函数更聚焦于真实震源位置。图 6是图 5中不同成像函数200次实现的定位误差，可见不同信噪比下，优化波形叠加成像函数的定位误差比其他两种成像函数的定位误差更小。可见，本文提出的优化波形叠加成像函数具有更强的抗噪能力，从而可实现低信噪比微地震事件的可靠定位。

3 实际资料应用

为了进一步验证本文优化后波形叠加成像函数方法的有效性，对M油田致密砂岩压裂井中监测微地震资料进行定位测试。压裂采用邻井观测，压裂井和监测井均为斜井，监测井中沿井轨迹方向斜深2570~2630 m（对应的垂直深度为2532.95~2590.18 m）处放置7级三分量检波器，检波器间隔为10 m，时间采样间隔为0.25 ms。两段压裂，垂深分别为2569.88~2572.83 m和2588.31~2589.79 m。利用压裂井和监测井的测井曲线及射孔数据获得校正后速度模型。由于采集的三分量数据中z分量品质较差，故应用低信噪比微地震事件自动检测方法^[27]对y分量数据识别了282个微地震事件。

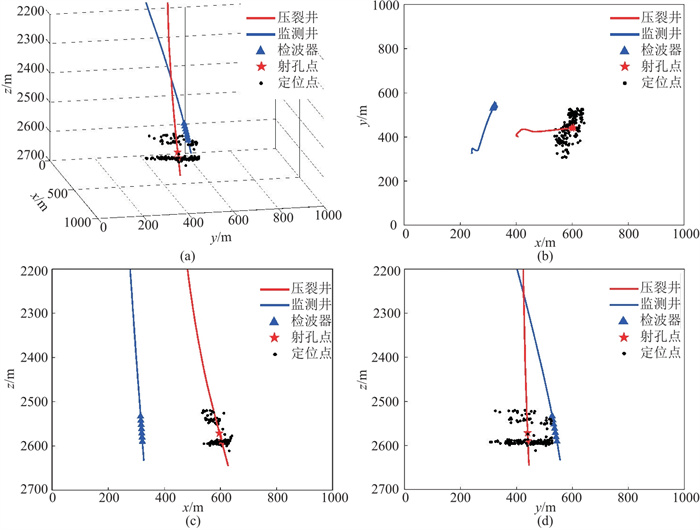
以两段压裂井段的中点为搜索最优解空间的中心，建立一个x、y和z方向长度分别为300、300、200 m的三维搜索空间，离散网格尺寸为1 m。对识别的282个微地震事件分别应用式（7）、式（10）和式（11）的成像函数进行定位，结果如图 7~图 9所示，大致能看出定位结果具有分层现象，符合压裂预期。

常规方法（式（7）和式（10）的成像函数）的定位结果（图 7和图 8）比较分散，尤其是第一段（上层）远离第一段射孔点位置，说明误差较大。而本文提出的式（11）优化波形叠加成像函数的定位结果（图 9）更加连续和聚集，分层现象明显，且均在对应射孔深度层段附近，表明其定位结果的可信度更高。因此，本文提出的优化波形叠加的微地震定位方法比常规方法更加可靠、有效。

4 结束语

波形叠加成像函数的分辨率低直接影响基于波形叠加的井中微地震定位方法的精度。本文改进了波形相似性加权振幅叠加的成像函数构造方法，提出了一种优化波形叠加的井中微地震定位方法，即：先将纵、横波波形相似性基函数相乘，再将其振幅叠加基函数相乘，然后将两个积相乘，最后沿整个时窗内对其求和。该方法提高了成像函数的分辨率。模型数据测试和实际微地震数据应用均表明，与常规方法相比，本文方法的定位结果精度更高，能够提供更可靠的定位结果。