0 引言

水力压裂是改善非常规储层物性、实现非常规油气资源有效开发的核心技术，其监测方法和技术已成为非常规资源开发领域的技术前沿热点和难点^[1]。微地震技术通过定位微地震事件及其震级、震矩、震源半径等信息圈定裂隙范围与主要方向，存在一定的局限性，如微震震源与压裂诱发的裂隙并不完全一致^[2]。电磁监测方法以压裂液与围岩的巨大激电特征差异为基础，改造后的储层会呈现低电阻率、高极化率特征，表现出明显的激发极化（Induced Polarization，IP）异常，相比地震方法具有更好的物性基础^[3]。大量的理论和实践研究证明了电磁探测可以有效捕捉深部水力压裂引起的电磁场特征变化^[4-7]。

以致密页岩储层为代表的非常规储层受定向排列的黏土矿物和微裂隙的影响，呈现各向异性特征^[8-9]。水力压裂容易在应力主轴上形成人工裂隙，与天然裂隙耦合、填充，包含支撑剂的压裂液进一步形成裂隙系统的电各向异性。电磁勘探尺度下，三维各向异性介质建模通常以实电阻率为基础^[10]。考虑复电阻率特征的电各向异性研究主要侧重于测井尺度的研究，通常分析的是频率大于100 Hz的介电极化特征^[11-13]。尽管地层压力容易使储层微裂隙闭合，降低储层电各向异性系数^[14]，但因储层孔隙流体连通性降低，支撑剂—流体界面会增强低频极化特征，故低频激电各向异性特征在深层裂隙介质中会更突出。

正确构建裂隙岩石激发极化特征与结构间的实验关系有利于结合实际压裂工程建立合理的三维各向异性激电模型。在低频（通常小于100 Hz）电磁场作用下，岩石矿物颗粒与孔隙流体界面构成双电层（EDL）结构，形成过电位、氧化还原等电化学过程，宏观上形成激发极化现象。Weller等^[15]认为高盐度条件下紧密层（Stern层）的极化强度主要受孔隙—矿物界面的影响。Niu等^[16]以孔隙空间为主体建立了POLARIS模型，认为Stern层的极化与扩散层的极化存在相关性，通过孔隙直径与孔喉直径估计了致密岩石的时间常数；Park等^[17]基于薄膜极化理论对裂隙砂岩展开了实验分析，认为极化率主要受短、窄孔结构的影响，而裂隙空间对其影响不显著。

非常规储层的致密性会导致压裂动态监测周期（压裂前后数小时）内压裂液主要沿裂隙空间延伸，压裂液流入裂隙空间的体积远大于渗流进基质的体积^[18]。人工裂隙与不同尺度天然孔隙的耦合是决定压裂质量的重要因素^[19]。由于压裂裂隙定向排列，与原始地层孔隙结构存在较大差异，宏观上采用裂隙—孔隙双重孔隙介质描述压裂后岩石的复杂孔隙特征，有利于研究储层中两种孔隙的电性差异^[20]。

本文针对五峰组致密页岩储层，结合压裂工程设计与压裂区块压裂液分布模式设计了复电阻率实验，目的是分析不同地层压力条件下压裂前、后激电各向异性、不同压裂液分布的激电特征，并基于双重孔隙介质建立了研究区电阻率模型，分析了孔隙—裂隙结构对储层电性特征的影响，为压裂监测正、反演提供理论基础与先验信息。

1 水力压裂页岩激电理论 1.1 双重孔隙介质

对页岩储层进行水力压裂后，人工裂隙与部分天然裂隙耦合形成裂隙系统，并与原始低渗透率微孔隙系统构成双重孔隙介质。宏观上可利用立方定律对双重孔隙介质（图 1）进行表征。每个单元由一个边长为$ U $的立方体构成，包含开度为$ \boldsymbol{b}=[{b}_{x}, {b}_{y}, {b}_{z}] $的三向裂隙，即裂隙孔隙度各向异性特征。实际地层中，裂隙系统与孔隙系统在结构上存在差异，因而也具有不同的流体饱和度，因此对岩石的电性影响也不同。

假设页岩层原始孔隙系统与压裂裂隙系统的孔隙度分别为$ {\varphi }_{\mathrm{p}} $和$ {\varphi }_{\mathrm{f}} $，若压裂裂隙与页岩的各向异性主轴一致，则双重孔隙介质沿主轴方向的电导率张量为

$ {\boldsymbol{\sigma }}_{0}=\left[\begin{array}{ccc}{\sigma }_{x}& & \\ & {\sigma }_{y}& \\ & & {\sigma }_{z}\end{array}\right]=\left[\begin{array}{ccc}{\sigma }_{\mathrm{p}x}+{\sigma }_{\mathrm{f}x}& & \\ & {\sigma }_{\mathrm{p}y}+{\sigma }_{\mathrm{f}y}& \\ & & {\sigma }_{\mathrm{p}z}+{\sigma }_{\mathrm{f}z}\end{array}\right] $

(1)

式中$ {\sigma }_{\mathrm{p}i} $与$ {\sigma }_{\mathrm{f}i} $分别表示$ i(i=x, y, z) $方向孔隙系统与裂隙系统的电导率。根据模型假设，压裂裂隙沿主轴方向张开，具有明确的空间分布，则沿测量方向裂隙与原始岩石形成并联关系，是影响裂隙电导率的主要因素，在孔隙系统与裂隙系统弱耦合的假设下，两者具有可叠加性。孔隙电导率与裂隙电导率分别满足阿尔奇关系

$ \left\{\begin{array}{l}{\sigma }_{\mathrm{p}i}={\sigma }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{\varphi }_{\mathrm{p}}^{{m}_{\mathrm{p}i}}{I}_{\mathrm{p}i}={\sigma }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{\varphi }_{\mathrm{p}}^{{m}_{\mathrm{p}i}}{s}^{{n}_{\mathrm{p}i}}\\ {\sigma }_{\mathrm{f}i}={\sigma }_{\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{i}\mathrm{d}}{\varphi }_{\mathrm{f}}^{{m}_{\mathrm{f}i}}\end{array}\right. $

(2)

式中：$ {\sigma }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}} $与$ {\sigma }_{\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{i}\mathrm{d}} $分别表示地层水与裂隙流体（压裂液）的电导率；$ {I}_{\mathrm{p}i}={s}^{{n}_{\mathrm{p}i}} $为地层孔隙的电阻率指数，这里$ s $为孔隙系统的地层水饱和度；$ {m}_{\mathrm{p}i}\mathrm{、}{n}_{\mathrm{p}i}\mathrm{、}{m}_{\mathrm{f}i} $分别为i方向的孔隙系统胶结指数、孔隙系统地层水饱和度指数及裂隙系统胶结指数。由于裂隙系统由压裂液填充，因而流体饱和度为100%。黏土、金属等低阻矿物在特定方向的连续性也会影响该方向的实际电导率，因而实际地层的$ {m}_{\mathrm{p}i} $在不同方向存在差异。由于页岩黏土等低阻矿物的分布与地层宏观电各向异性的方向具有一致性，本文模型不单独考虑黏土及金属矿物对电导率的直接影响，而是通过调整$ {m}_{\mathrm{p}i} $间接表征这一影响。$ {m}_{\mathrm{p}i} $通常取值2，若连通性较好，$ {m}_{\mathrm{p}i} $取值可小于2。裂隙电导率与裂隙开度b的关系可以表示为

$ {\sigma }_{\mathrm{f}i}=\frac{{\sigma }_{fluid}(B-{b}_{i})}{S}=\frac{{\sigma }_{fluid}{\varphi }_{f}(B-{b}_{i})}{{b}_{x}+{b}_{y}+{b}_{z}} $

(3)

其中B=b_x+b_y+b_z。

当裂隙仅沿或主要沿i方向发育时，对比式（2）与式（3）可知$ {m}_{\mathrm{f}i}\approx 1 $。实际岩石通常无法满足裂隙与原始孔隙弱耦合的假设。岩石经压裂后，原始孔隙的连通性会增强，$ {m}_{\mathrm{p}i} $将降低；同时，裂隙发育的随机性也使$ {m}_{\mathrm{f}i} $增大。

孔隙系统的$ {n}_{\mathrm{p}i} $会受地层水分布影响。对页岩气自生自储的页岩层，地层水分布较均匀，因此通常取$ {n}_{\mathrm{p}i}\approx 2 $。由于页岩层基本满足横向各向同性假设，因此式（1）满足$ {\sigma }_{x}={\sigma }_{y}={\sigma }_{\mathrm{H}} $，$ {\sigma }_{z}={\sigma }_{\mathrm{V}} $，其中$ {\sigma }_{\mathrm{H}}\mathrm{、}{\sigma }_{\mathrm{V}} $分别表示横向和纵向的电导率。

理想情况下，水力压裂监测期间，由于压裂液具有低电阻率—高极化率特征，致密岩石具有低孔、低渗特征，相比微孔隙系统，裂隙系统是影响激电特征与渗流特征的主体。由式（2）可知，当裂隙张开导致$ {\varphi }_{\mathrm{f}} $增大时，或裂隙方向与测量方向一致性较高时，或压裂液电导率较高时，裂隙系统对电导率的增大起主要作用。因此，若$ {\sigma }_{\mathrm{f}i}\gg {\sigma }_{\mathrm{p}i} $，可仅考虑裂隙系统引起的电导率变化。

1.2 裂隙岩石的激电特征

天然岩石的电导率不仅受孔隙流体的影响，还与流体与岩石矿物的界面成分（如黏土、金属、高阻矿物等）有关。流体—矿物界面形成的EDL结构会形成岩石的复电导率

$ {\sigma }_{\mathrm{p}}^{\mathrm{*}}={\sigma }_{\mathrm{p}}^{}+{\sigma }_{\mathrm{s}\mathrm{p}}^{\mathrm{*}} $

(4)

式中$ {\sigma }_{\mathrm{s}\mathrm{p}}^{\mathrm{*}} $表示孔隙流体与矿物界面形成的面复电导率，包含实部与虚部两个部分，具有明显的频散特征。考虑到深部地层水与压裂液具有高电导率特征，可忽略EDL结构中扩散层离子浓度的变化，仅考虑Stern层离子浓度变化对EDL极化特征的影响。在谐变外电场作用下，单电荷离子对半径为$ A $的球状孔隙模型所形成的复电导率为

$ {\sigma }_{\mathrm{s}\mathrm{p}}^{\mathrm{*}}\left(\omega \right)=\frac{\mathrm{i}\omega {\tau }_{\mathrm{s}}}{1+\mathrm{i}\omega {\tau }_{\mathrm{s}}}\frac{{e}^{2}{Q}_{\mathrm{s}}{D}_{(+)}^{\mathrm{s}}R}{TN} $

(5)

式中：$ e\mathrm{、}T\mathrm{、}R\mathrm{、}N $分别表示单位电荷量（$ 1.6\times {10}^{-19}\mathrm{C} $）、温度、阿伏伽德罗常数（$ 6.02\times {10}^{23}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1} $）和理想气体常数（$ 8.3145\mathrm{J}\cdot {\mathrm{K}}^{-1}\cdot \mathrm{m}\mathrm{o}{\mathrm{l}}^{-1} $）；$ {D}_{(+)}^{\mathrm{s}} $为Stern层的阳离子扩散系数；$ \omega $为谐变电场的圆频率；$ {\tau }_{\mathrm{s}}={A}^{2}/2{D}_{(+)}^{\mathrm{s}} $为极化时间常数；$ {Q}_{\mathrm{s}} $为矿物与孔隙流体界面的电荷面密度，其值与界面矿物和孔隙流体的性质有关。结合式（4）与式（5）可知，在高频极限时，岩石的导电性主要源于界面的导电性，此时黏土、金属矿物等的导电作用不可忽略；在低频极限时，界面电导率趋于0，岩石的电导率仅决定于孔隙流体。

岩石裂隙结构与孔隙结构具有相似的复电导率理论基础，但存在如下差异：①在空间尺度上存在较大的差异，水力压裂形成的裂隙尺度更大，其时间常数通常大于孔隙结构的时间常数。②孔隙一般均匀分布在岩体内，引起极化的流体—矿物界面与岩石整体相关；而压裂裂隙面由脆性矿物及天然裂隙结构决定，引起的极化特征与压裂液滤失程度有关，流体—矿物界面主要由宏观裂隙面决定。③裂隙系统中，压裂液通常携带均匀性较高的支撑剂颗粒，因此压裂液本身的流体—支撑剂界面引起的极化效应会与裂隙界面的极化效应发生耦合。

1.3 压裂区块压裂液分布模型

压裂完成后，压裂液在目的层的分布直接决定压裂目的层的激电特征。换言之，根据压裂后目的层的激电特征也可分析压裂液的走向与分布，实现压裂质量评价。

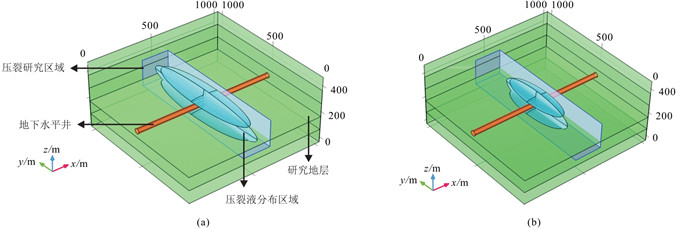
考虑页岩层水平井压裂的情形，分析压裂液返排完成时的裂隙分布。图 2是两种典型的压裂情况。对图 2所示的蓝色立方体区域进行压裂质量评价。充分压裂的裂隙及压裂液均匀分布在压裂区域（图 2a），欠压裂的裂隙分布于水平井附近（图 2b），压裂液集中在滤失严重的局部地区。滤失严重时，人工裂隙延伸空间有限，与天然裂隙耦合程度低，形成的有效裂隙比面小，使得压裂后研究区域激电特征变化不显著。

压裂液内支撑剂的分布同样对裂隙开度存在一定影响。通常压裂过程中支撑剂会首先在裂隙前段积累并逐渐饱和，达到临界状态后裂隙会进一步张开，为支撑剂提供更大的空间，即使在返排量相同的情况下，返排过程中支撑剂回流的充分程度也会影响压裂结束时的最终裂隙开度^[21]。

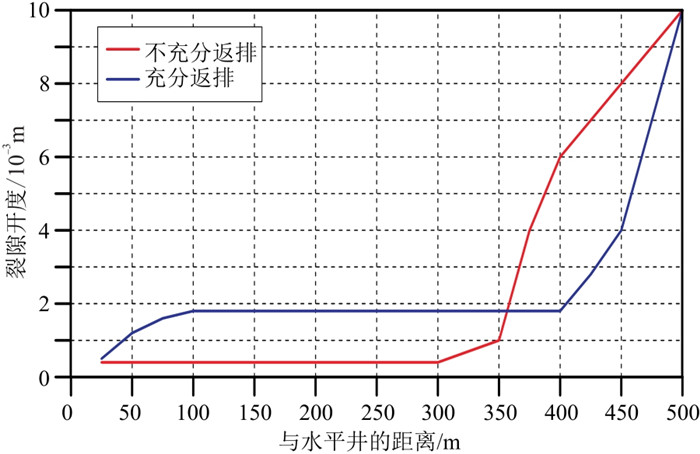
图 3为压裂区块y轴方向不同支撑剂分布对应的裂隙开度。支撑剂回流充分可增大有效裂隙开度，提供更强的渗透能力。若支撑剂回流不充分，在裂隙前端会形成较大的裂隙开度。返排完成后，缺少支撑剂的裂隙容易闭合，降低有效渗透能力。这两种情况下，由于裂隙开度差异及支撑剂分布不同，激电特征出现了较大的差异。

受天然裂隙、断层、岩性变化、地应力等因素的影响，实际地层中的人工裂隙通常具有一定的不对称性^[22]，导致压裂液分布偏离设计位置。结合研究区块的页岩电性实验，分析页岩压裂前后、支撑剂作用下的激电机制及激电参数特征，可有效表征不同压裂液滤失程度、不同支撑剂空间分布条件下上述不同情况下压裂区块的激电差异，为基于电磁勘探的压裂监测技术提供理论依据。

2 页岩激电实验设计 2.1 样品基本信息

对中国西南地区X工区的24块页岩气储层样品进行实验测试，分析研究不同条件下储层页岩的激电特征。样品采自下志留系五峰组地层，埋深约2500 m。样品采样分为纵向（V向）采样与横向（H向）采样，便于分析储层各向异性特征。样品基本信息见表 1。孔渗测试环境为约5 MPa，测量方式为氦气法，其中压裂后孔隙度增长主要为裂隙。渗透率测试表明，除52H与53H两块岩样由于测量方向裂隙发育呈大渗透率（> 1 mD），其余样品基本满足页岩低孔、低渗特征。

2.2 实验设备与原理

测试采用AutoLab1000高温、高压岩石物理实验系统，对岩石进行四极测量，在设定的温度、围压、孔压条件下，获取岩石阻抗信息。测试系统及岩石夹持器见图 4。测试频段为10^-2~10⁴ Hz，该频段包含了电磁勘探方法可观测频散范围。

岩石的阻抗可根据岩石的尺寸信息转换为复电阻率$ {\rho }^{\mathrm{*}}\left(\omega \right) $。实验分析采用复电导率，即复电阻率的倒数

$ {\sigma }^{\mathrm{*}}\left(\omega \right)={\sigma }_{\mathrm{R}}+\mathrm{i}{\sigma }_{\mathrm{I}}=\frac{1}{{\rho }^{\mathrm{*}}\left(\omega \right)}=\frac{{\rho }_{\mathrm{R}}-\mathrm{i}{\rho }_{\mathrm{I}}}{{\rho }_{\mathrm{R}}^{{}^{2}}+{\rho }_{\mathrm{I}}^{2}} $

(6)

式中$ {\sigma }_{\mathrm{R}} $、$ {\sigma }_{\mathrm{I}} $、$ {\rho }_{\mathrm{R}} $、$ {\rho }_{\mathrm{I}} $分别表示复电导率$ \sigma \left(\omega \right) $和复电阻率$ \rho \left(\omega \right) $的实部和虚部。

测试样品的复电阻率满足谱得拜模型的离散形式

$ \rho \left(\omega \right)={\rho }_{0}\left[1-\sum\limits _{k=1}^{N}{\eta }_{k}\left(1-\frac{1}{1+\mathrm{i}\omega {\tau }_{k}}\right)\right] $

(7)

式中：$ {\rho }_{0} $表示样品的真电阻率；N为观测频段按照对数等间距取值的总频点数；$ {\tau }_{k} $为第k个频点的时间常数；$ {\eta }_{k} $为第k个频点的极化率。观测频段内模型的IP参数包括：真电阻率$ {\rho }_{0} $，极化率$ \eta =\sum\limits _{k=1}^{N}{\eta }_{k} $，时间常数$ \tau =\mathrm{e}\mathrm{x}\mathrm{p}\left[\sum\limits _{k=1}^{N}({\eta }_{k}·\mathrm{l}\mathrm{n}{\tau }_{k})/\sum\limits _{k=1}^{N}{\eta }_{k}\right] $。这些参数可采用得拜分解参数估计方法^[23]计算。

2.3 实验设计

测试环境采用浓度为5%的NaCl饱和溶液，饱和方式通过真空加压实现。测试过程主要分析产生的裂隙空间对岩石电性的影响，因此测试环境为常温30℃。

不同饱和度状态可通过加压饱和后干燥实现。针对压裂后样品，这种干燥方式会首先降低裂隙饱和度，因而饱和度实验主要针对原始孔隙进行分析，尽量满足式（2）中关于饱和度相关参数的估计条件。饱和度的计算也考虑了压裂前孔隙度对应的孔隙空间的质量。

压裂采用MTS815型岩石三轴刚性压缩试验机，设备压力可达到140 MPa。采用单轴压裂，对岩石外柱面进行施压，页岩样品压裂发生在3~8 MPa压力环境下。为保证页岩样品压裂后仍能进行实验测试，测试端出现显著纹裂时停止压裂，图 5为压裂后样品测试面的典型裂隙形态。

岩石激电测试分为三阶段：①压裂前多饱和度样品测试；②压裂后多饱和度样品测试；③压裂后添加支撑剂测试，目的是分析不同压裂状态及支撑剂分布条件下的岩石激电特征。阶段③设置不同的压力环境及支撑剂类型和含量，其中添加支撑剂实验仅在全饱和条件下进行，支撑剂采用20~40目粗陶粒。支撑剂及填充裂隙后样品见图 6，可见页岩由于黏土层的定向排布，压裂后裂隙容易沿粘土层分布张开。图 6b与图 6c为两种典型的裂隙发育状态，裂隙发育直接贯穿岩石，支撑剂可以直接从断面填充进入。测试条件具体见表 2。

3 实验结果分析与讨论

页岩激电特征分析均针对全饱和样品，不同饱和度测试条件主要用于基于式（2）的裂隙孔隙介质建模饱和度相关参数估计。

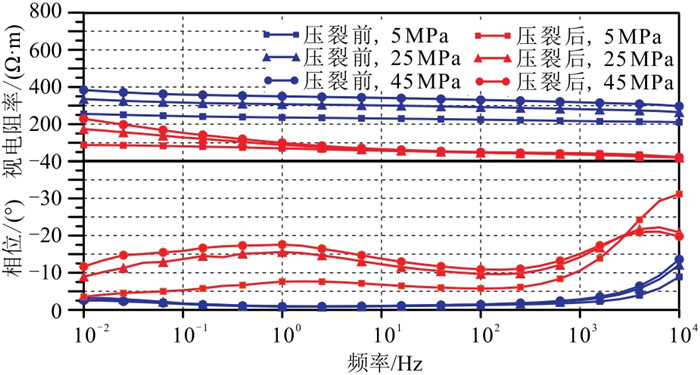
3.1 页岩样品激电特征 3.1.1 压裂前、后裂隙压力特征

图 7为典型的页岩样品压裂前、后不同压力状态下的复电阻率曲线。可见压裂后岩石的视电阻率显著下降，同时相位整体升高，这是由于压裂形成的裂隙空间提高了岩石的导电性，同时新通道与原始岩石孔隙形成了大量的导电界面。由于界面电导的频散特征，岩石极化现象显著。

不同压力条件下，岩石孔隙和裂隙会出现不同程度的压缩，引起部分有效电导通道关闭，降低了岩石电导率，同时也使得导电通道更复杂，界面的电导作用更突出，进一步增强了极化现象。

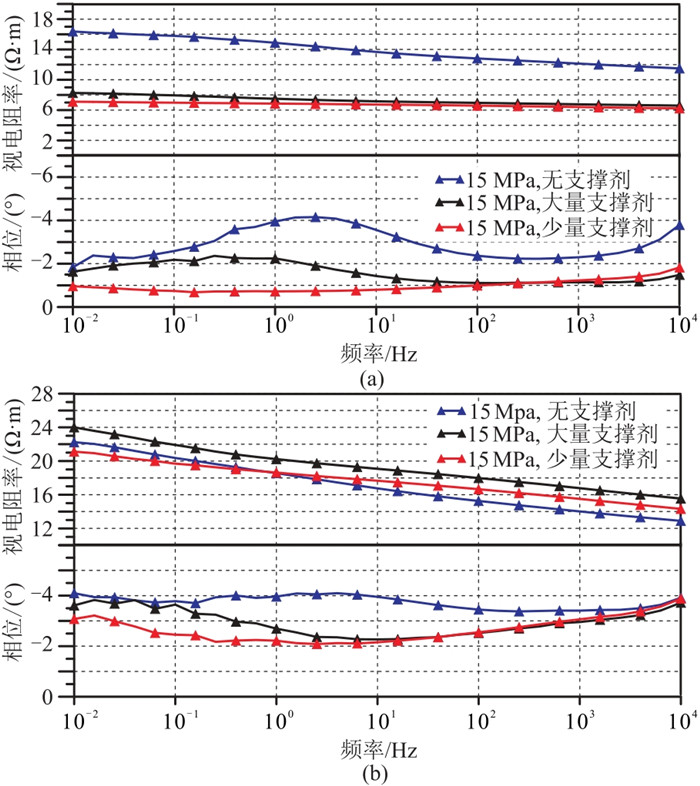
3.1.2 压裂后支撑剂的作用

图 8为页岩样品添加了不同量的支撑剂后的复电阻率曲线。

图 8a为样品沿测量方向填充支撑剂前后的复电阻率曲线。沿测量方向填充少量支撑剂会直接增大测量方向的裂隙开度，表现为电阻率降低。裂隙面不变的情况裂隙空间增大，界面电导占比下降，进而引起极化率降低。随着支撑剂含量增加，部分流体空间被支撑剂替代，电阻率变化不再明显，相位幅度增大，这主要是由于支撑剂颗粒与流体界面形成了新的界面，界面电导增强了低频极化效应。

图 8b为支撑剂沿测量垂向填充的复电阻率曲线。沿测量垂直方向填充少量支撑剂后，垂向裂隙开度增大，增大的流体空间与原样品孔隙空间在测量方向可视作串联关系，使得岩石高频电阻率增大；岩石相位也有降低的趋势，相位峰值向低频移动，这是由于支撑剂颗粒使得裂隙张开，裂隙空间尺度逐渐增大，进而增大了时间常数。随着支撑剂含量进一步增加，支撑剂颗粒形成的极化界面逐渐增多，同时支撑剂颗粒尺度介于原始孔隙与张开的裂隙之间。因此，大量支撑剂填充后相位峰值介于少量支撑剂与无支撑剂的情形之间。

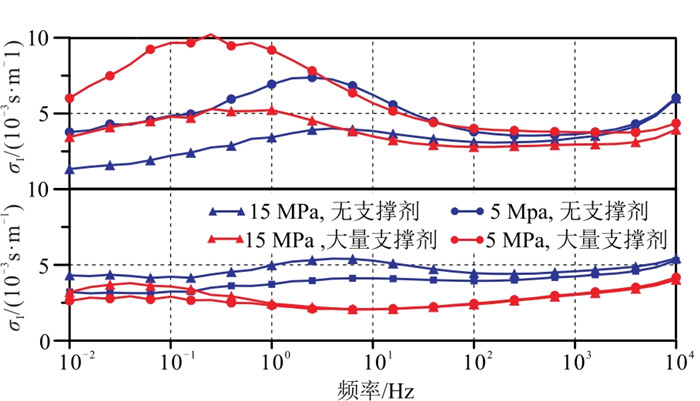
图 9为不同压力条件沿不同方向填充支撑剂前后的电导率虚部，可以更显著地观测到支撑剂界面呈现电导作用所对应的主要频段。图 9（上）为沿测量方向样品填充支撑剂前后电导率虚部。可见支撑剂与溶液耦合形成的界面在小于10 Hz的低频部分，其电导曲线逐渐凸显，此时界面电导与岩石电导呈现并联关系；在小于1 Hz的频段内，支撑剂界面电导强度达到峰值。图 9（下）为沿垂直测量方向样品填充支撑剂前、后的电导率虚部，支撑剂与压裂液耦合形成的界面电导与岩石电导呈串联关系，在大于0.1 Hz的频段内岩石界面电导率出现降低趋势。

实际上，岩石内支撑剂主要分布在开度较大的主裂隙中，支撑剂分布方向具有一定的随机性。支撑剂一方面有增大流体空间、降低岩石电阻率的作用，另一方面与溶液耦合，会增强低频界面的电导率、降低高频界面的电导率。因此，填充支撑剂的裂隙岩石电阻率会下降，极化强度也会下降，但时间常数会显著增大。

3.1.3 电各向异性特征

尽管同一深度有H向与V向两块样品，但考虑到单一样品的随机性较强，页岩各向异性特征可通过式（7）估计IP参数进行统计分析。IP参数各向异性系数定义为$ {\chi }_{w}={w}_{\mathrm{V}}/{w}_{\mathrm{H}} $，其中w可以是真电阻率$ {\rho }_{0} $、极化率$ \eta $或时间常数$ \tau $。

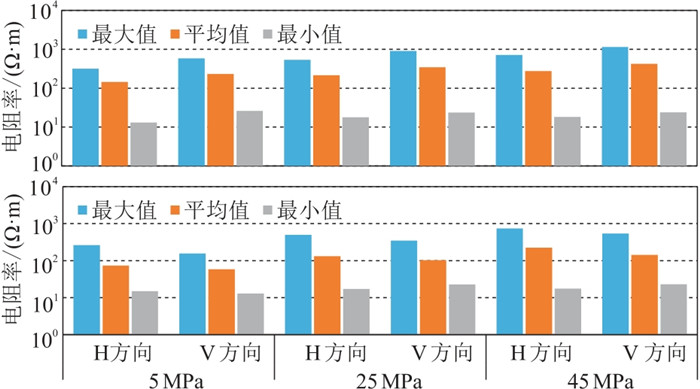
图 10为不同压力环境下压裂前、后各向异性电阻率统计结果。可见压裂后平均电阻率约为压裂前平均电阻率的0.4倍，压裂带来了较大的电阻率变化。压裂前、后真电阻率各向异性系数$ {\chi }_{{\rho }_{0}} $在不同压力环境下均呈现下降趋势，但差异不明显：压裂前$ {\chi }_{{\rho }_{0}} $平均值为1.58，压裂后$ {\chi }_{{\rho }_{0}} $平均值为0.74，这主要是由于H向样品压裂前、后孔隙度平均值变化幅度（约0.2%）比V向样品平均值变化幅度（约0.8%）低。这种情况下孔隙度的变化主要是裂隙引起的，裂隙的导电能力强，因此V向样品的电阻率下降更明显。

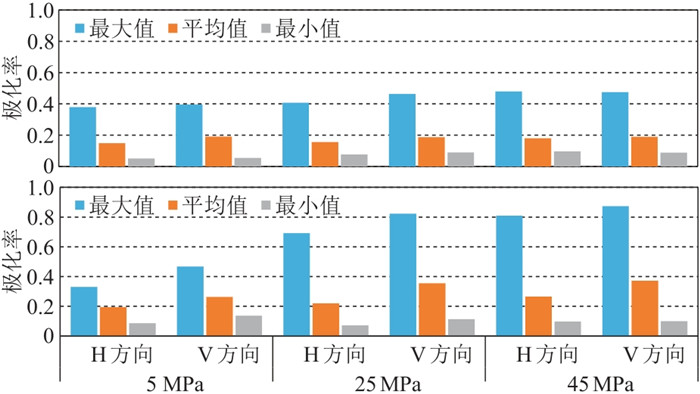
图 11为不同压力条件下压裂前、后各向异性极化率统计结果，可见压裂后平均极化率为压前平均极化率的约1.6倍，压裂后岩石极化率均有显著提高。压裂前、后$ {\chi }_{\eta } $平均值分别为1.17、1.45，表明压裂前页岩孔隙的方向性并不明显；压裂后V向样品垂直测量方向裂隙发育显著，使得极化率明显增大，平均增量大于15%，而H方向样品极化率增量较小，表明V方向裂隙发育较少。因此，样品压裂后H方向的裂隙发育多于V方向。

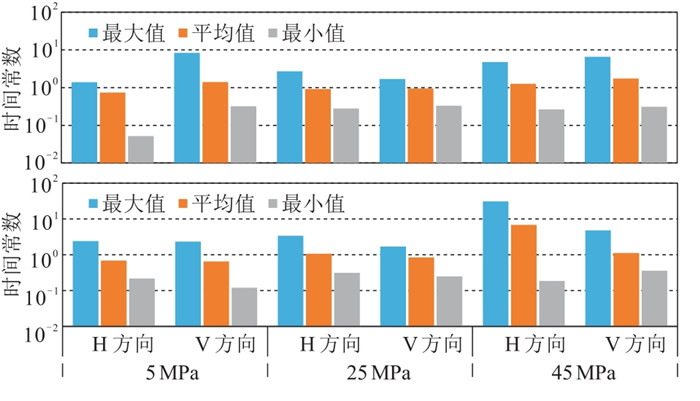
图 12为不同压力下压裂前、后各向异性时间常数$ {\chi }_{\tau } $统计结果。受裂隙发育随机性的影响，$ {\chi }_{\tau } $分布范围较大。压裂后样品的平均$ {\chi }_{\tau } $约为压前的1.6倍，表明压裂后样品整体上具有更高的时间常数。压裂后$ {\chi }_{\tau } $从压裂前的1.40下降到0.63，压裂后H向样品的$ {\chi }_{\tau } $增加更显著，表明沿测量方向的裂隙张开更有利于等效孔隙半径的增大，导致时间常数增大。

3.2 裂隙—孔隙介质建模

结合双重孔隙介质模型与表 1中实验测量的压裂前、后孔隙度，对压裂前、后5 MPa压力下的H向与V向页岩真电阻率进行电性建模，并在完全饱和状态下确定地层因子，再针对不同饱和状态计算电阻率指数。

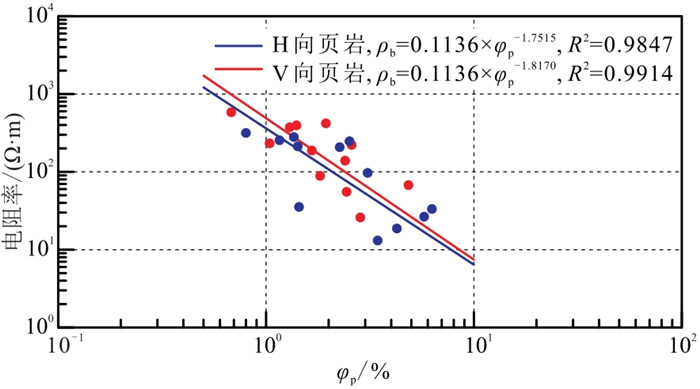
3.2.1 压裂前真电阻率模型

根据式（2），压裂前样品仅存在原始孔隙，符合阿尔奇关系，结合5 MPa压力下测量的压裂前复电阻率数据建模（图 13）。饱和盐水下的H向与V向压裂前真电阻率模型分别为

$ {\rho }_{\mathrm{b}\mathrm{H}}=\frac{1}{{\sigma }_{pH}}={\rho }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{\varphi }_{\mathrm{p}}^{-{m}_{\mathrm{p}\mathrm{H}}}=\frac{0.1136}{{{\varphi }_{p}}^{1.7515}} $

(8)

$ {\rho }_{\mathrm{b}\mathrm{V}}=\frac{1}{{\sigma }_{pV}}={\rho }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{\varphi }_{\mathrm{p}}^{-{m}_{\mathrm{p}\mathrm{V}}}=\frac{0.1136}{{{\varphi }_{p}}^{1.8170}} $

(9)

式中$ {\rho }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=0.1136\begin{array}{c}\Omega ·m\end{array} $是饱和盐水在30℃条件下的电阻率。模型中V向页岩具有更高的胶结指数，也表明V向页岩具有更复杂的导电通道。

3.2.2 压裂后真电阻率模型

由图 10可知，裂隙结构会显著提高岩石的导电能力。结合表 1可知，12对样品的平均原始孔隙度为2.45%，压裂后新增裂隙的平均孔隙度为0.51%，平均电导率从0.01555 S/m增至0.03035 S/m。单位原始孔隙电导率为0.6357 S/m，压裂后增至2.9183 S/m，意味着压裂前、后岩石的导电性差异较大。因此，可结合双重孔隙介质模型对压裂后的岩石进行真电阻率建模。假设压裂前、后的孔隙度差值为裂隙孔隙度$ {\varphi }_{\mathrm{f}} $（实际孔隙度差值可能还包含由少量封闭的原始孔隙引起的孔隙度变化，可忽略），根据页岩横向各向同性，基于式（3）并结合开度各向异性系数$ {\chi }_{\boldsymbol{b}} $与孔隙度，可以有效估计裂隙胶结因子。

根据压裂过程停止标准，认为H向与V向样品压裂后在测量方向的开度相同，结合平均孔隙度可估计开度各向异性系数$ {\chi }_{\boldsymbol{b}}={b}_{\mathrm{V}}/{b}_{\mathrm{H}}\approx 0.435 $，对H向与V向进行裂隙孔隙度建模，可得裂隙胶结系数分别为

$ \begin{aligned} \varphi_{\mathrm{fH}}^{m_{\mathrm{H}}} & =\frac{\varphi_{\mathrm{fH}}\left(b_{\mathrm{H}}+b_{\mathrm{V}}\right)}{b_{\mathrm{H}}+b_{\mathrm{H}}+b_{\mathrm{V}}} \\ & =\frac{\varphi_{\mathrm{fH}}\left(1+\chi_b\right)}{1+1+\chi_b} \\ & =(0.2 \%)^{1.1432} \end{aligned}$

(10)

$\begin{aligned} \varphi_{\mathrm{fV}}^{m_{\mathrm{N}}} & =\frac{\varphi_{\mathrm{fV}}\left(b_{\mathrm{H}}+b_{\mathrm{H}}\right)}{b_{\mathrm{H}}+b_{\mathrm{H}}+b_{\mathrm{V}}} \\ & =\frac{\varphi_{\mathrm{fV}}(1+1)}{1+1+\chi_b} \\ & =(0.8 \%)^{1.3567} \end{aligned}$

(11)

将$ {m}_{\mathrm{f}\mathrm{H}} $和$ {m}_{\mathrm{f}\mathrm{V}} $代入式（2），结合原始孔隙度及5 MPa压力下测得的压裂后复电阻率数据，可得饱和溶液下页岩压裂后的H向与V向真电阻率ρ模型为

$\begin{aligned} \rho_{\mathrm{aH}} & =\frac{\rho_{\mathrm{water}}}{\varphi_{\mathrm{p}}^{m_{\mathrm{pH}}}+\varphi_{\mathrm{f}}^{m_{\mathrm{HH}}}} \\ & =\frac{0.1136}{\varphi_{\mathrm{p}}^{1.6556}+\varphi_{\mathrm{f}}^{1.1432}} \end{aligned}$

(12)

$ \begin{aligned} \rho_{\mathrm{aV}} & =\frac{\rho_{\text {water }}}{\varphi_{\mathrm{p}}^{m_{\mathrm{pV}}}+\varphi_{\mathrm{f}}^{m_N}} \\ & =\frac{0.1136}{\varphi_{\mathrm{p}}^{1.5662}+\varphi_{\mathrm{f}}^{1.3567}} \end{aligned} $

(13)

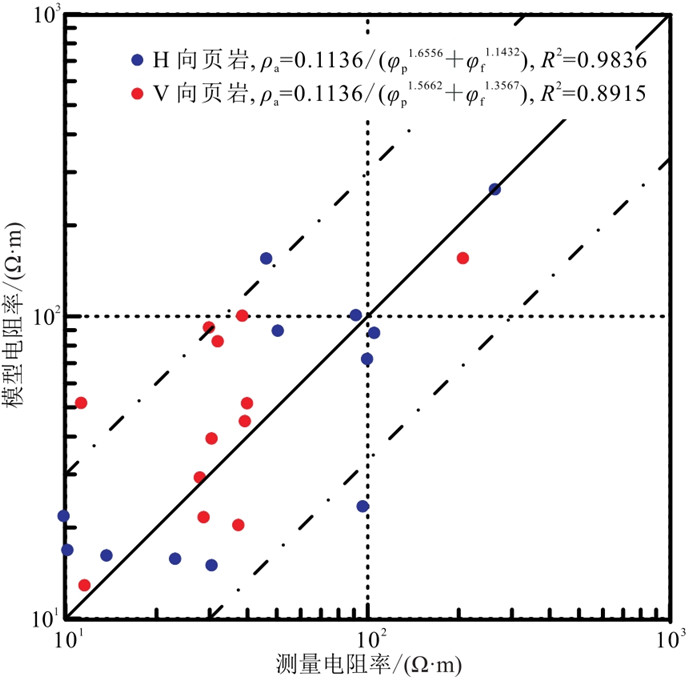
图 14为基于式（12）和式（13）的模型电阻率与真电阻率测量值的对比，模型结果约束在3倍以内。

对比式（12）与式（13），裂隙胶结指数显著低于孔隙胶结指数，表明裂隙系统具有更有效的导电性；与压裂前模型（式（8）和式（9））相比，原始孔隙度的胶结指数也有一定下降，H向与V向分别下降了约0.10和0.25，表明裂隙在形成电导的同时，进一步改善了原始孔隙的连通性，增强了岩石的整体导电能力。

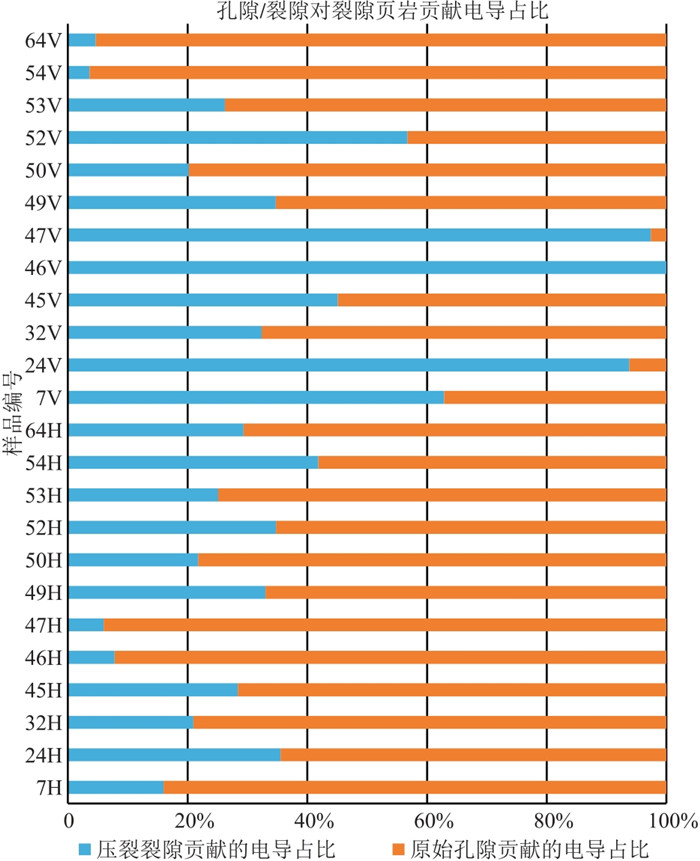
图 15为基于式（12）与式（13）计算的压裂后岩石原始孔隙与压裂裂隙对岩石电导的贡献占比。H方向与V方向中压裂裂隙电导占比分别为25.04%与48.14%。虽然压裂裂隙可以形成较强导电性，但若压裂裂隙的孔隙度远低于原始孔隙的孔隙度，前者亦不能成为页岩导电的主要因素。

3.2.3 考虑饱和度的真电阻率模型

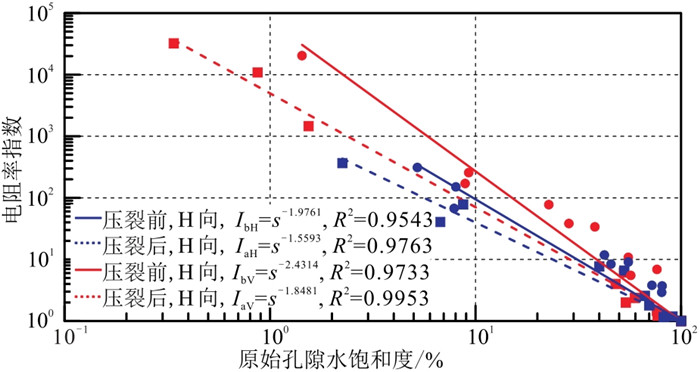
前文中压裂前、后原始孔隙度地层水完全饱和条件下的真电阻率模型（式（8）、式（9）、式（12）、式（13））未考虑原始孔隙含水饱和度的影响。基于压裂前、后饱和度实验建立H和V方向的电阻率指数$ I $与原始孔隙含水饱和度S的实验关系，估计式（2）中的饱和度指数$ {n}_{\mathrm{p}i} $。压裂后采用干燥后充水的饱和方式，由于裂隙空间与外部空间连通性强，流体首先高效饱和裂隙空间，然后逐渐饱和孔隙空间。因此，计算原始孔隙空间的饱和度时去除了裂隙空间饱和的影响。图 16为页岩压裂前、后两种方向岩样实验关系及拟合结果。

由图 16可见，压裂前H向与V向原始孔隙饱和度指数分别为1.9761和2.4314，V向岩石具有更高的饱和度指数，这是由于H向样品的粘土连通性更好，V向样品的导电主要依赖于孔隙流体，较低的水饱和度会导致较弱的导电能力；压裂后H向与V向原始孔隙饱和度指数均出现降低特征，分别为1.5593和1.8481。与地层因子胶结指数的降低机理相似，裂隙的产生使得原始孔隙结构的连通性增强，同时孔隙水的连通性也会因为裂隙流体的滤失（压裂液进入原始孔隙）得到进一步提高。对于压裂前、后完全饱和真电阻率模型，压裂前、后H向与V向真电阻率模型为

$ \left\{\begin{array}{l}{\rho }_{\mathrm{b}\mathrm{H}}={\rho }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{\varphi }_{\mathrm{p}}^{-1.7515}{s}^{-1.9761}\\ {\rho }_{\mathrm{b}\mathrm{V}}={\rho }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{\varphi }_{\mathrm{p}}^{-1.8170}{s}^{-2.4314}\\ {\rho }_{\mathrm{a}\mathrm{H}}=\frac{{\rho }_{water}}{{\varphi }_{p}^{1.6556}{s}^{1.5593}+{\varphi }_{f}^{1.1432}}\\ {\rho }_{\mathrm{a}\mathrm{V}}=\frac{{\rho }_{water}}{{\varphi }_{p}^{1.5662}{s}^{1.8481}+{\varphi }_{f}^{1.3567}}\end{array}\right. $

(14)

真电阻率模型有助于在更大的孔隙度和含水饱和度变化范围内分析测区页岩的电阻率理论关系，有利于对资料匮乏地区进行地层环境理论分析。

3.2.4 关于压裂工程中激电特征的讨论

实际压裂工程中，注入地下的压裂液作用于压裂区域时，其等效压裂空间具有更低的孔隙度，例如：将2000 t压裂液注入600 m×600 m×100 m的压裂空间，压裂液体积占比仅约0.005556%，这会进一步降低压裂裂隙本身对地层导电能力的影响。根据模型分析可知，压裂裂隙对原始孔隙连通性的改造才是压裂地层电导率上升（电阻率下降）的主要原因。

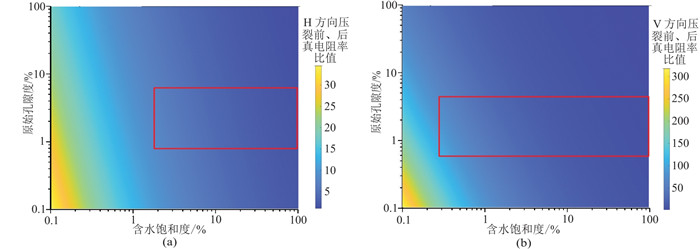
图 17为基于式（14）计算两种方向页岩压裂前与压裂后模型真电阻率的比值，图中红框为实测样品的参数变化范围。若不考虑支撑剂，孔隙度和含水饱和度越低（即含油气饱和度越高），压裂后真电阻率的变化越大。在相同的地层环境下，V方向电阻率变化明显大于H方向。若考虑到支撑剂的影响，H向电阻率会下降，有利于降低V方向与H方向的电阻率比值。

页岩中连通黏土对实际地层的导电性有一定影响，会降低原始孔隙及裂隙流体的导电性。因此，在低黏土、低孔隙度环境下（如花岗岩地热储层），在相同的压裂条件下，会观察到更大的电性变化。

4 结论

本文结合双重孔隙介质模型与储层页岩压裂前、后的复电阻率实验对水力压裂裂隙岩石在不同压力、各向异性、填充支撑剂等环境下的激电特征进行了分析和研究，为基于电磁技术的压裂监测提供正演理论与实验基础，为反演解释提供约束先验信息。

（1）页岩压裂后，电阻率会降低，极化率则显著增大，时间常数有增大的趋势。裂隙样品添加支撑剂后，岩石电阻率变化与支撑剂填充的裂隙方向有显著关系：支撑剂填充方向与测量方向一致时，电阻率显著降低；二者方向不一致时，电阻率变化不明显。

（2）根据统计分析，原始页岩电各向异性特征明显，压裂后电阻率各向异性下降，但极化率各向异性显著增强。

（3）基于双重孔隙介质模型建立的真电阻率模型有利于拓展测区样品孔隙度与水饱和度范围。建立的模型表明压裂裂隙流体的胶结指数较原始孔隙小，具有更强的导电能力。

（4）结合压裂设计可知，压裂岩石电阻率降低的主要因素是压裂裂隙对原始孔隙连通性的改造。由测区样品压裂前、后的真电阻率模型可知，压裂前原始孔隙度越低、含水饱和度越低，压裂后电阻率变化越大；V方向真电阻率的变化程度大于H方向。