2. 北京理工大学长三角研究院, 浙江嘉兴 314019;
3. 浙江大学先进技术研究院, 浙江杭州 310027
2. Yangtze River Research Institute of Beijing Institute of Technology, Jiaxing, Zhejiang 314019, China;
3. Institute of Advanced Technology, Zhejiang University, Hangzhou, Zhejiang 310027, China
在海洋勘探中,由于海水面和海底两个强波阻抗界面的存在,海洋地震数据普遍发育能量强的多次反射波。在常规的地震资料处理中,多次波在地震剖面上表现为构造假象,且与真实构造难以有效区分,这影响了解释人员对地下真实情况的判断,尤其是微幅度构造下的储层更易受多次波假象干扰。所以长期以来多次波一直被视为噪声,需尽可能地从地震数据中压制,以免在地震资料解释中造成误解[1-6]。事实上,多次波与一次波一样也是反射信号,它携带了丰富的地层信息。在逆掩构造和高速盐丘等复杂地质背景下,一次波经常由于照明不足出现成像阴影区,而多次波却能通过多次反射“照射”到一次波难以触及的地方。此外,多次波较小的入射角使其具有更高的垂向分辨率[7-8]。一次波虽然是地震数据的主体,但多次波所携带的信息对于地震成像的帮助也是不容忽视的。完整的地震成像应该是全波场(一次波、表面多次波和层间多次波)的贡献。为获得全面准确的地下信息,全波场成像是地震资料处理技术发展的必然趋势。
野外采集的陆地资料相对复杂,一般包含直达波、面波、折射波、绕射波、一次波和多次波等,所以陆地资料的全波场成像非常困难。海洋地震资料不受近地表的影响,具有较高的信噪比,发育的波场主要是一次波和多次波,因此就全波场成像研究而言,海洋地震资料具有优越的数据基础。对于海洋深水地震资料,根据实现方法的不同,利用多次波成像方法主要有四类。
第一类是高阶多次波转化为一次波后的偏移成像。该类方法的主要思想是将高阶多次波降阶为一次反射波,再利用现有的一次波成像技术。Wapenaar等[9]基于地震波干涉理论,将共炮点道集内的各道互相关生成虚拟炮记录,在相同位置叠加后将多次反射波转变为一次反射波,再按照一次波偏移算法成像[10]。利用聚焦变换策略[11],将原始地震记录的反射波能量聚焦到零时间点,可实现高阶多次波向低阶多次波的转变[12]。单国健[13]通过互相关技术将多次波转化为准一次波,再以一次波地表接收点为准震源对准一次波进行偏移成像。
第二类方法是全波场的直接偏移成像。这类技术与面炮偏移相似[14],将多个检波器接收到的多次反射波认为是多个震源同时激发的一次反射响应。常规的单程波偏移和逆时偏移均可修改为多次波直接偏移成像。Berkhout等[15]阐述了以含多次波数据为震源、表面多次波为记录的多次波成像理论,并指出成像会受不同程度干涉噪声影响[16]。Muijs等[17]以分离出的上行波场为震源、下行波为记录,利用单程波延拓和反褶积成像条件获得准确成像的同时压制了部分干扰噪声。Lu等[18]在三维SEAM模型上验证了多次波对盐下照明的优势。叶月明等[19]将基于单程波算子的多次波成像技术应用到海洋深水实际资料处理中,照明均衡度与垂向分辨率均有显著改善。随着计算机技术的进步,全波方程逆时偏移技术得到了快速发展。Liu等[20]修改了逆时偏移的上、下行波场,提出了多次波逆时偏移(RTM)技术,类似的策略也成功应用到海底地震仪(OBS)数据[21]。以子波和地震记录为震源、含多次波数据为记录可实现一次波与多次波的联合成像,Ye等[22]分别对一次波和多次波成像,再进行匹配叠加以避开子波估算。正向延拓一次波或低阶多次波与反向延拓高阶多次波产生的相干噪声是多次波偏移的固有难题,Wang等[23]通过曲率差异在局部角度域成像道集上衰减干涉噪声。基于波场分解和立体成像的方法也可压制相干噪声[24-26]。分离混叠在一起的多阶多次波,形成多个单阶多次波后再分别成像也可避免假象的产生,利用类似的方法可对层间多次波成像[27]。以表面多次波为上行波场,按照一次波的偏移方法可预测出表面多次波假象,再通过匹配相减在成像域压制震源与多次波产生的强能量地震假象[28]。Liu等[29]延伸了单阶多次波成像方法,提出了基于相位编码的多阶多次波RTM技术,在提高计算效率的同时显著压制了噪声。
第三类方法是基于反演理论的全波场成像方法。基于全波场的最小二乘偏移(LSM)技术有三种实现策略:①基于旅行时计算的射线追踪方法,其关键是多次波地下传播旅行时的求取。Brown等[30]提出了在CMP域的全波场最小二乘Kirchhoff偏移,并利用惩罚系数压制干涉噪声。②修改上、下行波场的LSM,这种方法与第二类“全波场的直接偏移成像”的区别在于通过反演压制干涉噪声。Zhang等[31]以预测出的表面多次波为上行波场、包含多次波的记录为下行波场实现了多次波的LSM;Wong等[32]将该方法扩展到海底电缆(OBS)数据的成像,增强了地下照明度,并证明不同阶次表面多次波单独成像同样可以压制干涉噪声。以子波震源和预测出的表面多次波为下行波场、以表面多次波为上行波场能够实现一次波与表面多次波的LSM,但若不能准确估计子波震源,同样会产生较强干扰噪声[33]。Lu等[34]利用单程波算子进行一次波和多次波LSM,应用构造导向正则化条件保障反演的稳定性,提升了墨西哥湾宽方位海洋实际资料的成像质量,在增强照明的同时还减弱了采集脚印影响。③基于单程波算子的全波场成像技术,能够利用包含表面多次波和层间多次波的全波场偏移成像,利用反射系数和地震速度正演,通过最小化模拟数据和偏移数据间的残差来更新成像结果[35]。Verschuur[36]对全波场成像方法的机遇和挑战做了系统的阐述。Davydenko等[37]提出了基于RTM框架的全波场成像方法,利用二次源项定义了波场关系,通过反射率对多次散射建模,克服了单程波偏移算子对成像角度的限制。
第四类方法是Marchenko成像。Marchenko方法可用于多次波预测和多次波成像。基于逆散射理论,Broggini等[38]提出了地震超越干涉法(BSI),把波场聚焦到一维介质的内部,形成Marchenko方法的雏形。Wapenaar等[39]结合BSI格林函数重构以及基于互相关函数和多维反褶积的成像,将这种成像方法命名为Marchenko成像,并给出了完整的理论推导。Slob等[40]基于Marchenko方程,利用层间多次波对地震反射界面成像。Broggini等[41]通过数据驱动聚焦完成了格林函数重构,并通过多维反褶积研究了层间多次波的数据成像。Singh等[42]拓展了Marchenko方程,同时计算了一次波、自由表面多次波和层间多次波的格林函数,实现了基于Marchenko方程的全波场成像。Singh等[43]系统研究了自由表面多次波的Marchenko成像,并指出该方法能够面向局部目标成像。靳中原等[44]提出了基于低频信息补偿的数据驱动Marchenko成像,并讨论了含有自由表面多次波的地震数据在Marchenko成像中的应用方法。
本文研究的基于单程波传播算子的全波场最小二乘偏移方法隶属上文所述第三类,在DELPHI工业组织的全波场偏移(FWM)技术基础上开展。首先,利用地层上、下界面反射系数和背景速度,考虑地层的透射和反射效应,并基于惠更斯二次源的思想,推导了基于单程波算子闭循环延拓的全波场正演模拟算子;其次,在二范数意义下求解全波场最小二乘偏移的误差泛函和梯度项表达式,构建基于反演框架下的全波场LSM;最后,针对透镜体与加入水层的Marmousi模型开展偏移测试分析,验证了本文方法的有效性。多次反射波信息的利用显著提高了成像品质,与此同时,多轮次反演迭代也压制了复杂波场产生的相干假象。该方法的研究拓宽了地震成像的手段,尤其在多次波发育的海域地震资料处理中具有实用和推广价值。
1 基于单程波算子的全波场正演模拟地球物理方法中,正问题是反问题的研究基础,单程波是对全波方程近似而分裂出的一种简化形式。它相对于射线追踪技术能够适应速度场更强的横向变化,相对于全波算子又具有更高的计算效率,并且具有灵活控制波场上、下行传播方向的特点,本节将阐述如何基于单程波算子进行全波场的正演模拟。
1.1 常规单程波传播算子在一次波偏移方法中,多次反射波被认为是噪声。单程波偏移方法将一次波场激发与接收的过程分解为两个单程波的传播过程,即入射波场的下行传播和反射波场的上行传播。基于Berkhout等[15]的“WRW”模型表述方法,从
| $ {\boldsymbol{P}}_{j}^{+}({z}_{m};{z}_{0})={\boldsymbol{W}}^{+}\left({z}_{m}, {z}_{0}\right){\boldsymbol{S}}_{j}^{+}\left({z}_{0}\right) $ | (1) |
式中:
从
| $ {\boldsymbol{P}}_{j}^{-}({z}_{m};{z}_{0})=\sum\limits_{n=m+1}^{M}{\boldsymbol{W}}^{-}\left({z}_{m}, {z}_{n}\right){\boldsymbol{R}}^{\bigcup }\left({z}_{n}, {z}_{n}\right){\boldsymbol{P}}_{j}^{+}\left({z}_{n};{z}_{0}\right) $ | (2) |
式中:
| $ \left\{\begin{array}{c}{\boldsymbol{W}}^{+}\left({z}_{m}, {z}_{0}\right)=\prod \limits_{n=m}^{1}{\boldsymbol{W}}^{+}\left({z}_{n}, {z}_{n-1}\right)\\ {\boldsymbol{W}}^{-}\left({z}_{0}, {z}_{m}\right)=\prod \limits_{n=1}^{m}{\boldsymbol{W}}^{-}\left({z}_{n-1}, {z}_{n}\right)\end{array}\right. $ | (3) |
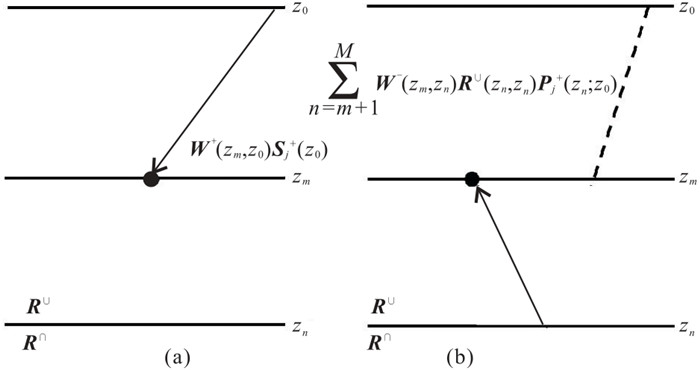
|
图 1 下行波场(a)、上行波场(b)一次波传播示意图 |
基于单程波算子的传统一次波偏移方法存在一个明显缺陷,即其反射界面处的波场是非连续的。反射界面zn之上的总波场包含了入射波场
| $ \left\{\begin{array}{c}\boldsymbol{I}+\mathsf{δ }{\boldsymbol{T}}^{+}\left({z}_{n}, {z}_{n}\right)\\ \boldsymbol{I}+\mathsf{δ }{\boldsymbol{T}}^{-}\left({z}_{n}, {z}_{n}\right)\end{array}\right. $ | (4) |
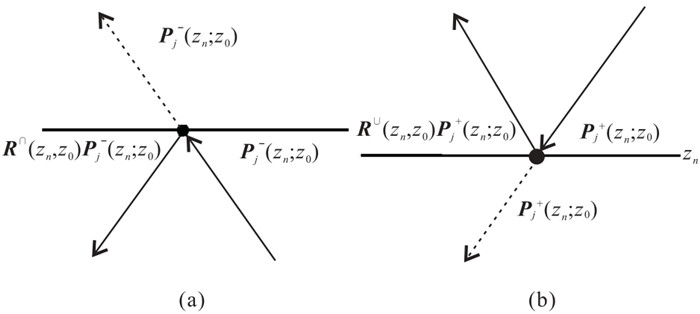
|
图 2 上(a)、下(b)行波场界面处的连续性分析 |
式中:
| $ \left\{\begin{array}{l}{\boldsymbol{P}}_{j}^{-}({z}_{m}, {z}_{0})=\sum\limits_{n=m+1}^{M}{\underset{\_}{\boldsymbol{W}}}^{-}\left({z}_{m}, {z}_{n}\right)\times \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\boldsymbol{R}}^{\bigcup }\left({z}_{n}, {z}_{n}\right){\boldsymbol{P}}_{j}^{+}({z}_{n}, {z}_{0})\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left(5\right)\\ {\boldsymbol{P}}_{j}^{+}({z}_{m};{z}_{0})={\underset{\_}{\boldsymbol{W}}}^{+}\left({z}_{m}, {z}_{0}\right){\boldsymbol{S}}_{j}^{+}\left({z}_{0}\right)\end{array}\right. $ | (5) |
式中
| $ \left\{\begin{array}{l}{\underset{\_}{\boldsymbol{W}}}^{-}\left({z}_{0}, {z}_{m}\right)={\boldsymbol{W}}^{-}\left({z}_{0}, {z}_{1}\right)\times \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \prod \limits_{n=1}^{m-1}[\boldsymbol{I}+\mathsf{δ }{\boldsymbol{T}}^{-}\left({z}_{n}, {z}_{n}\right)]{\boldsymbol{W}}^{-}\left({z}_{n}, {z}_{n+1}\right)\\ {\underset{\_}{\boldsymbol{W}}}^{+}\left({z}_{m}, {z}_{0}\right)={\boldsymbol{W}}^{+}\left({z}_{m}, {z}_{m-1}\right)\times \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \prod \limits_{n=m-1}^{1}[\boldsymbol{I}+\mathsf{δ }{\boldsymbol{T}}^{+}\left({z}_{n}, {z}_{n}\right)]{\boldsymbol{W}}^{+}\left({z}_{n}, {z}_{n-1}\right)\end{array}\right. $ | (6) |
比较式(6)与式(3)可见,修正后的传播算子包含波场经过界面的透射效应
全波场传播算子不仅考虑了波场传播过程中的透射,还需要考虑多次反射效应(包括表面相关多次波和层间多次波)。借鉴表面多次波预测方法中的反馈模型思路,通过单程波场在z0与zM间的多轮延拓,能够模拟出多次反射波场,每一轮的波场延拓能够正演模拟出一个阶次的多次反射波,在z0处注入下行波场能够模拟出表面相关多次波,在地下每个位置处的波场可以认为是惠更斯二次震源,分别沿上行和下行传播,从而模拟出层间多次反射波。因此,考虑多次反射波的单程波延拓算子的波场和上、下行波场[34]分别表示为
| $ \left\{\begin{array}{l}{\boldsymbol{P}}_{j}^{-}({z}_{m};{z}_{0})={\underset{\_}{\boldsymbol{W}}}^{-}\left({z}_{m}, {z}_{M}\right){\boldsymbol{P}}_{j}^{-}({z}_{M};{z}_{0})+\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{n=m+1}^{M}{\underset{\_}{\boldsymbol{W}}}^{-}\left({z}_{m}, {z}_{n}\right){\boldsymbol{R}}^{\bigcup }\left({z}_{n}, {z}_{n}\right){\boldsymbol{P}}_{j}^{+}({z}_{n};{z}_{0})\\ {\boldsymbol{P}}_{j}^{+}({z}_{m};{z}_{0})={\underset{\_}{\boldsymbol{W}}}^{+}\left({z}_{m}, {z}_{0}\right){\boldsymbol{S}}_{j}^{+}\left({z}_{0}\right)+\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{n=0}^{m-1}{\underset{\_}{\boldsymbol{W}}}^{+}\left({z}_{m}, {z}_{n}\right){\boldsymbol{R}}^{\bigcap }\left({z}_{n}, {z}_{n}\right){\boldsymbol{P}}_{j}^{-}({z}_{n};{z}_{0})\end{array}\right. $ | (7) |
式中:下行波延拓算子(第二式)与一次波偏移中的下行波延拓算子(式(5)第二式)相比,多了一项基于反射系数
| $ \left\{\begin{array}{l}{\boldsymbol{P}}_{j}^{+}({z}_{m}^{-};{z}_{0})={\boldsymbol{W}}^{+}\left({z}_{m}^{-}, {z}_{0}\right){\boldsymbol{S}}_{j}^{+}\left({z}_{0}\right)+\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{n=0}^{m-1}{\boldsymbol{W}}^{+}\left({z}_{m}^{-}, {z}_{n}^{+}\right)\mathsf{δ }{\boldsymbol{S}}_{j}^{+}({z}_{n}^{+};{z}_{0})\\ {\boldsymbol{P}}_{j}^{-}({z}_{m}^{+};{z}_{0})={\boldsymbol{W}}^{-}\left({z}_{m}^{+}, {z}_{M}\right){\boldsymbol{P}}_{j}^{-}({z}_{M};{z}_{0})+\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{n=m+1}^{M}{\boldsymbol{W}}^{+}\left({z}_{m}^{+}, {z}_{n}^{-}\right)\mathsf{δ }{\boldsymbol{S}}_{j}^{-}({z}_{n}^{-};{z}_{0})\end{array}\right. $ | (8) |
式中:
| $ \left\{\begin{array}{l}\mathsf{δ }{\boldsymbol{S}}_{j}^{+}({z}_{n}^{+};{z}_{0})={\boldsymbol{R}}^{\bigcap }\left({z}_{n}^{+}, {z}_{n}^{+}\right){\boldsymbol{P}}_{j}^{-}({z}_{n}^{+};{z}_{0})+\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathsf{δ }{\boldsymbol{T}}^{+}\left({z}_{n}^{+}, {z}_{n}^{-}\right){\boldsymbol{P}}_{j}^{+}({z}_{n}^{-};{z}_{0})\\ \mathsf{δ }{\boldsymbol{S}}_{j}^{-}({z}_{n}^{-};{z}_{0})={\boldsymbol{R}}^{\bigcup }\left({z}_{n}^{-}, {z}_{n}^{-}\right){\boldsymbol{P}}_{j}^{+}({z}_{n}^{-};{z}_{0})+\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathsf{δ }{\boldsymbol{T}}^{-}\left({z}_{n}^{-}, {z}_{n}^{+}\right){\boldsymbol{P}}_{j}^{-}({z}_{n}^{+};{z}_{0})\end{array}\right. $ | (9) |
式(9)如果忽略在
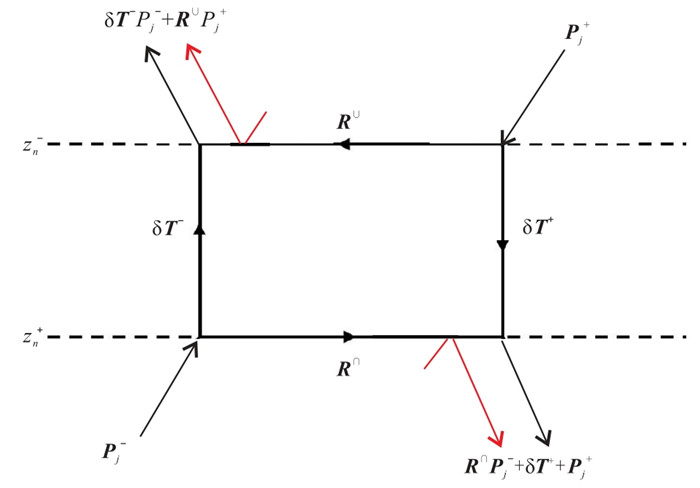
|
图 3 地下网格点波场散射关系 |
单程波传播算子的波场延拓方式是以一定的深度步长逐层延拓,如图 4所示。对于离开zm-1处的下行波场
| $ \left\{\begin{array}{l}{\boldsymbol{Q}}_{j}^{+}({z}_{m-1}^{+};{z}_{0})={\boldsymbol{P}}_{j}^{+}({z}_{m-1}^{-};{z}_{0})+\mathsf{δ }{\boldsymbol{S}}_{j}^{+}({z}_{m-1}^{+}, {z}_{0})\\ {\boldsymbol{P}}_{j}^{+}({z}_{m}^{-};{z}_{0})={\boldsymbol{W}}^{+}\left({z}_{m}^{-};{z}_{m-1}^{+}\right){\boldsymbol{Q}}_{j}^{+}({z}_{m-1}^{+};{z}_{0})\end{array}\right. $ | (10) |
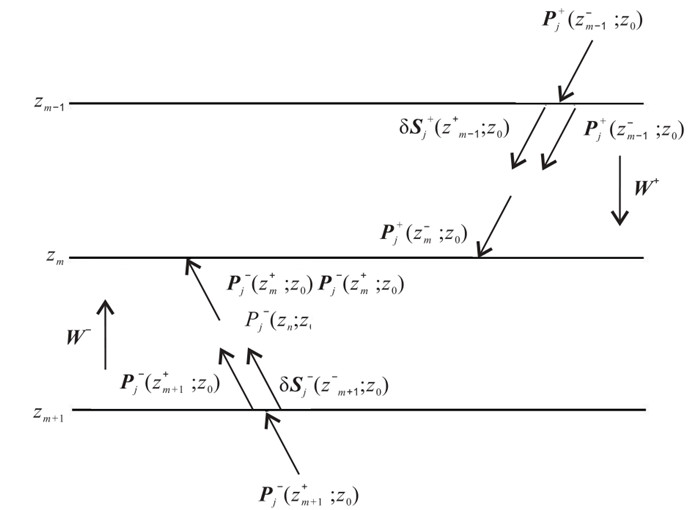
|
图 4 单程波场延拓示意图 |
同理可得到
| $ \left\{\begin{array}{l}{\boldsymbol{Q}}_{j}^{-}({z}_{m+1}^{-};{z}_{0})={\boldsymbol{P}}_{j}^{-}({z}_{m+1}^{+};{z}_{0})+\mathsf{δ }{\boldsymbol{S}}_{j}^{-}({z}_{m+1}^{-}, {z}_{0})\\ {\boldsymbol{P}}_{j}^{-}({z}_{m}^{+};{z}_{0})={\boldsymbol{W}}^{-}\left({z}_{m}^{+};{z}_{m+1}^{-}\right){\boldsymbol{Q}}_{j}^{-}({z}_{m+1}^{-};{z}_{0})\end{array}\right. $ | (11) |
式中:
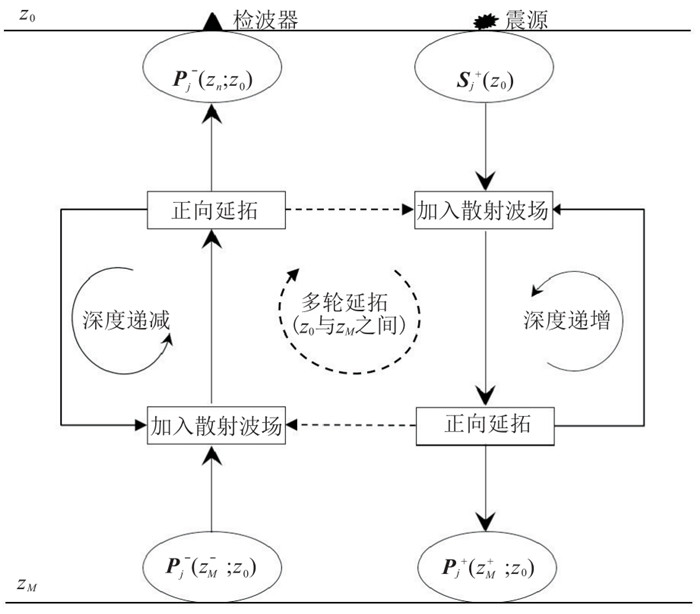
|
图 5 基于单程波算子的全波场模拟流程 |
LSM是利用模拟数据(或反偏移记录)与观测数据之间的匹配程度来解决常规成像结果中振幅失真及采样不规则等问题。基于1.4节介绍的全波场正演模拟技术,全波场LSM在迭代偏移过程中考虑了表面和层间等多次反射波对成像的贡献,可以通过如下的最优化反演问题来描述[32]
| $ J=\sum\limits_{w}{‖\mathrm{\Delta }\boldsymbol{P}‖}_{2}^{2}+f\left(\boldsymbol{R}\right)=\sum\limits_{w}{‖{\boldsymbol{P}}_{\mathrm{o}\mathrm{b}\mathrm{s}}-{\boldsymbol{P}}_{\mathrm{m}\mathrm{o}\mathrm{d}}‖}_{2}^{2}+f\left(\boldsymbol{R}\right) $ | (12) |
式中:
| $ f\left(\boldsymbol{R}\right)=\epsilon \sum\limits_{{z}_{n}}\sum\limits_{l}\mathrm{l}\mathrm{n}\left\{1+{\sigma }^{-2}\mathrm{d}\mathrm{i}\mathrm{a}{\mathrm{g}}_{l}\left[\boldsymbol{R}\left({z}_{n}\right)\right]\right\} $ | (13) |
式中:
| $ \left\{\begin{array}{l}{\boldsymbol{C}}^{\bigcup }\left({z}_{m}\right)=\left[\mathrm{\Delta }{\boldsymbol{P}}^{-}\left({z}_{m}\right)\right]{\left[\mathrm{\Delta }{\boldsymbol{P}}^{+}\left({z}_{m}\right)\right]}^{\mathrm{H}}\\ {\boldsymbol{C}}^{\bigcap }\left({z}_{m}\right)=\left[\mathrm{\Delta }{\boldsymbol{P}}^{+}\left({z}_{m}\right)\right]{\left[\mathrm{\Delta }{\boldsymbol{P}}^{-}\left({z}_{m}\right)\right]}^{\mathrm{H}}\\ \mathrm{\Delta }\boldsymbol{P}\left({z}_{m}\right)={\left[\boldsymbol{W}\left({z}_{0}, {z}_{m}\right)\right]}^{\mathrm{H}}\left[{\boldsymbol{P}}_{\mathrm{o}\mathrm{b}\mathrm{s}}\left({z}_{0}\right)-{\boldsymbol{P}}_{\mathrm{m}\mathrm{o}\mathrm{d}}\left({z}_{0}\right)\right]\end{array}\right. $ | (14) |
式中:
| $ \mathrm{\Delta }{\boldsymbol{P}}^{+}\left({z}_{m}\right)=\sum\limits_{n > m}{\left[\boldsymbol{W}\left({z}_{n}, {z}_{m}\right)\right]}^{\mathrm{H}}{\boldsymbol{R}}^{\bigcup }\left({z}_{n}\right)\mathrm{\Delta }{\boldsymbol{P}}^{-}\left({z}_{n}\right) $ | (15) |
图 6展示了全波场偏移成像中反射系数估计过程,正演模拟波场与逆向延拓的残差波场相关后形成反射系数的梯度项。上层界面反射系数贡献主要来自一次反射波和下行多次散射波场,而下界面的反射系数贡献主要来自层间多次反射波。在构造成像的情况下,选取对角线元素上的梯度并沿频率求和,也就是传统的互相关成像条件
| $ \left\{\begin{array}{l}\mathrm{\Delta }\boldsymbol{R}\left({z}_{n}\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[\sum\limits_{w}C\left({z}_{n}\right)\right]\right\}+{f}^{\mathrm{\text{'}}}\left({\boldsymbol{R}}^{\bigcup }\right)\\ {f}^{\mathrm{\text{'}}}\left({\boldsymbol{R}}^{\bigcup }\right)=\epsilon \frac{\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left[\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\boldsymbol{R}\right)\right]}{1+{\sigma }^{-2}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left[\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\boldsymbol{R}\right)\right]}^{2}}\end{array}\right. $ | (16) |
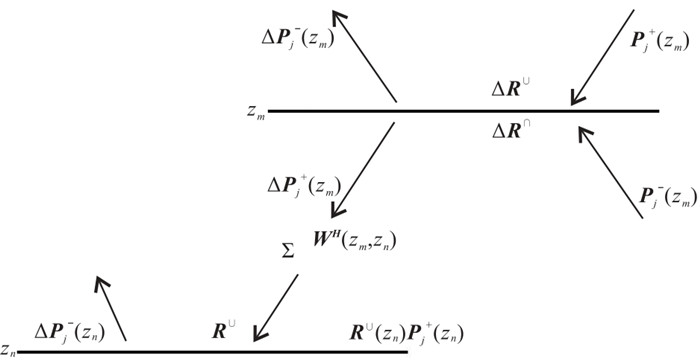
|
图 6 全波场偏移中的反射系数估计 |
反射系数更新为
| $ \left\{\begin{array}{c}{\boldsymbol{R}}^{\bigcup }={\boldsymbol{R}}_{i-1}^{\bigcup }+\alpha \mathrm{\Delta }{\boldsymbol{R}}_{i-1}^{\bigcup }\\ {\boldsymbol{R}}^{\bigcap }={\boldsymbol{R}}_{i-1}^{\bigcap }+\beta \mathrm{\Delta }{\boldsymbol{R}}_{i-1}^{\bigcap }\end{array}\right. $ | (17) |
式中
相对于传统一次波成像方法,全波场最小二乘的计算更加耗时,每增加一个阶次的闭循环波场延拓,相当于增加一倍的偏移时间,对于包含N阶次多次波的全波场成像,偏移计算是单程波偏移时间的N倍。
3 数值测试本节通过含透镜体的层状模型和含水层的Marmousi模型来验证基于单程波算子的FWM成像方法的有效性。透镜体模型利用全波场正演模拟方法可以实现不同阶次的多次波的模拟及分离;对于含水层的Marmousi模型,使用的是空间2阶和时间4阶的有限差分算子模拟全波场数据。通过两个模型数值算例说明,全波场最小二乘偏移方法(FW-LSM)可以有效利用多次波信息进行成像,提高复杂构造地区的成像品质。
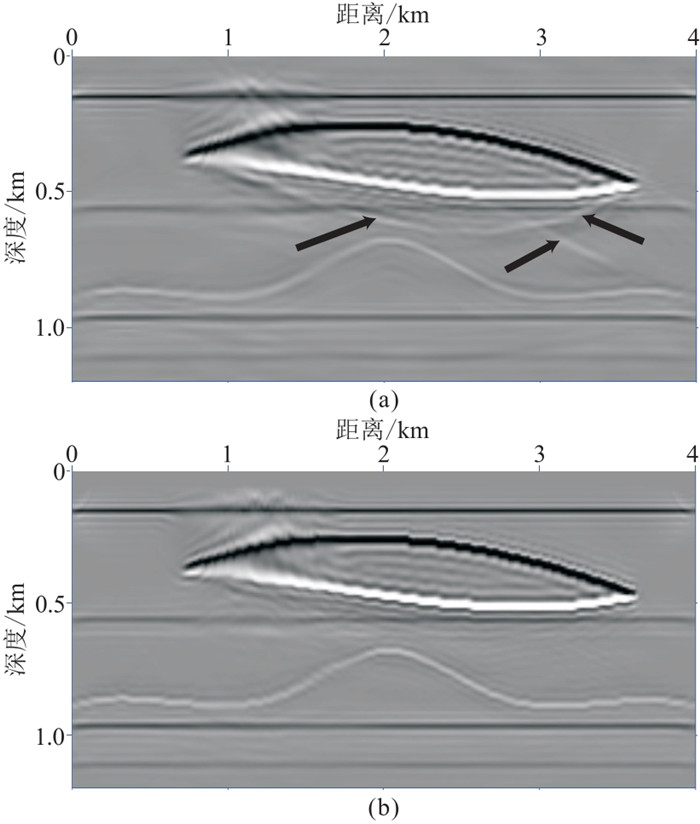
3.1 透镜体模型测试高速透镜体与下伏地层间容易产生层间多次反射波场,适用于本文研究的全波场LSM成像方法测试。速度模型如图 7a所示,浅部平层是海底,海水速度1500 m/s,水底下的两套平层间夹有速度为3200 m/s的高速透镜体,透镜体下伏三套平层和一套背斜地层,高速岩丘构造和目标层间会产生较强的层间多次反射波场。图 7b所示的是密度场,图 7c是用于计算的反射率模型。该模型横向4000 m,纵向深1200 m,正演模拟地震子波为主频20 Hz的Ricker子波,采样间隔为4 ms,记录时间为2 s。图 8a是正演模拟得到的一次反射波,①~⑦箭头所指为第1层~第7层的一次反射。图 8b和图 8c分别是含一阶表面多次波和含一阶及二阶表面多次波的正演模拟炮集,图 8d和图 8e分别是分离后的一、二阶表面相关多次反射波。当含有较强的波阻抗界面时,多次波信号对一次反射波地震信号造成了强烈的干扰。图 9a是常规一次波LSM,虽然所有阻抗界面都可以成像,但由于多次反射波无法正确归位导致干涉噪声影响成像质量,而且透镜体下的成像照明不足,多次波假象影响严重(图 9a中的箭头所示)。图 9b是利用本文方法迭代12次得到的全波场LSM结果,可以看出,FW-LSM成像通过多次迭代过程能够抑制干涉假象,与此同时,多次波信息的利用也提高了成像品质,盐丘下目的层成像照明增强。除此之外,由于充分利用了层间多次波的能量,地震成像的垂向分辨率也有了一定的提高。
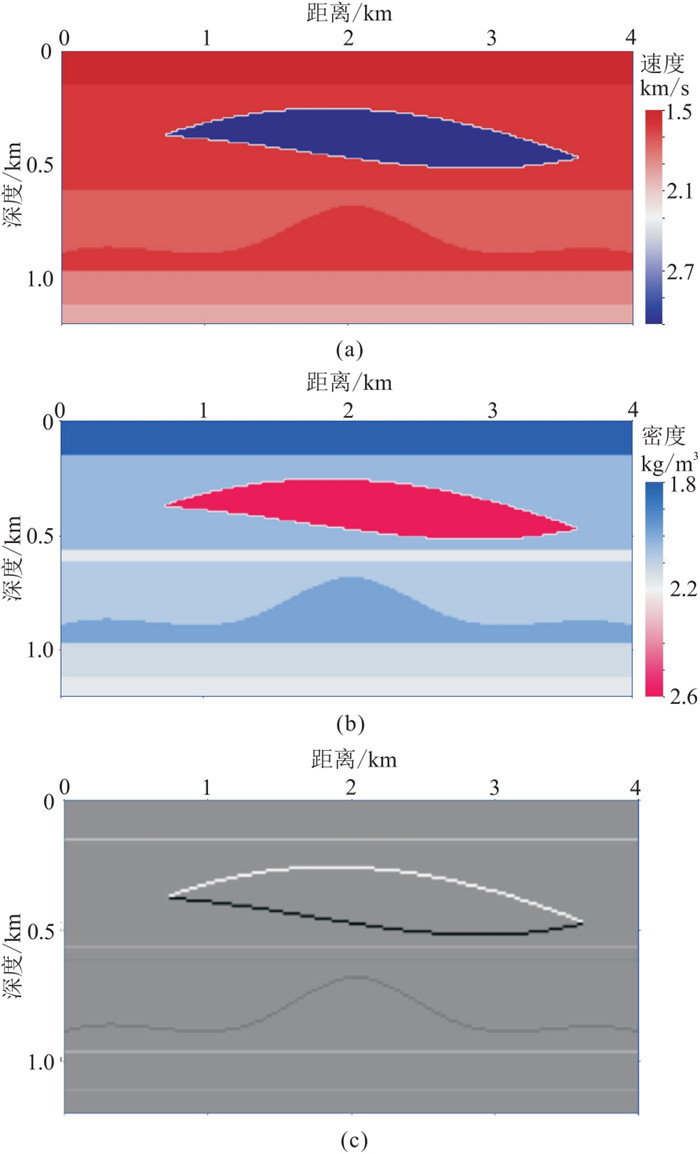
|
图 7 本文使用的速度(a)、密度(b)及反射率(c)模型 |
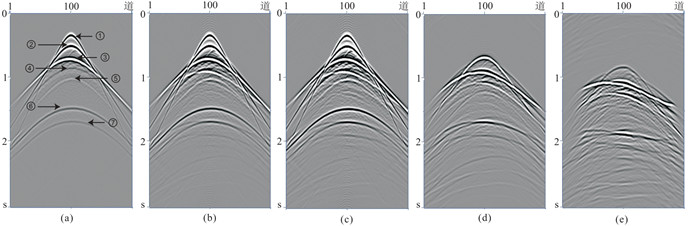
|
图 8 透镜体模型不同单炮记录 (a)一次波;(b)含一次波与一阶多次波;(c)含一次波、一阶多次波和二阶多次波;(d)一阶多次波;(e)二阶多次波 |
|
图 9 LSM(a)与FW-LSM(b)透镜体模型偏移效果对比 |
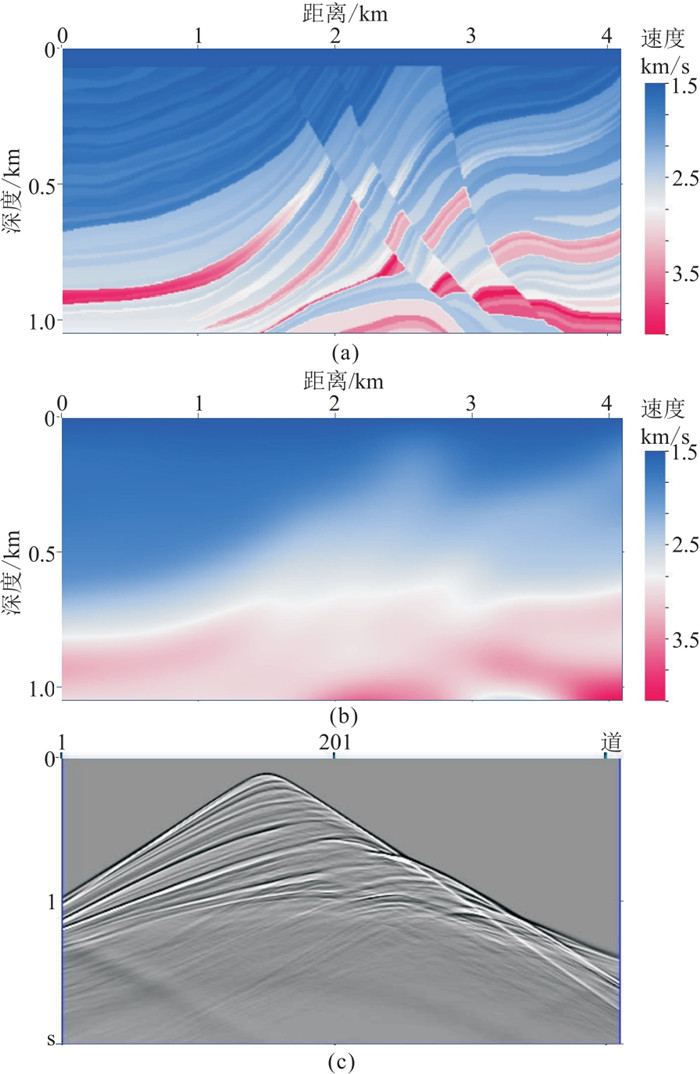
透镜体模型验证了本文方法对简单模型的有效性,下面对含水层Marmousi模型测试FW-LSM技术对复杂模型的适用性。图 10a为正演模拟速度场,浅层为速度是1500 m/s的水层,模型的宽度和深度分别为4100 m和1100 m,该模型的空间被离散为
|
图 10 Marmousi模型与正演记录 (a)模型速度场;(b)模型平滑速度场;(c)正演模拟单炮记录 |
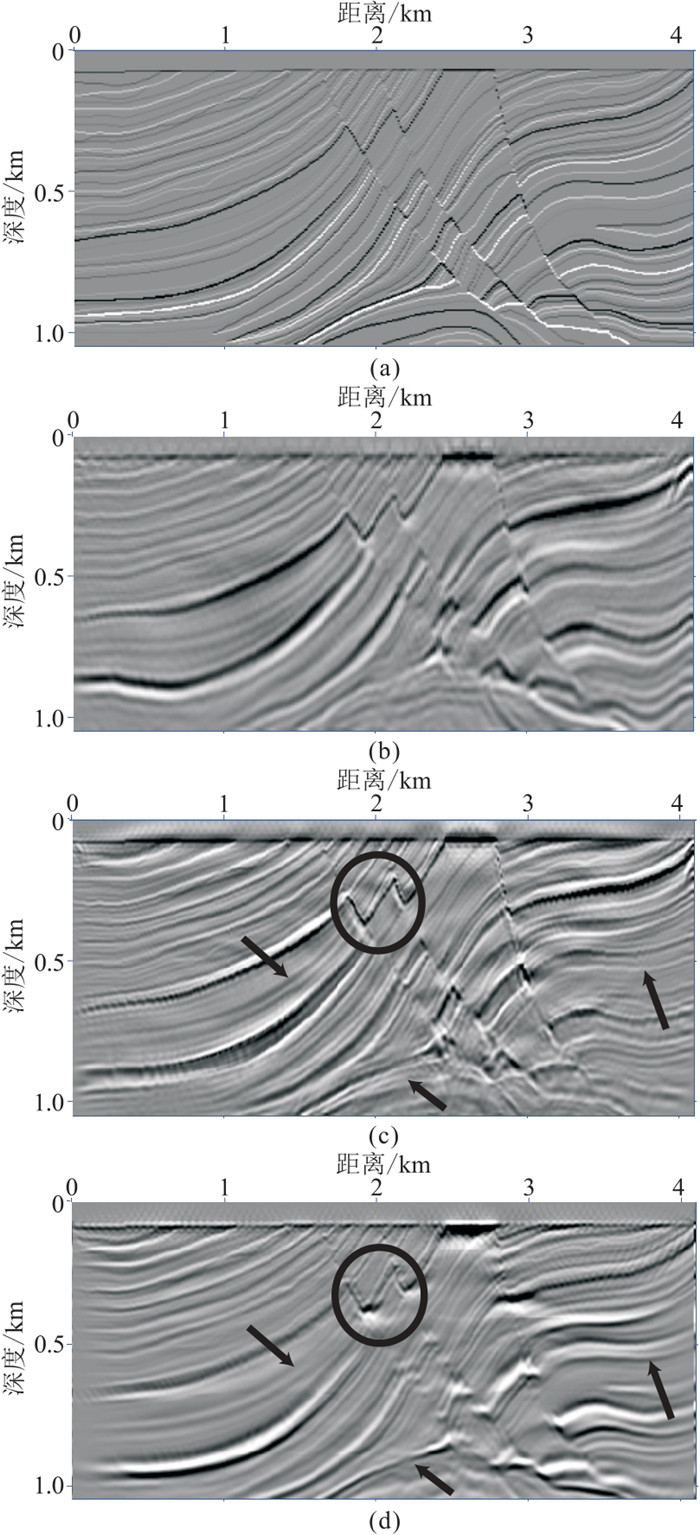
|
图 11 Marmousi模型偏移 (a)反射率模型;(b)第1次迭代FWM;(c)第10次迭代FW-LSM;(d)第10次迭代一次波LSM |
反射地震学利用地层反射波信息研究地下结构特征,传统地震资料处理方法受限于波场一次反射的假设条件,只能利用一次反射波信息成像,丰富的地下多次反射波信息通常被认为是噪声而进行了压制。为了能够合理利用地下全波反射波场信息,本文提出了一种基于单程波传播算子的全波场成像方法,优化了传统单程波传播算子,引入上、下层反射系数以及透射算子影响补偿,实现了全波场正演模拟和最小二乘偏移,充分利用了一次波和多次波信息对地下构造成像,在增强照明度的同时提高了垂向分辨率。
透镜体模型和Marmousi模型测试结果均验证了本文方法的有效性,该技术也为多次波发育资料(海洋地震资料)的处理提供了新的思路,具有实用性和潜在的应用价值。
当然,受限于资料的品质,对于强面波发育的陆地资料和极低信噪比资料,全波场成像技术现阶段并不适用。面向深海的地震资料具有强多次波能量和高信噪比较的特点,是全波场最小二乘偏移技术最具潜力的应用领域。
| [1] |
VERSCHUUR D J, BERKHOUT A J, WAPENAAR C P A. Adaptive surface-related multiple elimination[J]. Geophysics, 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [2] |
WEGLEIN A B, GASPAROTTO F A, CARVALHO P M, et al. An inverse-scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298 |
| [3] |
胡天跃, 王润秋, WHITE R E. 地震资料处理中的聚束滤波方法[J]. 地球物理学报, 2000, 43(1): 105-115. HU Tianyue, WANG Runqiu, WHITE R E. Beamforming in seismic data processing[J]. Chinese Journal of Geophysics, 2000, 43(1): 105-115. DOI:10.3321/j.issn:0001-5733.2000.01.013 |
| [4] |
刘伊克, 常旭, 王辉, 等. 波路径偏移压制层间多次波的理论与应用[J]. 地球物理学报, 2008, 51(2): 589-595. LIU Yike, CHANG Xu, WANG Hui, et al. Internal multiple removal and its application by wavepath migration[J]. Chinese Journal of Geophysics, 2008, 51(2): 589-595. DOI:10.3321/j.issn:0001-5733.2008.02.032 |
| [5] |
马继涛, 刘仕友, 廖震. 三维高精度保幅Radon变换多次波压制方法[J]. 石油地球物理勘探, 2022, 57(3): 582-592. MA Jitao, LIU Shiyou, LIAO Zhen. Research on multiple attenuation using 3D high-precision amplitude-preserving Radon transform[J]. Oil Geophysical Prospec-ting, 2022, 57(3): 582-592. DOI:10.13810/j.cnki.issn.1000-7210.2022.03.009 |
| [6] |
马军茂, 李静, 王晨, 等. GeoEast陆地层间多次波压制方法及应用效果[J]. 石油地球物理勘探, 2022, 57(增刊2): 41-45. MA Junmao, LI Jing, WANG Chen, et al. The suppression method for land internal multiples in GeoEast and its application effect[J]. Oil Geophysical Prospec-ting, 2022, 57(S2): 41-45. DOI:10.13810/j.cnki.issn.1000-7210.2022.S2.007 |
| [7] |
刘伊克, 刘学建, 张延保. 地震多次波成像[J]. 地球物理学报, 2018, 61(3): 1025-1037. LIU Yike, LIU Xuejian, ZHANG Yanbao. Migration of seismic multiple reflections[J]. Chinese Journal of Geophysics, 2018, 61(3): 1025-1037. |
| [8] |
秦宁, 王常波, 梁鸿贤, 等. 一次波和层间多次波联合成像方法[J]. 石油地球物理勘探, 2022, 57(6): 1375-1383. QIN Ning, WANG Changbo, LIANG Hongxian, et al. Joint imaging method of primaries and internal multiples[J]. Oil Geophysical Prospecting, 2022, 57(6): 1375-1383. DOI:10.13810/j.cnki.issn.1000-7210.2022.06.012 |
| [9] |
WAPENAAR K, FOKKEMA J. Green's function representations for seismic interferometry[J]. Geophysics, 2006, 71(4): SI33-SI46. DOI:10.1190/1.2213955 |
| [10] |
JIANG Z, SHENG J, YU J, et al. Migration methods for imaging different-order multiples[J]. Geophysical Prospecting, 2007, 55(1): 1-19. DOI:10.1111/j.1365-2478.2006.00598.x |
| [11] |
BERKHOUT A J, VERSCHUUR D J. Transformation of multiples into primary reflections[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 1925-1928.
|
| [12] |
刘学建, 刘伊克, 胡昊, 等. 一阶多次波聚焦变换成像[J]. 地球物理学报, 2015, 58(6): 1985-1997. LIU Xuejian, LIU Yike, HU Hao, et al. Focal transformation imaging of first-order multiples[J]. Chinese Journal of Geophysics, 2015, 58(6): 1985-1997. |
| [13] |
单国健. 地表多次波应用研究[J]. 石油物探, 2007, 46(6): 604-610. SHAN Guojian. Surface related multiple migration[J]. Geophysical Prospecting for Petroleum, 2007, 46(6): 604-610. |
| [14] |
BERKHOUT A J. Areal shot record technology[J]. Journal of Seismic Exploration, 1992, 1(3): 251-264. |
| [15] |
BERKHOUT A J, VERSCHUUR D J. Multiple technology: Part 2, migration of multiple reflections[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 1497-1500.
|
| [16] |
GUITTON A. Shot-profile migration of multiple reflections[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 1296-1299.
|
| [17] |
MUIJS R, HOLLIGER K, ROBERTSSON J O A. Prestack depth migration of primary and surface-related multiple reflections[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 2107-2110.
|
| [18] |
LU S, WHITMORE N D, VALENCIANO A A, et al. Imaging of primaries and multiples with 3D SEAM synthetic[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 3217-3221.
|
| [19] |
叶月明, 赵昌垒, 庄锡进, 等. 基于单程波偏移算子的地表相关多次波成像[J]. 地球物理学报, 2014, 57(4): 1241-1250. YE Yueming, ZHAO Changlei, ZHUANG Xijin, et al. Migration of surface correlated multiples based on one-way wave equation[J]. Chinese Journal of Geophysics, 2014, 57(4): 1241-1250. |
| [20] |
LIU Y, CHANG X, JIN D, et al. Reverse time migration of multiples for subsalt imaging[J]. Geophysics, 2011, 76(5): WB209-WB216. DOI:10.1190/geo2010-0312.1 |
| [21] |
ZHANG D. Reverse time migration of multiples for OBS data[C]. SEG Annual Meeting Expanded Abstracts, 2014, 33: 4077-4081.
|
| [22] |
YE Y, ZHUANG X, LI Z. One-way wave equation based surface-related multiples migration of marine data[C]. SEG Annual Meeting Expanded Abstracts, 2014.33: 4082-4086.
|
| [23] |
WANG Y, ZHENG Y, ZHANG L, et al. Reverse time migration of multiples: eliminating migration artifacts in angle domain common image gathers[J]. Geophysics, 2014, 79(6): S263-S270. DOI:10.1190/geo2013-0441.1 |
| [24] |
LI Z, LI Z, WANG P, et al. One-way wave-equation migration of multiples based on stereographic imaging condition[J]. Geophysics, 2017, 82(6): S479-S488. DOI:10.1190/geo2016-0478.1 |
| [25] |
LU S, WHITMORE D N, VALENCIANO A A, et al. Separated-wavefield imaging using primary and multiple energy[J]. The Leading Edge, 2015, 34(7): 770-778. DOI:10.1190/tle34070770.1 |
| [26] |
WANG Y, ZHENG Y, XUE Q, et al. Reverse time migration of multiples: reducing migration artifacts using the wavefield decomposition imaging condition[J]. Geophysics, 2017, 82(4): S307-S314. DOI:10.1190/geo2016-0354.1 |
| [27] |
LIU Y, HU H, XIE X, et al. Reverse time migration of internal multiples for subsalt imaging[J]. Geophysics, 2015, 80(5): S175-S185. DOI:10.1190/geo2014-0429.1 |
| [28] |
叶月明, 姚根顺, 庄锡进, 等. 衰减干涉假象的海洋一次波与多次波同时成像方法[J]. 地球物理学报, 2017, 60(12): 4814-4825. YE Yueming, YAO Genshun, ZHUANG Xijin, et al. Imaging marine primary and multiple simultaneously with interferential artifact attenuation[J]. Chinese Journal of Geophysics, 2017, 60(12): 4814-4825. |
| [29] |
LIU Y, HE B, ZHENG Y. Controlled-order multiple waveform inversion[J]. Geophysics, 2020, 85(3): R243-R250. |
| [30] |
BROWN M P, GUITTON A. Least-squares joint imaging of multiples and primaries[J]. Geophysics, 2005, 70(5): S79-S89. |
| [31] |
ZHANG D, SCHUSTER G T. Least-squares reverse time migration of multiples[J]. Geophysics, 2014, 79(1): S11-S21. |
| [32] |
WONG M, BIONDI B, RONEN S. Imaging with multiples using least-squares reverse time migration[J]. TheLeading Edge, 2014, 33(9): 970-976. |
| [33] |
TU N, HERRMANN F J. Fast imaging with surface-related multiples by sparse inversion[J]. Geophysical Journal International, 2015, 201(1): 304-317. |
| [34] |
LU S, LIU F, CHEMINGUI N, et al. Least-squares full-wavefield migration[J]. The Leading Edge, 2018, 37(1): 46-51. |
| [35] |
DAVYDENKO M, VERSCHUUR D J. Full-wavefield migration: using surface and internal multiples in imaging[J]. Geophysical Prospecting, 2017, 65(1): 7-21. |
| [36] |
VERSCHUUR D J. Full-wavefield migration: potential and challenges[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 3836-3837.
|
| [37] |
DAVYDENKO M, VERSCHUUR E. Full wavefield least-squares reverse time migration[J]. Geophysics, 2021, 86(5): WC67-WC74. |
| [38] |
BROGGINI F, SNIEDER R, WAPENAAR K. Focusing the wavefield inside an unknown 1D medium: beyond seismic interferometry[J]. Geophysics, 2012, 77(5): A25-A28. |
| [39] |
WAPENAAR K, THORBECKE J, VAN DER NEUT J, et al. Marchenko imaging[J]. Geophysics, 2014, 79(3): WA39-WA57. |
| [40] |
SLOB E, WAPENAAR K, BROGGINI F, et al. Seismic reflector imaging using internal multiples with Marchenko-type equations[J]. Geophysics, 2014, 79(2): S63-S76. |
| [41] |
BROGGINI F, SNIEDER R, WAPENAAR K. Data-driven wavefield focusing and imaging with multidimensional deconvolution: numerical examples for reflection data with internal multiples[J]. Geophysics, 2014, 79(3): WA107-WA115. |
| [42] |
SINGH S, SNIEDER R, BEHURA J, et al. Marchenko imaging: imaging with primaries, internal multiples, and free-surface multiples[J]. Geophysics, 2015, 80(5): S165-S174. |
| [43] |
SINGH S, SNIEDER R, VAN DER NEUT J, et al. Accounting for free-surface multiples in Marchenko imaging[J]. Geophysics, 2017, 82(1): R19-R30. |
| [44] |
靳中原, 韩立国, 胡勇, 等. 基于低频信息补偿的数据驱动Marchenko成像[J]. 地球物理学报, 2017, 60(9): 3601-3615. JIN Zhongyuan, HAN Liguo, HU Yong, et al. Low frequency information compensation based data-driven Marchenko imaging[J]. Chinese Journal of Geophysics, 2017, 60(9): 3601-3615. |



 钟世超, 浙江省嘉兴市秀洲区油车港镇东方北路1940号北京理工大学长三角研究院(嘉兴),314019。Emai:
钟世超, 浙江省嘉兴市秀洲区油车港镇东方北路1940号北京理工大学长三角研究院(嘉兴),314019。Emai: