0 引言

随着勘探地球物理技术的进步，地震勘探由传统的单分量声波勘探向多波、多分量勘探发展，勘探对象也逐渐转向复杂目标。弹性波地震勘探可有效利用纵、横波信息，降低勘探结果的多解性，且有助于提高地震勘探分辨率。为此，国内众多学者从弹性波正演模拟、速度建模和偏移成像等方面展开大量研究，深化了对弹性波传播规律的认识^[1-7]，尤其在弹性波偏移成像领域取得了很多成果。然而，针对弹性波偏移成像方法的研究大多是基于常规油气藏，而对于地震资料信噪比较低的探区，常规偏移成像方法的应用效果具有一定局限性。因此，探究一种适用于低信噪比数据的弹性波高斯束偏移方法尤为重要。

弹性波偏移方法包括波动方程类和射线类两种。Sun等^[8]通过研究弹性波波动方程，于1986年首先提出一种波动方程类弹性波偏移方法；经过Jia等^[9]的发展，形成对观测系统适应性更强的各向同性介质角度域弹性波逆时偏移（RTM）方法。RTM等偏移成像类方法虽然具有较高成像精度，但在计算效率方面欠理想。与此同时，Kuo等^[10]与Pao等^[11]研究了一种弹性波Kirchhoff积分法偏移成像方法。Kirchhoff类弹性波偏移具有较高计算效率，然而常规射线类方法受到多值走时等问题影响，且无法解决焦散区和阴影区的成像问题，在应用中存在一定局限性。为此，$ \stackrel{ˇ}{\mathrm{C}} $ervený等^[12]将高斯束方法引入地球物理学领域，在Hill^[13-14]、Gray等^[15]努力下，实现了高斯束偏移成像方法。Nowack等^[16]将高斯束偏移方法引入共炮域，提高了其对观测系统的适应性。作为一种改进的Kirchhoff偏移方法，高斯束偏移方法不仅具有较高计算效率，且能有效克服常规射线类偏移方法的局限性，解决了焦散区和阴影区的成像问题。后来，Vinje等^[17]、吴建文^[18]在常规声波高斯束偏移基础上，提出基于Tau-p域阈值滤波的声波控制束偏移成像方法；杨晶等^[19]进一步研究了时间域声波高斯束偏移成像方法。

然而以上研究均基于声波假设，无法有效解决弹性波偏移成像问题。在声波高斯束偏移发展的同时，Katchalov等^[20]、岳玉波^[21]等进一步研究了多波多分量弹性波偏移成像方法；秦宁^[22]通过研究各向异性介质射线追踪算法，发展了弹性波各向异性高斯束逆时偏移方法。只是以上研究均采用常规弹性波高斯束偏移成像思路，未提及复杂油气藏勘探中低信噪比地震资料成像问题。

本文基于前人研究成果，将阈值控制压制噪声方法引入常规弹性波高斯束偏移，提出一种基于阈值控制的弹性波高斯束偏移成像优化方法，通过滤除低波场值噪声，达到提高剖面成像质量的目的。文中采用洼陷模型和断块模型进行测试，试算结果验证了本文方法的正确性和有效性。相较于常规弹性波高斯束偏移成像方法，本文方法可有效压制噪声，增大偏移剖面信噪比，提高低信噪比地震资料成像质量。

1 阈值控制的弹性波高斯束偏移基本原理

运动学射线追踪与动力学射线追踪是实现高斯束偏移的关键。通过运动学射线追踪计算中心射线路径和走时，以动力学射线追踪方程计算动力学射线追踪参数。在射线追踪基础上计算得到高斯束，进而表征格林函数，推导出波场正向延拓和反向延拓公式，利用互相关条件实现弹性波高斯束偏移成像。

1.1 运动学射线追踪方程

本文采用岳玉波^[21]给出的各向同性介质弹性波运动学射线追踪方程，震源处采用纵波射线追踪，而检波点处束中心分别采用纵波和横波做射线追踪，得到中心射线走时和路径信息

$ \left\{\begin{array}{l}\frac{\mathrm{d}{x}_{i}\left(s\right)}{\mathrm{d}\tau }={{V}_{\mathrm{P}}}^{2}\left(s\right){p}_{\mathrm{P}i}\left(s\right)\\ \frac{\mathrm{d}{p}_{\mathrm{P}i}\left(s\right)}{\mathrm{d}\tau }=-\frac{1}{{V}_{\mathrm{P}}\left(s\right)}\frac{\partial {V}_{\mathrm{P}}\left(s\right)}{\partial {x}_{i}}\end{array}\right. $

(1)

$ \left\{\begin{array}{l}\frac{\mathrm{d}{x}_{i}\left(s\right)}{\mathrm{d}\tau }={{V}_{\mathrm{S}}}^{2}\left(s\right){p}_{\mathrm{S}i}\left(s\right)\\ \frac{\mathrm{d}{p}_{\mathrm{P}i}\left(s\right)}{\mathrm{d}\tau }=-\frac{1}{{V}_{\mathrm{S}}\left(s\right)}\frac{\partial {V}_{\mathrm{S}}\left(s\right)}{\partial {x}_{i}}\end{array}\right. $

(2)

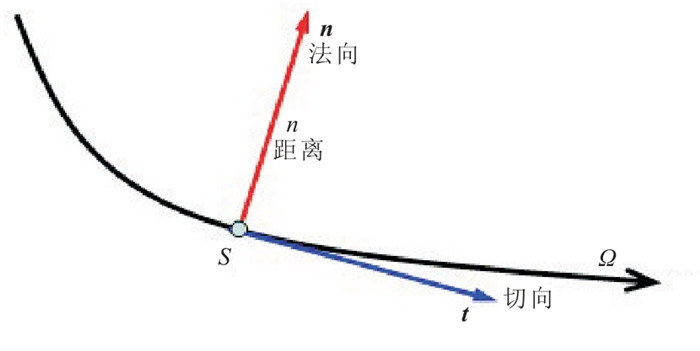
式中：x_i为直角坐标系（x，z）中的位置；p_Pi、p_Si分别为纵（P）、横（S）波慢度分量；τ为沿射线方向传播的走时；V_P、V_S分别为地下介质的纵、横波速度；s为二维射线中心坐标系（图 1）中射线Ω上某点到选定参考点S的弧长。

1.2 动力学射线追踪方程

动力学射线追踪广泛应用于高频近似下的波场计算与地震反演中^[23]。本文利用动力学射线追踪计算动力学射线追踪参数，用于中心射线的振幅及波前计算

$ \left\{\begin{array}{l}\frac{\mathrm{d}{Q}_{\mathrm{S}}\left(s\right)}{\mathrm{d}\tau }={{V}_{\mathrm{P}}}^{2}\left(s\right){P}_{\mathrm{P}}\left(s\right)\\ \frac{\mathrm{d}{P}_{\mathrm{P}}\left(s\right)}{\mathrm{d}\tau }=-\frac{1}{{V}_{\mathrm{P}}\left(s\right)}\frac{{\partial }^{2}{V}_{\mathrm{P}}\left(s\right)}{\partial {n}^{2}}{Q}_{\mathrm{P}}\left(s\right)\end{array}\right. $

(3)

$ \left\{\begin{array}{l}\frac{\mathrm{d}{Q}_{\mathrm{S}}\left(s\right)}{\mathrm{d}\tau }={{V}_{\mathrm{S}}}^{2}\left(s\right){P}_{\mathrm{S}}\left(s\right)\\ \frac{\mathrm{d}{P}_{\mathrm{S}}\left(s\right)}{\mathrm{d}\tau }=-\frac{1}{{V}_{\mathrm{S}}\left(s\right)}\frac{{\partial }^{2}{V}_{\mathrm{S}}\left(s\right)}{\partial {n}^{2}}{Q}_{\mathrm{S}}\left(s\right)\end{array}\right. $

(4)

上述式中：P（s）和Q（s）为动力学射线追踪参数；n代表射线Ω附近一点到S点的距离。

1.3 阈值控制函数

本文将阈值函数引入Tau-p变换，修改了倾斜叠加变换公式，并将其应用于偏移成像过程，实现基于阈值控制的弹性波高斯束偏移成像优化方法。

已知不同波型的多分量地震记录的加窗倾斜叠加为

$ \begin{array}{l}{D}_{m}^{\nu }({\boldsymbol{x}}_{L}, {p}_{1}^{\nu }, \omega )=\sqrt{\frac{\left|\omega \right|}{2\mathrm{\pi }}}{\int }_{s}d{\boldsymbol{x}}_{r}{u}_{m}({\boldsymbol{x}}_{r}, \omega )\times \\ \ \ \ \ \ \mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\omega {p}_{1}^{\nu }\left({\boldsymbol{x}}_{L}\right)({\boldsymbol{x}}_{\mathrm{r}}-{\boldsymbol{x}}_{L})-\left|\frac{\omega }{{\omega }_{\mathrm{r}\mathrm{e}\mathrm{f}}}\right|\frac{({\boldsymbol{x}}_{\mathrm{r}}-{\boldsymbol{x}}_{L}{)}^{2}}{2{w}_{0}^{2}}\right]\end{array} $

(5)

式中： x_s、x_r对应为震源和接收点位置；u_m（x_r，ω）为x_r处接收到的弹性波地震记录，m=1、2，对应为x、z方向的分量；上标ν指P波和S波两种不同波型；ω_ref、w₀分别为高斯束参考频率和初始宽度； p$ {}_{1}^{\nu } $（x_L）为在束中心x_L处ν型波慢度矢量的x方向分量。

通过在倾斜叠加过程中引入阈值参数ε，得到基于阈值控制的倾斜叠加公式

$ \begin{array}{l}{Y}_{m}^{\nu }({\boldsymbol{x}}_{L}, {p}_{1}^{\nu }, \omega )=\sqrt{\frac{\left|\omega \right|}{2\mathrm{\pi }}}{\int }_{s}d{\boldsymbol{x}}_{r}{u}_{m}({\boldsymbol{x}}_{r}, \omega )\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\omega {p}_{1}^{\nu }\left({\boldsymbol{x}}_{L}\right)({\boldsymbol{x}}_{\mathrm{r}}-{\boldsymbol{x}}_{L})-\left|\frac{\omega }{{\omega }_{\mathrm{r}\mathrm{e}\mathrm{f}}}\right|\frac{({\boldsymbol{x}}_{\mathrm{r}}{-L)}^{2}}{2{w}_{0}^{2}}\right]\times \epsilon \end{array} $

(6)

其中，阈值参数ε的选取需满足以下条件

$ \epsilon =\left(\begin{array}{c}{{u}_{m}}^{\nu }({\boldsymbol{x}}_{\mathrm{r}}, {\boldsymbol{x}}_{\mathrm{s}}, \omega ) < W{\sum }_{\mathrm{a}\mathrm{v}\mathrm{g}}{{u}_{m}}^{\nu }({\boldsymbol{x}}_{\mathrm{r}}, {\boldsymbol{x}}_{\mathrm{s}}, \omega )\begin{array}{cc}& \mathrm{舍}\mathrm{去}\end{array}\\ {{u}_{m}}^{\nu }({\boldsymbol{x}}_{\mathrm{r}}, {\boldsymbol{x}}_{\mathrm{s}}, \omega ) > W{\sum }_{\mathrm{a}\mathrm{v}\mathrm{g}}{{u}_{m}}^{\nu }({\boldsymbol{x}}_{\mathrm{r}}, {\boldsymbol{x}}_{\mathrm{s}}, \omega )\begin{array}{cc}& \mathrm{保}\mathrm{留}\end{array}\end{array}\right) $

(7)

式中：W为阈值控制系数，可据不同地震数据做相应赋值；$ {\sum }_{avg}{{u}_{m}}^{\nu }({\boldsymbol{x}}_{r}, {\boldsymbol{x}}_{s}, \omega ) $为波场值算术平均值。

1.4 弹性波波场正、反向延拓公式

在二维射线中心坐标系（图 1）中，可构建由参考点x₀处出射，且经过计算空间任一点x处的高斯束位移公式

$ \begin{array}{r}{\widehat{\boldsymbol{u}}}^{\nu }(\boldsymbol{x}, {\boldsymbol{x}}_{0}, \omega )=\frac{{\varphi }^{\nu }}{\sqrt{{v}^{\nu }\left(s\right)\rho \left(s\right)Q\left(s\right)}}{\boldsymbol{e}}^{\nu }\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left[\mathrm{i}\omega \tau \left(s\right)+\frac{\mathrm{i}\omega }{2}\frac{P\left(s\right)}{Q\left(s\right)}{n}^{2}\right]\end{array} $

(8)

式中：φ^ν为复值常数；ρ（s）为介质的密度数值；v$ {}^{\nu } $（s）为不同波型的相速度；e^P为P波在x处的高斯束极化矢量，表达式为$ {\boldsymbol{e}}^{\mathrm{P}}=\left[\boldsymbol{t}+\boldsymbol{n}{v}_{\mathrm{P}}\left(s\right)\frac{P\left(s\right)}{Q\left(s\right)}n\right] $，其中Ω的切向矢量t为高斯束极化矢量的主分量，Ω的法向矢量 n为次分量；同理，e^S为S波高斯束极化矢量，表达式为$ {\boldsymbol{e}}^{\mathrm{S}}=\left[\boldsymbol{n}-\boldsymbol{t}{v}_{\mathrm{S}}\left(s\right)\frac{P\left(s\right)}{Q\left(s\right)}n\right] $，但与P波不同，S波中n为主分量，－t为次分量。

1.4.1 波场的正向延拓

根据式（8），将由x_s处以不同角度出射，且对x位移有作用的高斯束叠加起来，便可得震源处正向延拓公式

$ \begin{array}{r}{\boldsymbol{U}}_{m}^{\mathrm{P}}\left(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{s}}, \omega \right)=\frac{\mathrm{i}}{4\mathrm{\pi }{\left[{v}_{\mathrm{P}}\left({\boldsymbol{x}}_{\mathrm{s}}\right)\right]}^{2}}\sqrt{\frac{{\omega }_{\mathrm{r}}{w}_{0}^{2}}{\rho \left({\boldsymbol{x}}_{\mathrm{s}}\right)}}\times \\ \int \frac{\mathrm{d}{p}_{1}^{\mathrm{P}}\left({\boldsymbol{x}}_{\mathrm{s}}\right)}{{p}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{\mathrm{s}}\right)}{\widehat{u}}_{m}^{\mathrm{P}}\left(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{s}}, \omega \right)\end{array} $

(9)

式中：p$ {}_{2}^{\mathrm{P}} $（x_s）为x_s处P波慢度矢量的垂直方向分量；$ {\widehat{u}}_{m}^{\mathrm{P}}\left(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{s}}, \omega \right) $为x_s处的P波高斯束位移。

1.4.2 阈值控制的波场反向延拓

在x_s处激发、x_r处接收到的记录用u_i（x_r，ω）表示，便可将弹性波反向波场的位移u_m（x， x_s，ω）用Kirchhoff-Helmholtz积分表示为

$ \begin{array}{l}{u}_{m}(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega )={\int }_{s}\mathrm{d}{\boldsymbol{x}}_{r}\left[{t}_{i}({\boldsymbol{x}}_{\mathrm{r}}, \omega ){G}_{im}^{\mathrm{*}}(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega )-\right.\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.{u}_{i}({\boldsymbol{x}}_{\mathrm{r}}, \omega ){\sum }_{im}^{\mathrm{*}}(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega )\right]\\ \end{array} $

(10)

式中：上标$ \mathrm{*} $表示复共轭，在x_r处对其沿i方向施加单位体力，造成点x处沿m方向产生一定位移量，用格林张量$ {G}_{im}(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega )=\sum\limits_{\nu }^{}{g}_{im}^{\nu }(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega ) $表示；$ {t}_{i}({\boldsymbol{x}}_{\mathrm{r}}, \omega )={n}_{j}{C}_{ijkl}\frac{\partial {u}_{l}}{\partial {x}_{k}} $为x_r处张量；n_j为x_r处沿外法线方向的单位矢量，应力格林张量$ {\sum }_{im}(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega )={n}_{j}{C}_{ijkl}\frac{\partial {G}_{im}}{\partial {x}_{k}} $，其中C_ijkl为四阶刚度系数，在二维各向同性介质弹性波中表示为

$ {C}_{ijkl}\left(\boldsymbol{x}\right)={\delta }_{ij}{\delta }_{kl}\lambda \left(\boldsymbol{x}\right)+({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})\mu \left(\boldsymbol{x}\right) $

(11)

式中：λ（x）、μ（x）为拉梅弹性参数，满足λ（x）+2μ（x）=ρ（x）v$ {}_{\mathrm{P}}^{2} $（x），μ（x）=ρ（x）v$ {}_{\mathrm{S}}^{2} $（x）；δ_ik为Kronecker Delta函数。

据文献[21]，可得基于阈值控制的反向延拓位移公式

$ \begin{array}{l}{u}_{m}^{\nu }(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega )=-\frac{\mathrm{\Delta }L\omega }{4\mathrm{\pi }}\sum\limits_{{N}_{L}}\int \frac{\mathrm{d}{p}_{1}^{\nu }\left({\boldsymbol{x}}_{L}\right)}{{p}_{2}^{\nu }\left({\boldsymbol{x}}_{L}\right)}\times \\ \ \ \ \ \ \ \ \sqrt{\rho \left({\boldsymbol{x}}_{L}\right)}{\widehat{u}}_{m}^{\nu \mathrm{*}}(\boldsymbol{x}, {\boldsymbol{x}}_{L}, \omega )\times \left[{W}_{1}^{\nu }\left({\boldsymbol{x}}_{L}\right){Y}_{1}^{\nu }({\boldsymbol{x}}_{L}, {p}_{1}^{\nu }, \omega )+\right.\\ \ \ \ \ \ \ \ \left.{W}_{2}^{\nu }\left({\boldsymbol{x}}_{L}\right){Y}_{2}^{\nu }({\boldsymbol{x}}_{L}, {p}_{1}^{\nu }, \omega )\right]\left(12\right)\end{array} $

(12)

式中：Y$ {}_{1}^{\nu } $（x_L，p$ {}_{1}^{\nu } $，ω）为阈值控制的对不同波型的多分量地震记录进行的加窗倾斜叠加；ΔL为水平间隔；N_L为高斯窗数目；权值W$ {}_{1}^{\nu } $、W$ {}_{2}^{\nu } $分别为

$ \left\{\begin{array}{l}{W}_{1}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right)=2{\gamma }^{2}\left({\boldsymbol{x}}_{L}\right){p}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right){e}_{1}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right)\\ {W}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right)=2{\gamma }^{2}\left({\boldsymbol{x}}_{L}\right){p}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right){e}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right)+\left[\frac{1-2{\gamma }^{2}\left({\boldsymbol{x}}_{L}\right)}{{v}_{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right)}\right]\\ {W}_{1}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right)={p}_{2}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right){e}_{1}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right)+{p}_{1}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right){e}_{2}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right)\\ \begin{array}{l}{W}_{2}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right)=-2{p}_{1}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right){e}_{1}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right)\\ \gamma \left({\boldsymbol{x}}_{L}\right)=\frac{{v}_{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right)}{{v}_{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right)}\end{array}\end{array}\right. $

(13)

1.5 阈值控制的弹性波高斯束偏移成像公式

根据Clearbout^[24]成像法则，利用震源波场与接收点反向延拓的波场之间的互相关计算，可得到单炮的成像值。由式（9）、式（12）可得到阈值控制的PP波与PS波成像公式

$ \begin{array}{l}{I}^{\mathrm{P}\mathrm{P}}\left(\boldsymbol{x}\right)=\int {U}_{2}^{P*}(\boldsymbol{x}, {\boldsymbol{x}}_{s}, \omega ){u}_{2}^{\mathrm{P}}(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega )\mathrm{d}\omega \\ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{\mathrm{\Delta }L\sqrt{{\omega }_{\mathrm{r}}{w}_{0}^{2}}}{16{\mathrm{\pi }}^{2}}\sum\limits_{{N}_{L}}\int \mathrm{d}\omega \frac{\mathrm{i}\omega }{{v}_{\mathrm{P}}^{2}\left({\boldsymbol{x}}_{\mathrm{s}}\right)}\sqrt{\frac{\rho \left({\boldsymbol{x}}_{L}\right)}{\rho \left({\boldsymbol{x}}_{\mathrm{s}}\right)}}\times \\ \iint \frac{\mathrm{d}{p}_{1}^{\mathrm{P}}\left({\boldsymbol{x}}_{\mathrm{s}}\right)\mathrm{d}{p}_{1}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right)}{{p}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{\mathrm{s}}\right){p}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right)}\times {\widehat{u}}_{2}^{\mathrm{P}\mathrm{*}}(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{s}}, \omega ){\widehat{u}}_{1}^{\mathrm{P}\mathrm{*}}(\boldsymbol{x}, {\boldsymbol{x}}_{L}, \omega )\times \\ \left[{W}_{1}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right){Y}_{1}^{\mathrm{P}}({\boldsymbol{x}}_{L}, {p}_{1}^{\mathrm{P}}, \omega )+{W}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{L}\right){Y}_{2}^{\mathrm{P}}({\boldsymbol{x}}_{L}, {p}_{1}^{\mathrm{P}}, \omega )\right]\end{array} $

(14)

$ \begin{array}{l}{I}^{\mathrm{P}\mathrm{S}}\left(\boldsymbol{x}\right)=\int {U}_{2}^{P*}(\boldsymbol{x}, {\boldsymbol{x}}_{s}, \omega ){u}_{1}^{\mathrm{S}}(\boldsymbol{x}, {\boldsymbol{x}}_{\mathrm{r}}, \omega )\mathrm{d}\omega \\ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{\mathrm{\Delta }L\sqrt{{\omega }_{\mathrm{r}}{w}_{0}^{2}}}{16{\mathrm{\pi }}^{2}}\sum\limits_{{N}_{L}}\int \mathrm{d}\omega \frac{\mathrm{i}\omega }{{v}_{\mathrm{P}}^{2}\left({\boldsymbol{x}}_{\mathrm{s}}\right)}\sqrt{\frac{\rho \left({\boldsymbol{x}}_{L}\right)}{\rho \left({\boldsymbol{x}}_{\mathrm{s}}\right)}}\times \\ \iint \frac{\mathrm{d}{p}_{1}^{\mathrm{P}}\left({\boldsymbol{x}}_{\mathrm{s}}\right)\mathrm{d}{p}_{1}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right)}{{p}_{2}^{\mathrm{P}}\left({\boldsymbol{x}}_{\mathrm{s}}\right){p}_{2}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right)}\times {\widehat{u}}_{2}^{P*}(\boldsymbol{x}, {\boldsymbol{x}}_{s}, \omega ){\widehat{u}}_{1}^{S*}(\boldsymbol{x}, {\boldsymbol{x}}_{L}, \omega )\times \\ \left[{W}_{1}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right){Y}_{1}^{\mathrm{S}}({\boldsymbol{x}}_{L}, {p}_{1}^{\mathrm{S}}, \omega )+{W}_{2}^{\mathrm{S}}\left({\boldsymbol{x}}_{L}\right){Y}_{2}^{\mathrm{S}}({\boldsymbol{x}}_{L}, {p}_{1}^{\mathrm{S}}, \omega )\right]\end{array} $

(15)

1.6 技术实现流程

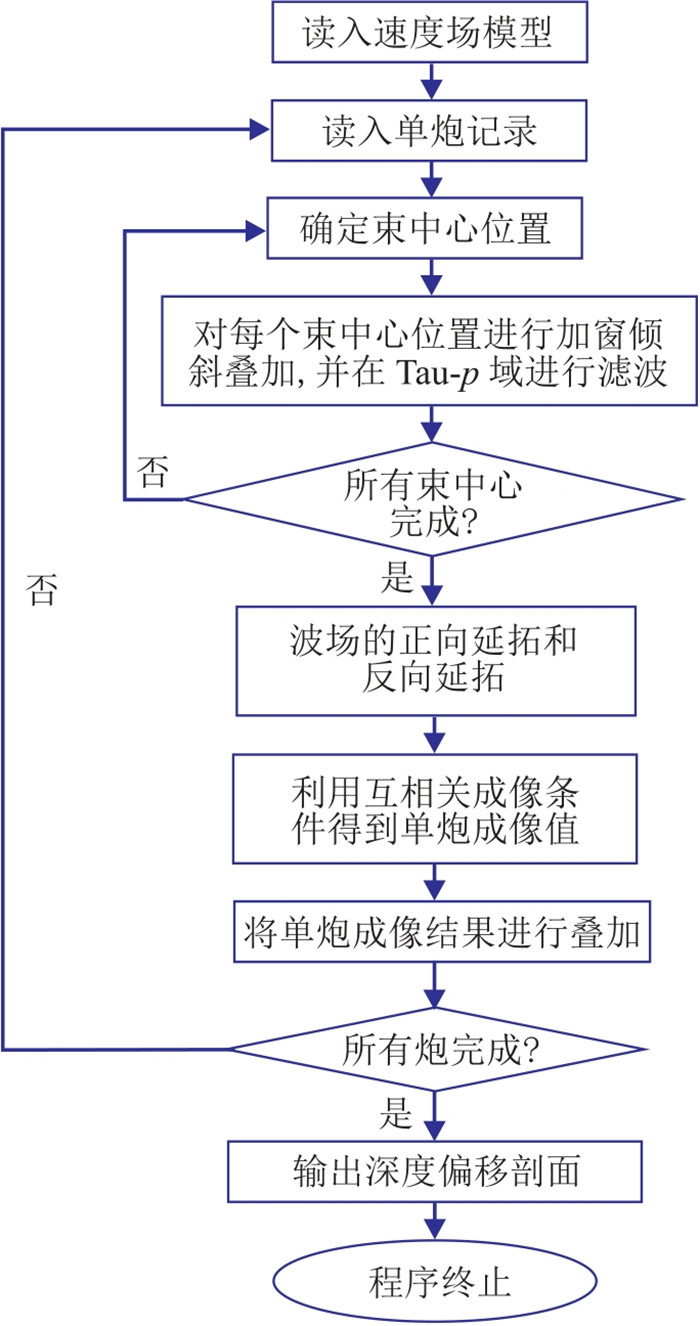
阈值控制的弹性波高斯束偏移方法的具体实现流程如图 2所示。

2 模型试算

为了验证该方法在低信噪比地震数据中的适用性，本文利用洼陷模型和断块模型进行测试。

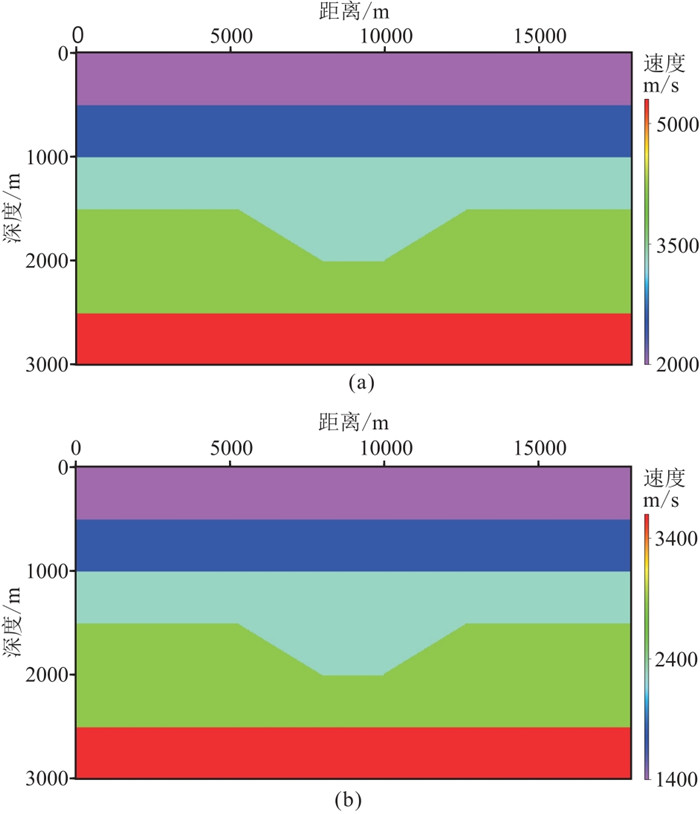
2.1 洼陷模型试算

设计的洼陷模型（图 3）大小为1801×301，纵向网格间距为10 m，横向网格间距为10 m，炮点距为7 m，第一炮位于10 m处，总计250炮激发，每炮接收道数为1801，道间距为10 m，时间采样间隔为1 ms，采集时长为3001 ms。

为验证低信噪比地震记录对偏移结果的影响及基于阈值控制的弹性波高斯束偏移方法的有效性，在SU系统中利用suaddnoise指令对正演得到的炮记录做加噪处理，其指令原理如下^[25]

$ \left\{\begin{array}{l}O(x, t)=I(x, t)+\mathrm{S}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}{G}_{N}\\ {G}_{N}=\frac{1}{\sqrt{2\mathrm{\pi }}\sigma }{\mathrm{e}}^{-\left(I\right(x, t)-I{(x, t)}^{\mathrm{*}}{)}^{2}/2{\sigma }^{2}}\\ \mathrm{S}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}=\frac{1}{\sqrt{2}\mathrm{S}\mathrm{N}\mathrm{R}}{\left|s(x, t)\right|}_{\mathrm{m}\mathrm{a}\mathrm{x}}\sqrt{\left|s(x, t)\right|}\end{array}\right. $

(16)

式中：O（x，t）为输出地震记录；I（x，t）为输入地震记录；G_N为高斯噪声；I（x，t）^*为输入地震记录绝对值的平均值；|signal|_max为输入地震记录最大绝对值；s（x，t）为每个记录采样点值；σ为输入记录的标准差。

信噪比（SNR）与噪声量（noise）的关系为^[26]

$ \mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}(x, t)=\frac{1}{\mathrm{S}\mathrm{N}\mathrm{R}}\frac{\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{ }\left(\left|s(x, t)\right|\right)}{\sqrt[]{2}}\frac{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(x, t\right)}{{\sigma }_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}} $

(17)

式中：s（x，t）为地震记录；rand（x，t）为（x，t）点的随机数；σ_rand为所有采样点随机数的标准差。

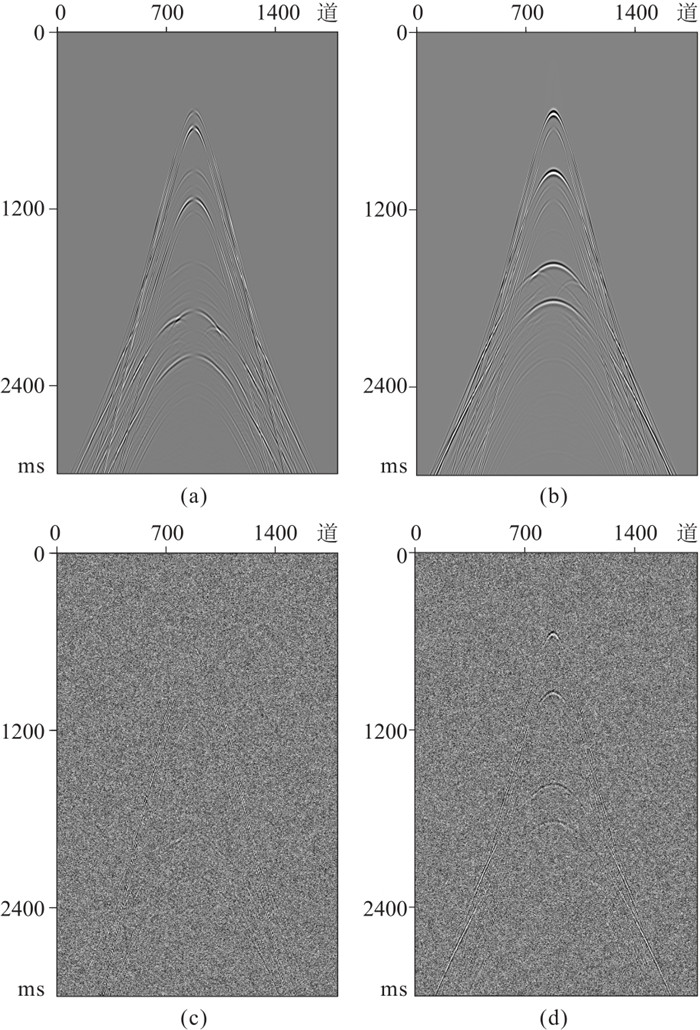
从图 4所示地震记录可知：原始地震记录上的反射波信息较清晰，同相轴较收敛；当SNR为5时，地震记录中的有效反射波信息受到噪声干扰（图 4c、图 4d）。针对这些低信噪比地震记录用常规方法做偏移成像（图 5）时，会导致成像剖面上出现大量噪声，影响偏移成像质量（图 5c、图 5e）。而采用本文方法，所得成像剖面（图 5d、图 5f）较清晰，有效消除了噪声干扰，提高了地层的分辨率，尤其是浅层的效果更显著。

2.2 复杂断块模型试算

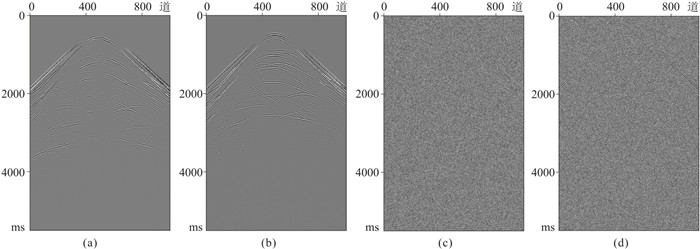
设计的复杂断块模型（图 6）大小为1000×550，纵向网格间距为10 m，横向网格间距为10 m，炮间距为5 m，第一炮位于2 m处，总计200炮激发，每炮接收道数为1000，道间距为10 m，时间采样间隔为1 ms，采集时长为5501 ms。模型正演及加噪后的地震记录分别如图 7所示。对比所得成像结果（图 8）可见：采用常规弹性波高斯束偏移对低信噪比数据的成像剖面（图 8c、图 8e）上有大量噪声，有效同相轴能量被噪声干扰，地震剖面信噪比较低，整体成像质量较差；用本文方法的偏移剖面（图 8d、图 8f）上噪声明显减少，同相轴能量也更聚焦，因此该方法适用于低信噪比数据的高质量成像。

分析图 9所示PP波单道振幅曲线，可知本文方法能有效压制噪声，提高成像信噪比，减少噪声对偏移成像的影响，使偏移成像剖面更清晰。

3 结束语

本文在倾斜叠加公式中加入阈值控制函数，并应用于弹性波高斯束偏移成像，形成了基于阈值控制的弹性波高斯束偏移方法。从模型偏移成像效果看，常规弹性波高斯束偏移成像方法对低信噪比资料成像噪声影响较大，勘探目标不清晰，偏移剖面质量较低；而采用本文方法则能有效压制噪声影响，提高地震数据信噪比及整体成像质量。

因条件所限，目前尚未进行弹性波实际资料测试。另外，所做的试算仅是针对各向同性介质。后续将把该方法推广应用于更复杂介质及实际数据。