2. 中国石油西南油气田分公司, 四川成都 610051
2. PetroChina Southwest Oil & Gas Field Company, Chengdu, Sichuan 610051, China
近年来,在地震偏移速度建模与成像过程中,越来越多地关注到地震信号在非弹性介质传播时发生的能量与频率衰减问题。尤其是有气云存在的复杂探区,地震波信号传播受地层吸收、衰减严重,气云下伏地层的成像分辨率低、反射波能量弱,有效反射信号较难识别,影响速度建模精度,进而造成偏移成像数据品质低。因此,需要进行地震波吸收衰减补偿以提高速度建模精度,得到分辨率和精度更高的地震偏移数据,为后期储层预测工作奠定良好的数据基础[1-4]。
速度建模精度是影响地震偏移数据品质的一个重要因素。目前常用的叠前深度偏移速度建模方法有速度扫描法、沿层谱分析方法[5]、网格层析反演[6]以及全波形反演(FWI)方法[7-9]等。气云是一种特殊的速度局部异常体,地震波经过气云区能量剧烈衰减,使依赖反射同相轴残差拾取的速度更新方法(如沿层谱分析法、网格层析法等)应用受限,加之气云形态和分布范围具有局部性和不确定性,单纯依赖传统速度更新方法难以高效、准确地进行高精度速度建模。FWI反演同时考虑地震波走时与振幅信息,在理论上能够较好地进行气云类异常体的速度建模。但是,由于对初始模型有较强的依赖性且计算量较大,目前FWI反演在实际工业生产的应用依旧面临困难。
地震波在传播过程中的吸收衰减效应通常采用品质因子Q量化,Q模型的精度对补偿效果具有决定性作用[10]。国内外学者对Q值反演和应用以及Q层析成像做了大量的理论研究和实际资料应用[11-14],Dutta等[15]、Pan等[16]、Huang等[17]、Jin等[18]提出并发展了多种建立地下介质Q模型的方法,目前常见的方法有经验公式法[19]、VSP约束Q建模[20-21]、射线Q层析反演[22-25]、全波形Q反演(QFWI)[26-27]、黏声反射波形Q反演(QRWI)[28]等。
本文应用计算效率较高的射线Q层析反演方法[29],在传统速度建模方法的基础上,提出一种基于Q层析反演约束的叠前深度偏移速度建模方法。新方法的核心思想是:利用基于峰值频率的Q层析反演建立Q模型,并在Q模型的约束下开展有针对性的局部速度更新。不同于依赖地震反射道集残差拾取的速度层析,Q层析反演是基于峰值频率的非线性计算,这对气云区以及一些特殊异常体的识别更加有利,可以实现高效、准确的速度建模。在建模过程中,Q模型与速度模型相互促进、迭代更新,实现速度模型和吸收衰减模型的同步优化,最终达到提升叠前深度偏移成像品质的目的。
本文基于理论数据验证了建模流程的正确性,并应用到中国西南部陆上复杂气云探区的地震资料处理中,实际资料的应用效果表明新方法具备有效性和可行性,实现了该区域更准确、高效的速度更新,显著提升了偏移成像剖面和道集的品质,为后续工作奠定了良好的数据基础。
1 Q反演约束的速度建模方法 1.1 Q模型层析反演原理地震波传播过程中,介质对地震波的吸收衰减引起地震子波形态的改变和能量损耗,进而造成成像剖面分辨率降低、相位畸变以及反射层成像深度误差等问题。在气云发育的勘探区,当地震波穿过气云区,地震信号中高频成分的衰减更加严重[14],分辨率明显降低。
经过衰减的信号同时携带着用于估计品质因子的重要信息。文中使用的Q层析反演方法依然采用近年来广泛流行的峰值频率衰减法,在求解信号峰值频率的过程中采用对信号做短时窗自相关等思路,使信号的频谱更接近雷克子波,增加了峰值频率估计的稳定性和有效Q值的计算精度。在射线追踪的过程中,考虑了速度异常导致的射线路径的剧变,采用直射线提高射线密度的均匀性,从而降低反演方程的奇异性,提高了反演结果的稳定性和分辨率。
该方法主要包括初始Q模型建立和Q模型层析反演两个核心步骤。初始Q模型采用李庆忠[19]提出的经验公式
| $ Q\approx 14{V}_{\mathrm{p}}^{2.2} $ | (1) |
式中:
Q层析的关键是有效Q场估算。有效Q场是指地震波全路径传播过程中Q效应的累积测量,而Q层析反演的目标是层间Q场,即求得某个度量间隔内的Q值。二者的关系可定义为
| $ \frac{t}{{Q}_{\mathrm{e}}^{}}=\sum\limits _{i=1}^{N}\frac{t}{{Q}_{i}} $ | (2) |
式中:
从初始Q模型出发,基于射线追踪技术模拟得到的有效Q场定义为模拟值
| $ \frac{t}{{Q}_{\mathrm{e}}^{\mathrm{o}}}-\frac{t}{{Q}_{\mathrm{e}}^{\mathrm{m}}}=\sum\limits _{i, j, k}^{N}({t}_{i, j, k}.\delta {Q}_{i, j, k}^{-1}) $ | (3) |
式中:
传统的速度层析反演是线性化反演,在残差拾取的基础上建立速度层析方程,速度更新后必须重新进行叠前深度偏移才能进行新一轮的残差拾取。如此多轮偏移、多轮层析的工作量非常大,不适合工业实际生产使用。而Q层析反演是非线性反演,基于峰值频率的移动建立Q层析方程,峰值频率总体上是不变量,即完成一次深度偏移后便可以基于该偏移结果进行峰值频率拾取,而且速度不变,射线路径也不发生改变。所以式(3)左端的矩阵是不变的,无需多轮偏移计算,利用峰值频率拾取量和层析方程便可进行多次层析反演迭代计算,因此称之为非线性的反演。
基于小扰动假设,Q层析求解层析方程时的反演更新量并不大,但是经过多次内循环迭代反演求解,基本可以精确定位局部异常体。这样仅需要一次偏移计算和一次Q层析非线性反演即可高效、准确地定位局部异常体。
李庆忠[19]提出了依据速度可以估计地下介质吸收衰减的总体趋势,表明速度与品质因子Q存在密切关系。对于气云等地震波传播的高衰减区,Q值通常较小且集中,在深度偏移剖面上,气云区下覆地质构造的成像分辨率及振幅明显降低。如图 1所示,根据经验公式和反演得到的Q场初步计算出异常体的参考速度,并结合Q场和深度偏移剖面特征圈定异常体的分布范围,再进行有针对性的局部速度扫描,对异常体进行速度更新;速度模型优化后,完成新的深度偏移计算;之后基于新速度模型和新的偏移数据进行新一轮Q层析反演,得到更优的Q模型。由此可见,层析反演Q场和速度模型更新是交替进行、相互补充的关系,速度场和Q场逐步迭代求精。最终,使用新速度场、新Q场进行Q叠前深度偏移,实现衰减信号的振幅、频率补偿,以提高偏移剖面的成像品质。
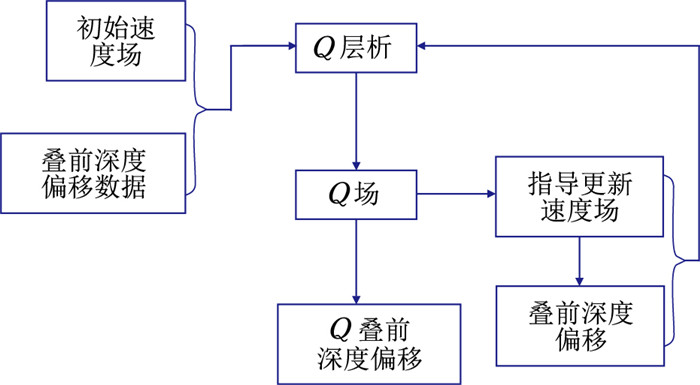
|
图 1 Q场与速度场相互优化过程 |
传统的叠前深度偏移速度建模方法主要有速度扫描、谱分析及层析反演等。速度扫描和谱分析属于沿层分析方法,层析反演属于区域性算法,更新量会分布到射线路径经过的所有网格上。气云是形态较难确定的局部异常体,它的分布范围往往跨越常规构造分层,在处理有类似气云等高吸收衰减、低速异常体发育的复杂探区资料时,通过传统速度分析方法可以得到宏观速度模型。此外,不同炮检距的射线对局部异常体速度的感应不同,在同相轴上表现为近炮检距和远炮检距的形态矛盾,加之受到吸收衰减影响,反射同相轴能量较弱,给层析反演的残差拾取带来困难,影响层析反演精度。并且如前文所述,速度层析反演属于线性反演,需要付出非常大的计算代价才有可能准确定位局部异常体。因此,单纯使用传统速度建模方法较难准确反演气云区速度,难以解决低速气云区的速度建模问题。
图 2展示了传统叠前深度偏移速度建模流程,基于此流程可完成大部分勘探区域的速度建模。
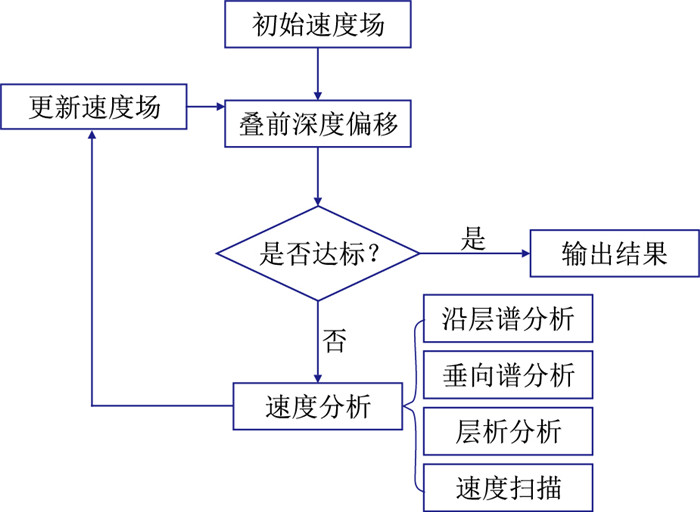
|
图 2 传统叠前深度偏移速度建模流程 |
而针对气云区域的精细建模,本文采用如图 3所示流程,具体步骤如下。
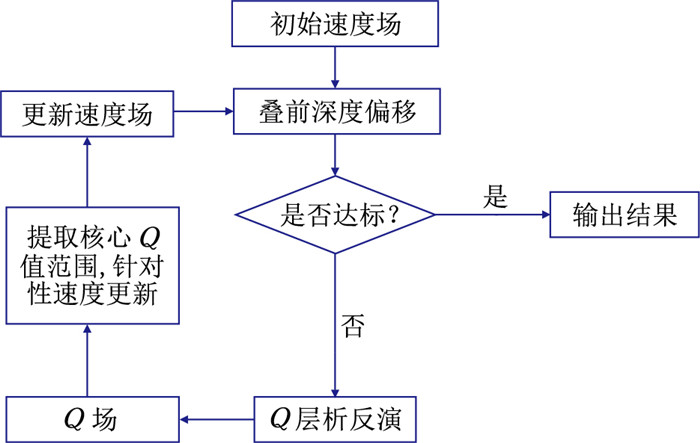
|
图 3 Q层析反演约束的速度分析流程 |
第一步:基于初始速度场进行叠前深度偏移,得到偏移成像道集和剖面。这里将图 2传统速度分析方法优化后的输出速度场作为初始速度场进行精细速度更新。这种针对气云等高衰减、局部低速异常体的速度建模方法具有准确、高效更新速度的特点,可以作为传统速度建模分析方法的有效补充。
第二步:依据式(1)生成初始Q模型,再基于初始速度场、初始速度场的深度偏移道集和剖面进行Q层析反演,得到反演Q场。通过非线性的Q层析反演可以高效、准确地初步定位局部异常体。理想的Q模型能够很好地表征低速气云的分布,Q值较大且集中的区域代表了强衰减气云区。
第三步:基于反演Q场开展速度更新。反演Q场中的核心区域(Q值较大且集中的区域)表征了局部低速异常体的分布范围,此外参考深度偏移剖面和道集特征,并通过加入人工拾取点干预、调整该目标异常体范围。之后,由反演Q场和经验公式初步计算异常体参考速度,在目标范围内依据深度偏移CIP道集和剖面,采用速度扫描、手工编辑、区域约束等速度层析方法对目标范围内的速度优化更新,得到新速度场。较理想的速度模型满足:①深度偏移CIP道集同相轴平直;②成像剖面同相轴连续、聚焦,断层断点成像清晰;③整体成像形态符合地层沉积规律。Q层析反演、速度更新、叠前深度偏移迭代结果相互促进,直至深度偏移剖面和道集达到预期效果。经过多次迭代求解基本可以准确定位局部异常体。
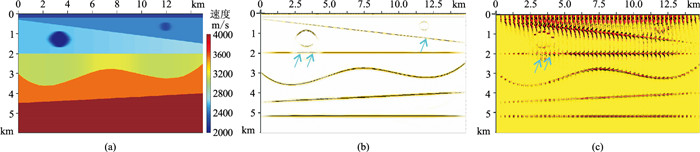
2 数值模型试验设计图 4a所示的理论模型进行数值模型试验。模型宽15 km,深6 km,包含左、右两个局部低速异常体。左侧大异常体最大宽度约1530 m,最大深度800 m,填充速度为1800 m/s,所在层围岩速度为2500 m/s,Q值为40;右侧小异常体最大宽度660 m,最大深度420 m,填充速度为2000 m/s,所在层速度为2300 m/s,Q值为60。基于背景场准确的速度初始模型(图 4b)进行基于Q层析反演技术的速度分析,以验证本文方法的正确性和有效性。同时,对比、分析了层析反演法对局部异常体的处理效果。
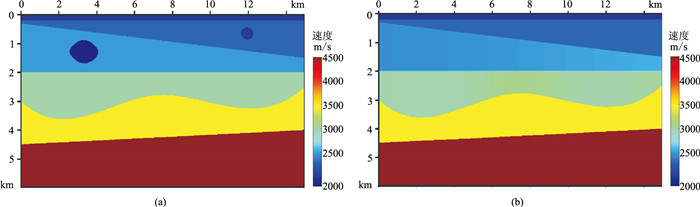
|
图 4 数值试验理论模型(a)及初始速度场(b) |
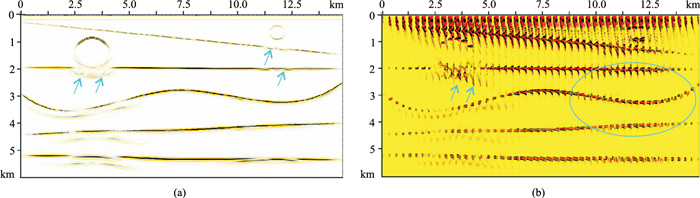
采用初始速度模型进行叠前深度偏移计算,得到偏移剖面和CIP道集(图 5)。可以看到,由于左侧大异常体与围岩速度差异较大,成像剖面上异常体下方同相轴凹陷较明显,影响范围较广;而右侧小异常体引起的同相轴破碎较隐蔽,地震解释时容易被忽略。从CIP道集上看,虽然只有两个异常体存在速度误差,但模型中部的深层偏移道集也受到两侧异常体的影响,异常体下方及中间的道集都存在剩余深度(图 5中箭头和蓝圈所示)。需要指出的是,实际资料处理过程中,往往难以观察到类似图 5b左侧的气云团响应特征。
|
图 5 初始速度场PSDM剖面(a)及CIP道集(b) |
首先,采用层析反演方法更新速度。图 6展示了迭代多次后层析反演的更新速度场(图 6a)、更新量(图 6b)和同相轴残差拾取(图 6c),可以发现:①速度层析反演能够反演出两个低速异常的趋势,但由于层析基于小扰动假设,且具有区域性速度更新的特点,低速异常体影响的区域由浅至深呈三角带分布(图 6a三角区内)。处于三角带区域的反射点对应的“射线对”穿过异常体,也会求解出速度更新量(图 6b),而且这种区域性更新需要经过多轮次层析和偏移才能被收敛,因此在没有其他先验约束信息的前提下,速度层析难以高效地反演出相对准确的气云分布范围及速度。此外,处理实际资料时还会出现信噪比问题,单纯使用速度层析解决局部异常体反演问题有实际困难。②图 6c上局部异常体的存在导致一些特殊位置的同相轴远、近炮检距对速度的响应不同,甚至出现相互矛盾的情况。即使没有信噪比问题,拾取到的残差曲线也会让层析难以准确判断速度的校正方向。这些因素造成了层析反演方法精度降低。
|
图 6 层析反演方法速度分析结果 (a)更新速度场;(b)更新量;(c)图 5b中蓝圈内道集残差拾取 |
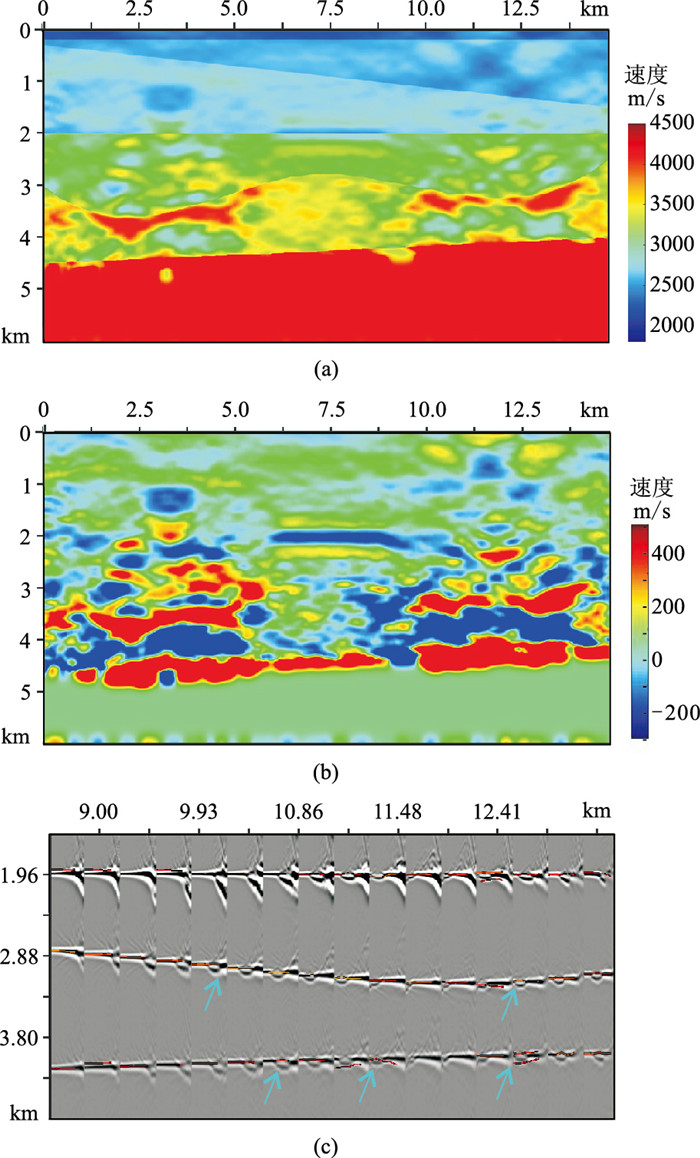
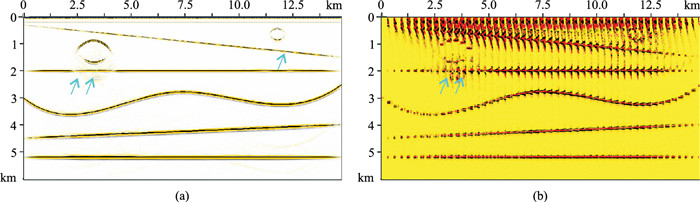
其次,基于Q层析反演技术进行气云区的速度分析。第一步,使用初始速度及对应的叠前深度偏移数据进行Q层析反演,得到图 7a所示的反演Q场。图 7b、图 7c分别是Q场与准确速度场以及与初始速度场叠前深度偏移剖面的叠合显示,可以看出,反演Q场的核心Q值区域准确表达了异常体范围和位置,与初始速度场偏移剖面上受异常体影响的范围非常吻合。第二步,基于经验公式和反演Q场计算异常体的参考速度,并提取Q场中的强衰减区,对该区域进行速度扫描、分析和速度更新,得到更新速度场(图 8a),图 8b、图 8c展示了对应的叠前深度偏移剖面和道集。可以看出,成像道集和剖面的效果得到了较明显改进。基于Q层析反演继续对局部异常体进行准确、精细的速度更新。此时,异常体下方同相轴的能量相对左、右两侧明显变弱(尤其是左侧大异常体影响区域衰减更为明显)。进一步采用Kirchhoff积分法Q叠前深度偏移技术进行补偿,得到补偿后偏移剖面和道集(图 9)。可以看到,两个异常体下方的同相轴成像品质都得到了提升,尤其是左侧大异常体下方区域补偿效果更为明显(图 9中箭头处)。
|
图 7 本文方法反演Q场(a)及其与理论模型(b)、初始速度场PSDM剖面(c)的叠合显示 |
|
图 8 基于Q场约束更新后的速度场(a)及对应的PSDM剖面(b)、道集(c) |
|
图 9 基于新方法更新后的速度场Q-PSDM剖面(a)与CIP道集(b) |
X区块为中国西南部三维复杂勘探区,该探区存在丰富的天然气团。图 10a、图 10b分别展示了该区域初始速度场(采用传统速度分析方法优化后的结果)及其对应的叠前深度偏移剖面(采用Kirchhoff积分法叠前深度偏移技术获得)。观察到该区域存在明显的低速异常气云区,气云下伏地层同相轴连续性变差、振幅减弱、分辨率降低(图 10b蓝色箭头处)。在图 10c的偏移成像道集上(局部道集)可见,受气云区吸收、衰减影响,浅层反射信号弱,残差拾取困难,并且受局部异常速度影响强烈,同相轴由浅至深呈现不同的弯曲形态(图 10c红色箭头处)。为了快速、准确地解决气云低速异常体的速度更新问题,本文直接利用Q层析反演技术校正气云区速度、优化速度模型。
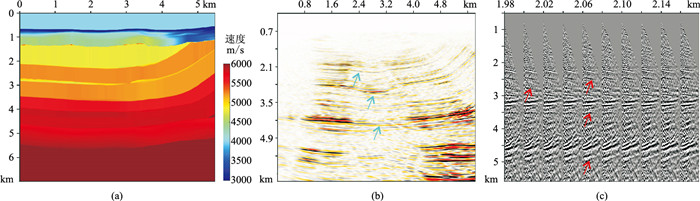
|
图 10 初始速度场(a)及对应的叠前深度偏移剖面(b)和局部成像道集(c) |
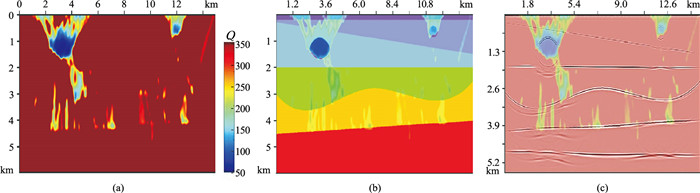
依据图 2流程首先基于初始速度场创建初始Q模型,并结合初始速度场的常规叠前深度偏移剖面和道集数据进行Q层析反演,得到反演Q场(图 11a),将反演Q场与初始速度叠前深度偏移剖面叠合显示(图 11b),可见该Q值模型的低值异常区与偏移剖面展示的低速气云影响范围一致(同相轴突然出现由浅至深的凹陷),气云区范围在Q场中有较好的展现。
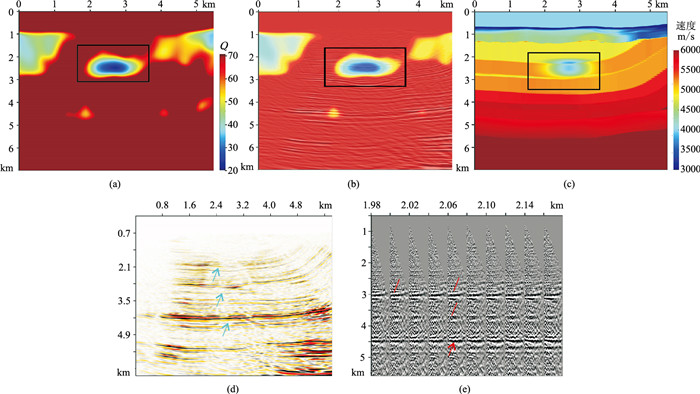
|
图 11 基于Q层析反演技术的更新速度场及对应的叠前深度偏移剖面、成像道集 (a)反演Q场;(b)反演Q场与初始速度场PSDM剖面叠合;(c)更新速度场;(d)更新速度场后的PSDM剖面;(e)更新速度场后的成像道集 |
以该Q值模型为参照提取气云分布范围,并给予一定的人工解释干预,再采用手工编辑速度开展针对性速度分析校正。从Q层析反演、目标区分布范围提取、人工补充解释到速度更新,该过程可迭代多次,最终得到校正后速度场及对应的叠前深度偏移剖面和道集(图 11c~图 11e)。对比图 10可以看出:更新速度场的PSDM CIP道集同相轴被拉平(图 11e红色箭头处);叠加剖面同相轴连续、自然,振幅能量及分辨率明显提高(图 11d蓝色箭头处)。另外,从优化后的速度场中注意到,气云范围跨越多个速度模型边界,以这种形态分布的速度区域一般难以通过传统沿层谱分析或具有区域性更新特点的网格层析反演技术实现快速、准确建模。
在上述常规叠前深度偏移的基础上,进一步采用Kirchhoff积分法Q叠前深度偏移技术对衰减能量和频率进行补偿,得到的Q-PSDM剖面和CIP道集(图 12)。由图可见:①Q叠前深度偏移剖面中气云下伏地层振幅和频率均得到补偿,同相轴分辨率提高,波组特征清楚,弱能量区的成像质量明显改善(图 12a箭头位置所示);②CIP道集同相轴连续、聚焦,更有利于开展AVO分析处理和地震解释工作(图 12b箭头位置所示);③图 12c为常规偏移和Q偏移剖面的频谱对比,可见目标区内常规PSDM资料主频小于10 Hz,Q偏移后资料主频在10 Hz左右,且振幅和频率都有所提高(左);而目标区外的Q偏移资料振幅略有提升,但二者频带范围没有明显变化(右)。
综上所述,实际资料应用效果表明基于Q层析反演技术的局部低速异常体速度建模方法准确、有效、可行。

|
图 12 Q-PSDM叠加剖面(a)、局部成像道集(b)及频谱分析对比(c) |
本文提出一种应用Q层析反演技术对气云等高衰减、低速异常体进行速度精细建模新方法,通过理论模型试验和实际数据应用验证了该方法的正确性和可行性,获得以下结论。
(1)速度模型和Q模型在迭代过程中相互促进,实现同步更新,之后应用Q叠前深度偏移技术对能量衰减进行振幅和频率双补偿,获得的CIP道集同相轴更为聚焦、连续,成像结果波组特征更清楚、构造形态更清晰。处理结果有利于开展AVO/AVA分析,为地震资料解释、属性分析和储层预测等后期工作奠定了数据基础。
(2)基于Q层析反演技术可以帮助高效、准确地圈定气云范围,进行细致且有针对性的速度校正,提高了速度建模效率。该方法可作为传统叠前深度偏移速度建模方法的有效补充,有助于得到更精细、更准确的速度模型。
| [1] |
HARGREAVES N D, CALVERT A J. Inverse Q filtering by Fourier transform[J]. Geophysics, 1991, 56(4): 519-527. DOI:10.1190/1.1443067 |
| [2] |
丁在宇, 郭建卿, 宫同举, 等. Q偏移处理技术在浅海气云区成像的应用与效果[C]. 中国石油学会2017年物探技术研讨会论文集, 2017, 1069-1071. DING Zaiyu, GUO Jianqing, GONG Tongju, et al. Application and effect of Q-migration processing techno-logy in shallow sea gas cloud region imaging[C]. Proceedings of the 2017 Geophysical Exploration Techno-logy Seminar of the Chinese Petroleum Society, 2017, 1069-1071. |
| [3] |
KOROBKIN V, NOVIKOV E, NAKATSUKASA M. Application of QFWI and QPSDM techniques for improvement of seismic image below gas cloud and faults clarification on Sakhalin offshore[C]. Geomodel 2020, 2020, 1-5.
|
| [4] |
张壹, 王赟, 陈本池, 等. 强衰减介质中地震波场的频率—空间域特征[J]. 石油地球物理勘探, 2020, 55(5): 1016-1028, 1046. ZHANG Yi, WANG Yun, CHEN Benchi, et al. Characteristics of seismic wave field in frequency-space domain in strong attenuation media[J]. Oil Geophysical Prospecting, 2020, 55(5): 1016-1028, 1046. DOI:10.13810/j.cnki.issn.1000-7210.2020.05.010 |
| [5] |
程玉坤, 刘建红, 周振晓, 等. 速度建模特色技术的实际应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 110-115. CHENG Yukun, LIU Jianhong, ZHOU Zhenxiao, et al. Depth-domain velocity model building for prestack depth imaging[J]. Oil Geophysical Prospecting, 2017, 52(S2): 110-115. |
| [6] |
马俊彦, 张龙, 罗昭洋, 等. 黏滞介质Q偏移技术在准噶尔盆地南缘低信噪比地区的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 94-99. MA Junyan, ZHANG Long, LUO Zhaoyang, et al. Q migration of low-SNR seismic data for visco-elastic media in Southern Junggar Basin[J]. Oil Geophysical Prospecting, 2018, 53(S1): 94-99. |
| [7] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophy-sics, 2009, 74(6): WCC1-WCC26. |
| [8] |
DONG L, HUANG C, CHI B, et al. Strategy and application of waveform inversion based on seismic data subset[J]. Chinese Journal of Geophysics, 2015, 58(6): 628-639. DOI:10.1002/cjg2.20200 |
| [9] |
杨瑞冬, 黄建平, 杨振杰, 等. 基于双对角通量校正的多尺度全波形反演[J]. 石油地球物理勘探, 2022, 57(5): 1120-1128. YANG Ruidong, HUANG Jianping, YANG Zhenjie, et al. Multi-scale full waveform inversion based on double diagonal flux correction transport[J]. Oil Geophysical Prospecting, 2022, 57(5): 1120-1128. DOI:10.13810/j.cnki.issn.1000-7210.2022.05.013 |
| [10] |
WANG Y. Inverse-Q filtered migration[J]. Geophy-sics, 2008, 73(1): S1-S6. |
| [11] |
ZHANG J, WU J, LI X. Compensation for absorption and dispersion in prestack migration: an effective Q approach[J]. Geophysics, 2013, 78(1): S1-S14. DOI:10.1190/geo2012-0128.1 |
| [12] |
GAMAR F, CAROTTI D, GUILLAUME P, et al. Success of high-resolution volumetric Q-tomography in the automatic detection of gas anomalies on offshore Brunei data[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 5184-5188.
|
| [13] |
KEERS H, KEERS D W, JOHNSON L R. Visco-acoustic crosswell imaging using asymptotic waveforms[J]. Geophysics, 2001, 66(3): 861-870. DOI:10.1190/1.1444975 |
| [14] |
ZHANG C, ULRYCH T J. Estimation of quality factors from CMP records[J]. Geophysics, 2002, 67(5): 1542-1547. DOI:10.1190/1.1512799 |
| [15] |
DUTTA G, SCHUSTER G T. Wave-equation Q tomography[J]. Geophysics, 2016, 81(6): R471-R484. DOI:10.1190/geo2016-0081.1 |
| [16] |
PAN W, INNANEN K A, WANG Y. Adjoint Q tomography with central-frequency measurements in viscoelastic medium[J]. Geophysical Journal International, 2023, 233(2): 1144-1165. DOI:10.1093/gji/ggac502 |
| [17] |
HUANG C, ZHU T, XING G. Data-assimilated time-lapse visco-acoustic full-waveform inversion: theory and application for injected CO2 plume monitoring[J]. Geophysics, 2023, 88(1): R105-R120. DOI:10.1190/geo2021-0804.1 |
| [18] |
JIN C, CAO D, ZHOU B, et al. Joint visco-acoustic waveform inversion with the separated upgoing and downgoing wavefields in zero-offset vertical seismic profile data[J]. Geophysical Prospecting, 2023, 71(1): 125-139. |
| [19] |
李庆忠. 走向精确勘探的道路: 高分辨率地震勘探系统工程剖析[M]. 北京: 石油工业出版社, 1993. LI Qingzhong. The Way to Obtain A Better Resolution in Seismic Prospecting: A Systematical Analysis of High Resolution Seismic Exploration[M]. Beijing: Petroleum Industry Press, 1993. |
| [20] |
STAINSBY S D, WORTHINGTON M H. Q estimation from vertical seismic profile data and anomalous variations in the central North Sea[J]. Geophysics, 1985, 50(4): 615-626. |
| [21] |
HAUGE P S. Measurements of attenuation from vertical seismic profiles[J]. Geophysics, 1981, 46(11): 1548-1558. |
| [22] |
BRZOSTOWSKI M A, MCMECHAN G A. 3-D tomographic imaging of near-surface seismic velocity and attenuation[J]. Geophysics, 1992, 57(3): 396-403. |
| [23] |
XIE Y, XIN K, SUN J, et al. 3D prestack depth migration with compensation for frequency dependent absorption and dispersion[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2919-2923.
|
| [24] |
HU W, LIU J, BEAR L, et al. A robust and accurate seismic attenuation tomography algorithm[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 2727-2731.
|
| [25] |
CAVALCA M, MOORE I, ZHANG L, et al. Ray-based tomography for Q estimation and Q compensation in complex media[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 3989-3993.
|
| [26] |
YONG P, BROSSIER R, MÉTIVIER L, et al. Q estimation by full-waveform inversion: analysis and misfit functions comparison[C]. First International Meeting for Applied Geoscience & Energy Expanded Abstracts, 2021, 827-831.
|
| [27] |
XUE Z, SUN J, FOMEL S, et al. Accelerating full-waveform inversion with attenuation compensation[J]. Geophysics, 2018, 83(1): A13-A20. |
| [28] |
邹鹏, 程玖兵. 黏声方程Q值反射波反演[J]. 地球物理学报, 2020, 63(1): 287-297. ZOU Peng, CHENG Jiubing. Visco-acoustic wave equation reflection inversion for the Q model[J]. Chinese Journal of Geophysics, 2020, 63(1): 287-297. |
| [29] |
WANG L, LIANG J, ZHOU Z, et al. A more stable Q tomography for strong anomalies[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 4196-4200.
|



 王磊,北京市西城区新康路5号东方地球物理公司北京研究中心,100088。Email:
王磊,北京市西城区新康路5号东方地球物理公司北京研究中心,100088。Email: