2. 喀斯特地质资源与环境教育部重点实验室(贵州大学), 贵州贵阳 550025
2. Key Laboratory of Karst Georesoucres and Environment (Guizhou University), Ministry of Education, Guiyang, Guizhou 550025, China
地下介质普遍具有各向异性特征,其主要表现为地震波传播速度随传播方向变化,因此在实际资料处理中采用传统各向同性偏移方法会产生较大的成像误差[1]。近年来,为提高深部储层及复杂构造区的成像质量,进一步挖潜剩余油气储量,各向异性偏移已成为地震资料常规处理的重要环节。鉴于各向异性弹性波逆时偏移存在参数较多且精度有限、波场分离难度大、计算成本高等难题,在实际生产中,通常采用更具可行性的qP(quasi-P)波逆时偏移[2-3]。
对于各向异性介质,用于实现其逆时偏移算法的qP波方程大多源于拟声波近似。Alkhalifah[2]假设沿对称轴方向的横波速度为零,简化了VTI(Vertical Transversely Isotropic)介质相速度公式,导出了VTI介质四阶拟声波波动方程。在此基础上,人们利用不同方法发展了多种形式的拟声波方程[4-5]。然而,基于拟声波近似思想的qP波方程一直存在qP波与qSV(quasi-SV)波耦合的现象,即使在均匀介质的波场快照中,也包含有残余qSV波能量,利用该类方程进行逆时偏移可能出现严重的偏移假象和数值不稳定,成像效果不佳。为了彻底消除伪横波干扰、避免不稳定现象,有学者考虑从qP波和qSV波耦合频散关系出发,推导出不含qSV波的纯qP波方程[6-7];与耦合波动方程相比,纯qP波能够实现更精确的波场模拟及逆时偏移,但其控制方程中包含复杂的拟微分算子,不易直接采用数值方法进行求解。因此,针对纯qP波方程的高效求解方法仍是当前的研究热点。
迄今为止,已发展了多种形式的纯qP波方程及相应的求解方法。Chu等[8]利用泰勒系数展开简化了纯qP波方程中的拟微分算子,推导了TTI(Titled Transversely Isotropic)介质纯qP波波动方程,并给出了伪谱法求解方案,然而该方法在波场延拓的每一时间步需进行多次Fourier变换(二维7次,三维22次),计算效率极低[9]。为此,Zhan等[10]联合伪谱法与有限差分法求解拟微分算子,减少了计算过程中所需的Fourier变换次数,在一定程度上提升了伪谱法的计算效率,但是在面对大规模或三维复杂模型的数值模拟时,计算成本仍会限制该类方法在实际生产中的应用[11]。此外,Xu等[12]另辟蹊径,将伪微分算子分解为一个椭圆微分算子和一个标量算子,并采用有限差分法进行求解,该策略计算效率较高,易于实现,已推广至各类复杂各向异性介质波场模拟和偏移成像[13]。用有限差分法进行纯qP波波场延拓需求解波场的空间偏导数,较大空间步长时易出现数值频散现象,与伪谱法相比,计算精度较低。近年来,为平衡纯qP波逆时偏移的计算精度与计算效率,还发展了快速泊松算法[14]、低秩分解算法[15-16]等。
为克服上述纯qP波求解方法的诸多不足,本文将兼具计算效率与计算精度的低秩有限差分法用于纯qP波波场延拓。Fomel等[17]利用低秩分解算法来近似空间—波数混合域地震波传播算子,实现了各向同性和各向异性介质的波场模拟,并指出低秩分解算法可以准确地描述地震波的运动学特征。随后,Song等[18]将该方法用于正交各向异性介质的正演模拟;Sun等[19]联合低秩分解与一步法延拓公式实现了黏弹介质的正演模拟及逆时偏移。在此基础上,顾汉明等[16]实现了基于低秩一步法延拓的黏声各向异性纯qP波正演模拟。由上述研究成果可知:低秩分解算法是利用频散关系构建不同介质的波场传播矩阵,进而实现精确的波场模拟,且无需推导显式波动方程。因此,该方法在各向异性介质正演模拟及逆时偏移中具有计算稳定、无数值频散以及无伪横波干扰等优势;然而,该方法在波场延拓的每一时间步也需要进行多次Fourier变换(一次正变换和多次反变换,反变换次数与模型复杂度有关)[15],其计算效率较低。针对这一不足,Song等[20]提出低秩有限差分算法,即利用低秩分解求取差分系数,有效地降低了波场模拟的计算成本,同时该方法还继承了低秩分解和有限差分法的优势,且具有较高的并行性。随后,方刚等[21]将低秩分解与交错网格有限差分相结合,提出了交错网格低秩有限差分法,实现了较大时间步长和空间步长下的波场延拓;袁雨欣等[22]将该方法用于弹性波正演模拟,有效地提高了常规交错网格有限差分的数值模拟精度;黄金强等[23]通过构建紧致差分模板求解低秩有限差分系数,实现了复杂TI介质纯qP波正演模拟及逆时偏移。然而,目前对低秩有限差分算法的研究还主要集中于二维情形,尤其是二维正演模拟的探讨,未见有应用于三维各向异性纯qP波逆时偏移的相关文献。
针对上述问题,本文借鉴前人利用低秩分解求解二维差分系数的思路[20, 23],构建了一种适用于三维各向异性介质的球型差分模板,随后结合低秩分解求解差分系数,将低秩有限差分法由二维拓展至三维,并实现了三维低秩有限差分法纯qP波正演模拟和逆时偏移。首先结合波动方程伪解析解和各向异性介质纯qP波频散关系,推导了各向异性介质纯qP波伪解析解波场延拓公式;随后,构建了三维球型差分模板,结合低秩分解求取与模型相适应的差分系数,由此实现三维纯qP波波场延拓;针对计算效率问题,利用GPU(Graphics Processing Unit)并行对波场延拓及成像过程进行加速,实现了基于GPU加速的低秩有限差分法纯qP波逆时偏移;最后,采用典型二维模型和三维模型进行逆时偏移成像测试,验证了本方法在二维各向异性介质成像方面的优势以及对于三维复杂模型成像的适用性。
1 方法原理 1.1 纯qP波波场延拓公式三维常密度声波波动方程可以表示为
| $ \frac{{\partial }^{2}p\left(\boldsymbol{x}, t\right)}{\partial {t}^{2}}={v}^{2}{\nabla }^{2}p\left(\boldsymbol{x}, t\right) $ | (1) |
式中:
| $ \frac{{\partial }^{2}P\left(\boldsymbol{k}, t\right)}{\partial {t}^{2}}=-{\left|\boldsymbol{k}\right|}^{2}{v}^{2}P\left(\boldsymbol{k}, t\right)=-{\phi }^{2}P\left(\boldsymbol{k}, t\right) $ | (2) |
式中:
| $ \left\{\begin{array}{l}p\left(\boldsymbol{x}, t\right)=\int P\left(\boldsymbol{k}, t\right){\mathrm{e}}^{\mathrm{i}\boldsymbol{k}\cdot \boldsymbol{x}}\mathrm{d}\boldsymbol{k}\\ P\left(\boldsymbol{k}, t\right)=\int p\left(\boldsymbol{x}, t\right){\mathrm{e}}^{-\mathrm{i}\boldsymbol{k}\cdot \boldsymbol{x}}\mathrm{d}\boldsymbol{x}\end{array}\right. $ | (3) |
引入一个复数波场
| $ \tilde{P}\left(\boldsymbol{k}, t\right)=P(\boldsymbol{k}, t)+\mathrm{i}Q(\boldsymbol{k}, t) $ | (4) |
式中
| $ Q\left(\boldsymbol{k}, t\right)=\frac{1}{\phi }\frac{\partial P\left(\boldsymbol{k}, t\right)}{\partial t} $ | (5) |
结合式(5),式(2)可等价为
| $ \frac{\partial \tilde{P}}{\partial t}=\frac{\partial \left(P+\mathrm{i}Q\right)}{\partial t}=-\mathrm{i}\phi \left(P+\mathrm{i}Q\right)=-\mathrm{i}\phi \tilde{P} $ | (6) |
对于变速介质,
| $ \frac{\partial \tilde{p}\left(\boldsymbol{x}, t\right)}{\partial t}=-\mathrm{i}\phi \left(\boldsymbol{x}\right)\tilde{p}\left(\boldsymbol{x}, t\right) $ | (7) |
式中拟微分算子
| $ \tilde{p}(\boldsymbol{x}, t\pm \mathrm{\Delta }t)={\mathrm{e}}^{\mp \mathrm{i}\phi \mathrm{\Delta }t}\tilde{p}\left(\boldsymbol{x}, t\right) $ | (8) |
式中Δt为时间延拓步长。通过Fourier变换,将式(8)转换至波数域
| $ \tilde{P}(\boldsymbol{k}, t\pm \mathrm{\Delta }t)={\mathrm{e}}^{\mp \mathrm{i}\phi \mathrm{\Delta }t}\tilde{P}(\boldsymbol{k}, t) $ | (9) |
式(9)即为波数域地震波场的时间正、反向一步法延拓公式。式(9)涉及复数运算,且
| $ \begin{array}{l}p(\boldsymbol{x}, t+\mathrm{\Delta }t)+p(\boldsymbol{x}, t-\mathrm{\Delta }t)\\ =\int 2\mathrm{c}\mathrm{o}\mathrm{s}\left[\phi (\boldsymbol{x}, \boldsymbol{k})\mathrm{\Delta }t\right]P(\boldsymbol{k}, t){\mathrm{e}}^{\mathrm{i}\boldsymbol{k}\cdot \boldsymbol{x}}\mathrm{d}\boldsymbol{k}\end{array} $ | (10) |
若基于上述公式直接求解,则需进行多次傅里叶变换。为此,本文利用非均匀介质频散关系,忽略高阶项,可对
| $ \phi \left(\boldsymbol{x}, \boldsymbol{k}\right)\approx v\left|\boldsymbol{k}\right|=\omega $ | (11) |
在各向同性介质中,相速度只与空间坐标
由上述推导可知,地震波传播算子与圆频率函数
| $ \begin{array}{l}{\omega }_{\mathrm{q}\mathrm{P}}\left(\boldsymbol{x},\boldsymbol{k}\right)=\frac{1}{2}\left\{\left[\left({v}_{\mathrm{H}}^{2}+{v}_{\mathrm{S}}^{2}\right){k}_{\mathrm{H}}^{2}+\left({v}_{\mathrm{P}}^{2}+{v}_{\mathrm{S}}^{2}\right){k}_{3}^{2}\right]+\right.\\ {\left.\sqrt{{\left[\left({v}_{\mathrm{H}}^{2}-{v}_{\mathrm{S}}^{2}\right){k}_{\mathrm{H}}^{2}-\left({v}_{\mathrm{P}}^{2}-{v}_{\mathrm{S}}^{2}\right){k}_{3}^{2}\right]}^{2}+S}\right\}}^{{}^{1/2}}\end{array} $ | (12) |
式中:
拟声波近似下的耦合型qP波方程在正演模拟中之所以会出现伪横波,是因为:①在推导显式qP波波动方程过程中,为了消去频散关系中的根号,防止分数阶算子的出现,对qP波频散关系式进行了平方处理,从而使方程产生了增根[25];②在各向异性介质中,令沿对称轴方向的横波速度为零,这一做法并不能使其他方向的横波相速度和群速度为零,因此在波场模拟时会出现伪横波干扰。
低秩方法利用频散关系构建波场传播算子,无需推导显式的qP波波动方程,也无需对频散关系进行平方处理,所以从根本上避免了伪横波的产生。低秩方法对精确频散关系和近似频散关系均有很好的适用性,在横波速度未知的情况下,可以假设横波速度为零,采用拟声波近似下的频散关系模拟qP波波场,这也是已有近似方法中最精确的。利用上述两种频散关系模拟的qP波波场特征十分接近[15],也即假设横波速度为零对qP波相速度没有太大的影响,因此本文利用qP波近似频散关系来构建纯qP波波场传播算子。假设
| $ \begin{array}{l}{\omega }_{\mathrm{q}\mathrm{P}}\left(\boldsymbol{x}, \boldsymbol{k}\right)=\frac{1}{2}\left[\left({v}_{\mathrm{H}}^{2}{k}_{\mathrm{H}}^{2}+{v}_{\mathrm{P}}^{2}{k}_{3}^{2}\right)+\right.\\ {\left.\sqrt{{\left({v}_{\mathrm{H}}^{2}{k}_{\mathrm{H}}^{2}+{v}_{\mathrm{P}}^{2}{k}_{3}^{2}\right)}^{2}-\frac{8\eta }{1+2\eta }{v}_{\mathrm{H}}^{2}{v}_{\mathrm{P}}^{2}{k}_{\mathrm{H}}^{2}{k}_{3}^{2}}\right]}^{1/2}\end{array} $ | (13) |
式中
再结合式(10)与式(11)即可得出VTI介质纯qP波波场延拓算子,该算子能够有效地消除伪横波干扰,同时可以准确地描述VTI介质纯qP波的运动学特征。对该算子的波数分量作如下坐标旋转变换
| $ \left(\begin{array}{c}{\tilde{k}}_{1}\\ {\tilde{k}}_{2}\\ {\tilde{k}}_{3}\end{array}\right)=\left(\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{c}\mathrm{o}\mathrm{s}\phi & \mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{s}\mathrm{i}\mathrm{n}\phi & \mathrm{s}\mathrm{i}\mathrm{n}\theta \\ -\mathrm{s}\mathrm{i}\mathrm{n}\phi & \mathrm{c}\mathrm{o}\mathrm{s}\phi & 0\\ -\mathrm{s}\mathrm{i}\mathrm{n}\theta \mathrm{c}\mathrm{o}\mathrm{s}\phi & -\mathrm{s}\mathrm{i}\mathrm{n}\theta \mathrm{s}\mathrm{i}\mathrm{n}\phi & \mathrm{c}\mathrm{o}\mathrm{s}\theta \end{array}\right)\left(\begin{array}{c}{k}_{1}\\ {k}_{2}\\ {k}_{3}\end{array}\right) $ | (14) |
即可拓展至TTI介质中。式中:
最后,将式(14)代入式(13),再结合式(10)与式(11)即可得到TTI介质纯qP波两步法延拓公式。由式(13)可见:在时间方向延拓一次需进行一次Fourier变换和
首先,依据式(10)与式(13)构建VTI介质纯qP波波场传播矩阵
| $ \begin{array}{l}\boldsymbol{W}\left(\boldsymbol{x}, \boldsymbol{k}\right)\approx \\ 2\left[\begin{array}{cccc}\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{\mathrm{1, 1}}\mathrm{\Delta }t\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{\mathrm{1, 2}}\mathrm{\Delta }t\right)& \cdots & \mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{1, M}\mathrm{\Delta }t\right)\\ \mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{\mathrm{2, 1}}\mathrm{\Delta }t\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{\mathrm{2, 2}}\mathrm{\Delta }t\right)& \cdots & \mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{2, M}\mathrm{\Delta }t\right)\\ & & ⋮& \\ \mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{N, 1}\mathrm{\Delta }t\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{N, 2}\mathrm{\Delta }t\right)& \cdots & \mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{N, M}\mathrm{\Delta }t\right)\end{array}\right]\end{array} $ | (15) |
式中
利用低秩分解将该空间—波数域传播矩阵
| $ \begin{array}{l}\boldsymbol{W}\left(\boldsymbol{x}, \boldsymbol{k}\right)\approx {\boldsymbol{W}}_{1}\boldsymbol{A}{\boldsymbol{W}}_{2}\\ =\sum\limits _{m=1}^{U}\sum\limits _{n=1}^{V}{\boldsymbol{W}}_{1}\left(\boldsymbol{x}, {\boldsymbol{k}}_{m}\right)\boldsymbol{A}{\boldsymbol{W}}_{2}\left({\boldsymbol{x}}_{n}, \boldsymbol{k}\right)\end{array} $ | (16) |
式中:
对子矩阵
| $ \begin{array}{l}\boldsymbol{W}(\boldsymbol{x}, \boldsymbol{k})\approx \sum\limits _{m=1}^{U}\sum\limits _{n=1}^{V}\sum\limits _{l=1}^{L}{\boldsymbol{W}}_{1}(\boldsymbol{x}, {\boldsymbol{k}}_{m})\boldsymbol{A}\boldsymbol{C}({\boldsymbol{x}}_{n}, {\boldsymbol{\xi }}_{l})\boldsymbol{B}({\boldsymbol{\xi }}_{l}, \boldsymbol{k})\\ =\sum\limits _{l=1}^{L}\boldsymbol{G}(\boldsymbol{x}, {\boldsymbol{\xi }}_{l})\boldsymbol{B}({\boldsymbol{\xi }}_{l}, \boldsymbol{k})\end{array} $ | (17) |
式中:L表示模板长度,即模板中参与计算的网格点总数;
| $ \boldsymbol{B}\left({\boldsymbol{\xi }}_{l}, \boldsymbol{k}\right)=2\left[\begin{array}{cccc}\mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits _{j=1}^{3}{\xi }_{1}^{j}{k}_{j}^{1}\mathrm{\Delta }{x}_{j}\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits _{j=1}^{3}{\xi }_{1}^{j}{k}_{j}^{2}\mathrm{\Delta }{x}_{j}\right)& \cdots & \mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits\limits _{j=1}^{3}{\xi }_{1}^{j}{k}_{j}^{{N}_{k}}\mathrm{\Delta }{x}_{j}\right)\\ \mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits _{j=1}^{3}{\xi }_{2}^{j}{k}_{j}^{1}\mathrm{\Delta }{x}_{j}\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits _{j=1}^{3}{\xi }_{2}^{j}{k}_{j}^{2}\mathrm{\Delta }{x}_{j}\right)& \cdots & \mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits _{j=1}^{3}{\xi }_{2}^{j}{k}_{j}^{{N}_{k}}\mathrm{\Delta }{x}_{j}\right)\\ & & ⋮& \\ \mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits _{j=1}^{3}{\xi }_{L}^{j}{k}_{j}^{1}\mathrm{\Delta }{x}_{j}\right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits _{j=1}^{3}{\xi }_{L}^{j}{k}_{j}^{2}\mathrm{\Delta }{x}_{j}\right)& \cdots & \mathrm{c}\mathrm{o}\mathrm{s}\left(\sum\limits _{j=1}^{3}{\xi }_{L}^{j}{k}_{j}^{{N}_{k}}\mathrm{\Delta }{x}_{j}\right)\end{array}\right] $ | (18) |
式中:
| $ \boldsymbol{G}\left(\boldsymbol{x}, {\boldsymbol{\xi }}_{l}\right)={\boldsymbol{W}}_{1}\left(\boldsymbol{x}, {\boldsymbol{k}}_{m}\right)\boldsymbol{A}\boldsymbol{C}\left({\boldsymbol{x}}_{n}, {\boldsymbol{\xi }}_{l}\right) $ | (19) |
最后,将式(17)代入式(10),根据Fourier变换的时移特性,式(10)可改写为[20]
| $ \begin{array}{l}p\left(\boldsymbol{x}, t+\mathrm{\Delta }t\right)+p\left(\boldsymbol{x}, t-\mathrm{\Delta }t\right)\\ \approx \sum\limits _{\boldsymbol{l}=1}^{\boldsymbol{L}}{g}_{\boldsymbol{l}}\left(\boldsymbol{x}\right)\left[p\left({\boldsymbol{x}}_{\mathrm{L}}, t\right)+p\left({\boldsymbol{x}}_{\mathrm{R}}, t\right)\right]\end{array} $ | (20) |
式中:gl为G的第l列元素;
| $ \left\{\begin{array}{l}{\boldsymbol{x}}_{\mathrm{L}}=\left(x-{\xi }_{l}^{1}{k}_{1}\mathrm{\Delta }x, y-{\xi }_{l}^{2}{k}_{2}\mathrm{\Delta }y, z-{\xi }_{l}^{3}{k}_{3}\mathrm{\Delta }z\right)\\ {\boldsymbol{x}}_{\mathrm{R}}=\left(x+{\xi }_{l}^{1}{k}_{1}\mathrm{\Delta }x, y+{\xi }_{l}^{2}{k}_{2}\mathrm{\Delta }y, z+{\xi }_{l}^{3}{k}_{3}\mathrm{\Delta }z\right)\end{array}\right. $ | (21) |
式(20)即为基于低秩有限差分的VTI介质纯qP波两步法波场延拓公式,对上式进行移项,可以得到其对应的波场正传与反传公式
| $ \left\{\begin{array}{r} p(\boldsymbol{x}, t+\Delta t) \approx \sum\limits_{l=1}^L g_l(\boldsymbol{x})\left[p\left(\boldsymbol{x}_{\mathrm{L}}, t\right)+\right. \\ \left.p\left(\boldsymbol{x}_{\mathrm{R}}, t\right)\right]-p(\boldsymbol{x}, t-\Delta t) \\ p(\boldsymbol{x}, t-\Delta t) \approx \sum\limits_{l=1}^L g_l(\boldsymbol{x})\left[p\left(\boldsymbol{x}_{\mathrm{L}}, t\right)+\right. \\ \left.p\left(\boldsymbol{x}_{\mathrm{R}}, t\right)\right]-p(\boldsymbol{x}, t+\Delta t) \end{array}\right. $ | (22) |
对比式(10)与式(22)可知:①低秩有限差分法在波场延拓时能够有效减少Fourier逆变换的次数,在时间方向延拓一次的计算复杂度为
本文借鉴二维低秩有限差分模板思想[20, 23],构建了适用于三维各向异性介质的球型差分模板,将前人利用低秩分解求解二维差分系数的思路拓展至球型差分模板的差分系数求解中,最终将低秩有限差分法由二维拓展至三维。本文构建的球型差分模板除了采用坐标轴方向的网格点参与波场递推计算外,在坐标轴以外的相应网格点也参与计算,与传统三维交错网格差分模板相比更具一般性和灵活性。假设模板中心网格点的坐标为
| $ {\left({i}^{\text{'}}-i\right)}^{2}+{\left({j}^{\text{'}}-j\right)}^{2}+{\left({h}^{\text{'}}-h\right)}^{2}\le {R}^{2} $ | (23) |
即所有参与计算的网格点都分布在以网格中心点为球心、以R为半径的球内,因此,一旦选定R,便可确定差分模板类型、模板长度L及对应参与计算的网格点索引数组
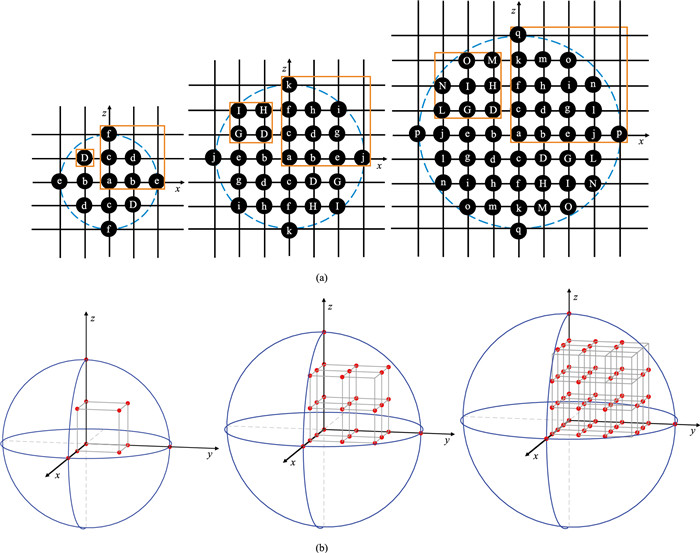
图 1展示了不同阶数的二维及三维差分模板示意图,图 1a中黑色圆圈所标识的字母分别表示该位置处的差分系数
|
图 1 二维(a)和三维(b)不同阶次低秩有限差分模板示意图 左、中、右依次为4阶(L=7)、6阶(L=15)、8阶(L=25)。 |
逆时偏移的实现过程主要包括震源波场正传、检波点波场反传以及互相关成像三个步骤:首先将震源波场沿时间正方向延拓,并将所有时刻波场值存入硬盘;随后将检波点波场沿时间反方向延拓,同时读取硬盘中相应时刻的震源波场值;最后应用互相关成像条件
| $ I\left(x, y, z\right)={\int }_{t}{p}^{\mathrm{f}}\left(x, y, z, t\right){p}^{\mathrm{b}}\left(x, y, z, t\right)\mathrm{d}t $ | (24) |
即可提取逆时偏移成像剖面。式中:
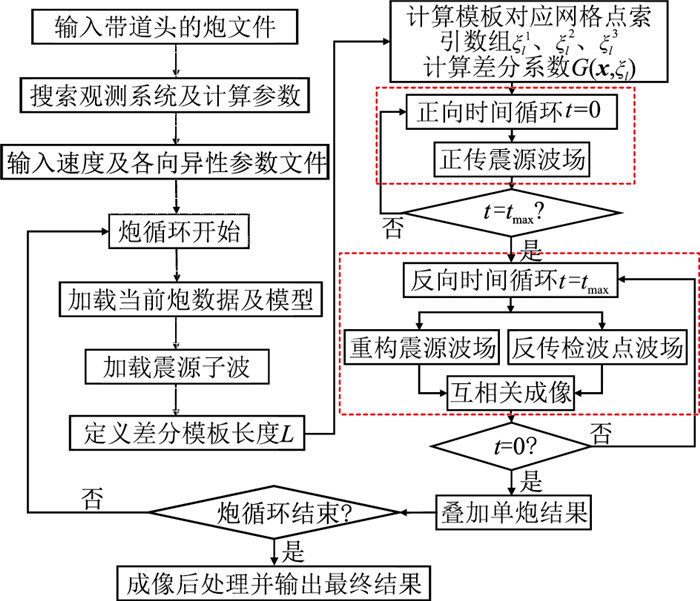
基于GPU并行加速的低秩有限差分逆时偏移实现流程如图 2所示,对于波场延拓与互相关成像部分利用GPU进行加速计算(图 2中红色虚线框所示),即分别利用GPU加速计算式(22)和式(24);并且在波场正传过程中利用自相关条件获取照明能量,以实现对成像结果的照明补偿。本文还采用了基于GPU并行的震源波场重构策略[26],即在震源波场正向延拓后,仅存储每一时刻的边界波场值,在检波点波场反向延拓的同时,通过边界波场值实现震源波场重构,利用同一时刻的两个波场值即可实现互相关成像。这一策略能够有效地降低逆时偏移过程中的存储要求和I/O传输次数,并且增加的计算量也是可以接受的。
|
图 2 基于低秩有限差分的逆时偏移成像流程 |
基于GPU并行的低秩有限差分逆时偏移具体算法过程如下:
(1)输入带道头的炮数据文件;
(2)搜索观测系统及计算参数,确定观测系统类型,激发总炮数、炮间距及炮点坐标位置,每炮的接收点个数、道间距及接收点坐标位置,时间采样点数及采样间隔;
(3)读入速度文件及各向异性参数文件;
(4)进入炮循环,根据观测系统加载当前炮的地震数据,并将模型参数与各向异性参数读入内存,同时生成地震子波;
(5)定义差分模板类型(二维或三维)及模板长度L,并计算差分模板对应的网格索引数组
(6)在计算区域内分配GPU线程,首先计算震源波场并保存震源波场的边界值。具体步骤:根据差分模板的网格点索引数组计算当前时刻的两波场之和p(xL,t)+p(xR,t);再将差分系数与两波场之和相乘;最后加上震源时间函数,即可实现震源波场正向时间延拓。该过程采用GPU加速,由零时刻逐步延拓至最大时刻,还需保存最后时刻的震源波场;
(7)其次,反传检波点波场,与步骤(6)相似,根据式(22)便可沿逆时间更新检波点波场,实现检波点波场的反向时间延拓,该过程仍然采用GPU加速,所不同的是,震源加载变为地震数据加载,由最大时刻反向延拓至零时刻;同步进行的还有震源波场重构,通过加载震源波场的边界值即可重构震源波场,该过程同样也利用GPU加速计算;
(8)将同一时刻的检波点波场与重构的震源波场进行互相关计算便可提取该时刻的成像值,将所有时刻的成像值进行累加,可得到当前炮的单炮成像结果;
(9)逐炮偏移,并将单炮成像结果进行叠加,直到完成所有炮;
(10)对所有炮的成像结果进行拉普拉斯滤波等处理后,便可输出最终成像剖面。
2 模型试算 2.1 均匀模型波场快照本文首先开展了三个均匀VTI介质正演试验来对比说明不同正演方法的特点,以验证本文方法的正确性。模型参数如表 1所示,模型纵、横向网格点数均为301,网格间距为10 m;震源采用主频为20 Hz的Ricker子波,在模型中心(1.5 km,1.5 km)处激发;时间采样点数为1501,时间步长为1 ms。
|
|
表 1 均匀VTI介质模型参数 |
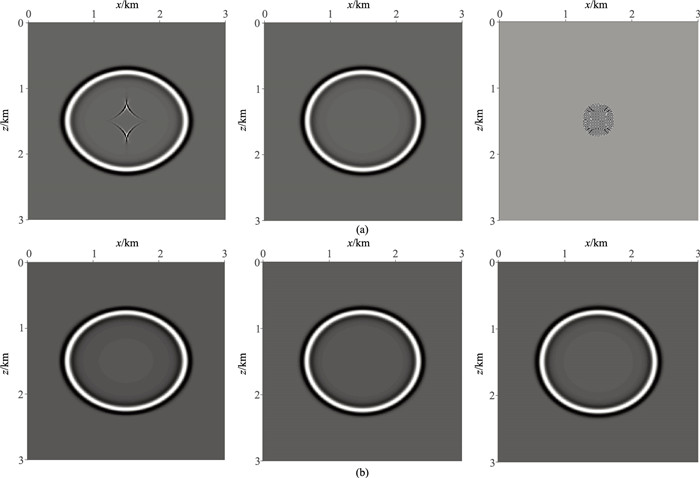
图 3a为常规拟声波方程交错网格高阶有限差分(SGFD,Staggered Grid Finite Difference)法的正演结果,图 3b为纯qP波低秩有限差分(LFD,Low⁃rank Finite Difference)法的正演结果。对比可见:常规拟声波方程只有在ε≥δ时才能实现波场的稳定传播(图 3a左、中所示)。需要说明的是,当ε>δ时,波场中会出现菱形的伪横波假象,在成像中会形成偏移噪声和假象,影响成像结果的同相轴连续性和降低剖面信噪比;当ε=δ时,代表椭圆各向异性介质,此时波场中无菱形干扰;当ε < δ时会出现严重的数值不稳定现象(图 3a右所示),在此情形下该方法失效,而纯qP波法则突破了这一参数限制,在任意类型的各向异性介质中均能实现波场的稳定传播,且正演结果都不存在伪横波干扰及数值不稳定性。
|
图 3 三个均匀模型不同方法模拟的0.3 s时刻波场快照 (a)拟声波方程SGFD法;(b)纯qP波LFD法。左、中、右依次对应模型Ⅰ~模型Ⅲ。 |
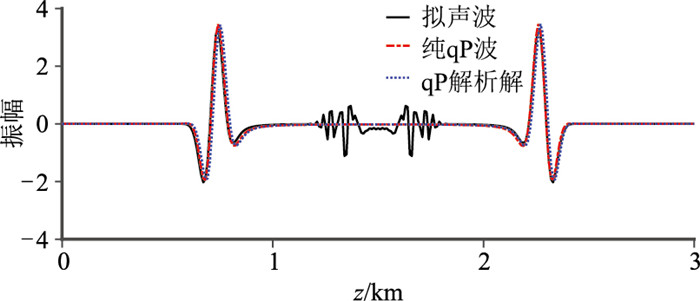
图 4展示了图 3a左和图 3b左在x=1500 m处的波场记录,对比可见:除伪横波干扰外,拟声波SGFD法、纯qP波LFD法与qP波的解析解高度吻合,验证了本文方法的正确性。
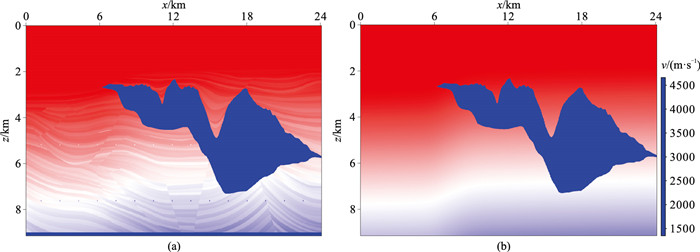
2.2 Sigsbee2a模型为了验证基于LFD的逆时偏移成像算法在计算效率上的优势,选用如图 5所示的Sigsbee2a各向同性模型进行测试。该模型主要由一个高速盐丘和几组正、逆断层构成,模型参数如下:模型网格数为3201×1201,网格间距均为7.62 m,模型尺寸为24.38 km×9.14 km。采用主频为25 Hz的Ricker子波作为激发震源,共激发500炮,第一炮位于x=281.94 m,炮间距为45.72 m,炮点深度均为7.62 m;采用348道检波器等间距移动接收,接收点的道间距为22.86 m,接收点深度为7.62 m,炮检距范围为0~7932.42 m。从第355炮开始采用变观采集,接收道数变为347道,随后逐炮按2道等差递减,最后一炮的接收道数变为57道,最后一炮的最大炮检距为1280.16 m,因此接收总道数为152684;时间采样点数均为1500,时间步长为8 ms。
|
图 5 Sigsbee2a模型 (a)真实速度;(b)偏移速度 |
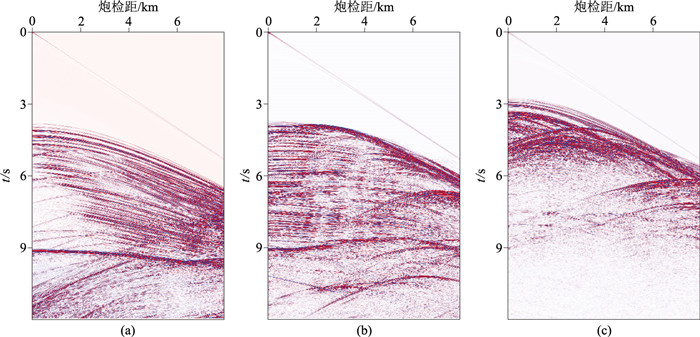
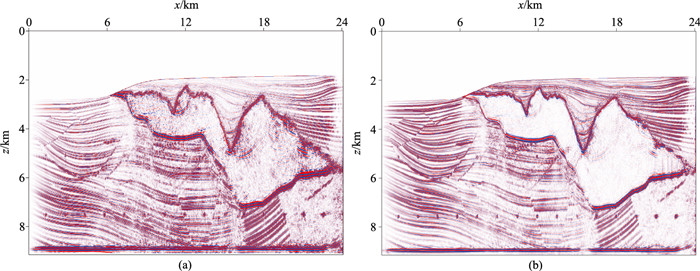
图 6为国际标准地震数据的不同单炮记录,可以看出:地震记录中浅部反射波同相轴连续,且浅部能量强、深部能量弱,与实际采集的地震记录特征相同。分别应用基于SGFD和基于LFD的逆时偏移方法进行成像试处理,成像结果如图 7所示。可见:在模型左侧约0~6 km范围内及盐丘右上部,因构造简单,两种方法都清晰地刻画出地层的起伏形态和薄层厚度,成像效果较好;相比于图 7a的SGFD法成像结果,在图 7b所示的LFD法成像结果中,盐丘内部的成像噪声更小,反射界面的同相轴连续性更好,盐丘轮廓的成像分辨率更高,浅中深层的能量更加均衡,因此总体成像质量更好。
|
图 6 Sigsbee2a模型单炮正演记录 (a)第1炮;(b)第100炮;(c)第200炮 |
|
图 7 Sigsbee2a模型两种方法逆时偏移结果对比 (a)SGFD法;(b)LFD法 |
在偏移成像测试过程中,两种方法均采用了GPU并行加速计算和震源波场重构策略,对其单炮偏移的耗时和内存占用进行了对比,结果如表 2所示。可见,相较于SGFD法,LFD方法的计算耗时更少、内存占用更低。测试结果表明,基于LFD的逆时偏移成像方法能够同时兼顾成像精度和计算效率。
|
|
表 2 Sigsbee2a模型两种方法单炮逆时偏移性能对比 |
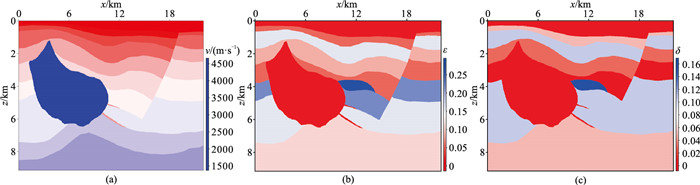
在验证了本方法正确性和有效性的基础上,采用VTI⁃Hess国际标准模型进一步验证LFD逆时偏移成像方法对复杂各向异性介质的适应性。VTI⁃Hess模型如图 8所示,模型主要由三部分组成,即左侧的高速岩体、中部的强各向异性体和右侧的陡倾角断层。模型网格数为3617×1500,网格间距为6.1 m,模型尺寸为22.04 km×9.14 km。考虑到实际地震数据中常伴有强烈的多次波,因此本文采用该模型开源的两套地震数据分别进行成像试算,其中第一套数据不含多次波,而第二套数据含有多次波。
|
图 8 VTI-Hess模型 (a)速度;(b)ε;(c)δ |
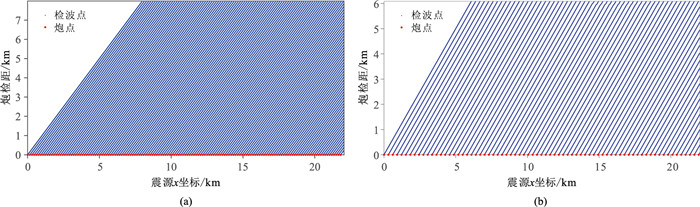
第一套数据的观测系统如图 9a所示,该数据的激发震源是主频为25 Hz的Ricker子波,激发炮数是721,第一炮位于x=0处,炮间距为30.48 m,等间距激发,采用656道检波器等间距移动接收,接收点的道间距为12.19 m,炮检距范围介于0~7984.45 m;从第463、464炮开始变观采集,接收道数分别变为653、651,随后依次每两炮分别按3、2道等差递减,最后两炮道数分别为13、11道,最后一炮的最大炮检距为121.92 m,因此总接收道数为388422;时间采样点数为1332,时间步长为6 ms。
|
图 9 两套观测系统示意图 (a)不含多次波;(b)含有多次波 |
第二套数据的观测系统如图 9b所示,该数据的激发震源是18 Hz的Ricker子波,激发炮数是361炮,第一炮位于x=0处,炮间距为60.96 m,等间距激发,采用500道检波器等间距移动接收,接收点的道间距为12.19 m,炮检距范围介于0~6082.81 m;从第263炮开始做了变观采集,接收道数变为498,随后逐炮按5道等差递减,最后一炮道数变为8,其最大炮检距为85.34 m,因此总接收道数为156047;时间采样点数为2000,时间步长为4 ms。
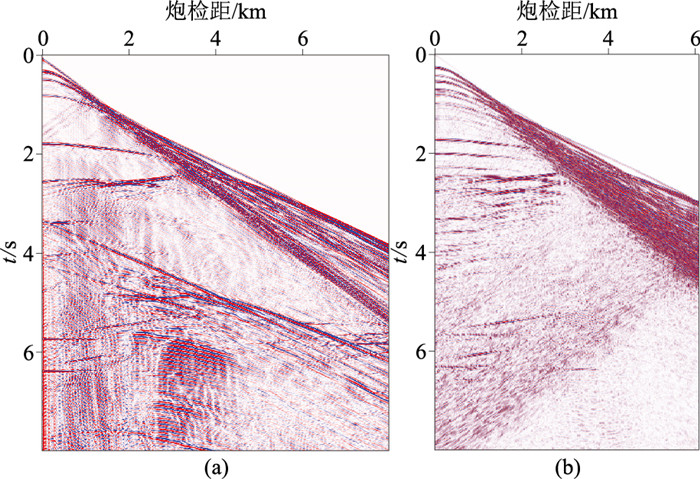
图 10展示了不含多次波和含有多次波的单炮地震记录。图中可见:当不含多次波时,深部反射信号的能量较强;而当含有多次波时,深部反射信号被多次波干扰,很难观察到明显的反射波同相轴,此外,由于在顶部未使用吸收边界条件,表面多次波信息较丰富。
|
图 10 VTI-Hess模型单炮地震记录 (a)不含多次波;(b)含有多次波 |
当不含多次波时,不同方法的偏移成像结果如图 11所示,由图可知:①在VTI介质中,与基于SGFD逆时偏移成像结果相比,在LFD成像结果中,左侧高速岩体轮廓更加清晰,岩体下部地层成像能量更强,对上部地层及中部各向异性体的分辨率更高;②对比图 11b与图 11c可知,用各向同性LFD进行逆时偏移成像时,地层界面无法聚焦,分辨率降低,右侧陡倾断层成像效果变差(图 11c中黑色虚线框所示);③理论情况下采用四周全接收的LFD逆时偏移结果,在真正意义上实现了波场的完全重构,此时成像剖面的分辨率显著提高,同相轴明显变细,能量也十分均衡,但在滤波处理时仍会出现部分偏移噪声(如图 11d黑色箭头所指)。对比上述成像结果可见:LFD逆时偏移对于高速岩体及各向异性体的成像效果与采用四周接收的LFD逆时偏移成像效果最接近,能够获得高质量的VTI介质成像结果,这表明该方法能够应用于复杂各向异性介质的逆时偏移成像处理。
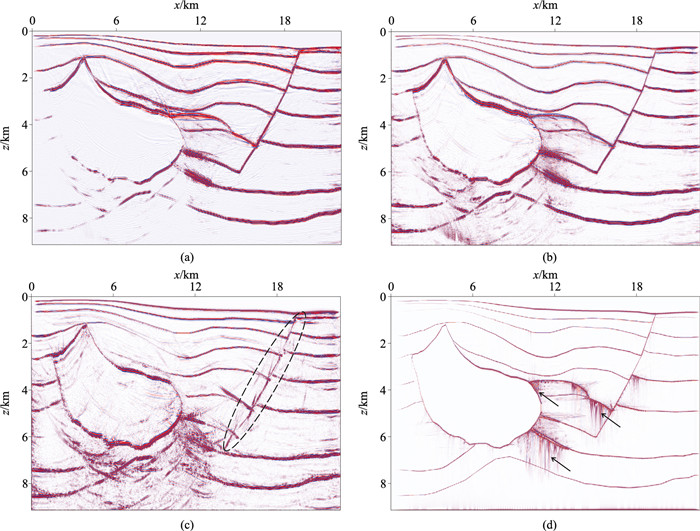
|
图 11 不含表层多次波时不同方法VTI⁃Hess模型逆时偏移结果 (a)VTI介质SGFD法;(b)VTI介质LFD法;(c)各向同性介质LFD法;(d)四周全接收的VTI介质LFD法 |
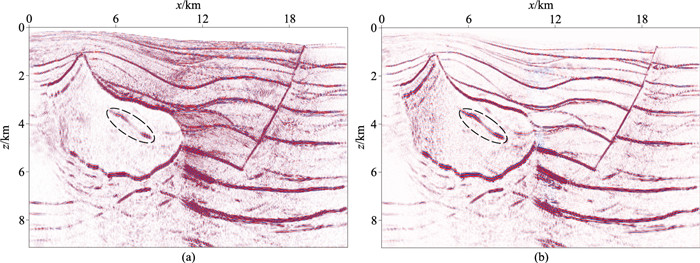
当地震数据含有多次波时,VTI-Hess模型的SGFD、LFD逆时偏移成像结果分别如图 12所示。图中可见:由于存在多次波干扰,成像结果中均含有较多的成像噪声及偏移假象(图 12中黑色虚线框所示);与图 12a中基于SGFD的逆时偏移成像结果相比,基于LFD的成像结果信噪比更高,对上部地层及中部强各向异性体具有更高的分辨率,总体成像质量更好。由此进一步验证了本文方法对于各向异性介质逆时偏移成像的适应性。此外,SGFD和LFD逆时偏移单炮成像耗时分别为330.17、196.75 s,可见基于LFD的逆时偏移成像方法对于各向异性介质具有明显的效率优势。
|
图 12 含表层多次波时两种方法VTI⁃Hess模型逆时偏移结果对比 (a)SGFD法;(b)LFD法 |
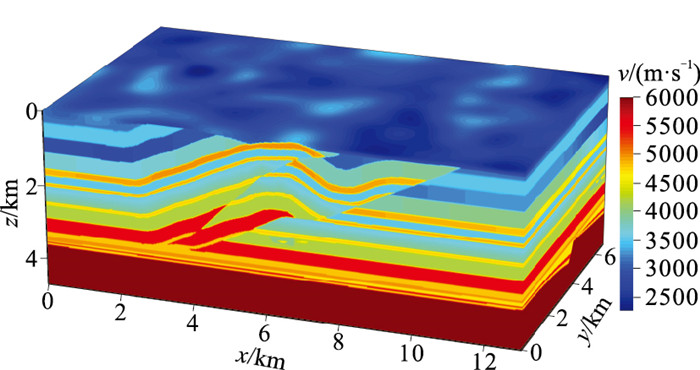
为进一步验证基于LFD的三维各向异性介质逆时偏移方法的适用性,本文选用三维Overthrust模型进行测试。图 13为速度模型,该模型结构复杂,横向速度变化剧烈,含有一个较大的逆冲推覆构造,介质非均质性强,地层厚度小,且界面起伏大,是检验成像算法优劣的国际标准模型。但该模型缺少各向异性参数,因此本文设置各向异性参数均匀不变,分别为ε=0.24、δ=0.10、倾角θ=30°、方位角φ=45°。模型网格点数为501×301×187,三个方向的网格间距均为25 m;采用主频为9 Hz的Ricker子波作为激发震源,在x和y方向分别激发51、21炮,共激发1071炮,炮间距分别为150、250 m,第一炮位于(2500 m,1250 m)处,激发点深度均为125 m;单炮在x方向和y方向分别有201、101道接收,道间距为25 m,接收点深度为100 m;时间采样点数1601,时间步长为1.5 ms。
|
图 13 三维Overthrust速度模型 |
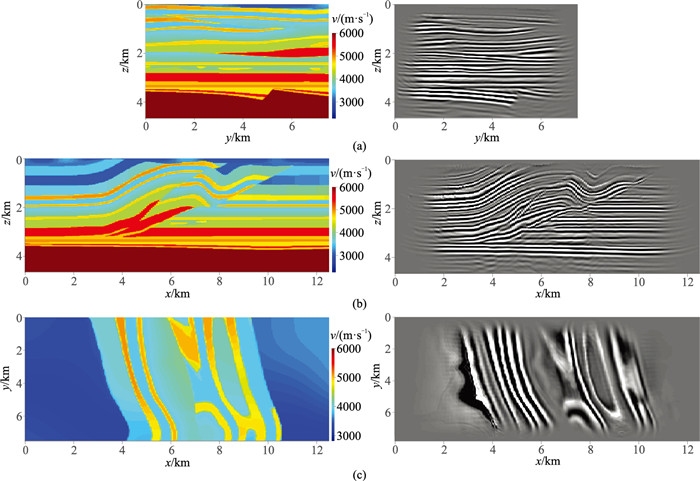
图 14为三维Overthrust模型LFD逆时偏移成像结果,由图可见:本方法对水平地层及倾斜地层均可以实现准确成像,并且能够清晰刻画逆掩断层的形态和断面的实际位置,对于复杂地质构造具有较高的成像分辨率。
|
图 14 三维Overthrust模型(左)与LFD逆时偏移结果(右)的对比 (a)x=2.5 km的yz剖面;(b)y=2.5 km的zx剖面;(c)z=1.5 km的水平切片 |
本文采用基于GPU加速和单CPU两套程序进行三维逆时偏移成像测试。测试过程中GPU型号为NVIDIA Quadro K6000,显存为12 GB;CPU型号为Intel Xeon E5⁃2680 v4 @ 2.40 GHz,内存为58 GB。三维Overthrust模型逆时偏移过程中,GPU单炮偏移耗时59.69 s,而CPU单炮偏移耗时2578.28 s;完成1071炮偏移,GPU总耗时约为1065 min,CPU总耗时约为46022 min。可见,与基于单CPU串行的LFD逆时偏移方法相比,基于GPU并行的LFD逆时偏移方法能够有效减少成像的耗时,显著提高成像效率,两种方法的用时之比约为1∶43。
3 结论与认识本文推导了各向异性介质纯qP波波场延拓公式,随后引入三维球型差分模板求取与模型相适应差分系数,并将其应用于三维纯qP波波场正、反向延拓,最后利用GPU并行进行加速计算,实现了基于GPU加速的三维LFD纯qP波逆时偏移成像。由模型测试及理论分析,得出以下结论与认识。
(1)本文构建的纯qP波延拓公式克服了模型参数的限制,在任意模型参数下均能实现波场稳定传播,并且消除了伪横波干扰及数值不稳定现象。
(2)与SGFD逆时偏移方法相比,LFD法对复杂各向异性介质具有更高的成像分辨率,当模型含有多次波时,仍然能够取得较好的成像效果;并且在保证成像精度的前提下,该方法能够有效降低逆时偏移计算耗时及内存占用,表明LFD法在各向异性介质逆时偏移成像中具有一定的优势。
(3)基于LFD的逆时偏移方法对于三维各向异性介质的逆时偏移成像同样具有较好的适用性,且本文采用的GPU并行加速策略能够有效提高三维逆时偏移计算效率,其加速比可达43倍左右,有利于推广和应用于实际地震数据。
将LFD应用于三维黏声各向异性介质逆时偏移成像是下一步的研究重点。
| [1] |
FLETCHER R P, DU X, FOWLER P J. Reverse time migration in titled transversely isotropic (TTI) media[J]. Geophysics, 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
| [2] |
ALKHALIFAH T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [3] |
杨富森, 李振春, 王小丹. TTI介质一阶qP波稳定方程波场数值模拟及逆时偏移[J]. 石油地球物理勘探, 2016, 51(3): 497-505. YANG Fusen, LI Zhenchun, WANG Xiaodan. Wave⁃field numerical simulation and reverse⁃time migration based on the stable TTI first⁃order qP⁃wave equations[J]. Oil Geophysical Prospecting, 2016, 51(3): 497-505. |
| [4] |
DUVENECK E, BAKKER P M. Stable P⁃wave mo⁃ deling for reverse⁃time migration in tilted TI media[J]. Geophysics, 2011, 76(2): S65-S75. DOI:10.1190/1.3533964 |
| [5] |
DU X, BANCROFT J C, LINES L R. Anisotropic reverse⁃time migration for tilted TI media[J]. Geophysical Prospecting, 2007, 55(6): 853-869. DOI:10.1111/j.1365-2478.2007.00652.x |
| [6] |
LIU F Q, MORTON S A, JIANG S S, et al. Decoupled wave equation for P⁃ and SV⁃waves in an acoustic VTI media[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2844⁃2848.
|
| [7] |
PESTANA R C, URSIN B, STOFFA P L. Separate P⁃ and SV⁃wave equations for VTI media[C]. SEG Te⁃ chnical Program Expanded Abstracts, 2011, 30: 163⁃167.
|
| [8] |
CHU C, MACY B K, ANNO P D. Approximation of pure acoustic seismic wave propagation in TTI media[J]. Geophysics, 2011, 76(5): WB97-WB107. DOI:10.1190/geo2011-0092.1 |
| [9] |
黄建平, 黄金强, 李振春, 等. TTI介质一阶qP波方程交错网格伪谱法正演模拟[J]. 石油地球物理勘探, 2016, 51(3): 487-496. HUANG Jianping, HUANG Jinqiang, LI Zhenchun, et al. Staggered grid pseudo⁃spectral numerical simulation of first⁃order quasi P⁃wave equation for TTI media[J]. Oil Geophysical Prospecting, 2016, 51(3): 487-496. |
| [10] |
ZHAN G, PESTANA R C, STOFFA P L. An efficient hybrid pseudo spectral/finite⁃difference scheme for solving the TTI pure P⁃wave equation[J]. Journal of Geophysics and Engineering, 2013, 10(2): 1322-1327. |
| [11] |
张庆朝, 朱国维, 周俊杰, 等. TTI介质qP波伪谱法正演模拟[J]. 石油地球物理勘探, 2019, 54(2): 302-311. ZHANG Qingchao, ZHU Guowei, ZHOU Junjie, et al. qP⁃wave numerical simulation in TTI media with pseudo⁃spectral method[J]. Oil Geophysical Prospec⁃ ting, 2019, 54(2): 302-311. |
| [12] |
XU S, ZHOU H B. Accurate simulations of pure quasi⁃P⁃waves in complex anisotropic media[J]. Geophysics, 2014, 79(6): T341-T348. DOI:10.1190/geo2014-0242.1 |
| [13] |
LI X Y, ZHU H J. A finite⁃difference approach for sol⁃ ving pure quasi⁃P⁃wave equations in transversely isotropic and orthorhombic media[J]. Geophysics, 2018, 83(4): C161-C172. DOI:10.1190/geo2017-0405.1 |
| [14] |
徐世刚, 包乾宗, 任志明, 等. 结合泊松算法和波场分解成像条件的各向异性优化纯声波方程逆时偏移[J]. 石油地球物理勘探, 2022, 57(3): 613-623. XU Shigang, BAO Qianzong, REN Zhiming, et al. Reverse⁃time migration of optimized pure acoustic equation in anisotropic media by combining Poisson algorithm and wavefield decomposition imaging condition[J]. Oil Geophysical Prospecting, 2022, 57(3): 613-623. |
| [15] |
黄金强, 李振春. 基于Low⁃rank分解的复杂TI介质纯qP波正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(2): 704-721. HUANG Jinqiang, LI Zhenchun. Modeling and reverse time migration of pure quasi⁃P⁃wave in complex TI media with a low⁃rank decomposition[J]. Chinese Journal of Geophysics, 2017, 60(2): 704-721. |
| [16] |
顾汉明, 张奎涛, 刘春成, 等. 基于Low⁃rank一步法波场延拓的黏声各向异性介质纯qP波正演模拟[J]. 石油地球物理勘探, 2020, 55(4): 733-746. GU Hanming, ZHANG Kuitao, LIU Chuncheng, et al. Low⁃rank one⁃step wave extrapolation for pure qP⁃wave forward modeling in viscoacoustic anisotropic media[J]. Oil Geophysical Prospecting, 2020, 55(4): 733-746. |
| [17] |
FOMEL S, YING L X, SONG X L. Seismic wave extrapolation using low rank symbol approximation[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 3092⁃3096.
|
| [18] |
SONG X L, ALKHALIFAH T. Modeling of pesudoacoustic P⁃waves in orthorhombic media with a low⁃rank approximation[J]. Geophysics, 2013, 78(4): C33-C40. |
| [19] |
SUN J, FOMEL S, YING L X. Low⁃rank one⁃step wave extrapolation for reverse time migration[J]. Geophysics, 2016, 81(1): S39-S54. |
| [20] |
SONG X L, FOMEL S, YING L X. Low⁃rank finite⁃differences and low⁃rank Fourier finite⁃differences for seismic wave extrapolation in the acoustic approximation[J]. Geophysical Journal International, 2013, 193(2): 960-969. |
| [21] |
方刚, Fomel S, 杜启振. 交错网格Lowrank有限差分及其在逆时偏移中的应用[J]. 中国石油大学学报(自然科学版), 2014, 38(2): 44-51. FANG Gang, FOMEL S, DU Qizhen. Low⁃rank finite difference on a staggered grid and its application on reverse time migration[J]. Journal of China University of Petroleum (Edition of natural Science), 2014, 38(2): 44-51. |
| [22] |
袁雨欣, 胡婷, 王之洋, 等. 求解二阶解耦弹性波方程的低秩分解法和低秩有限差分法[J]. 地球物理学报, 2018, 61(8): 3324-3333. YUAN Yuxin, HU Ting, WANG Zhiyang, et al. Solving second⁃order decoupled elastic wave equation using low⁃rank decomposition and low⁃rank finite differences[J]. Chinese Journal of Geophysics, 2018, 61(8): 3324-3333. |
| [23] |
黄金强, 李振春, 江文. TTI介质Low⁃rank有限差分法高效正演模拟及逆时偏移[J]. 石油地球物理勘探, 2018, 53(6): 1198-1209. HUANG Jinqiang, LI Zhenchun, JIANG Wen. An efficient forward modeling with the low⁃rank finite⁃diffe⁃ rence algorithm for complex TTI media and its application in reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(6): 1198-1209. |
| [24] |
ZHANG Y, ZHANG G. One⁃step extrapolation method for reverse time migration[J]. Geophysics, 2009, 74(4): A29-A33. |
| [25] |
黄金强, 李振春. 各向异性介质Low⁃rank有限差分法纯qP波叠前平面波最小二乘逆时偏移[J]. 地球物理学报, 2019, 62(8): 3106-3129. HUANG Jinqiang, LI Zhenchun. Least⁃squares reverse time migration of pure qP⁃wave pre⁃stack plane⁃waves based on low⁃rank finite difference for anisotropic media[J]. Chinese Journal of Geophysics, 2019, 62(8): 3106-3129. |
| [26] |
包乾宗, 戴雪, 梁雪. 一种基于新差分模板和无穷范数的震源波场重建方法[J]. 石油地球物理勘探, 2022, 57(6): 1384-1394. BAO Qianzong, DAI Xue, LIANG Xue. Source wavefield reconstruction based on a new finite⁃difference stencil and infinity norm[J]. Oil Geophysical Prospecting, 2022, 57(6): 1384-1394. |



 黄金强,贵州省贵阳市花溪区花溪大道南段2708号贵州大学西校区资源与环境工程学院,550025。Email:
黄金强,贵州省贵阳市花溪区花溪大道南段2708号贵州大学西校区资源与环境工程学院,550025。Email: