2. 中国石油集团油藏描述重点实验室, 甘肃兰州 730020;
3. 东方地球物理公司研究院, 河北涿州 072750;
4. 中国石油勘探开发研究院, 北京 100083
2. PetroChina Key Laboratory of Reservoir Description, Lanzhou, Gansu 730020, China;
3. GRI, BGP Inc., CNPC, Zhuozhou, Hebei 072750, China;
4. PetroChina Research Institute of Petroleum Exploration and Development, Beijing 100083, China
波动方程数值模拟是研究复杂介质中波场传播规律的重要手段[1-2],是逆时偏移(RTM)[3-4]和全波形反演(FWI)[5-6]的重要基础。相比伪谱法[7-8]和有限元法[9-10],有限差分法[11-12]具有计算效率高、占用内存小、算法实现简单灵活等优点,已发展成为应用最普遍的一种波动方程数值模拟方法[13-15]。然而,有限差分法利用差分算子近似波动方程中的微分算子,导致波场的传播速度与真实速度不相等,且不同频率的波场传播速度不同,即出现数值频散现象[16]。固有的数值频散严重影响有限差分法的模拟精度[17-18],进而影响了RTM和FWI的精度[19],因此,压制数值频散、提高模拟精度是有限差分法的一项重要研究内容。
构建更合理的差分算子和改进差分系数计算方法是提高有限差分法模拟精度的两条重要途径。Dablain[16]指出,高阶差分算子能够减小数值频散,提高模拟精度,但时间高阶差分算子会使内存占用和计算量显著增加。此后,学者普遍保持时间2阶差分算子不变,通过设计更合理的空间差分算子以提高模拟精度。Fornberg[20]给出了基于泰勒级数展开的规则网格和交错网格2M阶(M表示空间差分算子中与差分中心点等距的坐标轴网格点的组数)空间差分算子的差分系数解析表达式,据此可以构建采用时间2阶差分算子、空间2M阶差分算子的规则网格和交错网格有限差分法,本文称之为常规规则网格有限差分法(C-FD)和常规交错网格有限差分法(C-SFD)。C-FD和C-SFD利用空间域频散关系和泰勒级数展开计算差分系数,尽管空间差分算子具有2M阶差分精度,但差分离散波动方程仍然仅具有2阶差分精度。波动方程有限差分数值模拟通过迭代求解差分离散波动方程实现,不应通过分开逼近时间差分算子或空间差分算子达到高阶差分精度,而应该使差分离散波动方程达到高阶差分精度,才能有效提高有限差分法的模拟精度。针对二阶标量波动方程和一阶应力—速度声波方程有限差分模拟,一些学者提出基于时空间域频散关系和泰勒级数展开计算差分系数,构建了时空域规则网格和交错网格有限差分法,这种时空域有限差分法使得相应的二维和三维差分离散波动方程分别沿8个和48个传播方向达到2M阶差分精度,但沿其他传播方向仍然仅具有2阶差分精度,呈现明显的数值各向异性[17, 21]。除了上述基于泰勒展开的差分系数算法,基于最小二乘优化算法最小化频散关系误差,相速度误差和群速度误差求解差分系数也被广泛采用[22-24],这种基于最小二乘的差分系数算法能够有效提高中高频成分的模拟精度,但会在一定程度上损失低频成分的模拟精度,并且最小二乘算法通过迭代优化差分系数,计算量较大。Liu[25-26]采用最小二乘优化相对空间域和时空域频散关系求解差分系数,将非线性最优化问题转化为线性最优化问题,求解过程不需要迭代,有效地提高了差分系数的计算效率。
仅通过改进差分系数算法提高模拟精度的效果有限,构建更合理的空间差分算子是有效提高模拟精度的另一重要途径。针对2阶标量波动方程,Liu等[27]提出了一种菱形网格有限差分法,并基于时空域频散关系和泰勒展开计算差分系数,使得差分离散波动方程沿任意传播方向达到2M阶差分精度,有效地提高了二维标量波动方程的模拟精度和稳定性,但是其空间差分算子长度随M2急剧增大,导致计算量巨大,计算效率低。后来,Wang等[28]又提出组合常规十字交叉型网格和菱形网格以构建空间差分算子,有效兼顾了计算效率和模拟精度。胡自多等[29]借鉴频率域混合网格有限差分法[30-31]的构建思路,将波动方程中的Laplace微分算子近似表示为直角坐标系中坐标轴网格点构建的Laplace差分算子和非坐标轴网格点构建的Laplace差分算子的加权平均,建立了一种混合网格有限差分法,它与Wang等[28]提出的有限差分法相似,但构建思路不同。胡自多等[32]导出了三维直角坐标系中非坐标轴网格点构建Laplace差分算子的方法,进一步构建了三维混合网格有限差分法,有效提高了三维标量波动方程的模拟精度和稳定性。针对速度—应力声波方程,Tan等[33]提出联合利用坐标轴网格点和非坐标轴网格点构建空间差分算子近似波动方程中的1阶空间偏导数,建立了一种混合交错网格有限差分法,相应的差分离散声波方程可以达到4阶或6阶差分精度,有效提高了声波模拟精度。Ren等[34-35]进一步发展了这种混合交错网格有限差分法,使得差分离散声波和弹性波方程最高可以达到8阶差分精度。Zhou等[36-37]对混合交错网格有限差分法做进一步改进,使得差分离散声波和弹性波方程可以达到任意偶数阶差分精度,并采用两步线性优化方法简化了基于最小二乘的优化差分系数计算,进一步提高了声波和弹性波的模拟精度。然而,这类混合交错网格有限差分法不恰当地使用了非坐标轴网格点的对称性,通常将与差分中心点距离不相等的2组非坐标轴网格点赋予了相同的差分系数,导致难以推导差分系数的通解。
针对速度—应力声波方程数值模拟,本文发展了一种改进型的混合交错网格有限差分法(M-SFD),利用坐标轴网格点和非坐标轴网格点构建空间差分算子时,确保与差分中心点距离相等的1组非坐标轴网格点赋予相同的差分系数,与差分中心点距离不等的任意2组非坐标轴网格点赋予不同的差分系数,使得所构建的M-SFD更为合理,并利用时空域频散关系和泰勒级数展开建立差分系数求解方程组,导出差分系数通解的解析表达式。
本文首先阐述了M-SFD中空间差分算子的构建方法,给出相应的差分离散声波方程,并导出差分系数通解;其次,开展频散分析和稳定性分析;最后,利用层状介质模型和中国塔里木盆地典型复杂构造模型开展数值模拟,并将M-SFD推广应用于RTM,利用塔里木复杂构造模型模拟数据开展RTM测试。测试表明,该方法能够有效消除由于数值频散造成的成像假象,从而提高深层成像精度和分辨率。
1 混合交错网格有限差分法的基本原理 1.1 差分离散声波方程的导出二维速度—应力声波方程可表示为
| $ \begin{array}{lll}\left\{\begin{array}{l}\frac{\partial P}{\partial t}+\kappa \left(\frac{\partial {\upsilon }_{x}}{\partial x}+\frac{\partial {\upsilon }_{z}}{\partial z}\right)=0\\ \frac{\partial {\upsilon }_{x}}{\partial t}+\frac{1}{\rho }\frac{\partial P}{\partial x}=0\\ \frac{\partial {\upsilon }_{z}}{\partial t}+\frac{1}{\rho }\frac{\partial P}{\partial z}=0\end{array}\right.& \begin{array}{l}\\ \end{array}& \end{array} $ | (1) |
式中:
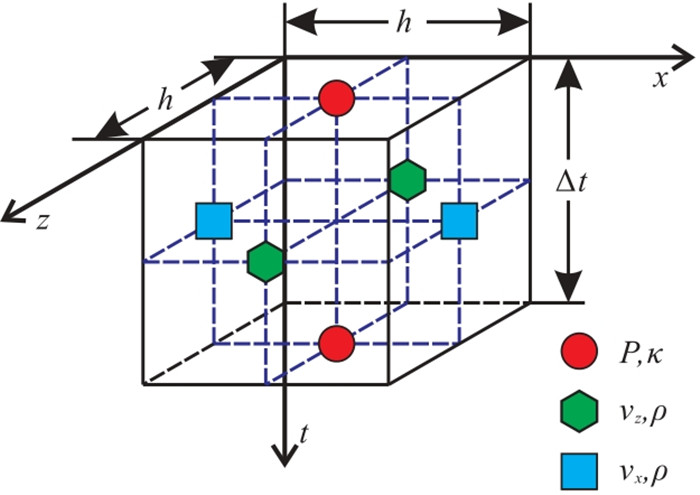
交错网格有限差分法求解式(1)时,波场变量和弹性参数定义在交错的网格位置上,如图 1所示。波场变量
|
图 1 二维声波交错网格差分格式中波场变量及弹性参数相对位置示意图 |
与C-SFD类似,M-SFD采用时间2阶差分算子近似式(1)中波场变量关于时间变量
| $ \left\{\begin{array}{l}{\left.\frac{\partial P}{\partial t}\right|}_{1/2, 1/2}^{1/2}\approx \frac{{P}_{1/2, 1/2}^{1}-{P}_{1/2, 1/2}^{0}}{\mathrm{\Delta }t}\\ {\left.\frac{\partial {\upsilon }_{x}}{\partial t}\right|}_{0, 1/2}^{0}\approx \frac{{\upsilon }_{x\left(0, 1/2\right)}^{1/2}-{\upsilon }_{x\left(0, 1/2\right)}^{-1/2}}{\mathrm{\Delta }t}\\ {\left.\frac{\partial {\upsilon }_{z}}{\partial t}\right|}_{1/2, 0}^{0}\approx \frac{{\upsilon }_{z\left(1/2, 0\right)}^{1/2}-{\upsilon }_{z\left(1/2, 0\right)}^{-1/2}}{\mathrm{\Delta }t}\end{array}\right. $ | (2) |
式中:
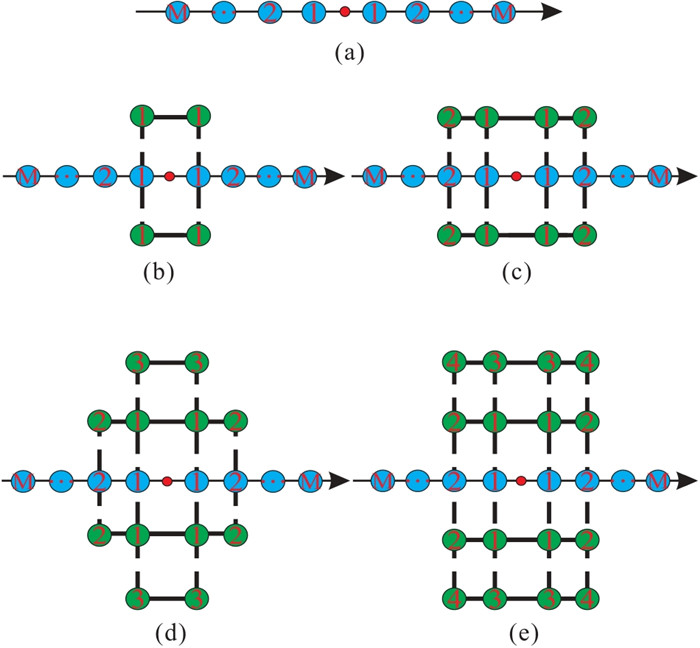
C-SFD仅利用坐标轴网格点构建空间2M阶差分算子(图 2a)近似波场变量关于空间的一阶偏导数,随着M取值的增大,新增网格点与差分中心点的距离也逐渐增大,对提高模拟精度的贡献逐渐减小。
|
图 2 交错网格有限差分法的空间差分算子示意图 (a)C-SFD;(b)~(e)M-SFD(N=1、2、3、4) 蓝色圆圈代表坐标轴网格点,绿色圆圈代表非坐标轴网格点,数字1、2、…、M代表坐标轴或非坐标轴网格点组编号。 |
本文所提M-SFD的基本思路是:联合利用坐标轴网格点和非坐标轴网格点构建一种混合型的空间差分算子近似波场变量关于空间的1阶偏导数。图 2b~图 2e为M-SFD(N=1、2、3、4)的空间差分算子示意图,N表示空间差分算子中与差分中心点等距的非坐标轴网格点的组数。相比C-SFD,M-SFD能有效利用距离差分中心点更近的非坐标轴网格点,理论上更合理。
本文提出的M-SFD与Tan等[33]提出的时间和空间高阶交错网格有限差分法具有一定的相似性,但是他们不恰当地使用了非坐标轴网格点的对称性,将与差分中心点距离不相等的两组非坐标轴网格点赋予了相同的差分系数,例如将图 2d中标记为绿色②和③的两组非坐标轴网格点赋予了相同的差分系数,标记为绿色②的网格点与差分中心点的距离为
M-SFD(N=1)与Tan等[33]提出的时间4阶、空间2M阶交错网格有限差分法本质上完全相同。下面以M-SFD(N=2)为例阐述M-SFD的基本原理。利用图 2c中M-SFD(N=2)的空间差分算子近似方程(1)中波场变量关于空间变量
| $ \left\{\begin{array}{l}{\left.\frac{\partial {\upsilon }_{x}}{\partial x}\right|}_{1/2, 1/2}^{1/2}\approx \frac{1}{h}\left\{\begin{array}{l}\sum\limits _{m=1}^{M}{a}_{m}\left[{\upsilon }_{x\left(m, 1/2\right)}^{1/2}-{\upsilon }_{x\left(-m+1, 1/2\right)}^{1/2}\right]+{b}_{1}\left[{\upsilon }_{x\left(1, 3/2\right)}^{1/2}-{\upsilon }_{x\left(0, 3/2\right)}^{1/2}+{\upsilon }_{x\left(1, -1/2\right)}^{1/2}-{\upsilon }_{x\left(0, -1/2\right)}^{1/2}\right]+\\ {b}_{2}\left[{\upsilon }_{x\left(2, 3/2\right)}^{1/2}-{\upsilon }_{x\left(-1, 3/2\right)}^{1/2}+{\upsilon }_{x\left(2, -1/2\right)}^{1/2}-{\upsilon }_{x\left(-1, -1/2\right)}^{1/2}\right]\end{array}\right\}\\ {\left.\frac{\partial {\upsilon }_{z}}{\partial z}\right|}_{1/2, 1/2}^{1/2}\approx \frac{1}{h}\left\{\begin{array}{l}\sum\limits _{m=1}^{M}{a}_{m}\left[{\upsilon }_{z\left(1/2, m\right)}^{1/2}-{\upsilon }_{z\left(1/2, -m+1\right)}^{1/2}\right]+{b}_{1}\left[{\upsilon }_{z\left(3/2, 1\right)}^{1/2}-{\upsilon }_{z\left(3/2, 0\right)}^{1/2}+{\upsilon }_{z\left(-1/2, 1\right)}^{1/2}-{\upsilon }_{z\left(-1/2, 0\right)}^{1/2}\right]+\\ {b}_{2}\left[{\upsilon }_{z\left(3/2, 2\right)}^{1/2}-{\upsilon }_{z\left(3/2, -1\right)}^{1/2}+{\upsilon }_{z\left(-1/2, 2\right)}^{1/2}-{\upsilon }_{z\left(-1/2, -1\right)}^{1/2}\right]\end{array}\right\}\\ {\left.\frac{\partial P}{\partial x}\right|}_{0, 1/2}^{0}\approx \frac{1}{h}\left\{\begin{array}{l}\sum\limits _{m=1}^{M}{a}_{m}\left[{P}_{m-1/2, 1/2}^{0}-{P}_{-m+1/2, 1/2}^{0}\right]+{b}_{1}\left[{P}_{1/2, 3/2}^{0}-{P}_{-1/2, 3/2}^{0}+{P}_{1/2, -1/2}^{0}-{P}_{-1/2, -1/2}^{0}\right]+\\ {b}_{2}\left[{P}_{3/2, 3/2}^{0}-{P}_{-3/2, 3/2}^{0}+{P}_{3/2, -1/2}^{0}-{P}_{-3/2, -1/2}^{0}\right]\end{array}\right\}\\ {\left.\frac{\partial P}{\partial z}\right|}_{1/2, 0}^{0}\approx \frac{1}{h}\left\{\begin{array}{l}\sum\limits _{m=1}^{M}{a}_{m}\left[{P}_{1/2, m-1/2}^{0}-{P}_{1/2, -m+1/2}^{0}\right]+{b}_{1}\left[{P}_{3/2, 1/2}^{0}-{P}_{3/2, -1/2}^{0}+{P}_{-1/2, 1/2}^{0}-{P}_{-1/2, -1/2}^{0}\right]+\\ {b}_{2}\left[{P}_{3/2, 3/2}^{0}-{P}_{3/2, -3/2}^{0}+{P}_{-1/2, 3/2}^{0}-{P}_{-1/2, -3/2}^{0}\right]\end{array}\right\}\end{array}\right. \begin{array}{l}\\ \\ \\ \end{array} $ | (3) |
式中
| $ \left\{\begin{array}{l}\frac{{P}_{1/2, 1/2}^{1}-{P}_{1/2, 1/2}^{0}}{\mathrm{\Delta }t}\approx -\frac{\kappa }{h}\left\{\begin{array}{l}\sum\limits _{m=1}^{M}{a}_{m}\left[{\upsilon }_{x\left(m, 1/2\right)}^{1/2}-{\upsilon }_{x\left(-m+1, 1/2\right)}^{1/2}\right]+{b}_{1}\left[{\upsilon }_{x\left(1, 3/2\right)}^{1/2}-{\upsilon }_{x\left(0, 3/2\right)}^{1/2}+{\upsilon }_{x\left(1, -1/2\right)}^{1/2}-{\upsilon }_{x\left(0, -1/2\right)}^{1/2}\right]+\\ {b}_{2}\left[{\upsilon }_{x\left(2, 3/2\right)}^{1/2}-{\upsilon }_{x\left(-1, 3/2\right)}^{1/2}+{\upsilon }_{x\left(2, -1/2\right)}^{1/2}-{\upsilon }_{x\left(-1, -1/2\right)}^{1/2}\right]\end{array}\right\}-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\kappa }{h}\left\{\begin{array}{l}\sum\limits _{m=1}^{M}{a}_{m}\left[{\upsilon }_{z\left(1/2, m\right)}^{1/2}-{\upsilon }_{z\left(1/2, -m+1\right)}^{1/2}\right]+{b}_{1}\left[{\upsilon }_{z\left(3/2, 1\right)}^{1/2}-{\upsilon }_{z\left(3/2, 0\right)}^{1/2}+{\upsilon }_{z\left(-1/2, 1\right)}^{1/2}-{\upsilon }_{z\left(-1/2, 0\right)}^{1/2}\right]+\\ {b}_{2}\left[{\upsilon }_{z\left(3/2, 2\right)}^{1/2}-{\upsilon }_{z\left(3/2, -1\right)}^{1/2}+{\upsilon }_{z\left(-1/2, 2\right)}^{1/2}-{\upsilon }_{z\left(-1/2, -1\right)}^{1/2}\right]\end{array}\right\}\\ \frac{{\upsilon }_{x\left(0, 1/2\right)}^{1/2}-{\upsilon }_{x\left(0, 1/2\right)}^{-1/2}}{\mathrm{\Delta }t}\approx -\frac{1}{\rho h}\left\{\begin{array}{l}\sum\limits _{m=1}^{M}{a}_{m}\left({P}_{m-1/2, 1/2}^{0}-{P}_{-m+1/2, 1/2}^{0}\right)+{b}_{1}\left[{P}_{1/2, 3/2}^{0}-{P}_{-1/2, 3/2}^{0}+{P}_{1/2, -1/2}^{0}-{P}_{-1/2, -1/2}^{0}\right]+\\ {b}_{2}\left[{P}_{3/2, 3/2}^{0}-{P}_{-3/2, 3/2}^{0}+{P}_{3/2, -1/2}^{0}-{P}_{-3/2, -1/2}^{0}\right]\end{array}\right\}\\ \frac{{\upsilon }_{z\left(1/2, 0\right)}^{1/2}-{\upsilon }_{z\left(1/2, 0\right)}^{-1/2}}{\mathrm{\Delta }t}\approx -\frac{1}{\rho h}\left\{\begin{array}{l}\sum\limits _{m=1}^{M}{a}_{m}\left({P}_{1/2, m-1/2}^{0}-{P}_{1/2, -m+1/2}^{0}\right)+{b}_{1}\left[{P}_{3/2, 1/2}^{0}-{P}_{3/2, -1/2}^{0}+{P}_{-1/2, 1/2}^{0}-{P}_{-1/2, -1/2}^{0}\right]+\\ {b}_{2}\left[{P}_{3/2, 3/2}^{0}-{P}_{3/2, -3/2}^{0}+{P}_{-1/2, 3/2}^{0}-{P}_{-1/2, -3/2}^{0}\right]\end{array}\right\}\end{array}\right. $ | (4) |
式(4)为M-SFD(N=2)对式(1)的差分离散声波方程,同样还可以导出M-SFD(N=1、3、4)对式(1)的差分离散声波方程。
1.2 差分系数计算合理的差分系数算法能有效提高交错网格有限差分法的模拟精度。C-SFD利用空间域频散关系和泰勒级数展开计算差分系数,使得空间差分算子达到2M阶差分精度,但是相应的差分离散声波方程仅具有2阶差分精度[21]。交错网格有限差分法通过迭代求解差分离散声波方程实现声波数值模拟,为了提高模拟精度,应该设法提高差分离散声波方程的差分精度,而不是仅仅提高空间差分算子的差分精度。
M-SFD基于时空域频散关系和泰勒级数展开计算差分系数,将有助于提高差分离散声波方程的差分精度。下面以M-SFD(N=2)为例,阐述M-SFD的差分系数计算方法。均匀介质中,速度—应力声波方程(1)具有如下形式的离散平面波解
| $ \left\{\begin{array}{l}{P}_{m-1/2, n-1/2}^{j}={A}_{P}{\mathrm{e}}^{i\left[{k}_{x}\left(x+\left(m-1/2\right)h\right)+{k}_{z}\left(z+\left(n-1/2\right)h\right)-\omega \left(t+j\mathrm{\Delta }t\right)\right]}\\ {\upsilon }_{x\left(m, n-1/2\right)}^{j-1/2}={A}_{{\upsilon }_{x}}{\mathrm{e}}^{i\left[{k}_{x}\left(x+mh\right)+{k}_{z}\left(z+\left(n-1/2\right)h\right)-\omega \left(t+\left(j-1/2\right)\mathrm{\Delta }t\right)\right]}\\ {\upsilon }_{z\left(m-1/2, n\right)}^{j-1/2}={A}_{{\upsilon }_{z}}{\mathrm{e}}^{i\left[{k}_{x}\left(x+\left(m-1/2\right)h\right)+{k}_{z}\left(z+nh\right)-\omega \left(t+\left(j-1/2\right)\mathrm{\Delta }t\right)\right]}\\ {k}_{x}=k\mathrm{c}\mathrm{o}\mathrm{s}\theta \\ {k}_{z}=k\mathrm{s}\mathrm{i}\mathrm{n}\theta \end{array}\right. $ | (5) |
式中:
将式(5)代入式(4)得到
| $ \left\{\begin{array}{l}\frac{{A}_{P}}{\mathrm{\Delta }t}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\omega \mathrm{\Delta }t}{2}\\ \approx -\frac{\kappa {A}_{{\upsilon }_{x}}}{h}\left\{\sum\limits _{m=1}^{M}{a}_{m}\mathrm{s}\mathrm{i}\mathrm{n}\left[\left(m-\frac{1}{2}\right){k}_{x}h\right]+\right.\\ \;\;\;\;\left.2\mathrm{c}\mathrm{o}\mathrm{s}\left({k}_{z}h\right)\left({b}_{1}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{k}_{x}h}{2}+{b}_{2}\mathrm{s}\mathrm{i}\mathrm{n}\frac{3{k}_{x}h}{2}\right)\right\}-\\ \;\;\;\;\frac{\kappa {A}_{{\upsilon }_{z}}}{h}\left\{\sum\limits _{m=1}^{M}{a}_{m}\mathrm{s}\mathrm{i}\mathrm{n}\left[\left(m-\frac{1}{2}\right){k}_{z}h\right]+\right.\\ \;\;\;\;2\mathrm{c}\mathrm{o}\mathrm{s}\left({k}_{x}h\right)\left.\left({b}_{1}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{k}_{z}h}{2}+{b}_{2}\mathrm{s}\mathrm{i}\mathrm{n}\frac{3{k}_{z}h}{2}\right)\right\}\\ \frac{{A}_{{\upsilon }_{x}}}{\mathrm{\Delta }t}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\omega \mathrm{\Delta }t}{2}\\ \approx -\frac{{A}_{P}}{\rho h}\left\{\sum\limits _{m=1}^{M}{a}_{m}\mathrm{s}\mathrm{i}\mathrm{n}\left[\left(m-\frac{1}{2}\right){k}_{x}h\right]+\right.\\ \;\;\;\;2\mathrm{c}\mathrm{o}\mathrm{s}\left({k}_{z}h\right)\left.\left({b}_{1}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{k}_{x}h}{2}+{b}_{2}\mathrm{s}\mathrm{i}\mathrm{n}\frac{3{k}_{x}h}{2}\right)\right\}\\ \frac{{A}_{{\upsilon }_{z}}}{\mathrm{\Delta }t}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\omega \mathrm{\Delta }t}{2}\\ \approx -\frac{{A}_{P}}{\rho h}\left\{\sum\limits _{m=1}^{M}{a}_{m}\mathrm{s}\mathrm{i}\mathrm{n}\left[\left(m-\frac{1}{2}\right){k}_{z}h\right]+\right.\\ \;\;\;\;\left.2\mathrm{c}\mathrm{o}\mathrm{s}\left({k}_{x}h\right)\left({b}_{1}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{k}_{z}h}{2}+{b}_{2}\mathrm{s}\mathrm{i}\mathrm{n}\frac{3{k}_{z}h}{2}\right)\right\}\end{array}\right. $ | (6) |
消去式(6)中的
| $ \begin{array}{l}\frac{1}{{\left(v\mathrm{\Delta }t\right)}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\frac{rkh}{2}\approx \frac{1}{{h}^{2}}\left\{\sum\limits _{m=1}^{M}{a}_{m}\left[\mathrm{s}\mathrm{i}\mathrm{n}\left(m-\frac{1}{2}\right){k}_{x}h\right]+\right.\\ {\left.2\mathrm{c}\mathrm{o}\mathrm{s}\left({k}_{z}h\right)\left({b}_{1}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{k}_{x}h}{2}+{b}_{2}\mathrm{s}\mathrm{i}\mathrm{n}\frac{3{k}_{x}h}{2}\right)\right\}}^{2}+\\ \frac{1}{{h}^{2}}\left\{\sum\limits _{m=1}^{M}{a}_{m}\left[\mathrm{s}\mathrm{i}\mathrm{n}\left(m-\frac{1}{2}\right){k}_{z}h\right]+\right.\\ {\left.2\mathrm{c}\mathrm{o}\mathrm{s}\left({k}_{x}h\right)\left({b}_{1}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{k}_{z}h}{2}+{b}_{2}\mathrm{s}\mathrm{i}\mathrm{n}\frac{3{k}_{z}h}{2}\right)\right\}}^{2}\end{array} $ | (7) |
式中:
式(7)为M-SFD(N=2)给出的差分离散声波方程的频散关系,也称为时空域频散关系。泰勒展开其中的三角函数,得到
| $ \begin{array}{l}{\left\{\sum\limits _{j=0}^{\mathrm{\infty }}{c}_{j}{\beta }_{j}{\left({k}_{x}/2\right)}^{2j+1}{h}^{2j}+2\left(\sum\limits _{j=1}^{\mathrm{\infty }}{\gamma }_{j}{k}_{z}^{2j}{h}^{2j}\right)\left[{b}_{1}\sum\limits _{j=0}^{\mathrm{\infty }}{\beta }_{j}{\left({k}_{x}/2\right)}^{2j+1}{h}^{2j}+{b}_{2}\sum\limits _{j=0}^{\mathrm{\infty }}{\beta }_{j}{\left(3{k}_{x}/2\right)}^{2j+1}{h}^{2j}\right]\right\}}^{2}+\\ {\left\{\sum\limits _{j=0}^{\mathrm{\infty }}{c}_{j}{\beta }_{j}{\left({k}_{z}/2\right)}^{2j+1}{h}^{2j}+2\left(\sum\limits _{j=1}^{\mathrm{\infty }}{\gamma }_{j}{k}_{x}^{2j}{h}^{2j}\right)\left[{b}_{1}\sum\limits _{j=0}^{\mathrm{\infty }}{\beta }_{j}{\left({k}_{z}/2\right)}^{2j+1}{h}^{2j}+{b}_{2}\sum\limits _{j=1}^{\mathrm{\infty }}{\beta }_{j}{\left(3{k}_{z}/2\right)}^{2j+1}{h}^{2j}\right]\right\}}^{2}\\ \approx {\left[\sum\limits _{j=0}^{\mathrm{\infty }}{r}^{2j}{\beta }_{j}{\left(k/2\right)}^{2j+1}{h}^{2j}\right]}^{2}\end{array} $ | (8) |
其中
| $ \left\{\begin{array}{l}{c}_{j}=\sum\limits _{m=1}^{M}{\left(2m-1\right)}^{2j+1}{a}_{m}+2{b}_{1}+{3}^{2j+1}·2{b}_{2}\\ {\beta }_{j}=\frac{{\left(-1\right)}^{j}}{\left(2j+1\right)!}\\ {\gamma }_{j}=\frac{{\left(-1\right)}^{j}}{\left(2j\right)!}\end{array}\right. $ | (9) |
使式(8)左右两边
| $ {c}_{0}\left({b}_{1}+3{b}_{2}\right)=\frac{{r}^{2}}{24} $ | (10) |
使式(8)左右两边
| $ \begin{array}{l}{c}_{0}\left(3{b}_{1}+33{b}_{2}\right)+{c}_{1}\left({b}_{1}+3{b}_{2}\right)+\\ \;\;\;\;\;\;12({b}_{1}+3{b}_{2}{)}^{2}=\frac{{r}^{4}}{10}\end{array} $ | (11) |
使式(8)左右两边
| $ \left\{\begin{array}{cc}\begin{array}{l}\begin{array}{cc}{c}_{0}^{2}=1& j=0\end{array}\\ \sum\limits _{p=0}^{j}{c}_{p}{c}_{j-p}{\beta }_{p}{\beta }_{j-p}\\ =\sum\limits _{p=0}^{j}{\beta }_{p}{\beta }_{j-p}{r}^{2j}j=\mathrm{1, 2}, \cdots , M-1\end{array}& \end{array}\right. $ | (12) |
根据式(12)可得出
| $ \begin{array}{cc}{c}_{j}={r}^{2j}& j=\mathrm{0, 1}, \cdots , M-1\end{array} $ | (13) |
由式(13)可知
| $ \begin{array}{cc}\left\{\begin{array}{l}{b}_{1}=-\frac{3{r}^{4}}{640}+\frac{11{r}^{2}}{192}\\ {b}_{2}=\frac{{r}^{4}}{640}-\frac{{r}^{2}}{192}\end{array}\right.& \end{array} $ | (14) |
将式(13)代入式(9)得到
| $ \left\{\begin{array}{l}\sum\limits _{m=1}^{M}{\left(2m-1\right)}^{2j+1}{a}_{m}+2{b}_{1}+{3}^{2j+1}2{b}_{2}={r}^{2j}\\ j=\mathrm{0, 1}, \cdots , M-1\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\left(15\right)\end{array}\right. $ | (15) |
式(15)可改写为如下矩阵方程
| $ \left[\begin{array}{ccccc}{1}^{0}& {3}^{0}& {5}^{0}& {(2M-1)}^{0}& 1\\ {1}^{2}& {3}^{2}& {5}^{2}& \cdots & {\left(2M-1\right)}^{2}\\ {1}^{4}& {3}^{4}& {5}^{4}& \cdots & {\left(2M-1\right)}^{4}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {1}^{2M-2}& {3}^{2M-2}& {5}^{2M-2}& \cdots & {\left(2M-1\right)}^{2M-2}\end{array}\right]\left[\begin{array}{c}{a}_{1}+2{b}_{1}\\ 3\left({a}_{2}+2{b}_{2}\right)\\ 5{a}_{3}\\ ⋮\\ \left(2M-1\right){a}_{M}\end{array}\right]=\left[\begin{array}{c}1\\ {r}^{2}\\ {r}^{4}\\ ⋮\\ {r}^{2M-2}\end{array}\right] $ | (16) |
式(16)是一个范德蒙矩阵方程。
联合求解方程(14)和(16)得到
| $ \left\{\begin{aligned} b_1= & -\frac{3 r^4}{640}+\frac{11 r^2}{192} \\ b_2= & \frac{r^4}{640}-\frac{r^2}{192} \\ a_1= & \prod\nolimits_{2 \leqslant k \leqslant M}\left[\frac{r^2-(2 k-1)^2}{1-(2 k-1)^2}\right]-2 b_1 \\ a_2= & \frac{1}{3} \prod\nolimits_{1 \leqslant k \leqslant M, k \neq 2}\left[\frac{r^2-(2 k-1)^2}{3^2-(2 k-1)^2}\right]-2 b_2 \\ a_m= & \frac{1}{2 m-1} \prod\nolimits_{1 \leqslant k \leqslant M, k \neq m} \frac{r^2-(2 k-1)^2}{(2 m-1)^2-(2 k-1)^2} \\ & m=3,4, \cdots, M \end{aligned}\right.$ | (17) |
式(17)为M-SFD(N=2)的差分系数通解,利用同样的方法,可以导出M-SFD(N=1、3、4)的差分系数通解,见附录A。
1.3 差分精度分析可以将差分离散声波方程的频散关系误差函数关于空间采样间隔
| $ \begin{array}{l}{E}_{\mathrm{M}\mathrm{-}\mathrm{S}\mathrm{F}\mathrm{D}\left(N=2\right)}=\frac{1}{{h}^{2}}\left\{\sum\limits _{m=1}^{M}{a}_{m}\mathrm{s}\mathrm{i}\mathrm{n}\left[\left(m-\frac{1}{2}\right){k}_{x}h\right]+\right.\\ {\left.2\mathrm{c}\mathrm{o}\mathrm{s}\left({k}_{z}h\right)\left({b}_{1}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{k}_{x}h}{2}+{b}_{2}\mathrm{s}\mathrm{i}\mathrm{n}\frac{3{k}_{x}h}{2}\right)\right\}}^{2}+\\ \frac{1}{{h}^{2}}\left\{\sum\limits _{m=1}^{M}{a}_{m}\mathrm{s}\mathrm{i}\mathrm{n}\left[\left(m-\frac{1}{2}\right){k}_{z}h\right]+\right.\\ {\left.2\mathrm{c}\mathrm{o}\mathrm{s}\left({k}_{x}h\right)\left({b}_{1}\mathrm{s}\mathrm{i}\mathrm{n}\frac{{k}_{z}h}{2}+{b}_{2}\mathrm{s}\mathrm{i}\mathrm{n}\frac{3{k}_{z}h}{2}\right)\right\}}^{2}-\\ \frac{1}{{\left(v\mathrm{\Delta }t\right)}^{2}}\mathrm{s}\mathrm{i}{\mathrm{n}}^{2}\frac{rkh}{2}\left(18\right)\end{array} $ | (18) |
结合式(8)~式(12),
| $ \begin{array}{l}{E}_{\mathrm{M}\mathrm{-}\mathrm{S}\mathrm{F}\mathrm{D}\left(N=2\right)}=\sum\limits _{j=M}^{\mathrm{\infty }}\sum\limits _{p=0}^{j}\left({c}_{p}{c}_{j-p}-{r}^{2j}\right){\beta }_{p}{\beta }_{j-p}\frac{1}{{2}^{2j+2}}\left({k}_{x}^{2j+2}+{k}_{z}^{2j+2}\right){h}^{2j}+\\ \sum\limits _{j=3}^{\mathrm{\infty }}\sum\limits _{p=0}^{j-1}\left\{\frac{{\gamma }_{j-p}}{{2}^{2p+2}}\sum\limits _{q=0}^{p}2{c}_{q}\left[{b}_{1}+{3}^{2\left(p-q\right)+1}{b}_{2}\right]{\beta }_{q}{\beta }_{p-q}+\frac{{\gamma }_{p+1}}{{2}^{2\left(j-p\right)}}\sum\limits _{q=0}^{j-p-1}2{c}_{q}\left[{b}_{1}+{3}^{2\left(j-p-1-q\right)+1}{b}_{2}\right]{\beta }_{q}{\beta }_{j-p-1-q}-\right.\\ \left.\frac{{r}^{2j}{C}_{j+1}^{p+1}}{{2}^{2j+2}}\sum\limits _{q=0}^{j}{\beta }_{q}{\beta }_{j-q}\right\}{k}_{x}^{2p+2}{k}_{z}^{2\left(j-p\right)}{h}^{2j}\left(19\right)\end{array} $ | (19) |
其中
式(19)表明,
同样地,M-SFD(N=1)给出的差分离散声波方程的频散关系误差函数
表 1给出了当差分离散声波方程达到相同阶的差分精度时,本文的M-SFD与Tan等[33]构建的时间和空间高阶交错网格差分格式需要的非坐标网格点数。对比可以看出,达到相同阶的差分精度,本文的M-SFD需要的非坐标轴网格点数更少,因而计算量更小,计算效率更高。
|
|
表 1 相同阶差分精度本文方法与Tan等(2014)方法所需的非坐标轴网格点数 |
数值频散能直接反映交错网格有限差分法的数值模拟精度。本文引入归一化相速度误差函数
| $ \left\{\begin{array}{l}{\varepsilon }_{ph}\left(kh, \theta \right)=\frac{{v}_{ph}}{v}-1=\frac{2}{rkh}\mathrm{s}\mathrm{i}{\mathrm{n}}^{-1}\left(r\sqrt[]{q}\right)-1\\ q=\left\{\sum\limits _{m=1}^{M}{a}_{m}\mathrm{s}\mathrm{i}\mathrm{n}\left[\left(m-\frac{1}{2}\right)kh\mathrm{c}\mathrm{o}\mathrm{s}\theta \right]\right.+\\ \;\;\;\;\;\;2{b}_{1}\mathrm{c}\mathrm{o}\mathrm{s}\left(kh\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}{\frac{kh\mathrm{c}\mathrm{o}\mathrm{s}\theta }{2}}^{2}+\\\;\;\;\;\;\; \left\{\sum\limits _{m=1}^{M}{a}_{m}\mathrm{s}\mathrm{i}\mathrm{n}\left[\left(m-\frac{1}{2}\right)kh\mathrm{s}\mathrm{i}\mathrm{n}\theta \right]\right.+\\\;\;\;\;\;\;2{b}_{1}\mathrm{c}\mathrm{o}\mathrm{s}\left(kh\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)\mathrm{s}\mathrm{i}\mathrm{n}{\frac{kh\mathrm{s}\mathrm{i}\mathrm{n}\theta }{2}}^{2}\end{array}\right. $ | (20) |
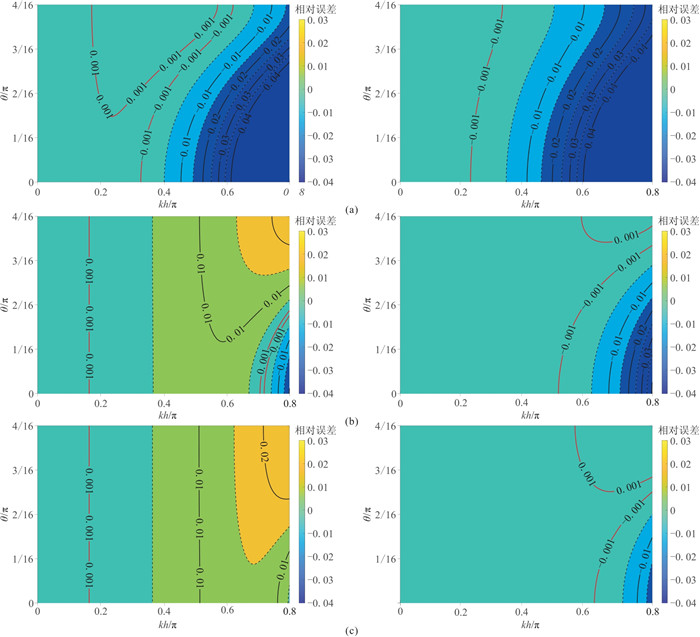
图 3给出了不同M值时C-SFD和M-SFD的归一化相速度误差
|
图 3 不同M值时C-SFD(左)和M-SFD(N=1)(右)相速度频散等值线图( |
图 4给出了不同M及N时,M-SFD的归一化相速度误差

|
图 4 M=10(左)及M=20(右)时不同N值的M-SFD相速度频散等值线( |
根据M-SFD(N=2)给出的差分离散声波方程的频散关系式(7)得到
| $ \begin{aligned} & \frac{1}{r^2} \sin ^2 \frac{r k h}{2} \approx \frac{1}{h^2}\left\{\sum\limits_{m=1}^M a_m \sin \left[\left(m-\frac{1}{2}\right) k_x h\right]+\right. \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left.2 \cos \left(k_z h\right)\left(b_1 \sin \frac{k_x h}{2}+b_2 \sin \frac{3 k_x h}{2}\right)\right\}+ \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{h^2} \sum\limits_{m=1}^M a_m \sin \left[\left(m-\frac{1}{2}\right) k_z h\right]+ \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left.2 \cos \left(k_x h\right)\left(b_1 \sin \frac{k_z h}{2}+b_2 \sin \frac{3 k_z h}{2}\right)\right\} \end{aligned} $ | (21) |
取空间波数
| $ r\le S=\frac{1}{\sqrt[]{2}\left|\sum\limits _{m=1}^{M}{\left(-1\right)}^{m-1}{a}_{m}-2{b}_{1}+2{b}_{2}\right|} $ | (22) |
式中
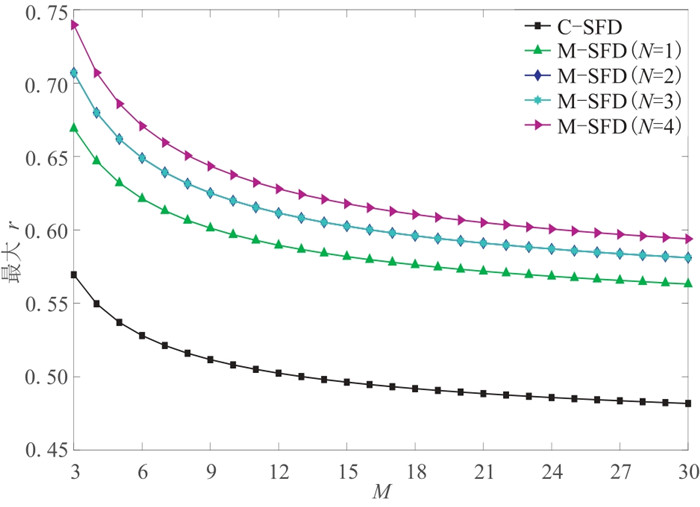
式(22)为M-SFD(N=2)给出的差分离散声波方程的稳定性条件表达式。同样地,可以导出C-SFD和M-SFD(N=1、3、4)的稳定性条件表达式。图 5给出了稳定性条件约束下,
|
图 5 C-SFD和M-SFD(N=1、2、3、4)的稳定性曲线 |
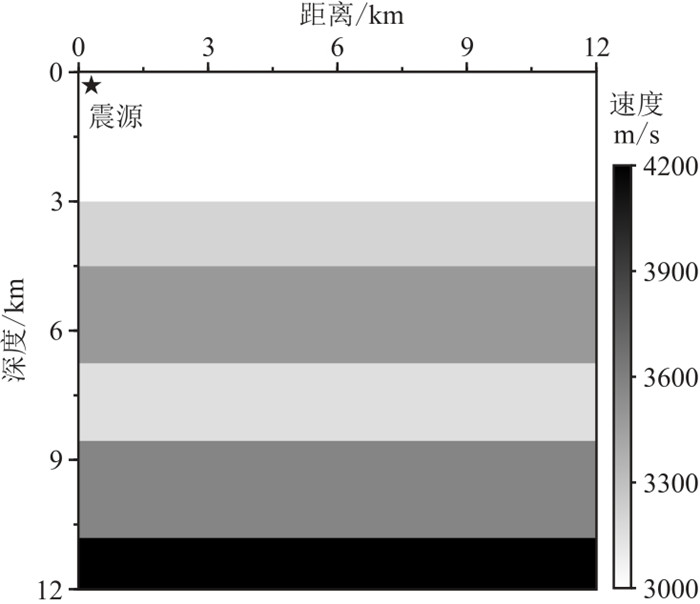
图 6给出了一个包含5个反射界面的层状介质速度模型,模型尺寸为
|
图 6 层状介质速度模型 |
|
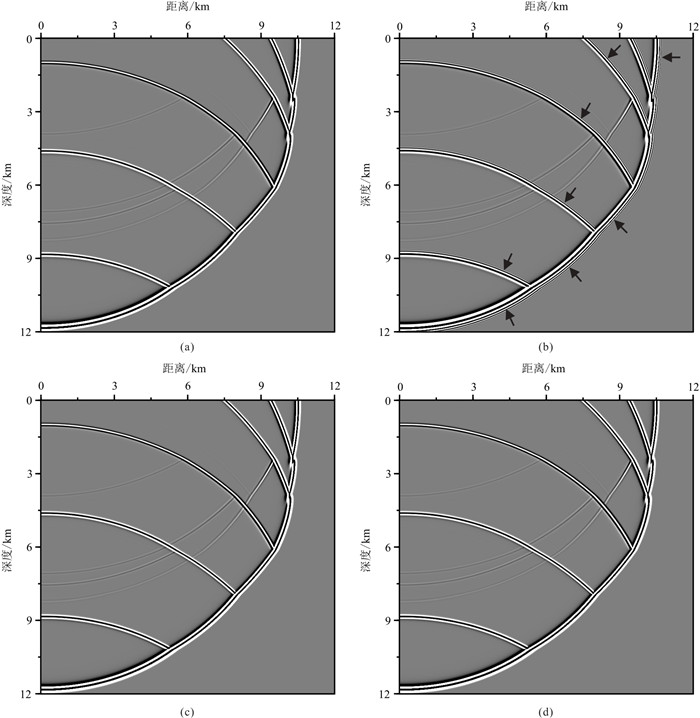
图 7 不同参数C-SFD(上)及M-SFD(下)层状介质3.6 s时刻压力场( |

|
图 8 不同参数C-SFD(上)及M-SFD(下)层状介质3.6 s时刻速度场( |
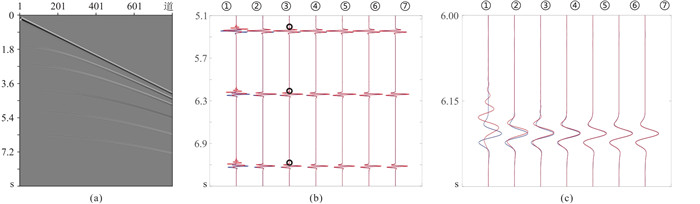
|
图 9 M-SFD层状介质模型模拟炮集记录(a)和两种方法不同时区单道波形对比(b)及其放大显示(c) 蓝色为参考波形,由C-SFD(M=20)采用Δt=0.1 ms模拟得到;红色为不同交错网格有限差分法的模拟波形;①、②C-SFD(M=12)分别采用Δt=1.0 ms和Δt=0.5 ms;③、④ M-SFD(M=10;N=1)分别采用Δt=2.0 ms和Δt=1.5 ms;⑤、⑥、⑦ M-SFD(M=10;N=2,3,4)采用Δt=2.0 ms。 |
表 2统计了C-SFD(M=12)和M-SFD(M=10;N=1,2,3,4)采用不同时间采样间隔进行模拟的耗时和加速比,模拟总时长为9.0 s,且均采用Inter Xeon Gold 5218 CPU处理器。
|
|
表 2 C-SFD和M-SFD法层状介质声波模拟的耗时和加速比对比 |
图 7和图 8中两组波场快照显示:C-SFD(M=12)采用
图 9b和图 9c中的单道波形显示:C-SFD(M=12)采用
综合图 7~图 9给出的数值频散特征及表 2给出的计算效率统计结果,可以看出:M-SFD(M=10;N=1)采用
仔细对比图 9c中的单道波形会发现,采用相同的时间采样间隔
图 10a为中国塔里木盆地典型复杂构造速度模型,模型尺寸为
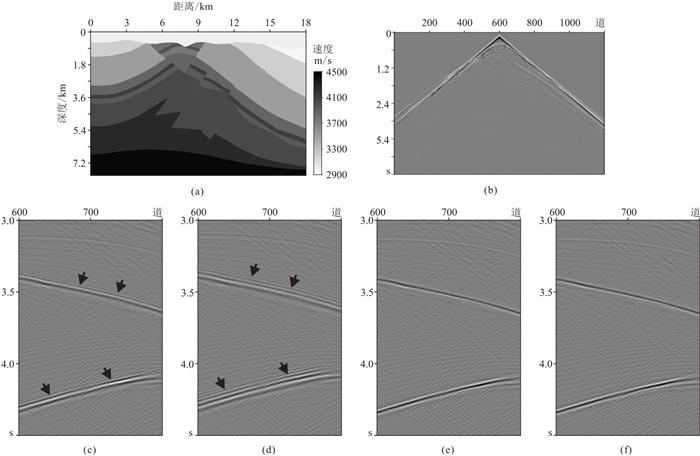
|
图 10 中国塔里木盆地典型复杂模型及声波交错网格有限差分数值模拟单炮记录(压力场 |
图 10b给出了M-SFD(M=8;N=1)采用采
复杂构造模型模拟结果表明:计算效率基本相同时,M-SFD比C-SFD能更有效地压制数值频散,模拟精度更高;M-SFD可采用更大的时间采样间隔以提高计算效率,并保持更高的模拟精度。
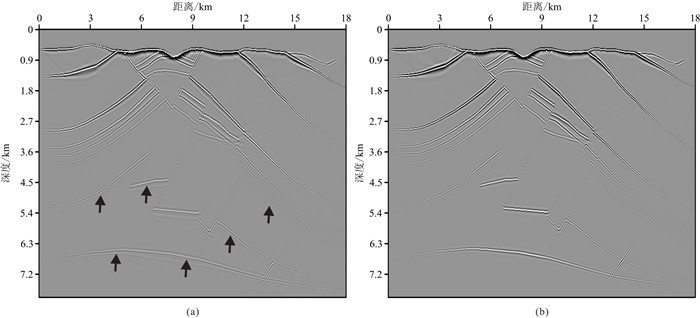
4 混合交错网格有限差分法在逆时偏移中的应用将M-SFD作为逆时偏移算法中的波场传播算子,以图 10a中的复杂构造模型进行逆时偏移测试。震源采用主频为25 Hz的Ricker子波。C-SFD(M=15)采用非常小的时间采样间隔
分别以C-SFD(M=10)和M-SFD(M=8;N=1)作为逆时偏移算法中的波场传播算子,时间采样间隔
|
图 11 中国塔里木盆地典型复杂构造模型声波混合交错网格有限差分RTM剖面 (a) C-SFD(M=10);(b) M-SFD(M=8;N=1) |
本文联合利用坐标轴网格点和非坐标轴网格点构建空间差分算子近似波场的一阶空间偏导数,建立了适用于速度—应力声波方程模拟的M-SFD,并基于时空域频散关系和泰勒级数展开导出了差分系数通解。通过差分精度分析、频散分析、稳定性分析、数值模拟和逆时偏移试验,得到以下结论:
(1) C-SFD给出的差分离散声波方程仅具有二阶差分精度,M-SFD(N=1、2、4)给出的差分离散声波方程可达到4、6、8阶差分精度,继续增大N的取值,理论上可以达到任意偶数阶差分精度;
(2) 计算效率基本相同时,M-SFD比C-SFD能更有效地压制数值频散,模拟精度更高;M-SFD可通过采用更大的时间采样间隔以提高计算效率,且模拟精度仍然高于C-SFD;
(3) M-SFD作为逆时偏移的波场传播算子能够更有效地消除数值频散造成的成像假象,进而提高深层的成像精度和分辨率。
附录A M-SFD(N=1,3,4)的差分离散声波方程及差分系数通解与文中M-SFD(N=2)的差分系数求解过程类似,利用M-SFD(N=1)对声波方程(式(1))进行差分离散可以导出相应差分离散声波方程,再将离散平面波解代入差分离散声波方程导出相应的时空域频散关系,并利用泰勒公式对频散关系中的三角函数进行级数展开,然后,使得方程左右两边
| $ \left\{\begin{array}{l} b_1=\frac{r^2}{24} \\ a_1=\prod\limits_{2 \leqslant k \leqslant M} \frac{r^2-(2 k-1)^2}{1-(2 k-1)^2}-\frac{r^2}{12} \\ a_m=\frac{1}{2 m-1} \prod\limits_{1 \leqslant k \leqslant M, k \neq m} \frac{r^2-(2 k-1)^2}{(2 m-1)^2-(2 k-1)^2} \\ \quad\quad\quad m=2,3, \cdots, M \end{array}\right. $ | (A-1) |
利用泰勒公式对M-SFD(N=3)给出的差分离散声波方程的时空域频散关系中的三角函数进行级数展开,然后,使得方程左右两边
| $ \left\{\begin{array}{l} b_1=\frac{r^6}{4480}-\frac{5 r^4}{128}+\frac{37 r^2}{576} \\ b_2=\frac{r^6}{4480}-\frac{r^4}{640}+\frac{r^2}{576} \\ b_3=-\frac{r^6}{4480}+\frac{r^4}{320}-\frac{r^2}{144} \\ a_1=\prod\limits_{2 \leqslant k \leqslant M} \frac{r^2-(2 k-1)^2}{1-(2 k-1)^2}-2 b_1-2 b_3 \\ a_2=\frac{1}{3} \prod\limits_{1 \leqslant k \leqslant M} \frac{r^2-(2 k-1)^2}{3^2-(2 k-1)^2}-2 b_2 \\ a_m=\frac{1}{2 m-1} \prod\limits_{\substack{1 \leqslant k \leqslant M \\ k \neq m}} \frac{r^2-(2 m-1)^2-(2 k-1)^2}{(2 m-1)^2} \\ \quad\quad m=3,4, \cdots, M \end{array}\right.$ | (A-2) |
利用泰勒公式对M-SFD(N=4)给出的差分离散声波方程的时空域频散关系中的三角函数进行级数展开,然后使得方程左右两边
| $ \left\{\begin{array}{l} b_1=\frac{1}{240 \times 16}\left(-\frac{r^6}{7}-15 r^4+\frac{629}{3} r^2\right) \\ b_2=\frac{1}{240 \times 48}\left(-\frac{31 r^6}{7}+87 r^4-239 r^2\right) \\ b_3=\frac{1}{240 \times 64}\left(\frac{25 r^6}{7}-57 r^4+\frac{457 r^2}{3}\right) \\ b_4=\frac{1}{240 \times 24 \times 8}\left(r^6-15 r^4+37 r^2\right) \\ a_1=\prod\limits_{2 \leqslant k \leqslant M} \frac{r^2-(2 k-1)^2}{1-(2 k-1)^2}-2 b_1-2 b_3 \\ a_2=\frac{1}{3} \prod\limits_{\substack{1 \leqslant k \leqslant M \\ k \neq 2}} \frac{r^2-(2 k-1)^2}{3^2-(2 k-1)^2}-2 b_2-2 b_4 \\ a_m=\frac{1}{2 m-1} \prod\limits_{\substack{1 \leqslant k \leqslant M \\ k \neq m}} \frac{r^2-(2 m-1)^2-(2 k-1)^2}{(2 m-1} \\ \quad\quad\quad m=3,4, \cdots, M \end{array}\right. $ | (A-3) |
| [1] |
CARCIONE J M. Wave Fields in Real Media: Wave Propagation in Anisotropic, An Elastic, Porous and Electromagnetic Media[M]. 3rd ed. Elsevier, Amsterdam, 2015.
|
| [2] |
吴建鲁, 吴国忱, 王伟, 等. 基于等效交错网格的流固耦合介质地震波模拟[J]. 石油地球物理勘探, 2018, 53(2): 272-279. WU Jianlu, WU Guochen, WANG Wei, et al. Seismic forward modeling in fluid-solid media based on equivalent staggered grid scheme[J]. Oil Geophysical Prospecting, 2018, 53(2): 272-279. DOI:10.13810/j.cnki.issn.1000-7210.2018.02.007 |
| [3] |
VIRIEUX J, CALANDRA H, PLESSIX R É. A review of the spectral, pseudo-spectral, finite-difference and finite-element modelling techniques for geophysical imaging[J]. Geophysical Prospecting, 2011, 59(5): 794-813. DOI:10.1111/j.1365-2478.2011.00967.x |
| [4] |
BERKHOUT A J. Review paper: an outlook on the future of seismic imaging, part Ⅰ: forward and reverse modelling[J]. Geophysical Prospecting, 2014, 62(5): 911-930. DOI:10.1111/1365-2478.12161 |
| [5] |
GERHARD P, SHIN C, HICKS. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
| [6] |
VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophy-sics, 2009, 74(6): WCC1-WCC26. |
| [7] |
RESHEF M, KOSLOFF D, EDWARDS M, et al. Three-dimensional acoustic modeling by the Fourier method[J]. Geophysics, 1988, 53(9): 1175-1183. DOI:10.1190/1.1442557 |
| [8] |
MITTET R. On the pseudospectral method and spectral accuracy[J]. Geophysics, 2021, 86(3): T127-T142. DOI:10.1190/geo2020-0209.1 |
| [9] |
MARFURT K J. Accuracy of finite‐difference and finite‐element modeling of the scalar and elastic wave equations[J]. Geophysics, 1984, 49(5): 533-549. DOI:10.1190/1.1441689 |
| [10] |
韩德超, 刘卫华, 司文朋. 三角网格间断有限元法弹性波模拟精度分析[J]. 石油地球物理勘探, 2021, 56(4): 758-770. HAN Dechao, LIU Weihua, SI Wenpeng. Analysis of elastic wave simulation accuracy with discontinuous Galerkin finite element method based on triangular meshes[J]. Oil Geophysical Prospecting, 2021, 56(4): 758-770. DOI:10.13810/j.cnki.issn.1000-7210.2021.04.009 |
| [11] |
王辉, 何兵寿, 邵祥奇. 一阶速度—胀缩—旋转弹性波方程交错网格数值模拟[J]. 石油地球物理勘探, 2022, 57(6): 1352-1361. WANG Hui, HE Bingshou, SHAO Xiangqi. Numerical simulation of first-order velocity-dilatation-rotation elastic wave equation with staggered grid[J]. Oil Geophysical Prospecting, 2022, 57(6): 1352-1361. DOI:10.13810/j.cnki.issn.1000-7210.2022.06.010 |
| [12] |
王绍文, 宋鹏, 谭军, 等. 弹性波数值模拟中的高斯型混合吸收边界条件及其GPU并行[J]. 石油地球物理勘探, 2021, 56(3): 485-495. WANG Shaowen, SONG Peng, TAN Jun, et al. Gaussian-type weighted hybrid absorbing boundary for elastic wave simulation and its acceleration on GPU[J]. Oil Geophysical Prospecting, 2021, 56(3): 485-495. DOI:10.13810/j.cnki.issn.1000-7210.2021.03.007 |
| [13] |
REN Z, LIU Y. Acoustic and elastic modeling by optimal time-space-domain staggered-grid finite-difference schemes[J]. Geophysics, 2015, 80(1): T17-T40. DOI:10.1190/geo2014-0269.1 |
| [14] |
彭更新, 刘威, 郭念民, 等. 基于时空域交错网格有限差分法的应力速度声波方程数值模拟[J]. 石油物探, 2022, 61(1): 156-165. PENG Gengxin, LIU Wei, GUO Nianmin, et al. A time-space domain dispersion-relationship-based staggered-grid finite-difference scheme for modeling the stress-velocity acoustic wave equation[J]. Geophysical Prospecting for Petroleum, 2022, 61(1): 156-165. DOI:10.3969/j.issn.1000-1441.2022.01.016 |
| [15] |
胡建林, 宋维琪, 张建坤, 等. 交错网格有限差分正演模拟的联合吸收边界[J]. 石油地球物理勘探, 2018, 53(5): 914-920. HU Jianlin, SONG Weiqi, ZHANG Jiankun, et al. Joint absorbing boundary in the staggered-grid finite difference forward modeling simulation[J]. Oil Geophysical Prospecting, 2018, 53(5): 914-920. DOI:10.13810/j.cnki.issn.1000-7210.2018.05.004 |
| [16] |
DABLAIN M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66. |
| [17] |
LIU Y, SEN M K. A new time-space domain high-order finite-difference method for the acoustic wave equation[J]. Journal of Computational Physics, 2009, 228(23): 8779-8806. |
| [18] |
LIU Y, SEN M K. Finite-difference modeling with adaptive variable-length spatial operators[J]. Geophysics, 2011, 76(4): T79-T89. |
| [19] |
任志明, 戴雪, 包乾宗, 等. 有限差分的时间和空间频散及其对逆时偏移和全波形反演的影响[J]. 地球物理学报, 2021, 64(11): 4166-4180. REN Zhiming, DAI Xue, BAO Qianzong, et al. Time and space dispersion in finite difference and its influence on reverse time migration and full-waveform inversion[J]. Chinese Journal of Geophysics, 2021, 64(11): 4166-4180. |
| [20] |
FORNBERG B. Classroom note: calculation of weights in finite difference formulas[J]. SIAM Review, 1998, 40(3): 685-691. |
| [21] |
LIU Y, SEN M K. Scalar wave equation modeling with time-space domain dispersion-relation-based staggered-grid finite-difference schemes[J]. Bulletin of the Seismological Society of America, 2011, 101(1): 141-159. |
| [22] |
GELLER R J, TAKEUCHI N. Optimally accurate second-order time-domain finite difference scheme for the elastic equation of motion: one-dimensional cases[J]. Geophysical Journal International, 1998, 135(1): 48-62. |
| [23] |
CHU C, STOFFA P L. Determination of finite-difference weights using scaled binomial windows[J]. Geophysics, 2012, 77(3): W17-W26. |
| [24] |
ZHANG J, YAO Z. Optimized finite-difference operator for broadband seismic wave modeling[J]. Geophysics, 2013, 78(1): A13-A18. |
| [25] |
LIU Y. Globally optimal finite-difference schemes based on least squares[J]. Geophysics, 2013, 78(4): T113-T132. |
| [26] |
LIU Y. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling[J]. Geophysical Journal International, 2014, 197(2): 1033-1047. |
| [27] |
LIU Y, SEN M K. Time-space domain dispersion-relation-based finite-difference method with arbitrary even-order accuracy for the 2D acoustic wave equation[J]. Journal of Computational Physics, 2013, 232(1): 327-345. |
| [28] |
WANG E, LIU Y, SEN M K. Effective finite-difference modelling methods with 2-D acoustic wave equation using a combination of cross and rhombus stencils[J]. Geophysical Journal International, 2016, 206(3): 1933-1958. |
| [29] |
胡自多, 贺振华, 刘威, 等. 旋转网格和常规网格混合的时空域声波有限差分正演[J]. 地球物理学报, 2016, 59(10): 3829-3846. HU Ziduo, HE Zhenhua, LIU Wei, et al. Scalar wave equation modeling using the mixed-grid finite-difference method in the time-space domain[J]. Chinese Journal of Geophysics, 2016, 59(10): 3829-3846. |
| [30] |
JO C H, SHIN C, SUH J H. An optimal 9‐point, finite‐difference, frequency‐space, 2-D scalar wave extrapolator[J]. Geophysics, 1996, 61(2): 529-537. |
| [31] |
SHIN C, SOHN H. A frequency‐space 2-D scalar wave extrapolator using extended 25-point finite‐difference operator[J]. Geophysics, 1998, 63(1): 289-296. |
| [32] |
胡自多, 刘威, 雍学善, 等. 三维波动方程时空域混合网格有限差分数值模拟方法[J]. 地球物理学报, 2021, 64(8): 2809-2828. HU Ziduo, LIU Wei, YONG Xueshan, et al. Mixed-grid finite-difference method for numerical simulation of 3D wave equation in the time-space domain[J]. Chinese Journal of Geophysics, 2021, 64(8): 2809-2828. |
| [33] |
TAN S, HUANG L. An efficient finite-difference method with high-order accuracy in both time and space domains for modelling scalar-wave propagation[J]. Geophysical Journal International, 2014, 197(2): 1250-1267. |
| [34] |
REN Z, LI Z, LIU Y, et al. Modeling of the acoustic wave equation by staggered‐grid finite‐difference schemes with high‐order temporal and spatial accuracy[J]. Bulletin of the Seismological Society of America, 2017, 107(5): 2160-2182. |
| [35] |
REN Z, LI Z. Temporal high-order staggered-grid finite-difference schemes for elastic wave propagation[J]. Geophysics, 2017, 82(5): T207-T224. |
| [36] |
ZHOU H, LIU Y, WANG J. Time-space domain scalar wave modeling by a novel hybrid staggered-grid finite-difference method with high temporal and spatial accuracies[J]. Journal of Computational Physics, 2022, 455: 111004. |
| [37] |
ZHOU H, LIU Y, WANG J. Elastic wave modeling with high-order temporal and spatial accuracies by a selectively modified and linearly optimized staggered-grid finite-difference scheme[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 1-22. |



 胡自多, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院,730020。Email:
胡自多, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院,730020。Email: 