0 引言

随着地震勘探开发难度的不断增大，对地震资料质量的要求也越来越高。在现场采集地震数据时，由于地表等因素的影响，不可避免地会引入噪声，降低了地震资料信噪比，因此地震数据去噪就显得非常重要。地震数据去噪处理的众多方法可分为几大类：基于滤波的方法^[1-2]、基于变换的方法^[3-8]、基于降秩类的方法^[9-10]和基于学习的方法等。

近年来，基于学习的方法发展迅速，它是学习含噪图像到“干净”图像的一种映射关系，可细分为基于字典学习的方法^[11-14]和基于深度学习的方法^[15-16]。基于字典学习的方法旨在得到含原始数据信息的自适应字典，需对数据进行多次学习训练，根据有效信号与随机噪声在字典上表现的不同特点，突显数据本质特征，压制随机噪声，达到去噪目的。基于深度学习的方法是一种数据驱动类方法，去噪时需从大量数据样本学习得到有效信号与噪声的区别，搭建适用的深度神经网络以压制噪声，包括准备数据、搭建网络、训练网络、最优模型等环节，各环节的处理经验对最终训练效果有显著影响。本文主要探讨字典学习方法在地震数据去噪中的应用。

字典学习源于压缩感知理论^[17-18]。在稀疏表示中，若待处理的数据是稀疏的，就可通过某种稀疏变换稀疏表示原始地震信号，从而实现数据去噪。但由于地震信号的稀疏表示能力因采用不同的变换方法表达效果会有明显差异，或因实际采集的地震数据具有不同的局部特性，这时若仅使用某一种变换所组成的稀疏字典往往不能充分、有效地将其全部表达，将对去噪结果产生一定影响。因此，基于数据本身特征，自适应地构造一种新的适用学习型方法^[19]，更有效地应用于数据去噪显得尤为重要。

Olshausen等^[20]率先提出学习型过完备字典概念，并将该理论应用于图像去噪领域；在此基础上，Aharon等^[21]提出一种新的自适应字典算法，实现信号的稀疏表示。将K奇异值分解(K-SVD)作为字典更新方法，自适应地获取表达信号本身特征的原子，训练出学习型过完备字典，将学习训练得到的字典作为图像稀疏表示的稀疏字典，以有效压制随机噪声。之后，基于K-SVD算法的字典学习广泛地应用于地震数据去噪^[22]。但这种传统的K-SVD字典学习方法在去噪精度及计算效率等方面仍有进一步提升的空间。

针对以上问题，本文提出一种新的用于地震数据去噪的K-SVD字典学习方法：采用一种将任意位置的块作为学习的对象，并对这种不定的稀疏表示模型进行学习算法的改进；然后对稀疏编码算法关键步骤进行优化，使新的K-SVD字典学习方法在信噪比、计算时间和数据局部特征保持等方面更具优势。文中首先阐述了字典学习方法基本理论；然后基于传统K-SVD字典学习方法，进行改进并给出新方法的去噪原理及处理流程；最后，通过数值模拟试验，分析、评估本文方法的去噪性能。

1 理论方法

先介绍字典学习的基本理论及去噪模型，再重点阐述新方法的K-SVD字典更新理论。在此基础上，使用新的字典学习方法对地震数据进行去噪。

1.1 字典学习

字典学习应用于地震去噪领域有两个关键步骤：一是对地震数据进行稀疏编码；二是学习更新字典。

对于含噪地震数据模型，可将其近似看作

$ \boldsymbol{Q}={\boldsymbol{Q}}_{0}+\boldsymbol{\varepsilon } $

(1)

式中Q₀是待估测的无噪地震数据，通常所采集的是含有随机噪声$ \boldsymbol{\varepsilon } $的有噪数据Q。去除随机噪声相当于从采集的含噪地震数据Q中近似得到无噪数据Q₀，简言之，即是利用一种方法压制噪声$ \boldsymbol{\varepsilon } $。

1.1.1 稀疏编码

基于K-SVD算法的字典学习，是设计出一种基于小块的过完备字典算法，对数据样本进行研究；通过对每一小块进行去噪，使其更接近理想化结果。字典学习包含的主要参数有可稀疏线性表示^[23]的原始信号样本Q (m×n，m为样本个数，n为每个样本的特征维度)、包含k个原子的字典矩阵D (m×k)、及稀疏矩阵X (k×n)，这样就可理想化表示为Q=DX。该思想过程可表示为

$ \underset{D, X}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖\boldsymbol{Q}-\boldsymbol{D}\boldsymbol{X}‖}_{\mathrm{F}}^{2}\begin{array}{cc}& \end{array}\mathrm{s}.\mathrm{t}.\begin{array}{cc}& \end{array}\forall i, {‖{\boldsymbol{x}}_{i}‖}_{0}\le T $

(2)

式中：$ {x}_{i}(i=\mathrm{1, 2}, \cdot \cdot \cdot , k) $是稀疏矩阵X的行向量，其元素是字典矩阵中对应原子的系数；T为稀疏度；F是指Frobenius范数。

实际上，在压缩感知与稀疏表示理论框架中，利用拉格朗日乘子法就可将上述去噪问题转变成求解无约束的正则化问题

$ \mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\frac{1}{2}{‖\boldsymbol{Q}-\boldsymbol{D}\boldsymbol{X}‖}_{2}^{2}+\lambda {‖{\boldsymbol{x}}_{i}‖}_{P} $

(3)

式中：第一项是数据真实值与误差之间的控制项，即控制重建后地震信号与含噪信号之间的误差；第二项是x_i的P范数，它是为了保证系数足够稀疏。由此得到理想化的既稀疏又能准确地表达地震数据的稀疏解。当P=0时，即需找出系数的0范数，通常这是一个NP问题^[24]，相对来讲较难解决，但若利用其默认满足的有限等距条件，即可将0范数替换为1范数，从而简化计算以便于求解

$ \mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\frac{1}{2}{‖\boldsymbol{Q}-\boldsymbol{D}\boldsymbol{X}‖}_{2}^{2}+\lambda {‖{\boldsymbol{x}}_{i}‖}_{1} $

(4)

式中正则化参数$ \lambda $可确定目标函数中数据精确性和系数稀疏性的权重，通过设置和调节$ \lambda $值可获得更佳方案。

针对稀疏编码系数，通常可用正交匹配追踪(Orthogonal Matching Pursuit，OMP)这一贪婪算法近似求解。当然还有很多类似算法可求取近似解，如基追踪(Basis Pursuit，BP)^[25]、Bregman算法等。

1.1.2 字典更新

通过K-SVD算法进行字典更新时，因难以同时求解D和X，故K-SVD算法采用迭代思想，在每次迭代中交替求解D和X。字典更新是固定稀疏编码阶段的X，从而求解出字典D，在多次迭代后得到最优稀疏系数X及对应的字典D。此阶段的约束条件^[26-27]为

$ \underset{\boldsymbol{D}}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖\boldsymbol{Q}-\boldsymbol{D}\boldsymbol{X}‖}_{2}^{2} $

(5)

K-SVD算法采用逐列更新字典方式，如对字典D的第t列做更新时，记D的第t列列向量为d_t，并称其为原子，记X的第t行行向量为x_t，更新过程如下

$ \begin{aligned} \|\boldsymbol{Q}-\boldsymbol{D}\boldsymbol{X}\|_{\mathrm{F}}^2 & =\left\|\boldsymbol{Q}-\sum\limits _{j=1}^{t}{\boldsymbol{d}}_{j}{\boldsymbol{x}}_{j}\right\|_{\mathrm{F}}^2 \\ & =\left\|\left(\boldsymbol{Q}-\sum\limits_{j=1, j \neq t} {\boldsymbol{d}}_{j}{\boldsymbol{x}}_{j}\right)-{\boldsymbol{d}}_{t}{\boldsymbol{x}}_{t}\right\|_{\mathrm{F}}^2 \\ & =\left\|{\boldsymbol{E}}_{t}-{\boldsymbol{d}}_{t}{\boldsymbol{x}}_{t}\right\|_{\mathrm{F}}^2 \end{aligned}$

(6)

这样，学习优化问题转化为$ \underset{{\boldsymbol{d}}_{t}, {\boldsymbol{x}}_{t}}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖{\boldsymbol{E}}_{t}-{\boldsymbol{d}}_{t}{\boldsymbol{x}}_{t}‖}_{\mathrm{F}}^{2} $，其中$ {\boldsymbol{E}}_{t}=\boldsymbol{Q}-\sum\limits _{j=1, j\ne t}{\boldsymbol{d}}_{j}{\boldsymbol{x}}_{j} $是误差矩阵，此时还需找到x_j中元素为0的位置，同时删除E_t中与其对应的位置，更新得到新的误差矩阵E_t'，此时学习问题进一步转化为$ \underset{{\boldsymbol{d}}_{t}, {\boldsymbol{x}}_{t}}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖{\boldsymbol{E}}_{t}^{\prime}-{\boldsymbol{d}}_{t}{\boldsymbol{x}}_{t}^{\prime}‖}_{\mathrm{F}}^{2} $。

利用奇异值分解方法分解误差矩阵，使得

$ {\boldsymbol{E}}_{t}^{\prime}=\boldsymbol{U}\boldsymbol{\varSigma }{\boldsymbol{V}}^{\mathrm{T}} $

(7)

由此求解出最优的d_t、x_t'。d_t即取U的第1列更新字典的第t列，x_t'即取$ \boldsymbol{\varSigma } $的对角线上的第1个元素与V的第1列的乘积，由此进行更新，并替换x_t，这样便使式(6)的值为最小。其中

$ \left\{\begin{array}{l}{\boldsymbol{E}}_{t}{{\boldsymbol{E}}_{t}}^{\mathrm{T}}=\boldsymbol{U}{\boldsymbol{\varLambda }}_{1}{\boldsymbol{U}}^{\mathrm{T}}\\ {{\boldsymbol{E}}_{t}}^{\mathrm{T}}{\boldsymbol{E}}_{t}=V{\boldsymbol{\varLambda }}_{2}{V}^{\mathrm{T}}\end{array}\right. $

(8)

上述式中：U是E_tE_t^T的特征向量构成的矩阵，称作左奇异矩阵(m×m)；V是E_t^TE_t的特征向量构成的矩阵，也称作右奇异矩阵(n×n)；$ \boldsymbol{\varSigma } $是$ {\boldsymbol{\varLambda }}_{1} $(m×m)和$ {\boldsymbol{\varLambda }}_{2} $(n×n)两个矩阵的对角线上的非零元素由大到小构成的对角矩阵(m×n)。

1.2 地震数据去噪

新的K-SVD字典学习方法对地震数据进行去噪包括两个阶段：首先对样本数据进行训练，得到学习字典；然后利用学习到的字典对含噪数据做降噪处理，得到较理想的最终去噪结果。整个过程通过多次循环实现。

在训练集足够大的情况下，本文从含噪数据中训练提取任意位置的块作为训练集，使得用K-SVD算法得到的字典更能较准确地捕获数据中的特征，提高分块后含噪数据的去噪质量。该算法对字典进行训练时需从样本数据中选取大量图像块作为训练集，随着训练样本的增加，求取系数时的计算量也会增加。虽然训练集的数量是保证稀疏表示后图像精度的前提，但数量过多的训练集会加重运算负担，降低算法效率。因此，根据所采集地震数据选择合适的块的大小尤为重要。在后面数值试验部分，本文方法设置原子的尺寸为4×4的块，学习字典的尺寸^[28]为16×64的块，即字典大小设置为原子的4倍，即一个字典包含维度为16的64个原子。

在得到学习字典之后，重要的是对从含噪数据中提取的重叠部分的每个块进行去噪。利用稀疏编码参数中的约束条件，通过学习的字典计算每个块的稀疏逼近进行去噪，然后对去噪后的块进行平均以重建整个数据，完成对地震数据的去噪。这里使用OMP进行稀疏编码，块向量x与其稀疏逼近$ \tilde{\boldsymbol{x}} $之间的误差需满足下列约束条件^[29]

$ {‖\boldsymbol{x}-\tilde{\boldsymbol{x}}‖}_{2}\le C\sigma \sqrt{n} $

(9)

式中：通过绝对中位差(Median Absolute Deviation，MAD)假设噪声标准差为$ \sigma $，在处理噪声数据时，也可根据噪声方差估计正则化参数$ \lambda $值；C为增益因子，取1.15^[21]。增益因子是据经验估计的，目的是使稀疏编码步长更灵活；同时，也是数据精确度和稀疏性的权重参数。增益因子越大，字典中块的表示就越稀疏，精度就越低。

2 处理流程

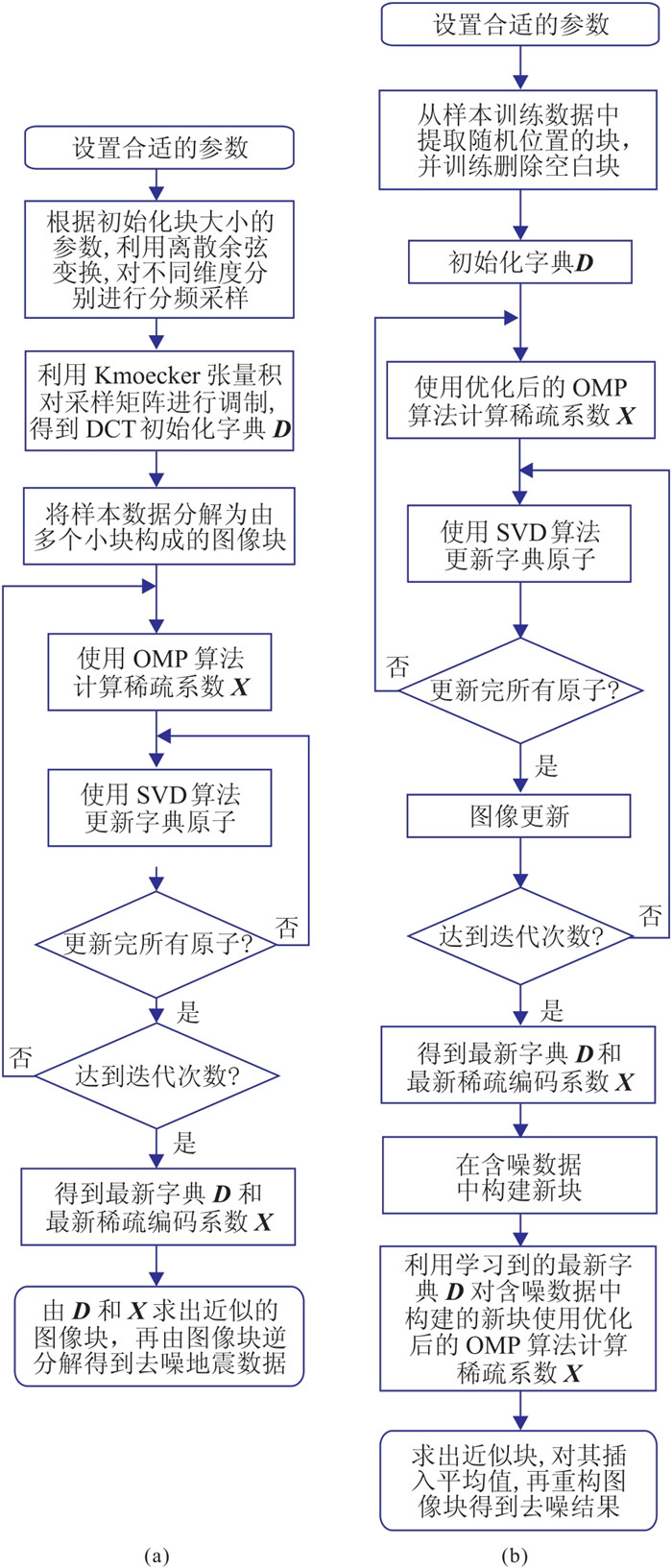
图 1a是传统K-SVD字典学习算法^[22]去噪流程图，本文主要从初始化字典、求稀疏系数的OMP算法、字典的学习过程等方面进行优化。其中从含噪数据中选取任意位置的块作为字典学习的对象，这种随机性使得能更准确地捕获地震数据特征，进而实现不定的稀疏表示，以此提高K-SVD字典学习的去噪效果。同时，在OMP算法中增加了稀疏表示每个信号允许的最大表示误差的约束，使得OMP算法的效率大幅度提升等。

图 1b是本文所提K-SVD字典学习算法实现地震数据去噪的流程图。具体去噪过程是：首先设置适用参数，如K-SVD算法的迭代次数、字典学习过程的迭代次数、稀疏度等；然后从样本训练数据中提取随机位置的块，并训练删除空白块，初始化字典D，根据设置的迭代次数进行字典学习，包括用OMP算法稀疏编码得到稀疏系数X，用K-SVD算法更新字典直至遍历所有原子，在达到设定的全局迭代次数时完成字典学习，同时得到最新字典D和最新稀疏编码系数X；最后，在含噪数据中构建新块，利用学习到的最新字典D对构建的新块使用OMP算法得到稀疏系数X，由字典D和新稀疏系数X求出近似块，对该近似块插入平均值，再重构图像块得到去噪后结果，完成地震数据去噪。

3 数值试验

为了验证本文方法去噪性能，分别利用理论数据和现场采集数据做数值试验，将其去噪结果与f-x反褶积方法和传统K-SVD字典学习方法^[22]进行比较。

为定量评价去噪效果，将信噪比定义为原始信号的功率(Power of Signal)与噪声的功率(Power of Noise)之比值取对数，再乘以10^[1]

$ \mathrm{S}\mathrm{N}\mathrm{R}\left(\mathrm{d}\mathrm{B}\right)=10\mathrm{l}\mathrm{g}\frac{{P}_{\mathrm{s}}}{{P}_{\mathrm{n}}} $

(10)

式中P_s、P_n分别为不含噪声原始地震数据和噪声数据的功率。

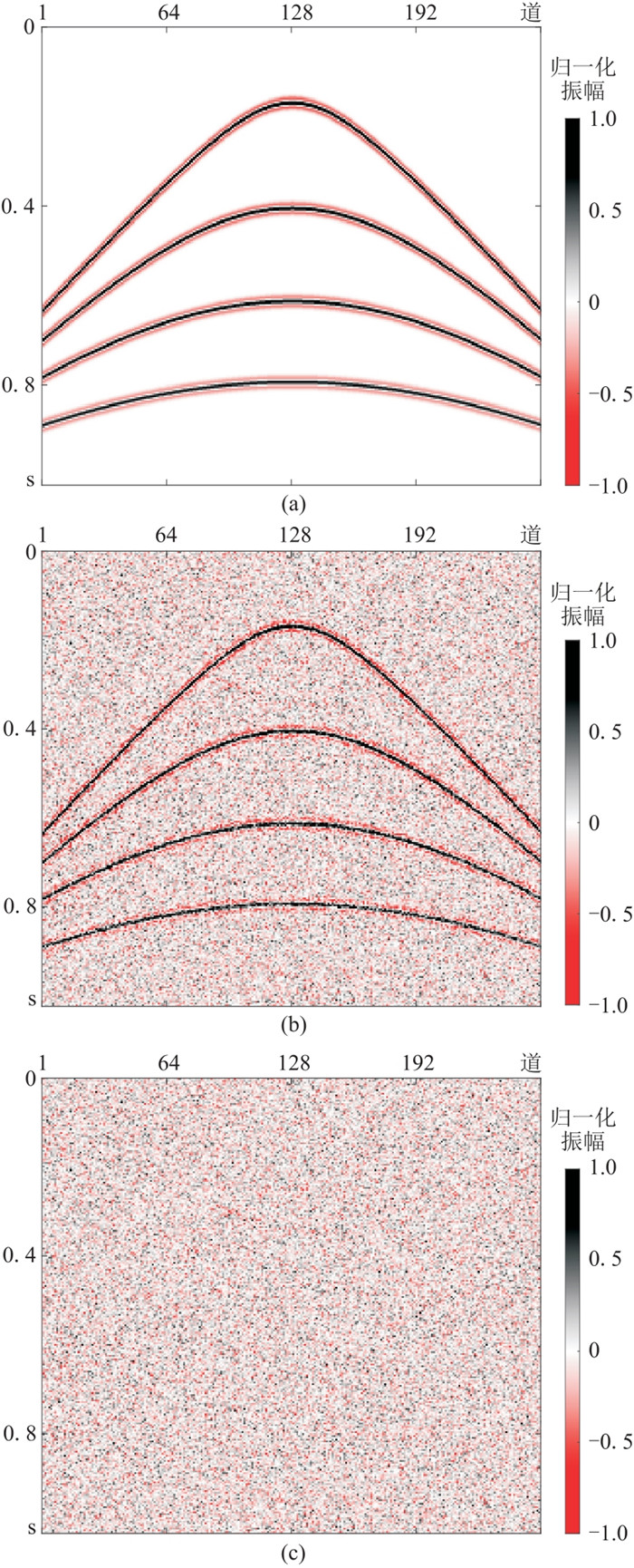
3.1 理论数据

采用图 2所示双曲同相轴合成理论数据进行试验。图 2a是原始无噪数据，大小为256×256，即共有256道，每道256个采样点，时间采样间隔为4 ms。对图 2a加入标准差为0.2的随机噪声(图 2c)，得到图 2b所示含噪数据。在本文理论数据研究部分，随机噪声均通过randn函数产生。因为randn函数产生的随机数服从均值为0、标准差为1的标准正态分布(高斯分布)，所以加入的随机噪声也是高斯噪声。

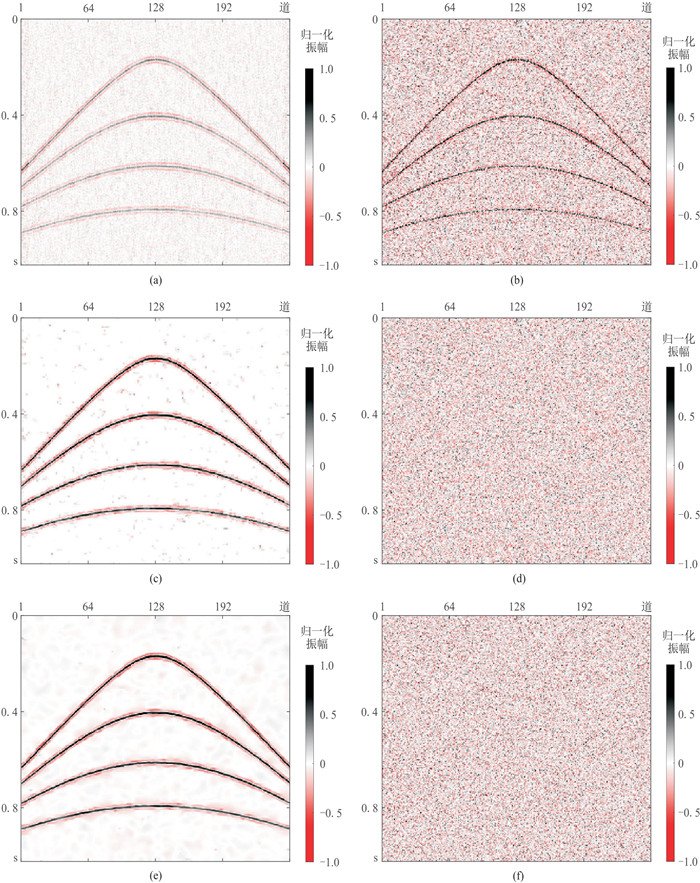
分别采用f-x反褶积、传统K-SVD字典学习及本文方法对含噪数据做去噪处理(图 3)。从f-x反褶积方法去噪结果(图 3a)中，可见噪声残留仍相对较多；而去除的噪声中仍包含较多有效信号(图 3b)。传统K-SVD字典学习方法去噪效果(图 3c)比f-x反褶积方法的好，但仍会损失部分原始信号(图 3d)。与前面两种方法相比，本文方法获得更好去噪结果(图 3e)，在去除的噪声剖面(图 3f)上基本看不到残留有效信号，表明它更好地保存了原始数据特征。原始含噪数据信噪比为-2.59 dB，利用上述三种方法去噪之后的信噪比分别是3.10(f-x反褶积)、9.16(传统K-SVD字典学习)和10.46 dB(本文方法)。对比可知，传统K-SVD字典学习算法对信噪比有显著提升，而本文方法相对又进一步提高了信噪比。试验过程中，三种方法的耗时分别是2.76(f-x反褶积)，271.67(传统K-SVD字典学习)和34.89 s(本文方法)。由此可知，本文方法既具有更高信噪比，计算效率也比传统K-SVD字典学习方法显著提升。

字典学习即是先给定一个初始字典，然后通过学习更新字典。本文方法的字典是通过在含噪数据中随机选择64个训练块开展随机初始化。图 4a、图 4c分别是两种字典学习方法的初始化字典原子，得到相应的更新后64个字典原子(图 4b、图 4d)。可见更新前的字典原子较单一，存在表现特征完全一样的字典原子，图 4a中的原子形状是刚性的，不能最优地表示高度非平稳的地震数据，图 4c的原子则较具柔性。两种方法更新后的字典原子均显得更丰富，且字典原子的表现特征也不同，字典中的每个原子都被重塑，相比于传统K-SVD字典学习方法，本文方法更新的字典在每个原子的色域上更宽泛，说明本文方法可更充分地突显地震数据局部特性。

数值试验中，另一较重要的参数是迭代次数。学习过程中迭代次数通常设置为100次，但实际上大多不需迭代100次即能获得较满意结果，因此本次试验设定的学习迭代次数为50，可相应地缩短整个学习和去噪过程的时长。

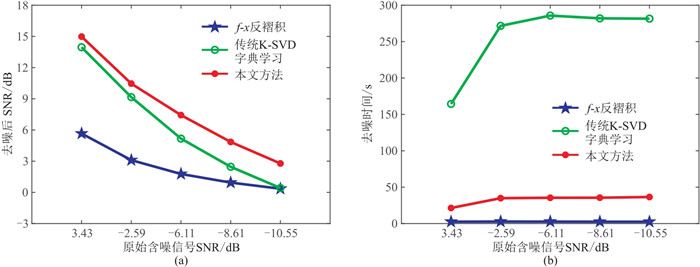
为了对比不同噪声水平下前述三种方法的去噪效果，利用randn函数对原始理论数据分别加入标准差为0.1、0.2、0.3、0.4、0.5的随机噪声，测试结果如表 1、图 5a和图 5b所示。

从表 1对比数据和图 5a可看出，在去噪效果上，不同方法去噪后的信噪比随噪声强度的逐渐增加都在降低，本文方法的去噪效果好于传统K-SVD字典学习方法和f-x反褶积方法。

从三种方法的去噪时间(表 1和图 5b)看，f-x反褶积方法的去噪时间随加入噪声的强弱变化较小，整体趋于稳定。两种K-SVD字典学习算法的去噪时间在加入较弱~较强的随机噪声的过程中，在开始阶段有一个跳跃的变化，然后随着加入的噪声越来越强，去噪时间的增幅并不大。与传统K-SVD字典学习方法相比，本文方法在提高精度的同时也大幅度节省了时间。

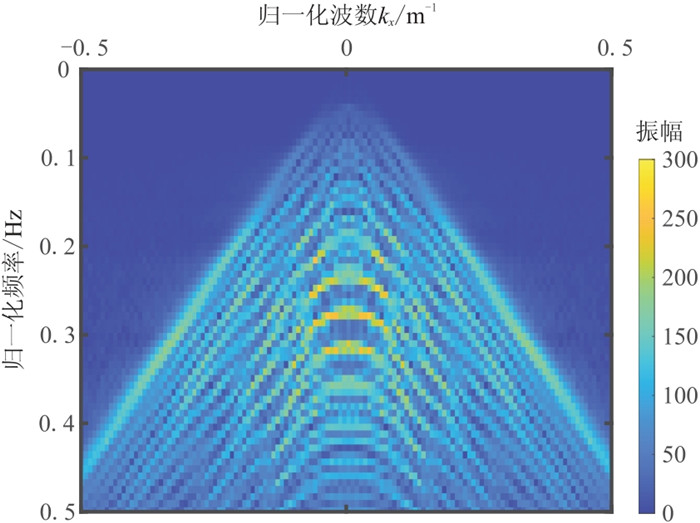
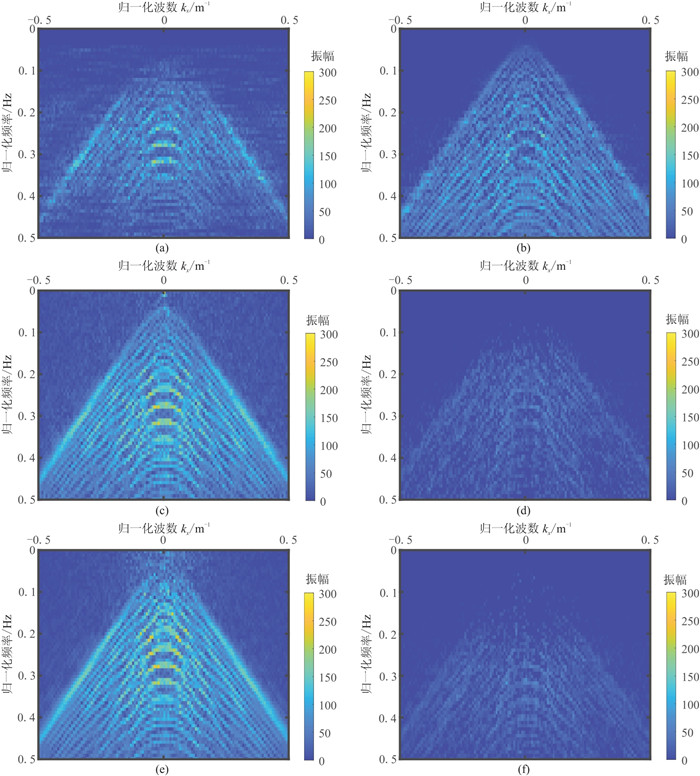
图 6为原始数据的f-k谱。图 7为图 3数据的f-k谱对比，其中图 7a、图 7c和图 7e分别是上述三种方法去噪结果对应的f-k谱：可见f-x反褶积方法在去噪的同时也去除了很多有效信号，有效波损伤较大(图 7b)；而两种K-SVD方法去噪结果的f-k谱均与原始数据f-k谱差别不大，进一步对比这两种去噪结果频谱与原始信号频谱之差(图 7d与图 7f)，可知本文方法的去噪残差中有效信号损失相对更少。

3.2 实际采集数据

图 8是实际采集的地震数据，受采集条件及现场环境因素影响，与理论数据相比，实际采集数据更复杂，噪声的存在淹没了部分有效信号。

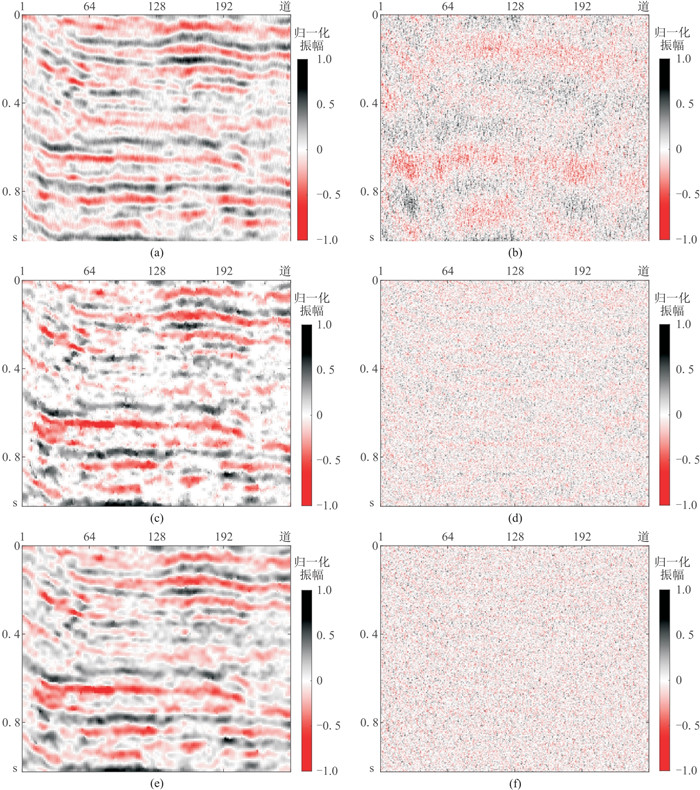
应用上述三种方法进行去噪，从所得处理结果(图 9a、图 9c、图 9e)可见：f-x反褶积方法虽可压制部分噪声能量，但它损失了较多有效信号(图 9b)；传统K-SVD字典学习方法去噪效果(图 9c)虽比f-x反褶积方法的略好，但噪声剖面(图 9d)中也有部分有效信号残留，去噪后数据同相轴连续性较差；相比而言，本文方法有效压制了绝大部分噪声能量，去噪相对彻底(图 9e)，去噪后数据同相轴较连续，几乎未损失有效信号(图 9f)，去噪效果更好。

利用这三种方法对实际地震数据去噪后的信噪比分别是6.04(f-x反褶积)、8.79(传统K-SVD字典学习)和9.54 dB(本文方法)。可见本文方法去噪后的信噪比最高，表明该方法在较完整保留有效信号的同时，还显著提升了信噪比。三种方法对本次试验数据实施去噪分别耗时为2.53(f-x反褶积)、47.26(传统K-SVD字典学习)和4.81 s(本文方法)。从该数据可看出，本文方法在提高信噪比的同时，相比于传统K-SVD字典学习去噪方法还大幅度地提高了计算效率。

信噪比是针对全局的度量，它不能展示去噪性能较差的区域；而局部相似图^[22]是针对去噪性能的一个局部度量，能更直观地显示去噪结果与去除噪声之间的局部相似性，可更准确地评估信号泄漏的程度。

为进一步展示去噪性能，下面采用局部相似图分析这三种方法对有效信号的保护效果。若出现一些高相似性的异常区域，即表明去噪结果在相应位置上存在较多有效信号泄漏。

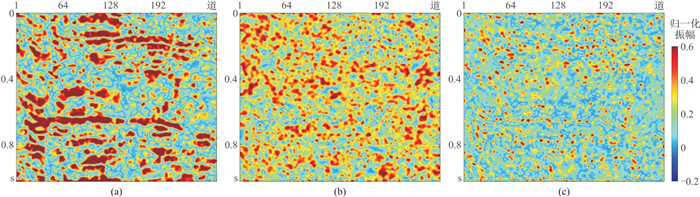
图 10展示三种方法去噪后结果数据与去除的噪声之间的局部相似图。由局部相似图原理可知，能量强的部分指示对原始信号的损失较大。从该图中可见：f-x反褶积方法的局部相似图(图 10a)中存在较强能量，表明去噪后损失了很多原始信号；传统K-SVD方法的局部相似图(图 10b)中能量弱于f-x反褶积方法，但有效信号仍残留较多；本文方法的局部相似图(图 10c)中能量最弱，表明原始信号损失最少，更完整地保留了有效信号局部特征。

4 结论与展望

本文提出一种用于地震数据去噪的新的K-SVD字典学习方法，数值试验显示它具有良好的去噪性能。该方法是通过从含噪数据中提取随机位置的块实现字典初始化；并用OMP算法稀疏编码和K-SVD算法字典更新进行学习，构建出自适应的字典，使原子特征逐渐接近样本数据；再用字典对含噪地震数据分块进行去噪。与f-x反褶积和传统K-SVD字典学习方法相比，本文方法去噪效果更好，信噪比更高，在提升计算效率和保持地震数据局部特征方面更具优势。

虽然K-SVD是字典学习算法中很有效的算法之一，但不论哪一种方法，总会有其欠完善之处。如计算成本还较高，需数以千计的奇异值分解，在三维或五维地震数据中可能有更突出的体现，这也阻碍了其在地震数据处理中的广泛应用。对此，拟从三方面做后续深入研究：①探究适合求解大型稀疏矩阵的0范数或1范数问题，使稀疏表示能力更强，更能突出地震数据的信息；②在字典学习阶段可尝试利用在线字典学习算法中的最小角回归(Least Angle Regression，LARS)算法或改进的OMP算法，使学习得到的字典符合地震数据的结构特征和反映地震数据的局部信息变化规律；③一些初始参数的设定可考虑根据经验或实验数据的不同稍做优化处理，可能会有更好结果。这样可望改进字典学习算法在地震去噪领域的应用效果，也为实现工业化应用提供更可靠的理论基础。

文中未与深度学习去噪方法对比。当前深度学习面临的问题是如何加入物理约束，并赋予其更明确的物理意义。因此，后续研究方向将是发展字典学习约束的深度学习去噪方法，以获得更佳去噪效果。