0 引言

地下地层多为黏弹性介质，地震波在黏弹性介质中传播会受到地层吸收作用的影响。该吸收效应是降低地震分辨率的主要原因，可见地层吸收补偿是提高分辨率的根本途径^[1-3]。然而，在开展地层吸收补偿的工程实践中，不稳定性和对高频噪声的放大效应严重影响了该技术的应用及效果^[4]。目前，国内外已推出多种地层吸收补偿技术，如常用的非稳态反褶积^[5]、反Q滤波^[6-13]等。

反Q滤波技术的主要目的是补偿地震记录的能量损失，校正地震数据的相位畸变，提高地震资料的垂向分辨率。由于反Q滤波补偿技术是一个能量指数放大过程，因此该技术本身存在严重的数值不稳定性问题^[14]。对此，目前主要有两种应对策略：一是对指数补偿算子进行稳定化处理，如Wang^[15]提出一种稳定化的反Q滤波算法，其核心是对振幅补偿算子做稳定化处理，增强了反Q滤波的稳定性和抗噪性；二是将吸收补偿问题进行数学转化，利用反演框架实现反Q滤波，如Zhang等^[16]在贝叶斯反演框架下，利用非稳态反演实现反Q滤波，较好地恢复了被吸收之前的地震信号。

以上反Q滤波方法的共性是基于单道吸收补偿策略，其补偿算法中没有也无法考虑地震信号在空间上的约束关系。因此，反Q滤波结果的空间连续性较差，补偿精度和稳定性都有所欠缺。

为了进一步提高地层吸收补偿算法的可靠性，有人提出将地震信号空间结构特征作为正则化约束条件^[17-18]，引入吸收补偿算法中。地层的倾角和倾向、同相轴斜率、道间时差等是很简单的空间结构特征，基于这些特征可发展基于空间反射结构正则化的地层吸收补偿方法。例如，Ma等^[19]将传统的单道吸收补偿算法推广到多道，并引入横向约束项，实现基于横向约束的地层吸收补偿。该算法隐含的假设条件是地层(近似)水平，以保证横向约束项(0°倾角约束)的有效性。在实际资料中，陡倾角也较常见，为此Ma等^[20]进一步发展了该算法，提出基于倾角约束的地层吸收补偿方法。由于该改进算法需预先求取空间每个点的倾角信息，并将其作为倾角约束项引入多道吸收补偿算法中，因此它具有较强的适应能力。

地震反射结构的倾向和倾角等几何信息一般通过地震数据的空间梯度进行映射和估算，计算结果的抗噪性较差，且对地震数据品质要求较高。实际上，倾角和倾向等空间连续性信息隐含了地震反射的空间可预测性。因此，从理论上讲，基于地震反射的空间可预测性，可构建一种对空间结构具有更强刻画能力的空间反射结构表征算子，该算子既能描述地震反射几何结构，也能描述反射振幅的空间变化。进一步地，将该空间反射结构表征算子作为一种先验信息引入地层吸收补偿的目标函数，赋予地层吸收补偿反演系统一种信号自适应识别能力，使该吸收补偿系统在一定程度上避免对噪声干扰的放大效应，提高吸收补偿算法的稳定性和抗噪性。

1 原理和方法 1.1 地震信号自适应识别的原理

空间可预测性是信号与随机噪声的本质差异。一般而言，地震信号在空间方向具有一定的连续性和相干性，这种相干性可通过空间反射结构算子进行预测和描述；随机噪声在空间分布上并不具备相关性，无法用空间预测算子表征。因此，两者可通过空间反射结构算子进行甄别和区分。

假设有一个由20个系数构成的地震信号空间预测算子b_i，j，其形式^[21]为

$ \left(\begin{array}{ccccc}{b}_{-2, -2}& {b}_{-1, -2}& \times & {b}_{1, -2}& {b}_{2, -2}\\ {b}_{-2, -1}& {b}_{-1, -1}& \times & {b}_{1, -1}& {b}_{2, -1}\\ {b}_{-\mathrm{2, 0}}& {b}_{-\mathrm{1, 0}}& 0& {b}_{\mathrm{1, 0}}& {b}_{\mathrm{2, 0}}\\ {b}_{-\mathrm{2, 1}}& {b}_{-\mathrm{1, 1}}& \times & {b}_{\mathrm{1, 1}}& {b}_{\mathrm{2, 1}}\\ {b}_{-\mathrm{2, 2}}& {b}_{-\mathrm{1, 2}}& \times & {b}_{\mathrm{1, 2}}& {b}_{\mathrm{2, 2}}\end{array}\right) $

(1)

式中：b_i，j中i、j分别指沿时间和空间方向的序号；“0”为被预测点位置；“$ \times $”表示不参与计算的点。

从b_i，j的形式可知，被预测样点值与其周围样点值的关系可表示为

$ {s}_{k, l}=\sum\limits _{j=-2, j\ne 0}^{2}\sum\limits _{i=-2}^{2}{b}_{i, j}{s}_{i-k, j-l} $

(2)

式中：s_k，l为地震数据样点值；k和l分别为地震数据在时间(纵向)和空间(横向)方向的索引号。

从式(2)可知地震信号空间预测过程为：将空间预测算子作为权系数，对被预测点周围样点值做加权求和，所得求和结果作为被预测点的值。这一数学运算隐含的物理意义是：地震信号的各样点值并不是独立存在的，它与周围的样点值应满足预测滤波器所表征的数学关系；而随机噪声不具备特定的空间结构特征，故不能用上述空间预测算子进行数学表征。因此，利用上述空间预测算子可对地震信号与噪声进行自适应识别和区分。

地震信号空间预测算子可通过求解如下最小二乘问题得到^[21]

$ {b}_{i, j}=\underset{{b}_{i, j}}{\mathrm{a}\mathrm{r}\mathrm{g}~\mathrm{m}\mathrm{i}\mathrm{n}}\sum\limits _{k=1}^{M}\sum\limits _{l=1}^{N}{‖{s}_{k, l}-\sum\limits _{j=-2, j\ne 0}^{2}\sum\limits _{i=-2}^{2}{b}_{i, j}{s}_{i-k, j-l}‖}_{2}^{2} $

(3)

式中M和N分别表示地震数据在时间和空间方向的采样点数。

1.2 基于反演的单道吸收补偿方法

对干扰噪声的放大效应是反Q滤波技术在实际应用中的主要弊端。其根本原因在于，虽然地震信号经历了地层吸收衰减的影响，但相同时刻的噪声干扰并未经历与信号同样的衰减作用，故反Q滤波技术在补偿地震信号的同时，也会放大地震噪声，造成补偿结果的不稳定。传统方法的解决思路是，在反演框架下，通过引入先验信息或正则化约束条件，构建非稳态反演(吸收补偿)的目标函数，从而在一定程度上缓解吸收补偿结果的不稳定性。

黏弹性介质对地震波的吸收作用是一个典型的非稳态滤波过程，可由非稳态褶积模型描述^[22]

$ d\left(t\right)={\int }_{0}^{\infty }w(t, \tau )r\left(\tau \right)\mathrm{d}\tau $

(4)

式中：t和τ均为时间变量，t为数据记录时间，$ \tau $为子波时间；$ d\left(t\right) $表示包含吸收衰减的单道地震记录；$ r\left(\tau \right) $为地震反射系数；$ w(t, \tau ) $表示非稳态地震子波，其表达式为

$ w(t, \tau )={\int }_{0}^{\infty }W\left(\omega \right)a(\omega , \tau )\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{i}\omega t)\mathrm{d}\omega $

(5)

式中：$ W\left(\omega \right) $为震源子波的频谱，ω为角频率；$ a(\omega , \tau ) $为吸收衰减函数(表征地下介质的吸收特性)，其表达式为

$ a\left(\omega , \tau \right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{i}\omega \tau {\left|\frac{\omega }{{\omega }_{\mathrm{r}}}\right|}^{-\gamma }\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{\omega \tau }{2Q}{\left|\frac{\omega }{{\omega }_{\mathrm{r}}}\right|}^{-\gamma }\right) $

(6)

式中：ω_r为参考角频率；Q为品质因子，且γ = 1/πQ。

将式(4)离散，可改成如下矩阵方程

$ \left[\begin{array}{c}{d}_{1}\\ {d}_{2}\\ ⋮\\ {d}_{M}\end{array}\right]=\left[\begin{array}{cccc}w({t}_{1}, {\tau }_{1})& w({t}_{1}, {\tau }_{2})& \cdots & w({t}_{1}, {\tau }_{M})\\ w({t}_{2}, {\tau }_{1})& w({t}_{2}, {\tau }_{2})& \cdots & w({t}_{2}, {\tau }_{M})\\ & & ⋮& \\ w({t}_{M}, {\tau }_{1})& w({t}_{M}, {\tau }_{2})& \cdots & w({t}_{M}, {\tau }_{M})\end{array}\right]\left[\begin{array}{c}{r}_{1}\\ {r}_{2}\\ ⋮\\ {r}_{M}\end{array}\right] $

(7)

简记为

$ \boldsymbol{d}=\boldsymbol{Wr}$

(8)

式中：d为单道地震记录向量；W为时变子波矩阵；r为反射系数向量。

一般而言，可假设地震反射系数满足稀疏概率分布，为此可采用L₁范数对反射系数施加正则化约束，并构建如下的目标函数^[14]

$ \phi \left(\boldsymbol{r}\right)=\frac{1}{2}{‖\boldsymbol{W}\boldsymbol{r}-\boldsymbol{d}‖}_{2}^{2}+{\lambda }_{1}{‖\boldsymbol{r}‖}_{1} $

(9)

式中λ₁为纵向调节因子，用于调节稀疏正则化约束项的权重。利用迭代重加权算法求解该目标函数，得到吸收补偿结果为

$ {\boldsymbol{r}}^{n+1}={\left({\boldsymbol{W}}^{\mathrm{T}}\boldsymbol{W}+{\lambda }_{1}{\boldsymbol{\varOmega }}^{n}\right)}^{-1}{\boldsymbol{W}}^{\mathrm{T}}\boldsymbol{d} $

(10)

式中：$ {\boldsymbol{r}}^{n+1} $表示第n+1次迭代的反射系数结果；上标T表示转置运算；$ {\boldsymbol{\varOmega }}^{n} $表示第n次迭代的辅助矩阵，且$ \boldsymbol{\varOmega }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\frac{1}{\sqrt{{{r}_{1}}^{2}+{\epsilon }^{2}}}, \cdots , \frac{1}{\sqrt{{{r}_{M}}^{2}+{\epsilon }^{2}}}\right) $，其中ε²为稳定化因子。

常规地层吸收补偿方法是单道运行模式，即对地震数据中的各道依次进行非稳态反演。反演过程中未考虑、也无法考虑不同地震道补偿结果之间的空间依赖关系。由此可见，传统反Q滤波本身并不具备空间信号识别能力，补偿过程中无法对有效信号与地震噪声进行有效区分和选择性补偿。为了提高补偿算法的稳定性和抗噪性，可将地震信号的空间可预测性作为一种先验信息引入吸收补偿的目标函数，赋予反演系统一种信号自适应识别能力，从而实现信号与噪声的自适应识别和选择性补偿，在系统结构层面上消除噪声干扰对吸收补偿的影响。

1.3 信号自适应识别多道吸收补偿方法

为了将空间预测算子描述的不同地震道之间的依赖关系引入吸收补偿反演系统，首先需将单道非稳态褶积模型(式(8))推广到多道形式，该多道非稳态褶积模型可表示为^[22]

$ \left[\begin{array}{c}{\boldsymbol{d}}_{1}\\ {\boldsymbol{d}}_{2}\\ ⋮\\ {\boldsymbol{d}}_{N}\end{array}\right]=\left[\begin{array}{cccc}{\boldsymbol{W}}_{1}& {\bf{0}}& {\bf{0}}& {\bf{0}}\\ {\bf{0}}& {\boldsymbol{W}}_{2}& {\bf{0}}& {\bf{0}}\\ & & ⋮& \\ {\bf{0}}& {\bf{0}}& {\bf{0}}& {\boldsymbol{W}}_{N}\end{array}\right]\left[\begin{array}{c}{\boldsymbol{r}}_{1}\\ {\boldsymbol{r}}_{2}\\ ⋮\\ {\boldsymbol{r}}_{N}\end{array}\right] $

(11)

简记为

$\boldsymbol{s}=\boldsymbol{Gm}$

(12)

上两式中：d_l、W_l、r_l对应为第l(l=1，2，…，N)道的地震数据向量、时变子波矩阵及反射系数向量；s为多道地震记录超级向量；m为多道反射系数超级向量；G为多道时变子波构建的块状矩阵。

在传统吸收补偿反演系统(式(9))中，只考虑了反射系数的纵向稀疏特性，并未考虑地震信号在空间方向的反射结构特征。为此，可利用空间预测算子b_i，j对地震信号和随机噪声的自适应区分特性，将其作为一种先验信息引入吸收补偿的目标函数，构建一种信号自适应约束多道吸收补偿反演系统，消除随机噪声对吸收补偿的影响。

为实现反射结构自适应约束，首先对空间预测算子进行改造，得到反射结构表征算子

$ \left(\begin{array}{ccccc}{b}_{-2, -2}& {b}_{-1, -2}& \times & {b}_{1, -2}& {b}_{2, -2}\\ {b}_{-2, -1}& {b}_{-1, -1}& \times & {b}_{1, -1}& {b}_{2, -1}\\ {b}_{-\mathrm{2, 0}}& {b}_{-\mathrm{1, 0}}& -1& {b}_{\mathrm{1, 0}}& {b}_{\mathrm{2, 0}}\\ {b}_{-\mathrm{2, 1}}& {b}_{-\mathrm{1, 1}}& \times & {b}_{\mathrm{1, 1}}& {b}_{\mathrm{2, 1}}\\ {b}_{-\mathrm{2, 2}}& {b}_{-\mathrm{1, 2}}& \times & {b}_{\mathrm{1, 2}}& {b}_{\mathrm{2, 2}}\end{array}\right) $

(13)

显然，该算子与空间预测算子的唯一区别是中心位置(待预测点位置)的系数为-1。这意味着将该算子与待约束地震记录(补偿后记录)进行褶积的结果不再是预测后的地震记录，而是预测结果与实际测量结果的残差，可表示为

$ {e}_{k, l}={b}_{i, j}*{\hat{d}}_{k, l} $

(14)

式中：$ * $为(二维)褶积运算符；b_i，j此时为从补偿前地震数据中提取的空间预测算子(或反射结构表征算子)；$ {\hat{d}}_{k, l} $为补偿后地震记录；e_k，l为预测误差。若补偿前、后地震数据反射结构特征类似，则预测误差较小；反之，预测误差较大。这也是利用反射结构表征算子约束补偿后地震数据的核心思想。

式(14)的二维褶积运算较繁琐，可采用Helix变换将其转化为一维褶积运算^[22]

$ \boldsymbol{e}=\boldsymbol{B}\hat{d}=\stackrel{}{\boldsymbol{B}\hat{W}\boldsymbol{m}} $

(15)

式中：e为预测误差向量；B为反射结构表征算子褶积矩阵(利用空间预测算子b_i，j构造得到)，其作用是在反演过程中对地震信号和随机噪声进行自适应的识别和选择性的补偿；$ \hat{W} $是由地震子波构成的分块矩阵，其作用是将待反演的反射系数m转化成地震记录$ \hat{d} $，以便更好实现地震信号空间约束。

通过最小化预测误差，就可使反演结果体现的反射特征与原始数据的反射特征最相似，即实现对吸收补偿结果进行反射结构特征约束的目的。该反射结构约束项可表示为

$ \underset{m}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}~{\boldsymbol{e}}^{\mathrm{T}}\boldsymbol{e}={‖\boldsymbol{B}\hat{W}\boldsymbol{m}‖}_{2}^{2} $

(16)

将反射结构自适应约束项引入多道吸收补偿反演系统，构建信号自适应识别多道吸收补偿目标函数

$ \phi \left(\boldsymbol{m}\right)=\frac{1}{2}{‖\boldsymbol{G}\boldsymbol{m}-\boldsymbol{s}‖}_{2}^{2}+{\lambda }_{1}{‖\boldsymbol{m}‖}_{1}+\frac{{\lambda }_{2}}{2}{‖\boldsymbol{B}\hat{W}\boldsymbol{m}‖}_{2}^{2} $

(17)

式中：等式右端第一项为数据匹配误差项(表征模型数据与实际数据的匹配残差)，第二项为纵向稀疏约束项，第三项为空间反射信号自适应约束项；λ₂为信号空间约束项调节因子，其作用是调节信号自适应约束项的权重。

针对目标函数$ \phi \left(\boldsymbol{m}\right) $，Ma等^[22]采用交替方向乘子法(Alternating direction method of multipliers，ADMM)进行求解，该算法在理论上十分有效，已广泛应用于压缩感知和机器学习领域。但在算法测试时，发现ADMM算法收敛速度较慢，往往需迭代几十甚至上百次才能得到较可靠结果。而且，在算法实现过程中需引入中间变量和调节参数，这些参数的取值也会影响收敛速度。在某些情况下，参数选择不当甚至可能带来不收敛的后果。为此，本文采用迭代重加权算法^[23]求解该目标函数，得到如下迭代表达式

$ {\boldsymbol{m}}^{n+1}={\left[{\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{G}+{\lambda }_{1}{\boldsymbol{\varOmega }}^{n}+{\lambda }_{2}{\left(\boldsymbol{B}\hat{W}\right)}^{\mathrm{T}}\left(\boldsymbol{B}\hat{W}\right)\right]}^{-1}{\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{s} $

(18)

得到多道反射系数m后，可将其转化为二维反射系数模拟$ \left[{\boldsymbol{r}}_{1}, {\boldsymbol{r}}_{2}, \cdots , {\boldsymbol{r}}_{M}\right] $；然后，将反演结果与子波褶积，得到补偿后的地震记录

$ \left[{\boldsymbol{d}}_{1}, {\boldsymbol{d}}_{2}, \cdots , {\boldsymbol{d}}_{M}\right]=\left[\boldsymbol{W}{\boldsymbol{r}}_{1}, \boldsymbol{W}{\boldsymbol{r}}_{2}, \cdots , \boldsymbol{W}{\boldsymbol{r}}_{M}\right] $

(19)

综上，本文提出的具体计算过程如下：

(1) 利用式(3)从原始数据中计算地震信号的空间预测算子b_i，j；

(2) 基于吸收衰减理论，推导单道非稳态褶积模型(式(8))，并将单道褶积模型推广到多道模型(式(12))；

(3) 利用步骤(1)中求出的空间预测算子，构建空间反射结构约束项(式(16))；

(4) 同时考虑反射系数的稀疏约束和地震数据的空间约束，建立信号自适应识别多道吸收补偿目标函数(式(17))；

(5) 求解式(17)，得到反射系数反演结果(式(18))；

(6) 根据式(18)，计算补偿后的地震记录(式(19))。

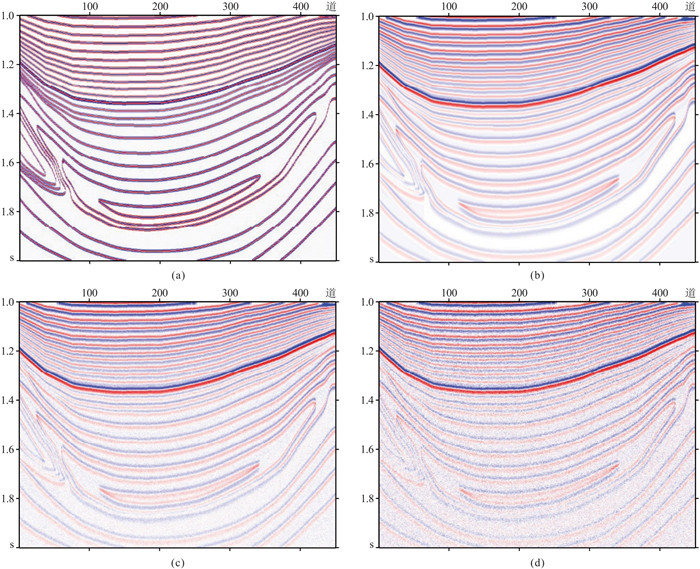
2 模型测试与分析

首先采用层状模型数据测试、评判本文方法的有效性和优越性。图 1a是未考虑地层吸收效应的合成地震记录，模拟采用的地震子波为50 Hz的零相位雷克子波。可见未考虑吸收衰减的地震数据分辨率较高，地震反射结构清晰，深层能量与浅层相当。该合成记录可作为参考数据(图 1a)，用于定性和定量评价地层吸收补偿结果的优劣。图 1b是考虑了地层吸收衰减(Q=50)的合成记录，可见由于地层的吸收衰减作用，接收的地震数据分辨率降低，深层能量较弱，原有的反射特征弱化。在该合成记录中加入不同强度的随机噪声，得到信噪比(SNR)分别为20(图 1c)和5(图 1d)的含噪声衰减记录。

分别采用单道吸收补偿和信号自适应识别多道吸收补偿对SNR=20含噪地震记录(图 1c)进行地层吸收补偿，提高地震资料分辨率。图 2展示两种方法的补偿结果，可见两种方法的吸收补偿结果都明显增强了深层能量，也提高了原始数据的垂向分辨率。但本文方法可有效地抑制地震噪声的放大，在提高分辨率的同时，有效地保持了地震记录的信噪比和空间连续性，地震反射结构更清晰(图 2b)。

图 3展示两种方法对SNR=5含噪地震记录进行吸收补偿的结果。随着噪声强度的增大，吸收补偿的不稳定性问题更凸显。可见此时单道吸收补偿结果虽恢复了深层地震信号，提高了地震分辨率，但补偿结果的信噪比较低。然而，得益于引入了地震信号空间结构自适应约束，本文方法补偿结果(图 3b)地震反射结构更清晰，连续性更好。

进一步，定量计算了两种方法吸收补偿结果与参考数据的相关系数。在SNR=20情况下，单道补偿和本文方法补偿结果与参考数据的相关系数分别为0.75和0.91；而SNR=5时，两者相关系数分别为0.63和0.82。定性分析和定量比较表明：本文方法具有更高的补偿精度，更强的稳定性和抗噪性，其吸收补偿结果空间连续性更好，与参考结果更匹配。

同时，还比较了采用ADMM算法和迭代重加权算法求解多道补偿目标函数的效率。测试设备的CPU参数为13 thGen Intel(R) Core(TM) i7-13700KF，主频为3.4 GHz。在SNR=20情况下，ADMM算法和迭代重加权算法的计算时间分别为172.55和158.37 s；在SNR=5时，ADMM算法和迭代重加权算法的计算时间分别为185.04和161.21 s。显然，本文算法运算效率更高，具一定优势。

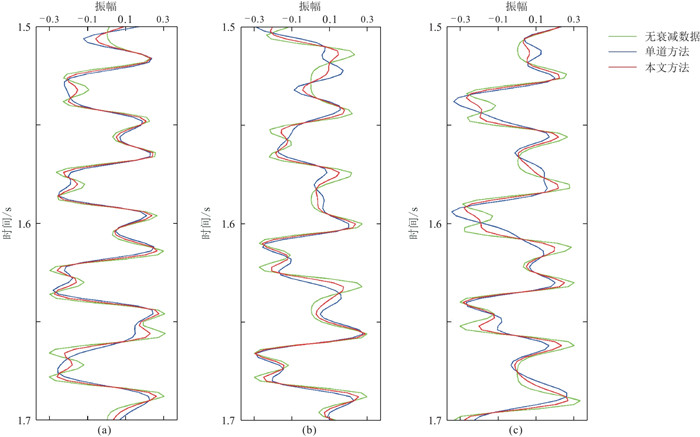
图 4显示SNR=5时两种方法补偿结果与无衰减数据的单道对比。可以发现，相较于单道补偿结果(蓝色)，本文方法补偿结果(红色)与参考曲线(绿色)无论是振幅还是相位都更吻合，补偿效果更好。

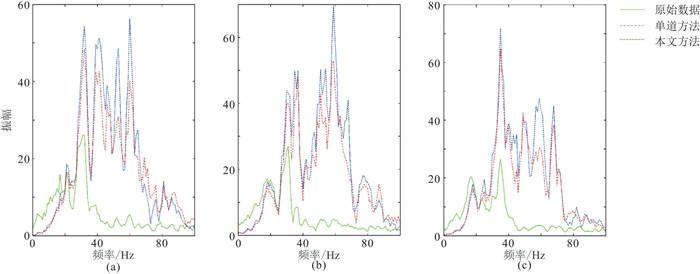
图 5是SNR=5时两种方法补偿结果与原始数据的单道振幅谱对比。可以看出，两种方法均能有效补偿地震高频成分的衰减，拓宽地震数据有效频带。另外，单道补偿振幅谱(蓝色)比本文方法振幅谱(红色)的高频成分能量略强，这可能缘于单道算法对高频噪声的过度放大。

3 实际资料应用

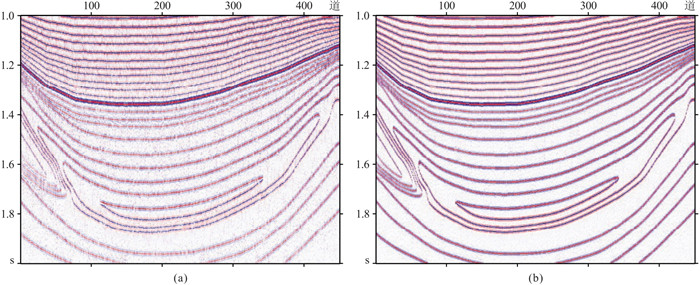
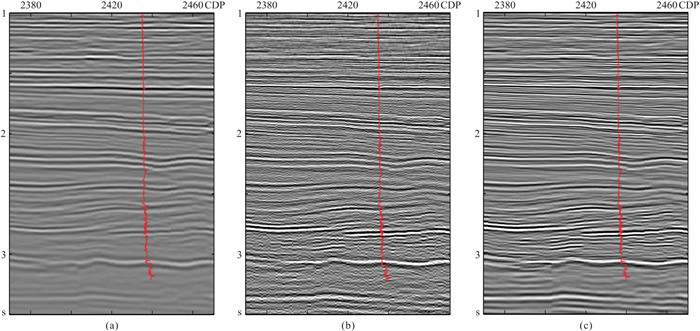
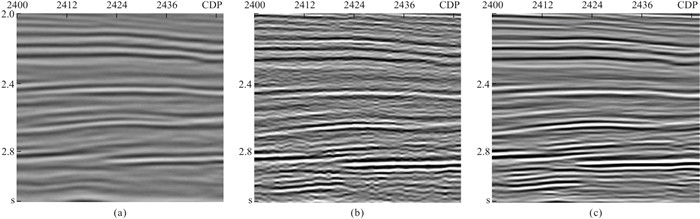
利用实际地震数据，进一步对本文方法的实用性和可靠性进行了测试和分析。图 6a为吸收补偿前的实际地震数据，可见该输入地震记录分辨率较低，深层能量较弱，且视觉上看不到太多噪声干扰。分别用单道吸收补偿和信号自适应识别多道吸收补偿方法处理该数据，得到相应的补偿结果(图 6b和图 6c)。其中单道吸收补偿算法虽提高了原始数据的分辨率，但补偿后地震剖面的噪声较明显，地震记录信噪比较低。在补偿过程中，通过引入地震信号自适应约束(本文方法)，该算法具备了信号与噪声的甄别能力。因此，在对地震信号进行补偿的同时，并未放大噪声干扰的影响，其补偿结果具有更高信噪比和更好的空间连续性。图 7为实际地震数据的局部放大显示，可见经本文方法吸收补偿后，地震剖面的整体结构更明确，空间连续性更好，地质现象和构造细节也更清晰。

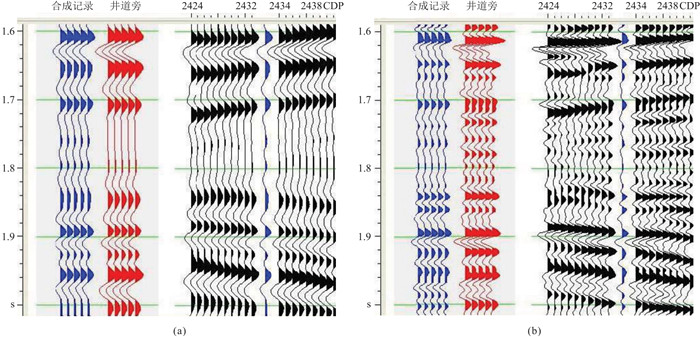
为了更充分展示本文方法对地震反射结构特征的恢复能力，将利用本文方法补偿前、后的井旁地震数据与合成地震记录(单道情形的噪声放大过于明显，故未被采用)进行标定对比(图 8)。可以看出，利用本文方法补偿处理后，测井数据合成地震记录与井旁地震记录在反射结构特征上能较好地吻合，表明本文方法对实际资料也颇具实用性和可靠性。

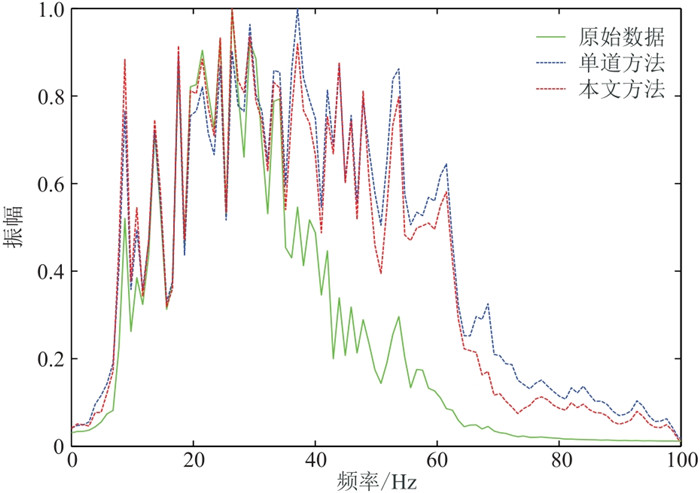
图 9展示了吸收补偿前、后地震数据的振幅谱，可见吸收补偿后的地震数据高频成分被抬升，地震频带有一定的展宽，说明两种吸收补偿方法都能有效提高地震资料的分辨率。但这两种方法补偿结果的振幅谱在50 Hz以上存在一定差异，可能缘于单道补偿方法对高频噪声的放大效应，这也从侧面说明本文方法能有效压制噪声干扰，保障补偿后地震资料的信噪比。

4 结论

(1) 本文提出一种信号自适应识别的吸收补偿方法。该算法的核心是，在吸收补偿目标函数中引入地震反射结构自适应识别约束项，在反演过程中实现信号与噪声的自适应识别和选择性补偿。

(2) 空间可预测性是有效信号与随机噪声的本质差异，利用空间预测算子可对地震信号与噪声进行自适应识别和区分，并以此构建信号自适应约束正则化项。

(3) 模型数据测试和实际资料应用结果表明：本文所提自适应识别吸收补偿方法不仅能提高地震资料的分辨率，还可保护补偿结果的空间构造特征和信噪比，具有实用性和较强稳定性。

本文方法为多道同时反演算法，计算量和存储量较大。后期可根据矩阵特点进行优化处理；同时，也考虑通过并行计算进一步提升计算效率。