2. 东方地球物理公司西安物探装备分公司, 陕西西安 710061
2. Xi'an Geophysical Prospecting Equipment Company of BGP, CNPC, Xi'an, Shaanxi 710061, China
地震勘探作业时,产生人工地震波的常用激发源有可控震源和脉冲源两种。多年来,人们希望通过改变人工地震波激发方式以提升混叠数据的分离效果,取得了一定成效。在可控震源激发控制方面,Silverman[1]开创性地提出多震源同时激发方法,利用可控震源相位编码方式从多源记录中分离单炮信号;Allen等[2]提出HFVS(High Fidelity Vibratory Seismic)方法,使用一套独特震源编码进行多震源同时采集,不同于Silverman提出的方法[1],它采用记录的震源产生的振动信号分离数据,而弃用理论信号,故数据保真度相对较高;Sallas等[3]提出SPST(Simultaneous Pseudorandom Sweep Technology)扫描方式,扫描信号以随机相位编码形式做长时扫描,基于互相关算法分离出目标数据;Bagaini等[4]提出DSS(Dithered Slip-Sweep)采集技术,应用固定滑动扫描和小窗口抖动的激发控制方式,波场分离后数据偏移的质量与传统激发方式相当。
上述方法仅适用于陆上地震勘探可控震源混叠采集作业,已作为成熟的工业技术得到规模化应用,但目前对于脉冲激发源的混叠研究相对较少。关于使用脉冲源激发得到的混叠数据分离方法的讨论热点,是将随机激发的混叠数据中不同激发源导致的混叠噪声在非共炮点域(共检波点道集、共炮检距道集、共中心点道集等)看作是随机噪声,采用随机噪声去除方法实现波场分离。由于有效信号的连续性特征和混叠噪声的随机性特征会影响数据的分离效果,不同激发源产生人工地震波的随机性即显得更为重要。Fromyr等[5]提出使用导航系统,根据激发设备的移动速度和位置信息,结合一个小的抖动时间作为炮点激发时间,提高了炮点激发随机性;Hampson等[6]通过设置随机颤动延迟时间提高激发时间的随机性;吉林大学联合中海油深圳分公司分别于2013和2014年在渤海和南海开展了2D和3D双源随机混合震源采集试验[7],但该方法仅考虑海上勘探作业时两个脉冲激发源同时激发的情形,存在一定局限性。
为了增加同时激发脉冲源的数量,并进一步提高脉冲源激发的随机性,本文提出一种随机时间产生算法,以提高地震勘探高效混叠采集时两个及以上激发源同时激发概率。该算法基于卫星授时技术,以当前炮的上一炮激发时间的整秒部分为基础,根据激发源所处位置、备好的炮点激发顺序、时—距规则参数等信息,以高精度ADC(模数转换)芯片和振动传感器采集的数值为种子,随机产生一个指定窗口内小抖动的随机数作为炮点激发的颤动时间,从而提高抖动激发时间的随机性,实现高效勘探。
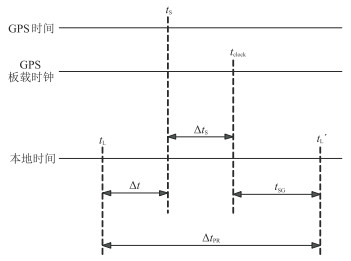
1 相关理论 1.1 卫星授时北斗、GPS及GLONASS是目前世界上普遍使用的定位授时系统,可持续不断地发射导航定位及授时信息。地面接收机从接收到的导航电文中解析出本地时钟相对卫星系统时钟的时差,并不断修正以实现与卫星时钟的同步(图 1)。
|
图 1 卫星时钟同步示意图 |
本地时钟与卫星系统时间的差值计算式为
| $ \mathrm{\Delta }t=\mathrm{\Delta }{t}_{\mathrm{P}\mathrm{R}}-({t}_{L\mathrm{\text{'}}}- t_{{\rm{S}}}) $ | (1) |
式中:tL′为接收机的时钟时刻;tS为卫星时刻;ΔtPR为伪距产生的延迟,计算式为
| $ Δt_{{\rm{PR}}}= \frac{R^{*}}{c} $ | (2) |
式中:R*为伪距;c为光速。
根据图 1对式(2)做进一步推导,得到
| $ Δt_{{\rm{PR}}} =Δt +Δt_{{\rm{S}}}+τ_{{\rm{SG}} }$ | (3) |
式中:ΔtS为卫星系统时间与星载原子钟时间tclock的差值;τSG为星地总时延,可由下式计算
| $ τ_{{\rm{SG}}}=τ_{{\rm{R}}}+τ_{{\rm{E}}}+τ_{{\rm{A}}}+τ_{{\rm{L}}} $ | (4) |
式中:τR为信号传输的理论延迟;τE、τA分别为电离层和对流层导致的延迟;τL为接收机本身延迟。
随着相关领域科技水平的不断发展和创新,北斗、GPS等卫星导航定位系统已成熟地应用于各行各业,相关配套产品完备,能方便购置的卫星接收模块输出的授时信号精度达30~150 ns,在电路设计、选用天线等诸多因素的影响下,最大误差也不会超过1 μs[8-12],并且卫星授时信号自身噪声小,传播过程中抗干扰能力强,具备全球性、全天时、全天候覆盖、精度高、成本低等优点,完全满足地震勘探对时钟精度的要求。
近年来,卫星授时技术已逐步融入地震勘探数据采集过程中,基于卫星授时的节点、无线等新型地震数据采集系统及有线地震仪器,也都支持长时间连续采集并使用基于卫星授时技术的时间标记采集样点的功能。因此,使用卫星系统时间作为地震勘探随机激发时间的基准具有很强的可行性,且应用成本低、授时精度高。
功耗和时钟精度是随机激发时间发生器需考虑的两个重点因素。Pallier等[13]提出采用周期性的同步方式结合相应的校正算法就可保证卫星时间同步精度,且可大幅度降低系统功耗,但该方法使用软件算法补偿本地时钟的偏差,而不是直接调整系统晶振输出的振荡频率,存在一定的应用局限性。常用的高精度晶体振荡器大致可分为三类,即恒温晶振(Oven-Controlled Crystal Oscillator,OCXO)、温补晶振(Temperature-Compensated Crystal Oscillator,TCXO)和压控晶振(Voltage-Controlled Crystal Oscillator,VCXO)[14-15]。其中,OCXO是利用恒温槽使晶体振荡器中石英晶体谐振器的温度保持恒定,将由周围温度变化引起的振荡器输出频率变化量削减到最小的晶体振荡器,功耗一般超过1 W,振荡信号精度高;TCXO是通过附加的温度补偿电路削减由周围温度变化产生的振荡频率变化量的一种石英晶体振荡器,实际应用中因焊接温度远高于TCXO的最大允许温度,会使晶体振荡的频率发生变化,对焊接工艺、电路设计等有特殊要求,后期维护困难;VCXO是通过电压调节信号微调振荡频率,以保持输出频率恒定的一种石英晶体振荡器,具有传输性能高、抗干扰性强、节省功率等优点。TCXO和VCXO功耗一般为5~200 mW,输出振荡信号精度相对较高[16]。因此,从功耗、频率精度、漂移特性及工业化应用的便捷性等方面考虑,选用VCXO作为系统时钟源。
1.2 随机数发生器生成随机激发时间需解决的另一个关键问题是如何设计并实现统计特性和随机特性良好的随机数发生器。按随机性来源和生成原理的不同,随机数发生器主要分为真随机数发生器(True RNG,TRNG)和伪随机数发生器(Pseudo RNG,PRNG)[17]。其中,TRNG是采集某些物理现象(如温度、电路噪声、核裂变)中的随机成分,经数字化处理后生成随机数[18-19];PRNG则是采用确定的拉伸函数算法将一个预先得到的数值或序列(也称为种子)扩展为所需的随机数[20-22]。地震勘探中,采用高效混叠采集作业方式时,对炮点的激发控制有特殊要求:一方面激发时间须具有较强随机分布特征;另一方面还需按设计规则输出的激发时间能在某一小的时间窗口内抖动。从本质上讲,要求产生的随机激发时间是一个在某确定数值附近呈随机分布的随机数。
正态分布(也称高斯分布)是一个在数学、物理及工程等领域都很常用的概率分布,其概率密度函数为
| $ m\left(x\right)=\frac{1}{\sqrt[]{2\mathrm{\pi }}\;\sigma }\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{{\left(x-\mu \right)}^{2}}{2{\sigma }^{2}}\right] $ | (5) |
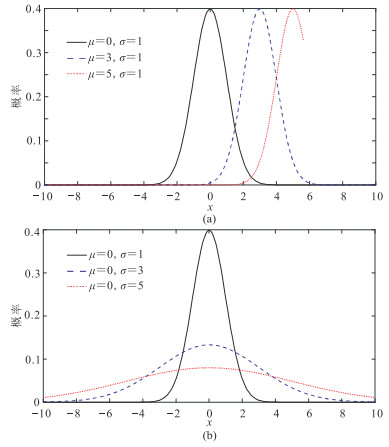
式中:x为随机变量;μ为随机变量的正态分布的期望值,决定随机数所处位置;σ为正态分布的标准差,决定分布的幅度。当μ=0,σ=1时,称为标准正态分布。
不同μ和σ值的正态分布曲线如图 2所示。显然,选用正态分布函数作为生成随机激发时间的概率密度函数,可在有效保证数据随机性的同时,还具有一定的分布区间可控性。地震勘探用的模拟地震检波器是一种电磁式振动传感器,本质是一种质量体—弹簧的电磁系统,其响应特性会随着温度变化而发生细微的变化。因此,选用模拟检波器作为产生随机激发数的种子,能够利用振动、温度引起的采集振动数据的随机特征,进一步增强生成的混叠激发时间数据的随机性。
|
图 2 不同期望值(a)和标准差(b)的正态分布(概率)曲线 |
本文提出的多源混叠激发时间发生算法的硬件实现结构主要由卫星接收模块、高精度压控晶体振荡器、微控制器、高精度ADC芯片、振动传感器及相关辅助电路组成(图 3)。

|
图 3 地震勘探随机激发时间发生器构成示意图 |
施工开始时,卫星接收模块周期性启动,获取并成功解析接收到卫星信号后,输出时间信息(包括秒脉冲信号和对应历元信息)到微控制器;微控制器接收来自卫星接收模块的时间信息,计算本地时钟的准确度及其与卫星时钟的时间偏差,利用选用的晶体振荡器的压控特性和数模转换模块的高精度、高分辨率特性输出调节电压,“牵引”晶振的频率,使运行频率靠近晶振的中心频率,实现卫星时间同步和本地时钟的校准。在完成上述操作功能后,微控制器即可根据激发炮点的当前位置、时距控制参数及振动传感数据,生成所需的随机激发时间。本文所提基于振动传感和卫星授时的地震勘探随机时间产生方法具有如下优点:
(1)使用卫星时间作为地震勘探随机激发时间的基准,一方面能以较低经济成本达到高精度的时间同步精度;另一方面更加适用于具有良好卫星信号接收条件的现场施工,便于工业化应用;
(2)卫星接收模块运行功耗一般约为100 mW,是整个随机激发时间发生器的主要功耗部件,而采用基于压控晶体振荡器和卫星接收模块周期性休眠的时钟同步方式,可大幅度降低系统平均运行功耗;
(3)使用振动传感数据作为生成随机激发时间的种子,有助于提高生成的正态分布数据的随机性,便于使用现行的地震勘探数据处理算法。
本文侧重两个关注点:一是低功耗、高精度卫星时钟同步的实现;二是符合正态随机分布特征的地震勘探激发控制时间的生成。
2.1 频率校准参数压控晶体振荡器是通过控制电压“牵引”输出振荡信号的频率。选用的晶体振荡器的输出频率会随着控制电压升高而升高,但缘于制造工艺、结构设计、生产批次不同等多方面因素,使同一型号的压控晶体振荡器的电压—频率曲线也会存在差异。因此,获取压控晶体振荡器牵引电压与频率变化对应关系是卫星时钟同步需解决的关键问题。
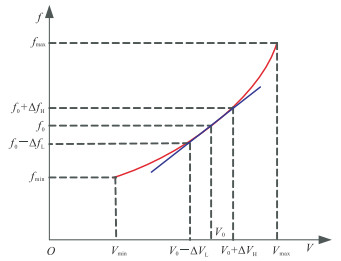
考虑到实际作业现场环境温度在短期内不会发生剧烈变化,可将该较小频率范围内的控制电压与输出频率关系近似看作线性关系。图 4中V0为中心频率(f0)控制电压;f为压控晶振输出频率;ΔfL为晶振输出频率变化下限,ΔVL为对应的控制电压调整量;ΔfH为晶振输出频率变化上限,ΔVH为对应的控制电压调整量;(V0-ΔVL,V0+ΔVH) 为微调的控制电压区间,(f0-ΔfL,f0+ΔfH) 为频率变化范围。
|
图 4 压控晶振电压—频率特性曲线 |
结合图 3的硬件架构,获取晶体输出频率调节参数步骤如下:
(1)微控制器根据选用晶体振荡器的技术参数,由DAC(数模转换)输出对应压控晶振中心电压的初始控制值C1,控制晶体振荡器输出振荡信号频率在其标称的输出频率附近;
(2)初始化微控制器内置定时器Timer1、Timer2和Timer5的时钟频率为同一频率f。设置Timer1为上升沿捕获模式,设置Timer2输出模拟秒脉冲(Pulse Per Second,PPS)信号,设置Timer5为向上计数模式;
(3)在Timer1捕获到第一个来自卫星接收模块的PPS信号时,启动Timer2输出仿真PPS信号,并同时开启Timer5计数;
(4)在微控制器DAC输出初始控制值C1的条件下,Timer5对连续的k(k≥1)个PPS上升沿进行周期计数,记为N1;
(5)微控制器调节DAC输出控制值增至C2,Timer5对连续的k(k≥1)个PPS上升沿进行周期计数,记为N2;
(6)根据Timer5两次计数N1、N2,按下式
| $ {c}_{0}=\frac{{N}_{2}-{N}_{1}}{{C}_{2}-{C}_{1}} $ | (6) |
计算微控制器的DAC每变化1个控制值对应Timer5的计数值c0。
2.2 周期性卫星时钟同步地震勘探中,要求数据采集与炮点激发严格同步,不同地质目标对同步精度有不同要求,一般要求不大于10 μs。图 3中微控制器在收到来自卫星接收模块有效时间信息后,在PPS上升沿时刻配置实时时钟(Real Time Clock,RTC),之后每隔一个固定时间间隔获取本地时钟与卫星时钟的偏差,并利用晶体振荡器的特性进行调节,确保RTC的准确度。该过程中,使用增量比例积分微分控制(Proportional Integral Derivative,PID)算法调整压控晶体振荡器的输出信号频率。
设u(k)是某次卫星接收模块启动后,第k次PID算法输出的控制量。根据PID算法思路可得到u(k)与Timer5计数值的关系
| $ \begin{array}{l}u\left(k\right)={K}_{\mathrm{p}}e\left(k\right)+{K}_{\mathrm{i}}\sum\limits_{j=0}^{k}e\left(j\right)+\\ \quad\quad\quad{K}_{\mathrm{d}}[e\left(k\right)-e(k-1\left)\right]\end{array} $ | (7) |
式中:e(k)为第k次PID预设值与需调节Timer5计数值的误差;Kp为PID控制的比例放大系数;Ki、Kd分别为积分和微分参数。由式(7)可见,u(k)为输出的控制量,若某次计算溢出等原因输出错误的控制量,会引起晶振频率发生大幅度变化,则可通过只输出控制量的增量解决
| $ \mathrm{\Delta }u\left(k\right)=u\left(k\right)-u(k-1) $ | (8) |
式中
| $ \mathrm{\Delta }u\left(k\right)={K}_{\mathrm{p}}\mathrm{\Delta }e\left(k\right)+{K}_{\mathrm{i}}e\left(k\right)+{K}_{\mathrm{d}}[\mathrm{\Delta }e\left(k\right)-\\ \quad\quad\quad\quad\mathrm{\Delta }e(k-1\left)\right] $ | (9) |
式中
| $ \mathrm{\Delta }C\left(k\right)=\frac{\mathrm{\Delta }u\left(k\right)}{{c}_{0}} $ | (10) |
在地震数据处理环节,也有用于滤除或衰减符合正态分布随机噪声的成熟方法和流程。因此,本文提出使用高精度ADC芯片采集振动传感器的数据作为产生符合正态分布抖动时间的种子。
假设随机采集到的振动信号数据t0作为产生随机数的种子,产生小窗口随机数的过程如下。
首先使用种子t0生成n个处于(0,1)区间均匀分布的随机数x1,x2,…,xn,其中n为生成随机数的个数
| $ \left\{\begin{array}{l}{t}_{i}=a{t}_{i-1}+b-⌊\left(\frac{a{t}_{i-1}+b}{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}\right)\times \mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}⌋\\ {x}_{i}=\frac{{t}_{i}}{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}\end{array}\right. $ | (11) |
式中:a、b、base均为预先设定的常数;ti为计算过程参数,当i=0时,即t0表示随机采集的振动传感数据,作为产生随机数的种子;xi为(0,1)区间随机数;“⌊⋅」”表示向下取整。
再用由式(11)生成的(0,1)区间均匀分布的随机数x1,x2,…,xn,得到正态分布随机数
| $ y=\mu +\sigma \times \frac{-\frac{n}{2}+\sum\limits_{i=1}^{n}{x}_{i}}{\sqrt[]{\frac{n}{12}}} $ | (12) |
式中:用于生成随机激发时间时,μ表征据时—距曲线得到的当前炮与上一炮的最小时间间隔;σ用于控制在μ基础上的时间抖动范围。
3 算法验证为了验证所提算法的有效性,选用内置有温度传感器的STM32L475作为微控制器,卫星接收模块选用Ublox公司的MAX-8C,ADC模块使用TI公司低功耗、高精度的ADS1292,振动传感器选用地震勘探常见的动圈式检波器,按图 3所示硬件架构进行电路设计。测试过程中,使用高精度示波器分析模拟PPS信号与真实PPS信号的一致性程度,从另一角度验证卫星时间同步精度。
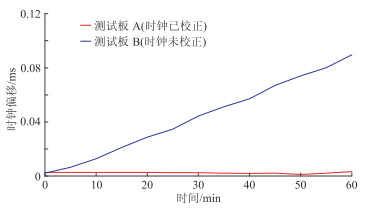
3.1 卫星时间同步精度使用A、B两块测试板,让其运行于卫星信号接收条件良好的相同测试环境。测试板A每5 min记录一次本地时钟相对卫星时钟的偏差,并使用本文校准算法对该时钟偏差进行校正;测试板B每5 min记录一次本地时钟相对卫星时钟的偏差,但不做校正。测试开始和结束时,分别使用示波器抓取测试板A、B输出模拟PPS脉冲与真实PPS脉冲的时间偏差。由图 5可见,未做时钟偏差校正的测试板B的时间偏差随运行时间的延长呈不断累加的趋势,1 h的时钟偏差近100 μs,而做过时钟偏差校正的测试板A的时间偏差一直维持在5 μs以下。测试板输出的仿真PPS脉冲信号与真实PPS信号时间差值的示波器分析结果如图 6所示。
|
图 5 校准和未校准时钟偏移曲线 |
|
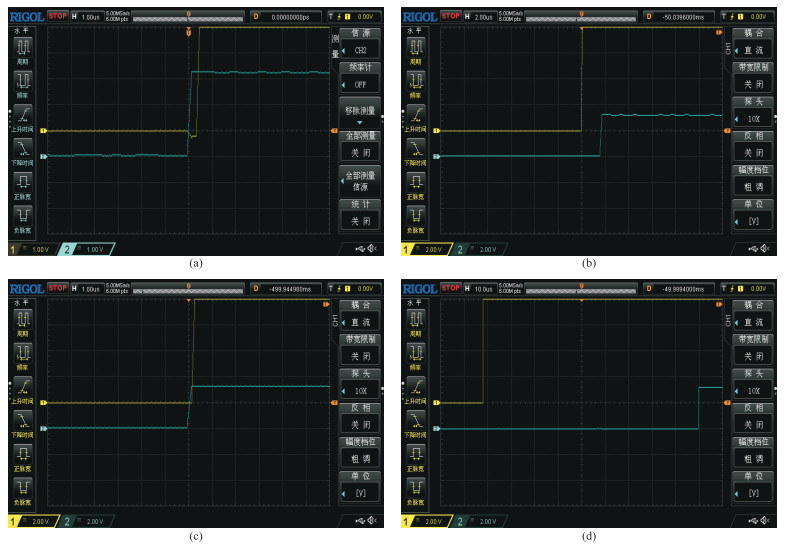
图 6 测试板输出模拟PPS与真实PPS的时间差 (a)、(b)分别为应用和未用周期性卫星时钟同步算法的初始时间差;(c)、(d)对应(a)、(b)的1 h后的时间差。横轴为时间,纵轴为幅度 |
图 6中黄色信号为微控制器输出的模拟PPS信号,蓝色线为输出的真实PPS信号。其中图 6a、图 6b分别为应用和未应用周期性卫星时钟同步算法的初始时间差;图 6c为应用周期性卫星时钟同步算法的测试板在1 h后的时间差,可见不大于10 μs;图 6d为未应用周期性卫星时钟同步算法的测试板1 h后的时间差,可见已达近100 μs,印证了时钟校正算法的有效性。
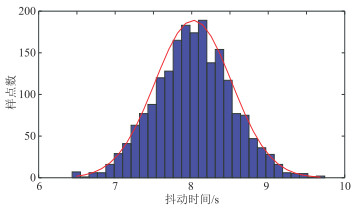
3.2 随机激发时间测试板A、B使用ADS1292采集和振动传感器的数据作为生成随机激发时间的种子,生成2000个激发间隔时间为8 s、抖动范围为300 ms的随机激发时间,样本数据的分布见图 7所示,达到了设计的预期目标。
|
图 7 生成随机激发时间数据的分布图 |
相邻两炮或多炮间相互的时间抖动程度也直接影响生成随机激发时间的质量。以随机时间生成的顺序为横轴,生成随机数幅度为纵轴对生成随机数进行显示(图 8),相邻激发时间具有较强非相干性。

|
图 8 生成随机激发时间的颤动情形 |
随机激发时间的准确性决定于本地时钟的精度。众所周知,晶体振荡器的输出频率会随环境温度的变化而变化,压控晶振也不例外。本文算法采用按一定时间间隔进行卫星时钟同步的方式保持本地时钟的准确性,故卫星同步周期会直接影响产生的随机激发时间的准确性。
图 9给出24 h不同同步周期的时钟偏差曲线,可见同步周期越短,算法对环境温度变化的适应能力就越强,但MAX-8C的运行功耗约为48 mW,待机功耗约11 mW,为了降低地震勘探随机激发时间发生器的综合运行功耗,最终选择卫星时钟同步周期为5 min,测试板整机平均运行功耗约50 mW。

|
图 9 不同卫星同步周期的时钟偏移曲线 |
激发时间的随机性强弱是衡量所提算法优劣的另一重要指标,而种子的随机性决定生成数据随机性的关键,本文使用高精度的ADS1292和振动传感器拾取的数据作为产生随机激发时间的种子。
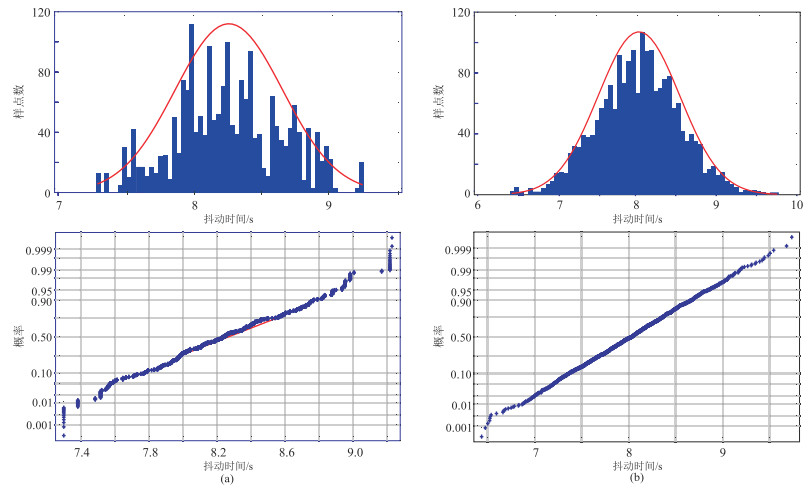
图 10给出自带的随机数发生器和本文算法生成随机数的概率分布特征。其中图 10a分别展示随机数发生函数产生的随机数样本分布图和概率图;图 10b是本文算法产生的随机数样本分布图和概率图。无论是数据样本的分布图还是概率图,均表明使用高精度振动传感数据作为种子,能生成随机性很强,且数值大小、范围可控的随机数,可完全满足工业应用的需求。
|
图 10 STM32L475自带随机数生成函数(a)与本文算法产生数据样本(b)的分布(上)及概率(下)对比 |
激发源启动的随机性对于实现地震勘探混叠采集具有重要意义。本文提出一种基于振动传感和卫星授时的多源混叠激发时间产生算法,用于地震勘探数据采集时激发源启动控制。首先,利用卫星授时技术及压控晶振在较短时间内的电压—频率呈线性关系的特点,以固定时间间隔方式进行本地时钟的校准与卫星时间同步,确保用于生成随机激发时间的时间基准的准确性;然后,以高精度ADC芯片采集的振动传感数据作为种子,生成数值大小、偏差程度可控的随机数作为抖动激发时间,从而提高激发时间的随机性。
使用基于本文设计的硬件架构的测试板验证所提算法的正确性、可靠性和工业应用的可行性。测试发现,按照5 min的卫星时钟同步周期能确保本地时钟误差长时间保持在10 μs以下,且可大幅度削减功率损耗,使测试板平均运行功耗在50 mW以下。相比于直接使用微控制器自带随机数发生器,本文算法求取的随机激发时间的抖动幅度具有数值大小及范围可控、随机性强的特征,更贴合工业化应用的实际需求。
在将来,拟将本文算法应用于高密度、高效率油气勘探实践,而施工现场存在随机的振动干扰,将进一步提高生成激发时间的随机性。同时,苛刻的现场环境也会对本文算法的硬件实施效果带来巨大考验,如何确定能满足不同环境温度变化曲线的自适应卫星同步周期是确保生成随机激发时间准确性的关键,也是下一步的技术探讨的焦点。另外,如何充分考虑地震勘探的需求,选择随机激发时间的抖动值,也是侧重关注的内容。
| [1] |
SILVERMAN D. Method of Three Dimensional Seismic Prospecting: 4159463[P]. 1979-06-26.
|
| [2] |
ALLEN K P, JOHNSON M L, MAY J S. High fidelity vibratory seismic (HFVS) method for acquiring seismic data[C]. SEG Technical Program Expanded Abstracts, 1998, 17: 140-143.
|
| [3] |
SALLAS J J, GIBSON J B, LIN F, et al. Broadband vibroseis using simultaneous pseudorandom sweeps[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 100-104.
|
| [4] |
BAGAINI C, JI Y. Dithered slip-sweep acquisition[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 91-95.
|
| [5] |
FROMYR E, CAMBOIS G, LOYD R, et al. Flam: a simultaneous source wide azimuth test[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2821-2825.
|
| [6] |
HAMPSON G, STEFANI J, HERKENHOFF F. Acquisition using simultaneous sources[J]. The Leading Edge, 2008, 27(7): 918-923. DOI:10.1190/1.2954034 |
| [7] |
ZHANG Z B, LUO W, ZENG T, et al. The first marine seismic survey of dual-source random shooting offshore China[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 288-292.
|
| [8] |
ALLAN D W, WEISS M A. Accurate time and frequency transfer during common-view of a GPS satellite[C]. 34th Annual Symposium on Frequency Control, 1980, 334-346.
|
| [9] |
DAVIS D D, WEISS M A, CLEMENTS A C, et al. Remote synchronization within a few nanoseconds by simultaneous viewing of the 1.575 GHz GPS satellite signals[J]. Alspach W J, Ed, CPEMDig N, 1982, 15: 1982. |
| [10] |
WEISS M, ZHANG V, NELSON L, et al. Delay variations in some GPS timing receivers[C]. Proceedings of International Frequency Control Symposium, 1997, 304-312. .
|
| [11] |
MANNERMAA J, KALLIOMAKI K, MANSTÉN T, et al. Timing performance of various GPS receivers[C]. Proceedings of the 1999 Joint Meeting of the European Frequency and Time Forum and the IEEE International Frequency Control Symposium (Cat No 99CH36313), IEEE, 1999, 287-290.
|
| [12] |
MUMFORD P J. Relative timing characteristics of the one pulse per second (1PPS) output pulse of three GPS receivers[C]. Proceedings of the 6th International Symposium on Satellite Navigation Technology Including Mobile Positioning & Location Services (SatNav 2003), Melbourne, Vic, Australia, 2003, 1-10.
|
| [13] |
PALLIER D, LE CAM V, Pillement S. Energy-efficient GPS synchronization for wireless nodes[J]. IEEE Sensors Journal, 2021, 21(4): 5221-5229. DOI:10.1109/JSEN.2020.3031350 |
| [14] |
CANTOR S R, STERN A, Levy B. Clock technology[C]. Proceedings of the 55th Annual Meeting of The Institute of Navigation (1999), 1999, 37-47.
|
| [15] |
GOBATO R, GOBATO M R R, HEIDARI A. Rhodochrosite as crystal oscillator[J]. American Journal of Biomedical Science & Research, 2019, 3(2): 187. |
| [16] |
TIAN R, ZHANG J, ZHANG S, et al. A high-precision energy-efficient GPS time-sync method for high-density seismic surveys[J]. Applied Sciences, 2020, 10(11): 3768. DOI:10.3390/app10113768 |
| [17] |
MA Y, CHEN T, LIN J, et al. Entropy estimation for ADC sampling-based true random number generators[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(11): 2887-2900. DOI:10.1109/TIFS.2019.2908798 |
| [18] |
CHOI S, SHIN Y, YOO H. Analysis of ring-oscillator based true random number generator on FPGAs[C]. 2021 International Conference on Electronics, Information, and Communication (ICEIC), IEEE, 2021, 1-3.
|
| [19] |
VASILEIADIS N, DIMITRAKIS P, NTINAS V, et al. True random number generator based on multi-state silicon nitride memristor entropy sources combination[C]. 2021 International Conference on Electronics, Information, and Communication (ICEIC), IEEE, 2021, 1-4.
|
| [20] |
CANG S, KANG Z, WANG Z. Pseudo-random number generator based on a generalized conservative Sprott-A system[J]. Nonlinear Dynamics, 2021, 104(1): 827-844. DOI:10.1007/s11071-021-06310-9 |
| [21] |
KRISHNAMOORTHI S, JAYAPAUL P, DHANARAJ R K, et al. Design of pseudo-random number generator from turbulence padded chaotic map[J]. Nonlinear Dynamics, 2021, 104(2): 1627-1643. DOI:10.1007/s11071-021-06346-x |
| [22] |
LIU J, LIANG Z, LUO Y, et al. A hardware pseudo-random number generator using stochastic computing and logistic map[J]. Micromachines, 2021, 12(1): 31. |



 孙祥娥, 湖北省荆州市南环路1号长江大学电子信息学院,434023。Email:
孙祥娥, 湖北省荆州市南环路1号长江大学电子信息学院,434023。Email: