2. 长江大学地球物理与石油资源学院, 湖北武汉 430100;
3. 中国石油勘探开发研究院, 北京 100083;
4. 中国石化石油勘探开发研究院, 北京 100083
2. College of Geophysics and Petroleum Resources, Yangtze University, Wuhan, Hubei 430100, China;
3. Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100083, China;
4. Petroleum Exploration and Production Research Institute, Sinopec, Beijing 100083, China
在地震资料定量解释中,密度(DEN)和声波时差(AC)测井曲线是地震岩石物理学和地震反演技术中的两条关键曲线,能够提供可靠的时深关系,使深度域测井数据与时间域地震数据相互标定,是岩石物理建模技术必不可少的岩石弹性和物性信息曲线。但实际测井中,井径的扩缩对声波和密度测井影响较大,导致部分井段出现畸变、失真,甚至缺失,为后续综合解释带来一定困难,曲线重构技术是测井数据校正和预测的主要方法[1-2]。
传统的测井曲线重构方法主要有三种:经验模型法、多元拟合法、岩石物理建模法。由于经验模型法效率最高、最易推广,因此针对横波速度测井曲线缺失问题,提出了许多纵波和横波之间的线性或非线性经验关系[3-4],但受到地区和岩石类型的限制。黄小平等[5]论述了Gardner公式不适用于井壁垮塌处DEN曲线校正,原因在于井壁垮塌对DEN和AC曲线都有影响。陈钢花等[6]论证了Faust公式需要保证地层电阻率和AC曲线具有很好相关性,储层中流体对电阻率有较大影响的地层并不满足该公式的假设条件。
虽然不同测井曲线的测量原理不同,但它们都是反映岩石某一方面的特征,因此不同测井曲线一般存在一定相关性。多元拟合法基于曲线相关性特征,采用线性或非线性关系式拟合目标曲线与其他曲线的关系,完成目标曲线重构,该方法精度高于经验模型法,但矿物成分复杂的岩石使目标曲线与其他曲线的非线性关系增强,多元拟合关系式泛化能力不足,拟合的目标曲线精度不高[7-8]。
岩石物理建模法(Xu-White、Cemented、Krief模型等)假设饱和流体岩石主要由岩石基质、孔隙结构、流体三部分组成,而这三部分的参数是根据受井眼影响较小的测井曲线(自然伽马(GR)、自然电位(SP)、电阻率(RT)、中子孔隙度(CNL)等)解释的孔隙度、泥质含量、含水饱和度由不同岩石物理模型构建,通过迭代调整岩石孔隙纵横比参数,求解纵、横波速度和密度。Yang等[9]针对岩石矿物成分复杂的情况,拓展了Xu-White模型,形成了考虑石英、黏土、方解石三种矿物的Xu-White模型,重构的灰质发育区砂泥岩地层的横波速度精度较高。针对页岩、碳酸盐岩等各向异性较强的岩石,桂俊川等[10]提出了考虑包含裂缝等多种孔隙类型的横向各向同性介质的横波速度预测方法。这些岩石物理建模法方法重构的横波速度精度依赖于孔隙度、孔隙类型、矿物成分、含水饱和度等储层地球物理参数的计算精度,然而这些参数难以高精度获取。岩石物理建模法重构的目标曲线精度高于前两类方法,但一般在纵波速度和密度已知情况下重构横波速度,在纵波速度和密度曲线存在误差时,该方法重构的目标曲线精度明显下降。
深度学习具有建立输入与输出之间的复杂非线性映射关系的能力,因此在人脸识别、机器翻译、图像分类等领域得到了广泛的应用[11-13]。近年来,深度学习被引入地学领域[14-15],在岩石物理建模、岩性识别、储层参数反演等领域取得了一定的研究成果。在测井曲线重构方面应用最为广泛的为横波速度重构。有学者提出利用长短时记忆(Long Short-term Memory,LSTM)网络解决横波速度缺失问题[16-17]。该方法充分考虑了测井数据的时序特征,并在碳酸盐岩和砂岩储层中取得了较好的重构效果。为了提高深度学习网络重构横波速度的精度,Chen等[18]提出使用二维卷积神经网络(2DCNN)和门控循环单元(Gated Recurrent Unit,GRU)的混合网络预测横波速度。该方法分别利用2DCNN、GRU提取输入数据的空间特征(地层的不同属性特征,如自然伽马、自然电位、中子孔隙度、地层电阻率等)和时序特征(测井数据深度方向的变化特征),能够建立输入与输出之间复杂的非线性关系。Han等[19]将深度学习和机器学习相融合,揭示输入与输出之间更复杂的非线性关系。实验结果表明,与决策树、随机森林和深度学习网络相比,该方法在缺失曲线重构方面更具优势。近年来,融合注意力机制的神经网络可提高网络对重要特征的敏感度,已应用于机器翻译、智能电网、地学等不同领域[20-23]。Kavianpour等[24]开发了融合注意力机制的CNN-BILSTM(双向LSTM)网络并用于地震预测,取得了良好的效果。Bai等[25]提出了一种基于注意力机制的长短期记忆全卷积网络(LSTM-FCN)模型并用来提取地震数据之间的时序特征,以提高地震事件检测和定位的准确性;马国庆等[26]提出了基于自注意力机制的深度学习网格化方法,实现了高精度重磁数据网格化和滤波处理。
测井是油气开发和勘探行业最重要的观测技术之一。在实际应用中,校正和预测缺失测井曲线是节约油气勘探开发成本的有效途径之一。由于储层的结构复杂性和非均质性,测井曲线之间存在较强的非线性关系[19]。相比于现有的经验模型法、多元拟合法、岩石物理建模法,已成功应用于地震相识别、岩性预测、储层参数反演等地球物理领域的深度学习具有构建输入与输出之间复杂非线性关系的能力。针对测井曲线自相关性和互相关性的不同,本文构建了融合注意力机制的二维卷积深度学习网络(STACNN),该网络主要包括输入层、二维卷积层、空间注意力层、时序注意力层和全连接层。以准噶尔盆地超深层致密砂岩为研究对象,通过试验分析了时、空注意力层权重与测井曲线自相关性和互相关性的关系。然后开展了应用该网络、GRU、2DCNN和多元拟合重构AC和DEN测井曲线试验,并进行参数优化。最后通过井震匹配关系的提升验证了AC和DEN测井曲线校正和缺失重构的效果。
1 原理与方法 1.1 卷积神经网络(CNN)卷积神经网络(CNN)是深度学习领域经典的网络之一,随着深度学习网络的快速发展,已广泛应用于图像、医学、地球物理等领域。CNN通常由输入层、卷积层和全连接层组成,其核心部分为卷积层,当数据输入到卷积层后,卷积核可以挖掘数据局部间的高维空间特征,作为下一层的输入。
| $ {\mathit{\boldsymbol{X}}}^{T}=\sigma \left(\sum\limits_{t}{\mathit{\boldsymbol{W}}}^{T}{\mathit{\boldsymbol{X}}}^{t}+{\mathit{\boldsymbol{B}}}_{1}\right) $ | (1) |
式中:
神经网络借鉴了人类的注意力机制。人们在观察图像时,会专注于图像的目标区域,以挖掘图像的重要信息。虽然各条测井曲线测量机理不同,但它们都反映了同一岩石不同方面的性质,AC、DEN与其他测井曲线的互相关性及自相关性不同,因此提出将注意力机制融合到2DCNN中,达到提升深度学习网络捕捉测井数据自相关性和互相关性特征的能力。空间注意力层的输出结果可表示为
| $ {\mathit{\boldsymbol{S}}}^{T}={\mathit{\boldsymbol{\alpha }}}^{T}•{\mathit{\boldsymbol{X}}}^{T} $ | (2) |
| $ {\mathit{\boldsymbol{\alpha }}}^{T}=\mathrm{R}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{V}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}\left({\mathit{\boldsymbol{\alpha }}}_{1}^{T}, d\right) $ | (3) |
| $ {\alpha }_{1, m}^{T}=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\sum\limits_{k=1}^{d}{X}_{k, m}^{T}\right) $ | (4) |
式中:
时序注意力层的输出结果可表示为
| $ {\mathit{\boldsymbol{F}}}^{D}={\mathit{\boldsymbol{\beta }}}^{D}•{\mathit{\boldsymbol{S}}}^{D} $ | (5) |
| $ {\mathit{\boldsymbol{\beta }}}^{D}=\mathrm{R}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{V}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}({\mathit{\boldsymbol{\beta }}}_{1}^{D}, m) $ | (6) |
| $ {\beta }_{d, 1}^{D}=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\sum\limits_{g=1}^{m}{S}_{d, g}^{D}\right) $ | (7) |
式中:
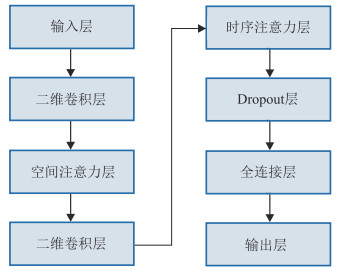
由于AC、DEN测井曲线与其他曲线的互相关性、自相关性不同,且它们之间的非线性关系复杂,因此本文提出了一种基于时空注意力机制的CNN融合网络。其网络组成(图 1)为:
|
图 1 STACNN的网络结构 |
(1)输入层,将训练测井数据集输入STACNN;
(2)第一2DCNN层,卷积核尺寸为3×3,输入通道数为1,输出通道数为16,用于提取测井数据的空间特征;
(3)空间注意力层,用于提高网络对空间特征的敏感性;
(4)第二2DCNN层,卷积核尺寸为5×3,输入通道数为16,输出通道数为32,用于提取测井数据的时序特征;
(5)时序注意力层,用于提高网络对时序特征的敏感性;
(6)Dropout层,在训练时以一定的概率p使神经元失活;
(7)全连接层,输入通道数为32,输出通道数为1,用于提高输入层和输出层之间的非线性关系拟合能力;
(8)输出层,输出STACNN的预测结果(AC或DEN曲线)。
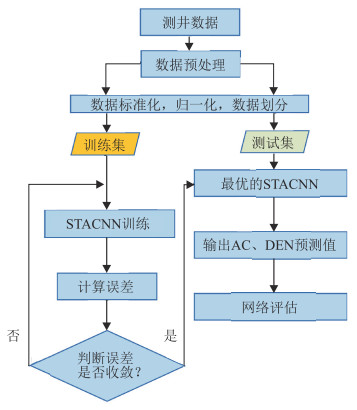
1.4 STACNN的网络训练和预测的流程本文网络训练和预测的过程如下(图 2)。
|
图 2 STACNN的训练和预测流程 |
(1)数据预处理。使用StandardScaler和MinMaxScaler函数对测井数据进行标准化和归一化处理以消除不同数据量纲之间的差距。
(2)将训练测井数据集输入STACNN。
(3)训练STACNN。本文将均方误差(MSE)作为损失函数,同时选用自适应矩(Adam)优化算法进行网络优化,直至损失函数收敛。
(4)将测试集的测井数据输入到STACNN。
(5)网络评估。本文用可决系数(R2)对STACNN进行定量评估
| $ {R}^{2}=\frac{\sum\limits_{i=1}^{M}({\tilde{y}}_{i}{-\stackrel{-}{y})}^{2}}{\sum\limits_{i=1}^{M}({y}_{i}{-\stackrel{-}{y})}^{2}} $ | (8) |
式中:M表示样本个数;
R2用来度量一个统计模型的拟合优度,取值范围为[0, 1]。R2越接近1,说明回归直线对观测值的拟合程度越高;R2的值越接近0,说明回归直线对观测值的拟合程度越低。
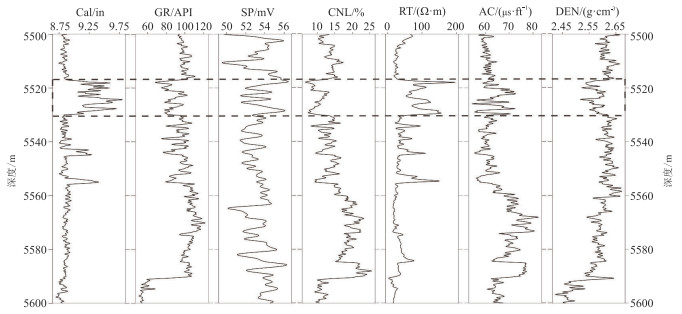
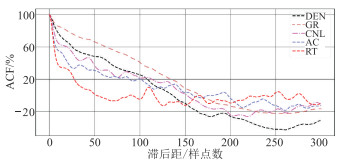
2 案例分析 2.1 数据集简介本文选取准噶尔盆地M工区gd-1、gd-2、gd-5、gd-13等井致密砂岩储层为研究对象,且数据集都为白垩系同一目的层段,保证数据集测井曲线横向特征具有一定的相似性。样本集中输入的特征曲线为GR、SP、CNL、RT,标签集为AC和DEN曲线。在测井曲线的深度方向采用多对一(多个采样点对应一个标签)的方式对样本集进行划分,既充分保证了测井曲线的自相关性,又体现了地层的连续渐变特征。gd-2井的测井曲线(图 3)表明该井在黑框处出现了严重的扩径现象,AC、DEN曲线存在严重的测量误差,即AC值周期跳跃、DEN值偏低。因此在分析目标测井曲线与其他测井曲线相关性时,在井径(Cal)曲线约束下将测井数据分为两类,即非扩径段和扩径段。用非扩径段目标曲线与其他曲线的交会图分析它们之间的互相关性(图 4)。与AC曲线的相关性从高到低依次为CNL、RT、GR、SP曲线,R2值分别为0.5688、0.4043、0.3594、0.1535。与DEN曲线的相关性从高到低依次为GR、CNL、RT、SP曲线,R2值分别为0.6712、0.3511、0.2307、0.0174。虽然AC、DEN都属于典型的孔隙度解释曲线,但AC、DEN与其他常规测井曲线相关性是不同的。使用自相关函数(ACF)分析测井数据的自相关性。各曲线的ACF皆随滞后距的增加而不断减小(图 5),但各曲线减小的速率不同。当滞后距小于10个样点时,自相关性都能达到40%以上,说明地下沉积地层是连续渐变的。
|
图 3 gd-2井的测井曲线 |

|
图 4 AC、DEN曲线与其他测井曲线的交会图 |
|
图 5 测井曲线的自相关系数 |
上述分析表明,其他测井曲线的时空特征与AC、DEN曲线有一定的相关性。同时,由于SP曲线与AC和DEN曲线的相关性都较低,因此在重构目标曲线时,选用相关性较高的GR、CNL、RT曲线作为深度学习网络的输入样本。
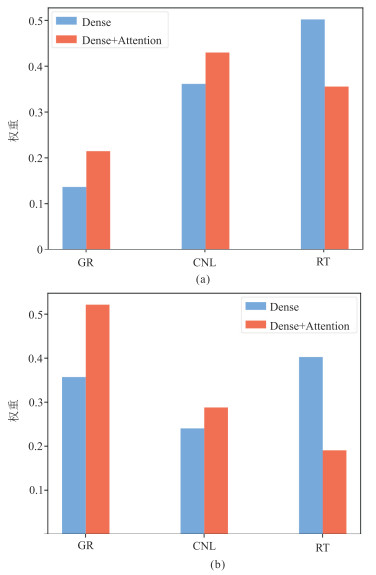
2.2 权重分析为了验证注意力机制能够加强深度学习网络对重要时空特征的敏感性,分别构造了有、无时空注意力机制的两种网络,其中,未加入时空注意力机制的网络结构由一个全连接层(Dense)组成,加入时空注意力机制的网络结构由一个全连接层(Dense)和一个时空注意力层(Attention)组成。图 6为测井数据有、无空间注意力层的权重分布。当标签为AC时,空间注意力层的权重分布由大到小分别为CNL、RT、GR曲线(图 6a),当标签为DEN曲线时,权重分布由大到小分别为GR、CNL、RT曲线(图 6b),这与图 4中的互相关性分析一致。而未加入注意力机制的网络权重分布却无此规律。当标签为AC曲线时,CNL曲线被空间注意力层赋予最大的权重,达到0.43,因为CNL、AC、DEN曲线都是用于测量岩石的孔隙度;当标签为DEN曲线时,GR曲线被空间注意力层赋予最大的权重,达到0.52,因为二者都属于放射性测井,皆可用于岩性解释。
|
图 6 标签为AC(a)和DEN(b)曲线时测井数据的空间特征权重分布 |
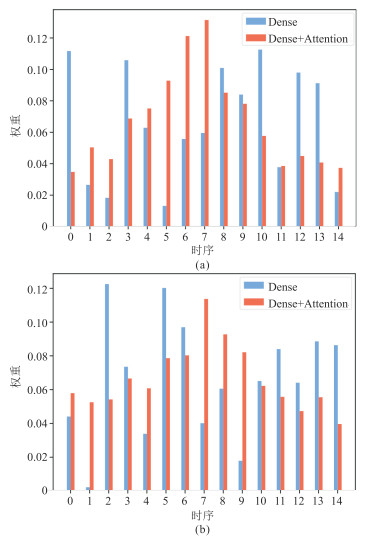
图 7为测井数据有、无时序注意力层的权重分布。选取常规测井数据中的15个采样点作为样本,并将第8个点的AC或DEN值作为标签,在预测AC或DEN时,位于标签位置的样本数据被时序注意力层赋予了最大的权重,分别达到了0.1314和0.1137,说明与标签位置相同的样本对AC或DEN值的影响最大。随着与标签的距离增加,注意力权重的总体趋势是减小的,这与图 5中测井数据的自相关性分布相一致。以上这些现象验证了在深度学习网络中加入时空注意力机制的合理性。
|
图 7 标签为AC(a)和DEN(b)曲线时测井数据的时序特征权重分布 |
为了验证STACNN的预测性能,分别与2DCNN、GRU和多元拟合法的结果进行了对比。2DCNN组成为:两个二维卷积层(卷积核尺寸分别为3×3、5×3,通道数皆为16)、一个Dropout层(丢弃率p=0.25)、一个全连接层(通道数为1);GRU网络的组成为:两个GRU层(门控循环单元个数分别为16和32)、一个全连接层(通道数为1)。所有网络都采用Adam优化算法,结合了AdaGrad和RMSProp算法的优点,在处理大规模数据、参数优化和非稳态目标方面具有较强的优势。同时,添加舍弃层,随机丢弃神经元,以增加网络的泛化性。
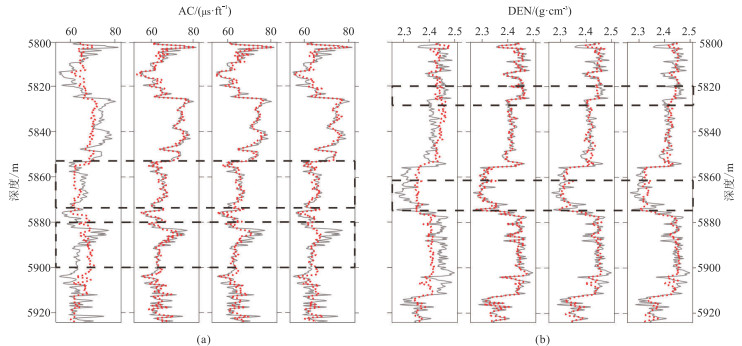
选取gd-13井测井数据对2DCNN、GRU网络和本文的STACNN进行训练。整体上本文网络的AC、DEN曲线预测结果都优于其他两个网络,更优于多元拟合的预测结果(图 8黑虚线框所示),这表明在捕捉目标曲线与其他曲线复杂的非线性关系方面,深度学习网络具有明显的优势。三个网络预测AC、DEN曲线的损失函数如图 9所示,都随训练次数的增加而不断减小,最终达到一个稳定的值,即网络达到最优状态。本文网络训练一次后的损失函数值明显低于其他两个网络,而且达到稳定状态时的损失函数值也最小。原因在于STACNN可以更好地挖掘其他测井曲线的时、空特征与AC、DEN曲线之间的相关性,提高了网络对时、空特征的敏感度。GRU、CNN、本文网络AC曲线预测结果的R2值分别0.7199、0.8192、0.8940,DEN曲线预测结果的R2值分别为0.7528、0.8396、0.9570,同样验证了注意力机制能够提升深度学习网络的预测性能。
|
图 8 gd-13井四种方法AC(a)、DEN(b)曲线的预测结果(红色点线)与真实曲线(黑色实线)的对比 从左往右依次为多元拟合、本文网络、CNN、GRU网络。 |

|
图 9 预测AC(a)、DEN(b)曲线时STACNN、CNN和GRU网络的损失函数曲线对比 |
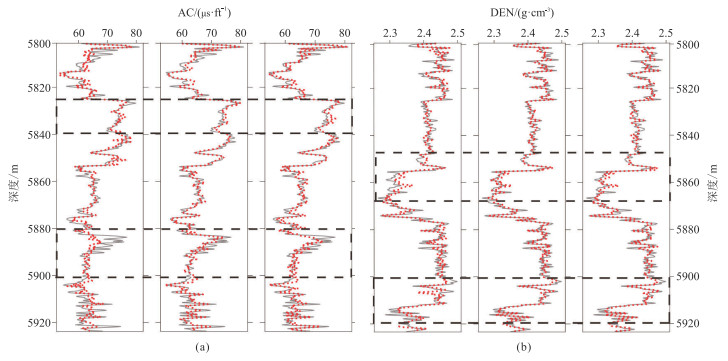
为了更好地用本文网络完成目标曲线校正和缺失重构,分别将样本划分时窗长度,即采样点数设为5、15、25,采用同样的训练参数,网络的预测结果如图 10所示。AC曲线预测结果的R2值分别为0.7305、0.9128、0.8945,DEN曲线预测结果的R2值分别为0.8834、0.9674、0.9469。可见,样本划分时窗长度为15时,本文网络预测性能最佳。
|
图 10 时窗长度为5(左)、15(中)、25(右)时AC(a)、DEN(b)的预测结果(红色点线)与真实曲线(黑色实线)的对比 |
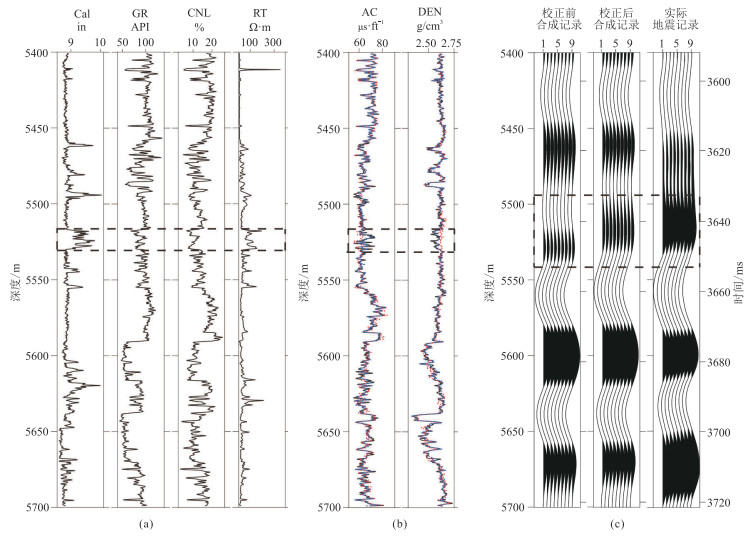
在钻井过程中受地层岩性的影响,有些井段产生了扩径或缩径现象,导致AC、DEN测井曲线存在测量误差。由图 11中gd-2井的井径曲线可以看出,该井段井孔质量较差,其中大段扩径有一段(5520~5530 m,黑框所示),还有一些小范围扩径段。
|
图 11 gd-2井AC、DEN曲线校正分析 (a)其他测井曲线;(b)AC、DEN曲线校正前(实线)、后(虚线)对比(红色短虚线为只有非扩径段参与训练,蓝色长虚线为全部数据参与训练);(c)校正前、后合成记录与实际地震记录的对比 |
使用井径曲线作为约束条件将gd-2井测井曲线划分为扩径段和非扩径段两部分,用非扩径段样本集训练本文网络,并预测了所有样本的AC和DEN曲线(校正结果),预测结果与真实曲线的R2值分别为0.8472、0.8755。AC、DEN测井曲线校正前、后在小范围的扩径井段的数值略有差异,而在大范围的扩径井段的数值差异较大(黑框区域)。根据地层的沉积演变规律,同一块具有相同沉积背景的岩性段,其物理性质基本相近,校正后的曲线形态变化比较平缓,而校正前的声波受井径扩径的影响具有明显的周期跳跃现象。
将扩径段与非扩径段同时参加网络训练的预测结果,AC、DEN曲线校正前、后在扩径井段的数值基本吻合,产生这种现象的原因在于扩径段的数据参与了网络的训练和监督。
与校正前的合成记录相比,校正后的合成记录与真实的地震记录吻合度更高,尤其在5490~5540 m(图 11c黑框区域)内,校正后的合成记录的振幅相对关系与真实地震记录基本一致。因此在AC、DEN曲线同时存在测量误差时本文网络的重构效果明显。
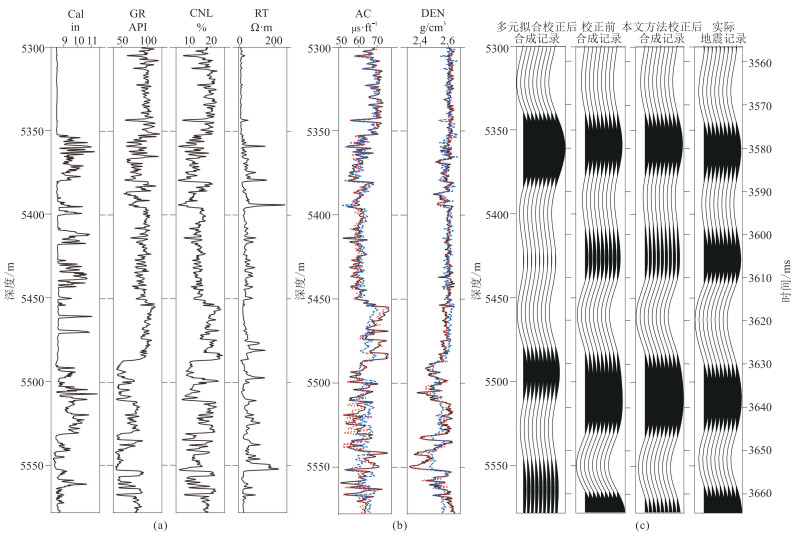
2.5 缺失曲线预测由于井孔条件的限制,有些情况会出现AC、DEN曲线都缺失。选取准噶尔盆地gd-1、gd-2、gd-5、gd-13等井致密砂岩储层测井曲线为研究对象,其中gd-2、gd-5、gd-13井作为训练集,gd-1井作为测试集,且数据集都为白垩系同一目的层段,保证数据集测井曲线横向特征具有一定的相似性。为减少扩径对AC、DEN的影响,选用前三口井非扩径段样本进行训练,建立了两个网络分别预测gd-1井的AC、DEN曲线(图 12)。预测结果与真实曲线的R2值分别为0.8446、0.8598,略低于图 11的预测结果,原因在于图 12验证数据完全没有参与网络训练,而图 11是用同一口井非扩径段进行训练。由图 12可见,本文网络的AC、DEN预测值与真实值相关性要强于多元拟合预测的结果。此外,受扩径的影响,AC、DEN曲线的预测结果与真实值略有差异,校正前、后的合成记录与实际记录基本一致,但校正后的合成记录与真实值的相关系数略高于校正前的合成记录。而多元拟合预测结果的合成记录与实际地震记录相关性较差的原因在于多元拟合得到的声波速度与真值差异较大,造成井震时深转换及计算的反射系数都出现了较大的误差。
|
图 12 gd-1井AC、DEN曲线校正预测分析 (a)测井曲线;(b)本文网络(红色短虚线)和多元拟合方法(蓝色长虚线)预测的AC、DEN曲线与真实曲线(实线)对比;(c)校正前、后合成记录与实际地震记录的对比 |
由于准噶尔盆地致密砂岩储层的孔隙结构复杂,且常规的测井曲线重构方法难以捕捉测井曲线之间的较强的非线性关系,因此本文提出了一种基于时空注意力机制的CNN网络重构AC和DEN测井曲线,得出以下几点结论。
(1)测井曲线的交会分析表明不同测井曲线之间的相关性不同,AC与CNL曲线相关系数达到了0.57,DEN与GR曲线相关系数达到了0.67,证明了利用其他测井曲线重构AC和DEN测井曲线的可行性。
(2)基于AC、DEN测井曲线与其他测井曲线相关性不同,提出在2DCNN提取特征的基础上增加注意力层,达到提高网络对重要时空特征的敏感性。深度学习网络的权重分析表明注意力层权重分布与测井曲线自相关、互相关特征规律一致。
(3)GRU、CNN及本文的STACNN的AC、DEN测井曲线重构效果优于多元拟合法,合成记录时深标定效果验证了本文网络在AC、DEN测井曲线校正、缺失重构方面的效果最优。
| [1] |
廖茂辉. 多元回归方法校正扩径对密度曲线声波曲线的影响[J]. 物探与化探, 2014, 38(1): 174-179, 184. LIAO Maohui. The application of multiple regression method to the calibration of the influence of hole enlargement on density and acoustic logs[J]. Geophysical and Geochemical Exploration, 2014, 38(1): 174-179, 184. |
| [2] |
高刚, 杨亚华, 赵彬, 等. 砂岩敏感识别因子的建立及直接提取方法[J]. 石油地球物理勘探, 2019, 54(6): 1329-1338, 1347. GAO Gang, YANG Yahua, ZHAO Bin, et al. A method for establishing and directly extracting sensitive identification factors of unconsolidated sandstones[J]. Oil Geophysical Prospecting, 2019, 54(6): 1329-1338, 1347. |
| [3] |
CASTAGNA J P, BATZLE M L, EASTWOOD R I. Relationship between compressional-wave and shear-wave velocities in clastic rocks[J]. Geophysics, 1985, 50(5): 571-581. |
| [4] |
HAN D, NUR A, MORGAN D. Effects of porosity and clay content on wave velocities in sandstones[J]. Geophysics, 1986, 51(11): 2093-2107. DOI:10.1190/1.1442062 |
| [5] |
黄小平, 高玉春. 对Garden公式应用条件的探讨[J]. 新疆石油地质, 2000, 21(3): 233-234. HUANG Xiaoping, GAO Yuchun. An approach to application considerations of Garden's relation[J]. Xinjiang Petroleum Geology, 2000, 21(3): 233-234. DOI:10.3969/j.issn.1001-3873.2000.03.016 |
| [6] |
陈钢花, 王永刚. Faust公式在声波曲线重构中的应用[J]. 勘探地球物理进展, 2005, 28(2): 125-128. CHEN Ganghua, WANG Yonggang. Application of Faust equation in rebuilding of acoustic curve[J]. Progress in Exploration Geophysics, 2005, 28(2): 125-128. |
| [7] |
熊冉, 高亮, 杨姣, 等. 曲线重构反演在储层横向预测中的应用[J]. 西南石油大学学报(自然科学版), 2012, 34(1): 83-89. XIONG Ran, GAO Liang, YANG Jiao, et al. Application of curve recomposition inversion in lateral reservoir prediction[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(1): 83-89. |
| [8] |
王俊瑞, 梁力文, 邓强, 等. 基于多元回归模型重构测井曲线的方法研究及应用[J]. 岩性油气藏, 2016, 28(3): 113-120. WANG Junrui, LIANG Liwen, DENG Qiang, et al. Research and application of log reconstruction based on multiple regression model[J]. Lithologic Reservoirs, 2016, 28(3): 113-120. |
| [9] |
YANG Y, YIN X, GAO G, et al. Shear-wave velocity estimation for calciferous sandy shale formation[J]. Journal of Geophysics and Engineering, 2019, 16(1): 105-115. |
| [10] |
桂俊川, 马天寿, 陈平. 横观各向同性页岩岩石物理模型建立——以龙马溪组页岩为例[J]. 地球物理学报, 2020, 63(11): 4188-4204. GUI Junchuan, MA Tianshou, CHEN Ping. Rock physics modeling of transversely isotropic shale: an example of the Longmaxi formation in the Sichuan basin[J]. Chinese Journal of Geophysics, 2020, 63(11): 4188-4204. |
| [11] |
ZHAO W, CHELLAPPA R, PHILLIPS P J, et al. Face recognition: A literature survey[J]. ACM Computing Surveys, 2003, 35(4): 399-458. |
| [12] |
YOUNG T, HAZARIKA D, PORIA S, et al. Recent trends in deep learning based natural language proce-ssing[J]. IEEE Computational Intelligence Magazine, 2018, 13(3): 55-75. |
| [13] |
张家臣, 邓金根, 谭强, 等. 基于XGBoost的测井曲线重构方法[J]. 石油地球物理勘探, 2022, 57(3): 697-705. ZHANG Jiachen, DENG Jingen, TAN Qiang, et al. Reconstruction of well logs based on XGBoost[J]. Oil Geophysical Prospecting, 2022, 57(3): 697-705. |
| [14] |
张益明, 张繁昌, 丁继才, 等. 基于混合深度学习网络的致密砂岩甜点预测[J]. 石油物探, 2021, 60(6): 995-1002. ZHANG Yiming, ZHANG Fanchang, DING Jicai, et al. Sweet spot prediction in tight sand reservoirs by a hybrid deep-learning net-work[J]. Geophysical Prospec-ting for Petroleum, 2021, 60(6): 995-1002. |
| [15] |
CHEN T F, GAO G, LIU H J, et al. Rock brittleness index inversion method with constraints of seismic and well logs via a CNN-GRU fusion network based on the spatiotemporal attention mechanism[J]. Geoenergy Science and Engineering, 2023, 225: 211646. |
| [16] |
周伟, 赵海航, 蒋云凤, 等. 基于串级双向长短时记忆神经网络的测井数据重构[J]. 石油地球物理勘探, 2022, 57(6): 1473-1480. ZHOU Wei, ZHAO Haihang, JIANG Yunfeng, et al. Logging data reconstruction based on cascade bidirectional long short term memory neural network[J]. Oil Geophysical Prospecting, 2022, 57(6): 1473-1480. |
| [17] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [18] |
CHEN T, GAO G, WANG P, et al. Prediction of shear wave velocity based on a hybrid network of two-dimensional convolutional neural network and gated recurrent unit[J]. Geofluids, 2022, 14: 9974157. |
| [19] |
HAN J, LU C, CAO Z, et al. Integration of deep neural networks and ensemble learning machines for missing well logs estimation[J]. Flow Measurement and Instrumentation, 2020, 73: 101748. |
| [20] |
DABRE R, CHU C, KUNCHUKUTTAN A. A survey of multilingual neural machine translation[J]. ACM Computing Surveys, 2020, 53(5): 1-38. |
| [21] |
赵兵, 王增平, 纪维佳, 等. 基于注意力机制的CNN-GRU短期电力负荷预测方法[J]. 电网技术, 2019, 43(12): 4370-4376. ZHAO Bing, WANG Zengping, JI Weijia, et al. A short-term power load forecasting method based on attention mechanism of CNN-GRU[J]. Power System Technology, 2019, 43(12): 4370-4376. |
| [22] |
王泽峰, 许辉群, 杨梦琼, 等. 应用时域卷积神经网络的地震波阻抗反演方法[J]. 石油地球物理勘探, 2022, 57(2): 279-286. WANG Zefeng, XU Huiqun, YANG Mengqiong, et al. Seismic impedance inversion method based on temporal convolutional neural network[J]. Oil Geophysical Prospecting, 2022, 57(2): 279-286. |
| [23] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [24] |
KAVIANPOUR P, KAVIANPOUR M, JAHANI E, et al. A CNN-BILSTM model with attention mechanism for earthquake prediction[J]. The Journal of Supercomputing, 2023. DOI:10.1007/s11227-023-05369-y |
| [25] |
BAI T, PEJMAN T. Attention-based LSTM-FCN for earthquake detection and location[J]. Geophysical Journal International, 2021, 228(3): 1568-1576. |
| [26] |
马国庆, 王泽坤, 李丽丽. 基于自注意力机制深度学习的重磁数据网格化和滤波方法[J]. 石油地球物理勘探, 2022, 57(1): 34-42. MA Guoqing, WANG Zekun, LI Lili. Gridding and filtering method of gravity and magnetic data based on self attention deep learning[J]. Oil Geophysical Prospecting, 2022, 57(1): 34-42. |



 高刚, 湖北省武汉市蔡甸区蔡甸街道大学路111号长江大学地球物理与石油资源学院,430100。Email:
高刚, 湖北省武汉市蔡甸区蔡甸街道大学路111号长江大学地球物理与石油资源学院,430100。Email: